Abstract
Background: Clinical weight loss in individuals typically stabilizes at 6 mo. However, validated models of dynamic energy balance have consistently shown weight plateaus between 1 and 2 y. The cause for this discrepancy is unclear.
Objective: We developed 2 mathematical models on the basis of the first law of thermodynamics to investigate plausible explanations for reaching an early weight plateau at 6 mo.
Design: The first model was an energy-expenditure adaptation model and was applied to determine the degree of metabolic adaptation required to generate this plateau. The second model was an intermittent lack-of-adherence model formulated by using a randomly fluctuating energy intake term accounting for intermittent noncompliance in dietary intake to reach this plateau. To set model variables, validate models, and compare free-living weight-loss patterns to in-residence supervised programs, we applied the following 4 different studies: The US NHANES 1999–2004, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy (CALERIE) weight-loss study, the Bouchard Twin overfeeding study, and the Minnesota Starvation Experiment.
Results: The metabolic adaptation model increased final weight but did not affect the predicted plateau time point. The intermittent lack-of-adherence model generated oscillating weight graphs that have been frequently observed in weight-loss studies. The model showed that a 6-mo weight-loss plateau can be attained despite what can be considered as high diet adherence. The model was programmed as a downloadable application.
Conclusions: An intermittent lack of diet adherence, not metabolic adaptation, is a major contributor to the frequently observed early weight-loss plateau. The new weight-loss prediction software, which incorporates an intermittent lack of adherence, can be used to guide and inform patients on realistic levels of adherence on the basis of patient lifestyle. The CALERIE study was registered at clinicaltrials.gov as NCT00099151.
See corresponding article on page 744
INTRODUCTION
Physicians and health care workers are increasingly being asked to provide weight-loss advice and support to overweight and obese patients. Although the initial weight loss with hypocaloric diets is often successful, patients frequently experience a plateau at ∼6 mo after which no or little additional weight loss is achieved. The cause for the weight-loss plateau is often obscure because many patients continue to report good diet adherence. Therefore, the question arises whether the body has begun to adapt to weight loss and defend against additional loss (1, 2), or as recent studies suggested, patients decrease their dietary adherence (3, 4). The first explanation is based on evidence between the individual variation in the down-regulation of energy expenditure (EE)4 during caloric restriction (5). The second explanation is based on adherence arguments put forth by Heymsfield et al (6).
To differentiate between these 2 hypotheses, we have modified an existing dynamic model (7, 8) that includes the effect of metabolic adaptation (6) and weight loss to negative energy balance to test which hypothesis best fits existing weight-loss data. The answer is clinically important because the genesis of weight-loss plateaus dictates how physicians council patients with regard to maximizing weight loss and weight-loss maintenance.
The aim of the current study was to investigate evidence for the 2 explanations for early weight-loss plateaus. These explanations are the potential adaptation of EEs to weight loss (ie, metabolic adaptation) and intermittent fluctuations in dietary adherence.
SUBJECTS AND METHODS
Study design
To test the 2 explanations, we designed 2 experiments to provide insight into each of the following questions:
1) How does a reduction in EEs beyond those accounted for by weight affect the length of time for weight to plateau?
2) How does an intermittent lack of adherence to dietary prescriptions translate to changes in the weight plateau?
To address the first question, we relied on our validated dynamic model (7, 8) and reduced the EE component of the model by fixed percentages. The model already accounts for the amount of metabolic adaption frequently observed in weight-loss studies, and our analysis further increased the amount of metabolic adaptation to very high levels that are not typically observed. This method allowed us to examine if metabolic adaptation can be responsible for weight-loss plateaus that occur after ∼6 mo of dieting, even if the levels of metabolic adaptation necessary to achieve this end are unrealistically high. The second model altered the design of the dynamic model (7, 8) by incorporating random fluctuations in energy intake after the input of a prespecified adherence that was <100%.
Subjects
Four studies were applied for different model analyses and comparisons. A summary of all studies and how they were applied are shown in Table 1.
TABLE 1.
Summary and baseline characteristics of the 4 studies applied for model validation and analysis
| Participants |
BMI |
||||
| Study name (reference) | M | F | M | F | Model application |
| n | kg/m2 | ||||
| CALERIE1 (9) | 10 | 13 | 28.7 ± 1.42 | 27.8 ± 1.7 | Applied to validate dynamic model (7) predictions during energy restriction. |
| Applied to calculate percentage of adherence data over time by using the adherence model. | |||||
| Applied to compare free-living weight-loss patterns with confined weight-loss patterns. | |||||
| Bouchard (11) | 24 | — | Applied to validate thermodynamic model (7) predictions during overfeeding. | ||
| NHANES (12) | 2651 | 2500 | 26.8 ± 4.4 | 27.4 ± 5.7 | Applied to develop average male and female demographic inputs into the reduced energy-expenditure model. |
| Minnesota Starvation Experiment (10) | 32 | 21.7 ± 1.7 | — | Applied to compare weight-loss patterns in confined subjects with weight-loss patterns in free-living subjects. | |
CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy.
Mean ± SD (all such values).
Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy phase I study
The Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy (CALERIE) study was a 6-mo weight-loss intervention conducted at the Pennington Biomedical Research Center (9). Study participants (n = 46) were randomly assigned into 4 groups as follows: a control cohort, a cohort of 12 subjects prescribed calorie reduction 25% below baseline energy requirements (25% CR), a cohort of 12 subjects prescribed reduced energy intake of 12.5% below baseline requirements combined with increased EEs through exercise 12.5% above baseline EEs, and a cohort of 11 subjects assigned to a very-low-calorie diet of 890 kcal/d administered until measured weight decreased 15% below the baseline weight, which was followed by a weight-maintenance diet. Combined reference data from the 25% CR and very-low-calorie diet groups were applied to determine the validity of the dynamic weight-change prediction model (7) during restriction of energy intake. Because the prescribed reduction of energy intake in the 25% CR group was constant for the 24-wk study duration, these data were applied to calculate the actual percentage of adherence over time by using the adherence model described in the following sections and compared with weight-loss patterns in the supervised in-residence Minnesota Starvation Experiment study data (10).
Bouchard Twin study
Twelve pairs of monozygotic male twins were administered 840 kcal/d over baseline energy requirements for a period of 100 d under supervision in residence in a closed section of dormitories at Laval University, Quebec, Canada (11). Data were used to test the validity of the dynamic weight-change prediction model during overfeeding.
NHANES
To obtain a nationally representative reflection of input data necessary to simulate the reduced EE model described in the sections that follow, average body weight, height, and age data were calculated from the adult (>18 y of age) US NHANES 1999–2004 data set (12), which is a combined data set of 3 biannual cross-sectional waves from 1999 to 2000, 2001 to 2002, and 2003 to 2004.
Minnesota Starvation Experiment
The classic weight-regulation study the Minnesota Starvation Experiment was led by Ancel Keys in the mid-1940s to better understand the physiologic responses to famine conditions to optimally design refeeding protocols (10). Thirty-two objective World War II dissenters volunteered to undergo 24 wk of semistarvation under 24-h supervision in residence at the University of Minnesota. Of 32 total subjects, we restricted our analysis to 13 subjects who were administered a constant dose of energy restriction for a period of 10 wk to compare to free-living subjects in the CALERIE study who were also prescribed a constant dose of energy restriction.
Dynamic energy balance model validation
Although several existing validations of the dynamic model have been previously published (7, 8, 13), we extended these validations to include a Bland-Altman analysis (14) of 2 additional data sets. Weight-change prediction model validation requires data for which energy intake was objectively determined, and accordingly, both studies applied for validation included these measurements. For the purpose of testing the model validity during underfeeding we applied the CALERIE study (9) in which body composition was measured at baseline, 3 mo (84 d), and 6 mo (168 d) by using dual-energy X-ray absorptiometry, and the total EE was evaluated at both time points by using the doubly labeled water (DLW) method. The achieved energy intake was determined by summing changes in body-energy stores with the DLW-assessed EE. Changed body energy stores were calculated by using the following formula:
 |
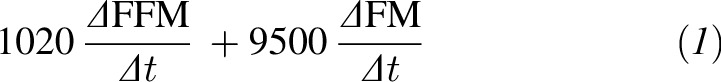where ΔFFM represents the change in fat-free mass, ΔFM represents the change in fat mass, and Δt is the elapsed time in days between measurements (Δt = 84 d). This method of determining achieved energy intake has been validated and applied to assess dietary adherence in several studies (15, 16). The dynamic model was simulated for the 23 subjects by using the multisubject calculator described in reference 8. The model validity during overfeeding was tested on the Bouchard Twin study (11). Baseline data were input into the multisubject calculator described in reference 8. These 2 studies allowed for the validation of the adherence model described in Model validation under Results because both included nonadherence measurements by design.
Linearized model to calculate weight-loss half-life
All dynamic weight-change prediction models that are based on the first law of thermodynamics can be linearized whereby weight loss can be expressed in terms of exponential decay (17). Exponential decay models yield a value that can be directly calculated and is referred to as the half-life, which represents the length of time required for a baseline amount to reach one-half its original quantity. To understand how the half-life depends on other model inputs, we derived the following linear dynamic model:
 |
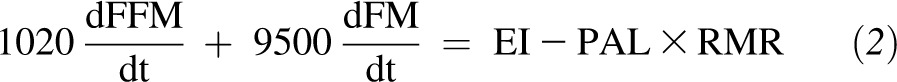where FFM and FM represent kilograms of fat-free mass and fat mass, respectively, EI represents kilocalories per day of energy intake, PAL is the physical activity level, and RMR is the resting metabolic rate in kilocalories per day. With the linearization of the Forbes’ model around baseline fat-free mass (FFM0) and baseline fat mass (FM0) and the substitution of the Mifflin-St Jeor equation (19) for RMR, we arrived at a purely linearized model for which the half-life could be directly calculated.
Reduced EE model
The dynamic model (7, 8) is a differential equation that applies model terms developed for each component of the energy-balance equation. A detailed description of our validated dynamic energy-balance body-weight regulation model appears elsewhere (7). Briefly, model terms are developed by using the human energy-balance equation which stems from the first law of thermodynamics as follows:
 |
where ES represents the rate of energy stored or lost, EI is energy intake, and EE is EE in kilocalories per day. In all dynamic models, 100% compliance to a constant prescribed calorie intake, EI, is assumed (7, 19). These model terms include the continual weight- and intake-related decreases in the resting metabolic rate, activity expenditures, and dietary-induced thermogenesis. In addition, the model includes the effect of metabolic adaptation to a negative energy balance derived from data-driven estimates (20).
To explore the effect of reductions in EEs beyond these known factors, we can model a reduction in EE beyond those reductions already accounted for in the model by the multiplier variable P, whereby
 |
The dynamic model requires the input of age, height, sex, baseline weight, and energy intake. For baseline age, height, sex, and weight, we use the following NHANES 1999–2004 average values for men: age, 46.2 y; height, 174.8 cm; and weight, 84.2 kg; and average values for women: age, 47.9 y; height, 161.1 cm; weight, 73.8 kg. We selected NHANES to obtain demographic data for an average US man and woman. We placed both hypothetical subjects on a reduced energy intake 25% below baseline and simulated the model by using varying values of p (p = 0.05 and 0.10). Baseline energy intakes were estimated by using a regression formula on the basis of DLW data in weight-stable humans (7). Model simulations were performed in the Maple 17 program (Maplesoft, 2013).
Adherence model
We applied the dynamic model described in references 7 and 16 and available for simulation by using an online calculator. To incorporate an intermittent lack of adherence, the value for EI was defined by applying a random variable with uniform distribution between 0 and 1. If, for example, an individual is assumed to be adherent 80% of the time, EI is set to the target prescription whenever the random variable is >0.80. In this case, 80% of days are randomly selected by the model for which EI is equal to the target prescription. On nonadherent days (eg, the remaining 20% of days), EI is assumed to be over or under prescribed intakes by a back-calculated amount. To account for varying degrees of adherence over time, the percentage of the time the individual is adherent is recalculated monthly.
Calculation of percentage of adherence from experimental data
Average baseline data from the 6 men and 6 women in the CALERIE 25% CR group (9) was applied to simulate the varying intake model. Prescribed intake for men was 2390.5 kcal/d, and the prescribed intake for women was 1515.5 kcal/d. The monthly percentage of adherence in adherence-model simulations were set to match actual weight-loss patterns.
Finally, the adherence model was simulated for 1 y by continuing with the last calculated percentage of adherence to observe long-term effects of an intermittent lack of adherence on a weight plateau. A summary of all models that were applied or developed appear in Table 2.
TABLE 2.
Summary and description of the 4 developed and validated models
| Model | Description |
| Dynamic model (7, 8) | Validated differential equation model originating from the first law of thermodynamics. Accurately predicts the degree of weight gain or loss from a change in intake or activity. The model forms the foundation of the adherence model. |
| Linearized model | A linear differential equation model originating from the first law of thermodynamics. This model was applied to calculate the half-life in terms of other model inputs. |
| Reduced energy-expenditure model | A modification of the dynamic model that includes a variable that allows for increases in energy expenditure beyond known factors. This model was applied to explore the resulting weight graph patterns when energy expenditure increases. |
| Adherence model | A modification of the dynamic model that incorporates random fluctuations in energy intake. In addition to dynamic model inputs, the adherence model includes the monthly percentage of adherence inputs and the percentage over and under target intake achieved on nonadherence days. |
Comparison between free-living and confined weight-loss patterns
Weight loss over time in the 13 subjects administered a constant dose of energy restriction in the Minnesota Starvation Experiment was plotted against time and compared with weight-loss graphs in the 12 subjects in the 25% CR cohort of the CALERIE study for differences in weight-loss patterns.
Development of adherence calculator
A clinical software tool was developed by using the Visual Basic Application in Microsoft Excel 2010 (Microsoft Corp) that allows users to input monthly adherence percentages and degrees over and under baseline that are achieved on nonadherence days. The new tool will be made available for download (21).
RESULTS
Model validation
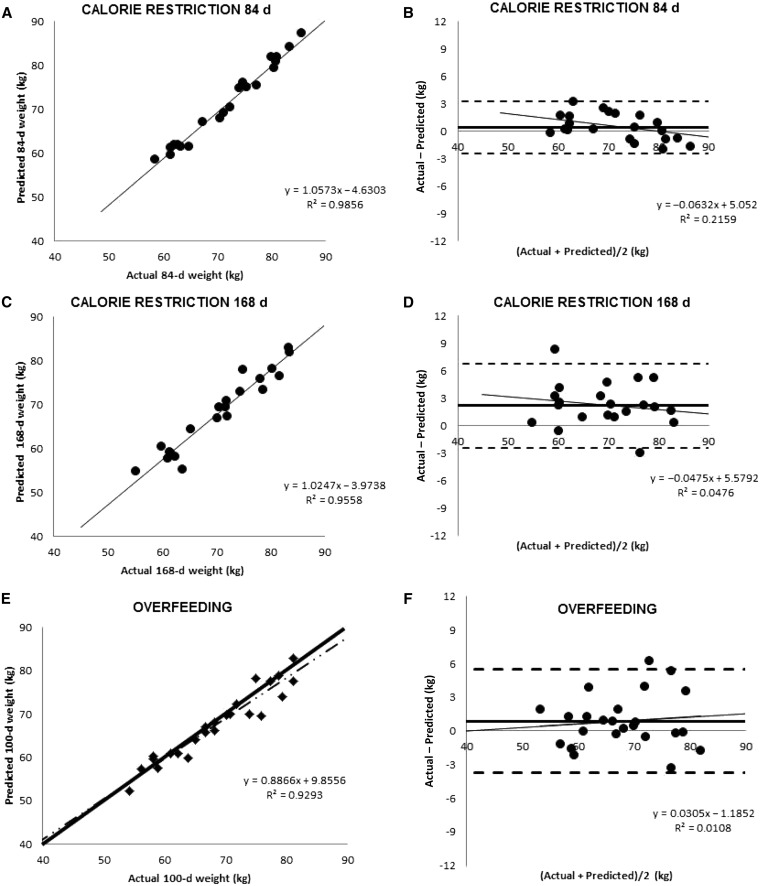
Dynamic model (8)–predicted weights showed good agreement with actual final weights (Figure 1) in calorie restricted subjects (9) [3 mo: R2 = 0.99,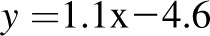 
, bias 
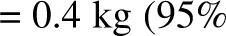CI: −2.4, 3.2 kg); 6 mo: R2 = 0.96, 
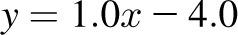, bias = 2.2 kg (95% CI: −2.4, 6.8 kg)]. There was a trend in the error at 3 mo (R2 = 0.22, 
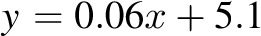, P = 0.02), but it was NS at 6 mo (R2 = 0.05, 
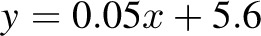, P = −0.32). The overfeeding validation (17) yielded better agreement than the calorie-restriction validation [correlation: R2 = 0.93, 
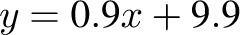, bias = 0.9 kg (95% CI: −3.7, 5.5 kg)], again with no significant trend in error (R2 = 0.01, 
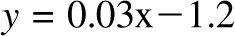, P = 0.6).
FIGURE 1.
A–D: Level of agreement between dynamic model predictions of weight and measured weight at 84 and 168 d in the 23 CALERIE study participants who were undergoing weight loss through calorie restriction (9). E and F: Agreement between dynamic model predictions with measured weight from the Bouchard Twin study (11). A, C, and E: Dynamic model–predicted final weight against actual final weight. B, D, and F: Bland-Altman analyses of model predictions. The validation against the CALERIE study at 3 mo yielded good agreement [R2 = 0.99,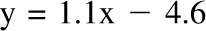 
, bias = 0.4 kg (95% CI: −2.4, 3.2 kg); 6 mo: R2 = 0.96, 
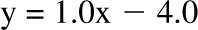, bias = 2.2 kg (95% CI: −2.4, 6.8 kg)]. There was a trend in the error at 3 mo (R2 = 0.22, y = 0.06x + 5.1, P = 0.02), but it was NS at 6 mo (R2 = 0.05, 
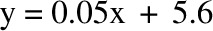, P = −0.32). The overfeeding validation (11) yielded better agreement than the calorie restriction validation [correlation: R2 = 0.93, 
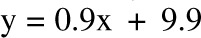, bias = 0.9 kg (95% CI: −3.7, 5.5 kg)], again with no significant trend in error (R2 = 0.01, 
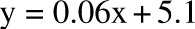, P = 0.6). CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy.
Calculation of half-life
Half-life was directly calculated from the linearized dynamic model as follows:
 |
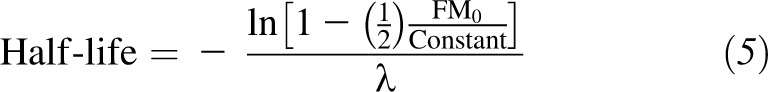where
 |
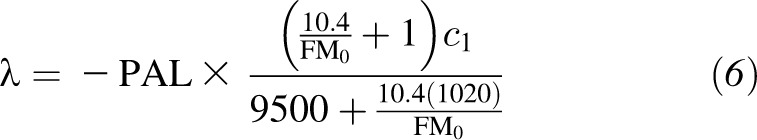and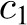 
is the weight coefficient in the Mifflin-St Jeor RMR model. From this expression, influences on the time for weight to plateau are the PAL, energy density of fat and lean mass (9500 and 1020 kcal/d), slope of the Forbes’ curve (10.4), relation of body weight on the RMR, and baseline body composition (FM0).
Reduced EE does not induce an earlier weight plateau
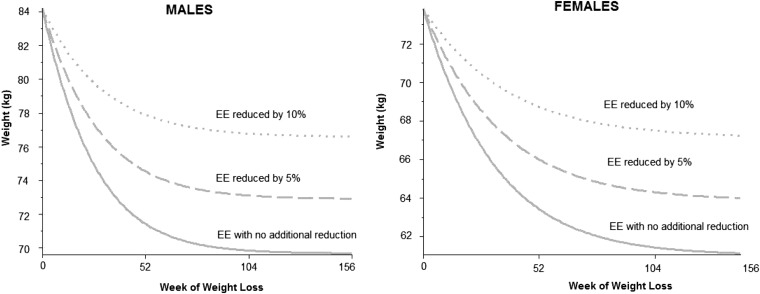
Three simulations of the dynamic model (8) with different percentage excess reductions in EE are shown in Figure 2. Although a 10% decrease in EE resulted in an 11% increase in the predicted weight at stabilization, it did not affect the time at which the weight plateau was achieved. That is, reductions of EE by 5% and 10% showed that the weight-loss plateau was achieved at a higher body weight, but the location or timing of the plateau after the onset of the diet consistently occurred between 365 and 730 d (Figure 2). Recall that known values of metabolic adaptation were already included in the dynamic model, and the 5% and 10% metabolic adaptation values were even beyond those already incorporated in the dynamic model (7).
FIGURE 2.
Simulations of the effect of reduced EE on body weight over time beyond those accounted for in the dynamic model (7) for men (left) and women (right). Dotted curves represent a 10% decrease in EE beyond the expected, dashed curves represent a 5% decrease in EE beyond the expected, and solid curves represent no change in EE from original model predictions. Although a decreasing EE generated a value at which weight plateaued, the time at which the weight loss plateau was achieved did not change. EE, energy expenditure.
Intermittent loss of dietary adherence is associated with an earlier weight plateau
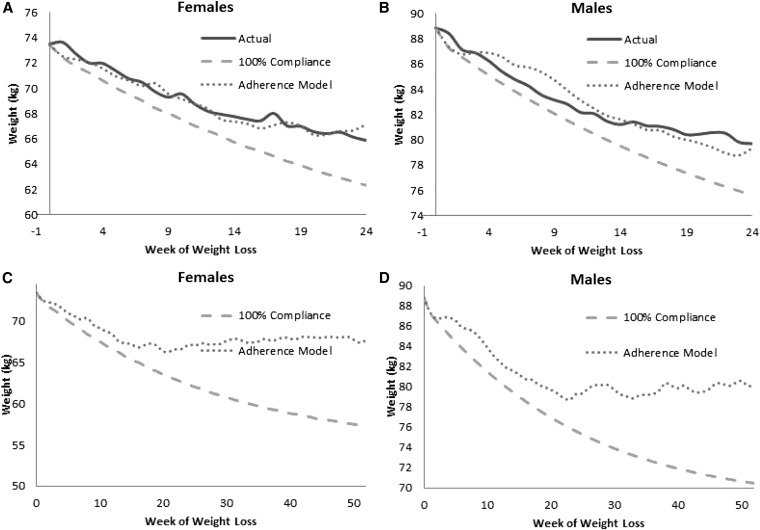
Inputs of the percentage of adherence required to simulate the adherence model were matched with weight graphs generated from the group mean data of the 25% CR group for men and women (9) (Figure 3, A and B). By month, women on average were calculated as 80% adherent in month 1, 60% adherent in month 2, 50% adherent in month 3, and 40% adherent after month 3. Similarly, men were calculated to be 80% adherent from months 1 to 5 and 70% adherent thereafter. Because energy intake in the model applied a random process, nonadherent days predicted by the model did not exactly match the subject's nonadherent days. Specifically, we could not know a priori which exact days the subject may have been less adherent. However, the actual weight graph and model-simulated weight graph share similar structures and trends. For example, the solid curve (actual weight) and dotted curve (adherence-model simulation) were observed to have similar fluctuations in weight and the overall average trend (Figure 3, A and B). Results of long-term model simulations are shown in Figure 3, C and D. The percentage of adherence after 24-wk was set to the last calculated percentage of adherence in the final month of the intervention (40% for women and 70% for men). Adherence-model simulations for both men and women (dotted curve) plateaued after ∼24 wk (6 mo), whereas the dynamic model simulations, with the assumption of 100% compliance, continued to decrease.
FIGURE 3.
Depicted are actual weight graphs (solid), dynamic model simulations (7) with assumption of 100% compliance to the prescribed calorie restriction (dashed), and simulations of the adherence model matched to actual weight graphs (dotted) from the participants in the 25%-below-baseline-energy-requirements cohort in the Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy study (9). A and B: Simulations for women and men, respectively. C and D: Extension of simulations of dynamic and adherence models to 1 y. The percentage of adherence after 6 mo was set as 6-mo calculated values from matching the model to the data. In both groups, a weight plateau was generated at 24 wk by the adherence model. In contrast, the dynamic model, which assumed 100% compliance, continued to decrease and deviate from adherence model predictions.
Weight graphs from confined weight-loss studies are monotonically decreasing
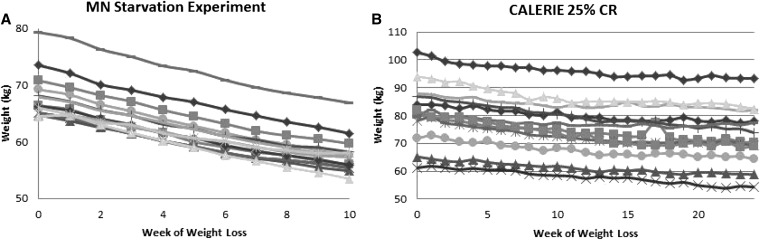
A plot of weight compared with the week of restricted energy intake for the Minnesota Starvation Experiment is shown in Figure 4A. All 13 subjects decrease monotonically. In contrast, the a plot of weight compared with the week of restricted energy intake for 25% CR CALERIE participants shown in Figure 4B exhibits oscillations with periodic weight gain followed by weight loss.
FIGURE 4.
Weight compared with study week during prescribed restriction of energy intake in the MN Starvation Experiment (10) (A) and 25% CR participants from the CALERIE study (9) (B). Weight graphs from the MN Starvation Experiment were monotonically decreasing, whereas weight graphs from the free-living CALERIE study oscillated with intermittent periods of weight gain. CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; MN, Minnesota; 25% CR, calorie reduction 25% below baseline energy requirements.
Dietary adherence calculator
The adherence calculator simulates the effect of an intermittent loss of dietary adherence on the body-weight change. The user inputs baseline age, height, weight, and sex and preference of units (metric or US standard). A prescribed total energy intake is input by using preferred units (kcal/d or MJ/d) along with monthly percentage of adherence rates, the percentage over prescribed intake achieved on nonadherence days, and the percentage under prescribed intake achieved on nonadherence days. The calculator outputs the resulting weight graph, numerical predictions of body weight over time, and the daily intake generated by the stochastic energy intake variable.
DISCUSSION
The evidence presented in this study indicates that even very high and unrealistic levels of metabolic adaptation do not affect the timing of weight plateaus. Rather, the seemingly innocuous intermittent loss of dietary adherence results in weight graphs with 6-mo plateaus, and these results point to the sensitivity of dietary adherence in determining the kinetics of weight loss.
There is support in the literature for the hypothesis that a reduced EE in response to weight loss cannot account for an early weight-loss plateau. It has been previously observed that reductions in EE “would slow weight loss but not result in a premature weight-loss plateau because, by definition, that plateau occurs at the point of energy balance” (6).
An intermittent lack of adherence, which is a common response to weight-loss interventions, was also confirmed by our analysis of confined compared with free-living body-weight data and further supported by our model simulations. To expect complete adherence from individuals in weight-loss interventions each day appears unrealistic and is rarely achieved unless all food is provided and eaten under supervision. With recognition that small, even unconscious deviations from a weight-loss prescription can lead to an early plateau can help both patient and practitioner promote more-effective and lasting weight loss. Models that predict a weight-loss response should incorporate this likely behavioral response, which may have a biological basis (22), and derive weight-loss estimates accordingly. The developed calculator provides the first predictor that includes both physiologic as well as behavioral (intermittent loss of dietary adherence) components of weight loss and, thereby, can serve as an important counseling tool for dietary interventions.
Several limitations applied to the current study. First, mathematical models are only as good as the data in which they are derived from. Although the dynamic human model (7) was formulated by using state-of-the-art measurements of body composition via dual-energy X-ray absorptiometry, EEs from DLW, and RMR from indirect calorimetry, model terms are not free from error. Second, the evidence we present in this article is secondary to actual long-term validation in humans; however, appropriate objective data in studies of duration >12 mo are not yet available. As noted previously, model validation also requires rigorous knowledge of subject adherence to prescribed dietary intake and, most likely, can never be obtained.
We did not model a third possible scenario. This scenario would be a situation in which we hypothesize time dependent changes in the adaptive reduction in EE with the increasing time of caloric restriction. A model that incorporates greater decreases in EE could also be fit to the observed weight-loss curves. However, we did not develop this model because the actual measurement of EE did not support it. The evidence for suppressed EE during weight loss and maintenance has been well documented (23). However, the contribution to weight regain would require increases in suppressed EE. Weinsier et al (24) explored the capacity for a reduced resting metabolic rate during weight loss to account for weight regain. After obese women during different phases of weight loss and weight regain were measured, the authors reported that their “findings do not provide evidence in support of adaptive metabolic changes as an explanation for the tendency of weight-reduced persons to regain weight.” Total daily EE data collected during the CALERIE study did not find time-varying increases in EE (20). Likewise, Stice et al (25) showed no correlation between a suppressed RMR and later weight gain. Also, Camps et al (26) did not find evidence for a change in suppressed EE even after subjects maintained weight loss over 1 y.
In conclusion, the developed models support the hypothesis that an intermittent lack of adherence can lead to an early weight plateau. To our knowledge, this study is the first to include simulated behavioral responses to reduced energy intake within a model that is based on human dynamics. Models that guide patients can include predictable behavioral responses such as an intermittent lack of adherence to dietary prescriptions.
The work presented in this article introduces new questions: Are there demographic predictors for adherence rates during specific time intervals during weight loss? If so, can this information be used within the developed model to guide patients against eventual weight regain? Are there periods of time where adherence is stronger than others? The newly developed model, combined with appropriately designed experiments, is important to investigate these questions for future research and fully understand if behavioral as well as physiologic responses to weight-loss interventions can be accurately predicted from dynamic mathematical models.
Acknowledgments
The authors’ responsibilities were as follows—DMT and DAS: conceived the study; DMT: developed mathematical models; DMT, CKM, LMR, and SL: designed the software interface; DMT and SL: developed the software code; DMT, CKM, LMR, SBH, JAL, CB, and DAS: analyzed data; and all authors: prepared the manuscript. CB is an advisor to Weight Watchers, Pathway Genomics, and Nike SPARQ. DMT, CKM, LMR, SBH, SL, JAL, and DAS declared no conflicts of interest.
Footnotes
Abbreviations used: CALERIE, Comprehensive Assessment of Long-term Effects of Reducing Intake of Energy; DLW, doubly labeled water; EE, energy expenditure; 25% CR, calorie reduction 25% below baseline energy requirements.
REFERENCES
- 1.Miller DS, Parsonage S. Resistance to slimming: adaptation or illusion? Lancet 1975;1:773–5. [DOI] [PubMed] [Google Scholar]
- 2.Cannon G. Dieting. Makes you fat? Br J Nutr 2005;93:569–70. [DOI] [PubMed] [Google Scholar]
- 3.Dansinger ML, Gleason JA, Griffith JL, Selker HP, Schaefer EJ. Comparison of the Atkins, Ornish, Weight Watchers, and Zone diets for weight loss and heart disease risk reduction: a randomized trial. JAMA 2005;293:43–53. [DOI] [PubMed] [Google Scholar]
- 4.Sacks FM, Bray GA, Carey VJ, Smith SR, Ryan DH, Anton SD, McManus K, Champagne CM, Bishop LM, Laranjo N, et al. Comparison of weight-loss diets with different compositions of fat, protein, and carbohydrates. N Engl J Med 2009;360:859–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Redman LM, Heilbronn LK, Martin CK, Alfonso A, Smith SR, Ravussin E. Effect of calorie restriction with or without exercise on body composition and fat distribution. J Clin Endocrinol Metab 2007;92:865–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Heymsfield SB, Harp JB, Reitman ML, Beetsch JW, Schoeller DA, Erondu N, Pietrobelli A. Why do obese patients not lose more weight when treated with low-calorie diets? A mechanistic perspective. Am J Clin Nutr 2007;85:346–54. [DOI] [PubMed] [Google Scholar]
- 7.Thomas DM, Martin CK, Heymsfield SB, Redman LM, Schoeller DA, Levine JA. A simple model predicting individual weight change in humans. J Biol Dyn 2011;5:579–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thomas DM, Martin CK, Lettieri S, Bredlau C, Kaiser K, Church T, Bouchard C, Heymsfield SB. Can a weight loss of one pound a week be achieved with a 3500-kcal deficit? Commentary on a commonly accepted rule. Int J Obes (Lond) 2013;37:1611–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Heilbronn LK, de Jonge L, Frisard MI, DeLany JP, Larson-Meyer DE, Rood J, Nguyen T, Martin CK, Volaufova J, Most MM, et al. Effect of 6-month calorie restriction on biomarkers of longevity, metabolic adaptation, and oxidative stress in overweight individuals: a randomized controlled trial. JAMA 2006;295:1539–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.University of Minnesota, Laboratory of Physiological Hygiene. Keys A. The biology of human starvation. Minneapolis, MN: University of Minnesota Press, 1950. [Google Scholar]
- 11.Bouchard C, Tremblay A, Despres JP, Nadeau A, Lupien PJ, Theriault G, Dussault J, Moorjani S, Pinault S, Fournier G. The response to long-term overfeeding in identical twins. N Engl J Med 1990;322:1477–82. [DOI] [PubMed] [Google Scholar]
- 12.National Center for Health Statistics. National Health and Nutrition Examination Survey. 2014. Available from http://www.cdc.gov/nchs/nhanes.htm (cited 12 March 2014).
- 13.Thomas DM, Schoeller DA, Redman LA, Martin CK, Levine JA, Heymsfield SB. A computational model to determine energy intake during weight loss. Am J Clin Nutr 2010;92:1326–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1:307–10. [PubMed] [Google Scholar]
- 15.de Jonge L, DeLany JP, Nguyen T, Howard J, Hadley EC, Redman LM, Ravussin E. Validation study of energy expenditure and intake during calorie restriction using doubly labeled water and changes in body composition. Am J Clin Nutr 2007;85:73–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pieper C, Redman L, Racette S, Roberts S, Bhapkar M, Rochon J, Martin C, Kraus W, Das S, Williamson D, et al. Development of adherence metrics for caloric restriction interventions. Clin Trials 2011;8:155–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hall KD, Chow CC. Estimating changes in free-living energy intake and its confidence interval. Am J Clin Nutr 2011;94:66–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mifflin MD, St Jeor ST, Hill LA, Scott BJ, Daugherty SA, Koh YO. A new predictive equation for resting energy expenditure in healthy individuals. Am J Clin Nutr 1990;51:241–7. [DOI] [PubMed] [Google Scholar]
- 19.Hall KD, Sacks G, Chandramohan D, Chow CC, Wang YC, Gortmaker SL, Swinburn BA. Quantification of the effect of energy imbalance on bodyweight. Lancet 2011;378:826–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Martin CK, Heilbronn LK, de Jonge L, DeLany JP, Volaufova J, Anton SD, Redman LM, Smith SR, Ravussin E. Effect of calorie restriction on resting metabolic rate and spontaneous physical activity. Obesity (Silver Spring) 2007;15:2964–73. [DOI] [PubMed] [Google Scholar]
- 21.The Adherence Calculator. Version 17 June 2014. Available from: http://pbrc.edu/research-and-faculty/calculators/adherence/ (cited 17 June 2014).
- 22.Sumithran P, Prendergast LA, Delbridge E, Purcell K, Shulkes A, Kriketos A, Proietto J. Long-term persistence of hormonal adaptations to weight loss. N Engl J Med 2011;365:1597–604. [DOI] [PubMed] [Google Scholar]
- 23.Rosenbaum M, Hirsch J, Gallagher DA, Leibel RL. Long-term persistence of adaptive thermogenesis in subjects who have maintained a reduced body weight. Am J Clin Nutr 2008;88:906–12. [DOI] [PubMed] [Google Scholar]
- 24.Weinsier RL, Nagy TR, Hunter GR, Darnell BE, Hensrud DD, Weiss HL. Do adaptive changes in metabolic rate favor weight regain in weight-reduced individuals? An examination of the set-point theory. Am J Clin Nutr 2000;72:1088–94. [DOI] [PubMed] [Google Scholar]
- 25.Stice E, Durant S, Burger KS, Schoeller DA. Weight suppression and risk of future increases in body mass: effects of suppressed resting metabolic rate and energy expenditure. Am J Clin Nutr 2011;94:7–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Camps SG, Verhoef SP, Westerterp KR. Weight loss, weight maintenance, and adaptive thermogenesis. Am J Clin Nutr 2013;97:990–4. [DOI] [PubMed] [Google Scholar]