Electrocortical source imaging of intracranial EEG data in epilepsy

Abstract

Here we report first results of numerical methods for modeling the dynamic structure and evolution of epileptic seizure activity in an intracranial subdural electrode (iEEG, ECoG) recording from a patient with partial refractory epilepsy. A 15-min dataset containing two seizures was decomposed using up to five competing adaptive mixture ICA (AMICA) models. Multiple models modeled early or late ictal, or pre-or post-ictal periods in the data, respectively. To localize sources, a realistic Boundary Element Method (BEM) head model was constructed for the patient with custom open skull and plastic (non-conductive) electrode holder features. Source localization was performed using Sparse Bayesian Learning (SBL) on a dictionary of overlapping multi-scale cortical patches constructed from 80,130 dipoles in gray matter perpendicular to the cortical surface. Remaining mutual information among seizure-model AMICA components was dominated by two dependent component subspaces with largely contiguous source domains localized to superior frontal gyrus and precentral gyrus; these accounted for most of the ictal activity. Similar though much weaker dependent subspaces were also revealed in pre-ictal data by the associated AMICA model. Electrocortical source imaging appears promising both for clinical epilepsy research and for basic cognitive neuroscience research using volunteer patients who must undergo invasive monitoring for medical purposes.

I. INTRODUCTION

Epilepsy is one of the most common neurological disorders, affecting 50 million people worldwide, and in approximately 30% of these patients the seizures are not controlled by any available medical therapy. About 4.5% of all patients with epilepsy are thus potential candidates for surgical treatment. Epilepsy surgery has a good chance of success in this patient group, but only if the brain region initiating the ictal activity can be accurately localized and safely removed. For this purpose, in selected cases, recordings are acquired from implanted subdural and/or depth electrode (intracranial) during pre-surgical evaluation. Here, we model and image the source dynamics of electrocorticographic (ECoG, iEEG) data before, during and after occurrence of epileptic seizures in 15 min of data from a patient with an implanted ECoG electrode grid and strips. The accuracy of source localization is heavily influenced by the electrical head model used. Applying a best-fitting sphere or average-template head model may give mis-estimates of seizure onset location of up to 2–3 cm [1]. The influences on current flow of post-surgical defects in the skull and the plastic sheets in which the subdural electrodes are embedded cannot be neglected [2]. Here, we used the Boundary Element Method (BEM) to solve the forward problem using the NFT head modeling toolbox [3]. A custom head model included the non-conducting plastic sheets in which the subdural electrodes were attached and the large opening left in the skull during implantation to reduce patient discomfort from associated brain tissue swelling [2].

Another factor that affects source localization of ictal activity is the degree of isolation of ictal activity from the spontaneous EEG background. In earlier studies we have shown Infomax Independent Component Analysis (ICA) developed by Makeig et al [4] can successfully separate seizure and non-seizure source activities [2]. Here we used a recently developed extension, adaptive multiple-mixture ICA (AMICA) to model the nonstationarity in the data [5] we have found to return components whose time courses are more independent than infomax or other ICA methods tested (Delorme et al., submitted).

Source modeling and choice of the inverse method also affect cortical source localization. Parametric ‘equivalent current dipole’ methods assume that potential maps of interest can be approximated by a few dipolar sources. ‘Distributed source’ methods assume that potentials are generated by a large number of dipolar sources distributed across the cortical surface [6]. Other source models that may be more physiologically accurate model an EEG source as a cortical patch with a fixed relative source intensity profile of activity synchronously produced across the patch [7]. Plummer et al (2010) compared the effect of various forward models, distributed inverse source localization algorithms, and subspace constraints [8]. They used data from four patients with benign focal epilepsy of childhood plus four mesial temporal lobe epilepsy patients. Three realistic head models derived from the MNI template brain were used for forward solutions. These researchers reported that the sLORETA algorithm, constrained to find cortical patches or cortical rotating dipoles, generated the most robust and clinically meaningful results. A recent study by Wipf et al. compared Sparse Bayesian Learning (SBL) methods with other distributed localization methods including sLORETA, beamforming, and minimum current estimation, reporting that SBL methods were the most successful in estimating distributed sources [9]. In a previous report, we showed that using a multi-scale patch-based source space, SBL was able to find both sulcal and gyral sources of standard ECoG grid data [10]. The following section describes the head modeling, AMICA, component clustering based on mutual information, and inverse solution steps.

II. Methods

A. Forward problem solution and head modeling of the epilepsy patient

When a patient is hospitalized for epilepsy surgery, scalp EEG is monitored and a magnetic resonance (MR) head image is acquired. Before epilepsy surgery, a pre-surgical procedure is applied in which a portion of their skull is removed and areas around the suspected epileptogenic zone are recorded and sometimes stimulated to determine whether the seizure generating region is localized and suitable for operation, e.g. not within or too close to eloquent cortex. CT images of the head are then acquired to locate the intracranial electrodes.

To generate an electrical forward head model, first the MR and CT images of the patient were co-registered. The skull, intracranial electrodes, and the plastic sheet in which the subdural electrodes were embedded were segmented from the CT images. The brain and the scalp were segmented from the MR images using an open source Matlab toolbox, NFT (Neuroelectromagnetic Forward Head Modeling Toolbox) [3]. Figure 1 shows the BEM meshes for the skull, plastic sheet, and the scalp. Here, the CSF was not modeled for simplicity. The resulting model was used in forward- and inverse-problem (FP/IP) calculations to localize independent sources of iEEG data from their respective projection patterns to the grid channels returned by AMICA.

Fig. 1.

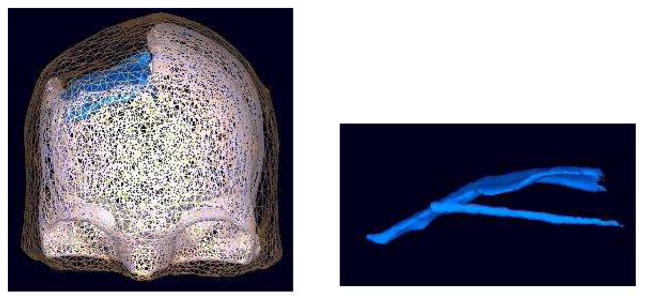
BEM model of the scalp, skull and the plastic sheet, represented by 10,000, 30,000, and 7,000 faces, respectively. The right figure is the plastic sheet model of the plastic grid and strip electrode matrices.

B. Adaptive mixture independent component analysis (AM-ICA)

Infomax Independent Component Analysis (ICA) has proven to be an effective method for removing eye and muscle activity artifacts from scalp EEG data, thus increasing the potential signal-to-noise ratio of subsequent analyses [4]. ICA can also identify and separate functionally independent components, which for normal scalp EEG prove to be most often associated with scalp maps matching the projection of a single equivalent current dipole. ICA decomposition returns a vector of weights giving the relative strength and polarity of the projection of each IC source process to each of the electrodes, and an activation time series giving the time course of activity of each IC process during the data time period.

We have previously shown source localization results using Infomax ICA [10]. Here, we used a recently developed adaptive mixture ICA (AMICA) method in which a number of models compete with each other to fit the data. This allows us to model nonstationarity in the data source structure by allowing different models to account for different time periods. The data are segmented by AMICA in an unsupervised manner using a variational EM algorithm combined with a Newton method for updating the model bases. The AMICA model:

$$x(t)=A^m{s}^m(t),m=1,\dots ,n$$ (1)

where x(t) is the data, A^m is the mixing matrix for the m^th model, and s^m(t) is the activation for the m^th model. n is the total number of models. Given the estimated model, the segmentation is performed using the maximum posterior likelihood, given by,

$$p(x_t\mid M_h)=\mid det{A}_h^{-1}\mid p_h(A_h^{-1}{x}_t)$$ (2)

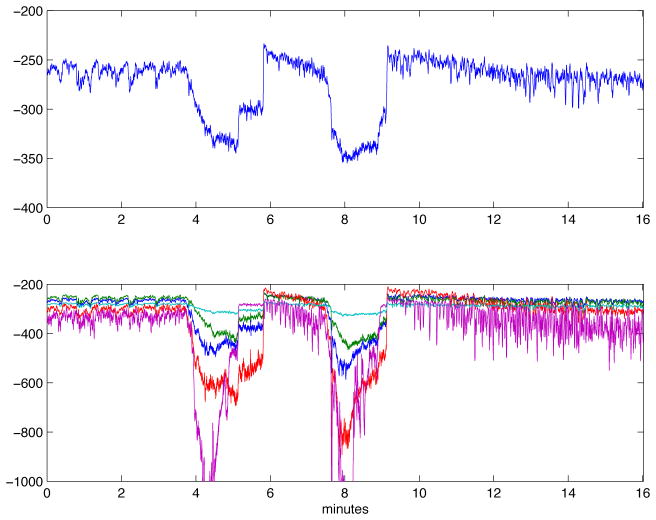
We applied AMICA to 16 minutes of 78-channel iEEG data (Figure 2) from subdural electrodes recorded from an epilepsy patient and including two brief ictal (seizure) periods (Figure 3). We compared AMICA decompositions using 1–5 models. Multiple models allowed individual adaptation to differeces in spatiotemporal source structures during seizure and nonseizure periods. The temporal segmentation returned by AMICA was consistent across varying model numbers. Additional models adapted to some time-local features expressed in the data. In the five-model decomposition, the two seizures were segmented consistently into early and late phases. The logarithm of the posterior likelihood given in equation (2) is plotted over all time points in Figure 4 for the 1-model and 5-model decompositions. In the 1-model decomposition, overall data likelihood (given the model) drops severely during seizure periods, while in the 5-model decomposition the seizure periods are better accounted by other models that represent pre-seizure, early seizure, late seizure, early post-seizure, and later post-seizure data, respectively.

Fig. 2.

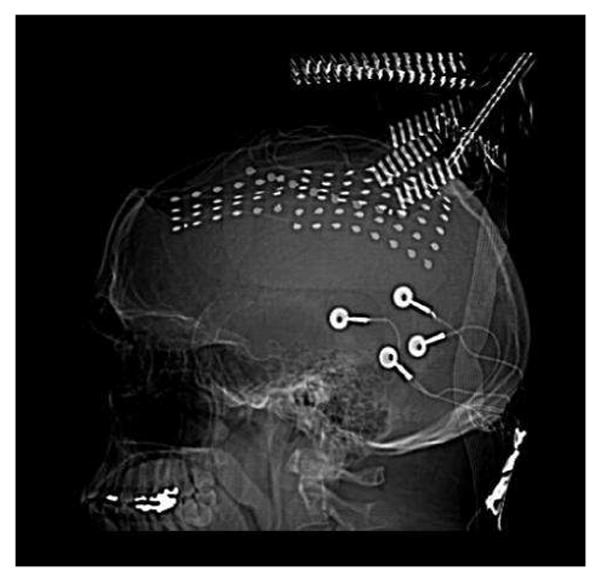
CT image of the implanted grid electrodes. The two grids (6 × 8,4 × 6) and one medial strip (1×8) implanted in the patient for monitoring.

Fig. 3.

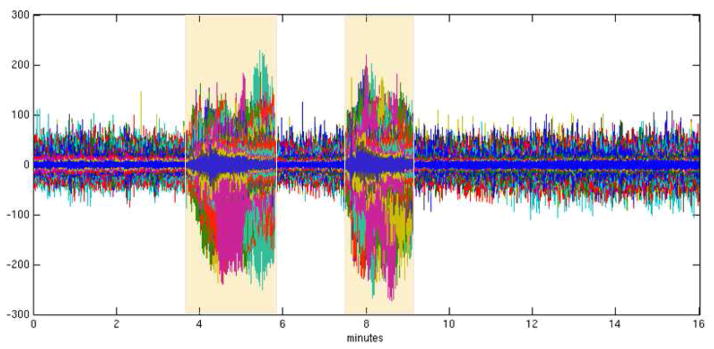
The iEEG data. All channels are plotted on the same axis. The seizure periods are highligtened.

Fig. 4.

Likelihood graphs for single model and 5-model Amica decomposition.

C. Sparse patch-based inverse problem solution

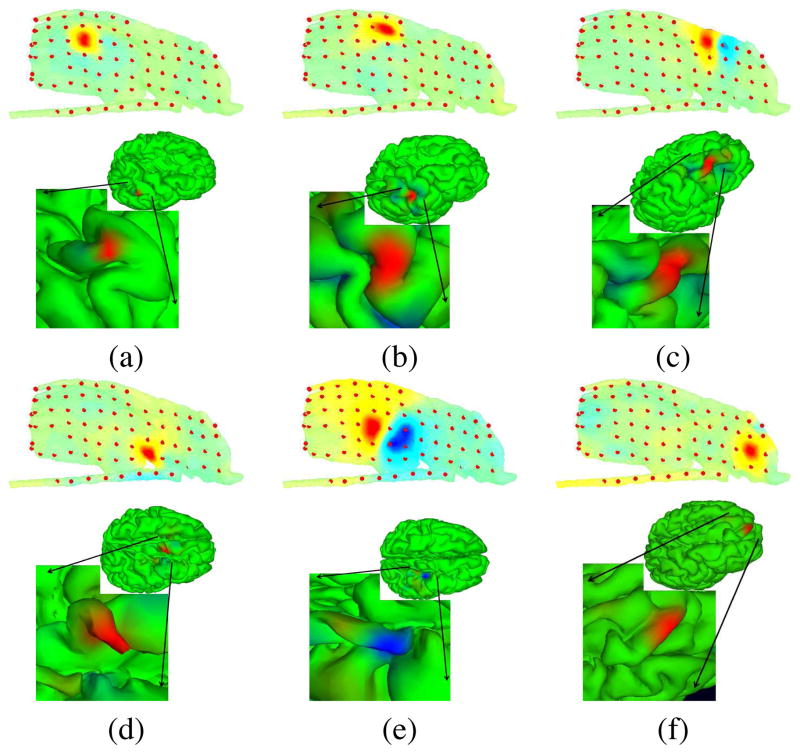
Next, we generated a realistic cortical source space incorporating 80,130 dipole elements oriented perpendicular to the local cortical surface, located from the subject MR head images using tessellated FreeSurfer gray and white matter surfaces (surfer.nmr.mgh.harvard.edu). The lead field matrix (LFM) for this source space was calculated using the BEM tools in the NFT toolbox. To create a multi-scale cortical patch basis on this brain mesh surface, we selected for each single voxel dipoles, three conformal, gaussian-tapered cortical patches of three sizes with geodesic radii of 10 mm, 6 mm, and 3 mm [11]. Figure 5 shows the three gaussian patches centered on a single cortical voxel. We solved the EEG inverse problem for each AMICA component by identifying a sparse collection of cortical patches that best accounted for its grid map using sparse Bayesian learning (SBL) [12]. Figure 6 shows projection maps for six IC processes to the model subdural electrode sheet and strips, and their associated source localization estimates. These components were selected from the early-seizure model of 5-model AMICA decomposition; all participate in the seizure. Component (d) is the seizure onset component as well as the component accounting for interictal spikes observed in the data by our clinical collaborators. Most of the seizure-related component locations are compact gyral patches, but there are also sulcal components as shown in Figure 6(e). This IC process projects to two separate broad pools of electrodes with opposite polarities and has a compact source area estimate located in a sulcus. The spatial extent of the source regions (a), (b), and (c) look similar, but the degree of focality of the source projections to the recording grid differs according to the estimate source location.

Fig. 5.

Three Gaussian patches of different size centered on a cortical mesh voxel with radius 10 mm, 6 mm, and 3 mm.

Fig. 6.

Projection maps (interpolated on the electrode grid and strip surfaces) and patch-basis SBL localization of the cortical source domain, shown on the whole cortical surface and in close-up.

D. Component pairwise mutual information and dependency clustering

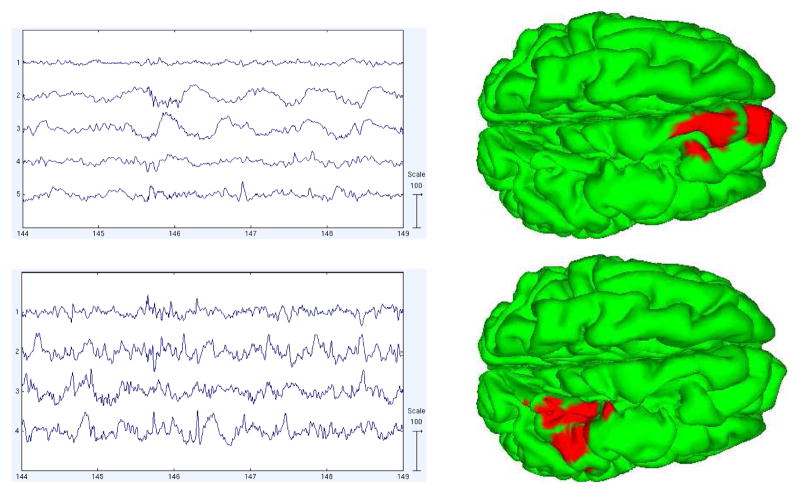
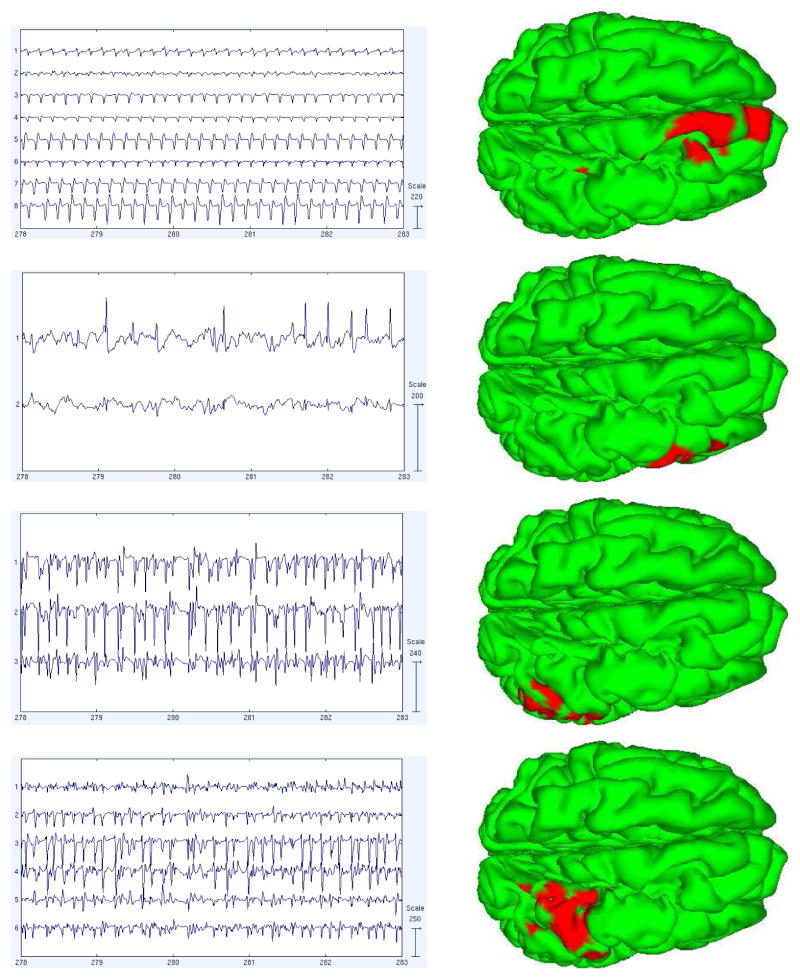
We calculated the pairwise mutual information (PMI) between the component processes to better understand how the component time courses differ. The PMI calculation is based on estimating the entropies of the signal using the usual binning method in which channel value histograms and a simple Riemann integral approximation are used to compute the entropies. This approach is generally suitable for larger sample sizes like those encountered for EEG data. We then clustered the components using a heuristic method of searching for permutations in component order that produce approximately more block diagonal PMI matrix. We searched for component position swaps, or pairs of swaps, that most decrease a cost function penalizing the magnitudes of the off-diagonal elements. This was done iteratively until a local minimum was reached. Figure 7 shows the sorted PMI of components in the 5-model decomposition (a) for the pre-seizure model, and (b) for the first part of the seizure. We then imaged the activations and source estimates of the revealed component subspaces. Figures 8 and 9 show the activations of the subspace components during 5 seconds of pre-ictal or ictal period data and and their summed source location estimates.

Fig. 7.

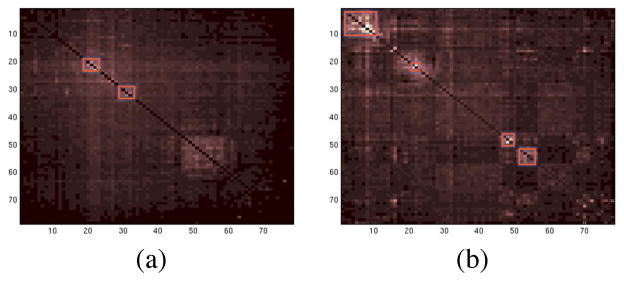
Pairwise mutual information between maximally independent components of two models in the 5-model decomposition. (a) Pre-seizure model, (b) first part of the seizure. Component subspaces exhibiting partial residual dependency are highlighted.

Fig. 8.

Activations and sources of the components in the dependency clusters shown in Figure 7(a) (pre-seizure period).

Fig. 9.

Activations and sources of the components in the dependency clusters shown in Figure 7(b) (seizure period)

The activations of the components in each AMICA cluster had similar time patterns, and the components were localized by SBL to nearby or partly overlapping cortical patches. There were two main active regions during seizure as shown in the first and last columns of Figure 9. The first active region was on the superior frontal gyrus and the second in the precentral gyrus. We computed PMI on those data points best accounted by each model. Thus, the pre-seizure PMI clusters were trained predominantly on pre-seizure data only. Yet we observed that the source locations of the (much weaker) PMI residual-dependency clusters for this model were quite similar to those for the seizure model. To test the stability of this observation, we decomposed an additional 15 minutes of non-seizure data using single-model AMICA and again calculated the component PMI. We found 6 weak dependency clusters; two of them had grid maps and source distributions again similar to the two principal early-seizure model clusters for the seizure data, suggesting that the seizures exploit background susceptibilities to dependent interaction of these areas.

III. CONCLUSIONS AND FUTURE WORK

Here, we analyzed intracranial EEG recordings using multi-model AMICA and numerical forward and inverse source estimation methods and presented patch-based source localization results for seizure data recorded from an epilepsy patient during invasive pre-surgical monitoring. We calculated PMI between components and clustered components exhibiting dynamic interdependency. We found two predominant dependent clusters that accounted for much of the ictal activity and were localized to contiguous cortical areas. In a companion paper [13], the dynamic interactions of these two regions are further modeled using multivariate causality and information flow methods. It seems possible that electrocortical source imaging may allow valuable insights into the electrophysiological dynamics of the human brain (both normal and abnormal).