Matched Longitudinal Analysis of Biomarkers Associated with Survival

Abstract

The identification of host or pathogen factors linked to clinical outcome is a common goal in many animal studies of infectious diseases. When the disease is fatal, statistical analysis of such factors may be biased from missing observations due to deaths. For example, when observations of a subject are censored before completing the intended study period, the complete trajectory will not be observed. Even if the factor is not associated with outcome, comparisons of data from survivors with those from nonsurvivors may lead to the wrong conclusions regarding associations with survival. Comparisons between subjects must account for differing observation lengths for those who survive relative to those who do not. Analyzing data over an interval common to all subjects provides one solution but requires eliminating data, some of which may be informative about the differences between groups. Here, we present a novel approach, matched longitudinal analysis (MLA), for analyzing such data based on matching biomarker intervals for survivors and nonsurvivors. We describe the results from simulation studies and from a study of monkeypox virus infection in nonhuman primates. In our application, MLA identified low monocyte chemoattractant protein-1 (MCP-1) levels as having a statistically significant association with survival, whereas the alternative methods did not identify an association. The method has general application to longitudinal studies that seek to find associations of biomarker changes with survival.

INTRODUCTION

In studies of high-consequence pathogens, human studies of infection are typically not possible, making animal models the primary basis for evaluating both the immunological processes related to infection and therapeutic efficacy. The U.S. FDA code of regulations allows for the approval of drugs or products for human use when human studies are not feasible; these regulations are commonly and collectively referred to as the Animal Rule (1). Animal studies allow for more extensive characterization of the host response to infection than might typically be possible in humans; more variables may be controlled and evaluated, including the timing and route of infection. A goal of such studies may be to identify host or pathogen factors associated with disease outcome (such as survival) in order to characterize pathophysiologic mechanisms and to suggest novel therapeutic targets. The identification of factors associated with survival is an objective that differs from a comparison of preidentified groups (e.g., treatment versus placebo control) and may require nonstandard statistical methods.

When subjects succumb to infection, observations are censored at the time of death, resulting in shorter observation times relative to those subjects surviving infection. Subjects observed for shorter periods may not have attained their potential maximum value (for biomarkers that tend to increase) or their potential minimum value (for biomarkers that tend to decrease), which can bias group comparisons in favor of falsely identifying an effect. As an example, assume a biomarker of interest increases up until day 10 and then gradually declines to preinfection levels by day 30 in survivors. Further, assume the biomarker is not associated with survival, so the true trajectories of survivors and nonsurvivors are identical. As an extreme hypothetical example, consider the case that all subjects who succumb do so on the second day after inoculation. It follows that subjects who survive infection are more likely to have higher biomarker levels than subjects who succumb, simply as a result of the longer observation times and not due to any true differences between survivors and nonsurvivors. As a result, comparisons of summaries between survivors and nonsurvivors over the entire observation periods may lead to incorrect conclusions about the association of survival with biomarker levels. We refer to this approach as the naive approach.

An alternative to the naive approach is the standard derived variable approach, which summarizes trajectories over a common interval length; this is a common statistical approach for variable observation lengths. One might, for example, summarize the biomarker up until the time of the first death or up until a preselected time point before any deaths. This requires ignoring potentially informative data, which might reduce power. Further, unless a specific time point after infection is known a priori to be critical, one consequence of this approach might be the elimination of the meaningful differences that occur after selected time points.

In this paper, we develop an approach, called matched longitudinal analysis (MLA), to overcome these limitations. The performance of MLA is compared to those of the naive and standard derived variable approaches using computer simulation studies and data from a monkeypox virus (MPXV) experiment. The application of our approach to the MPXV nonhuman primate study indicates that monocyte chemoattractant protein-1 (MCP-1) is associated with outcome.

MATERIALS AND METHODS

The statistical methods developed in this study are motivated from a study of MPXV infection of nonhuman primates (NHPs) (2). One goal of this study was to identify cytokines associated with improved survival that might lead to candidate therapeutic targets. Briefly, cytokines in 21 cynomolgus macaques (Macaca fascicularis) from a recent study comparing 2 routes of MPXV inoculation were measured at regular intervals up until death or the end of the study period (36 days postinoculation). In this study, 12 NHPs survived infection, while 9 succumbed to disease. The challenge (i.e., pathogen) dose and route were divided as follows: 5 × 10⁷ PFU intravenous (i.v.) (n = 6), 5 × 10⁶ PFU i.v. (n = 6), 5 × 10⁶ PFU intrabronchial (i.b.) (n = 3), and 5 × 10⁵ PFU i.b. (n = 6). All animal handling procedures were approved by the National Institute of Allergy and Infectious Diseases Animal Care and Use Committee and adhered to National Institutes of Health (NIH) policies. More details about the animal care, assays, and data collection can be found in Johnson et al. (3).

Our goals were to determine the disease pathogenesis of MPXV in NHPs in order to discover potential therapeutic targets. Historically, studies perform comparisons of infected and uninfected groups to identify what is elevated during the disease process. Comparisons of uninfected and infected NHPs provide data pertaining to changes during the disease process but not factors associated with lethal disease. For example, previous orthopoxvirus studies have listed the “cytokine storm” or toxemia as the cause of death (3). However, these comparisons were made to the preinfection state, when one would expect that cytokines or other immunological factors would not be elevated. Therefore, identifying factors that are associated with lethal disease by comparing subjects who succumbed to those who survived may provide enhanced insight into pathogenesis and identify potential therapeutics.

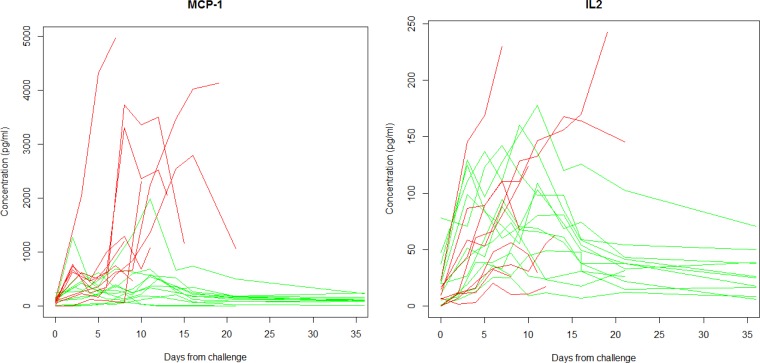
Evaluations using standard methodology do not account for variations in the time until death, and there are no guidelines for which features of the trajectory to analyze. For example, should comparisons occur at a study midpoint, at the endpoint only, or at the peak measurement? To illustrate such problems, consider Fig. 1. Figure 1 displays profiles from two cytokines, monocyte chemoattractant protein-1 (MCP-1) and interleukin 2 (IL-2), evaluated over time from challenge until the end of the study or death. The analysis of these profiles is complicated by many factors, including the nonlinear trajectory after infection, appropriate treatment of the repeated measurements for each subject, and missing observations that occur after an animal succumbs to infection.

FIG 1.

MCP-1 and IL-2 trajectories for 21 NHPs from day of challenge (day 0) until clinical moribund endpoint or end of study (35 days). Red trajectories are from NHPs that succumbed to infection, while green represents those that survived infection. Note that for MCP-1, the survivors (green) have consistently lower values than nonsurvivors (red), while for IL-2, there are not large differences between the survivors and nonsurvivors.

The repeated measurements of a biomarker over time for a given subject can be analyzed using a derived variables approach, in which the profile is described by a single summary measure. Various summaries of the curves in Fig. 1 can be considered, including the area under the curve (AUC), maximum, average, and slope from a linear regression. The appropriate summary measure will depend on the underlying process. Prior knowledge about the mechanism can guide the selection of the preferred approach prior to performing data analysis. For example, if exposure to a cytokine concentration of some threshold is most important, the maximum value may be appropriate. On the other hand, if the total exposure is important, the AUC may be preferred. For linear trajectories, change over time as described by the slope may be appropriate. When little is known about the mechanism, multiple summaries may be considered, but this requires accounting for multiple testing (4).

After the derived variable has been computed, standard statistical tests (e.g., a t test or a Wilcoxon signed-rank test) can be performed on the derived variables among survivors and nonsurvivors to test for an association. When observation lengths between subjects vary, a straightforward statistical test is not appropriate. The standard derived variable approach computes the variable over a common interval, which may limit the ability to detect true differences.

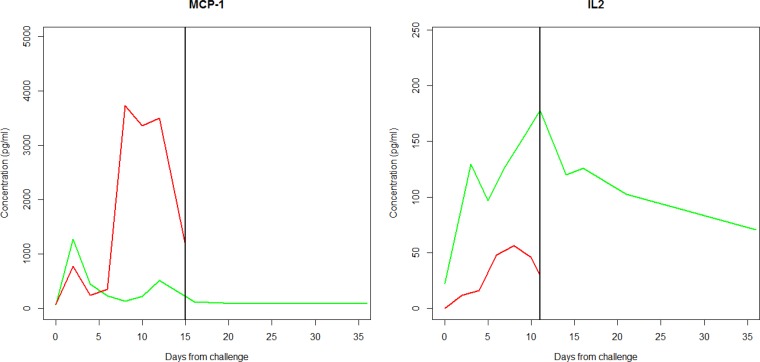
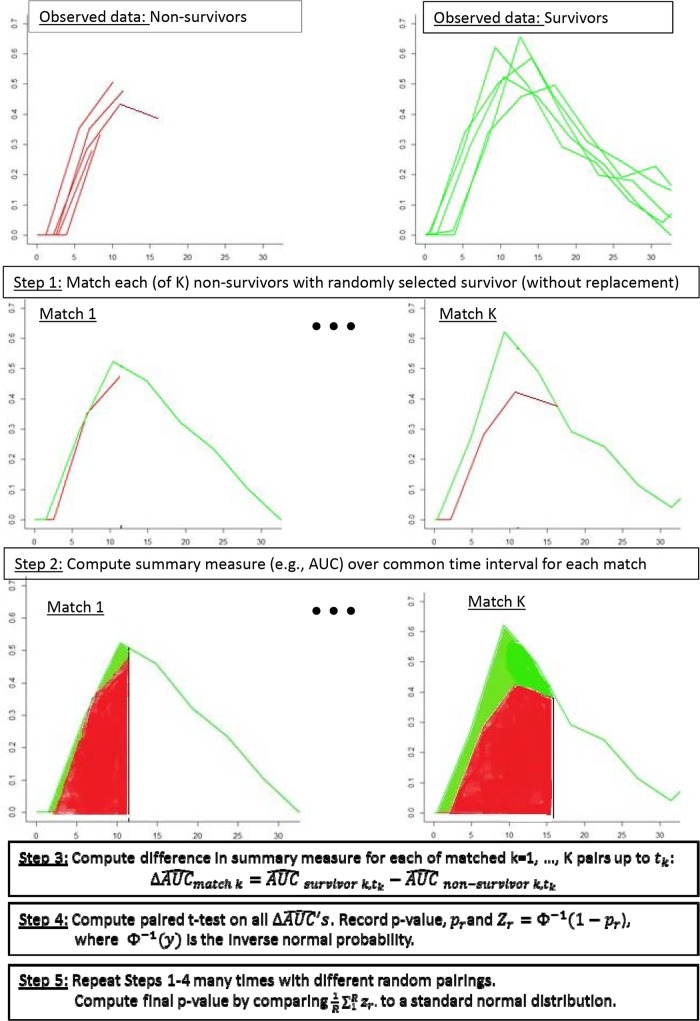
Matched longitudinal analysis (MLA) allows for comparisons between subjects with differing lengths of observations using derived variables. With this method, observations from survivors and nonsurvivors are paired (at random), and the derived variable is computed over the time interval shared by the pairs. In other words, the longitudinal profile for a survivor is matched to the same interval as that for its (randomly matched) nonsurvivor, and then the data are summarized backwards in time over the common interval. Figure 2 displays one such match for two examples from the MCP-1 and IL-2 results. The difference between the derived variables for each pair is computed, and then a paired t test (or Wilcoxon signed-rank test) is applied to the two groups to obtain a P value. This is unappealing, however, because the P value depends on the particular randomly paired set, for which there are many possible combinations. Therefore, this process is repeated many times to obtain a set of different P values. This method is akin to the bootstrap, a resampling based method frequently employed when parametric inference is intractable, although here the sampling requires pairing (or sampling without replacement) (5). In such methods, resampling is frequently undertaken a minimum of 200 times, depending on computational burden. In our analyses, 1,000 repeated samples were taken to ensure reasonable precision in estimating the P value. To summarize the results across these different pairings, an overall P value is computed using the inverse normal method of combining P values, as described in the Appendix. Figure 3 provides a graphic detailing the steps of the algorithm. An average of the derived variable across the repeated replicates by group (and the difference between the groups) provides point estimates. Note that the averages require thoughtful interpretation, as they represent averages taken over different time intervals, corresponding to the death times among the nonsurvivors. A confidence interval on the difference can be obtained by taking the average difference and standard deviation across the random pairings, using a t distribution, as described in the Appendix.

FIG 2.

One representative matched pair of a nonsurvivor (red) and survivor (green) for MCP-1 and IL-2. The black vertical line indicates the period from baseline over which cytokine profiles are compared back to the day of challenge (day 0). To obtain a P value, nonsurvivors are matched to each survivor. As described in Materials and Methods, this analysis is repeated 1,000 times, and an overall P value is obtained according to the method described in the Appendix.

FIG 3.

Algorithm for computing P values using MLA. The x axis shows the number of days from challenge. The y axis shows the concentration in pg/ml.

Note that the case above assumes there are more survivors than nonsurvivors, which is not always the case. When there are more nonsurvivors than survivors, a matching nonsurvivor is selected at random, without replacement, for each survivor. Adequate numbers of nonsurvivors and survivors are needed. Indeed, equal numbers of survivors and nonsurvivors is the most efficient allocation, which suggests the use of the 50% lethal dose (LD₅₀) as the challenge dose for such studies. The recommended total sample size will depend on the effect size of interest and the variability in the measured markers, but 5 survivors and 5 nonsurvivors seem to be reasonable minimum numbers for undertaking this analysis. Additionally, we recommend collecting data at the same times postinfection for all subjects in order to match the time points. Interpolation of the values between the time points will be necessary if the times do not match up exactly.

We conducted computer simulation studies to evaluate the performance of the MLA method relative to the naive and standard derived variable approaches. Specifically, we evaluated whether the proposed methodology produces appropriate rejection rates when there is no difference between the groups. In other words, we evaluated whether the type I error rate was at the nominal level, which is commonly set to 0.05. Additionally, because we simulate under scenarios with true differences, we evaluated the proportion of times the method concluded statistical significance to better understand the power of the test under specific models with true differences.

Simulation studies require mathematical models describing the longitudinal trajectories and the variability associated with subject-specific differences and measurement. To generate reasonable models, we fit third-order polynomial models with random intercepts to the MCP-1 and IL-2 cytokine MPXV data. The parameters estimated from these models were the basis for the generated data. In the MPXV study, roughly half of the subjects succumbed. To simulate who lived or succumbed, we used the statistical equivalent of flipping a fair coin (i.e., a binomial distribution with probability ½). For those who “lost the coin toss,” the times of death were generated, assuming a uniform distribution on the interval from 5 to 20 days.

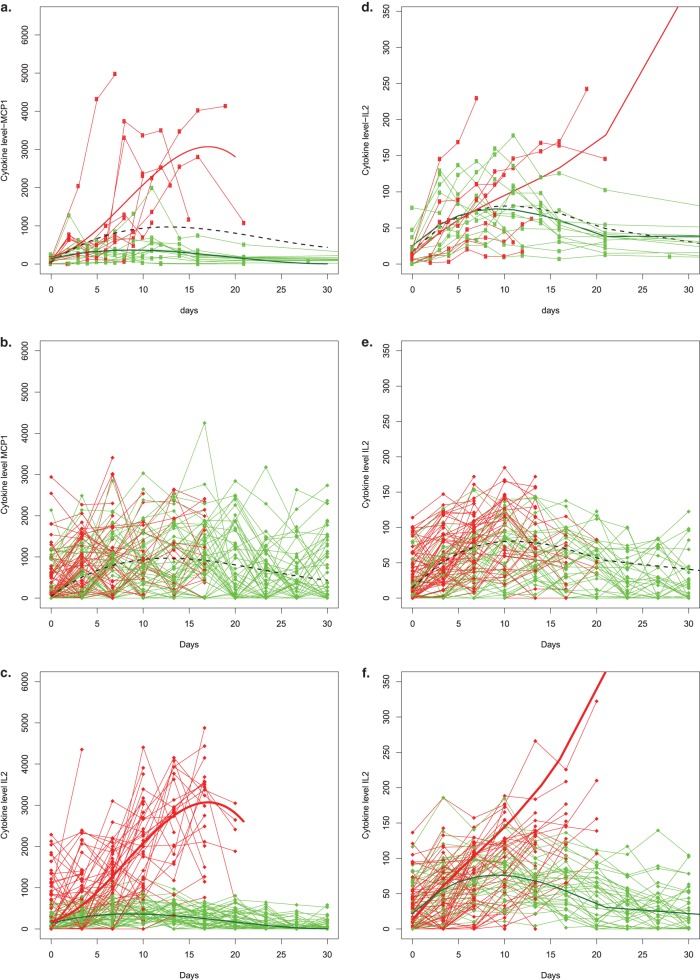
Two null models were derived, one based on MCP-1 and another on IL-2. The null models were derived by fitting a single polynomial model for both survivors and nonsurvivors. The models were fit separately for MCP-1 and IL-2. The models under alternative hypotheses (i.e., when true differences between survivors and nonsurvivors exist) were derived by fitting such models separately for survivors and nonsurvivors. This gave a total of four models: two with no true differences and two with true differences. Figure 4 displays the observed data from the MPXV experiment, along with the models used to generate the data and example realizations of the trajectories that were simulated accordingly. For each model, we considered sample sizes of 10, 15, 20, and 40. We generated 100,000 data sets for each of the four sample sizes considered under each of the four models, requiring a minimum of 5 survivors and 5 nonsurvivors for estimation and inference. For each data set generated, we computed P values based on the following approaches: (i) the naive approach, which ignores the censoring and computes the derived variable on all observed data, (ii) the standard derived variable approach, which summarizes data over a common interval (in our case, we computed derived variables up to the time of the first death for all subjects), and (iii) the MLA method. We computed derived variables based on a slope from a linear regression model, the maximum value, and the AUC. Simulations were run on the NIH Biowulf cluster using the package R.

FIG 4.

Simulated cytokine data from day of challenge (day 0) until end of study (day 30) using MCP-1 MPXV data as the basis for model derivation. (a) Longitudinal data for MCP-1 from all subjects. The three smooth curves represent the three models that were fit. The dotted black line represents the curve used to generate data under the null hypothesis. Specifically, the model is cytokine_ij = 47 + 166d − 9d² + 0.13d³ + a_i + e_ij, where a_i is ∼N(0, 680) and e_ij is ∼N(0, 680) for both survivors and nonsurvivors. The smooth green and red lines describe the data used to generate survivors (green) and nonsurvivors (red) under the alternative hypothesis. The model is cytokine_ij = 136.9 + 57.8d − 4.3d² + 0.07d³ + a_i + e_ij, where a_i is ∼N(0, 190) and e_ij is ∼N(0, 200) for survivors, and cytokine_ij =188 + 44.2d − 24.5d² − 1.02d³ + a_i + e_ij, where a_i is ∼N(0, 700) and e_ij is ∼N(0, 860) for nonsurvivors. (b) Example data that were generated under the null model. (c) Generated data under the alternative model. (d to f) Same kinds of figures in the other panels but based on the IL-2 data. The model based on IL-2 under the null hypothesis can be expressed as cytokine_ij = 18.4 + 13.3d − 0.837d² + 0.013d³ + a_i + e_ij, where a_i is ∼N(0, 37) and e_ij is ∼N(0, 27). The alternative models based on IL-2 is cytokine_ij = 25.6 + 12.25d − 0.87d² + 0.015d³ + a_i + e_ij, where a_i is ∼N(0, 29.3) and e_ij is ∼N(0, 20) for survivors, and cytokine_ij = 12.1 + 12.2d − 0.56d² + 0.015d³ + a_i + e_ij, where a_i is ∼N(0, 45) and e_ij is ∼N(0, 28) for nonsurvivors.

Finally, we applied the standard and MLA approaches to the MCP-1 and IL-2 cytokines from the MPXV study. Under the standard derived variable approach, the derived variables were computed in two ways: (i) summarizing up until the first time of death (day 7), and (ii) summarizing up until to the time at which all subjects had measurements for all time points (day 5). Survivors (n = 12) were matched to the nonsurvivors (n = 9) 1,000 times to obtain a final P value.

RESULTS

Table 1 provides a summary of the simulation study results under the two null hypotheses. The proportions of times statistical significance was concluded (out of each of the 10,000 generated data sets) are provided for each model, sample size, and method. For the commonly chosen threshold of significance of a P value of <0.05, a proper type I error rate ensures that if there are no true associations, a conclusion of “association” will only be made 5 out of 100 times over repeated experiments. Hence, all values in Table 1 should be <0.05. As expected, the naive approach rejected the null hypothesis far more than it should for all models, all derived variables, and all sample sizes. In contrast, the standard derived variable approach and MLA approach are near the 0.05 level. Note that the MLA is conservative, and the degree of conservativeness varies with the choice of the derived variable and sample size.

TABLE 1.

Simulation study results from two models without differences between survivors and nonsurvivors^a

Sample size for derived variablesb	Null model 1 (MCP-1)			Null model 2 (IL-2)
	Naive	Standard	MLA	Naive	Standard	MLA
Slope
10	0.156	0.039	0.007	0.552	0.045	0.009
15	0.285	0.047	0.004	0.791	0.050	0.005
20	0.397	0.047	0.006	1.000	0.049	0.005
40	0.703	0.049	0.008	0.994	0.050	0.009
Max
10	0.098	0.043	0.027	0.068	0.046	0.030
15	0.137	0.050	0.020	0.087	0.050	0.021
20	0.172	0.049	0.022	0.331	0.049	0.019
40	0.320	0.050	0.029	0.174	0.050	0.031
AUC
10	0.310	0.036	0.016	0.377	0.042	0.018
15	0.528	0.047	0.012	0.595	0.049	0.013
20	0.692	0.048	0.016	1.000	0.049	0.017
40	0.969	0.049	0.024	0.981	0.049	0.025

^aData are frequencies with which statistical significance is concluded using a nominal level of 0.05.

^bMax, maximum; AUC, area under the curve.

A high rejection rate under the null hypothesis makes a method invalid; hence, the naive approach was not considered when evaluating power. Table 2 describes the rejection rates for the MLA method and the standard derived variable approach under the two models when true differences existed between trajectories for survivors and nonsurvivors. The MLA (correctly) concluded statistical significance more frequently than the standard derived variable approach for both models and all sample sizes. This is not surprising, because the MLA uses more data from each subject. Note that in some cases, the power of the standard derived variable method decreases as the sample size increases. This occurs because as the sample size increases, the time of the last death tends to occur earlier (e.g., at day 5), which reduces the common time interval. For the models considered, the differences were smaller at day 5, resulting in lower power for the standard derived variable approach with larger sample sizes.

TABLE 2.

Simulation study results from two models with true differences between survivors and nonsurvivors^a

Sample size for derived variablesb	Alternative model 1 (MCP-1)		Alternative model 2 (IL-2)
	Standard	MLA	Standard	MLA
Slope
10	0.195	0.496	0.274	0.550
15	0.194	0.596	0.301	0.649
20	0.189	0.709	0.327	0.769
40	0.163	0.927	0.418	0.965
Max
10	0.415	0.733	0.129	0.285
15	0.548	0.898	0.130	0.383
20	0.653	0.978	0.131	0.555
40	0.916	1.000	0.135	0.933
AUC
10	0.245	0.342	0.082	0.076
15	0.371	0.548	0.085	0.108
20	0.489	0.813	0.083	0.197
40	0.825	0.999	0.076	0.573

^aData are frequencies with which statistical significance is concluded using a nominal level of 0.05.

^bMax, maximum; AUC, area under the curve.

Comparisons of MLA and the standard derived variable approach applied to the MPXV data are provided in Table 3. The MLA analysis concluded that lower MCP-1 concentrations are associated with survival from infection (P < 0.05 for the AUC, maximum, and slope summary measures). However, the two approaches based on derived variable analysis, namely, “infection to day of first death” and “infection to day 5,” failed to identify an association between MCP-1 concentration and survival. With regard to IL-2, none of the methods found associations between IL-2 concentration and survival. This may be due to a lack of power for detecting an association, given the limited sample size. Alternatively, a lack of significant change in IL-2 may reflect its role as an upstream regulator of T-cell differentiation and functional pathways that are too far removed from downstream events associated with outcomes (6). Table 4 provides point estimates and confidence intervals. The values of MCP-1 are higher among the nonsurvivors, suggesting further investigation of the potential role of MCP-1 suppression for improved outcome.

TABLE 3.

Comparison of MLA and standard derived variable approach from MPXV study data comparing MCP-1 and IL-2 trajectories between survivors and nonsurvivors

Analysis type by trajectorya	P values for the indicated variableb
	Slope	Maximum	AUC
MCP-1
MLA	0.025c	0.002c	0.007c
Infection to day of 1st death analysis	0.157	0.205	0.231
Infection to day 5 analysis	0.233	0.246	0.260
IL-2
MLA	0.181	0.471	0.464
Infection to day of 1st death analysis	0.275	0.940	0.600
Infection to day 5 analysis	0.775	0.501	0.422

^aThe standard derived variable approach considered two common time points: day from challenge to day of first death and day from challenge to day 5.

^bP values were computed using the following derived variables: regression slope, maximum value and AUC.

^cStatistically significant at P < 0.05.

TABLE 4.

Point estimates and confidence intervals for MCP-1 and IL-2

Data by derived variablea	MCP-1	IL-2
Slope
Survivors	18.0	4.7
Nonsurvivors	208.3	8.7
Difference (95% CI)	190.4 (26.9, 353.9)	4.0 (−2.6, 10.5)
Max
Survivors	559.3	92.2
Nonsurvivors	2,823.2	116.2
Difference (95% CI)	2,163.9 (978.3, 3,349.6)	24.0 (−51.0, 99.0)
AUC
Survivors	3,341.3	696.5
Nonsurvivors	16,446.3	881.8
Difference (95% CI)	13,105.0 (4,545.8, 21,663)	185.3 (−464.5, 835.2)

^aCI, confidence interval; Max, maximum; AUC, area under the curve.

DISCUSSION

Statistical analysis by MLA serves as a starting point for identifying biomarkers that warrant further study and consideration for disease staging and/or therapeutic intervention. When the goal is to evaluate associations of an immunologic marker or other biomarker with survival, we propose an analysis for censored longitudinal data based on derived variables. In such instances, variable interval lengths result due to censored observations at the time of death. The naive approach that ignores the various interval lengths and that summarizes the trajectories over the observed intervals for each animal produces P values that are not valid. The standard derived variable approach that summarizes trajectories up to a common time point for all subjects gave valid type I error rates but had lower power than the MLA, which uses more data and was expected to have greater power. In the application, MLA identified MCP-1 as being significantly associated with survival, while the standard derived variable approach failed to identify MCP-1 as significant.

More sophisticated statistical methods can be used to approach this problem. For example, response trajectories can be modeled using nonlinear mixed effects models (e.g., see reference 7). This approach can address the problem of bias in cases where nonsurvivors expire before reaching a peak cytokine value, can allow for a rich class of cytokine trajectories, and may make more efficient use of limited serial measurements, although stronger model assumptions are necessary for these alternative approaches. The development of such methods is an interesting avenue for future research on the identification of biomarkers associated with survival in animal challenge studies.

Finally, while we propose the AUC, maximum, and slope as potential summaries of the biomarker trajectory, alternative summary measures may be considered. For example, if interest resides in identifying factors immediately preceding death, comparing average values on the day before death may be the appropriate analysis. However, summaries immediately proximal to the time of death may be irrelevant for identifying therapeutic candidates, as such associations may simply be associated with death, such that related intervention targets occur too late in the pathway to death to improve the outcome. On a final note, adjustment for baseline measurements may be relevant when computing summaries. A simple way to use change from baseline is to take the difference (or log ratio) from baseline, rather than from the observed values.

The R code necessary to run these analyses is available upon request.

APPENDIX

Obtaining P values.

Let X_ij denote the observed cytokine from the ith nonsurvivor at the jth time point, with i = 1, …, n, and j = 1, …, N(i). Let the vector of responses be X_i = X_i1, …, X_iN(i). Further, let Y_kl denote the observed cytokine from the kth survivor at the lth time point, k = 1, …, m, and l = 1, …, M_k. Let the vector of responses be Y_i = Y_i1, …, X_im.

Assume for now that n ≤ m. The development for n > m is analogous. The derived variable is some function over the available time points for the nonsurvivors, denoted f(X_i, N_i). Let K(i) be the index for the survivor who is matched to nonsurvivor i. The associated derived variable is f(Y_K(i), N_i). For example, this may be the AUC, the maximum value, or the slope. The paired t test is performed on [f(X_i, N_i), f(Y_K(i), N_i)] for i = 1, …, n, with n − 1 degrees of freedom, producing a single one-sided P value, denoted P_r. This process is repeated many times (say r = 1,.., R times) to obtain a set of R P values. The overall P value from the r = 1,.., R P values, denoted P_r, for each P value is transformed to the normal quantile scale using the equation Z_r = Φ⁻¹ (1 − P_r). The average of these Z_r values, Z̄, is computed and then the normal percentile of Z̄ provides the overall one-sided P value, say P(Z̄). For an overall two-sided P value, we take the minimum of [P(Z̄), 1 − P(Z̄)] and double it. This can be shown to be conservative by the following argument: Z_r denotes the normal quantile of the rth P value, which, by definition, all have variance of 1. It follows that

$$\mathrm{var}\hspace{0.17em}(\overline{Z})=\mathrm{var}\hspace{0.17em}\frac{1}{R}\left(\sum _{i=1}^R{Z}_i\right)=\frac{1}{R}\mathrm{var}\hspace{0.17em}(Z_i)+\frac{1}{R^2}\sum _{j\ne 1}^R\sum _{i=1}^R\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}(Z_i)\le (\frac{1}{R}+\frac{R-1}{R})=1.$$

Computing confidence intervals.

Consider the parameter E[f(X_i, N_i), f(Y_K(i), N_i)], which is the matched mean difference in derived variables. We can construct a confidence interval for this parameter. To see this, note that for each random pairing, we can create a sample mean and sample variance from the n data points [f(X_i, N_i), f(Y_K(i), N_i)] for i = 1, …, n. For the rth of R random pairs, denote these by D̄_r, S_r², respectively. We can construct a two-sided (1 − α) 100% confidence interval for E[f(X_i, N_i), f(Y_K(i), N_i)], by the usual t-based confidence interval D̄_r ± t_α/2,n−1 $\sqrt{S_{r^2/n}}$, where t_α/2,n−1 is the α/2 quantile of a t distribution with n − 1 degrees of freedom. To improve on this interval, we can replace D̄_r, S_r² with their averages over the R samples, say D̄, S̄². We thus form D̄ ± t_α/2,n−1 $\sqrt{\overline{S^2/n}}$ as our two-sided (1 − α) 100% confidence interval.