Abstract
Current literature acknowledges the effect of food structure on bacterial dynamics. Most studies introduce this “structure” factor using a single gelling agent, resulting in a homogeneous environment, whereas in practice most food products are heterogeneous. Therefore, this study focuses on heterogeneous protein-polysaccharide mixtures, based on gelatin and dextran. These mixtures show phase separation, leading to a range of heterogeneous microstructures by adjusting relative concentrations of both gelling agents. Based on confocal microscope observations, the growth of Escherichia coli in gelatin-dextran systems was observed to occur in the dextran phase. To find a relation between microscopic and population behavior, growth experiments were performed in binary and singular gelatin-dextran systems and culture broth at 23.5°C, with or without adding 2.9% (wt/vol) NaCl. The Baranyi and Roberts growth model was fitted to the experimental data and parameter estimates were statistically compared. For salted binary mixtures, a decrease in the population maximum cell density was observed with increasing gelatin concentration. In this series, for one type of microstructure, i.e., a gelatin matrix phase with a disperse dextran phase, the maximum cell density decreased with decreasing percentage of dextran phase. However, this relation no longer held when other types of microstructure were observed. Compared to singular systems, adding a second gelling agent in the presence of NaCl had an effect on population lag phases and maximum cell densities. For unsalted media, the growth parameters of singular and binary mixtures were comparable. Introducing this information into mathematical models leads to more reliable growth predictions and enhanced food safety.
INTRODUCTION
The Centers for Disease Control and Prevention (CDC) estimate that each year roughly 1 in 6 Americans (i.e., 48 million people) become ill, 128,000 are hospitalized, and 3,000 die of food-borne diseases (1). In the EU, more than 55,000 human cases associated with food-borne outbreaks were reported in 2012 (2). Predictive microbiology is one of the approaches to improve food safety. It aims at constructing mathematical models that predict microbial behavior as a function of environmental conditions. These predictions are useful tools in risk assessment, food process control, and product design (3).
Microbial behavior in liquid systems has been studied thoroughly, and most available predictive models are based on experimental data in broth. These models are routinely applied to predict microbial growth in structured food systems, although food structure has been acknowledged to play a key role on microbial growth (4). Food model systems that mimic the composition and structure of real foods are often used to study microbial behavior in foods under reproducible and controllable conditions. A myriad of studies on microbial behavior in structured systems have already been conducted, involving different gelling agents and target microorganisms (Table 1).
TABLE 1.
Overview of studies performed with different microorganisms grown in homogeneous and heterogeneous model systems and in real food products
| Model system or real food product | Microorganism(s)a |
|---|---|
| Model systems | |
| Homogeneous systems | |
| Agar | Salmonella Typhimurium, Listeria monocytogenes, Escherichia coli and other microorganisms (5), E. coli (6) |
| Carrageenan | Listeria innocua (7), S. Typhimurium and E. coli (8) |
| Dextran | E. coli and S. Typhimurium (9) |
| Gelatin | S. Typhimurium (8, 10–12), L. monocytogenes (13), L. innocua (14, 15) |
| Pluronic F127 gel | S. Typhimurium (16) |
| Xanthan gum | S. Typhimurium and E. coli (8) |
| Heterogeneous systems | |
| Meat emulsion | L. monocytogenes (17) |
| Oil-in-water emulsion | Salmonella spp. (18), Shigella sonnei and Shigella dysenteriae (18), Klebsiella pneumoniae (18, 19), Enterobacter cloacae (19), Staphylococcus aureus (20), E. coli (20), Pseudomonas aeruginosa (20), Candida albicans (20), L. monocytogenes (21), Yersinia enterocolitica (21) |
| Packed bed of microporous silica particles and Sephadex microspheres | S. Typhimurium (22, 23), E. coli K-12 (23), Pseudomonas putida (23) |
| Water-in-oil emulsion | Citrobacter freundii and Kluyveromyces lactis (24) |
| Real food products | |
| Canadian retail Wieners | L. monocytogenes (25) |
| Cooked ham | L. monocytogenes (26) |
| Cooked meat emulsions | Lactic acid bacteria (27) |
| Fermented sausages | Lactobacillus spp. (28) |
| Liver pâté | L. monocytogenes (29, 26) |
| Mayonnaise | L. monocytogenes (30, 31) |
| Serra cheese | Host microflora (32) |
The microorganism(s) studied and the corresponding source references (in parentheses) are indicated.
Most studies involving food model systems only handle one gelling agent, resulting in a homogeneous growth environment. In contrast, most food products contain different phases, e.g., water, proteins, polysaccharides, and fat, leading to a heterogeneous environment. Observation of bacterial growth in such heterogeneous systems is mostly limited to studies in specific food products (Table 1). No general conclusions can be drawn about the sole effect of a heterogeneous microstructure on microbial growth since these food products each contain their own characteristic amounts of nutrients, salt, preservatives, etc. General studies in model systems with a heterogeneous microstructure have already been performed (Table 1). It has been shown that the microstructure of packed beds (22, 23) and emulsion systems influences microbial behavior (20, 21, 24). However, in these studies, heterogeneity is introduced by the addition of a second phase that does not allow bacterial growth, and in the case of the packed bed, not resembling real food products since silica particles and Sephadex microspheres are not used as food components in real food products. In summary, to accurately predict microbial behavior in food products, heterogeneous food model systems with all phases potentially supporting bacterial growth must be studied, meaning that microbial growth in these phases is physically possible. However, the components that introduce heterogeneity (e.g., gelling agents) do not necessarily have to be metabolizable.
Proteins, polysaccharides, and their mixtures are widely used in food products (33) and are known to show phase separation in a certain range of conditions, e.g., at high ionic strength (34). The process of phase separation and the resulting heterogeneous microstructures have extensively been discussed in the literature (see, for example, references 34 and 35). In addition, it is well known that bacterial growth is supported by nutrient-enriched protein (8, 10, 12, 15) and polysaccharide-based gels (9). Examples of food products containing protein-polysaccharide mixtures include puddings, whipped cream, sauces, and dressings.
The general objective of the present study was to investigate the effect of different heterogeneous microstructures on the microbial dynamics of Escherichia coli by performing growth experiments in phase-separating protein-polysaccharide food model systems, i.e., gelatin-dextran (G/D) systems. The population growth dynamics of E. coli were studied in seven gelatin-dextran mixtures with different microstructures obtained by using different ratios of gelatin and dextran, created as described previously (36). In this series of experiments, gelatin/dextran ratios of ≥1 were tested. To study the effect of salt, added in order to ensure phase separation, on the phase separation of the G/D systems and on the microbial growth behavior in the G/D systems, experiments were also performed in binary systems without added salt. Since the dextran phase is the preferential phase for E. coli growth, we tested whether singular dextran systems can mimic the population growth behavior in the binary G/D systems. For this purpose, the results in binary systems are compared to those obtained in singular systems of gelatin and dextran and, for completeness, in culture broth, with or without added salt. The growth parameters are estimated by fitting the Baranyi and Roberts growth model (37) to the experimental data. The population results were then compared to confocal microscope images in order to find a relation between microscopic and population observations.
This study investigates population microbial dynamics in binary gelled systems with heterogeneous microstructures supporting microbial growth in relation with confocal microscope observations. In addition, some hypotheses for the observed phase separation and preferential growth phase are presented.
MATERIALS AND METHODS
Microorganisms and preculture conditions.
Escherichia coli JM-109 DE3(pRSETb) Venus stock culture was kindly provided by the Department of Chemistry (KU Leuven, Leuven, Belgium). The inoculum was prepared by transferring a loopful of the stock culture into an Erlenmeyer containing 20 ml of brain heart infusion (BHI; Oxoid, Basingstoke, United Kingdom) enriched with 20 μl of ampicillin (Applichem, Darmstadt, Germany). After 9 h at 37°C under static conditions (Binder KB-series incubator; Binder, Inc., Great River, NY), a 20-μl aliquot of the stationary-phase culture was inoculated into 20 ml of fresh BHI containing 20 μl of ampicillin and incubated for 15 h under the same conditions.
Gelled media: preparation, characterization, and inoculation.
Gelled media were prepared by mixing BHI powder (37 g/liter) and, if appropriate, 2.9% (wt/vol) NaCl (AnalaR Normapur; VWR, Belgium), with different ratios of gelatin (gelatin from bovine skin, type B; Sigma) and dextran (dextran from Leuconostoc spp. [Mr ≈ 500,000]; Sigma, Denmark) in glass tubes with screw caps. The salt is added to ensure high enough ionic strength and hence phase separation in accordance with the method of Tromp et al. (38). Different ratios of gelatin and dextran were chosen in order to unravel the effect of their relative concentrations on system microstructure and microbial behavior (Table 2). After 15 ml of demineralized water was added, the samples were placed in a thermostatic water bath (GR 150 S12; Grant, United Kingdom) at 70°C for 12 min. In a next step, 30 μl of a 0.01% (wt/vol) rhodamine B solution (R953; Aldrich, Germany) was added, and the mixture was filter sterilized through a 0.2-μm-pore-size filter (Filtropur S 0.2; Sarstedt, Germany) with the aid of a syringe (10 ml of Norm-Ject; Henke Sass Wolf, Germany). Then, 15 μl of ampicillin was added to the samples, and the appropriate volume of a dilution of the preculture was inoculated to obtain an initial cell density of ∼104 CFU/ml. Undiluted samples are difficult to plate due to the consistency of the gelled media, so an inoculum level was chosen in such a way that the first decimal dilution of the first sample could be detected via plate counting.
TABLE 2.
Percentages of gelatin and dextran in mixtures used in the experiments
| Mixture | % (wt/vol) |
|
|---|---|---|
| Gelatin | Dextran | |
| 1G/1D | 2.5 | 2.5 |
| 2G/1D | 5.0 | 2.5 |
| 3G/1D | 7.5 | 2.5 |
| 4G/1D | 10.0 | 2.5 |
| 2G/2D | 5.0 | 5.0 |
| 3G/2D | 7.5 | 5.0 |
| 4G/2D | 10.0 | 5.0 |
| 1D | 0.0 | 2.5 |
| 2D | 0.0 | 5.0 |
| 4G | 10.0 | 0.0 |
| Liquid | 0.0 | 0.0 |
The water activity and pH of each mixture were determined with the aid of an aw-Kryometer (AWK-40; Nagy, Germany) set on the “liquid” modus and a pH meter (DocuMeter, Sartorius, Germany), respectively. Measurements were performed on media without bacterial cells.
Experimental setup for growth experiments.
Sterile glass screw-cap tubes (5 ml) were filled with 1 ml of inoculated medium, and then phase separation was induced by incubating the samples at room temperature for 20 min. After 6 min at 4°C to solidify the gels and then 4 min at room temperature to warm them up, the samples were placed in a temperature-controlled water bath at 23.5°C. A water bath was used in order to obtain fast heat transfer. Within 5 min, the temperature in the tubes reaches the temperature in the water bath. The temperature selected for growth experiments is a trade-off between the temperature at which the gelatin-dextran mixture is stable and the temperature that can be kept fixed in a water bath without cooling.
At regular time steps, one tube of each mixture was removed from the water bath at 23.5°C and placed in another water bath at 37°C in order to melt the structured medium. After the appropriate serial decimal dilutions were prepared in BHI, the samples were plated onto BHI supplemented with 1.4% (wt/vol) agar (agar technical No. 3; Oxoid, Basingstoke, United Kingdom). The plates were incubated for at least 18 h at 37°C before viable cell counting. At least four independent experiments were conducted for each mixture.
Estimation of growth parameters.
The growth model of Baranyi and Roberts (37) was fitted to the growth curves. Model parameters were estimated from the set of experimental data corresponding to each mixture via the minimization of the sum of squared errors (SSE), using the lsqnonlin routine with the Levenberg-Marquardt optimization algorithm of the Optimization Toolbox of Matlab version R2010b (The MathWorks, Inc., Natick, MA). Standard errors of parameter estimates were calculated from a Jacobian matrix. It should be noted that a global estimation procedure was standardized for each mixture to consider deviations in test reproducibility.
Statistical analysis.
An analysis of variance (ANOVA) test was performed to determine whether there are any significant differences among means of parameter estimates, at a 95.0% confidence level (α = 0.05). If the ANOVA indicated significant differences between the parameters for the different mixtures, a Fisher least-significant-difference (LSD) test was used to identify which means were significantly different. Standardized skewness and standardized kurtosis were used to assess whether the data sets came from normal distributions. These analyses were performed using the Statgraphics Centurion XVI.I Package (Statpoint Technologies, Warrenton, VA). Test statistics were regarded as significant when P was ≤0.05. Analyses were performed for experiments with or without added salt separately.
Microscopy: sample preparation and image analysis.
Preparation of the mixtures for the confocal microscope samples was performed in the same way as for the growth experiments. After inoculation, well chambers (chambered borosilicate cover glass system; Nunc Lab-Tek, USA) were filled with 300 μl of the mixture and incubated at room temperature. As described by Boons et al. (36), images were taken with a commercial laser scanning microscope (FV 100 [Olympus], ×60 magnification). An image analysis procedure was written using the algorithms embedded in the Matlab image processing toolbox (MathWorks). At least five images per mixture were analyzed. First, microscope RGB images were converted to grayscale images. Next, contrast was enhanced by applying adaptive histogram equalization. Finally, the contrast enhanced grayscale images were segmented with pixel thresholding. These segmented images allow quantification of the size and shape characteristics of the microstructures in the samples. In the present study, the percentage of dextran phase in the images is reported as a surface fraction in the analyzed images.
RESULTS
Intrinsic properties of G/D systems: pH and water activity.
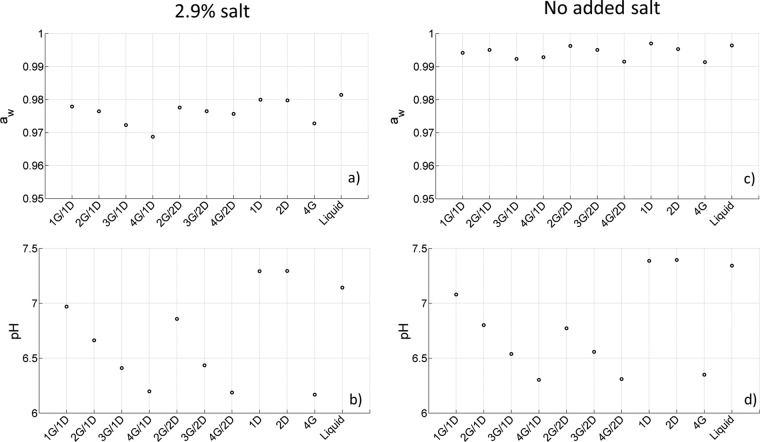
In Fig. 1, the water activity (aw) and pH of the different studied systems are plotted as a function of medium composition. These population measurements were performed in mixtures without the addition of bacteria. For the mixtures supplemented with salt, the water activity values ranged from 0.9687 (4G/1D) to 0.9799 (1D). Values for mixtures with no added salt varied between 0.9914 (4G) and 0.9970 (1D). The pH values fluctuated between 6.17 (4G) and 7.29 (1D) for the salted mixtures and from 6.30 (4G/1D) to 7.08 (1G/1D) for the nonsalted mixtures. The variation in pH and water activity was induced by changing the composition of the mixture, i.e., adding dextran, gelatin, and salt. The addition of salt or gelatin caused a decrease in water activity and pH, whereas the effect of dextran was limited.
FIG 1.
Water activity (a and c) and pH values (b and d) for the different binary and singular systems with (a and b) or without (c and d) salt.
Microscopic characterization of G/D systems.
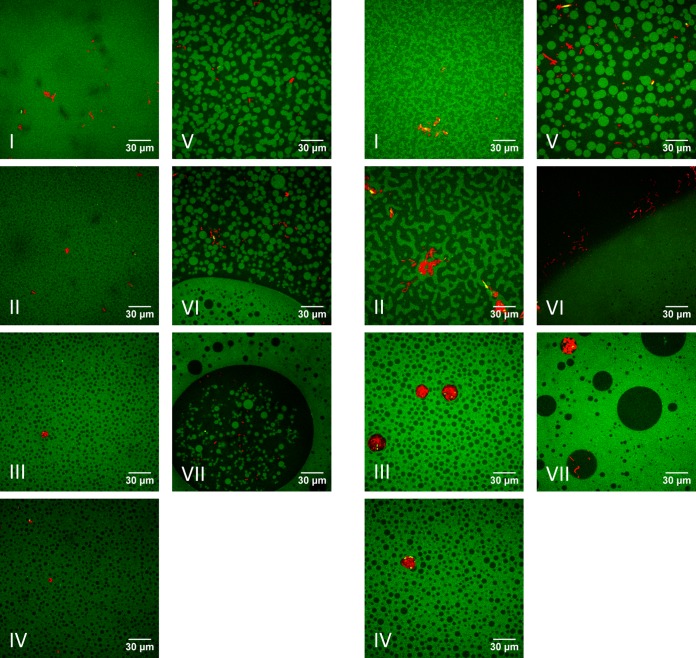
Confocal microscope images taken in salted and unsalted mixtures are shown in Fig. 2. For all systems, phase separation between gelatin and dextran was observed. For the same ratios of added gelling agents, the microstructures were similar for salted and unsalted mixtures. Only for the 1G/1D and 2G/1D systems was a bicontinuous phase observed for the unsalted mixtures, whereas the microstructure in the salted systems consisted of a disperse phase in a matrix phase. For both salted and unsalted mixtures, phase inversion was observed when the ratio of gelling agents was changed from 4G/1D to 2G/2D. As previously observed in the salted systems (36), in the unsalted systems E. coli growth also occurred in the dextran phase, regardless of the microstructure.
FIG 2.
Confocal microscopy images of growth of E. coli JM-109 DE3 (red) in gelatin (G, green)-dextran (D, black) mixtures with (left panels) or without (right panels) added salt: I, 1G/1D; II, 2G/1D; III, 3G/1D; IV, 4G/1D; V, 2G/2D; VI, 3G/2D; and VII, 4G/2D.
Population growth dynamics in G/D systems with added salt.
In Fig. 3a, E. coli growth curves obtained at the population level in singular and binary gelatin-dextran mixtures and liquid BHI with added salt are shown. Sigmoidal curves, including the typical microbial growth phases, were observed under all of the conditions.
FIG 3.
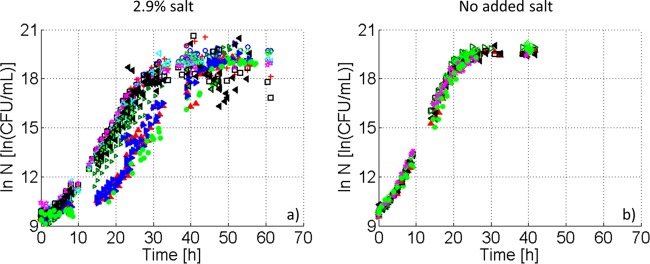
Population growth dynamics of E. coli JM-109 DE3 at 23.5°C in different mixtures of gelatin (G) and dextran (D) with (a) or without (b) salt: 1G/1D (>), 2G/1D (○), 3G/1D (+), 4G/1D (□), 2G/2D (◇), 3G/2D (<), 4G/2D (*), 1D (▲), 2D (▶), 4G (◀), and liquid (●).
Population growth kinetics: lag-phase duration and maximum growth rate.
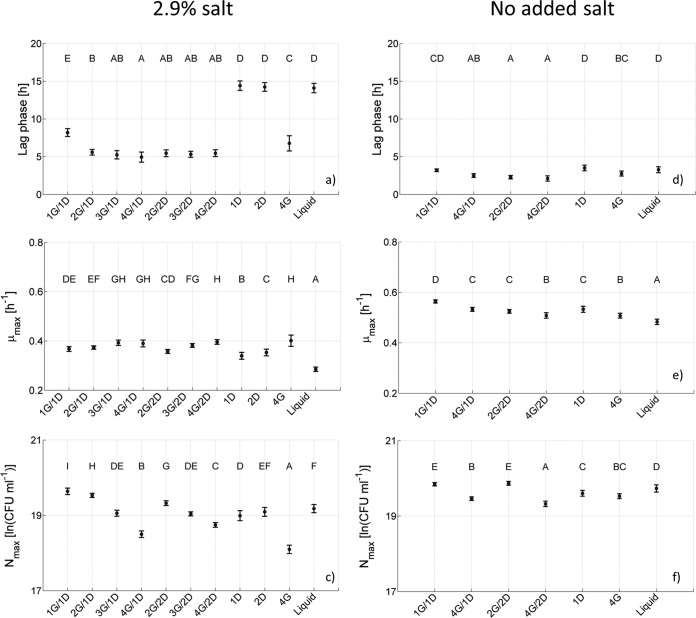
From Fig. 3a it is clear that the population lag and exponential growth phase in binary G/D systems were similar for all mixtures. However, the growth curves obtained in singular dextran systems and also in BHI broth showed a delay in population lag phase compared to binary systems. This is counterintuitive, i.e., the dextran phase has been shown to be the preferential site for E. coli in gelatin-dextran systems; hence, it was expected that population growth in binary systems would be comparable to that observed in singular dextran systems. The results of the parameter estimation confirmed the previously mentioned observations (Fig. 4a to c, including the results from ANOVA and LSD tests). For the salted G/D mixtures, population lag-phase durations did not vary significantly among binary mixtures, excluding the 1G/1D system, which had a longer population lag phase (Fig. 4a). However, a significantly higher value was observed for the population lag-phase duration in the liquid system and the singular dextran systems, with a negligible difference between both dextran systems. The population lag phase duration in the singular gelatin system was within the range of the values observed in the binary systems but significantly lower than the values obtained for the singular dextran systems. Looking to the different parameter values for the population maximum specific growth rate, an increasing trend was observed with increasing gelatin concentration.
FIG 4.
Population growth parameters and error bars for the growth of E. coli JM-109 DE3 at 23.5°C in G/D binary and singular systems and BHI broth with (a, b, and c) or without (d, e, and f) added salt, including the duration of the population lag phase (a and d), the population maximum specific growth rate (b and e), and the population maximum cell density (c and f).
Population maximum growth capacity.
Figure 4c indicates that increasing the gelatin concentration for a fixed dextran concentration resulted in a slight decrease in the population maximum cell density. A similar but less pronounced observation held for an increase in dextran concentration, keeping the gelatin concentration constant. The population maximum cell density in the singular gelatin system was lower than the other reported concentrations, whereas values for the BHI broth and singular dextran systems were within the range of those obtained for the binary mixtures. Again, the difference between both singular dextran systems was negligible.
Population growth dynamics in G/D systems with no added salt.
As for the salted systems, for all systems with no added salt, sigmoidal growth curves were observed (Fig. 3b). In contrast to what was observed for the salted systems, Fig. 3b illustrates that E. coli growth curves in systems with no added salt coincide for binary and singular systems, as well as for liquid BHI.
Population growth kinetics: lag-phase duration and maximum growth rate.
As expected, a reduction of the salt content to 0.5%, i.e., the percentage of salt present in BHI, led to a decrease in population lag time and an increase in population maximum growth rate and maximum cell density. Parameter estimation (Fig. 4d and f, including results from ANOVA and LSD tests) indicated that the variations in population lag time and population maximum growth rate obtained for results in unsalted mixtures were rather limited.
Population maximum growth capacity.
An increase in population maximum cell density was observed when the parameter estimates for systems without and with added salt were compared. For the population maximum cell density in mixtures with no added salt, a similar trend as for the salted media was observed when the gelatin concentration was increased for a fixed dextran concentration, i.e., the population maximum cell density decreases. However, this trend was more pronounced for the salted mixtures.
DISCUSSION
Microscopic characterization of G/D systems.
In a previous study (36), phase separation in G/D systems, supplemented with BHI and 2.9% salt, was observed. Changing the relative and absolute amounts of the gelling agents led to a change in microstructure characteristics. More specifically, when increasing the amount of gelatin for the 1D systems, the diameter of the dextran spheres increased (Fig. 2, left panels). When bacteria were added, it was found that the dextran phase was the preferential site for E. coli growth, regardless of the microstructure. However, the underlying mechanisms for these observations were not unraveled, and further analysis is encouraged. In the present study, the observed phase separation, as well as the preferential phase behavior, are discussed in detail and supported with relevant literature.
Phase-separating G/D systems.
First of all, the mechanisms behind phase separation in protein-polysaccharide mixtures, such as G/D systems, should be discussed. It is well known that, under specific conditions, mixtures of proteins and polysaccharides show thermodynamic incompatibility, forming aqueous two-phase systems (ATPS). This incompatibility between proteins and neutral polysaccharides can be reached at high ionic strengths or at pH values different from the isoelectric point of the protein (pI). Also, the difference in hydrophilicity between proteins and polysaccharides, the so-called “Δχ effect,” is of great importance for phase equilibrium in protein-polysaccharide-water systems (34). For the gelatin-dextran mixture, Grinberg and Tolstoguzov (34) reported that incompatible conditions for the protein-polysaccharide mixture are fulfilled when (i) the ionic strength is lower than 0.15 and the pH is equal to the pI or (ii) the ionic strength is higher than 0.15, and there is an inequality between pH and pI. With high ionic strength (>0.5 M) and pH values for all salted mixtures (Fig. 1b) that exceed the pI of gelatin (4.7 to 5.2) (39), phase separation is expected to happen in the salted mixtures, as already described in literature (35, 38). Here, it was observed that when no extra salt was added, phase separation still occurs. Since the pH of these mixtures exceeds the pI of gelatin and the added BHI causes an ionic strength of 0.38 M, the conditions for phase separation are fulfilled. In the nonsalted systems, phase separation is observed for all systems, including the 1G/1D systems, although for this system phase separation was not evident when salt was added.
Distribution of E. coli cells in phase-separating G/D systems.
The distribution of bacterial cells in different ATPS is already described in literature. However, to the best of our knowledge, no studies focus on the growth behavior of microorganisms in ATPS with different compositions and, hence, different microstructures. Also, most studies are performed in systems not resembling food products. Clostridium tetani, Lactobacillus rhamnosus, and E. coli W3110, ML308, and MG1655 were shown to have a preference for the dextran phase in polyethylene glycol-dextran systems (40–43). Also, in polyvinylpyrrolidone-dextran systems, Lactobacillus rhamnosus and Enterococcus faecium M74 were found preferentially in the dextran phase (42, 44). In alginate-sodium caseinate mixtures, bacteria were not located in the polysaccharide phase, as observed in the present study, but Lactococcus lactis LAB3 preferred the protein phase (45).
In the present study, E. coli cells were located in the dextran phase of the G/D system. Some hypotheses for this behavior are discussed below. In the G/D mixtures studied here, the pI of gelatin is exceeded, which causes the protein to become negatively charged. Harden and Harris (46) reported that E. coli cells have a negative cell surface charge in a suspending solution of 0.01 M K2HPO4 and 0.01 M KH2PO4 (pH 7.0). Schwarz-Linek et al. (47) performed electrophoretic mobility measurements and confirmed that E. coli carried a net negative charge in modified phosphate buffer. Also, Dickson and Koohmaraie (48) measured a negative charge on the E. coli cell surface when suspended in a phosphate buffer and its effect on bacterial attachment to meat surfaces. Because of this negative charge, electrostatic repulsion is likely to be one of the reasons why the cells do not appear in the proximity of the negatively charged gelatin molecules but prefer the neutral dextran phase. However, it must be mentioned that E. coli can be found in the gelatin phase in singular gelatin systems.
In the literature, the surfaces of E. coli cells have been reported to be relatively hydrophilic compared to proteins, probably because of the hydrophilic head groups of the phospholipids, which are the main components of the cell membrane (49, 50). Since dextran is known to be a hydrophilic molecule (51), it is likely that the hydrophilicity of both dextran molecules and E. coli cells makes this phase the preferred site for E. coli growth. On the other hand, gelatin is a molecule containing both hydrophilic and hydrophobic groups (52).
In conclusion, the combination of both electronegativity and hydrophilicity favors the distribution of E. coli in the dextran phase over the gelatin phase. Thus, both mechanisms contribute to the observed preferential phase behavior.
Population growth dynamics in G/D systems with added salt.
The estimated growth parameters in salted binary and singular mixtures were compared as a function of the mixture composition in order to unravel the effect of system microstructure on population bacterial dynamics. In the present study the relation between observed microstructure and population growth parameters is discussed.
Population growth kinetics: lag-phase duration.
When we compared the population lag-phase duration of the different mixtures, we observed significantly different values for the 1G/1D binary mixture, the singular dextran systems, and the liquid system. The absence or smaller amount of gelatin in these systems is a coherent explanation for this increase in the population lag phase. Boons et al. (8) studied the growth behavior of E. coli and Salmonella enterica serovar Typhimurium in gelatin, xanthan gum, and gelatin-xanthan gum systems and in BHI broth at 23.5°C at salt concentrations ranging from 0.0 to 5.0% (wt/vol). These researchers found that the addition of gelatin to BHI broth caused a decrease in population lag phase at salt concentrations of 3.0, 4.0, and 5.0% (wt/vol). In this sense, sodium chloride has reported to be bound to gelatin (52–54), which can cause a lower apparent salt concentration. Since the population lag-phase duration is influenced by cell prehistory and environmental growth conditions, a lower apparent salt concentration in the growth medium, due to a higher gelatin concentration, may lead to shorter population lag phases, given a non-salt-enriched preculture medium. Because 2.9% (wt/vol) NaCl is added to all systems, differences in population lag-phase duration can be expected, depending on the gelatin concentration. In the singular dextran systems and BHI broth, no gelatin is present in the media, which can explain the longer population lag phase. For the 1G/1D system, the gelatin concentration may not be high enough to cause the full effect on salt concentration observed in the other binary mixtures, although it significantly affects population lag times compared to singular dextran systems and BHI broth. This hypothesis is also supported by the experimental results in systems with no added salt, where population lag times are comparable, independently of mixture composition.
Population growth kinetics: maximum growth rate.
Statistical analysis of population maximum specific growth rate estimates for binary mixtures (Fig. 4b) yielded significantly different values. Increasing the gelatin concentration for a fixed dextran concentration, from 2.5% (for the 1D systems) or 5% (for the 2D systems) to 10% (wt/vol) led to an increase in the maximum specific growth rate. However, the largest difference between two values was only 0.039 h−1, taking into account the minimum (0.3574 ± 0.0077 h−1 for the 2G/2D system) and maximum value (0.3962 ± 0.0093 h−1 for the 4G/2D system). Theys et al. (12) reported that the effect of the gelatin concentration on the population maximum growth rate was negligible, since significant differences were not found between the growth curves of S. Typhimurium bacteria in 1.0% (wt/vol) gelatin and 5.0% (wt/vol) gelatin, which were obtained under conditions similar to those used in the present study. Antwi et al. (15) observed that for Listeria innocua within the range of between 5.0 and 20.0% (wt/vol) gelatin, the population maximum growth rate remained approximately constant and was not affected by the increase in gelatin concentration. The small difference between minimum and maximum value, combined with the information obtained from literature, does not lead to a definitive conclusion. The population maximum growth rate of the singular gelatin system is in line with the values observed for the binary systems. However, population maximum growth rates in the singular dextran systems and especially in BHI broth turn out to be slightly lower. Possibly, the absence of gelatin and, hence, the possibly higher apparent salt concentration, causes a decrease in the population maximum growth rate. However, in the study of Boons et al. (8), discussed above, no effect of the addition of gelatin to BHI broth on the population maximum growth rate was observed.
Population maximum growth capacity.
The trend in maximum cell density can be related to two factors.
First, for the binary mixtures, increasing the gelatin concentration for a fixed dextran concentration leads to a decrease in the maximum cell density. In addition, the lowest population maximum cell density is observed for growth experiments in singular gelatin systems. This is an indication that the concentration of gelatin influences to some extent the population maximum cell density. It is hypothesized that this effect may be 2-fold: (i) by adding more gelatin, the pH and water activity are lowered, leading to less-optimal growth conditions that may affect the population maximum cell density, and (ii) the rigidity of the systems increases when more gelatin is added. Theys et al. (12) performed rheological oscillatory measurements and concluded that gels became more firm and rigid when increasing the gelatin concentration from 1.0 to 5.0% (wt/vol). In this more rigid structure, the diffusion of nutrients toward and diffusion of metabolites away from the colony would be slowed down, which limits colony growth.
Second, changing the gelatin (and dextran) concentration also causes a change in the microstructure. In addition to the change in composition, the resulting change in microstructure can also have an effect on the population maximum cell density. Since the dextran phase is the preferential phase for bacterial growth, it is expected that the more dextran phase is present, i.e., the more space is available for bacterial growth, the higher the population maximum cell density will be. The results of image analysis suggest that there is indeed a relation between the fraction of dextran phase in the mixture and the population maximum cell density, i.e., the maximum cell density increases with increasing available dextran phase. However, this trend is only observed for mixtures exhibiting a microstructure with a dextran phase dispersed in a gelatin matrix, i.e., the 1D binary systems show a decrease in population maximum cell density with decreasing percentages of dextran phase: 2G/1D (24.9% ± 2.5% dextran phase), 3G/1D (21.2% ± 0.5% dextran phase), and 4G/1D (19.5% ± 1.0% dextran phase). Compared to mixtures with a different type of microstructure, i.e., gelatin phase dispersed in a dextran matrix or a combination of both, the relation between the population maximum cell density and the percentage of dextran phase no longer holds. For example, the dextran fraction in the 2G/2D mixture is higher (60.8% ± 4.5%) than the dextran fraction in the 2G/1D mixture, but the population maximum cell density is lower. Also, the population maximum cell density in the singular dextran systems, fully consisting of dextran phase, is not higher than the values observed for the binary systems, which contain a lower fraction of the dextran phase. It should be noted that going from the 1G/1D to the 4G/1D mixture, the observed dextran spheres get bigger (Fig. 2), but the population maximum cell density does not increase as expected. It seems that for the 1D binary systems the overall percentage of dextran phase instead of the local size of a dextran sphere is the factor related to the maximum cell density. However, it should be taken into account that (i) the microstructure of G/D systems depends on the concentration of the gelling agent. To uncouple these factors, future research must focus on the creation of different microstructures, obtained with the same concentration of gelling agents, e.g., by shearing the system (55). (ii) Care must be taken when relating the population and the microscopic level. The maximum cell density is a population parameter. It is an average, global value for the population present in the system, whereas (confocal) microscope images focus on one cell/colony (see, for example, reference 56). By using the average value, information at the colony level might get lost, whereas confocal microscope images fail to provide an overview of the whole population.
Population growth behavior in G/D systems with no added salt. (i) Population growth kinetics: lag-phase duration and maximum growth rate.
As widely accepted in the literature (8, 10, 12, 57), it was also observed in the present study that leaving out the extra amount of salt has a positive effect on bacterial dynamics in G/D systems. The parameter values for the population lag time in systems with no added salt are lower, and values for population maximum growth rates are higher than those obtained in the corresponding systems with extra salt. In addition, values for the population lag time are similar for all systems, whereas in the salted systems some differences in population lag times were observed. Differences among the population maximum growth rates in the different mixtures without added salt are considered too small for conclusions to be drawn, as also stated above for salted systems.
(ii) Population growth capacity.
Decreasing the salt concentration leads to an increase in population maximum cell densities. For these higher values, the trend of the population maximum cell density as a function of the mixture composition is also similar to that observed in the salted systems, although less pronounced.
Comparison of the population growth capacity to observed microscopic images shows that in the 1D binary systems a change in microstructure type is observed when the gelatin concentration is increased, i.e., from bicontinuous to a dextran phase dispersed in gelatin matrix, leaving no more than two mixtures with the same type of microstructure. Also for the 2D binary systems, different microstructures were observed. As such, no conclusions on the effect of microstructure on the population maximum cell density can be drawn for the systems without added salt.
Conclusion.
Based on the growth experiments performed here, we can state that to estimate the effect of a biphasic microstructure on E. coli growth at a macro scale it is not sufficient to perform experiments in the preferential phase, especially when a stress factor is present, i.e., salt. This is in contrast to what is sometimes reported in literature (see, for example, reference 58). In the presence of salt, adding a second gelling agent influences the population lag time duration and, to a limited extent, the maximum growth rate. However, for media without added salt, the growth parameters of singular and binary gelatin-dextran mixtures are comparable.
The presence of a second gelling agent, introducing a heterogeneous microstructure, also has an effect on the population maximum cell density. There is a relation between the percentage of dextran phase in the mixture and the maximum cell density for the salted 1D binary systems, i.e., the mixtures with a microstructure exhibiting a dispersed dextran phase in a gelatin matrix. However, this relation between the percentage of the dextran phase and the population maximum cell density does not hold for other types of microstructures. Additional research is needed to investigate whether there is a relationship between the different types of microstructure, i.e., whether there is a general parameter (e.g., rigidity of the microscopic growth environment, particle size distribution, etc.) that can characterize the different types of microstructures in relation to population growth parameters.
The present study emphasizes that the addition of a combination of gelling agents to food products, leading to a phase-separated system, cannot be neglected when making predictions on population bacterial growth and certainly not when additional stress factors are present.
ACKNOWLEDGMENTS
This study was supported by project PFV/10/002 (Center of Excellence OPTEC—Optimization in Engineering) of the KU Leuven Research Council, Knowledge Platform KP/09/005 (www.scores4chem.be) of the KU Leuven Industrial Research Fund, project G093013N of the Fund for Scientific Research–Flanders, and the Belgian Program on Interuniversity Poles of Attraction, initiated by the Belgian Federal Science Policy Office. J.F.V.I. holds the Safety Engineering chair sponsored by the Belgian Chemistry and Life Sciences Federation essenscia. J.H. gratefully acknowledges financial support in the form of long-term structural funding “Methusalem” from the Flemish Government and from the Hercules Foundation (HER/08/021). K.B. is supported by a research grant of the Institute for the Promotion of Innovation by Science and Technology in Flanders (IWT). C.C.D. is supported by the Fund for Scientific Research (FWO).
Footnotes
Published ahead of print 20 June 2014
For this virtual institution, see http://cpmf2.be/.
REFERENCES
- 1.CDC. 2011. CDC estimates of foodborne illness in the United States. Centers for Disease Control and Prevention, Atlanta, GA: http://www.cdc.gov/foodborneburden [Google Scholar]
- 2.EFSA. 2014. Scientific report of EFSA and ECDC: the European Union Summary Report on Trends and Sources of Zoonoses, Zoonotic Agents, and Food-borne Outbreaks in 2012. EFSA J. 12:3547. 10.2903/j.efsa.2014.3547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.McMeekin TA, Olley J, Ratkowsky DA, Ross T. 2002. Predictive microbiology: toward the interface and beyond. Int. J. Food Microbiol. 73:395–407. 10.1016/S0168-1605(01)00663-8 [DOI] [PubMed] [Google Scholar]
- 4.Wilson PDG, Brocklehurst TF, Arino S, Thuault D, Jakobsen M, Lange M, Farkas J, Wimpenny JWT, Van Impe JF. 2002. Modeling microbial growth in structured foods: toward a unified approach. Int. J. Food Microbiol. 73:275–289. 10.1016/S0168-1605(01)00660-2 [DOI] [PubMed] [Google Scholar]
- 5.Mitchell AJ, Wimpenny JWT. 1997. The effect of agar concentration on the growth and morphology of submerged colonies of motile and non-motile bacteria. J. Appl. Bacteriol. 83:76–84. 10.1046/j.1365-2672.1997.00192.x [DOI] [PubMed] [Google Scholar]
- 6.Skandamis PN, Brocklehurst TF, Panagou EZ, Nychas G-JE. 2007. Image analysis as a mean to model growth of Escherichia coli O157:H7 in gel cassettes. J. Appl. Microbiol. 103:937–947. 10.1111/j.1365-2672.2007.03358.x [DOI] [PubMed] [Google Scholar]
- 7.Noriega E, Laca A, Díaz M. 2010. Decisive role of structure in food microbial colonization and implications for predictive microbiology. J. Food Prot. 73:938–951 [DOI] [PubMed] [Google Scholar]
- 8.Boons K, Van Derlinden E, Mertens L, Peeters V, Van Impe JF. 2013. Effect of immobilization and salt concentration on the growth dynamics of Escherichia coli K-12 and Salmonella Typhimurium. J. Food Sci. 78:M567–M574. 10.1111/1750-3841.12067 [DOI] [PubMed] [Google Scholar]
- 9.Hills BP, Buff C, Wright KM, Sutcliffe LH, Ridge Y. 2001. Microstructural effects on microbial survival: phase-separating dextran solutions. Int. J. Food Microbiol. 68:187–197. 10.1016/S0168-1605(01)00490-1 [DOI] [PubMed] [Google Scholar]
- 10.Brocklehurst TF, Mitchell GA, Smith AC. 1997. A model experimental gel surface for the growth of bacteria on foods. Food Microbiol. 14:303–311. 10.1006/fmic.1997.0098 [DOI] [Google Scholar]
- 11.Wright KM, Coleman HP, Mackie AR, Parker ML, Brocklehurst TF, Wilson DR, Hills BP. 2000. Determination of mean growth parameters of bacterial colonies immobilized in gelatin gel using a laser gel-cassette scanner. Int. J. Food Microbiol. 57:75–89. 10.1016/S0168-1605(00)00229-4 [DOI] [Google Scholar]
- 12.Theys TE, Geeraerd AH, Verhulst A, Poot K, Van Bree I, Devlieghere F, Moldenaers P, Wilson D, Brocklehurst TF, Van Impe JF. 2008. Effect of pH, water activity and gel micro-structure, including oxygen profiles and rheological characterization, on the growth kinetics of Salmonella Typhimurium. Int. J. Food Microbiol. 128:67–77. 10.1016/j.ijfoodmicro.2008.06.031 [DOI] [PubMed] [Google Scholar]
- 13.Meldrum RJ, Brocklehurst TF, Wilson DR, Wilson PDG. 2003. The effects of cell immobilization, pH and sucrose on the growth of Listeria monocytogenes Scott A at 10°C. Food Microbiol. 20:97–103. 10.1016/S0740-0020(02)00083-7 [DOI] [Google Scholar]
- 14.Lebert I, Dussap CG, Lebert A. 2004. Effect of aw, controlled by the addition of solutes or by water content, on the growth of Listeria innocua in broth and in a gelatin model. Int. J. Food Microbiol. 94:67–78. 10.1016/j.ijfoodmicro.2004.01.002 [DOI] [PubMed] [Google Scholar]
- 15.Antwi M, Geeraerd AH, Vereecken KM, Jenné R, Bernaerts K, Van Impe JF. 2006. Influence of a gel microstructure as modified by gelatin concentration on Listeria innocua growth. Innov. Food Sci. Emerg. 7:124–131. 10.1016/j.ifset.2005.08.001 [DOI] [Google Scholar]
- 16.Knudsen GM, Nielsen M-B, Grassby T, Danino-Appleton V, Thomsen LE, Colquhoun IJ, Brocklehurst TF, Olsen JE, Hinton JCD. 2012. A third mode of surface-associated growth: immobilization of Salmonella enterica serovar Typhimurium modulates the RpoS-directed transcriptional programme. Environ. Microbiol. 14:1855–1875. 10.1111/j.1462-2920.2012.02703.x [DOI] [PubMed] [Google Scholar]
- 17.Karina P, Julio C, Leda G, Noemi Z. 2011. Behavior of Listeria monocytogenes type1 355/98 (85) in meat emulsions as affected by temperature, pH, water activity, fat, and microbial preservatives. Food Control 22:1573–1581. 10.1016/j.foodcont.2011.03.013 [DOI] [Google Scholar]
- 18.Pivnick H, Engelhard WE, Thompson TL. 1954. The growth of pathogenic bacteria in soluble oil emulsions. Appl. Microbiol. 2:140–142 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jarvis WR, Highsmith AK. 1984. Bacterial growth and endotoxin production in lipid emulsion. J. Clin. Microbiol. 19:17–20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gilbert G, Gallagher SC, Eads M, Elmore ME. 1986. Microbial growth patterns in a total parenteral nutrition formulation containing lipid emulsion. J. Pen.-Parenter. Enter. 10:494–497. 10.1177/0148607186010005494 [DOI] [PubMed] [Google Scholar]
- 21.Brocklehurst TF, Parker ML, Gunning PA, Coleman HP, Robins MM. 1995. Growth of food-borne pathogenic bacteria in oil-in-water emulsions. II. Effect of emulsion structure on growth parameters and form of growth. J. Appl. Bacteriol. 78:609–615. 10.1111/j.1365-2672.1995.tb03106.x [DOI] [PubMed] [Google Scholar]
- 22.Hills BP, Manning CE, Ridge Y, Brocklehurst T. 1997. Water availability and the survival of Salmonella typhimurium in porous systems. Int. J. Food Microbiol. 36:187–198. 10.1016/S0168-1605(97)01265-8 [DOI] [PubMed] [Google Scholar]
- 23.Hills BP, Arnould L., Bossu C, Ridge Y. 2001. Microstructural factors controlling the survival of food-borne pathogens in porous media. Int. J. Food Microbiol. 66:163–173. 10.1016/S0168-1605(00)00520-1 [DOI] [PubMed] [Google Scholar]
- 24.Verrips CT, Smid D, Kerkhof A. 1980. The intrinsic microbial stability of water-in-oil emulsions. II. Experimental. Eur. J. Appl. Microbiol. Biotechnol. 10:73–85. 10.1007/BF00504729 [DOI] [Google Scholar]
- 25.McKellar RC, Moir R, Kalab M. 1994. Factors influencing the survival and growth of Listeria monocytogenes on the surface of Canadian retail wieners. J. Food Prot. 57:387–392 [DOI] [PubMed] [Google Scholar]
- 26.Francois K, Devlieghere F, Uyttendaele M, Standaert AR, Geeraerd AH, Nadal P, Van Impe JF, Debevere J. 2006. Single cell variability of Listeria monocytogenes grown on liver pâté and cooked ham at 7°C: comparing challenge test data to predictive simulations. J. Appl. Microbiol. 100:800–812. 10.1111/j.1365-2672.2006.02833.x [DOI] [PubMed] [Google Scholar]
- 27.Cayré EM, Vignolo G, Garro O. 2003. Modeling lactic acid bacteria growth in vacuum-packaged cooked meat emulsions stored at three temperatures. Food Microbiol. 20:561–566. 10.1016/S0740-0020(02)00154-5 [DOI] [Google Scholar]
- 28.Wimpenny JWT, Leistner L, Thomas LV, Mitchell AJ, Katsaras K, Peetz P. 1995. Submerged bacterial colonies within food and model systems: their growth, distribution, and interactions. Int. J. Food Microbiol. 28:299–315. 10.1016/0168-1605(95)00065-8 [DOI] [PubMed] [Google Scholar]
- 29.Farber JM, McKellar RC, Ross WH. 1995. Modelling the effects of various parameters on the growth of Listeria monocytogenes on liver pâté. Food Microbiol. 12:447–453. 10.1016/S0740-0020(95)80129-4 [DOI] [Google Scholar]
- 30.Hwang C-A, Tamplin ML. 2005. The influence of mayonnaise pH and storage temperature on the growth of Listeria monocytogenes in seafood salad. Int. J. Food Microbiol. 102:277–285. 10.1016/j.ijfoodmicro.2004.11.019 [DOI] [PubMed] [Google Scholar]
- 31.Raghubeer EV, Ke JS, Campbell ML, Meyer RS. 1995. Fate of Escherichia coli O157:H7 and other coliforms in commercial mayonnaise and refrigerated salad dressing. J. Food Prot. 58:13–18 [DOI] [PubMed] [Google Scholar]
- 32.Parker ML, Gunning PA, Macedo AC, Malcata FX, Brocklehurst TF. 1998. The microstructure and distribution of micro-organisms within mature Serra cheese. J. Appl. Microbiol. 84:523–530. 10.1046/j.1365-2672.1998.00375.x [DOI] [PubMed] [Google Scholar]
- 33.Norton IT, Frith WJ. 2001. Microstructure design in mixed biopolymer composites. Food Hydrocolloid. 15:543–553. 10.1016/S0268-005X(01)00062-5 [DOI] [Google Scholar]
- 34.Grinberg VY, Tolstoguzov VB. 1997. Thermodynamic incompatibility of proteins and polysaccharides in solutions. Food Hydrocolloid. 11:145–158. 10.1016/S0268-005X(97)80022-7 [DOI] [Google Scholar]
- 35.Butler MF, Heppenstall-Butler M. 2003. Phase separation in gelatin/dextran and gelatin/maltodextrin mixtures. Food Hydrocolloid. 17:815–830. 10.1016/S0268-005X(03)00103-6 [DOI] [Google Scholar]
- 36.Boons K, Mertens L, Van Derlinden E, David CC, Hofkens J, Van Impe JF. 2013. Behavior of Escherichia coli in a heterogeneous gelatin-dextran mixture. Appl. Environ. Microbiol. 79:3126–3128. 10.1128/AEM.03782-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Baranyi J, Roberts T. 1994. A dynamic approach to predicting bacterial growth in food. Int. J. Food Microbiol. 23:277–294. 10.1016/0168-1605(94)90157-0 [DOI] [PubMed] [Google Scholar]
- 38.Tromp RH, van de Velde F, van Riel J, Paques M. 2001. Confocal scanning light microscopy (CSLM) on mixtures of gelatin and polysaccharides. Food Res. Int. 34:931–938. 10.1016/S0963-9969(01)00117-X [DOI] [Google Scholar]
- 39.Sigma-Aldrich. 2013. Product information sheet, gelatin. Sigma-Aldrich, St. Louis, MO: http://www.sigmaaldrich.com/content/dam/sigma-aldrich/docs/Sigma/Product_Information_Sheet/2/g9382pis.pdf [Google Scholar]
- 40.Mattiasson B. 1983. Applications of aqueous two-phase systems in biotechnology. Trends Biotechnol. 1:16–20. 10.1016/0167-7799(83)90021-5 [DOI] [Google Scholar]
- 41.Leja K, Dembczyński R, Białas W, Jankowski T. 2009. Production of dry Lactobacillus rhamnosus GG preparations by spray drying and lyophilization in aqueous two-phase systems. Technol. Aliment. 8:39–49 [Google Scholar]
- 42.Umakoshi H, Kuboi R, Komasawa I. 1997. Control of partitioning of bacterial cells and characterization of their surface properties in aqueous two-phase systems. J. Ferment. Bioeng. 84:572–578. 10.1016/S0922-338X(97)81914-9 [DOI] [Google Scholar]
- 43.Yagushi T, Dwidar M, Byun CK, Leung B, Lee S, Cho Y-K, Mitchell RJ, Takayama S. 2012. Aqueous two-phase system: derived biofilms for bacterial interaction studies. Biomacromolecules 13:2655–2661. 10.1021/bm300500y [DOI] [PubMed] [Google Scholar]
- 44.Millqvist-Fureby A, Malmsten M, Bergenståhl B. 2000. An aqueous polymer two-phase system as carrier in the spray-drying of biological material. J. Colloid Interf. Sci. 225:54–61. 10.1006/jcis.2000.6740 [DOI] [PubMed] [Google Scholar]
- 45.Léonard L, Gharsallaoui A, Ouaali F, Degraeve P, Waché Y, Saurel R, Oulahal N. 2013. Preferential localization of Lactococcus lactic cells entrapped in a caseinate/alginate phase separated system. Colloid Surface B 109:266–272. 10.1016/j.colsurfb.2013.03.005 [DOI] [PubMed] [Google Scholar]
- 46.Harden VP, Harris JO. 1953. The isoelectric point of bacterial cells. J. Bacteriol. 65:198–202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schwarz –Linek J, Dorken G, Winkler A, Wilson LG, Pham NT, French CE, Schilling T, Poon WCK. 2010. Polymer-induced phase separation in suspensions of bacteria. EPL 89:68003p1–68003p6. 10.1209/0295-5075/89/68003 [DOI] [Google Scholar]
- 48.Dickson JS, Koohmaraie M. 1989. Cell surface charge characteristics and their relationship to bacterial attachment to meat surfaces. Appl. Environ. Microbiol. 55:832–836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kito M, Aibara S, Kato M, Ishinaga M, Hata T. 1973. Effects of changes in fatty acid composition of phospholipid species on the β-galactoside transport system of Escherichia coli K-12. Biochim. Biophys. Acta 298:69–74. 10.1016/0005-2736(73)90010-2 [DOI] [PubMed] [Google Scholar]
- 50.Zhang X-S, García-Contreras R, Wood TK. 2007. YcfR(BhsA) influences Escherichia coli biofilm formation through stress response and surface hydrophobicity. J. Bacteriol. 189:3051–3062. 10.1128/JB.01832-06 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sun G, Shen Y-I, Ho CC, Kusuma S, Gerecht S. 2009. Functional groups affect physical and biological properties of dextran-based hydrogels. J. Biomed.Mater. Res. A 93A:1080–1090 [DOI] [PubMed] [Google Scholar]
- 52.Schrieber R, Gareis H. 2007. Gelatin handbook: theory and industrial practice, p 59 Wiley-VCH Verlag GmbH & Co, Weinheim, Germany [Google Scholar]
- 53.Gal S. 1974. Solvent versus non-solvent water in casein-sodium chloride water systems, p 183–191 In Duckworth R. (ed), Water relations of foods. Academic Press, London, England [Google Scholar]
- 54.Theys TE, Geeraerd AH, Devlieghere F, Van Impe JF. 2010. On the selection of relevant environmental factors to predict microbial dynamics in solidified media. Food Microbiol. 27:220–228. 10.1016/j.fm.2009.10.005 [DOI] [PubMed] [Google Scholar]
- 55.McClements DJ. 2006. Non-covalent interactions between proteins and polysaccharides. Biotechnol. Adv. 24:621–625. 10.1016/j.biotechadv.2006.07.003 [DOI] [PubMed] [Google Scholar]
- 56.Koutsoumanis KP, Lianou A. 2013. Stochasticity in colonial growth dynamics of individual bacterial cells. Appl. Environ. Microbiol. 79:2294–2301. 10.1128/AEM.03629-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Samapundo S, Ampofo-Asiama J, Anthierens T, Xhaferi R, Van Bree I, Szczepaniak S, Goemaere O, Steen L, Dhooge M, Paelinck H, Dewettinck K, Devlieghere F. 2010. Influence of NaCl reduction and replacement on the growth of Lactobacillus sakei in broth, cooked ham, and white sauce. Int. J. Food Microbiol. 143:9–16. 10.1016/j.ijfoodmicro.2010.07.014 [DOI] [PubMed] [Google Scholar]
- 58.Robins MM, Wilson PDG. 1994. Food structure and microbial growth. Trends Food Sci. Technol. 5:289–229. 10.1016/0924-2244(94)90137-6 [DOI] [Google Scholar]