Site-specific range uncertainties caused by dose calculation algorithms for proton therapy

Abstract

The purpose of this study was to investigate the impact of complex patient geometries on the capability of analytical dose calculation algorithms to accurately predict the range of proton fields. Dose distributions predicted by an analytical pencil-beam algorithm were compared with those obtained using Monte Carlo simulations (TOPAS). A total of 508 passively scattered treatment fields were analyzed for 7 disease sites (liver, prostate, breast, medulloblastoma-spine, medulloblastoma-whole brain, lung and head & neck). Voxel-by-voxel comparisons were performed on two-dimensional distal dose surfaces calculated by pencil-beam and Monte Carlo algorithms to obtain the average range differences (ARD) and root mean square deviation (RMSD) for each field for the distal position of the 90% dose level (R90) and the 50% dose level (R50). The average dose degradation (ADD) of the distal falloff region, defined as the distance between the distal position of the 80% and 20% dose levels (R80-R20), was also analyzed. All ranges were calculated in water-equivalent distances.

Considering total range uncertainties and uncertainties from dose calculation alone, we were able to deduce site-specific estimations. For liver, prostate and whole brain fields our results demonstrate that a reduction of currently used uncertainty margins is feasible even without introducing Monte Carlo dose calculations. We recommend range margins of 2.8% + 1.2 mm for liver and prostate treatments and 3.1% + 1.2 mm for whole brain treatments, respectively. On the other hand, current margins seem to be insufficient for some breast, lung and head & neck patients, at least if used generically. If no case specific adjustments are applied, a generic margin of 6.3% + 1.2 mm would be needed for breast, lung and head & neck treatments. We conclude that currently used generic range uncertainty margins in proton therapy should be redefined site specific and that complex geometries may require a field specific adjustment. Routine verifications of treatment plans using Monte Carlo simulations are recommended for patients with heterogeneous geometries.

Introduction

The main dosimetric advantages of proton therapy as compared to photon techniques are the reduced total energy deposited in the patient (“integral dose”) and the finite range of the proton beam. The energy loss per path length of protons increases as they slow down, giving rise to the Bragg peak. The width of the Bragg peak is determined by the energy distribution of protons entering the patient and by varying in-patient ranges due to the statistical nature of particle interactions causing a spread in the energy distribution (Sawakuchi et al 2008). This effect is called ‘range straggling’ (Rossi 1952).

For clinical prescription, the range of a proton beam is defined as the range in water. The most appropriate definition of range is the R80, i.e. the position of the 80% dose in the distal falloff. For a mono-energetic proton beams with energies used clinically, the R80 corresponds to the mean projected range of a proton, i.e. the range at which 50% of the protons have stopped. Thus, the R80 is independent of the initial energy spread of the proton beam. Nevertheless, the proton range is historically defined by the R90 (90% dose in the distal falloff) of a pristine beam or spread-out Bragg peak (SOBP).

Whilst the range in water can be well defined, this is not the case for the in-patient range. In passive scattered proton therapy, the range is modulated by a compensator and thus varies across the lateral dimension of the field. Scanning beams using uniform dose distributions or intensity-modulated proton therapy (IMPT) with low in-field dose gradients can be considered to be equivalent to passively scattered proton fields. However, for IMPT with high in-field dose gradients the concept of the range of a field may not be applicable (Albertini et al 2011).

To achieve the full potential inherent in proton therapy, the in-patient range of the proton beam needs to be predicted as accurately as possible during treatment planning and delivery. If planning margins are quantified incorrectly, the consequences can be more severe in proton therapy compared to photon-based modalities. If range uncertainties are underestimated, the shift in depth of the sharp distal falloff can result in parts of the tumor receiving no dose.

As a consequence of uncertainties in predicting the exact range in patients, the commonly employed geometric PTV expansion is only valid for consideration of uncertainties in the lateral dimensions. The finite proton range requires additional considerations for uncertainties in the depth dimension during treatment planning. Range uncertainties depend on the specific patient geometry and beam angle (Park et al 2013).

A generic range margin is typically applied during proton treatment planning. A recipe of defining this margin as 3.5% of the prescribed range in water + 1 mm was originally introduced at the Harvard Cyclotron Laboratory based on the uncertainty estimations of Goitein (Goitein 1985). The 1 mm value arose from uncertainties in the patient setup, detection of skin surface and design of the range compensator. The CT technology of the early 1980s gave rise to an uncertainty in determining HU values of ~2%. An additional 1% arose from the conversion of CT to water-equivalent densities in tissue. Combining these uncertainties led to ((2%)² + (1%)²)^0.5 x 1.5 standard deviations or ~3.5%. Thus, this range uncertainty margin recipe does not include uncertainties related to dose calculation, other than those associated with the water-equivalent density. Nevertheless, it was widely adopted. Proton facilities typically use margin recipes similar or equal to the 3.5% + 1 mm outlined above. The specific values vary institutionally, e.g. 3.5% + 3 mm or 2.5% + 1.5 mm. Experienced treatment planners will adjust these margins for individual cases, based on the specific patient geometry.

Many range uncertainties are not directly related to approximations in dose calculation algorithms. We first provide a brief overview of the uncertainties that are not related to dose calculation before discussing the uncertainties investigated in this study.

Uncertainties in CT imaging and scanner calibration may be on the order of ±0.5%. Stochastic errors in CT images result in standard deviations of the proton range of ~0.3–0.7% (Chvetsov and Paige 2010). For some tissue types, e.g. bone, the uncertainties may be as high as 5.0% (Yang et al 2012).

The conversion of HU to tissue composition has an uncertainty of up to 1.8% for bone and 1.1% for soft tissue, corresponding to a range uncertainty of 1–3 mm (Schaffner and Pedroni 1998). If the HU conversion is based on a proper stoichiometric calibration, the range uncertainties should be below 0.5 mm (~0.2% of the range) (España and Paganetti 2010, Yang et al 2012). The use of dual-energy CT also has the potential to reduce range uncertainties (Yang et al 2011, Landry et al 2013). Further, Yang et al. (Yang et al 2010) reported that beam hardening can cause a shift in HU by up to 150, which could lead to a range uncertainty of ~1%. The error in the stopping power was reported to be <1%.

The range uncertainty due to CT resolution is estimated to be approximately 0.3% for CT resolutions typically used in treatment planning (España and Paganetti 2011). In lung tissue there will be a bigger impact on CT imaging uncertainties, possibly up to 5%, and uncertainties due to the large proton range in low-density lung tissue.

Potential CT artifacts can also affect the accuracy of proton range prediction particularly in the presence of metallic implants (Jäkel and Reiss 2007, Newhauser et al 2008). However, these are special cases, which should not be included in a generic range uncertainty margin.

When it comes to dose calculation, the range in a medium is, to a first approximation, determined by two main parameters in the Bethe-Bloch equation, the density and the mean excitation energy. For water the ICRU (ICRU 1993) recommends a mean excitation energy, or I-value, of 75 ± 3 eV, while the stopping power tables by Janni (Janni 1982) are based on a value of 81.8 eV. A more recent experimental study resulted in a value of 78.4 ± 1.0 eV (Kumazaki et al 2007). Andreo (Andreo 2009) has demonstrated the impact of the I-value on the range. A variation of the I-value between 75 and 80 eV results in a 0.8–1.2% difference in the predicted proton stopping power in the therapeutic energy range. However, current clinical dose calculation methods are normalized to pristine peaks measured in water, thus the range uncertainty reduces to the uncertainty relative to water.

Mean excitation energies for various elements are tabulated by the ICRU (ICRU 1993), which also includes averaged values for tissues (ICRU 1992, 1989). These energies are typically adjusted to agree with measurement or interpolated where such data are not available. These theoretical models have uncertainties, for example due to binding effects (Ahlen 1980).

The aim of the study presented here was to quantify range uncertainties originating solely due to approximations in the dose calculation algorithm. Dose calculations algorithms are often optimized for calculation speed and not necessarily for accuracy. Analytical dose calculation algorithms typically project the range based on the water equivalent depth in the patient, neglecting the position of inhomogeneities relative to the Bragg peak (Petti 1992, 1996, Urie et al 1984). They are less sensitive to complex geometries and density variations, e.g. at bone-soft tissue interfaces. Consequently, analytical algorithms are not able to correctly predict the effect of range degradation caused by multiple-Coulomb scattering (Sawakuchi et al 2008, Urie et al 1986, Goitein and Sisterson 1978). Using Monte Carlo (MC) simulations in phantom geometries, Sawakuchi et al. (Sawakuchi et al 2008) analyzed range degradation effects as a function of proton energy and geometric complexity. Range degradation can lead to an underestimation of the doses to critical structures distal to the target particularly in low-density regions (Yamashita et al 2012). In a review on range uncertainties, Paganetti estimated the uncertainties due to dose calculations alone to be between 2.7% (for homogeneous patient geometries such as liver fields) and 4.6% (for heterogeneous patient geometries such as head & neck fields) of the proton range when using standard analytical dose calculations. It was further estimated that this uncertainty could be reduced to 2.4% when using MC simulations for treatment planning (Paganetti 2012). The use of MC causes a reduction of range uncertainties from three sources: CT conversion to tissue excluding I-values (from 0.5% to 0.2%), range degradation from complex inhomogeneities (from 0.7% to 0.1%), and, range degradation from local lateral inhomogeneities (from 2.5% to 0.1%) (Paganetti 2012). The maximum difference between the range uncertainties of analytical and MC dose calculations should thus be 1.2% (3.9%) for patients without (with) lateral inhomogeneities (adding the differences of the uncertainties in quadrature and applying 1.5 standard deviations).

In this study we analyzed more than 500 treatment fields from patients that have been treated at our facility and compared the range predicted by the planning system with the one predicted by MC. We assessed the dependency of range uncertainties on range, patient geometry and treatment site. Based on the results, we then assessed the current practice of implementing range uncertainty margins during the treatment planning process.

Materials and Methods

Patient cohort

A series of patients were selected from our clinical patient database. Liver, prostate, breast, medulloblastoma (spine and whole brain fields), lung and head & neck were chosen to cover a wide variety of scenarios in terms of geometry, range and field size. For each clinical site, between 10 and 27 patient treatment plans were analyzed, with each plan containing between 2 and 17 individual treatment fields. A summary of the patient data is presented in table 1.

Table 1.

Summary of the field specific parameters for the considered treatment sites. Listed are prescribed range (R90), prescribed modulation width (distal R90-proximal R98) and prescribed dose per field as well as the CT voxel size in X (RL) and Y (AP). The voxel size in Z (SI) is typically 2.5 mm with some sections of the CTs imaged with 1.25 mm or 3.75 mm resolution.

Site	Prescribed Range [mm]	Prescribed Modulation Width [mm]	Prescribed CTV dose per field [Gy]	CT voxel size in X and Y [mm]
liver	109 – 250	64 – 169	20 – 29.5	0.799 – 1.137
prostate	224 – 278	66 – 107	14.1 – 26.6	0.916 – 1.051
breast	54 – 102	15 – 98	1 – 51.1	0.977 – 1.27
spine	63 – 114	36 – 81	0.9 – 39.2	0.561 – 0.977
whole brain	146 – 176	134 – 156	3.6 – 6.3	0.561 – 0.977
lung	75 – 191	16 – 122	5.4 – 32.7	0.977 – 1.27
head & neck	46 – 203	16 – 139	1.0 – 40.3	0.449 – 0.957

Treatment planning

Analytical dose calculations and treatment planning were performed using a pencil-beam algorithm implemented on the CMS/XiO platform (XiO, Computerized Medical System Inc.) that is currently used for double scattering proton therapy at Massachusetts General Hospital (MGH). Analytical dose calculations do not propagate protons through the treatment head geometry, but instead calculate relative patient doses (field weights) for each field based on a parameterized beam model. The obtained dose distributions have to be weighted to obtain absolute doses. The dose calculation is based on the water-equivalent path length (WEPL) of each CT voxel. XiO uses a look-up table to convert HU into relative stopping power. The algorithm is based on the physics model developed by Hong et al. (Hong et al 1999) to propagate the proton beam and model the lateral beam spread. At each point along a pencil, the dose of a single pencil kernel is factorized into a depth-scaled central axis dose and a lateral fluence distribution. The off-axis term is approximated by a Gaussian profile. The standard deviation of the Gaussian is determined by adding the contributions of the virtual source size, the scatter in the patient specific treatment head components (such as a range compensator) and the scatter in the patient.

Monte Carlo dose calculation

The MC simulations were performed using TOPAS (Perl et al 2012), which is based on Geant4 (Agostinelli and al 2003). Previous studies have validated the code against experimental data (Testa et al 2013, Perl et al 2012). For all simulations, TOPAS beta-release version 8 was used with Geant4 version 9.6.p02. Physics settings were chosen according to models described elsewhere (Zacharatou Jarlskog and Paganetti 2008, Testa et al 2013), with the physics list specifications updated to Geant4.9.6.p02.

To determine the radiation field impinging on the patient, the MGH double scattering treatment head (nozzle) has been implemented in TOPAS (Testa et al 2013, Perl et al 2012). Protons are initialized at the vacuum window at nozzle entrance and transported through the entire nozzle. The most important components for the proton transport are the first scatterers, range modulator wheels, second scatterers, and patient-specific apertures and compensators. Further details about the MGH nozzle for MC simulations can be found elsewhere (Paganetti 2004, Testa et al 2013). Liquid water was implemented as defined by ICRU (ICRU 1993), using a mean excitation energy of 75 eV.

Patient geometries were imported using the planning CT (Schuemann et al 2012, Paganetti et al 2008). The conversion of Hounsfield units from CTs to tissue material composition followed the method outlined in (Schneider et al 2000) and previously described by (Paganetti et al 2008). In addition, the conversion was normalized so that the MC predicted relative stopping power matches the one used by XiO as determined for our departmental CT scanner.

In order to obtain absolute doses, simulations were performed in three steps. First, a SOBP dose distribution in a water phantom was simulated and used to determine the dose to water delivered per proton entering the nozzle. This mimics the actual clinical dose normalization where the dose delivered in a SOBP in water is related to the ionization chamber reading in the treatment head. Second, protons were transported through the nozzle geometry to generate a phase space downstream of the patient-specific hardware. Finally, protons from the generated phase space files were transported into the patient CT geometry.

Each treatment field was adjusted to match the field weight prescribed within the treatment planning system, utilizing the normalization factor obtained in the initial water phantom simulation. For a more detailed description of this method see (Paganetti et al 2008).

All simulations were performed on the Partners research computing cluster. 30 parallel simulations per patient field were used, each with 250,000 protons starting at the vacuum window at the top of the treatment head. Geometrical splitting and Russian roulette techniques for variance reduction were applied with a splitting factor of 8 at two planes along the treatment head, effectively increasing the number of initial protons by a factor of 64 (Ramos-Méndez et al 2013). Patient simulations thus consisted of an equivalent of 480x10⁶ initial protons. Single patient simulations completed generally within 5 hours running on up to 500 computing nodes in parallel. For SOBP simulations in the water tank a smaller number of 128x10⁶ initial protons were simulated.

Monte Carlo Range calibration

The MGH treatment head was implemented according to blueprints provided by the manufacturer (IBA, Louvain-la-Neuve, Belgium). The prediction of the proton energy distribution at nozzle exit for some treatment options (combinations of SOBP range and modulation width) experienced discrepancies between measured and MC predicted values of up to 2 mm for range and 3 mm for modulation width (Testa et al 2013) due to uncertainties in the modeling of the treatment head geometry.

Since the purpose of this work was to quantify range differences between analytical and MC dose calculations caused by the patient geometry only, we performed a correction to ensure that both systems predict identical ranges in water. We therefore introduced an additional simulation step. First, the requested SOBP was simulated in a water phantom for each field. The TOPAS ranges (R90) in water were then corrected by adjusting the beam energy at treatment head entrance to coincide with those predicted by the analytical algorithm, which are based on commissioning measurements at MGH. The energies were adjusted by up to 1 MeV (or 0.7%) resulting in a maximum difference in R90 after this range-calibration between TOPAS and XiO of <0.3 mm in water.

Range analysis

The analysis of the range in patients has to consider that the distal dose falloff is modulated by the range compensator. There is no single range defined in the patient. Consequently, we analyzed the range on a voxel by voxel basis.

The CT grid can be different from the treatment-planning grid. XiO dose calculations in this study were performed on a grid comprised of voxels of 2x2x2.5 mm³. The CT voxel size varied between the different treatment sites considered (see table 1). While dose deposition calculations in the MC simulations were performed on the CT grid, they were scored in the same dose grid as used by XiO for comparison. Because information from both the CT and dose grids is needed for the range analysis, the dose grids of XiO and TOPAS were interpolated onto the CT grid to take advantage of the higher resolution. Further, the CT and dose grids were rotated such that the beam’s eye view was aligned in parallel with one voxel orientation.

This method allows the definition of distal dose surfaces (DDS). These two-dimensional surfaces are comprised of the depths that show the same fraction dose of the prescribed dose, e.g. R90. To illustrate this method, TOPAS dose distributions of selected CT slices are shown in figures 1a–c in coronal, transverse and sagittal views. Figure 1b additionally shows a comparison of dose distributions predicted by TOPAS and XiO. Figure 1d shows the DDSs in beam’s eye (coronal) view.

Figure 1.

Proton dose distribution for a spine field in (a) coronal, (b) transverse and (c) sagittal view. (d) 2D range map in (coronal) field’s eye view for TOPAS and XiO (dimensions indicated by red dashed lines) and the difference map.

Each voxel at the surface of the rotated CT grid in beam’s eye view defines the starting position P_j of a ray j. A ray then consists of all voxels along the field direction (beam’s eye view) starting from P_j. We define the region of interest as all rays where both TOPAS and XiO predict a dose larger than 90% of the dose prescribed for that field in any voxel along ray j. These rays comprise the analysis set J. Rays outside the analysis set J with doses along the ray of at least 2% of the prescribed dose are called the penumbra. The DDS is formed by calculating the range along each ray of J. For each j in J the range is defined as:

$$R_X(j)=dx(N_{T_X}(j)+\frac{D_i(j)-T_{X}D}{D_i(j)-D_{i+1}(j)}),$$ (1)

where dx is the dimension of the analysis grid voxel in the field direction. The last voxel with dose larger than the fraction T_X (T_X = 0.9, 0.8 or 0.2) of the prescribed dose D is voxel i. N_Tx(j) is the number of voxels along the beam axis for the j^th ray from the patient surface to voxel i. The range is then interpolated between voxel i and the next, (i+1)^th voxel, according to the doses in the two voxels, D_i(j) and D_i+1(j), as described by the second term of equation 1.

Using the DDS, the average range differences (ARD) and root-mean-square deviations (RMSD) were calculated on a voxel-by-voxel basis. ARDs and RMSDs were calculated for two ranges, R90 and R50. The two ranges emphasize different aspects: clinical treatment plans are defined using R90, while R50 is not affected by range degradation and thus provides an estimate of how much the range of the proton field is shifted. To investigate degradation of the distal falloff, DDS surfaces for 20% (R20) and 80% (R80) of the prescribed dose were similarly formed. The average distal dose degradation difference (ADD) is defined as the difference of the dose degradation (R80-R20) between TOPAS and XiO averaged over all rays (j).

For some fields, rays exiting the patient geometry influenced the range differences. Such rays occurred in particular for whole brain treatments, but also in some head & neck or breast fields. This can lead to large differences in the predicted ranges. Rays were excluded for the calculation of the ARD and RMSD in the 2D range profile if the dose exiting the patient was larger than 90% of the prescribed dose. Rays where the exiting dose was larger than 20% of the prescribed dose were excluded from the calculation of the ADD. In addition, the outermost ring of rays in beam’s eye view of each field was excluded from the R90 profiles to remove any penumbral effects, which also can cause large discrepancies in the calculated range differences.

Abbreviations

RXX

the distal position (range) of the XX% dose level, i.e. R90 is the position of the distal edge where the dose falls below 90% of the prescribed dose

ARD

the average range difference, subtracting the range predicted by the planning system from the one predicted by TOPAS for all rays of the 2-dimensional range profiles

ARD_R90

ARD for R90

ARD_R50

ARD for R50

RMSD

the root mean square difference between the range predicted by the planning system and the one predicted by TOPAS for all rays of the 2-dimensional range profiles

RMSD_R90

RMSD for R90

RMSD_R50

RMSD for R50

ADD

the average dose degradation difference, i.e. subtracting the distal falloff

(R80-R20) of the planning system from that calculated by TOPAS All range differences are reported in WEPL.

Results

Fields used for Head & Neck treatments

The head & neck treatment site will be discussed in more detail as many of the features of other sites can be demonstrated using these patient fields as examples.

The results of all 248 head & neck treatment fields are summarized in figure 2. The mean values and variance (root mean square) of the histograms are listed in table 2 together with the minimum and maximum values for each ARD, RMSD and the ADD.

Figure 2.

Distributions summarizing the results for all head & neck fields: a) average range difference (ARD); b) root mean square difference (RMSD) in percent of the prescribed range for R90 (red, solid) and R50 (blue, dashed); scatter plots of c) ARD_R90, d) RMSD_R90, e) ARD_R50 and f) RMSD_R50 vs. the prescribed range for all fields; g) average dose degradation (R80-R20) difference (ADD) in percent of the prescribed range; h) ADD vs. the prescribed range. The scatter plots were fitted with a linear function (lines) to illustrate the dependence on the prescribed range.

Table 2.

Summary of the number of fields analyzed for each site and the average range difference (ARD), root mean square difference (RMSD) and average dose degradation difference (ADD) in percent of the prescribed range. Listed are the mean values with the standard deviation and underneath the min. and max. values observed.

Site	# of fields	ARDR90 [%]	ARDR50 [%]	RMSDR90 [%]	RMSDR50 [%]	ADD [%]
Head & Neck	248	−1.5 ± 1.5 [−14.8, 0.9]	−0.5 ± 0.6 [−3.4, 1.1]	3.2 ± 1.9 [0.6, 19.9]	1.8 ± 0.8 [0.1, 4.7]	0.05 ± 1.2 [−4.8, 3.1]
Lung	30	−2.0 ± 1.8 [−5.8, −0.1]	−0.6 ± 1.0 [−2.2, 1.8]	4.0 ± 1.3 [1.8, 7.0]	2.1 ± 0.5 [1.2, 6.3]	1.2 ± 1.8 [−1.6, 6.3]
Spine	69	−2.3 ± 1.9 [−7.1, −0.4]	−1.3 ± 0.8 [−3.7, −0.5]	3.4 ± 2.4 [1.3, 9.6]	2.1 ± 0.9 [1.1, 4.6]	−0.9 ± 1.7 [−5.1, 1.3]
Whole Brain	49	−0.6 ± 0.4 [−1.5, −0.1]	−0.6 ± 0.2 [−1.2, 0.1]	1.7 ± 0.2 [1.5, 2.1]	1.4 ± 0.2 [1.2, 1.9]	0.2 ± 0.3 [−0.3, 0.7]
Breast	48	−1.2 ± 0.9 [−3.5, 0.8]	−0.7 ± 0.8 [−3.8, 0.4]	2.6 ± 1.0 [1.1, 6.0]	1.8 ± 0.9 [0.8, 7.3]	0.2 ± 0.8 [−1.1, 3.4]
Prostate	42	−0.2 ± 0.3 [−0.8, 0.4]	−0.2 ± 0.3 [−0.9, 0.3]	0.9 ± 0.3 [0.6, 1.5]	0.6 ± 0.2 [−0.9, 0.3]	0.4 ± 0.1 [0.2, 0.7]
Liver	22	−0.3 ± 04 [−1.2, 0.5]	−0.3 ± 0.4 [−1.2, 0.4]	1.0 ± 0.4 [0.4, 2.0]	0.7 ± 0.3 [0.4, 1.2]	0.4 ± 0.3 [−0.1, 1.1]

Figures 2a and 2b show the ARD and RMSD for the two ranges (R90 and R50) in percentage of the prescribed range, respectively. The ARD and RMSD show a much narrower distribution with a sigma of 0.6% (ARD_R50) and 0.8% (RMSD_R50) for R50 compared to 1.5% (ARD_R90) and 1.9% (RMSD_R90) for R90. This effect is seen for all sites and confirms that properties based on R90 are influenced by two factors, the overall range difference caused primarily by multiple-Coulomb scattering (also affecting R50) and range straggling, which has little affect on R50.

Figures 2b–e show a scatter plot of the ARDs and RMSDs in absolute values (millimeter) versus the prescribed range. We performed a linear fit to the data points to investigate a possible correlation of these values to the prescribed range. No clear correlation (Spearman’s p-value < 0.02) is seen for either of the ARDs. However, both RMSDs are correlated with the prescribed range. The coefficients of the linear fits and Spearman’s p-values for the RMSDs are summarized in table 3.

Table 3.

Summary of linear fits for all sites for the RMSD90 and RMSD50 together with the Spearman’s p-value. The top half of the table is per site for a linear fit, in the second half similar sites are combined and the offset is set to 0.

	RMSDR90			RMSDR50
Site	offset [mm]	slope [%]	Spearman’s p-value	offset [mm]	slope [%]	Spearman’s p-value
Head & neck	1.5	2.0	<10−11	0.7	1.2	<10−8
Lung	1.3	2.7	0.07	0.2	1.9	<10−4
Spine	7.1	−4.5	0.90	1.6	0.2	0.66
Whole Brain	0.6	1.4	0.02	−3.2	3.4	<10−6
Breast	−0.2	2.8	0.002	1.7	−0.3	0.66
Prostate	0.3	0.8	0.34	−4.1	2.3	<10−5
Liver	−0.1	1.1	0.08	−0.6	1.1	0.24
Head & neck + lung + breast	--	3.2	<10−22	--	1.8	<10−19
Head & neck	--	3.1	<10−11	--	1.8	<10−8
Lung + breast	--	3.3	<10−7	--	1.9	<10−5
Prostate + liver	--	0.9	<10−4	--	0.7	<10−7
Whole brain	--	1.7	0.02	--	1.4	<10−6
Spine	--	3.5	0.90	--	2.0	0.66

Figures 2g and 2h display the dose degradation in percent of the prescribed range and as scatter plot of absolute values vs. the prescribed range, respectively. The scatter plot shows no significant correlation of the ADD to the prescribed range (p-value = 0.2). The ADD, the measure of how much the dose degradation changes when using the more accurate MC simulations, is distributed evenly around zero with a variance of 1.2% (figure 2g). This shows that even for highly heterogeneous geometries, the majority of the distal dose degradation is due to range straggling with a much smaller impact of multiple-Coulomb scattering as has been found already by Sawakuchi et al. (Sawakuchi et al 2008). We found that the analytical algorithm slightly overestimates range degradation due to range straggling alone, thus compensating for the underestimation of multiple-Coulomb scattering effects. This results in the shape of the averaged dose falloff to be in relatively good agreement, i.e. the ADD is centered on zero.

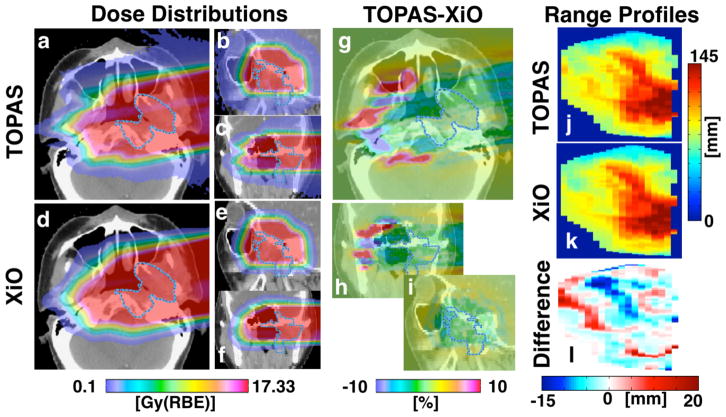
Figure 2 demonstrates that there can be substantial variations from field to field. We use two example fields to demonstrate the shortcomings of analytical dose calculation algorithms. The dose distributions for the field with the largest RMSD_R90 (16.4 mm) and ARD_R90 (12.7 mm) are shown in figure 3 for TOPAS (3a–c) and XiO (3d–f). The differences between the two calculation methods are particularly evident in the difference plots, both for the dose (3g–i) and the range profile (3l). To illustrate the effects of multiple-Coulomb scattering, we follow protons along the arrow in figure 3g. These protons pass through soft tissue, bone and air before reaching the nasal septum. Distal to the septum, protons pass through bone posterior to the arrow and first air, then soft tissue anterior to the arrow. The incorrect modeling of the preferential scattering of protons to the lower-density region by XiO causes an underdose compared to TOPAS calculations posterior to the arrow, resulting in a shorter range in that region. Accordingly, we observe an overdose and extended range anterior to the arrow. Another reason for the large RMSD is the small field size. The opening area of the aperture is 10.5 cm² because this field is only treating a subset of the GTV. It has previously been found (Bueno et al 2013, Bednarz et al 2010) that the analytical algorithm does not model the doses for small fields correctly, even for very homogeneous patient geometries (Daartz et al 2009). For the field in figure 3, this results in an overestimation of the delivered dose and thus a systematically longer range predicted by XiO as compared to TOPAS. Correction factors to the predicted doses should be applied for small fields (Daartz et al 2009).

Figure 3.

Proton dose distribution for the field with the largest RMSD_R90 (16.4 mm) as calculated with TOPAS (a–c), XiO (d–f) and the dose difference map (g–i) in transverse (a,d,g), sagittal (b,e,h) and coronal (c,f,i) view. The prescribed dose for this field was 10.1 Gy(RBE). The scale for the dose difference plots is given as percent of the prescribed dose. The 2D range profiles in beam’s eye view for the range calculation are shown for TOPAS (j) and XiO (k) together with the range difference (l).

Figure 4 shows a second example for the same patient treatment. This field is treating the entire GTV, and thus covers a much larger volume than the field depicted in figure 3. The opening area of the aperture is 33.1 cm². This field resulted in the lowest ARD_R50 (0.01%). On the other hand, local differences in R90 of ±30 mm exist. Areas of clear overshooting and undershooting of the R90 can be observed in the difference plot of the range profiles (figure 4l). Averaging over all such areas, positive and negative, leads to a small total ARD, despite large local variations. This suggests that quantifying the quality of a predicted dose distribution using ARD alone is not ideal. More meaningful is the RMSD, an estimate of the variation within the field. The RMSD_R90 (RMSD_R50) for this field is 4.7 mm or 3.2% (4.1 mm or 2.8%) of the prescribed range.

Figure 4.

Proton dose distribution for the field with the smallest ARD_R50 (0.01 mm) for the same patient as shown in Figure 3 as calculated with TOPAS (a–c), XiO (d–f) and the dose difference map (g–i) in transverse (a,d,g), sagittal (b,e,h) and coronal (c,f,i) view. This field also has one of the lowest RMSD_R90 (4.7 mm). The prescribed dose for this field was 17.33 Gy(RBE). The scale for the dose difference plots is given as percent of the prescribed dose. The 2D range profiles in beam’s eye view for the range calculation are shown for TOPAS (j) and XiO (k) together with the range difference (l).

Range differences for single rays can be substantial. The maximum range underestimation by the analytical algorithm for the two example fields (figures 3 and 4) was found to be 39 mm for the R90. Such a large underestimation of the clinically important R90 could yield systematic underdosage of parts of the tumor if the range margin is not properly defined. Similarly, the maximum single-ray overshoot for these two fields was found to be 20 mm, which could have been clinically relevant if such a ray points towards an organ at risk. The impact of such uncertainties is to a certain extend mitigated when using multiple fields. The fields shown in figure 3 and figure 4 are part of a treatment consisting of 13 fields. While the RMSD_R90 for the field shown in figure 3 is large (11.3%), the difference of the mean dose (D50) in the dose volume histogram (DVH) for the GTV between TOPAS and XiO when all 13 fields are combined is −3.5%. The TOPAS (XiO) dose is 1.7% less (1.8% more) than the prescribed dose, thus both calculations are within clinical limits (±2% of the prescribed dose).

Fields used for lung treatments

The results for the range analysis for the 30 lung fields investigated are shown in figure 5 and summarized in tables 2 and 3. Because range differences are reported in WEPL the absolute values of the range differences are up to a factor 3 larger than reported here for the low-density lung tissue. A significant correlation with the prescribed range (p-value <10⁻⁴) was found for RMSD_R50 shown in figure 5d.

Figure 5.

Distributions summarizing the results for lung fields from 2D range surfaces of TOPAS and XiO: a) average range difference (ARD); b) root mean square difference (RMSD) in percent of the prescribed range for R90 (red, solid) and R50 (blue, dashed); c) average dose degradation (R80-R20) difference (ADD) in percent of the prescribed range; d) scatter plot for the absolute RMSDs in millimeter vs. the prescribed range. The solid (dashed) line represents a linear fit to the R90 (R50) data points to illustrate the dependence on the prescribed range.

The largest RMSD_R90 is 7.0% of the prescribed range. The dose distribution for this field is depicted in figure 6. The penumbral width in analytical algorithms is predicted from the beam spread based on the water-equivalent range. TOPAS predicts a wider lateral penumbra than XiO due to scattering in the chest wall followed by low-density lung tissue (Grassberger et al n.d.). Figure 6d shows an underdose (3.5% of the prescribed dose) inside the tumor at the center of the GTV (pink outline), which is a consequence of this effect. The lateral edges of the target show a ring of underdose of approximately 9% due to scattering, with a corresponding higher dose in the penumbra outside the target (+4%).

Figure 6.

a) TOPAS and b) XiO dose distributions for the lung field with the largest relative RMSD_R90 (7.0%). The prescribed dose for this field is 16.1 Gy(RBE). The TOPAS-XiO dose difference is shown in c (transverse view) and d (sagittal view) in percent of the prescribed dose.

As for the head & neck examples, the inaccurate description of multiple-Coulomb scattering by the analytical algorithm causes large dose fluctuations (>10% of the prescribed dose) downstream of high-density gradients (here ribs/soft-tissue and tumor/lung). The large margins used for lung treatments (extra margins of up to 10 mm WEPL are sometimes added at our institution to cover range uncertainties in lung) still ensure full coverage of the tumor volume as can be seen in figure 6a.

Medulloblastoma – Spine fields

Figure 7 shows the results for 69 spine fields (based on 10 medulloblastoma treatment plans). The analysis is summarized in tables 2 and 3. No significant correlation was observed between the RMSDs and the prescribed range (p=0.9 for R90 and 0.66 for R50). In figure 7d, clusters of 3 data points can be seen. Due to the large size of the treatment volume (brain and spine) for medulloblastoma patients, the fields cannot be delivered in a single irradiation and field-patching techniques are implemented. The largest lateral field size for passive scattering proton therapy at our institute is 25cm (radius). Medulloblastoma treatments typically consist of a whole brain irradiation, split into two opposing fields, and a spine treatment, which is split into two or three sections depending on the patient’s height. Each of these sections is irradiated with three slightly shifted fields to reduce uncertainties at the patch line. Thus for each plan, there are three nearly identical field combinations generated, causing the clusters of 3.

Figure 7.

Distributions summarizing the results for spine fields from 2D range surfaces of TOPAS and XiO: a) average range difference (ARD); b) root mean square difference (RMSD) in percent of the prescribed range for R90 (red, solid) and R50 (blue, dashed); c) average dose degradation (R80-R20) difference (ADD) in percent of the prescribed range; d) scatter plot for the absolute RMSDs in millimeter vs. the prescribed range. The solid (dashed) line represents a linear fit to the R90 (R50) data points to illustrate the dependence on the prescribed range.

Figure 8 shows the dose distribution for one of the patients, with figure 8k illustrating the multiple-Coulomb scattering effect as discussed for the head & neck and lung examples (figures 3, 4 and 6). The analytical calculations poorly predict the dose distributions distal to high-density gradients parallel to the field direction, in this case the spine/lung interface. This effect can be seen all along the spine (see figure 8l) but is most prominent where the spine is adjacent to the lung.

Figure 8.

Proton dose distribution calculated with TOPAS (a–c) and XiO (d–e) with their dose difference map, TOPAS-XiO, (g–i) for one medulloblastoma patient in sagittal view. Single fields for each section of the treatment are shown for a single whole brain field (a,d,g), superior spine field (b,e,h) and inferior spine field (c,f,i). The combined treatment containing all fields is shown in (j). (k) and (l) depict the transverse view of the dose difference for two slices through the patient at two positions indicated by the dashed black line in (h) and (i), respectively.

The largest deviations between TOPAS and XiO for the RMSD_R90 and ARD_R90, 9.6% and −7.1%, respectively, occur in the superior spine field. All data points in figure 7b with an RMSD_R90 > 4% of the prescribed range are from superior spine fields. The largest RMSD_R90 for a non-superior spine field is 3.8%. This suggests that superior and inferior spine fields should be considered separately in terms of range uncertainties. Differences in the patient geometry for the different spine sections are the dominating factor determining the size of the RMSDs, which explains the absence of a correlation between the RMSDs and the prescribed range.

Medulloblastoma – Whole brain fields

The top row of figure 8 (a,d,g) shows a representative brain field calculated with TOPAS, XiO and their difference. Whole brain treatment fields are prescribed to stop inside the distal cranial bone, thus rays overshooting the prescribed range by a few millimeters exit the patient geometry distally. Because such rays were excluded in the analysis the number of rays was substantially reduced for some of the fields. For one patient the number of rays remaining for the range analysis was a factor 5 lower than for other patients. We excluded the whole brain fields from this patient from all analyses.

Figure 9 shows the ARDs, RMSDs and ADD of the 49 whole brain fields of the 9 remaining medulloblastoma patients investigated. The RMSDs were observed to significantly correlate (p(RMSD_R90)=0.02 and p(RMSD_R50)<10⁻⁶) with prescribed range as shown in figure 9d. The data is summarized in tables 2 and 3. The two calculation algorithms agree well for this site (RMSD_R90 < 2.1%). This was also reflected in small deviations of the mean dose (<1.5% for all patients) when comparing the DVHs of the target volume between the two algorithms. The good agreement between the two algorithms is due to three factors, a homogeneous tissue distribution across the majority of the field, large fields and the distal dose falloff located in the skull bone, which reduced the possibility for large range fluctuations inside the patient.

Figure 9.

Distributions summarizing the results for whole brain fields from 2D range surfaces of TOPAS and XiO: a) average range difference (ARD); b) root mean square difference (RMSD) in percent of the prescribed range for R90 (red, solid) and R50 (blue, dashed); c) average dose degradation (R80-R20) difference (ADD) in percent of the prescribed range; d) scatter plot for the absolute RMSDs in millimeter vs. the prescribed range. The solid (dashed) line represents a linear fit to the R90 (R50) data points to illustrate the dependence on the prescribed range.

Fields used for breast treatments

Figure 10 summarizes the results of the 48 breast treatment fields. The breast fields considered here include treatments of intact breast and comprehensive post-mastectomy radiotherapy. The data is summarized in tables 2 and 3. A correlation between the range and the RMSD_R90 (p=0.002) is seen in figure 10d while the RMSD_R50 does not show any significant correlation.

Figure 10.

Distributions summarizing the results for breast fields from 2D range surfaces of TOPAS and XiO: a) average range difference (ARD); b) root mean square difference (RMSD) in percent of the prescribed range for R90 (red, solid) and R50 (blue, dashed); c) average dose degradation (R80-R20) difference (ADD) in percent of the prescribed range; d) scatter plot for the absolute RMSDs in millimeter vs. the prescribed range. The solid (dashed) line represents a linear fit to the R90 (R50) data points to illustrate the dependence on the prescribed range.

The target volume of breast treatments generally is too large to be covered by a single field. The target is covered by patched fields, i.e. a larger (main) treatment field covering the majority of the treatment volume is combined with a smaller patch field. The latter are generally superior to the breast. One of the fields, a main treatment field, showed particularly large range differences (RMSD_R90=6.0% or 3.8 mm, the RMSD_R50=7.3% or 4.7 mm). The range predicted by TOPAS was shorter across the entire field (ARD_R50=−2.4 mm), resulting in improved lung sparing but larger RMSDs.

The breast field with the largest absolute RMSD_R90 = 4.2 mm (4.3%) was a superior patch field which is shown in figures 11a–d. The corresponding inferior main treatment field is also shown in figures 11e–h. The main difference between these two types of fields is that the inferior fields are generally aimed at the lung while the distal falloff of the superior fields occurs in soft tissue. Furthermore, the field sizes are different with aperture opening areas of 50 cm² and 295 cm², respectively. However, the patch field aperture is highly eccentric resulting in an increased small-field effect (equivalent to a round aperture opening of 25cm²). As discussed for head & neck fields, small apertures cause the analytical algorithm to predict longer ranges resulting in a large RMSD.

Figure 11.

Dose distributions of a smaller (superior) patch field (a–d) and a larger patch (inferior) breast treatment field (e–f) as calculated with TOPAS (a,e), XiO (b,f) and their difference TOPAS-XiO (c,g). The sagittal view images (d,h) illustrate the different sizes of the two fields. The prescribed dose for the fields were 24.8 Gy(RBE) and 23.51 Gy(RBE). The scale for the dose difference plots is given as percent of the prescribed dose

Fields used for prostate treatments

The results for 42 prostate fields are summarized in figure 12. Prostate patients are treated with ranges greater than 22 cm due to the currently employed treatment scheme of two lateral parallel-opposed fields. The ARDs were found to be within 0.9%, the RMSD_R90 within 1.5% and the RMSD_R50 within 1.0% of the prescribed range. The ADD is less than 0.7% of the prescribed range and on average 0.4 ± 0.1% larger than that predicted by XiO. Even for the fields with the longest range, the systematical difference in dose degradation between TOPAS and XiO is only approximately 1 mm. Figure 12d shows the dependence of the RMSDs on the prescribed range. A clear correlation can be seen between RMSD_R50 and prescribed range (p<10⁻⁵).

Figure 12.

Distributions summarizing the results for prostate fields from 2D range surfaces of TOPAS and XiO: a) average range difference (ARD); b) root mean square difference (RMSD) in percent of the prescribed range for R90 (red, solid) and R50 (blue, dashed); c) average dose degradation (R80-R20) difference (ADD) in percent of the prescribed range; d) scatter plot for the absolute RMSDs in millimeter vs. the prescribed range. The solid (dashed) line represents a linear fit to the R90 (R50) data points to illustrate the dependence on the prescribed range.

For prostate fields multiple-Coulomb scattering effects at bone-tissue interfaces can cause differences of more than 10% of the prescribed dose where protons pass parallel to the pelvic-bone and spinal-bone. A similar ring structure to the one observed in lung (figure 6d) can be observed. This structure already exists at the proximal patient surface and is caused by small differences in aperture and compensator scattering or beam properties prior to the aperture.

Fields used for liver treatments

The results from analyzing 22 liver fields from 10 liver patients are shown in figure 13 and summarized in tables 2 and 3. Both ARDs are within 1.25% of the prescribed range and the RMSD_R50 (RMSD_R90) is less than 1.25% (2.0%). The ADD is less than 1.1%. Liver treatments are expected to have good agreement between analytical algorithms and MC simulations due to a relatively homogeneous patient geometry. The largest density heterogeneities for liver are present when individual fields pass through ribs or when fields enter the lung. No significant correlation was found between the RMSDs and the prescribed range (figure 13d).

Figure 13.

Distributions summarizing the results for liver fields from 2D range surfaces of TOPAS and XiO: a) average range difference (ARD); b) root mean square difference (RMSD) in percent of the prescribed range for R90 (red, solid) and R50 (blue, dashed); c) average dose degradation (R80-R20) difference (ADD) in percent of the prescribed range; d) is the scatter plot for the absolute RMSDs in millimeter vs. the prescribed range. The solid (dashed) line represents a linear fit to the R90 (R50) data points to illustrate the dependence on the prescribed range.

Discussion and Conclusions

General

The current clinical practice at proton centers is to use a generic range uncertainty margin (e.g. 3.5% of the range plus 1 mm) and add additional margins based on the site (e.g. as routinely done for lung treatments) or based on the specific patient geometry (e.g. as routinely done for complex cases in the head and neck region). The decision when and where to add additional margins largely depends on the experience of the treatment planner.

Overall, our study shows that

1. if generic (non-patient-specific) range margins are being applied, they should be site specific

2. for some sites, patient variations can be substantial and warrant additional margins to ensure target coverage

3. Monte Carlo dose calculation can have a substantial impact in proton therapy treatment planning for most sites

The clinical significance of the presented results, i.e. the average range differences for R90 and R50, the root mean squares of these differences and the change in dose degradation depend strongly on the treatment site. Overall, in order to quantify the range error by analytical dose calculation methods, the clinically most relevant parameter is the RMSD_R90. For fields in the head & neck region the variation in the field ranges (the RMSD) caused by multiple-Coulomb scattering on bone/air interfaces may result in a small organ at risk (such as the brainstem or optic nerve) receiving an increased dose while not affecting the tumor coverage. On the other hand, for medulloblastoma-spine fields, the range variations may not be as important as assuring a full coverage of the spine, thus a large negative ARD may be more important than a large RMSD.

The presented analysis focused purely on the uncertainty from dose calculation. The portion of the range margins related to dose calculations has been estimated to be on the order of 1.2% of the prescribed range in the absence of lateral inhomogeneities and 3.9% of the prescribed range with lateral inhomogeneities, respectively (Paganetti 2012).

For each site in the results section we used a linear fit to assess a potential relationship between prescribed range and RMSD. The results are summarized in the upper half of table 3. While correlations between the RMSDs and the prescribed range were observed for most treatment sites, the fits through the data points yield very different slopes (between −4.5% and +2.8% for RMSD_R90). Also shown in table 3 (lower half) are alternative fits where we forced the line to go through the origin, i.e. resulting in zero uncertainty at a range of 0. The obtained slopes for RMSD_R90 and RMSD_R50 are illustrated in figure 14. The figure separates sites with and without significant lateral inhomogeneities, i.e. lung, breast and head & neck as well as liver and prostate. Also shown are lines representing the range uncertainty margin employed at our facility (3.5% + 1 mm; including dose calculation as well as other uncertainties). Apparently, on average, this generic recipe covers the uncertainties. Special consideration is required for a selected number of fields as discussed above.

Figure 14.

Linear fit without offset to sites with (a) and without (b) significant lateral inhomogeneities as indicated in the legend together with the current range margins (3.5% + 1 mm) and our recommended range margins.

It should be noted that the discrepancies between analytical and MC based dose calculations do not only describe effects of the patient geometry but also include discrepancies caused by the patient specific aperture and range compensator used to shape the treatment fields in passively scattered proton treatments.

Site specific

Based on our analysis summarized in table 3 and the estimation of non-dose calculation related uncertainties (Paganetti 2012), we can make site-specific recommendations for range uncertainty considerations in treatment planning. We define the range uncertainty from dose calculation as the obtained slope plus 1.5 standard deviations (determined by the root mean square of the data points around the fit divided by the number of data points). Table 4 shows the resulting site-specific range margins based on RMSD_R90. Range margins based on RMSD_R50 are also listed to illustrate the effect excluding range degradation effects. No recommendation is made for spine fields due to the different behavior for superior and inferior fields discussed above.

Table 4.

Recommended range margins for all site investigated (except for medulloblastoma-spine fields) considering R50 and R90. Also shown are the uncertainties based on dose calculation alone.

Site	RMSDR50		RMSDR90
	Dose calc. only	Total	Dose calc. only	Total
Liver + prostate	1.0%	2.6% + 1.2 mm	1.4%	2.8% + 1.2 mm
Whole brain	1.7%	3.0% + 1.2 mm	2.0%	3.1% + 1.2 mm
Lung + breast	3.2%	4.0% + 1.2 mm	5.3%	5.9% + 1.2 mm
Head & neck	3.0%	3.8% + 1.2 mm	6.0%	6.5% + 1.2 mm
Lung + breast + head & neck	3.0%	3.9% + 1.2 mm	5.8%	6.3% + 1.2 mm

For liver and prostate, the range seems to be predicted with sufficient accuracy by the treatment planning system. We estimate the contribution of the dose calculation to the range margin to be ~1.4% (R90). As a result it seems feasible to reduce currently applied generic margins (1.5 standard deviations of range uncertainties) to 2.8% + 1.2 mm (considering also uncertainties other than dose calculation, i.e. 2.4% + 1.2 mm (Paganetti 2012)). The value is in excellent agreement with a previous estimation of 2.7% ± 1.2 mm (Paganetti 2012). For these sites, the routine use of MC dose calculation would appear to be of limited additional value since the margin is dominated by uncertainties that affect analytical and MC dose calculations equally.

For whole brain fields used in medulloblastoma treatments we estimate the dose calculation based range margin for R90 to be ~2.0%. It thus seems feasible to reduce the currently applied generic margin to 3.1% + 1.2 mm.

It should be emphasized that generic margins should always be considered carefully. Adjustments to margins or a selection of a different treatment field may be necessary for some fields for individual patients.

For heterogeneous treatment sites (lung, breast and head & neck) we estimate the dose calculation based range margin for R90 to be ~5.8%. The majority of fields provide full coverage of the target with current range margin settings. However, these margins do not cover range differences for the extreme cases. If target coverage ought to be ensured for all cases based on a generic margin, a margin of 6.3% of the prescribed range + 1.2 mm would be required. This is even larger than a value previously estimated (4.6% ± 1.2 mm (Paganetti 2012)). Consequently, for these sites, case specific margins are recommended, i.e. the currently used recipe can be applied with planners being aware of the need for adjustments in certain geometrical scenarios. Using MC for treatment planning could thus significantly reduce range margins for these patients. The difference between our recommended range margin of 6.3% + 1.2 mm and the range margin that are possible with MC based planning (2.4% + 1.2 mm) for a field with 10 cm range is an additional 3.7 mm of healthy tissue that could be spared.

All fields investigated here use passively scattered spread-out Bragg peaks (SOBPs). While this is currently the dominant treatment modality for proton therapy, more and more proton centers are being constructed and commissioned for treatments with scanned proton beams. Proton fields delivered with beam scanning can apply intensity modulated proton therapy (IMPT). These treatments can apply SOBP fields, for which the conclusions drawn here should equally apply. However, if IMPT is used to deliver non-homogeneous fields, the range uncertainty needs to be defined on a pencil-by-pencil basis.

While our analysis is based on a specific pencil-beam dose calculation algorithm, the results can be expected to be similar for other analytical algorithms based on the same conceptual approach. The main source of the discrepancy between TOPAS and XiO dose distributions is the inability to accurately describe multiple-Coulomb scattering with the approach used in analytical algorithms, i.e. predicting the dose based on straight pencils and accommodating lateral spread with a Gaussian distribution.

Efforts have been made to improve the accuracy of analytical dose calculations. These efforts generally introduce additional calculation steps in the analytical algorithms to improve handling of lateral heterogeneities. Some of these efforts are the pencil-beam redefinition algorithms (Egashira et al 2013, Shiu 1991) and the introduction of sub-spots for pencil-beam scanning spots (Soukup et al 2005). However, it seems that fast Monte Carlo based dose calculation is the more promising approach (Jia et al 2012).