Neutron production from beam-modifying devices in a modern double scattering proton therapy beam delivery system

Abstract

In this work the neutron production in a passive beam delivery system was investigated. Secondary particles including neutrons are created as the proton beam interacts with beam shaping devices in the treatment head. Stray neutron exposure to the whole body may increase the risk that the patient develops a radiogenic cancer years or decades after radiotherapy. We simulated a passive proton beam delivery system with double scattering technology to determine the neutron production and energy distribution at 200 MeV proton energy. Specifically, we studied the neutron absorbed dose per therapeutic absorbed dose, the neutron absorbed dose per source particle and the neutron energy spectrum at various locations around the nozzle. We also investigated the neutron production along the nozzle's central axis. The absorbed doses and neutron spectra were simulated with the MCNPX Monte Carlo code. The simulations revealed that the range modulation wheel (RMW) is the most intense neutron source of any of the beam spreading devices within the nozzle. This finding suggests that it may be helpful to refine the design of the RMW assembly, e.g., by adding local shielding, to suppress neutron-induced damage to components in the nozzle and to reduce the shielding thickness of the treatment vault. The simulations also revealed that the neutron dose to the patient is predominated by neutrons produced in the field defining collimator assembly, located just upstream of the patient.

1. Introduction

Protons and heavier charged particles offer the potentially significant advantage for radiation therapy of a dramatically improved physical dose distribution compared to indirectly ionizing particles such as photons or neutrons and lighter charged particles such as electrons (Wilson 1946). This results because most proton interactions occur by means of Coulombic interactions with atomic electrons (Gottschalk et al 1993). In particular, the large mass difference results in minimal deflection of the proton. The vast numbers of such interactions, each imparting very little energy loss, result in an almost continuous slowing down of the protons. The clinical advantages of proton therapy are apparent (Suit 1992, Gragoudas et al 2002, Lodge et al 2007, Brada et al 2007).

However, not all proton interactions are due to electromagnetic interactions with atomic electrons. In fact, non-elastic interactions of the proton with atomic nuclei produce a broad spectrum of secondary neutrons as well as other spallation products. Non-elastic interactions occur with a probability of approximately 1–2% per cm of material traversed (Janni 1982, ICRU 1993, ICRU 1998, ICRU 2007). Neutrons of high energy and considerable penetrability are generated in the treatment head and may reach the patient and shielding barriers of the treatment room. Neutron exposures are a predominant consideration in the shielding design of the treatment room and may pose long-term carcinogenic risk to patients. Thus, knowledge of the neutron emission rate from the nozzle is crucial to the shielding design of the treatment head and treatment vault.

Two system types, passive and active (dynamic), are commonly used to deliver a proton beam treatment (Chu et al 1993, Miller 1995, ICRU 1998). In passive systems, the proton range and fluence are varied by directing the beam through a spinning range modulation wheel (RMW). The RMW, together with a second scattering foil that spreads the beam laterally, produces a spread-out Bragg peak (SOBP). Generally, the materials employed for range modulation are of low atomic number (Z) such as polymethyl methacrylate (PMMA), polycarbonate or aluminum (Koehler et al 1975, Chu et al 1993, Newhauser et al 2007). For lateral scattering, higher-Z materials such as lead are used. Also a system of collimators shapes the proton field laterally and a range compensator (or bolus) can be employed to shape the distal surface of the field. Recently, several companies have developed treatment nozzles with double scattering systems (Matsuda et al 2006). In some such systems a RMW modulates the beam at the same time when it spreads it laterally (Gottschalk et al 1991). After the RMW there is a second scatterer that further spreads the beam laterally. This second scatterer is made of a set of inner and outer disks. The outer section is made of a low-Z material while the inner is of high-Z material. The outer low-Z region compensates for the variable range shift caused by the inner high-Z component. With this approach, the dose distribution is laterally uniform and the beam's penetration remains constant at off-axis locations.

Conversely in active systems (or spot scanning systems), a proton pencil beam with variable energy, and hence range, is manipulated such that there is no need for scattering foils, aperture collimation nor range compensators. It had been stated that scanned beams produce a tenth of the neutron exposure of passive beam delivery (Schneider et al 2002), although more recent studies (Tayama et al 2006, Fontenot et al 2008) suggest that the difference is smaller. In fact, the literature about neutron production in active systems is sparse. Passively scattered proton therapy systems, the focus of this work, are of particular interest because the majority of operating proton therapy centers rely exclusively on passively scattered beam delivery methods.

In passive systems, as presented previously, the proton beam interacts with energy degraders, scatterers and collimators. The bombarding beam loses significant energy in these components making them the major sources of secondary neutron production (Agosteo et al 1998, Schneider et al 2002, Yan et al 2002, Polf and Newhauser 2005). These components are absent in some active beam delivery systems, thus suppressing neutron production. Schneider et al (2002) reported that the spot scanning system at the Paul Scherrer Institute (PSI) confers 1/10 the neutron dose 100 mm from the beam central axis than does the passive scattering system at the National Accelerator Center (NAC) in South Africa. The results from the NAC proton treatment facility appear atypical. The reported neutron equivalent dose values per therapeutic dose⁴ were significantly larger than those reported in more recent studies for other passive systems. These differences have not been resolved in the literature but may be traceable to the dose reporting methods as noted by Zheng (2007a). In addition, using Monte Carlo simulations, Agosteo et al (1998) estimated 10⁻³ Gy per therapeutic Gy for deep-seated tumors treatments due to neutrons and photons for active scanning systems. For passive systems the dose was of 10⁻² Gy per therapeutic Gy, again this study was also based on the NAC passive system. Yan et al (2002) reported for the three passive treatment systems at the Harvard Cyclotron Laboratory a neutron equivalent dose of approximately 10⁻³ Sv per therapeutic dose at 0 degree with respect to the beam direction, 0.5 m from isocenter. The higher neutron equivalent doses were found for the largest angles closer to the treatment nozzle with a maximum of 1.5 × 10⁻³ Sv. Recently, neutron equivalent doses of the same magnitude as the ones reported by Agosteo et al (1998) for active systems were reported by Tayama et al (2006) for the passive system at the Proton Medical Research Center (PMRC) at Tsukuba.

Recently Zheng et al (2007a, 2007b, 2008) used Monte Carlo simulations to study stray neutrons from the double scattering passive beam delivery system at the M. D. Anderson Cancer Center. In one of their studies (Zheng et al 2007a), they estimated the neutron dose equivalent at various distances from isocenter. For forward angles, the neutron dose equivalent per therapeutic dose decreased with distance from isocenter. At back angles as the distance increases the dose increased. Presumably this was due to the neutron production from the passive beam spreading devices upstream of isocenter. Thus at back angles (larger than 90°) the detecting surfaces are in fact closer to the nozzle and therefore closer to the main source of neutrons.

The objective of this work was to explore the sources of secondary neutrons, the neutron energy fluence, its associated absorbed dose per therapeutic Gy and the neutron absorbed dose per source particle for a contemporary passively scattered proton therapy system. The beam spreading system modeled in this work closely resembles that of The University of Texas M. D. Anderson Cancer Center (Newhauser et al 2007, Zheng et al 2007a, 2007b). The neutron energy spectrum and absorbed dose were investigated for this system as a function of neutron emission. The neutron production was characterized separately for each of the major beam-modifying components inside the treatment unit. The study utilized the Monte Carlo simulation technique to predict the radiation fields.

2. Methods and materials

2.1. Neutron absorbed dose and energy spectra determination

2.1.1. Monte Carlo simulations

The University of Texas M. D. Anderson Cancer Center proton beam delivery nozzle served as the basis for our model of a passive proton double scattering system. Specifically, it was used as a guide for the overall dimensions and the positions of the RMW, second scatterer and collimating system (Zheng et al 2007a, 2007b). However, we designed the RMW and second scatterer following the methods of Gottschalk et al (1991). This approach allowed for a design that was also representative of a second commercial proton therapy system (IBA, Belgium). Radiologically thin components, which produce minimal lateral scattering, energy loss and nuclear interactions, such as monitor chambers were not included because we believe they make minor contributions to neutron production in comparison to other components and also are specific to a given nozzle design.

To estimate the neutron production and subsequent transport, the Monte Carlo code package MCNPX developed by Los Alamos National Laboratory was used (Pelowiz 2005). This code allows simulations of the design of the desired geometry as well as the selection of the type of physics models that are appropriate for the type of particles to be simulated. While MCNPX can create and transport a large variety of particles, one can choose to transport only those of interest for a given situation. In the present case, only protons and neutrons were transported. In MCNPX, the sampled nuclear reaction cross-section data for most materials came from evaluated nuclear data libraries for energies from 0 to 150 MeV (Pelowiz 2005, Chadwick et al 1999). At energies above 150 MeV, physics models were used to estimate the interaction cross-sections. In this work, the physics model, employed was the intranuclear cascade model originally described by Bertini (1963). The cross-section information was combined from evaluated data and nuclear models using the ‘mix and match’ option in MCNPX. Hence, for any given particle's transport, the code used the data from the evaluated tables, when available, up to their energy limit and then used the physics models. Also, for particle transport, the energy cutoff used for protons and neutrons in this study was 1 × 10^-3 MeV and 0 MeV, respectively. The MCNPX code has been used extensively for research applications in proton therapy and benchmarked against measurements in numerous previous investigations (Heérault et al 2005, Koch and Newhauser 2005, Fontenot et al 2005, Newhauser et al 2005, 2007, Titt and Newhauser 2005, Tayama et al 2006, Polf et al 2007, Koch et al 2008, Titt et al 2008, Taddei et al 2008).

2.1.2. Geometry characteristics

A schematic diagram of the nozzle simulated is shown in figure 1 (Newhauser et al 2007, Zheng 2007a, 2007b). It consists of an RMW, a second scatterer, a set of collimators and a retractable snout with a final field-defining aperture. Table 1 presents the distances of the different nozzle components with respect to the RMW. The RMW was modeled as layers of lead and PMMA of various thicknesses, table 2, while the second scatterer was modeled as having geometry made of annuli of PMMA and disks of lead, table 3. The same scatterer was used for all simulations. The collimator system and snout materials were modeled as copper. The collimator system thicknesses are listed in table 1. Notice that the geometry simulated did not include the nozzle enclosure components which would attenuate the neutron fields somewhat. The internal collimators were modeled such that the inner aperture had dimensions of 300 × 300 mm² to avoid edge-scattering effects (Titt et al 2008) with the uncollimated therapeutic proton field of 180 × 180 mm², taken from the 50% to 50% profile width. Meanwhile the final collimator aperture was varied for the different sets of simulations, using 50 × 50 mm², 100 × 100 mm² and 150 × 150 mm² apertures. The thickness of the nozzle's collimating components were fixed for all field sizes, table 1. To obtain SOBP widths of 50 mm, 100 mm and 150 mm in depth, several simulations were combined, where each simulation included a single step of the RMW, which where modeled as right circular cylinders with variable thicknesses. The SOBP flatness in depth was achieved by varying the fluence weights of the individual RMW steps. Together, these adjustments provided field sizes with volumes of high dose regions of size 50 × 50 × 50 mm³, 100 × 100 × 100 mm³ and 150 × 150 × 150 mm³.

Figure 1.

Schematic diagram of the proton treatment nozzle simulated with MCNPX. The arrow (a) shows the direction of the monoenergetic 200 MeV proton beam. Also shown are (b) the RMW, (c) the second scatterer, the (d) first, (e) second and (f) third collimator set, (g) the snout's collimator, (h) the snout aperture, (i) the stopping-length water phantom (the phantom is long enough such that the proton beam stops in it) and (j) the neutron detecting surfaces.

Table 1.

Nozzle components and their respective distances from the RMW interface and thicknesses. The collimating components had an extension of 100 mm from the internal field definition with the exception of the snout apperture that has a fixed extension of 60 mm. The characteristics of the secondary scatterer are given in table 3.

Component	Distance (m)	Thickness (mm)
Secondary scatterer junction	0.856	–
First set of collimators	1.045	70
Second set of collimators	1.558	120
Third set of collimators	2.064	60
Snout's collimator	2.550	60
Final snout aperture	2.610	250

Table 2.

Areal density for the steps used to degrade the energy of the beam and obtained the desire SOBP for each of the treatment volumes simulated. The first eight steps were used for a 50 mm SOBP, the first 14 for the 100 mm and finally the 21 steps were used for the 150 mm SOBP.

Step number	PMMA (kg m−2)	Lead (kg m−2)
1	2.9	32.8
2	13.0	28.5
3	21.5	27.1
4	29.8	26.1
5	38.6	24.2
6	47.1	22.7
7	55.8	21.1
8	64.2	19.8
9	72.7	18.4
10	81.6	16.4
11	90.4	14.5
12	99.1	12.8
13	107.8	11.0
14	116.8	8.6
15	125.6	6.8
16	134.5	4.6
17	143.8	1.9
18	152.5	–
19	160.3	–
20	168.0	–
21	175.8	–

Table 3.

Second scatterer areal thickness as a function of the radial distance from the central axis. Each layer of the high-Z portion of the second scatterer was modeled as a disk and each layer of the low-Z was modeled as an annulus.

Radius (mm)	PMMA (kg m−2)	Lead (kg m−2)
0.1	0.00	29.40
5.04	0.91	27.72
10.08	3.37	23.18
15.12	6.81	17.32
20.16	10.47	10.05
25.20	13.37	4.65
30.24	15.11	1.44
35.28	15.89	0.00
40.31	15.89	0.00
45.35	15.89	0.00

In addition to the nozzle components, the simulated geometry included a water phantom whose front face was located at isocenter, 3.06 m from the RMW and 200 mm from the retractable snout. The water phantom had a radius of 150 mm and was 300 mm thick. Eight neutron-detecting surfaces were modeled at 4.06 m from the RMW and at angles of 0° and 5° as well as from 15° to 90° in 15° increments. These angles are formed from the high-Z to low-Z interface in the RMW with respect to the primary proton beam direction. Each detecting surface was the front circular plane of a right circular cylinder 250 mm in diameter oriented facing the RMW. For all simulations, a 200 MeV proton pencil beam was initiated upstream of the RMW on the central axis of the nozzle, interacting first with nozzle components, and then stopping in the water phantom. Some of these interactions produced neutrons, particularly in the RMW. Therefore, the neutron energy fluence was scored at each detecting surface and used to determine the neutron energy distribution and the neutron absorbed dose as a function of neutron emission angle.

2.1.3. Computational aspects

To obtain a set of data with good relative statistical uncertainty it was necessary to run simulations with as many as 150 × 10⁶ source protons, which is similar to previous studies of relevance to this work (Zheng et al 2007a, 2007b, Fontenot et al 2005). The simulations were run on a cluster (GLOW 2004) that comprised 66 computer nodes with two 2.8 GHz Intel Xeon CPUs per node and 29 nodes with two Intel Xeon CPUs of 3.20 GHz. Each simulation took approximately 270 cpu-hours.

2.1.4. Neutron absorbed dose and neutron energy spectra

The fluence of neutrons at each detecting surface was scored in energy bins ranging from 1.10 × 10⁻⁵ to 200 MeV. The bin energy boundaries up to 150 MeV were taken from the International Commission on Radiation Units and Measurements (ICRU) Report 63 (2000). Neutron absorbed dose was calculated on the assumption of secondary charged particle equilibrium and using the kerma approximation, or

$$D_{\mathrm{n}}=K={\int }_0^{\infty }{\mathrm{\Phi }}_{\mathrm{n}}(E_{\mathrm{n}})k(E_{\mathrm{n}})\mathrm{d}{E}_{\mathrm{n}}$$ (1)

where D_n is the absorbed dose (in Gy), Φ_n(E_n) is the neutron fluence (neutrons cm⁻² proton⁻¹) for a given energy and k(E_n) is the kerma coefficient for the same energy (fGy cm²) at neutron energy E_n. The assumption of secondary charge particle equilibrium is an approximation that is appropriate to the purpose of this study.

Kerma coefficients below 150 MeV neutron energy were taken from ICRU Report 63. The kerma coefficients above 150 MeV were estimated by fitting the ICRU data from 100 to 150 MeV with a third degree logarithmic extrapolation. This process created 10 bins that were equally spaced in the logarithm of neutron energy.

Additionally, the proton dose at the center of the SOBP, the so-called therapeutic dose in units of Gy, was obtained for each SOBP and field size studied. To accomplish this, the same nozzle design was used with a modified water phantom. The modification consisted of the addition of a small right circular cylinder inside the main water phantom and this small cylinder was used to score the proton absorbed dose as a function of depth along the central axis. This scoring cylinder had the same thickness as the outer one, a diameter of 20 mm and was sub-divided by planes placed 2 mm apart such that proton fluence could be scored as a function of depth. The absorbed dose was calculated using the cema approximation:

$$D_{\mathrm{p}}={\int }_0^{E_{\mathrm{p}}}{\mathrm{\Phi }}_{\mathrm{p}}\left[\frac{1}{\rho }\frac{\mathrm{d}{E}_{\mathrm{p}}}{\mathrm{d}x}\right]\mathrm{d}{E}_{\mathrm{p}}$$ (2)

where D_p is the proton absorbed dose (in Gy), Φ_p is the distribution of proton fluence for a given energy and dE_p/ρdx is the mass stopping power in water (MeV cm² g⁻¹) for protons of the respective energy. Stopping power values were taken from ICRU Publication 49 that were derived from the PSTAR database from Berger et al (2005).

2.1.5. Neutron contribution from nozzle components

Finally, the neutron contribution from each component along the proton beam central axis in the treatment nozzle was investigated using the same nozzle geometry shown in figure 1, but with a few modifications. Specifically, the detecting surfaces at different angles were eliminated and instead annular detecting volumes were placed at several locations on the beam central axis, including just downstream from the RMW, just downstream of the secondary scatterer and immediately upstream and downstream of the snout. The annuli were 1 mm thick right circular cylinders with radii ranging from 50 to 200 mm. The annuli material was set to vacuum such that neither the proton beam nor the neutrons created were perturbed by them.

3. Results and discussion

3.1. Neutron absorbed dose per therapeutic dose and neutron absorbed dose per source proton

Figure 2(a) presents the neutron absorbed dose per therapeutic absorbed dose normalized to the scoring distance squared, which we will denote as D_n/D_p, and figure 2(b) shows the neutron absorbed dose per source proton, also normalized, or D_n/N_p, as a function of neutron emission angle. The angles represent the position of the detecting surfaces presented in figure 1. Note in both figures, 2(a) and (b), that D_n/D_p and D_n/N_p are larger at forward angles, decreasing rapidly with increasing angle. The larger dose at small angles is influenced by the presence of the water phantom, which also contributed to the neutron production. As the angle increased, the detecting surfaces were further away from the phantom and hence the phantom contribution diminished.

Figure 2.

(a) Neutron absorbed dose per therapeutic absorbed dose multiplied by the distance square (D_n r²/D_p) and (b) neutron absorbed dose per source proton (D_n r²/N_p) for the three treatment volumes studied as a function of the neutron emission angle, θ, normalized by the distance square from the RMW interface to the detecting surface, 4.06 m.

The value of D_n/D_p is higher at forward angles smaller than 15°, for the largest treatment volume, followed by the 100 × 100 × 100 mm³ volume for which D_n/D_p is slightly higher than for the smallest one, figure 2. Between 15° and 30° there was a slight increase in D_n/D_p for the smallest treatment volume which may have been due to the presence of the additional collimating material that was needed at the snout to produce smaller proton fields. For angles larger than 30° D_n/D_p diminishes for all treatment volumes. The overall trend of higher dose with larger treatment volume is due in part to a larger contribution from the water phantom itself since relatively more protons reach the phantom and fewer stop in the final collimator.

An opposite behavior was observed for D_n/N_p shown in figure 2(b) at forward angles. The higher D_n/N_p was obtained for the smaller treated volume from angles between 5° and 30°. In this case the last collimator was the predominating source of neutrons. The smaller the aperture, the more beam is intercepted in the collimator thus producing more secondary neutrons with higher energies. However, for smaller fields the contribution from the RMW and the water phantom is less because the proton beam interacts with less RMW material and at the same time that fewer protons are needed to obtain the desired SOBP width.

3.2. Neutron energy spectra

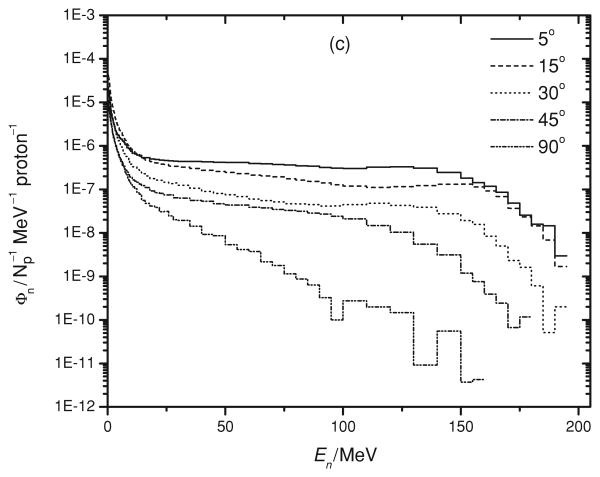
As shown in figure 3(a) to (c), the neutron production for angles less than 30° was uniform from a few MeV to around 160 MeV. Above these energies, the neutron fluence per solid angle per MeV decreased. At larger emission angles, the neutron production was less uniform and decreased sharply with neutron energy. There were a significant number of neutrons created at energies below a few MeV for all angles and we attributed this to the near isotropic production of evaporation neutrons. Even though these neutrons have low energy and generate little absorbed dose per neutron, they should be included in dosimetric considerations as their fluence is high. For instance, Yan et al (2002) observed a significant dose equivalent contribution from such evaporation neutrons for a 160 MeV proton beam. Similar neutron spectra have been predicted at other proton energies (Yan et al 2002, Fontenot et al 2005, Newhauser et al 2002).

Figure 3.

Neutron energy spectra, Φ_n, as a function of neutron energy, E_n, for the three studied volumes, (a) 50 × 50 × 50 mm³, (b) 100 × 100 × 100 mm³ and (c) 150 × 150 × 150 mm³ at various emission angles.

3.3. Neutron contribution from nozzle components

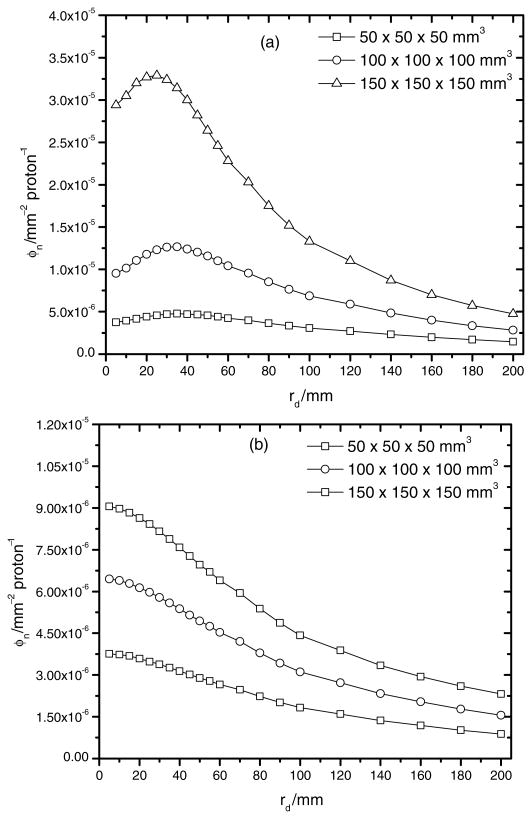
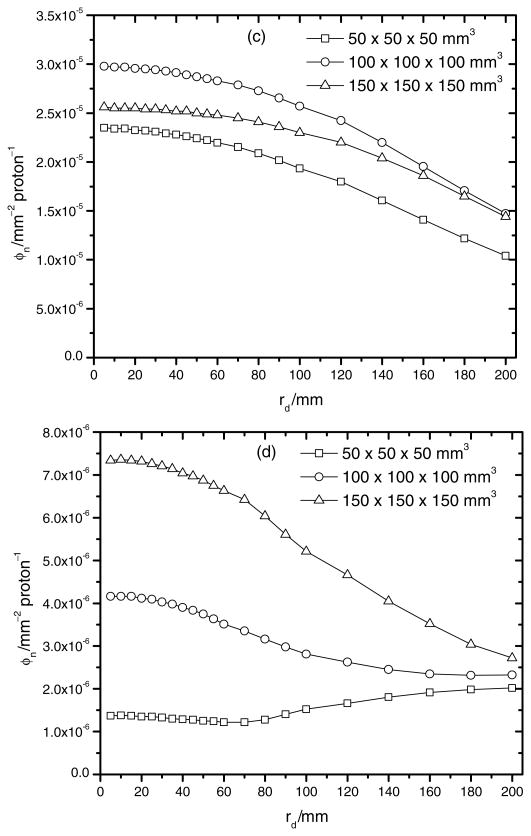
Figure 4 shows the neutron fluence per source proton at various locations downstream of the nozzle as a function of the radial distance from the central axis for each treatment field considered. Figures 4(a) and (b) present the neutron fluence per source particle just downstream from the RMW and the secondary scatterer, respectively. Both figures show a higher neutron production for the 150 × 150 × 150 mm³ treatment volume configuration. This result was expected since the largest areal densities of PMMA and lead were used in the nozzle for this treatment volume.

Figure 4.

Total neutron fluence, φ_n, as a function of radial distance r_d for the three studied volumes (a) just downstream from the RMW and (b) the second scatterer, (c) upstream and (d) downstream (d) of the snout.

Figures 4(c) and (d) show the neutron fluence per source particle immediately upstream and downstream of the snout. The neutron fluence per source particle is around a factor of 3–20 smaller downstream from the snout than upstream, and the largest difference was found for the smallest treatment volume. This increase in neutron fluence before the snout is attributed to backscattering. Several simulations were run to test this backscatter effect. In the simulations the density of copper was varied and the neutron fluence upstream of the snout was found to decrease considerably for the lower densities used.

In summary, the largest neutron fluence was found after the RMW for all radii studied with the exception of the backscatter effect. The neutron fluence downstream of the RMW decreases with distance from the RMW and for smaller treatment volumes the neutron fluence downstream of the RMW is not significantly higher than those detected downstream of the snout. This shows the competitive effect between both sources when small treatment volumes are irradiated.

Meanwhile, the interactions with the RMW produced the largest fluence of high-energy neutrons. Figure 5 presents the neutron energy spectra for the largest treatment volume at 25 mm radial distance from the central axis for the four positions studied. A significant number of high-energy neutrons were found up to a radial distance of 100 mm, indicating a predominant neutron production in the forward direction. The relative contribution to fluence of these high-energy neutrons decreases along the central axis and with increasing radial distance.

Figure 5.

Neutron energy spectra, Φ_n, as a function of neutron energy, E_n, at a radial distance of 25 mm from the central axes at the four positions studied for the 150 × 150 × 150 mm³ treatment volume: just downstream from the RMW (after RMW) and second scatterer (after second scatterer), just upstream and downstream of the snout (before snout and after snout, respectively).

The neutron contribution to fluence by the final snout was also studied for the smaller treatment volume and it is presented in figure 6. During the simulations the material of the final aperture was changed to vacuum. This allowed the determination of the influence of the final aperture over the final neutron fluence at the snout exit. The neutron fluence just downstream of the snout increases by approximately a factor of 5 due to the snout's presence.

Figure 6.

Neutron fluence, ϕn as a function of radial distance, rd, downstream of the snout when the material of the snout is set to copper and when set to vacuum. This was done to test the neutron contribution from the snout to the neutron fluence just downstream of it.

Also, it is relevant to mention that although the neutron contribution from other collimating components was not individually studied, their contribution was accounted for in the neutron absorbed dose calculations previously reported. The neutron contribution from the snout was studied in more detail because this is the component of the collimating system that interacts the most with the proton beam.

Overall, the RMW is the main source of neutrons within the nozzle, contributing also the largest fluence of energetic neutrons. Therefore, it may be important to characterize the neutron production in the RMW in order to refine shielding designs for the nozzle and the treatment vault. On the other hand, due to the neutron fluence dependence on distance from the source, neutrons created in the RMW will not contribute significantly to the dose at isocenter. Most of the neutron dose to the patient is due to interactions of the spread beam with the final collimating aperture.

3.4. Uncertainty

In general, a statistical uncertainty of approximately 5% was obtained in the results for the energy range of interest. This uncertainty is related to the statistical fluctuations in the Monte Carlo simulations and not with systematic uncertainties.

4. Conclusion

From the simulations performed we determined that the RMW is the nozzle's component that produces the most neutrons because it possesses the largest areal density of high-Z and low-Z material intercepting the proton beam. Such neutrons are forward directed with energies as high as the primary proton beam energy. Their production decreases with emission angle and distance from the main source of neutrons, RMW, increases. This suggests that the design of the appropriate room and nozzle shielding will be determined primarily by the RMW. At the patient's location the predominant source of neutrons comes from the snout. The RMW will also contribute neutrons but due to its distance from the patient this is not as significant. Although the snout contributes to backscattered neutrons, this is not directly relevant to the secondary dose to the patient. This should however be considered for the shielding of the treatment unit. An isotropic emission of evaporation neutrons was also observed. The proportion of absorbed dose from evaporation neutrons was small, but the neutron's fluence intensity was non-negligible for all angles studied. The presence of the water phantom contributed to the production of neutrons as well.

The data presented here provide insight to the determination of the neutron production at a given therapeutic dose and a given distance from the nozzle for similar nozzle configurations at 200 MeV proton energy. Varying components or conditions, for instance the secondary scatterer or the beam energy, will yield different neutron production ergo different absorbed dose. Nevertheless this work presents how each nozzle component contributes to the neutron production. Knowing the location and intensity of neutron sources inside the radiation treatment head may help guide the design of better local shielding. Tayama et al (2006) reported that by adding a pre-collimator upstream in the nozzle head it was possible to diminish the neutron equivalent dose per therapeutic dose. A similar study by Taddei et al (2008) showed that the addition of several shielding materials placed at different positions within the nozzle can reduce the stray radiation that reaches the patient. However, they did not attempt to localize the neutron sources and therefore could not design a low-mass shield that was suitable for installation on a rotating gantry. Based on the current results, it appears that designing a local neutron shield around the RMW is the next logical step toward achieving clinically practical improvements in the shielding of the treatment head.