Modeling Cortical Source Dynamics and Interactions During Seizure

Abstract

Mapping the dynamics and spatial topography of brain source processes critically involved in initiating and propagating seizure activity is critical for effective epilepsy diagnosis, intervention, and treatment. In this report we analyze neuronal dynamics before and during epileptic seizures using adaptive multivariate autoregressive (VAR) models applied to maximally-independent (ICA) sources of intracranial EEG (iEEG, ECoG) data recorded from subdural electrodes implanted in a human patient for evaluation of surgery for epilepsy. We visualize the spatial distribution of causal sources and sinks of ictal activity on the cortical surface (gyral and sulcal) using a novel combination of multivariate Granger-causal and graph-theoretic metrics combined with distributed source localization by Sparse Bayesian Learning applied to a multi-scale patch basis. This analysis reveals and visualizes distinct, seizure stage-dependent shifts in inter-component spatiotemporal dynamics and connectivity including the clinically-identified epileptic foci.

I. Introduction

Nearly 5% of patients with epilepsy are potential candidates for surgical treatment. Surgery for epilepsy can have a good chance of success if the brain region(s) generating seizures can be accurately localized. For this purpose, in selected cases recordings are acquired using intracranial (subdural and/or depth electrode) recording for pre-surgical evaluation. Here we describe some recent preliminary assays of the spatial and time-frequency dynamics of seizure generation and propagation in an intracranial EEG recording by Dr. Worrell at the Mayo Clinic (Rochester MN).

Under suitable conditions, a time-varying vector autoregressive (VAR) model provides a useful model for the analysis of oscillatory structure in stochastic time series [5] including brain electrical activity. From the VAR coefficients, we can obtain a number of useful quantities describing the spectral dynamics and causal relationships between elements of the system under observation. One proposed approach for identifying epileptic foci involves fitting VAR models to channel data and identifying electrodes that exert strong influence on other electrodes using the normalized Directed Transfer Function (DTF) (e.g. [6], [14]). Here we use the short-time direct DTF (SdDTF) [16] which measures direct (conditional) Granger-causal influences within a system of observed variables and normalizes over all outflows and inflows across all given time points and frequencies, making it possible to directly compare the amplitudes of the resulting causal measures across sources, time periods, and frequencies.

Volume conduction and relatively large inter-electrode distances can frustrate precise identification of epileptic foci as well as interpretation of inter-regional connectivity when considering only iEEG channel time-series. When the number of electrodes is large, the quality of a VAR model fit may additionally suffer. To reduce dimensionality and minimize effects of volume conduction, we apply SdDTF to partially-dependent component subspaces of an infomax independent component analysis (ICA) model trained on ECoG data collected before, during, and after two seizure periods. To identify the cortical regions critically participating in seizure generation and propagation, we apply Sparse Bayesian Learning (SBL) and a multi-scale patch-based source solution [1], [3], [2] to the maximally-independent source process projections, allowing us to directly visualize source and sink areas of multivariate Granger-causal influence on the cortical surface.

II. Theory

A. Adaptive multivariate autoregressive modeling

Assuming that X = [x₁, …, x_T ] is an M-dimensional zero-mean weakly-stationary stochastic process of length T, we can describe the linear dynamics of the state vector $x_t={[x_t^{(1)},\dots ,x_t^{(M)}]}^T$ as a vector autoregressive (VAR[p]) process of order p: $p:x_t={\sum }_{l=1}^p{A}_l{x}_{t-l}+u_t$, where u_t ∈ ℜ^M×1 is a zero-mean white noise process with covariance matrix $\mathrm{\sum }=\langle u_t{u}_t^T\rangle$.

The coefficient matrices, A_l, can be estimated using a number of approaches, including multivariate ordinary and stepwise least-squares approaches, lattice algorithms (e.g. Vieira-Morf) or state-space models (Kalman filtering) [8]. Neumaier and Schneider [12] provide an efficient stepwise least-squares algorithm which we use here. To deal with the non-stationary data, we model the time-varying cortical dynamics using a simple segmentation approach in which we fit separate VAR[p] models to a sequence of highly-overlapping locally-stationary windows [7].

B. Short-time Direct Directed Transfer Function

The Short-time Direct Directed Transfer Function (Sd-DTF) [16] from process j to i is obtained from a fitted VAR[p] model by

$${\eta }_{ij}^2(f,t)=\frac{{\mid H_{ij}(f,t)\mid }^2{\mid P_{ij}(f,t)\mid }^2}{{\sum }_{\mathit{klf}\tau }{\mid H_{kl}(f,\tau )\mid }^2{\mid P_{kl}(f,\tau )\mid }^2}$$ (1)

where $A(f)={\sum }_{l=0}^p{\widehat{A}}_l{e}^{-i2\pi fl}$, Â_l = −A_l, Â₀ = I and H(f) = A(f)⁻¹ is the transfer function of the system with spectral density matrix S(f) = H(f)ΣH(f)⁻¹, Ŝ = S⁻¹ and $P_{ij}(f)=\frac{{\widehat{S}}_{ij}(f)}{\sqrt{{\widehat{S}}_{ii}(f){\widehat{S}}_{jj}(f)}}$ is the partial coherence between variables i and j. It can be shown that ${\eta }_{ij}^2(f,t)$ will be nonzero if and only if there exists a direct (multivariate) Granger-causal influence from X _j to X_i at time t and frequency f.

C. Graph-theoretic measures

The causal participation of process j within the rest of the system can be represented by graph theoretic measures such as Outflow ${\mathrm{\Omega }}_j={\sum }_{i=1}^M{\eta }_{ij}^2$, Inflow ( ${\mathrm{\Upsilon }}_i={\sum }_{j=1}^M{\eta }_{ij}^2$), Causal flow (F_i = Ω_i − ϒ_i), and Causal asymmetry ratio ( $R_i=\frac{{\mathrm{\Omega }}_i-{\mathrm{\Upsilon }}_i}{{\mathrm{\Omega }}_i+{\mathrm{\Upsilon }}_i}$). Outflow characterizes the causal influence of a node on the rest of the system, while the degree to which a node is causally driven by other elements of the system is represented by the inflow. The causal flow and causal asymmetry ratios represent asymmetry in causal influence of a given node. Large positive values of F_i (or R_i = 1) indicate a causal source (a driving process) while large negative values (or R_i = −1) indicate a causal sink. Values near zero indicate balanced inflow and outflow or nonsignificant flow.

D. Source Separation and Localization

EEG recorded at each electrode pair can be modeled as linear instantaneous mixtures of latent brain sources, s_t. The generative model for an M-channel observed signal vector x_t can thus be written as x_t = As_t. An estimate of A can be obtained by ICA [4], which seeks to maximize the independence of assumed non-gaussian sources s_t. This approach has been demonstrated to be effective at separating both brain and non-brain sources of EEG and also iEEG activity [9].

We denote each column A_q the loading vector of the q^th independent component (IC) and the time course of the estimated sources s_t we denote IC activations. For each IC source q = 1, … , N we may obtain a solution to the multi-scale distributed source localization problem A_q = LH_q + ε where ε is a zero-mean noise process, L is an [M ×V ] lead-field matrix and H_q is a [V × 1] vector of weights for each of V elements of a cortical surface mesh. For more details on the construction of L and its multiscale extension see [2], [3], [1]. Although L is fat and ill-conditioned, we can obtain a unique solution for H_q by assuming source sparsity and applying Sparse Bayesian Learning [15]. We then obtain the [V × T ] matrix P_q of time-courses of the distributed cortical potentials (voltages) for the q^th IC by multiplying its [1 ×T ] activation time-course S_q by H_q.

E. Visualizing IC dynamics on the cortical surface

We can model the dynamics of and interdependencies between IC sources by fitting a VAR[p] model to the IC activations. While it may seem that physical (e.g., Granger-causal) interactions between and statistical independence of source processes (as assumed by ICA) are contradictory assumptions, it can be shown that for weakly coupled (e.g., partially coherent or transiently coupled) systems they may be reconciled, since weakly interacting sources may still be statistically independent or near-independent [17]. Infomax ICA only explicitly minimizes instantaneous dependencies, so time-delayed dependencies (e.g., Granger-causal influences) may be generally preserved, typically within low-dimensional component subspaces distinct from other non-affected source processes.

To obtain an estimate at each cortical surface mesh element of outflow, causal flow, spectral density or any other univariate measure derived from the VAR[p] model, we can simply multiply the estimate of the measure Φ_q computed for the q^th IC by H_q. If we wish to preserve the sign of Φ_q at each element, we may take the absolute value of the source weights H_q before this projection. When projecting measures for multiple ICs simultaneously, the weighted contributions from each IC are summed at each cortical surface element, normalizing each H_q to have a maximum of 1 to preserve the relative amplitudes of projected measures for different component processes.

III. Data collection and modeling

Intracranial EEG was collected from a patient undergoing presurgical evaluation at The Mayo Clinic (Rochester, MN). The patient presented with seizures due to a porencephalic cyst in the fronto-parietal brain. Seventy-eight channel iEEG data was collected at a sampling rate of 500 Hz during drowsy resting. We selected for analysis a 16-minute epoch of data containing two seizure bursts, each lasting about 2 minutes. The data were decomposed by extended Infomax ICA into 78 maximally-independent processes. By visual inspection, 16 ICs were identified as exhibiting clear epileptiform activity; remaining ICs were ignored for present purposes. The selected ictal ICs were then localized as described in section II-D and in [2], [11].

The time courses of the ictal ICs were downsampled to 256 Hz after application of a zero-phase FIR antialiasing filter. Each IC activation sequence was then independently z-normalized. A 16-dimensional VAR[7] model was fit to the normalized IC activations using ARFIT stepwise least-squares [12]. An adaptive model was realized using a 15-sec sliding window with 1-s step size. The model order (p=7) was selected based on inspection of the distribution, over all windows, of model orders that minimized the Hannan-Quinn information criterion. For each window, the power spectral density and SdDTF estimators were obtained from the model coefficient and noise covariance matrices, as described in Section II-B. Outflow, inflow, causal flow, and causal asymmetry ratio were computed for each IC source. Statistical significance of causality was assessed by reference to a surrogate null distribution constructed by repeatedly (500x) fourier transforming each time series, replacing the phases at each frequency with uniformly random numbers in [−π, π] and applying the inverse fourier transform. This destroyed all phase structure in each time-series, while preserving its power spectrum.

IV. Results

Figure 1 shows the time course of activations of the selected ICs around the scattered onset (left) and abrupt offset (right) of the first seizure. IC12 exhibits earliest onset of ictal activity, followed closely by ICs 1, 11 and 13.

Fig. 1.

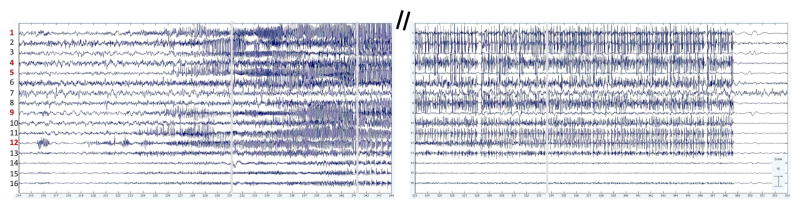
Time course of activations of selected ICs during first seizure onset (left) and offset (right). Time units are in seconds. ICs with red labels are those with SBL source solutions shown in Figure 2

IC12 accounted for prominent interictal discharges (IEDs) at the epileptogenic focus, but did not appear to be a strong causal outflow hub during the seizure. Our analysis revealed significant spectral power and SdDTF interactions between IC processes during the seizure in the theta, alpha, and beta frequency ranges (Figure 2). To visualize the time course and distribution of sub-networks potentially involved in seizure propagation (causal hubs), at each time point and for each IC the spectrum and graph-theoretic measures were integrated from 4–30 Hz (theta through beta bands) and projected onto the cortical surface mesh as described in section II-E.

Fig. 2.

SBL Solutions for selected components. A representative SdDTF time-frequency image shown on bottom right. Note the mid-seizure burst of connectivity in theta, alpha, and beta bands.

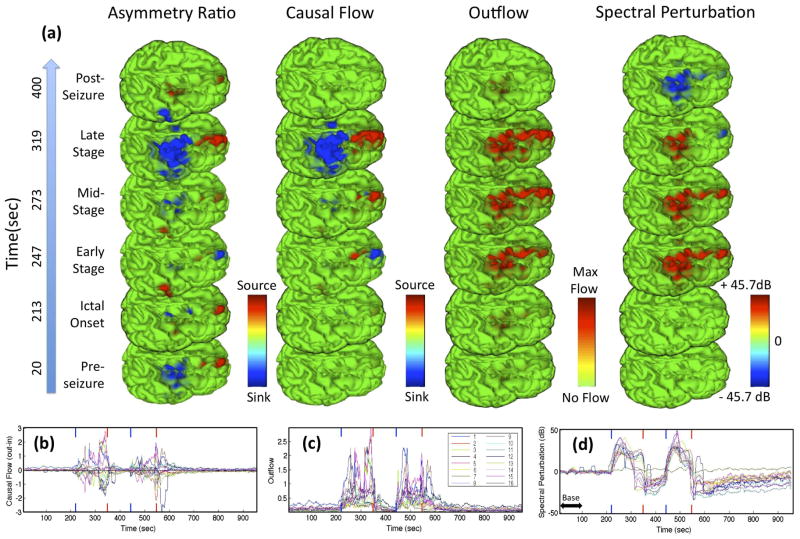
Figure 3 shows a sequence of frames from animations visualizing the projections of outflow, causal flow, causal asymmetry, and spectral perturbation (all integrated from 4–30 Hz) during the first seizure. The time-varying amplitudes of the measures are also plotted for all ICs. At least three distinct stages appear during each seizure(s). IC1 (blue trace, Fig. 3(b–d)) and (transiently) IC9 (brown trace) appear to be the dominant causal sources during the first stage of the seizure (particularly driving frontopolar IC5, pink trace). IC5 dominates in the second stage (with some feedback into IC1,9) and finally joined by other frontal sources in the third, final stage. This final stage of the seizure is characterized by strong dorsofrontal → precentral (e.g., IC4, dark blue trace) synchronization. While the causal flow measure more clearly delineates the driving causal hubs throughout the seizure, it does not distinguish between zero flow (network decoupling) and balanced flow (symmetric information flow) and thus should be examined in combination with another measure such as outflow.

Fig. 3.

Panel (a) shows a sequence of frames from animations mapping 4–30 Hz causal and spectral measures projected onto the cortical surface before, after and during different stages of the first seizure. Colormaps bounded at 99th percentile. Panels (b–d) show, respectively, the causal flow, outflow, and spectral perturbation (deviation from 1–100 second baseline power indicated by horizontal doublearrow) for all IC sources as a function of time. Blue (Red) vertical ticks denote onset (offset) of both seizures. High resolution version of this and other images available at [18].

The causal asymmetry ratio metric revealed an interesting spatial motif involving two clusters of dorsal frontal and precentral sources close to the electrodes identified clinically as exhibiting epileptiform activity. This motif, involving a strong positive dorsal frontal causal asymmetry and negative dorsal parietal asymmetry, is evident throughout the pre-seizure period in the causal flow measure and then reappears, more saliently, in the final stage of the seizure, possibly indicating a susceptibility of cortex in these areas to dynamic interdependency. In a parallel analysis using adaptive mixture ICA, these same frontal and parietal regions appear as two quasi-independent component subspaces, suggesting they are functionally distinct local processes that may interact as seen here near seizure end [2]. The second seizure (not shown) had quite similar multi-stage dynamics.

V. Conclusions and Future Work

In this paper we analyzed neuronal dynamics during epileptic seizures using adaptive multivariate autoregressive models applied to ICA sources of intracranial EEG data recorded from subdural electrodes implanted in a human patient for presurgical monitoring. We examined the spatial distribution of time-frequency information flow dynamics in the source domain using a novel combination of causal flow metrics and SBL-based source localization. This revealed that causal source and sink hubs emerged during the seizure. We observed distinct stages of alternating feedforward and feedback information flow between adjacent or overlapping gyral and sulcal sources in a prefrontal network (elements of which also expressed the primary epileptogenic focus). This activity might possibly be maintained through short U-fiber connections. In the final seizure stage this was followed by a strong asymmetric spread of sustained theta-alpha-beta ictal activity from this anterior frontal network to a dorsal parietal/precentral gyrus network, possibly though cortico-cortical white matter tracts or subcortical U-fibers.

To our knowledge, this preliminary report represents the first time that these techniques have been combined to analyze spatially-localized information flow dynamics in electrophysiological data. We note that ground-truth validation of the method will require new multi-resolution electrical recording methods. We speculate that the temporal resolution and goodness-of-fit of the VAR model under non-stationary conditions may be improved through the use of a state-space representation of the adaptive VAR model. This would also allow real-time online updating of the VAR coefficient matrices and thereby possibly improve the robustness of the method. Finally, our approach may be readily extended to modeling source dynamics from scalp EEG, broadening its applicability for clinical monitoring or basic cognitive neuroscience research applications.