Benchmark measurements and simulations of dose perturbations due to metallic spheres in proton beams

Abstract

Monte Carlo simulations are increasingly used for dose calculations in proton therapy due to its inherent accuracy. However, dosimetric deviations have been found using Monte Carlo code when high density materials are present in the proton beam line. The purpose of this work was to quantify the magnitude of dose perturbation caused by metal objects. We did this by comparing measurements and Monte Carlo predictions of dose perturbations caused by the presence of small metal spheres in several clinical proton therapy beams as functions of proton beam range, spread-out Bragg peak width and drift space. Monte Carlo codes MCNPX, GEANT4 and Fast Dose Calculator (FDC) were used. Generally good agreement was found between measurements and Monte Carlo predictions, with the average difference within 5% and maximum difference within 17%. The modification of multiple Coulomb scattering model in MCNPX code yielded improvement in accuracy and provided the best overall agreement with measurements. Our results confirmed that Monte Carlo codes are well suited for predicting multiple Coulomb scattering in proton therapy beams when short drift spaces are involved.

1. Introduction

The theoretical advantages of proton beam therapy derive mainly from the ability to deliver large doses to the target volume while largely sparing the surrounding normal tissues. This advantage depends on accurate dose calculations in the treatment planning process and accurate delivery of the planned proton treatment fields. Dose calculations are commonly performed with fast analytical models such as the pencil beam algorithm, which has been studied in considerable depth (cf. Carlsson et al., 1997; Hollmark et al., 2004; Hong et al., 1996; Petti, 1992, 1996; Russell et al., 2000; Schaffner, 2008; Schaffner et al., 1999; Soukup et al., 2005; Szymanowski and Oelfke, 2002). The dosimetric accuracy of pencil beam algorithms on voxelized patient anatomy is adequate in most situations (Schaffner et al., 1999; Szymanowski and Oelfke, 2002). The Monte Carlo method has increasingly been applied to in conjunction with analytical dose algorithms, e.g., to generate their configuration data (cf. Koch and Newhauser, 2005; Newhauser et al., 2007b; Russell et al., 2000) to validate their dosimetric accuracy (Koch and Newhauser, 2010; Newhauser et al., 2005), and to model stray and leakage radiation exposures (cf. Jarlskog and Paganetti, 2008b; Moyers et al., 2008; Newhauser et al., 2009; Polf and Newhauser, 2005; Taddei et al., 2009; Zheng et al., 2007). Most dose algorithms contain approximations that limit their accuracy, particularly in cases where the proton beam interacts with metal objects such as the treatment head, implanted fiducial markers, and prostheses. In theory, the Monte Carlo method should be the most physically realistic method, but in practice approximations are made that can cause potentially large dosimetric errors. The rationale for making such approximations include the need to balance accuracy against execution speed and, in some cases, the lack of interaction data and models that would be needed for an exact approach. Examples where approximations may be dosimetrically important include charged particle stopping powers, energy straggling, multiple Coulomb scattering, and non-elastic nuclear reactions.

Multiple Coulomb scattering is a particularly important mechanism in proton therapy calculations because it determines, to a large extent, how a proton trajectory deviates from a straight line. These deviations produce important features in the resulting absorbed dose distribution and therefore multiple Coulomb scattering is usually taken into account, using approximate methods, for dose calculations in proton therapy. The dosimetric effects of multiple Coulomb scattering calculations is particularly strong in cases in which the drift space is long, the proton beam passes through large heterogeneities, high-Z objects, and for field sizes that are small. Sawakuchi et al (2008) reported that multiple Coulomb scattering within the heterogeneities is the main contributor to distal edge degradation of Bragg peak and the small-angle scattering events are mainly caused by multiple Coulomb scattering. Herault et al. (2005) reported Monte Carlo simulations using the MCNPX code (Hendricks et al., 2006) that over predicted the multiple Coulomb scattering in a high-Z (tantalum) foil with respect to measurements. Stankovskiy et al. (2009) also reported the over-prediction of the scattering angle for thin foils by the Gaussian approximation in the MCNPX code, and extended the observation to light materials in addition to high-Z materials. The results of these findings are important because they revealed potential for large dosimetric errors in dose calculations involving some clinical proton treatment beams.

In recent years, there has been increasing interest in patients with metal objects in the therapeutic radiation field, particularly for external-beam radiotherapy (cf. Cheung and Yu, 2005; Reft et al., 2003) but also for brachytherapy (Nath et al., 1999; Xia et al., 2005). Comparatively little consideration has been given in the literature to the dosimetric perturbations of metal objects in the path of therapeutic proton beams. The perturbations are caused by the substantially different radiation interaction cross sections of human tissues and metals, e.g., the mass energy and absorption coefficients for photons and the mass stopping power and mass scattering power for charged particles. The dose perturbations introduced by metal implants may cause hot or cold spots, which may lead to increased risk of normal tissue complications, local failure, or both. Verhagen and Palmans (1999) reported on a theoretical investigation of the perturbation of secondary electron spectra near the planer interfaces of thin, semi-infinite high-Z slabs and a water phantom. Their study was based on Monte Carlo simulations of 50-MeV to 250-MeV proton beams and revealed up to a 5% dose increase upstream and a 2% dose decrease downstream of the interface. The literature contains few investigations of clinically-realistic metallic implants in proton fields, and only a fraction of these included measurements. Tourovsky et al. (2005) carried out a treatment planning case study involving a two-field proton beam treatment of a sacral chordoma in which the patient had a large metal implant in the treatment field. They reported significant differences between the dose distribution predicted with an analytical pencil beam dose algorithm and the corresponding dose distribution from Monte Carlo simulations. Schneider et al. (2004) measured the influence of a titanium alloy prosthesis on secondary neutron doses caused by proton interactions within the implant. Newhauser et al. (2007a) and Giebeler et al. (2008; 2009) reported on measurements that confirmed the accuracy of the MCNPX code for modeling the multiple Coulomb scattering in millimeter size implanted fiducial marker of tantalum, gold, and stainless steel. Together, these studies reveal two important facts, namely, that metal-induced dose perturbations can be substantial, and that Monte Carlo simulations can predict them with adequate accuracy in some cases but not in others. They also revealed that our knowledge of attainable accuracy is incomplete, as is our understanding of the factors that govern it.

The major aim of the current study was to quantify the magnitude of absorbed dose perturbations caused by the presence of small metal spheres in clinical proton therapy beams. In addition, we investigated the accuracy of the predicted dose distributions as a function of proton beam range, and drift space beyond the spheres. Predictive methods included the MCNPX and GEANT4 Monte Carlo codes and the FDC track-repeating algorithm.

2. Methods

2.1. Measurements

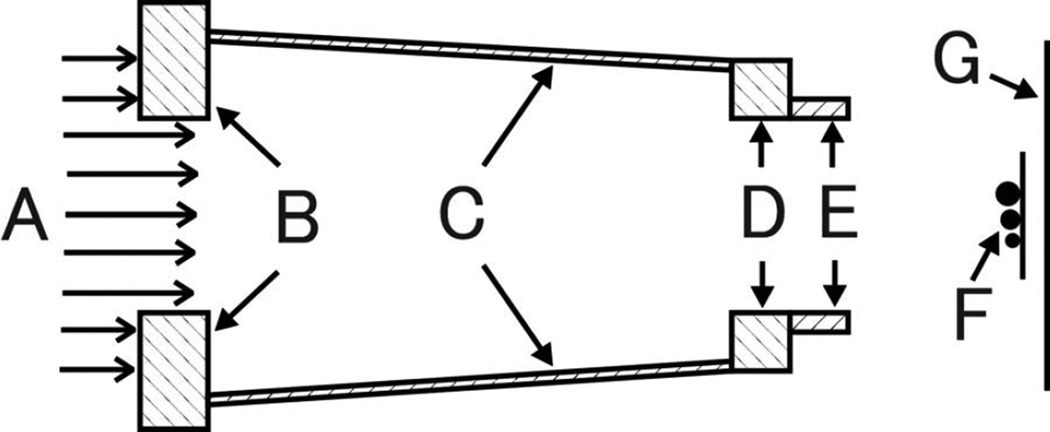
A test phantom was created in which stainless steel (ρ = 8.5 g/cm³, 69% Fe, 20% Cr, 10% Ni, and 1% Si by mass) spheres of diameters 6.4 mm, 9.5 mm, and 15.9 mm were affixed to a 5-mm-thick slab of polymethyl methacrylate (commonly known under the Lucite trade name, GE Plastics, Inc., Pittsfield, MA, C₅H₈O₂, ρ = 1.19 g/cm³). Table 1 shows the properties of the steel spheres. These sizes were chosen because they are representative of medium or large implants, i.e., they are larger than the implanted fiducial markers, which were already studied in several previous investigations. The spherical shape was selected to avoid dosimetric artifacts associated with angular misalignment that are possible with non-spherical objects, a confounding factor encountered in a previous study (Newhauser et al., 2007c). A schematic diagram of the phantom setup is shown in Fig. 1.

Table 1.

Properties of metallic objects, including shape, size, material, and orientation of the rotational axis of symmetry with the proton beam central axis. The values in the size column correspond to the sphere’s diameter. The rightmost column lists alpha-numeric labels for each combination of object and orientation investigated.

Shape	Size [mm]	Material	Symbol
Sphere	6.4	Stainless steel	SS-1
Sphere	9.5	Stainless steel	SS-2
Sphere	15.9	Stainless steel	SS-3

Fig. 1.

Schematic diagram of the geometry for irradiating the stainless steel spheres. The proton beam (A) is collimated with a square precollimator (B), snout (C), snout base plate (D), and 175-mm-diameter final collimating aperture (E). The spheres (F) are mounted on a thin plastic plate, and radiographic film (G) measurements provided estimates of the absorbed dose at distances of 20 mm, 150 mm, and 630 mm behind the mounting plate. This geometry was also used to simulate irradiations of the small cylindrical and spherical gold fiducial markers.

Measurements were performed using an unmodulated 160-MeV proton beam on the large-field nozzle at the Harvard Cyclotron Laboratory (Cambridge, MA) (Koehler et al., 1975, 1977; Polf and Newhauser, 2005). The field was collimated to 180 mm in the isocentric plane. The range of the proton beam was set to 40 mm, 80 mm, 120 mm, and 161 mm in water using a plastic range shifter system. Table 2 gives the details of the beam arrangement.

Table 2.

Proton therapy beam characteristics for measurements and simulations of metallic object irradiations, including the proton energy (E_p), the range in water to the distal 90% absorbed dose point (R₉₀), the proximal-90%-to-distal-90% Bragg peak width (w_90-90), and the collimated circular field diameter (d) at the isocentric plane. The column at the far right lists an alpha-numeric label for the experimental condition.

EP [MeV]	R90 [mm]	w90-90 [mm]	d [mm]	Label
160	161	4.5	180	SS-16
128	120	4.5	180	SS-12
102	80	4.5	180	SS-08
70	40	4.5	180	SS-04

For each proton beam range setting, radiographic film (X-Omat V; Eastman Kodak Co., Rochester, NY) was placed at distances, or air gaps, ranging from 20 mm to 630 mm behind the metal spheres in air. The films were exposed to an absorbed dose of 400 mGy to 500 mGy as measured according to the methods described Newhauser et al. (Newhauser et al., 2005; 2002), digitized (0.36-mm² spatial resolution) with a 16-bit scanning optical densitometer (VXR-16 DosimetryPro, Ser. No. 102318; Vidar Systems Corporation, Herndon, VA), and converted from optical density (OD) to absorbed dose using a measured calibration curve (Newhauser et al., 2005). The DOSELAB package (Childress and Rosen, 2003) was used for processing the digital images of the films, including background subtraction, conversion from optical density to absorbed dose, and correction for scanner non-uniformity.

2.2. Simulations

Monte Carlo simulations of the experimental conditions were carried out with two widely-used general-purpose Monte Carlo radiation-transport codes, MCNPX, and GEANT4, and an in-house track-repeating code called FDC. The remainder of this section provides brief descriptions of these codes and their implementations in this study.

2.2.1. MCNPX Simulations

Simulations were performed with the MCNPX code (version 2.7a) (Hendricks et al., 2006) which provides a comprehensive suite of physics models. The models used in this study included ion energy loss via the continuous slowing-down approximation, energy straggling based on the theory of Vavilov (1957), and elastic and nonelastic nuclear interactions based on evaluated cross-section data (Chadwick et al., 1999) or, in cases where evaluated data were not available, using the default Bertini internuclear cascade model (Bertini, 1969). Multiple Coulomb scattering based on the Gaussian approximation (Rossi, 1952) of Moliere’s theory (Moliere, 1948) and on a recently reported enhancement described by Stankovskiy et al. (2009) and implemented by us in MCNPX. Primary protons and secondary protons were tracked down to 1 MeV, at which point the residual energy was deposited locally. In previous benchmarking studies, we validated the accuracy of the simulation model for predicting dose distributions in homogeneous water phantoms (Fontenot et al., 2005; Polf and Newhauser, 2005; Polf et al., 2005) and phantoms with limited heterogeneity (Titt et al., 2008); this study focused on extremely heterogeneous geometries. The models of the proton source and treatment head were taken from previous investigations (Polf and Newhauser, 2005; Polf et al., 2005). The proton beam properties in the simulations were set to match the experimental beams described in section 2.1.

Energy deposition per unit volume in air was scored with two-dimensional mesh tallies (0.5 mm³ rectilinear grid) at 10 crossfield (x–y) measuring planes. 120 × 10⁶ proton histories were required to obtain uncertainties of less than 8% (one standard uncertainty) immediately downstream of the metal sphere locations. Simulations were carried out on a cluster of 115 dual-node 32-bit processors (Pentium; Intel, Santa Clara, CA) running Linux (Red Hat 7.3, kernel version 2.4; Raleigh, NC), MPI-CH parallel computing software (Gropp et al., 1996), and commercial queuing software (PBS Pro, version 5.4; Altair Engineering, Troy, MI). Variance reduction techniques incorporating mesh-based weight-windows were used, which reduced the statistical uncertainties by a factor of approximately two for an identical number of histories.

2.2.2 GEANT4 Simulations

We used the GEANT4 tool kit (version 4.8.3) (Agostinelli et al., 2003; Allison et al., 2006) to create an in-house Monte Carlo transport code specifically to simulate the measurements described above. In this work we utilize the low-energy parametrized model (Chauvie et al., 2004). This model takes into account atomic and shell effects and is applicable down to 250 eV. It uses the Bethe-Bloch formula to calculate hadron ionization down to 2 MeV, and a ICRU 49 parameterization (ICRU, 1993) in the range 1 keV to 2 MeV. Below 1 keV the free electron gas approach was implemented. The energy straggling is calculated with a Gaussian distribution with Bohr’s variance (ICRU, 1993) for distances long enough for the approximation to be accurate. For short distances a simple model of the atom is used (GEANT4 Physics Reference Manual, www.cern.ch/geant4): The multiple Coulomb scattering of protons is estimated with a condensed simulation algorithm, in which the global effects of the collisions are estimated at the end of a track segment. It uses model functions to determine the angular and spatial, which functions have been chosen in such a way as to give the same moments of the (angular and spatial) distributions as the Lewis theory (Lewis, 1950).

For elastic hadronic interactions the low-energy parameterized model (G4LElastic) was implemented. Inelastic interactions were simulated with the pre-equilibrium model (G4PreCompoundModel) in the range of interest to our simulations (0–250 MeV). The model is based on Griffin’s semi-classical description of composite nucleus decay (Griffin, 1966; Gudima et al., 1983; Lara and Wellisch, 2000).

Primary protons and secondary protons were tracked down to < 1 MeV, at which point the residual energy was deposited locally. A more detailed description of the models used in proton therapy can be found elsewhere (Jarlskog and Paganetti, 2008a) Previous benchmarking studies (Cirrone et al., 2006; Jarlskog and Paganetti, 2008a; Randeniya et al., 2009) validated the accuracy of the simulation model for predicting dose distributions in a homogeneous water phantom; the simulations here focus on severely heterogeneous geometries.

The simulation was implemented with a simplified model of the proton source and treatment head that were developed in previous studies (Polf and Newhauser, 2005; Polf et al., 2005). The initial proton beam was approximated as a point-source located 549 cm from the steel spheres, corresponding to the location of the lateral scattering foil. The range shifter system was modeled as a slab of 1.15 cm Lucite, yielding a penetration of 16.1 cm in water. Dose distributions were estimated from tallies of energy deposition per unit volume in air. This was tallied in a 91×31×643 mm³ matrix sub-divided into 1-mm isotropic voxels. 38×10⁶ proton histories were required to obtain uncertainties of less than 2% (one standard uncertainty) immediately downstream of the metal sphere locations. Simulations were carried out on a cluster of 1072 central processing unites (CPUs). The CPUs were contained in 134 nodes, each node comprising eight 64-bit CPUs (Xeon E5440; Intel, Santa Clara, CA) and operated at 2.83 GHz clock speed. Each node was provisioned with 16 GB RAM per node, which was shared among all CPUs on the node. The cluster utilized the Linux operating system (Red Hat Enterprise 5, kernel version 2.6; Raleigh, NC).

2.2.3 Track-Repeating Calculations

The track repeating algorithm proposed by Li et al (2005) and Yepes et al (2009a) predicts dose distributions using two conceptually distinct steps, first the pre-computation of proton trajectories or “tracks” in a homogeneous water phantom using a Monte Carlo code. Then, for the geometry under investigation, the proton tracks are reused or “repeated”, where the pre-computed tracks are adjusted to take into account any differences in the materials relative to the materials used to generate the pre-computed tracks. Specifically, the adjustments include approximate methods to scale energy loss and scattering angles of the proton tracks. The motivation to the test track-repeating algorithm is twofold. First, it is expected to provide good dosimetric accuracy regions of severe heterogeneity, e.g., the air-bone interfaces in the paranasal sinus, where the accuracy of analytical dose algorithms is limited. Second, it is faster than Monte Carlo simulations, which are presently too slow for routine clinical treatment planning.

We used the GEANT4-based code (described above) to pre-compute 15 million 251 MeV proton tracks impinging on a 550×550×500 mm³ water phantom and stored them on the database of tracks as described in Yepes 2009a. We used the Fast Dose Calculator (FDC) implementation of the track repeating algorithm, which was previously described by Yepes et al. (2009a, b). In the FDC code, we modeled the steel balls and their mounting plate according to the description in Section 2.1. Identical tallies to those used in GEANT, described in section 2.2.2, were added to record the predicted dose distributions corresponding to the measurements, also described in Section 2.1. 15×10⁶ protons histories were required to obtain uncertainties of less than 2% (one standard uncertainty) immediately downstream of the metal sphere locations. Simulations described in this section were performed using the computer system described in Section 2.2.2.

3. Results

Each of the three sizes of stainless steel spheres introduced clearly discernable dose perturbations in all experimental conditions considered, as shown in the two-dimensional dose image in Fig. 2. Figs. 3–5 plot the lateral one-dimensional dose profiles extracted from the two-dimensional x–y dose distributions. From Figs. 3–5, several major findings are apparent: the dose perturbations increased with the size of the sphere and with the distance from the sphere to the measuring plane; the perturbations also increased with decreasing proton beam energy; and the predictions were in generally good agreed well with the measurements.

Fig. 2.

Measurements of proton absorbed dose perturbations caused by 6.4-mm, 9.5-mm, and 15.9-mm diameter stainless steel spheres. These images qualitatively illustrate that the dose perturbations is clearly influenced by the sphere diameter, the proton beam range (R₉₀), and the gap (G) or drift space between the spheres and the measuring plane. With a 20-mm air gap (panels a and c), the dose enhancements near the circumference of the spheres’ images are caused by lateral scattering of the proton beam. In the central region of the largest sphere, where protons lose the most energy, there is an increase in the dose due to an increase in the proton mass stopping power. At a 150-mm air gap, the dose perturbations are predominantly shadows caused by out-scatttering of protons that pass through the spheres (panels b and d). In these images, the color progression from dark blue and dark red corresponds to increasing relative absorbed doses.

Fig. 3.

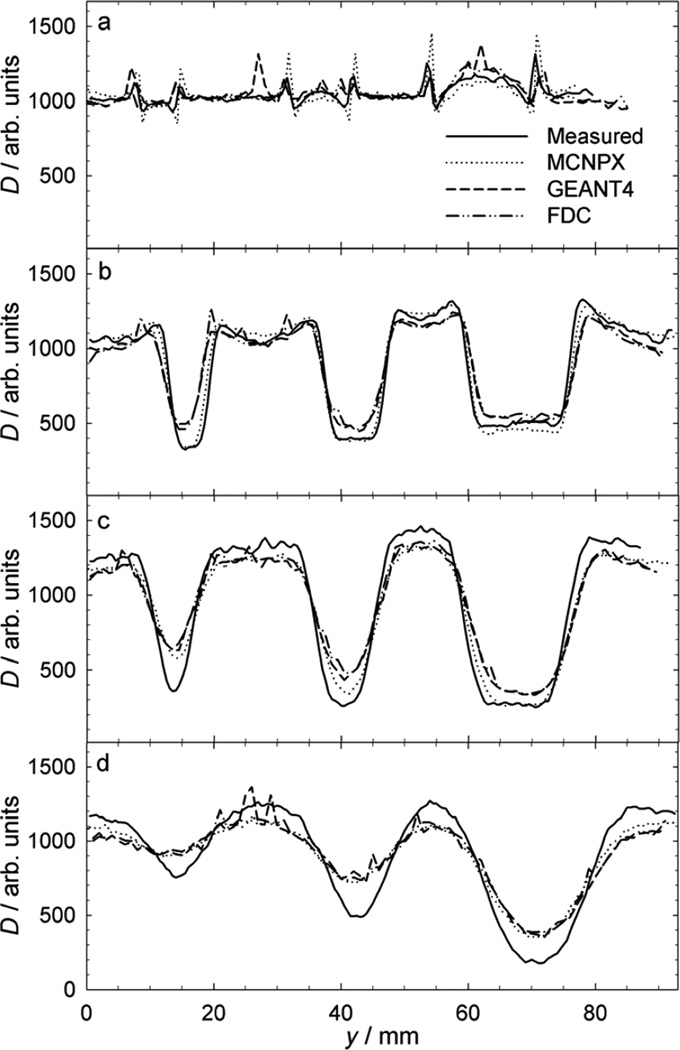
Measurements of normalized absorbed dose (D) versus lateral position (y), revealing perturbations caused by 6.4-mm, 9.5-mm, and 15.9-mm diameter stainless steel spheres in a proton beam with a mean residual range of 161 mm. These profiles reveal the influence of the sphere diameter and the gap (G) or drift space between the spheres and the measuring plane. The air gaps presented are (a) 20 mm, (b) 150 mm, (c) 300 mm, and (d) 630 mm. The dose enhancements tend to decrease with increasing air gap size. The dose reductions tend to increase with increasing air gap and with decreasing beam range.

Fig. 5.

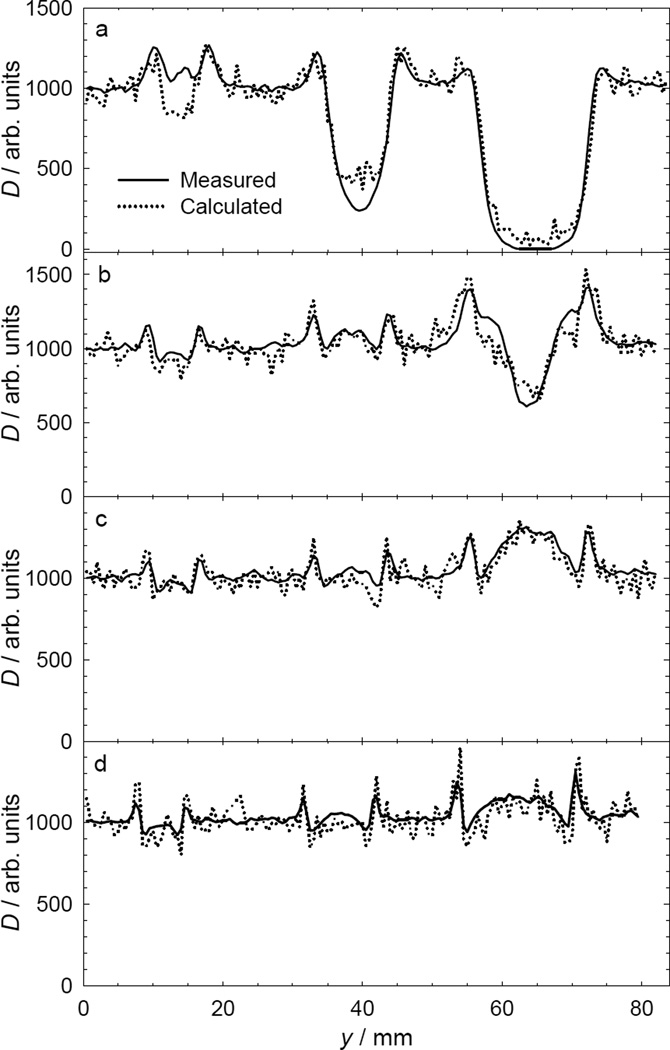
Measurements of normalized proton absorbed (D) dose versus lateral position (y) at 20 mm downstream distance from 6.4-mm, 9.5-mm, and 15.9-mm-diameter stainless steel spheres, revealing the influence of the sphere diameter and the proton beam range (R₉₀) on the dose perturbation caused by the spheres. Beam ranges are (a) 40 mm, (b) 80 mm, (c) 120 mm, and (d) 161 mm. The dose reductions tended to increase with decreasing beam range.

Table 3 lists the maximum measured and simulated dose perturbations for the 12 cases considered. The percentages of perturbation, with respect to the local unperturbed dose, are listed separately for dose enhancement (+ΔD) and dose reduction (−ΔD). The measured +ΔD values for the small, medium, and large spheres were in the intervals of 1% to 12%, 7% to 16%, and 3% to 31%, respectively, while simulated +ΔD values were in the intervals of 0.3% to 25%, 1% to 30%, and 1% to 42%. The measured −ΔD values for the small, medium, and large spheres were in the intervals of −8% to −69%, −5% to −79%, and −6% to −85%, respectively, while simulated values were in the intervals of −3% to −69%, −2% to −77%, and −5% to −82%. Figs. 3–5 provide illustrative examples comparing absorbed dose profiles from measurements and predictions with MCNPX, GEANT4, and FDC. These figures also reveal the dependence on penetration range, air gap, and sphere size.

Table 3.

Comparison of the predicted (simulated) and observed (measured) absorbed dose perturbations caused by stainless steel spheres listed in the leftmost column. The values listed include the air gap (G) between the Lucite plate holding the spheres and the measuring plane, and measured and predicted dose enhancements (+ΔD) and reductions (−ΔD) behind the steel spheres, and the difference between the percentage predicted and observed dose perturbations. The beam range was 161 mm for all 12 cases here.

			+ΔD [%]					−ΔD [%]
Sphere Label	G [cm]	Meas.	Pred. (MCNPX)		Pred. (Geant4)	Pred. (FDC)	Meas.	Pred. (MCNPX)		Pred. (Geant 4)	Pred. (FDC)
			Old MCS	New MCS				Old MCS	New MCS
SS-1	2.0	11.6	20.8	7.9	20.7	11.2	−7.7	−19.3	−6.7	−5.0	−3.0
SS-1	15.0	11.8	12.3	14.1	11.8	24.6	−68.6	−69.3	−68.4	−51.4	−54.7
SS-1	30.0	7.2	7.9	4.3	11.1	7.3	−71.2	−49.4	−63.4	−45.1	−45.6
SS-1	63.0	1.2	5.5	0.3	2.8	9.8	−36.9	−20.0	−28.4	−18.4	−19.0
SS-2	2.0	15.9	30.3	17.5	30.0	14.3	−5.0	−14.5	−9.6	−2.4	−1.5
SS-2	15.0	21.5	19.6	20.5	20.1	16.0	−62.0	−64.8	−64.1	−56.5	−55.2
SS-2	30.0	18.1	10.5	8.8	12.6	14.6	−79.1	−70.3	−76.7	−62.6	−59.3
SS-2	63.0	6.6	2.0	1.0	8.7	4.6	−59.0	−37.9	−41.0	−33.1	−32.9
SS-3	2.0	30.9	41.6	19.6	37.9	24.4	−5.9	−10.4	−12.0	−3.7	−0.5
SS-3	15.0	28.4	22.2	25.4	20.1	16.0	−53.9	−60.7	−58.0	−56.5	−55.2
SS-3	30.0	16.4	10.1	12.3	14.0	15.3	−79.7	−82.0	−79.1	−71.5	−71.5
SS-3	63.0	3.4	1.2	1.4	1.0	1.9	−85.0	−69.4	−79.7	−67.2	−64.2

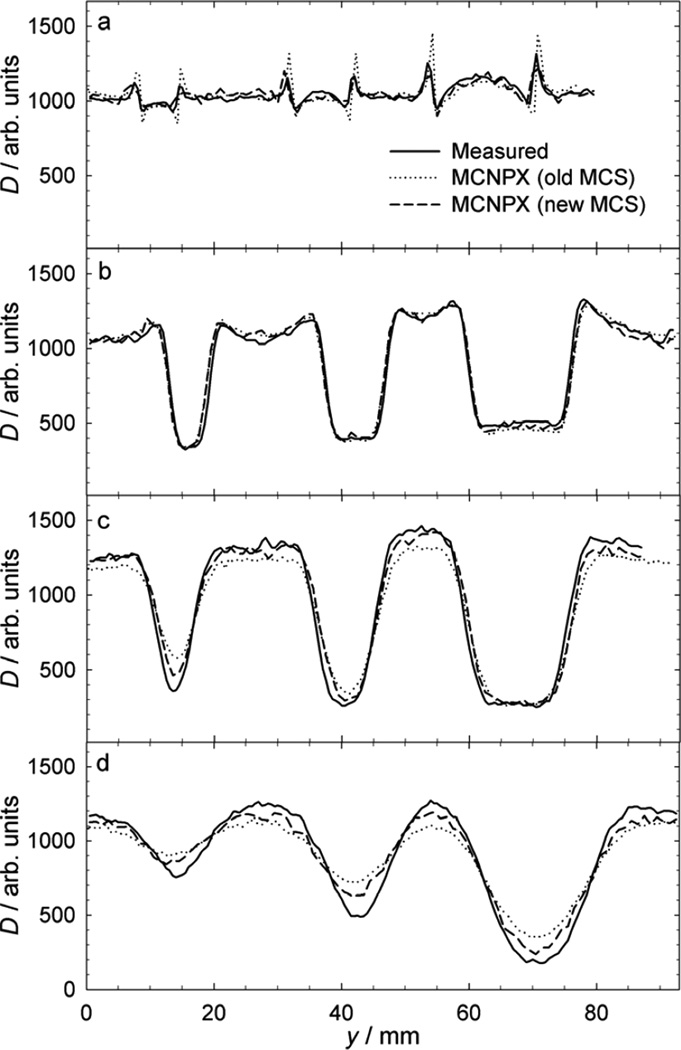
Fig. 3 shows measured and predicted dose profiles for a beam with a range of 161 mm and air gaps ranging from 20 mm to 630 mm, revealing a systematic increase in dose perturbation with larger air gaps. The predicted profiles were all very similar, which reflects the similarities in the underlying modeling techniques. For the same beam conditions, Fig. 4 plots the same measured profiles but with the predictions from the simulations using the MCNPX code with the original multiple Coulomb scattering model and with the modified model (Section 2.2.1). The modification yields a modest improvement in accuracy at 150 mm and 630 mm air gaps. The modified MCNPX provided the best overall agreement with the measurements at all air gaps considered.

Fig. 4.

Measurements of normalized absorbed dose (D) versus lateral position (y), revealing perturbations caused by 6.4-mm, 9.5-mm, and 15.9-mm diameter stainless steel spheres in a proton beam with a mean residual range of 161 mm. As in Fig. 3, the air gaps presented are (a) 20 mm, (b) 150 mm, (c) 300 mm, and (d) 630 mm. The same general features are observed as in Fig. 3, though differences are apparent between the curves resulting from the old and new multiple Coulomb scattering algorithms. In general, the results from the new algorithm more accurately represent the measurements and are an improvement where the old algorithm underestimates dose perturbations.

Fig. 5 plots measured and predicted dose profiles for beam ranges of 40 mm to 161 mm, where the air gap between the spheres and the measurement plane was held constant at 20 mm. The dose perturbations increased with sphere size and decreased with range. The predicted values were obtained using the MCNPX code with the modified multiple Coulomb scattering model. Good agreement was observed in each beam considered.

Each measured dose profile was offset in the lateral direction (y) in order to align it with the corresponding predicted profiles. However, it is noteworthy that the lateral distance scales in the measurements and simulations are absolute, i.e., they were not renormalized.

The level of agreement between simulated and measured perturbation values was good in terms of the shape and size of the absorbed dose profiles. For both dose enhancement and reduction perturbations, Table 3 lists the difference between predicted and observed, or measured, percentage perturbations (P-O). For the enhancement perturbations, the average and maximum P-O values were 5% and 15%, respectively. Similarly, the average and maximum dose-reduction perturbation values were −3% and −17.4%, respectively. In the majority of cases, the experimental and simulation data agreed to within the respective standard uncertainties. The small average values of P-O suggest an absence of any significant systematic bias between the measurements and simulations. The somewhat higher maximum P-O values mainly reflect the statistical uncertainties in the Monte Carlo simulation results.

4. Dicussion

4.1. Explanation of the Perturbations in Terms of Proton Interaction Physics

In metal objects, protons were laterally deflected more than in the surrounding material. This creates a lateral disequilibrium of protons, which causes perturbations in the absorbed dose distribution. Directly behind the metal object, the fluence enhancements and depletions are observed near the edge of the metal object. This well-understood effect is sometimes called the edge enhancement effect (Koehler, 1968; Schneider and Pedroni, 1995; Steward and Koehler, 1973a, b). The lateral deflections are predominated by multiple Coulomb scattering. The angular deflection, commonly characterized by the root mean square scattering angle θ_RMS, increases strongly with decreasing projectile velocity (See results section) and is approximately proportional to ρZ/A^1/2. For commonly implanted metals, ρ, Z/A^1/2, θ_RMS each tend to increase with Z. θ_RMS can differ greatly between metals. For example, using θ_RMS ∝ ρZ/A^1/2, one obtains 1, 2, and 7.5 for titanium, iron, and gold, respectively, where the values listed were normalized to the value of θ_RMS^titanium. Furthermore, it is instructive to compare the relative importance of ρ versus Z/A^1/2 on the initiation of lateral disequilibrium due to the presence of various metals in soft tissue. To do this, we simply calculated the ratio of θ_RMS^metal to θ_RMS^tissue for titanium, iron, and gold, obtaining 7, 15, and 54, respectively. These ratios generally depend more strongly on mass density ratios than on Z/A^1/2 ratios, e.g., by factors of 3, 5 and 7 for titanium, iron, and gold, respectively. Thus, the initiation of lateral disequilibrium depends in a conceptually simple way on multiple Coulomb scattering, which in turn depends on the velocity of the projectile, the size of the metal object, the ρ and Z/A^1/2 values of the metal, and the ρ and Z/A^1/2 values of the surrounding medium.

In addition to greater lateral scattering in metal, differences between the linear proton stopping power in metal and the surrounding medium also cause fluence and dose perturbations. Specifically, the linear proton stopping power, which varies approximately with ρZ/A and decreases with velocity (except near the very end of the proton trajectory), is generally larger in metal objects than in air or tissue. Consequently, protons impinging on the metal object will either stop in the object or exit with a reduced velocity and residual range. For example, the largest steel sphere (15.9 mm dia.) completely stopped protons in the lowest-energy beam (corresponding to 40 mm range in water) considered in this work, which is readily apparent in Fig. 5a. Thus, stopping-power-related dose perturbations depend on the velocity of the projectile, the size of the metal object, the ρ and Z/A values of the metal, and the ρ and Z/A values of the surrounding medium.

The discussion above mainly pertains to the initiation of lateral disequilibrium of proton fluence. Ultimately, though, dose perturbations may manifest themselves in the surrounding medium over regions extending from the metal/media interface all the way to the end of the beam range. In general, the dose perturbations are governed by scattering effects and energy-loss effects. For the highest energy proton beam considered, Fig. 3a–d reveal that the dose perturbations are governed predominantly by multiple Coulomb scattering with a strong dependence on drift space between the sphere and the measuring plane. In stark contrast, the dose perturbation caused by the largest (16-mm-diameter) sphere in the lowest proton beam energy considered was governed by mainly by the removal of protons that ran out of energy and stopped in the sphere (Fig 5a). In other cases the dose perturbations were governed by a combination of both effects (e.g., Fig. 5b). In sum, the physics governing metal-induced dose perturbations for the general case, i.e., involving multiple effects and dependencies, is conceptually clear. However, a simple analytical formula is not available to predict the magnitude of dose perturbations in the general case.

4.2. Verification Benchmarks of the Predictive Models

The simulations and measurements of dose perturbations caused by stainless steel spheres agreed well. The perturbations provide a severe test of the ability of the Monte Carlo and track repeating codes’ abilities to model lateral proton scattering in a heterogeneous medium containing a large density gradient. For all cases considered, the maximum differences between the predicted and observed perturbation values was 17% for the stainless steel spheres in air. The average differences were much smaller, within approximately 5%.

These benchmark comparisons provide new evidence that confirm the suitability of general-purpose MCNPX and GEANT Monte Carlo codes to model the proton dose perturbations caused by small metal objects implanted in patients. These results complement several recent clinically motivated benchmarks of MCNPX simulations of proton absorbed dose in homogeneous or heterogeneous water phantoms (Fontenot et al., 2005; Koch and Newhauser, 2005; Koch et al., 2008; Koch and Newhauser, 2010; Newhauser et al., 2005; Titt et al., 2008). In addition, the results of this study confirmed earlier investigations that revealed dosimetric discrepancies in a somewhat different case. Specifically, Herault et al (2005) revealed that MCNPX over-predicts multiple Coulomb scattering discrepancies in a beamline with a high-Z metals and a long drift space. After implementing the modifications proposed by Stankovskiy et al. (2009) in our version of the MCNPX code, we obtained improved agreement of the predicted and measured dose profiles. Thus, our study also confirms the superiority of the multiple Coulomb scattering from Stankovskiy et al. for geometries with long drift spaces. For short drift spaces (200 mm or less), our results also confirms previous studies that validated the adequacy of the default multiple Coulomb scattering model in MCNPX for predicting dose perturbations caused by small metal implants in patients receiving proton radiotherapy (Giebeler et al., 2009; Newhauser et al., 2005). We speculate that improved multiple Coulomb scattering models will be particularly beneficial for simulations of low-energy scanned-beam proton fields because they involve metal foils, e.g., vacuum windows and beam monitoring instrumentation, and long drift spaces.

The steel-sphere test device was simple to construct, inexpensive, easy deploy in measurements, and straightforward to model with various predictive models. The variety of spheres used allowed testing of dose perturbations caused by multiple-Coulomb-scattering effects and/or energy-loss effects. For these reasons, the basic approach appears potentially well suited as a benchmark-type test for validating proton dose algorithms.

5. Conclusions

This work compared measurements and predictions of dose perturbations caused by the presence of metal spheres in several proton therapy beams. Generally good agreement was found between measurements and predictions using MCNPX, GEANT4, and FDC codes. The results of this work add to the growing body of evidence that Monte Carlo codes are well suited for predicting multiple Coulomb scattering in proton therapy beams when short drift spaces are involved. However, the results also confirm other studies that revealed the need for improved multiple Coulomb scattering models for situations involving long drift spaces.

1. We compared measurements and Monte Carlo predictions of dose perturbations caused by the metal objects in proton beams.

2. Different Monte Carlo codes were used, including MCNPX, GEANT4 and Fast Dose Calculator.

3. Good agreement was found between measurements and Monte Carlo simulations.

4. The modification of multiple Coulomb scattering model in MCNPX code yielded improved accuracy.

5. Our results confirmed that Monte Carlo codes are well suited for predicting multiple Coulomb scattering in proton therapy.