Clade extinction appears to balance species diversification in sister lineages of Afro-Oriental passerine birds

Significance

Although the number of species in major groups of organisms has been relatively stable over long periods, the dynamics of speciation and extinction are poorly understood. Analyses of the age and species richness of sister groups of species in the African and Oriental biogeographic regions suggest that continuing species production within clades is balanced by random catastrophic extinction of whole clades. Because these postulated “pulses” of diversification and extinction are highly clade specific and, by inference, largely independent of changes in the physical environment, the demise of clades might be caused by the rapid evolution and diversification of specialized pathogenic organisms.

Abstract

Recent analyses suggest that the number of species in a clade often increases rapidly at first, but that diversification subsequently slows, apparently as species fill ecological space. Support for diversity dependence comes largely from the failure of species richness to increase with clade age in some analyses of contemporary diversity. However, clades chosen for analysis generally are named taxa and thus are not selected at random. To avoid this potential bias, we analyzed the numbers of species and estimated ages of 150 pairs of sister clades established by dispersal of ancestral species between the Oriental and African biogeographic regions. The observed positive exponential relationship between clade size and age suggests that species diversify within clades without apparent limit. If this were true, the pattern of accumulation of sister-clade pairs with increasing age would be consistent with the random decline and extinction of entire clades, maintaining an overall balance in species richness. This “pulse” model of diversification is consistent with the fossil record of most groups and reconciles conflicting evidence concerning diversity dependence of clade growth.

The close relationship between local species richness and characteristics of the physical environment supports the existence of ecological constraints on species coexistence mediated through competition and other interactions (1–3), although historical influences on diversity sometimes parallel gradients in the physical environment (4–6). If species richness were limited as ecological space filled, one would expect the net rate of species production to slow and the number of species in a clade to level off as species richness approached ecological constraints.

Evidence for such “diversity-dependent diversification” consists mostly of (i) nonrandom concentrations of branch points (speciation events) toward the origin of a clade (7–12) and (ii) independence of the number of species and clade age in comparisons among clades (11–14). However, clades included in such analyses often are not randomly chosen. In particular, small clades may be ignored because they do not command interest, and large, older clades are often passed over because of incomplete sampling (15, 16). Moreover, most phylogenetic analyses of diversification include species in named higher taxa rather than clades that have diversified within particular regions.

Further support for diversity limits comes from the fossil records of many higher taxa, which exhibit long-term stability in number of species (17–19). It is also clear that species and entire clades continually replace each other through time, and the dynamics of this process appear to include the decline and extinction of evolutionary groups as a component of the local and regional regulation of the number of coexisting species (20–25).

We take advantage of the sister relationships of clades of passerine birds in two major biogeographic regions—tropical southern Asia [Oriental (OR)] and the continent of Africa [African (AF)]—to examine the independent diversification of sister clades of known stem ages, selected only because one of the ancestors had dispersed between the two continents at some time in the past. Movement of species between these regions occurred either over water across the Indian Ocean, possibly using island stepping-stones, or through the Arabian Peninsula during periods of suitable environment. Each dispersal event defines the origin of a pair of same-aged sister clades in the two regions.

If each diversifying clade filled a certain part of ecological space to a carrying capacity for species, after which diversification slowed, the sizes of clades filling this space would level off over time (26). Furthermore, the number of species per sister clade, particularly among older clades that have filled ecological space, might be correlated between regions, with species richness reflecting the ecological space available to each of the sister lineages (27). Finally, for those dispersal events whose directionality can be inferred, the rate of diversification should be higher, leading to larger clade size compared between sister lineages, in the newly colonized region, which initially would have fewer close (and ecologically similar) relatives of the ancestral species.

We include all species of passerine birds (Passeriformes) and, separately, species in nonpasserine orders, of small, terrestrial birds, in the Oriental and African biogeographic regions (SI Appendix, section S1). The passerine avifauna of these regions accumulated from several sources over most of the Cenozoic Era (28, 29), with an old Gondwanan clade of suboscine passerines diversifying in tropical Africa and southern Asia early in the Tertiary, followed by radiations of core corvoid and passerid oscine passerines out of Australia during the early to mid-Cenozoic, through Wallacea to southern Asia, or directly across the Indian Ocean to Africa (30, 31). Thus, the diversification of sister clades in the African and Oriental regions takes place against a background of an increasing number of lineages of modern passerine birds as a whole within the region. Nonpasserine orders of terrestrial birds are likely to have diversified earlier within these regions (32) and perhaps were replaced to some extent by the passerines.

Characteristics of a sample of clades include the distribution of node ages and the relationship between clade size and stem age, as well as the distribution of clade sizes regardless of age, including the proportion of clades that contain a single species. Any process-based model of diversification should be judged by how well it reproduces these characteristics. We use these criteria to evaluate simulations in which we attempt to reconstruct the underlying diversification process.

Results

Species in Each Region.

Family-level limits to species richness might be shared between the two regions, despite differences in the proportions of each type of habitat (ecoregions). However, numbers of species in taxonomic families in the two regions were insignificantly or weakly related, depending on the particular taxonomy used (SI Appendix, section S2). Moreover, these correlations do not take into account the relative ages of family-level clades within each region. The numbers of species in sister clades also were not correlated between regions (SI Appendix, section S3). However, within each sister pair, the clade in the region of origin has significantly more contemporary species than the clade in the region of introduction (SI Appendix, section S4).

Node Statistics.

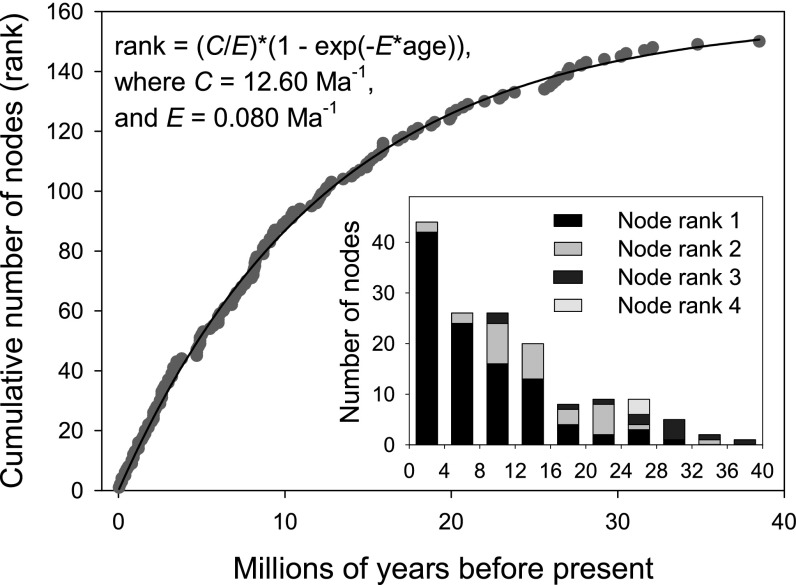
The number of nodes uniting African and Oriental sister clades decreases exponentially with age (Fig. 1, Inset). Although this might represent an increasing rate of dispersal between the continents toward the present, the pattern also would be expected if rates of dispersal (clade origin) and clade extinction were constant over time. Sister clades younger than 8 Ma are mostly monophyletic within each region (node rank 1; Methods). The descendant clades of older nodes are more likely to have dispersal events between the regions imbedded within them (node ranks 2–4).

Fig. 1.

Cumulative distribution of nodes uniting African and Oriental clades as a function of age. The data were fit by nonlinear regression (SAS Proc NLIN) to a model in which the cumulative number of clades exponentially approaches an asymptotic number of sister lineage pairs equal to the ratio of the colonization (C) and extinction (E) rate. The rank reaches 1/2 C/E when (1 – exp(−E*age)) = 0.5 or exp(−E*age) = 0.5, which, for E = 0.0798, occurs at 8.7 Ma. The Inset shows the distribution of the ages of nodes uniting sister taxa of African and Oriental passerine clades, grouped in four Ma intervals, with node rank indicated.

Clade-Level Dynamics.

We estimated uniform, i.e., time-homogeneous, dynamics of clade-level processes from the accumulation of nodes rank-ordered from the present back in time (Fig. 1). The rate (C) at which nodes linking African and Oriental clades appear (i.e., successful colonization across the Indian Ocean or Arabian Peninsula), and the rate at which they die out (E) within a region, can be estimated by the exponentially asymptotic relationship as follows:

$$N=\left(C/E\right)\ast \left(1-\exp \left[\mathrm{-}Et\right]\right),$$

where N is the number of nodes accumulated backward in time (t) (33). Rates estimated in this way assume steady-state origination of new clades and extinction of one of a pair of sister clades in one of the regions, the latter causing the disappearance of the biregion node in the phylogeny based on extant species, as well as an increase in the size of the higher-level clade.

By this approach, we estimated an interregion colonization rate of 12.6 (0.07 SE) events per million years, and a node extinction rate of 0.080 (0.0008 SE) per million years. The estimated asymptotic number of nodes was 12.6/0.080 = 157.5, which is 31% of an estimated ∼504 nodes produced over 40 Ma. When only terminal nodes (n = 105) were considered, C = 12.56 (0.095 SE), E = 0.079 (0.0013 SE), and C/E = 159.0, i.e., almost identical to the full dataset. Accordingly, the average duration of a node from its initiation as a single species that colonizes one or the other region, i.e., the inverse of the node extinction rate, would appear to be about (1/0.080 =) 12.5 million years. Because the disappearance of any node spanning the regions results initially from clade extinction in only one of the regions, the estimated extinction rate should be halved for each clade within each region, suggesting a rate of clade extinction of 0.040 per million years and an average persistence time of ∼25 Ma within a region.

Diversification of Species Within Clades.

Sister clades are slightly, but not significantly, larger in Africa (mean ± SD, 7.55 ± 21.15; range, 1–205) than in the Oriental region (6.21 ± 23.46; 1–274) (log-transformed values, t = 0.97, P = 0.17, df = 149). More than one-half of the clades (78 in Africa and 86 in the Orient) are represented by a single species in either region, an observation to which we shall return below.

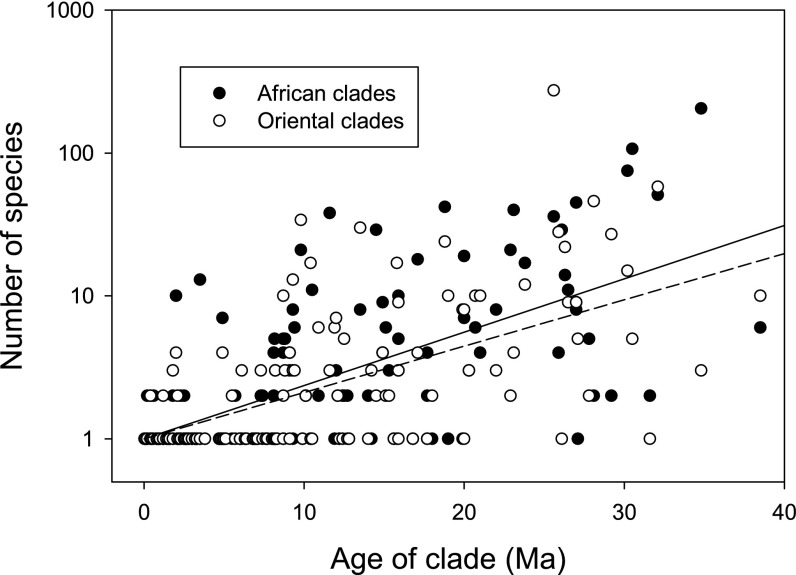
In a strictly homogeneous, random speciation (birth) process, the average number of species per clade (N) increases exponentially with time, resulting in a linear relationship between lnN and clade age, with an intercept of lnN = 0 at time (t) = 0. The SD in number of species among clades of identical age increases as (N(N – 1))^0.5, or approximately in proportion to N. Linear regressions of lnN as a function of time (SI Appendix, section S5) were consistent with a time-homogeneous pure speciation model with speciation rates of 0.086 (Africa) and 0.075 (Orient) per million years (Fig. 2). In addition, variation about the regressions was consistent with a time- and clade-homogeneous pure speciation process (SI Appendix, section S6). Nonpasserine clades in the Oriental and African regions present a similar picture of diversification (SI Appendix, section S7). Maximum-likelihood estimates of speciation and extinction rates under time-homogeneous models for each of the regions were consistent with the rates estimated by linear regression, including the absence of significant extinction within clades (SI Appendix, section S8).

Fig. 2.

Relationship between the log-transformed number of species and clade age in African and Oriental sister clades. The regression lines were passed through the origin, and the slopes in the two regions (AF = 0.086 ± 0.0054 SE; OR = 0.075 ± 0.0051 SE) did not differ significantly (see text).

An exponential relationship between clade size and age implies that the rate of increase in number of species is undiminished as clade size increases. In contrast, some recent analyses have estimated declining rates of increase of clade size with time, potentially reflecting either diversity-dependent slowing of the diversification rate or a constant high relative extinction rate (14, 26, 34). This relationship can be modeled by a logistic process in which the rate of diversification decreases linearly with increasing diversity until the number of species reaches a steady-state asymptotic value (A). The fit of a logistic model to the relationship between clade size and age in our dataset, assuming the same asymptote for all clades, was no better than the fit of the pure exponential model (SI Appendix, section S9). Moreover, the number of species in most clades was below the calculated inflection points of the fitted logistic models (A/2), hence still in the accelerating phase of species accumulation, which resembles exponential growth.

Analysis of Strongly Supported Clades.

Many of the 150 Orient–Africa nodes identified in the passerine phylogeny had weak posterior support, suggesting that a portion of these nodes might be artifacts of the phylogeny reconstruction. Such artifacts could have created false region-linking nodes and failed to identify other true nodes. This is a general problem with phylogeny reconstruction using limited gene sequence data. We addressed this problem to some extent by reanalyzing nodes with greater than 50% (n = 53) and 80% (n = 43) posterior support. Results were similar to the full analysis in failing to show either extinction or diversity-dependent diversification within clades (SI Appendix, section S10).

Single-Species Clades.

More than one-half of the clades descended from transregion nodes have but a single living species. Despite uncertainties about the location of many species in the avian phylogeny, accumulation of single-species lineages in each region with increasing age provides information about the rate of clade production and extinction. Single-species clades represent primarily recent dispersal events between Africa and the Orient; however, extinction of one member of a two-species clade within a region would also form a single-species clade. Single-species clades become “extinct” either when the lone species becomes extinct or when a speciation event occurs, which changes clade size from one to two species.

Rates of lineage accumulation (C) of single-species clades estimated by nonlinear regression were 12.17 (0.15 SE) Ma⁻¹ for the African single-species clades and 12.89 (0.15 SE) Ma⁻¹ for the Oriental clades. These values are close to the overall rate of clade accumulation, regardless of clade size (12.61, 0.07 SE), suggesting that single species clades are formed primarily by dispersal between regions, rather than decrease in the sizes of larger clades. The estimated rate of extinction among singleton clades (E) was 0.148 (0.003 SE) Ma⁻¹ for the African clades and 0.143 (0.003 SE) Ma⁻¹ for the Oriental clades. We previously estimated the extinction rate of clades of all sizes within regions, based on node extinction rates, to be 0.04 Ma⁻¹. In addition, the “extinction” of single-species clades by speciation would be about 0.08 Ma⁻¹ based on linear regression estimates of the speciation rate within clades (Fig. 2), and about 0.11 Ma⁻¹ based on exponential regression estimates of this rate (SI Appendix, section S6). Together, these “extinction” estimates sum to 0.12 and 0.15 Ma⁻¹, which bracket the values estimated from the lineage accumulation curves. We infer from these estimates that single-species clades are no more likely to become “extinct” than larger clades, although, under a random diversification process that includes extinction, the probability of true extinction (N → 0) increases rapidly as clade size decreases (35, 36). This implies that newly formed single-species clades are more resistant to extinction than one would expect under a random within-clade speciation–extinction model (SI Appendix, section S11).

Relative Rates of Speciation and Extinction Under a Homogeneous Diversification Process.

Our analyses highlight two attributes of clade origination and diversification. First, the cumulative number of nodes with progressively greater age can be fit by a model having a constant rate of clade origination (between-region colonization events) and a constant rate of clade extinction (d) within each region, which we estimated to be 0.04 Ma⁻¹ (Fig. 1). Second, the sizes of clades within each region increase exponentially at a rate of ∼0.08 Ma⁻¹ (log-linear fits) or 0.11 Ma⁻¹ (exponential fits) (Fig. 2; SI Appendix, section S7), which implies a negligible extinction rate of species within clades, likely too low to account for the estimated rate of clade extinction.

We simulated homogeneous random speciation and extinction with various combinations of speciation and extinction rates (SI Appendix, section S12). Clade ages were uniformly distributed between 0 and 40 Ma and the initial number of nodes was sufficient to yield ∼150 nodes after extinction (Fig. 3; SI Appendix, section S13, Table S4). The simulations reproduce some attributes of the observed distribution of clade sizes as a function of age, but fail to match the observed clade properties in several important respects. In particular, SDs of clade size were too low relative to the mean clade size. In addition, at low species turnover rates, the simulations also failed to produce the observed number of single-species clades (SI Appendix, Table S4). Estimated rates of node formation and extinction (Fig. 1: 12.6 and 0.08 Ma⁻¹) were most closely approximated (9.8 and 0.065 Ma⁻¹) by simulations with λ = 0.16 and μ = 0.10 Ma⁻¹, but these values produced too few singleton clades (55, 64) and too little heterogeneity in clade size (SD/mean, 1.45, 1.78).

Fig. 3.

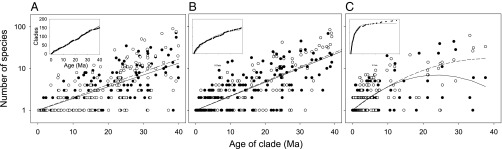
Distribution of clade sizes in two regions (open and filled symbols) within which clades diversify independently with random speciation (λ) and extinction (μ) and a uniform distribution of clade origination times between 0 and 40 Ma. The Inset in each panel shows the cumulative distribution of clade ages. (A) λ = 0.09 Ma⁻¹, μ = 0.00 Ma⁻¹; (B) λ = 0.16 Ma⁻¹, μ = 0.10 Ma⁻¹; (C) λ = 0.41 Ma⁻¹, μ = 0.40 Ma⁻¹ (see SI Appendix, section S13, for model fits and simulated clade statistics).

Simulations with Clade Extinction and with Nonuniform Clade Origination.

Observed distributions of contemporary clade ages and sizes can be produced by introducing a third process beyond clade initiation and within-clade diversification, namely the random extinction of entire clades within regions (24, 25, 37–39). This process represents the random collapse and disappearance of a clade, owing to unspecified causes but affecting all of the lineages within a clade, over a brief period; extinction of any one clade occurs independently of all others. For example, with λ = 0.15 and μ = 0.05 Ma⁻¹ within clades, and a probability of random clade extinction of 0.07 per Ma, regardless of clade size or age (clade extinction model), the estimated parameters for the simulated and actual clades match closely (SI Appendix, Table S4).

Observed distributions of contemporary clade characteristics also can be produced by introducing an exponential decrease in the probability of dispersal with increasing time in the past. An example of such a simulation shown in SI Appendix, Table S4 (clade origination model) matches observed clade characteristics well, except that the ratios of the SDs in clade size to the means are lower than observed, and lower than under the clade extinction model. Furthermore, we have no reason to suspect that dispersal between the Oriental and African regions might have been lower during the mid-Cenozoic than at present.

Discussion

The accumulation of Africa–Orient between-region nodes over time in the phylogeny of passerine birds suggests that such nodes originate at a rate of about 12.6 per million years and suffer extinction at a rate of about 0.08 (8%) per Ma (i.e., descendant clades have an extinction rate of ∼4% per Ma within each region) (Fig. 1). The approximately exponential increase in number of species per clade with time further suggests that clades increase in size without diversity-dependent limits on the diversification rate and, at least initially, with a low probability of clade extinction. One question addressed here is whether the estimated extinction rate of clades can be explained by a time-homogeneous stochastic speciation–extinction process within clades. Evidently, it cannot.

Constant rates of within-clade diversification indicated by our analysis contradict other evidence that diversification rate decreases (10, 14, 34) or even becomes negative with time and increasing clade diversity (22). Often cited to support diversity-dependent feedbacks on rates of diversification is the leveling off of clade size with increasing clade age (11, 12). Accordingly, as clade size increases and the species extinction rate approaches the speciation rate, the rate of increase in clade size slows and the number of species levels off. However, analyses of the relationship between clade size and age also can be biased, in such a way as to produce this leveling off, by nonrandom selection of clades based on taxonomy (SI Appendix, section S14). Our selection of clades as those descending from between-region nodes avoids this potential bias.

Additional evidence supporting the hypothesis of diversity-dependent slowing of diversification within a clade is the often-observed nonlinearity in the lineage-through-time (LTT) plot for individual clades. These plots are reconstructed from phylogenetic hypotheses and depict the number of ancestral lineages in a clade beginning with the crown node at which the stem lineage splits to form two descendants. In a time-homogenous process, the number of ancestral lineages increases exponentially, with an upswing toward the recent depending on the relative extinction rate. In fact, however, many clades exhibit a leveling of the LTT plot toward the present, indicative of a slowing of diversification rate (12, 14). As we discuss in SI Appendix, section S15, this leveling of the LTT plot is open to a variety of interpretations, including potential consequences of clade decline and extinction after a period of constant diversification. We do not believe that LTT plots can distinguish between diversity dependence of diversification within clades and terminal clade decline through the concentrated extinction of species within a clade—both result in a deceleration of lineage accumulation in a LTT plot.

Diversity dependence, rather than operating within each clade of birds independently, might influence the diversity of all species equally, regardless of their specializations for resource use. Accordingly, when ecological space fills with species, speciation and extinction rate must come into equilibrium at equal rates, at which point the production of each new species must be balanced by the extinction of another. However, even with equal rates of speciation and extinction, resulting in high species turnover, the expected size of extant clades increases rapidly at first—because only the larger clades survive—and then begins to level off (34, 40) (SI Appendix, section S12). Eventually, just owing to random speciation and extinction (community drift; ref. 41), a local avifauna will eventually consist of the descendants of a single ancestral species, the chain broken only by the immigration of new species into a region.

The observed relationship between the logarithm of clade size and age among African and Oriental sister lineages cannot be distinguished statistically from the linear relationship expected from a pure speciation process, nor from a time-homogeneous speciation–extinction process in which the extinction rate might be a relatively high proportion (i.e., up to 60–80%) of the speciation rate, but certainly not approaching the speciation rate. Accordingly, such a time-homogeneous speciation–extinction process within clades would imply that the numbers of clades and species of African and Oriental passerine birds have increased continuously over the past 40 million years. However, assuming time-homogeneous clade origination and extinction, the observed pattern of accumulation of sister clades, which levels off with increasing clade age, is incompatible with a positive net within-clade diversification rate, according to which few clades would disappear and their number would continue to accumulate. Reconciling these conflicting observations requires either time heterogeneity in rates, or placing the diversification of species within clades and the extinction of clades under the control of different, independent processes.

If dispersal between Africa and the Orient were to have increased toward the present, the preponderance of nodes toward the present (Fig. 1) might reflect variation in clade origination rather than extinction of older clades. In the absence of paleontological data concerning birds, historical information bearing on this hypothesis is restricted to paleogeography. The plate on which Africa sits has moved northward continuously during most of the Tertiary, narrowing the overwater gap between Africa and Asia, which might have facilitated dispersal (42). At the same time, global temperatures have declined since the Eocene, except for a reversal in the Oligocene, leading to aridification of the Middle East and northern Africa, reducing the ecological quality of terrestrial corridors between the two regions (43). Finally, low sea levels during the early Miocene (20–16.5 Ma) facilitated faunal interchange between Africa and Eurasia (44). On balance, the data do not suggest any particular trend in avian dispersal between Africa and the Orient.

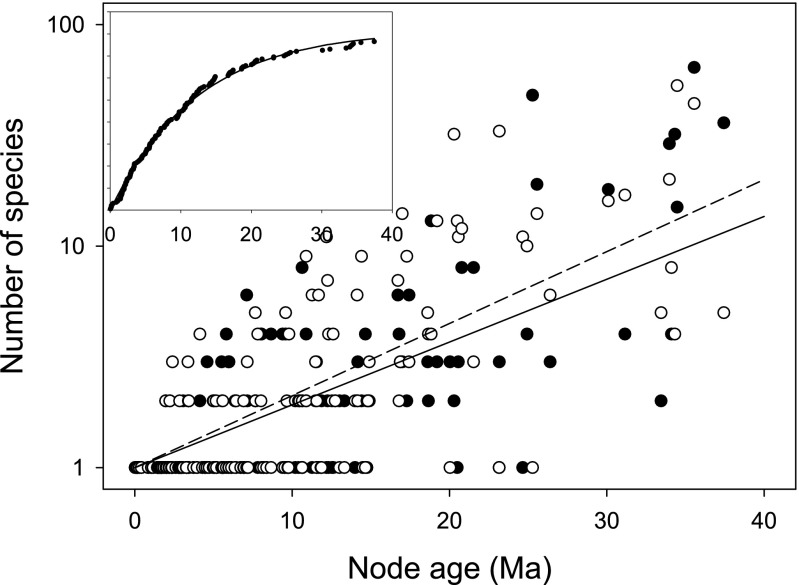
Instead, we argue that the observed patterns could have been produced by independent processes controlling the survival of clades that descend from nodes uniting African and Oriental species, in contrast to the within-region diversification of species within clades. A time-homogeneous species origination and extinction process within clades, combined with an independent time-homogeneous clade origination and extinction process, can reproduce the observed distribution of clade sizes and ages, although it might not be the only feasible model. Fig. 4 shows the results of a simulation of 500 nodes randomly and uniformly distributed over 40 Ma (node origination rate, 12.5 clades per Ma) with a clade extinction rate of 0.08 per Ma (156 nodes survive, with an average life span of 12.5 Ma) and a within-clade speciation rate of 0.09 per Ma. The accumulation of nodes with time in this simulation matches the input parameters closely (origination, C = 13.26 ± 0.10 per Ma; extinction, E = 0.081 ± 0.0011 per Ma) and the within-clade rates of increase in the logarithm of the number of species with time (no intercept) were 0.0653 ± 0.0037 SE per Ma and 0.0749 ± 0.0040 SE per Ma, again close to the observed values. Finally, with independent processes shaping the birth and death of clades and of species within clades, the SD is about twice the mean in the compound simulation (3.56 ± 7.83 SD; 3.94 ± 7.09 SD), which more closely approaches the observed data. When the within-clade speciation and extinction rates are 0.15 and 0.05 Ma⁻¹, respectively, with a clade extinction rate of 0.07 Ma⁻¹, the output values also match the observed data closely (SI Appendix, Table S4). These simulations are, moreover, consistent with the apparent resistance of single-species clades to extinction.

Fig. 4.

Results of a simulation of 500 nodes randomly and uniformly distributed over 40 Ma (node origination rate, 12.5 clades per Ma) with a within-clade speciation rate of 0.09 per Ma and clade extinction rate of 0.08 per Ma. The Inset shows the node accumulation as a function of node age. Compare with observed data in Figs. 2 and 3.

Mechanisms that might cause the independent extinction of entire clades are poorly understood, although the paleontological record is replete with groups that have died out individually and often quickly in the past (45–48). In the absence of changes in the physical environment that might differentially affect individual clades of birds, one has to postulate other clade-specific causes. A plausible reason for clade decline is competition from other clades that are on the rise. Particularly when new clades obtain some advantageous adaptation—a “key innovation”—for more efficient exploitation of the environment, older clades whose members are bound together by a shared, generally conservative, evolutionary history, are likely to suffer (49–52). Another possibility is that the decline of a clade might be caused by the rise of a pathogen, or clade of pathogens, that gains an infection advantage and spreads rapidly through the members of a particular host clade, taking advantage of their shared physiological attributes, including qualities of their immune systems (53). Many pathogens are specialists on one or a small number of related hosts (54–57). Conversely, the evolution by a host population of resistance to a pathogenic parasite might lead to population expansion, with increased probability of interregional dispersal, initiating a new regional clade, and perhaps facilitating the formation of new species within the clade.

In summary, diversification within clades of passerine birds in the Oriental and African biogeographic regions appears to behave according to a random speciation–extinction process that is uncorrelated between sister clades in the two regions and exhibits no diversity-dependent constraint on early diversification. Thus, the logarithm of the number of species within extant clades increases linearly with time. As predicted by such a process, the variance in number of species among clades also increases linearly with time. However, the diversification process within clades does not predict the observed distribution of clade ages, or the rates of origin and extinction of clades that can be inferred from this distribution. We reconcile these within- and between-clade patterns by postulating independent processes controlling diversification within clades and the age-dependent origin and survival of clades themselves. Simulations based on these two types of process reproduce observed patterns of diversity and clade-age distributions, although the underlying mechanisms are unknown and may be difficult to investigate. In particular, it would be problematic to distinguish a priori (i.e., without fossil evidence) between a particular clade that is small owing to its history of stochastic within-clade speciation and extinction, and a clade that is small owing to a clade-specific challenge to species survival and/or lineage splitting.

Our analyses suggest, for this system, that diversification might be homogeneous over time but that extinction of lineages within clades does not balance speciation, causing individual clades to grow continuously on average. The age distribution of nodes linking Oriental and African clades further suggests independent processes controlling clade initiation and extinction, potentially resulting in a regional balance in species richness over long periods. In such a process, species (and clades) are constantly going extinct as others grow and diversify, the result being a gradual turnover of the avifauna within and between clades over time. Because speciation and extinction within clades, as well as clade origination and extinction, can be modeled as random, time-homogeneous processes, regional numbers of species might not have changed markedly over time, barring major environmental drivers, except by drift. Thus, although the total regional species richness of passerine birds may have reached a plateau, this limit might be set by regional speciation–extinction dynamics within and among clades, mediated through coevolutionary relationships with specialized pathogens rather than by local ecological interactions.

Methods

The biogeography and history of the African and Oriental regions are detailed in the SI Appendix, section S1.

Samples and Phylogenetic Analyses.

For our passerine dataset, we used the International Ornithologists’ Union’s World Bird Names list, version 3.3 (58), and included all passerine bird species that occur in the Oriental region (OR) and the African region (AF). Some taxa occur in more than one region. We included all species that occur both in Australia and in the Orient (AU/OR) but removed all species that occur both in Eurasia and in Africa (EU/AF), as well as species that occur in both Eurasia and in the Orient (EU/OR), because they largely represent species adapted to the dry regions of northern Africa and the Middle East. Species distributed in both AF and OR were also excluded (10 species), although these might represent the initial stage of sister-clade formation between the two regions.

We included, in a second dataset, nonpasserine birds belonging to the terrestrial families Apodiformes, Caprimulgiformes, Columbiformes, Coraciiformes, Cuculiformes, Musophagiformes, Piciformes, Psittaciformes, and Trogoniformes, and that occur in OR and AF. We then accessed 10,000 trees from the all bird phylogeny (under the option “Hackett All Species: a set of 10000 trees with 9993 OTUs each”) on www.birdtree.org (59) and generated two maximum clade credibility trees with posterior probabilities: a passerine tree with 2,057 tips (1,140 African taxa and 915 Oriental taxa) and a nonpasserine tree with 645 tips (334 African taxa and 311 Oriental taxa). Note that, in the phylogeny of all birds from which these trees were drawn, almost one-third of the species-level taxa were placed by a randomization algorithm within their designated taxonomic groups. This lends a level of uncertainty to the status of some comparisons as representing sister clades, as well as to the regional number of species in these clades.

Based on the maximum clade credibility trees, we identified all sister relationships representing presumed dispersal of ancestral taxa between the Orient and Africa, counted descendant species in each region, and inferred the region of origin of the dispersing lineage where possible (SI Appendix, section S16).