Visuo–spatial working memory is an important source of domain-general vulnerability in the development of arithmetic cognition

Abstract

The study of developmental disorders can provide a unique window into the role of domain-general cognitive abilities and neural systems in typical and atypical development. Mathematical disabilities (MD) are characterized by marked difficulty in mathematical cognition in the presence of preserved intelligence and verbal ability. Although studies of MD have most often focused on the role of core deficits in numerical processing, domain-general cognitive abilities, in particular working memory (WM), have also been implicated. Here we identify specific WM components that are impaired in children with MD and then examine their role in arithmetic problem solving. Compared to typically developing (TD) children, the MD group demonstrated lower arithmetic performance and lower visuo-spatial working memory (VSWM) scores with preserved abilities on the phonological and central executive components of WM. Whole brain analysis revealed that, during arithmetic problem solving, left posterior parietal cortex, bilateral dorsolateral and ventrolateral prefrontal cortex, cingulate gyrus and precuneus, and fusiform gyrus responses were positively correlated with VSWM ability in TD children, but not in the MD group. Additional analyses using a priori posterior parietal cortex regions previously implicated in WM tasks, demonstrated a convergent pattern of results during arithmetic problem solving. These results suggest that MD is characterized by a common locus of arithmetic and VSWM deficits at both the cognitive and functional neuroanatomical levels. Unlike TD children, children with MD do not use VSWM resources appropriately during arithmetic problem solving. This work advances our understanding of VSWM as an important domain-general cognitive process in both typical and atypical mathematical skill development.

1. Introduction

Recent research in mathematical cognition has led to theories that emphasize the foundational role of quantity representations on an internalized mental number line (Ansari, 2008; Cohen Kadosh & Walsh, 2009; Feigenson, Dehaene, & Spelke, 2004). The link between quantity and space requires domain-general visuo-spatial processes (De Smedt et al., 2009; Holmes & Adams, 2006; Rasmussen & Bisanz, 2005). The study of developmental disorders can provide a unique window into the role of WM in mathematical cognition, notably by pinpointing the specific source of domain-general vulnerabilities in cognitive abilities such as WM. Mathematical disability (MD) is a specific deficit in number and mathematics ability in the presence of preserved intellectual and verbal ability (Butterworth, Varma, & Laurillard, 2011; Rubinsten & Henik, 2009; von Aster & Shalev, 2007). MD is often described as a domain-specific disability arising from deficits in the representation of numerical information resulting in abnormal basic numerical processing mechanisms (Butterworth et al., 2011; Wilson & Dehaene, 2007). Children with MD show poor performance on a broad range of basic numerical tasks including magnitude judgment (Ashkenazi, Rubinsten, & Henik, 2009; Geary, Hamson, & Hoard, 2000; Mussolin et al., 2010; Piazza et al., 2010; Price, Holloway, Rasanen, Vesterinen, & Ansari, 2007) and enumeration (Geary, Bow-Thomas, & Yao, 1992; Geary & Wiley, 1991; Knootz & Berch, 1996; Landerl, Bevan, & Butterworth, 2004; Schleifer & Landerl, 2011). Importantly, they also lag behind their typically developing (TD) peers in basic arithmetic problem solving skills (Geary et al., 1992; Shalev, Auerbach, Manor, & Gross-Tsur, 2000; Shalev, Manor, & Gross-Tsur, 2005).

In addition to these basic number processing deficits, there is growing evidence to suggest that domain-general working memory (WM) deficits also contribute to MD (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007). Critically, despite growing behavioral evidence for the involvement of WM in numerical cognition, the role of specific WM components and their underlying neural basis is poorly understood. It is well known that WM is not unitary; specifically, the multicomponent view of WM proposes a general cognitive model for the storage and manipulation of information that includes a central executive for high level monitoring and control, and a subsidiary phonological loop and visuo-spatial sketchpad for short term storage and maintenance of verbal, and visuo-spatial information, respectively (Baddeley, 1996, 1998; Baddeley, Emslie, Kolodny, & Duncan, 1998; Baddeley & Hitch, 1974; Baddeley & Logie, 1987). Each element of the multicomponent WM model is potentially important for arithmetic problem solving. The visuo-spatial sketchpad is involved in the solution of multi-digit operations (Heathcote, 1994), and its activity is thought to reflect the representation of quantities on a mental number line (Rotzer et al., 2009). The phonological loop helps in the maintenance of intermediate arithmetic results (Trbovich & LeFevre, 2003). The central executive is needed for sequencing complex arithmetical procedures that involve intermediate steps such as carrying and borrowing (Imbo, Vandierendonck, & Vergauwe, 2007).

Previous behavioral studies have used MD to draw links between working memory and mathematical ability, but no consensus has yet emerged for the relative importance of different WM components and their role in normal versus aberrant development of arithmetic cognition. Geary (1990) hypothesized that WM deficits increase the difficulty of early learning instances, leading to a failure to develop long-term memory associations for basic numerical facts (Geary, 1990; Geary et al., 1992). This hypothesis is consistent with behavioral observations that, relative to their TD peers, children with MD have difficulties in retrieval of arithmetic facts, use less mature arithmetic strategies (Geary, 2004) and have deficits in multiple WM components, including verbal WM and visuo-spatial working memory (VSWM) (Swanson & Jerman, 2006).

The relative importance of each WM component and its role in normal versus aberrant development of arithmetic cognition in not well understood. Several studies have focused on the central executive and verbal WM as strong contributors to arithmetic deficits, but these studies have tended to rely on WM measures based on verbal manipulation of numerical information such as counting or backward Digit Recall (Geary et al., 2000; Geary, Hoard, & Hamson, 1999; Landerl et al., 2004; Wu et al., 2008). Other studies that have controlled for this potential confound have not found a reliable link between verbal WM and math ability. Instead, researchers have found comparable performance on verbal WM tasks, such as word span, between MD and TD groups (Hitch & McAuley, 1991; Passolunghi & Siegel, 2001, 2004; Siegel & Ryan, 1989). This has led some researchers to suggest that participants with MD have a number-specific verbal WM deficit (Siegel & Ryan, 1989). In contrast, Swanson & Jerman (2006) found that VSWM deficit was the only factor that differentiated MD children from children with reading difficulties. Consistent with this view, Rotzer et al. (2009) found that children with MD (age range 9–11, mean=10.4) had lower scores on a Corsi Block Tapping test (a standard measure of VSWM ability) than TD children. This study also found that children with MD had lower activity levels in the right inferior frontal gyrus, right intraparietal sulcus (IPS), and right insula during a VSWM task. Moreover, right IPS activity was positively correlated with VSWM ability. However, VSWM was not evaluated in the context of arithmetic problem solving. Importantly, there have been no studies directly examining the link between VSWM and brain activity during arithmetic processing in either TD children or children with MD despite the large potential elucidating this link could have on our theoretical understanding of the role of VSWM in arithmetic and numerical cognition.

Here we examine the specific role of VSWM in arithmetic problem solving. We use standardized measures of WM to first examine whether VSWM is a specific locus of deficits in MD children who are otherwise well-matched on cognitive abilities to a group of typically developing (TD) peers. We then contrast the role of VSWM on brain responses during arithmetic processing in both groups of children, allowing us to examine fundamental questions about the specific role of VSWM in normal function while at the same time investigating how WM deficits impact arithmetic problem solving deficits in children with MD. We build upon a previous study in which we examined deficits in brain activation and multivariate representations underlying arithmetic problem solving in 2nd and 3rd graders (ages 7–9) with MD who were matched on age, sex, IQ and reading ability to TD controls (Ashkenazi, Rosenberg-Lee, Tenison, & Menon, 2012). We reported earlier that TD children showed strong modulation of univariate and multivariate brain response in parietal and prefrontal cortex with increasing arithmetic complexity. In contrast, MDs demonstrated weak modulation of brain response in the right IPS, superior parietal lobule, supramarginal gyrus (SMG), and bilateral dorsolateral prefrontal cortex in relation to arithmetic complexity. In the current study, we examine whether WM has a differential effect on brain responses during arithmetic problem solving in the two groups, and whether these effects are modulated by different levels of arithmetic complexity. Note that in contrast to our previous study (Ashkenazi et al., 2012), the samples in the current study were improved by including 2 left handed TD subjects in order to better match TDs to our difficult-to-obtain MD sample that also included two left handed participants.

The Working Memory Test Battery for Children (WMTB-C) (Pickering & Gathercole, 2001) was used to measure the three different components of WM in the TD and MD groups. The central executive was assessed using two subtests: (1) Counting Recall, and (2) Backward Digit Recall. The phonological loop was tested using Digit Recall and visuo-spatial sketch-pad was tested using Block Recall, a variant of the Corsi Block Test. Mathematical abilities were assessed using two standardized measures (Wechsler, 2001): (1) Numerical Operations, which emphasizes counting and computation, and (2) Mathematical Reasoning, which emphasizes word problems. Our primary focus is the relationship between individual VSWM abilities and arithmetic-related brain activity at the whole brain level, and in theoretically motivated region-of-interests (ROI). For the latter analysis, ROIs were selected based on a previous study that demonstrated correlation between behavioral VSWM abilities and brain activation during a VSWM task (Klingberg, Forssberg, & Westerberg, 2002). This study revealed that, in children and adults VSWM abilities and VSWM task activations were positively correlated with left IPS activity levels (Klingberg et al., 2002).

We predicted that children with TD would show a strong relationship between VSWM ability and brain response in multiple frontal and parietal regions during arithmetic problem solving. Based on previous behavioral studies we predicted that even after matching on IQ and reading, VSWM would be a specific source of vulnerability in children with MD. We further predicted that children with MD would use VSWM differently from TD children during arithmetic problem solving. Finally, we specifically predicted that this pattern of strong relationship for TDs and weaker relationship for MDs would hold in IPS regions previously implicated in tasks involving VSWM (Klingberg et al., 2002). Together, these findings would provide novel evidence that VSWM plays a significant role in arithmetic problem solving.

2. Methods

2.1. Participants

Participants were recruited from a wide range of schools in the San Francisco Bay Area using mailings to schools, and postings at libraries and community groups. Children between the ages of 7–9 years old with no history of psychiatric illness were included in the study. Intelligence was assessed using the Wechsler Abbreviated Scale of Intelligence (WASI) (Wechsler, 1999) with an inclusion criterion of full-scale IQ above 80. The Wechsler Individual Achievement Test, Second Edition (WIAT-II) (Wechsler, 2001) was used to determine grade specific achievement and mathematical disabilities status. Seventeen children (11 girls and 6 boys) who scored at 91 or below (i.e. the 27th percentile) on the Numerical Operations subtest of the WIAT-II formed the MD group. The TD group consisted of seventeen children (11 girls, 6 boys) individually matched on age, gender, IQ and reading ability to the MD group. TD children were required to score at or above 95 (i.e. the 37th percentile) on the Numerical Operations subtest (Table 1). Two children from the MD group and 2 children from the TD group were left handed as assessed using the Edinburgh handedness test (Oldfield, 1971).

Table 1.

IQ, math, reading and multicomponent working memory measures in children with mathematical disabilities (MD) and typically developing (TD) children. Visuo-spatial working memory scores were significantly lower in children with MD, compared to TD children.

Measure	MD		TD
	M (Range)	SD	M (Range)	SD
Age (months)	98.78 (86–109)	6.97	97.84 (88–108)	6.26
WASI
Verbal	106.65 (78–128)	12.32	108.29 (80–138)	15.93
Performance	107.59 (77–140)	18.20	113.77 (86–145)	13.32
Full Scale	107.71 (83–130)	13.36	112.35 (94–127)	10.20
WIAT–II
Word Reading	108.47 (93–122)	9.23	112.06 (90–130)	9.65
Numerical Operations	85.71 (79–91)	3.50	118.29 (95–156)***	15.41
Mathematical Reasoning	102.47 (84–130)	14.82	115.00 (90–137)*	12.20
WMTB-C
Digit Recall	105.71 (77–144)	20.40	107.12 (75–144)	17.50
Counting Recall	86.94 (60–117)	18.63	87.35 (56–110)	17.03
Block Recall	91.00 (56–114)	14.62	102.18 (81–118)*	9.91
Backward Digit Recall	96.94 (72–131)	19.45	99.35 (81–135)	13.87

Note: WASI=Wechsler abbreviated scales of intelligence, WIAT-II=Wechsler individual achievement test—2nd ed., WMTB-C=Working memory test battery for children.

^*p<.05.

^***p<.001.

2.2. Standardized cognitive assessments

2.2.1. Mathematical abilities

Mathematical abilities were assessed using the WIAT-II (Wechsler, 2001). This achievement battery includes nationally standardized measures of K-12 academic skills and problem-solving abilities, which are normed by grade and time of the academic year (Fall, Spring, or Summer). The Numerical Operations subtest is a paper-and-pencil test that measures number writing and identification, rote counting, number production, and simple addition, subtraction, multiplication, and division problems. For example, 4–2=___ and 37+54=___ (presented horizontally and vertically, respectively) are two problems in the 2nd and 3rd grade range. The Mathematical Reasoning subtest is a verbal problem-solving test that measures counting, geometric shape identification, and single- and multi-step word problem-solving involving time, money, and measurement with both verbal and visual prompts. The child is required to solve problems with whole numbers, fractions or decimals, interpret graphs, identify mathematical patterns, and solve problems of statistics and probability. For example, a dime is presented and the child is asked, “How many pennies does it take to equal the value of one dime?” A probability problem asks: “If you flipped a coin ten times, how many times would the coin be most likely to land on heads?”

2.2.2. Reading abilities

The WIAT-II was also used to assess reading abilities. The Word Reading subtest involves reading individual words presented visually to the child, and was used for matching the MD and TD groups on reading ability.

2.2.3. Working memory

Four subtests of the Working Memory Test Battery for Children (WMTB-C; (Pickering & Gathercole, 2001)) were used to assess working memory abilities. The central executive was examined by two tests: (1) Counting Recall, and (2) Backward Digit Recall. The phonological loop was tested using Digit Recall. Last, visuo-spatial sketchpad ability was tested using Block Recall, a variant of the Corsi block tapping test. In counting recall, multiple cards with different numbers of red dots on each card were presented. Participants had to count the number of dots on each card and report the final tally from each card sequentially at recall. In Backward Digit Recall, participants were required to report a set of digits in reverse of the order originally presented. In Digit Recall, participants had to report a set of digits in the original order presented. And finally, during Block Recall, participants were asked to reproduce a sequence of block tapping originally executed by the examiner.

2.3. Brain imaging

2.3.1. Experimental procedures

The functional magnetic resonance imaging (fMRI) experiment was an event-related design with two task conditions: Complex addition (26 trials) and Simple addition (26 trials). In the Complex addition task, participants were presented with an equation involving two addends and asked to indicate, via a button box, whether the answer presented was correct or incorrect (e.g. “3+4=8”). One operand ranged from 2 to 9, the other from 2 to 5 (tie problems, such as “5 +5=10”, were excluded), and answers were correct in half of the trials. Incorrect answers deviated by ± 1 or ±2 from the correct sum (Ashcraft & Battaglia, 1978). The Simple addition task was identical except one of the addends was always’1’ (e. g. 3+1=4). Critically, because stimuli in the Simple task have the same format as the Complex task, it provides a high-level control for sensory and number processing, as well as decision-making and response selection. Our use of this task was based on pilot studies, which suggested that children are consistently faster on these problems compared to the Complex addition problems. Furthermore, children show less strategy variability for “n+1” problems, thus serving as ideal control problems for our study (Siegler, 1987). A verification, rather than verbal production, format was used in the scanner because overt verbal responses can result in significant head movement in children resulting in unusable fMRI data. Stimuli were displayed for 5 s with an inter-trial interval of 500 ms and a jitter period which varied between 0 to 3500 ms with an average of 1846 ms. During the inter-trial interval and the jitter period a fixation cross appeared on the screen. The total length of the experimental run was 6 min and 22 s.

2.3.2. fMRI data acquisition

Images were acquired on a 3T GE Signa scanner (General Electric, Milwaukee, WI) using a custom-built head coil at the Stanford University Lucas Center. Head movement was minimized during the scan by a comfortable custom-built restraint. A total of 29 axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the AC-PC line and covering the whole brain were imaged with a temporal resolution of 2 s using a T2* weighted gradient echo spiral in-out pulse sequence (Glover & Lai, 1998) with the following parameters: TR=2 s, TE=30 ms, flip angle = 80°, 1 interleave. The field of view was 20 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss from field inhomogeneity, an automated high-order shimming method based on spiral acquisitions was used before acquiring functional MRI scans (Kim, Adalsteinsson, Glover, & Spielman, 2002).

2.3.3. fMRI preprocessing

fMRI data were analyzed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). The first 5 volumes were not analyzed to allow for T1 equilibration. A linear shim correction was applied separately for each slice during reconstruction (Glover & Lai, 1998). ArtRepair software was used to correct for excessive participant movement (Mazaika, Whitfield-Gabrieli, Reiss, & Glover, 2007). Images were realigned to correct for movement, smoothed with a 4 mm FWHM Gaussian kernel and motion adjusted. Deviant volumes resulting from sharp movement or spikes in the global signal were then interpolated using the two adjacent scans. No more than 20% of the volumes were interpolated. Participants with head movement exceeding 5 mm in any of the x, y, and z directions were excluded from the study. Finally, images were corrected for errors in slice-timing, spatially transformed for registration to standard MNI space, and smoothed again at 4.5 mm FWHM Gaussian kernel. The two step sequence of first smoothing with a 4 mm FWHM Gaussian kernel and later with 4.5 mm FWHM Gaussian kernel approximates a total smoothing of 6 mm, because total smoothing is equivalent to the square root of the sum of the squares of the individual smoothing steps.

2.3.4. Individual subject and group analyses

Task-related brain activation was identified using the general linear model implemented in SPM8. In the individual subject analyses, interpolated volumes flagged at the preprocessing stage were de-weighted. Each trial was modeled using a boxcar function convolved with the canonical hemodynamic response function and a temporal dispersion derivative to account for voxel-wise latency differences in hemodynamic response. Low-frequency drifts at each voxel were removed using a high-pass filter (.5 cycles/min). Serial correlations were accounted for by modeling the fMRI time series as a first-degree autoregressive process. Voxel-wise t-statistics maps of the following contrasts were generated for each participant using only correct trials: (1) Complex addition - Rest, and (2) Simple addition - Rest. For group analysis, contrast images corresponding to each arithmetic task were analyzed using a random effects analysis. We first compared activity between the MD and TD groups for each contrast. We then used an ANCOVA model to examine groups differences in the relationship between Block Recall and brain responses during arithmetic problem solving. We used a stringent threshold with the joint expected probability distribution of height (p < .005) and corrections for multiple spatial comparisons at the cluster level (p<.01) using a Monte Carlo simulation determined cluster extent of 87 voxels masked for gray matter.

2.3.5. ROI analyses

To further examine the relationship between WM and arithmetic problem solution, we used ROIs from an independent neuro-developmental study of VSWM in adults and children (Klingberg et al., 2002). In that study, the left IPS and left superior frontal sulcus (SFS) activity was positively correlated with behavioral measures of VSWM ability. Accordingly, we defined ROIs centered in the left IPS (MNI coordinates: −26 −60 60) and SFS (MNI coordinates: −24 −452) using spheres with a radius of 10 mm. We also used 10 mm spheres centered at the peaks and subpeaks of the functionally-defined clusters to examine responses in these brain regions.

3. Results

3.1. Neuropsychological assessments

3.1.1. Group differences in working memory

Working memory measures from the WMTB-C were compared between the groups. Children with MD had lower scores on Block Recall (t(32)=−2.61, p< .05) compared to TD children (Table 1). The other three working memory measures did not differ between the two groups—Digit Recall (t(32)=−.22, p=.83), Counting Recall (t(32)= −.07, p=.95) and Backward Digit Recall (t(32)= −.42, p=.68) (Table 1). To examine whether math skills or VSWM abilities were the most discriminating characteristic of the two groups we conducted an ANOVA with Cognitive Domain (Numerical Operations vs. Block Recall) as a within participant factor and Group (MD vs. TD) as a between participant factor. The interaction between Group and Cognitive Domain was significant [F(1,32)=17.95, p<.001]. The difference was larger for Numerical Operations (difference=33.18, MD=85.71, TD=118.29) than Block Recall (difference=11.18, MD=91.00, TD=102.18). As expected, this analysis suggests that math, rather than VSWM, ability is the more discriminating feature of our MD group. Because Numerical Operations was used to assign group membership this analysis may be biased by the selection procedure. Thus we also examined the Mathematical Reasoning subtest, again conducting an ANOVA with Cognitive Domain (Mathematical Reasoning vs. Block Recall) as a within participant factor and Group (MD vs. TD) as a between participant factor. In this case, the interaction between Group and Cognitive Domain was not significant [F(1,32)=.047, p=.83]. Group differences were comparable for Mathematical Reasoning (difference=12.53, MD=102.47, TD=115.00) and Block Recall (difference=11.18, MD=91.00, TD=102.18).

3.1.2. Relation between working memory and math abilities

Multiple stepwise linear regression analyses were conducted on Numerical Operations and Mathematical Reasoning scores, in the two groups combined, to test for unique contributions of the four subtests of the WMTB-C: the central executive assessed using Counting Recall and Backward Digit Recall; the phonological loop assessed using Digit Recall; and the VSWM assessed using Block Recall. General cognitive abilities (Full-Scale IQand Word Reading) were included in the model in order to account for variability not uniquely related to variation in WM abilities.

3.1.2.1. Numerical Operations

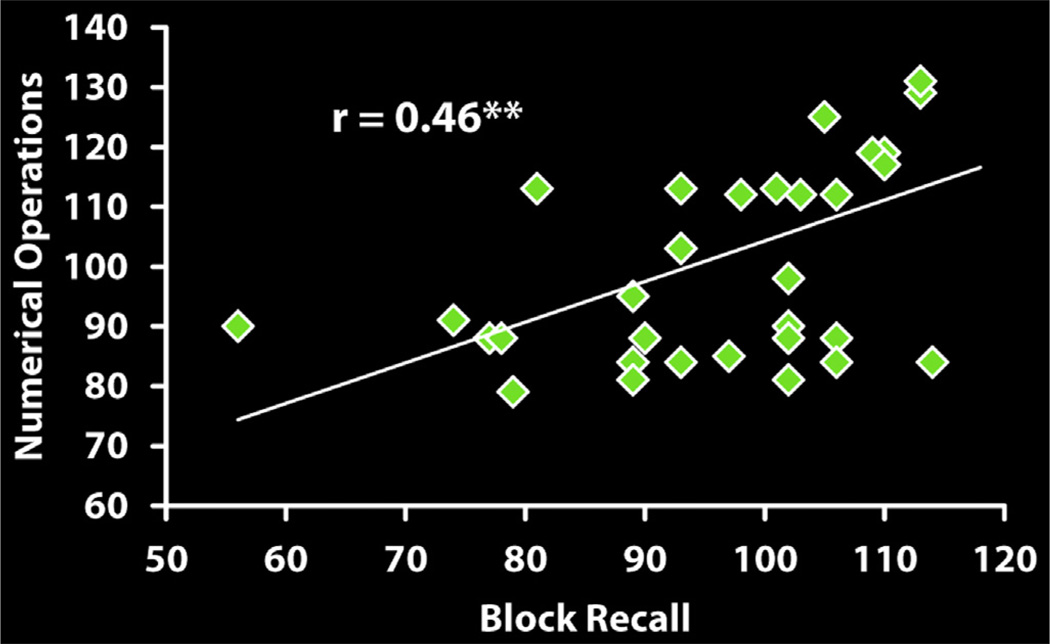
The regression analysis produced a model (R=0.46, adjusted R²=0.22), with Block Recall as the only significant predictor. As expected, higher Block Recall scores predicted higher Numerical Operations scores (Fig. 1 and Table 2).

Fig. 1.

Visuo-spatial working memory ability predicts arithmetic performance. Step-wise regression analyses confirmed that Block Recall, a measure of visuo-spatial working memory, uniquely predicted arithmetic performance among multi-component working memory capacities, and hierarchical modelling confirmed this relationship was independent of domain general performance variables, IQ and reading ability (**p<.01).

Table 2.

Stepwise regression models of mathematical abilities with full scale IQ, reading ability, and multi component working memory measures (Block Recall, Counting Recall, Digit Recall, Backward Digit Recall) as predictors.

Model	B	(SE)	β	R2	$R_{\text{change}}^2$	p
Numerical Operations
Predictor
Block Recall	.68	.23	.46	.22	–	.006
Mathematical Reasoning
Predictors
Full scale IQ	.75	.16	.60	.54	–	<.001
Word reading	.46	.20	.30	.61	.07	.024

3.1.2.2. Mathematical Reasoning

The regression analysis produced a model (R=0.78, adjusted R²=0.59) with FSIQ and word reading as the two significant predictors. Higher FSIQ and Word Reading scores both predicted higher Mathematical Reasoning scores (Table 2).

3.1.3. Hierarchical regression analysis of Numerical Operations and working memory

To assess the contribution of Block Recall to the variance explained in Numerical Operations, after accounting for the variance explained by general cognitive abilities, we used hierarchical regression analysis. Note that in our sample there were significant correlations between arithmetic, reading and IQ abilities (see Table 3). Additional analyses were conducted to eliminate the possibility that Block Recall did not contribute significantly to Numerical Operations scores after general cognitive abilities were specifically accounted for. No further regression analyses of Mathematical Reasoning were conducted because the omnibus stepwise regression did not specify WM subcomponents as significant predictors.

Table 3.

Relation between standardized measures of math abilities, working memory and general cognitive abilities. Pearson correlations were computed between measures.

Variables	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.
1. Numerical Operations	–	.48**	−.09	.14	.46**	.13	.26	−.06	.31	.19
2. Math Reasoning		–	.05	.29	.20	.17	.57***	.42*	.63***	.74***
3. Digit Recall			–	.12	.12	.08	.23	.08	.08	.09
4. Counting Recall				–	.22	.29	.31	.29	.36*	.44**
5. Block Recall					–	.37*	.24	<.01	.20	.15
6. Backward Digit Recall						–	.22	.16	.29	.29
7. Word Reading							–	.47**	.21	.45**
8. Verbal IQ								–	.02	.66***
9. Performance IQ									–	.76***
10. Full scale IQ										–

^*p<.05.

^**p<.01.

^***p<.001.

Model 1 included the IQ and Word Reading predictors from the previous analyses. Combined, these factors contributed to 7.6% of the variance in Numerical Operations scores. However, this contribution was not significant (R=0.28, adjusted R²=0.02, p=.29). Model 2 also included the only significant WM predictor from the original stepwise regression, Block Recall. Notably, the inclusion of Block Recall added 16.7% to the explained variance, and this contribution was significant (p<.05) (Table 4).

Table 4.

Hierarchical regression models of numerical operations scores with domain general predictors (Model 1), and the additional variance accounted for by visuo-spatial working memory (Model 2). Model 1 R²=.076, p=.29, Model 2 R²=.22, p=.05.

	B	(SE)	â	rpart	p
Model 1
Full scale IQ	.15	.32	.09	.08	.64
Word Reading	.47	.40	.22	.20	.26
Model 2
Full scale IQ	.11	.30	.07	.06	.70
Word Reading	.28	.38	.13	.12	.47
Block Recall	.62	.24	.42	.41	.02

3.2. Brain imaging

3.2.1. Accuracy and reaction time

For every participant the mean accuracy rate was calculated for each task condition. These means were subjected to a two-way analysis of variance (ANOVA) with Problem Complexity (Complex, Simple) as a within-participant factor, and Group (MD, TD) as a between-participants factor.

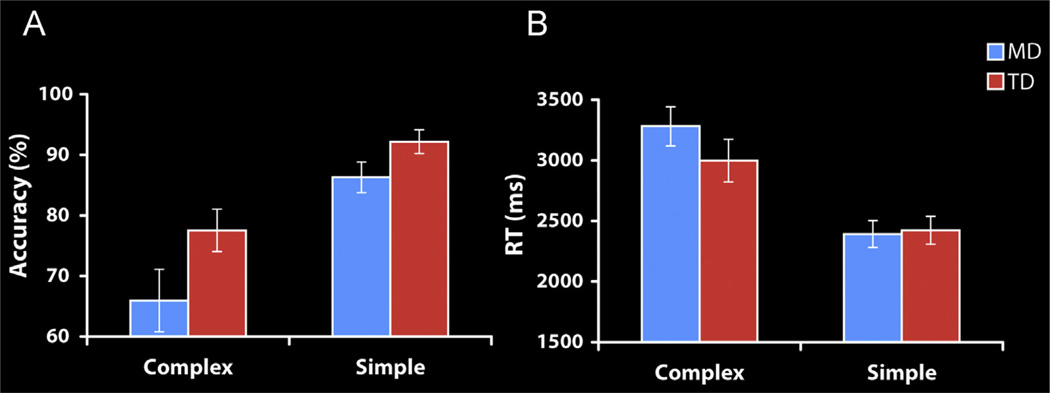
The main effect of Problem Complexity was significant [F(1,32)=55.41, p<.001]; accuracy levels were higher for Simple (89.2% SD=9.70) compared to Complex (71.7% SD=18.81) problems. The effect of Group was marginally significant [F(1,32)=4.02, p=.054]; the MD group had lower accuracy rates compared to the TD group. The interaction between Group and Complexity was not significant [F (1,32)=1.47, p=.23]. Planned follow up t-tests revealed that children with MD had marginally lower performance than TD children on Complex problems (t(32)=−1.86, p=.072; 65.94%, SD=21.24% for MD and 77.53%, SD=14.40% for TD), and Simple problems (t(32)=−1.83, p=.076; 86.29%, SD=10.53% for MD and 92.18%, SD=8.04% for TD) (see Fig. 2).

Fig. 2.

Arithmetic task performance in MD and TD groups. (A) Accuracy and (B) Reaction time (RT) for Complex and Simple addition problems. Both groups showed strong performance differences with addition problem complexity; Simple problems were solved faster and more accurately than Complex problems (ps < .001). For accuracy, the effect of Group was marginally significant (p=.054)—the mathematical disabilities (MD) group had slightly lower accuracy rates compared to the typically developing (TD) group. The interaction between Group and Complexity was not significant (p=.23). Planned follow-up t-tests indicated that MD children with had marginally lower performance than TD children on Complex problems (p=.072), and Simple ones (p=.076). For RT, there was no main effect of group, (p=.51), but there was a marginally significant interaction between Group and Complexity (p=.053). Planned follow up t-tests revealed no significant differences between the groups for either Complex (p=.24) or Simple (p=.85) problems.

For every participant the median reaction time (RT) of the correct trials was calculated for each condition. These means were subjected to a two-way ANOVA with Problem Complexity (Complex vs. Simple) as a within-participants factor, and Group (MD, TD) as a between-participants factor. The effect of Complexity was significant [F(1,32)=86.98, p<.001], participants were faster at Simple problems (2408 ms SD=461 ms) compared to Complex problems (3140 ms, SD=702ms). There was no main effect of Group [F(1,32)=0.45, p=.51] and a marginally significant interaction between Complexity and Group [F(1,32)=4.02, p=.053] (see Fig. 2). Planned follow up t-tests revealed no differences for either Complex (t(32)=1.19, p=.24; 3282 ms, SD=665 ms for MD and 2998 ms, SD=728 ms for TD), or Simple problems (t(32)= −.19, p=.85; 2392 ms, SD=461 ms for MD and 2423 ms SD=475 ms for TD).

3.2.2. Relation between brain activation and working memory in the MD and TD groups

As described above, behavioral analysis revealed that the only significant predictor of Numerical Operations abilities was Block Recall which measures VSWM capacity. Specifically, Block Recall explained unique variance in math skills even after controlling for other general cognitive factors. Furthermore, Block Recall was the only working memory measure that was significantly lower in children with MD compared to the TD group. Complex and Simple conditions were analyzed separately due to expected differences in WM load based on the differences in WM demands between the two tasks. Specifically, we predicted that Complex problems would require significant involvement of WM in their solution while such an involvement was not expected for Simple problems (Imbo et al., 2007). We therefore focused our analysis on the relationship between Block Recall and brain responses to Complex and Simple problems separately.

3.2.2.1. Complex arithmetic problems

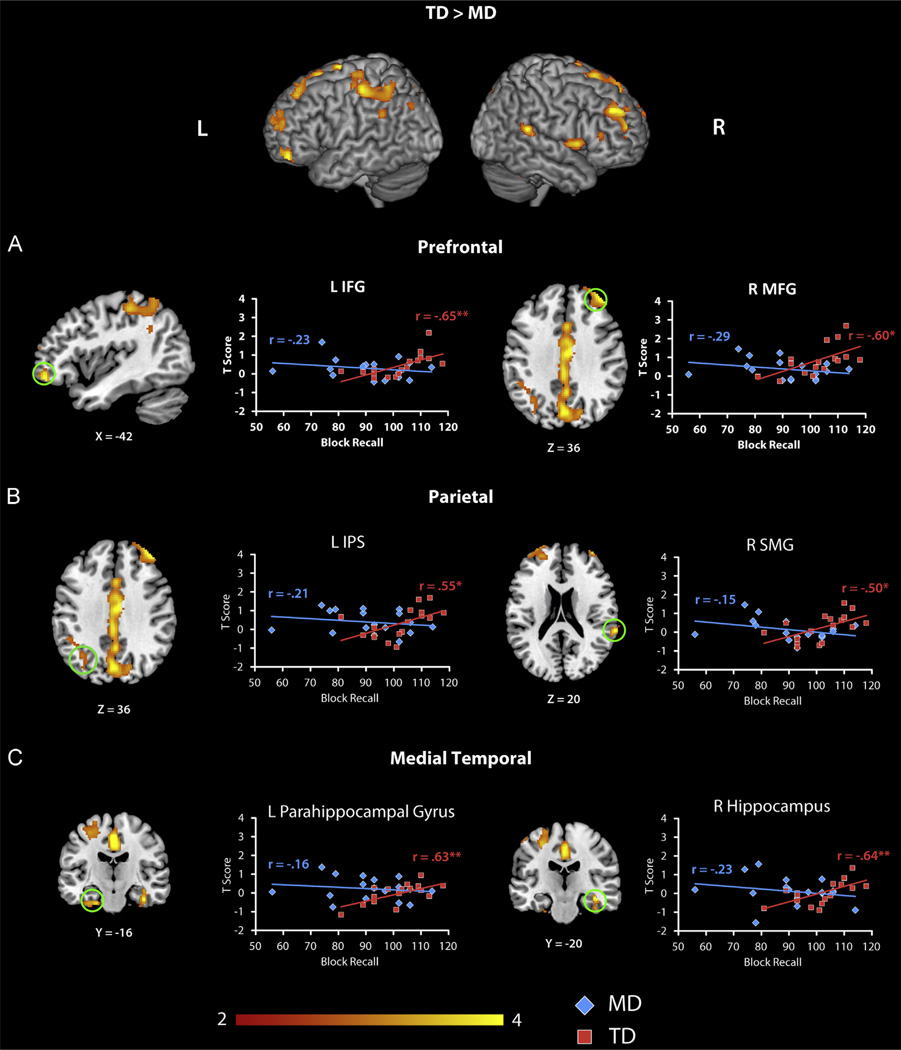
There were no overall differences in brain responses to Complex problems between the groups (Table S1). We next used an ANCOVA model to directly compare differences in the relation between Block Recall and brain activity in the two groups. The results indicated that there were differences in the slopes of the correlations in bilateral SMG (BA 22/48), left IPS (BA 7), left pre- and post-central gyri (BA 6/3), bilateral middle frontal gyrus (MFG, BA 44/46), supplementary motor area (SMA), precuneus (BA 18), bilateral inferior frontal gyrus (IFG, BA 47), right anterior insula (BA 48), bilateral fusiform gyrus (BA 20, 37), right cerebellum, right hippocampus (BA 20) and left parahippocampal gyrus (BA 36) (Table 5). Follow up ROI analyses revealed that these effects were driven by positive correlations in the TD group and negative or no correlations in the MD group (Fig. 3).

Table 5.

Brain areas where the relation between visuo-spatial working memory abilities and activity during arithmetic problem solving differed significantly between the TD and MD groups. No brain areas showed significantly greater correlations with visuo-spatial working memory in the MD group, compared to the TD group.

Region	BA	Cluster size (voxels)	Peak Z-score	Peak MNI coordinates (mm)
				X	Y	Z
TD>MD
M SMA/Precentral gyrus	23	4604	4.11	0	−14	48
L Precuneus	18		4.09	0	−76	32
L SFG	6		3.57	−6	−2	74
R MFG	44	358	3.84	40	44	36
R Fusiform gyrus	37	333	3.74	36	−48	−22
R Cerebellum	—		2.81	22	−58	−26
R Hippocampus	20	221	3.61	40	−20	−16
R Fusiform gyrus	20		3.54	38	−16	−28
R SMG	22	93	3.56	66	−38	20
L IFG	47	96	3.50	−42	50	−12
L Postcentral gyrus	3	1133	3.50	−50	−24	58
L Precentral gyrus	6		3.26	−28	−20	52
L SMG	40		3.17	−46	−50	60
L Parahippocampal gyrus	36	99	3.36	−22	−16	−32
L Fusiform gyrus	20		3.18	−32	−18	−32
R IFG	48	388	3.36	52	10	4
R AIC	48		3.08	38	20	10
L MFG	46	227	3.07	−24	54	20
L SMG	48	162	3.02	−48	−44	32
L IPS	7		2.84	−34	−62	36
MD>TD
No significant voxels

Note: BA=Brodmann Area. MD=Mathematical Disabilities group. TD=Typically Developing group. L=left hemisphere. R=right hemisphere. M=medial. Anatomical abbreviations populated from abbreviations list.

Fig. 3.

Brain areas where the relation between activity during arithmetic problem solving and visuo-spatial working memory abilities differed significantly between the TD and MD groups. (A) Prefrontal cortex. In typically developing (TD) children, left inferior frontal gyrus (IFG) and right middle frontal gyrus (MFG) showed significant positive correlation between activation during Complex addition problems and Block Recall, a measure of visuo-spatial working memory. In contrast, correlations were nonsignificant in children with mathematical disabilities (MD). (B) Parietal cortex. In TD children, the left intraperiatal sulcus (IPS), and right supramarginal gyrus (SMG) showed significant positive correlation between activation during Complex addition trials and Block Recall. In the MD group there were no significant correlations. (C) Medial temporal cortex. In TD children, left parahippocampal gyrus and right hippocampus showed significant correlations between activation during Complex addition trials and Block Recall. In the MD group there were no significant correlations (*p<.05, **p<.01).

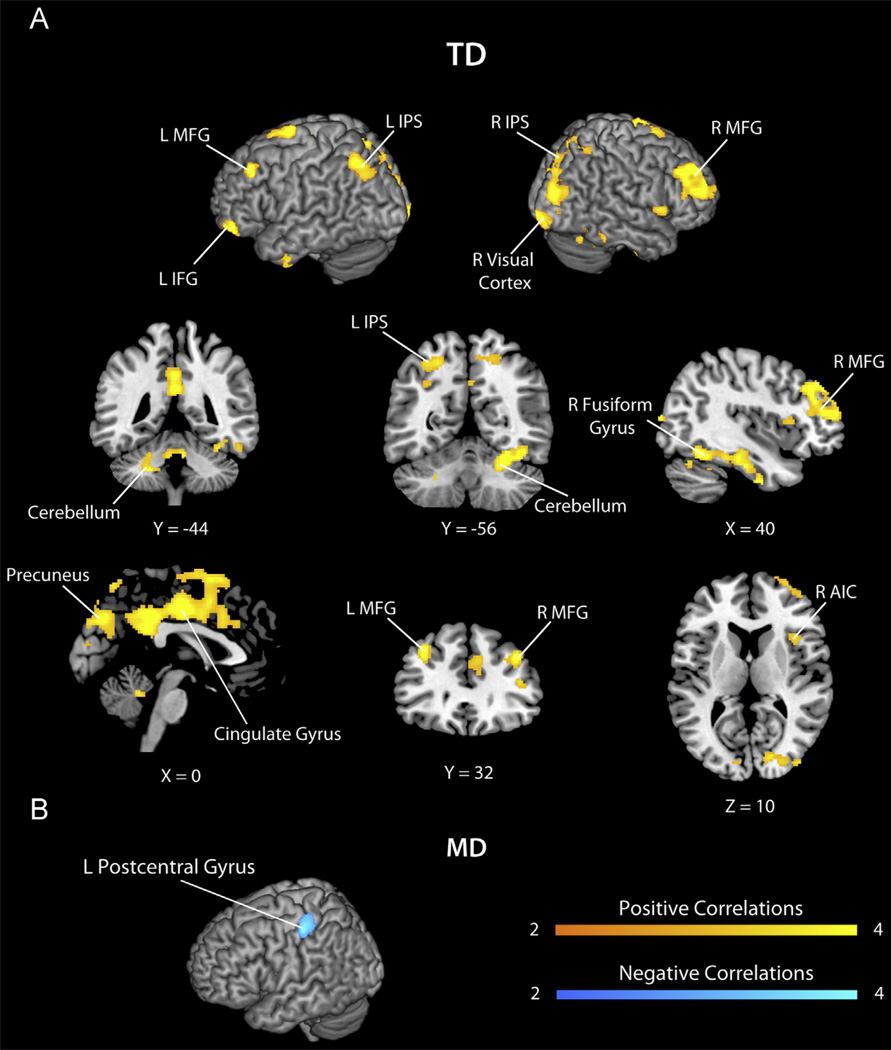
Additional analyses were conducted in each group separately to confirm these findings. In the TD group, Block Recall was significantly correlated with activity in the left IPS (BA 7), precuneus (BA 7), right superior parietal lobe (SPL, BA 5), bilateral precentral gyrus (BA 48/6), right anterior insula (BA 48), right visual cortex (BA 17), bilateral cerebellum, right fusiform gyrus (BA 20), left temporal pole (BA 36), inferior temporal gyrus (ITG, BA 20), bilateral MFG (BA 9/46) and left IFG (BA 47), cingulate gyrus (BA 23), left superior frontal gyrus (SFG, BA 6), right lateral occipital cortex (LOC, BA 19), cuneus (BA 18) (Fig. 4 and Table 6). In contrast, the MD group did not demonstrate any such relation; however, the MD group showed negative correlations in the left postcentral gyrus (BA 3) (Fig. 4 and Table 6).

Fig. 4.

Brain areas in which activity during arithmetic problem solving was significantly correlated with visuo-spatial working memory abilities in the TD and MD groups. (A) In the typically developing (TD) group, Block Recall, a measure of visuo-spatial working memory, was correlated with activity in bilateral middle frontal gyrus (MFG), left inferior frontal gyrus (IFG), right anterior insula (AIC), anterior, middle and posterior cingulate cortex and precuneus, bilateral intraparietal sulcus (IPS), right fusiform gyrus, left temporal pole and the cerebellum. No negative correlations were observed in the TD group. (B) In the mathematical disabilities (MD) group, Block Recall was negatively correlated with activity in left postcentral gyrus. No positive correlations were observed in the MD group.

Table 6.

Brain areas in which activity during arithmetic problem solving was significantly correlated with visuo - spatial working memory abilities in the TD and MD groups. No positive correlations were observed in the MD group. No negative correlations were observed in the TD group.

Region	BA	Cluster size (voxels)	Peak Z Score	Peak MNI coordinates (mm)
				X	Y	Z
TD Positive   correlations
R MFG	9	997	4.70	38	42	38
R Cerebellum	19	1131	4.24	26	−60	−20
R Fusiform gyrus	20		3.88	38	−8	−42
L MFG	46	253	4.14	−30	26	34
L Cerebellum	—	235	4.00	−30	−50	−40
R LOC	19	1820	3.97	20	−82	16
R Cuneus	18		3.73	4	−78	32
L Temporal pole	36	232	3.94	−38	2	−36
L ITG	20		3.03	−50	−4	−38
R Cingulate gyrus	23	3494	3.93	6	−14	36
L Cingulate gyrus	23		3.91	−4	−16	38
L SFG	6		3.86	−12	0	72
L IFG	47	101	3.79	−40	48	−12
R Visual cortex	17	223	3.55	20	−104	−4
M Cerebellum	—	139	3.45	6	−48	−26
LIPS	7	426	3.44	−32	−62	50
L Precentral gyrus	6	124	3.26	−22	−12	52
M Precuneus	7	266	3.25	2	−68	60
R SPL	5		2.95	18	−54	54
R Precentral gyrus	48	202	3.14	54	10	4
R AIC	48		2.85	38	18	10
TD Negative   correlations
No significant
voxels
MD Positive   correlations
No significant
voxels
MD Negative   correlations
L Postcentral   gyrus	3	269	4.04	−50	−24	58

Note: BA=Brodmann Area. MD=Mathematical learning disabilities group. TD=Typically Developing group. L=left hemisphere. R=right hemisphere. M=medial. Anatomical abbreviations populated from abbreviations list.

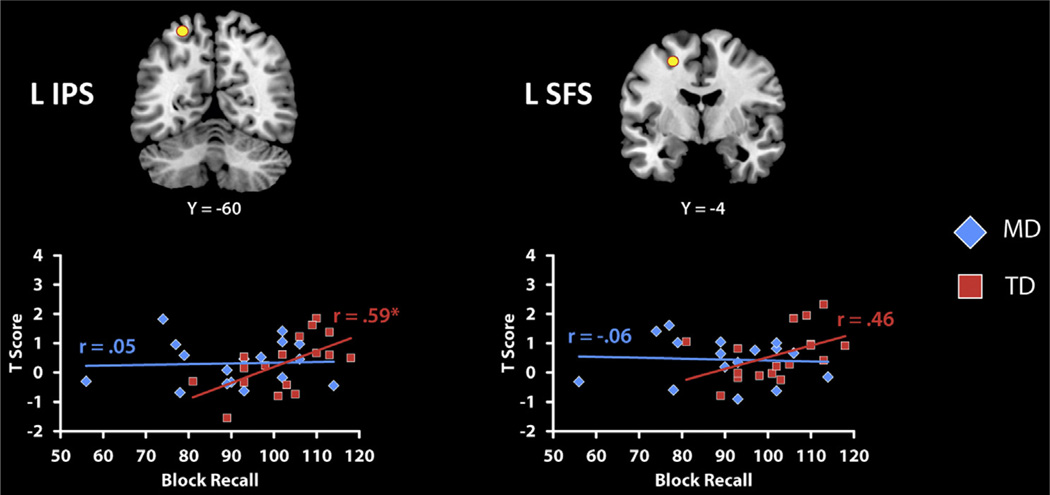
Next, we examined brain responses in two a priori ROIs within the left IPS and left SFS, based on a previous study that demonstrated significant correlation between VSWM abilities and activation in a developmental study of VSWM (Klingberg et al., 2002). Block Recall was significantly correlated with brain activity for Complex problems in the left IPS (R=0.59, p=.01) and marginally significant in the left SFS (R=0.46, p=0.06) in the TD group. In contrast, no significant correlations were detected in either the left IPS (R=0.05, p=.86) and left SFS (R=−0.06, p=.81) in the MD group (Table 7 and Fig. 5). Note that the TD group had slightly higher accuracy for Complex problems compared to children with MDs. This could potentially confound interpretation of group differences in brain response during problem solving. To control for this possibility, we re-analyzed the relation between Block Recall and activations in the left IPS and left SFS, covarying out accuracy on Complex problems. The pattern of results did not change: For TDs, left IPS (R=0.59, p<.05) and left SFS (R=0.46, p=.07). For MDs, correlations remained non-significant, left IPS (R=0.06, p=.82) and left SFS (R=−0.04, p=.88).

Table 7.

Relation between activity during arithmetic problem solving and visuo-spatial working memory abilities in a priori IPS and SFS ROIs. Full correlations represent associations between brain activation to Complex arithmetic problems and visuo-spatial working memory scores (Block Recall). Partial correlations were computed after removing the effects of phonological loop (Digit Recall) and central executive working memory (Counting Recall, Backwards Digit Recall).

	MD				TD
	Full		Partial		Full		Partial
	r	p	r	p	r	p	r	p
L IPS	.05	.86	.20	.49	.59	.01*	.57	.03*
L SFS	−.06	.81	.19	.52	.46	.06	.42	.14

^*p<.05.

Fig. 5.

Relation between activity during arithmetic problem solving and visuo-spatial working memory abilities in a priori IPS and SFS ROIs. We used ROIs from an independent neuro-developmental study of visual spatial working memory (VSWM) in adults and children (Klingberg et al., 2002) to further examine the relationship between working memory and arithmetic problem solving. In that study, left IPS and left superior frontal sulcus (SFS) activity was positively correlated with behavioral measures of VSWM ability. Accordingly, we defined ROIs centered in the left IPS (MNI coordinates: −26 −60 60) and SFS (MNI coordinates: −24 −4 52). As with results from whole brain analysis, the correlations were positive and significant in the IPS (*p< .05) and marginally significant in the SFS (p=.062) in the typically develping (TD) group, and nonsignificant in the mathematical disabilities (MD) group.

Additional analyses showed that effects in these two ROIs were specific to VSWM and not to the CE or PL. Specifically, we calculated partial correlation between VSWM abilities and activation level in the a priori ROIs while controlling for the individual abilities in Digit Recall, Counting Recall and Backward Digit Recall. In the TD group, Block Recall stayed significantly correlated with brain activity to Complex problems in the left IPS (R=0.57, p < .05) but not in the left SFS (R=0.42, p=.14). Moreover, no significant correlations were detected in the left IPS (R=0.20, p=.49) and the left SFS (R=0.19, p=.52) in the MD group.

3.2.2.2. Simple arithmetic problems

For Simple problems, children in the MD group had greater responses in the cingulate gyrus (BA 27), precuneus (BA 17), left precentral gyurs (BA 6), right LOC (BA 7), left amygdala (BA 20), left orbital frontal cortex (BA 47) and the right inferior and superior temporal gyri (BA 37/21) (Table S1). We then used an ANCOVA model to directly compare differences in the relation between Block Recall and brain activity during Simple problem solving in the two groups. The results indicated that there were differences in the slopes of the correlations in the left precuneus (BA 7), right fusiform gyrus, right hippocampus and ITG (BA 20), left precentral gyrus (BA 43), and right caudate. As with Complex problems, these correlations where positive in the TD group and negative in the MD group (Table S2 and Fig. S1). For the TD group, Block Recall was positively correlated with activity in the precuneus, right LOC and the right visual cortex (Table S3 and Fig. S2). For the MD group activity was negatively correlated with Block Recall in the left IFG, left MFG, left pre- and post-central gyrus, left caudate and the right precuneus and cuneus (Table S3 and Fig. S2).

In the TD group, Block Recall was marginally associated with brain activity in the left IPS a priori ROI (R=0.43, p=.087), but not in left SFS (R=0.23, p=.37). After covarying out individual abilities in Digit Recall, Counting Recall and Backward Digit Recall, no relationship was found between left IPS activity and Block Recall (R=0.35, p=.22). In the MD group, no significant correlations were detected in the left IPS (R=−0.08, p=.76) or the left SFS (R=−0.28, p=.28, see Table S4).

4. Discussion

WM is thought to play an important role in the normal development of arithmetic problem solving and WM deficits have been implicated in poor problem solving abilities in children with MD. However, the relation between WM and arithmetic problem solving has remained poorly characterized. In this study, we used behavioral and brain imaging measures to examine how WM components differentially impact arithmetical skills in TD children and children with MD. We addressed this question using a unique, carefully controlled, sample in which the MD and TD groups were matched on IQ and reading ability. Critically, central executive and phonological WM capacities in the MD group were all in the normal range and did not differ from the TD group. In contrast, VSWM capacity was significantly lower in children with MD. Brain imaging measures provided convergent evidence that children with MD use VSWM differently than TD children, further highlighting the importance of VSWM to normal and aberrant numerical cognition at a critical stage of skill acquisition.

4.1. Relationship between working memory and math abilities

Behavioral studies have variably implicated all three components of WM in arithmetic problem solving (Heathcote, 1994; Imbo et al., 2007; Trbovich & LeFevre, 2003), and there is evidence to suggest that in TD children the relationship between problem solving and WM abilities changes over the course of development with greater engagement of the central executive during early stages of arithmetic skill acquisition leading to eventual reliance on VSWM (Bull, Espy, & Wiebe, 2008; De Smedt et al., 2009; Meyer, Salimpoor, Wu, Geary, & Menon, 2010). To account for these developmental trends, we computed the unique contributions of all three components of WM to the standardized Numerical Operations and Mathematical Reasoning subtests of the WIAT-II. We found that individual differences in 7–9 year old children′s Numerical Operations scores were uniquely explained by VSWM abilities. This result has several important extensions. First, VSWM abilities predicted variability in Numerical Operations scores even after general factors such as IQ and reading ability were included in the analysis. Second, in the between group analysis, VSWM scores were significantly lower in children independently classified as having MD (by their Numerical Operations score) compared to TD controls. Taken together, these results indicate that, amongst the three working memory components, weak VSWM is a specific source of vulnerability in problem solving deficits in children with MD. This convergence on a single locus of deficits, despite previous behavioral findings suggesting the involvement of all three cognitive WM abilities in normal arithmetic acquisition, further suggests a specific role for VSWM over and above the involvement of the other WM abilities. Critically, previous behavioral studies have highlighted a shift to greater reliance on VSWM during math skill development (Meyer et al., 2010), suggesting that children with MD do not show maturation of VSWM abilities in ways that contribute to optimal development of math problem solving skills.

Importantly, VSWM predicted Numerical Operations subtest scores but not Mathematical Reasoning scores. Numerical Operations directly measures symbolic calculation abilities, Mathematical Reasoning places a greater load on reading and solving word problems. It is therefore likely that Mathematical Reasoning, much more than Numerical Operations, requires additional cognitive resources beyond VSWM. This view was confirmed by a step-wise regression analysis which found high and significant correlations between Mathematical Reasoning and full scale IQ, and between Mathematical Reasoning and Word Reading; no such relations were found between Numerical Operations and any of these measures. Together these results suggest that VSWM abilities are particularly important for rapid symbolic calculations.

4.2. Effects of weak VSWM in arithmetic problem solving

To further clarify the role of VSWM, we used fMRI to examine the relation between individual differences in VSWM abilities and brain activity during arithmetical problem solving. TD children exhibited significant positive correlations between brain activity while solving Complex problems and VSWM abilities, but children with MD showed no such positive effects. A formal Group by VSWM ability ANCOVA confirmed that there were significant group differences in the way VSWM modulated responses in multiple brain regions including the left IPS, left SMG, right insula, bilateral MFG, left IFG, left pre- and post-central gyrus, cingulate gyrus, precuneus, right hippocampus, left parahippocampal gyrus and the bilateral fusiform gyrus. For Simple arithmetic problems, some of these posterior regions, including left precuneus and right fusiform gyrus, also showed this pattern of positive correlations in the TD group and weak negative correlations in the MD group. The consistency of these results across two levels of problem complexity further bolsters our findings that, unlike TD children, children with MD do not engage VSWM resources appropriately during arithmetic problem solving.

Considering the TD children alone, VSWM was significantly correlated with activity in the left IPS, left SMG, bilateral ventral temporal cortex, cerebellum, insula and multiple frontal areas including the SMA, mid cingulate and pre- and post-central gyrus that are known to be involved in arithmetic problem solving and basic numerical processing in children and adults (Arsalidou & Taylor, 2011; Houdé, Rossi, Lubin, & Joliot, 2010). This pattern of results confirms that children with MD use VSWM resources differently during solution of arithmetic problems, and suggests that children with MD do not rely on VSWM representations for arithmetic problem solving. More generally, the differential findings in the two groups further point to a fundamental role played by VSWM in the normal development of arithmetic skills.

4.3. Overlap in IPS activity during VSWM and symbolic number processing

Our whole brain and a priori ROI findings provide new evidence for a link between IPS activity during symbolic number processing and VSWM in children. The IPS plays an important role in both basic number processing and arithmetic problem solving (Ansari & Dhital, 2006; Dehaene, Piazza, Pinel, & Cohen, 2003; Delazer et al., 2003; Menon, Mackenzie, Rivera, & Reiss, 2002; Pinel, Dehaene, Riviere, & LeBihan, 2001; Rosenberg-Lee, Lovett, & Anderson, 2009; Zago et al., 2008), leading to the hypothesis that impaired activity or structure of the IPS is a core feature of MD (Cohen Kadosh et al., 2007; Molko et al., 2003; Price et al., 2007). However, multiple lines of research have suggested that the IPS is also strongly activated during tasks involving short-term VSWM (Todd & Marois, 2004; Vogel & Machizawa, 2004). Weak IPS activation among children with MD could therefore not only underlie specific deficits in basic number processing but also deficits in complex arithmetic problems which require access to shared short-term VSWM processes. In adults, overlap in bilateral IPS activations has been reported during arithmetic and VSWM tasks (Zago & Tzourio-Mazoyer, 2002). In a developmental context, multiple studies suggest that IPS regions activated during VSWM tasks in children (Klingberg, 2006; Klingberg et al., 2002; Rotzer et al., 2009) were also found to be active during arithmetic problem solving (Kaufmann, Wood, Rubinsten, & Henik, 2011). But evidence for a link to normal and aberrant function in children has been lacking. Our study provides new evidence for a link between VSWM and arithmetic processing in children. In the present study, TD children showed positive correlations between VSWM abilities and activity level in the left IPS (BA 7), consistent with the developmental study by Klingberg et al. (2002) which found that left IPS activity during VSWM tasks is positively correlated VSWM abilities (Klingberg et al., 2002). Thus, the functional correlates of VSWM show prominent overlap in the IPS during both working memory and arithmetic problem solving tasks.

The observed profile of functional deficits may arise from morpho-metric deficits which have been reported in several previous anatomical studies of children with MD or developmental dyscalculia (Price et al., 2007; Rotzer et al., 2008, 2009; Rykhlevskaia, Uddin, Kondos, & Menon, 2009). Neuroanatomical studies have found that children with MD show reduced gray matter volume in the IPS and adjoining PPC areas (Rotzer et al., 2008; Rykhlevskaia et al., 2009). Similarly, under-activity in the IPS was found among MD during arithmetical and basic numerical tasks (Cohen Kadosh et al., 2007; Molko et al., 2003; Price et al., 2007) as well as during VSWM tasks (Rotzer et al., 2009). Hence, abnormality in the IPS among MDs can lead to deficits in numerical processing as well as VSWM abilities (Rubinsten & Henik, 2009). Collectively, these data suggest that the IPS is a specific locus of vulnerability in children with MD and that deficits in IPS function observed in these children arise from anatomical overlap between arithmetic processing and VSWM. More broadly, considered in the context of current theoretical conceptualizations of numerical information processing, our results suggest that while TD children rely on IPS associated VSWM processes to manipulate numerical information, children with MD do not use this locus of problem representation appropriately during numerical problem solving.

4.4. VSWM and arithmetic abilities in children

The role of VSWM has often been considered as secondary to the central executive component of WM in normal arithmetic skill acquisition and has generally been neglected in prior accounts of MD. Here we consider key developmental issues in light of our findings. Convergent evidence from the present neuroimaging study, as well as related behavioral studies, indicates that individual differences in VSWM ability play a significant role in the initial stage of acquiring arithmetic concepts in children, even before the beginning of formal education (De Smedt et al., 2009; Holmes & Adams, 2006; Rasmussen & Bisanz, 2005). This is consistent with the view that during the basic stage of acquiring arithmetical understanding, children use an internalized representation of a problem, or a mental model, for arithmetic that requires VSWM (Rasmussen & Bisanz, 2005). The use of mental models of arithmetic starts in infancy; for instance, it has been demonstrated that 8-month old infants create an automatic connection between space and number representations (de Hevia, 2010). Furthermore, linkage of number and space, or the representation of magnitude on the mental number line, requires VSWM (de Hevia, 2010). For example, VSWM load (but not verbal WM load) eliminates the spatial-numerical association of response codes (SNARC) effect during number comparisons, indicating that VSWM is necessary for the online mapping of number and space (Herrera, Macizo, & Semenza, 2008). Furthermore, children with visuo-spatial disabilities do not show the SNARC effect during number comparison (Bachot, 2005). Hence, deficits in VSWM can influence primarily non-verbal numerical skills, such as the ability to represent magnitude on the mental number line and estimation of quantity. The recurring theme of VSWM involvement in impaired development from multiple experimental paradigms across extended periods of early skill acquisition in the domains of number sense, numerical magnitude judgement and arithmetic emphasizes its importance in developmental models of mathematical cognition.

Furthermore, other areas of difficulty in children with MD such as counting and subitizing may have their roots in VSWM deficits (Geary et al., 1992; Schleifer & Landerl, 2011). Geary et al. (1992) has shown that in the initial stage of counting, children point sequentially at each element in a counted array while holding these locations in mind, a process that requires VSWM. Similarly, it has been suggested that subitizing abilities are based on domain general mechanisms including VSWM (Piazza, Fumarola, Chinello, & Melcher, 2011). In summary, in the initial stages of numerical and arithmetic skill development, there is a clear reliance on visuo-spatial representations. On the basis of these developmental findings as well as our neuroimaging results we suggest that VSWM is a major and necessary component for successfully building numerical and arithmetic representations that are a hallmark of mathematical skill acquisition.

4.5. Limitations

Definitions of mathematical disability can be highly variable across studies, ranging from the 2nd percentile on standardized arithmetic ability assessments on the conservative end (Ashkenazi et al., 2009), to the 35th percentile on the more liberal end (Geary et al., 2000). An arguably liberal cut-off was used in our study to identify the MD group (27th percentile). In spite of this, the MD sample used showed significant and specific deficits in VSWM. What is more relevant here is that the TD and MD groups differed in math abilities by more than 2 standard deviations. Given the focus of our study on differential links between brain and behavior in the two groups, the precise cut-offs are not as important here. Critically, a slightly more liberal cut-off allowed us to match the two groups on multiple other cognitive measures including normal IQ and reading, thereby allowing us to disambiguate the specific and crucial role of VSWM. Further studies are needed to examine whether children with more severe forms of MD (10% percentile and below) have a similar profile of VSWM deficits as those identified here.

5. Conclusions

We examined the association between VSWM abilities and brain activity during arithmetical problem solving in TD children and in children with MD. Our study overcomes limitations of previous neuro-imaging studies by employing a narrow age range, using a standardized test to identify children with MD and excluding children with co-morbid cognitive disabilities. Furthermore, TD children were individually matched on age, IQ, reading ability and handedness and drawn from a broad range of mathematical abilities (the 37th to the 100th percentile). Consistently, across prefrontal, parietal and cerebellar regions implicated in WM, we found that TD children demonstrated a strong positive relationship between activity level during arithmetic problem solving and individual VSWM abilities. In contrast, children with MD failed to show any positive relationship between brain response and VSWM abilities. Our study provides new evidence that VSWM is a specific source of vulnerability in symbolic numerical calculations deficits and thus needs to be seriously considered as a key component in cognitive, neurobiological and developmental models of mathematical skill acquisition. Convergent evidence from our study and related neuroimaging studies of number and VSWM processing, suggest that a common locus of deficits in visuo-spatial representations and memory contributes to both numerical and arithmetic deficits in children with MD. More broadly, our findings have important implications for understanding normal mathematical skill development as well as the etiology of mathematical learning disabilities.