Social Network Analysis of Biomedical Research Collaboration Networks in a CTSA Institution

Abstract

BACKGROUND

The popularity of social networks has triggered a number of research efforts on network analyses of research collaborations in the Clinical and Translational Science Award (CTSA) community. Those studies mainly focus on the general understanding of collaboration networks by measuring common network metrics. More fundamental questions about collaborations still remain unanswered such as recognizing “influential” nodes and identifying potential new collaborations that are most rewarding.

METHODS

We analyzed biomedical research collaboration networks (RCNs) constructed from a dataset of research grants collected at a CTSA institution (i.e. University of Arkansas for Medical Sciences (UAMS)) in a comprehensive and systematic manner. First, our analysis covers the full spectrum of a RCN study: from network modeling to network characteristics measurement, from key nodes recognition to potential links (collaborations) suggestion. Second, our analysis employs non-conventional model and techniques including a weighted network model for representing collaboration strength, rank aggregation for detecting important nodes, and Random Walk with Restart (RWR) for suggesting new research collaborations.

RESULTS

By applying our models and techniques to RCNs at UAMS prior to and after the CTSA, we have gained valuable insights that not only reveal the temporal evolution of the network dynamics but also assess the effectiveness of the CTSA and its impact on a research institution. We find that collaboration networks at UAMS are not scale-free but small-world. Quantitative measures have been obtained to evident that the RCNs at UAMS are moving towards favoring multidisciplinary research. Moreover, our link prediction model creates the basis of collaboration recommendations with an impressive accuracy (AUC: 0.990, MAP@3: 1.48 and MAP@5: 1.522). Last but not least, an open-source visual analytical tool for RCNs is being developed and released through Github.

CONCLUSIONS

Through this study, we have developed a set of techniques and tools for analyzing research collaboration networks and conducted a comprehensive case study focusing on a CTSA institution. Our findings demonstrate the promising future of these techniques and tools in understanding the generative mechanisms of research collaborations and helping identify beneficial collaborations to members in the research community.

1. Introduction

The Clinical and Translational Science Award (CTSA), funded by the National Center for Advancing Translational Sciences (NCATS, NIH) (formerly through the National Center for Research Resources (NCRR, NIH)), was launched in 2006 and has expanded to 60 academic institutions aiming to accelerate the process of translating biomedical research discoveries into clinical applications. One key function of the CTSA is to promote collaborative research efforts especially across different disciplines. For example, the University of Arkansas for Medical Sciences (UAMS)–a CTSA institution since 2009–created the Translational Research Institute (TRI) to support translational and collaborative activities such as helping basic and clinician scientists to develop and manage their studies, fostering collaborative partnerships among stakeholder communities, and providing infrastructures (e.g., clinical data warehouse) to affiliated researchers.

It is crucial to quantitatively assess the effectiveness and quality of research collaborations in a CTSA institution. Social network analysis (SNA) methods have been deemed as an effective tool to assess intra-institution research collaborations in the CTSA community [1]. Previous studies on RCN [2, 3, 4, 5, 6, 7], however, mainly focus on improving general understanding of collaboration networks by measuring common network metrics ¹. More fundamental questions about collaboration still remain unanswered such as recognizing “influential” nodes and identifying potential collaborations that are most rewarding. In this paper, we aim at finding answers to those questions by analyzing biomedical research collaboration networks at a CTSA institution (i.e., UAMS) in a comprehensive and systematic manner. To achieve this goal, we have developed new models and techniques for research collaboration network by leveraging readily available network analysis methods, results, and tools.

The research collaboration networks we studied are distinctive in their data source and model. Those collaboration networks were constructed from collaborative research grants instead of conventional publication co-authorships [3, 4, 5] as we believe collaborative grants provide additional and earlier evidence of possible collaborations. Principle investigator and co-investigator(s) of a collaborative grant often work together in a number of aspects throughout the supported research project, from grant proposal writing to research conduct and findings dissemination. We studied the RCN before (RCN_2006–2009) and after (RCN_2010–2012) UAMS being awarded CTSA aiming to understand the temporal evolution of the RCN. Through comparing various network characteristics across different time frames, we were able to examine the effectiveness of CTSA and evaluate its impact on collaborative research activities at UAMS.

In our network model, links between investigators are weighted to reflect the degree of collaboration. Previous studies on collaboration networks [3, 4, 5, 6, 7, 8] model research collaborations as unweighted or binary networks where edges only indicate the existence of collaborations. However, collaborative research relationships may vary between investigators. It is intuitive that certain connections are “stronger” than others in an RCN, as we are often inclined to work with existing collaborators than finding new peers. Our network model reflects such a natural distinction through assigning the number of collaborative grants between two investigators as the edge weight.

To understand network dynamics and generative mechanisms of research collaborations in a CTSA institution, more specifically, to answer questions such as: “Is the RCN at UAMS a small-world? Is the CTSA effective in fostering interdisciplinary collaborations? How to identify potential new collaborations that are more likely to succeed?,” we have developed new network analysis methods and obtained interesting and valuable findings from our unique dataset. The methods and findings are aimed to assist administration and leaderships in making such organizational policies and strategic plans that are inclined to cause positive and substantial impacts on research collaborations and their outcomes. For example, key nodes in a collaboration network can be identified on the basis of centrality measures, and promising new collaborations can be recommended by applying the link prediction techniques. Leveraging our network analysis and link prediction techniques, necessary resources can be provisioned to spawn new collaborations and attract new investigators.

Our first finding of the collaboration networks at UAMS is that those networks are indeed small-world but not scale-free. Small-world and scale-free properties, manifesting in many real-world complex networks, have important implications in network robustness and efficiency. We quantitatively measured the “small-world-ness” [9] and revealed that the RCNs at UAMS indeed exhibit the small-world property. Moreover, the statistical measures [10] show that the degree distributions of both RCN_2006–2009 and RCN_2010–2012 do not follow the power law. Therefore, the RCNs at UAMS are not scale-free.

Our results also testified the effectiveness of the CTSA and its important role in promoting collaborative research within an institution. In addition to studying temporal evolution of network measures pertaining to RCNs, we also devised a quantitative “diversity” measure to model the trend of cross-disciplinary collaborations. The diversity measures how easy it is for an investigator from one discipline to reach another investigator in a different research field. The bigger the diversity value, the easier the cross-disciplinary collaboration will be. The diversity measure increases from 0.37 in RCN_2006–2009 to 0.56 in RCN_2010–2012, indicating that the RCN at UAMS is moving towards favoring cross-disciplinary research after the CTSA.

We leveraged centrality measures [2] and rank aggregation techniques [11, 12] to derive a single consented ranking of important (or “influential”) nodes in a collaboration network. Moreover, Our collaboration recommendation technique employs the random walk with restart (RWR) algorithm [13] to construct a recommendation model for suggesting new research collaborations. The benchmarks of the our recommendation method on the RCNs of UAMS show promising results (AUC: 0.838 ~ 0.974 and MAP@3: ≈ 0.977).

Last but not least, we have developed an open source software package—the research collaboration network analysis (RCNA) tool kit (available at https://github.com/bianjiang/rcna under MIT license)—to help catalyze research in this area, especially to facilitate CTSA institutions to effectively evaluate the CTSA in promoting collaborative research activities. A unique and valuable component of the kit is a set of interactive visualization tools, which help us better explore and understand complex RCNs. A visualization of the UAMS’s RCNs can be accessed at http://bianjiang.github.com/rcna/.

The rest of the paper is organized as follows. We first describe the source data retrieved from an in-house developed research grant management system. We then introduce our weighted network model of research collaborations, the concept of network characteristics and measures pertaining to this study. After that, we describe our methods of using network centrality measures and rank aggregation to identify centrality “leaders” ². Furthermore, we present a link prediction based model for suggesting new research collaborations. Finally, we present the experiment results and our interpretations which indicate that the CTSA award has a positive impact on the collaborative research environment at UAMS.

2. Material and Methods

2.1. Background and dataset

In this paper, we study research collaboration networks constructed from collaborative research grants. The Office for Research and Sponsored Programs (ORSP) at UAMS uses an in-house developed software system to track detailed information of research grants such as the requested budget amount, the budget start/end date, the funding agencies, as well as all the investigators and their roles on each grant. Besides the ORSP, the Translational Research Institute (TRI, UAMS) supports all CTSA activities at UAMS since July 2009. As the TRI tracks all CTSA related activities such as publications, pilot awards and so on, we use the TRI’s CTSA reports to obtain the information of whether an investigator is supported by the CTSA or using TRI services.

Table 1 shows the statistics of the research grant data we have obtained from the ORSP. We use these meta-data of grants to construct RCN for each fiscal year from 2006 to 2012. Each fiscal year at UAMS starts on July 1st till June 30th of the next year. Therefore, we collected data for grant applications whose budget start date is in the range between July 1st, 2006 and June 30th, 2013. The CTSA at UAMS started on July 14th, 2009. Therefore, in this analysis, the “number of CTSA Investigators” (i.e., investigators who are listed on the original CTSA grant) and “number of CTSA supported investigators” (i.e., investigators who received support from the CTSA) columns in Table 1 are not applicable to budget years from 2006 to 2009. Moreover, we only consider the researchers with the “Principle Investigator”, “Co-Investigator”, and “Sub-Investigator” roles on the grants, and exclude other personnel such as “Support Staff” and “Laboratory Staff”. In addition, we only take into account the grants that have been “Awarded” for two main reasons: 1) an awarded collaborative grant indicates successful executions of team science; and 2) a grant might have to go through a few review and revision cycles to get funded. By considering only the final awarded version, we can effectively eliminate some of the noises in the constructed networks. For a multi-year project, the grant is counted individually for each fiscal year.

Table 1.

Statistics of the research grants dataset at the University of Arkansas for Medical Sciences.

Fiscal Year	Number of Awarded Grants	Number of Investigators	Average Number of Investigators Per Grant	Number of CTSA Investigators	Number of CTSA Supported Investigators
2006	477	326	2.78 (N/A)	N/A	N/A
2007	479	409	2.94 (N/A)	N/A	N/A
2008	601	469	2.83 (N/A)	N/A	N/A
2009	516	414	3.06 (N/A)	N/A	N/A
2010	603	431	3.63 (3.31)	34	114
2011	538	443	3.36 (3.22)	26	115
2012	549	434	3.44 (3.30)	23	322
2006 – 2009	2073	759	2.91 (N/A)	N/A	N/A
2010 – 2012	1690	650	3.48 (3.27)	34	551

^*CTSA – Clinical & Translational Service Award

^*The numbers in the parentheses of the “Average Number of Investigators Per Grant” column are calculated excluding the CTSA award itself.

^*The number of CTSA supported investigators is significantly higher in 2012 than previous years. We think it is because more investigators become aware of and start utilizing the CTSA services as we advertised more to the campus.

2.2. Abstraction of research collaboration networks

Existing studies [3, 4, 5, 8, 6, 7] on scientific collaboration networks, to our best knowledge, abstract the networks as undirected and unweighted (binary) graphs, which only consider the existence of collaboration relationship between two investigators. However, it is common that collaborative relationships among investigators vary. Intuitively, the association and partnership between two frequent collaborators should be much stronger than those who have collaborated only once in the past.

Therefore, we formalize a research collaboration network (RCN) as an undirected weighted graph, G = (V,E), where each investigator is represented by a vertex or node (v_i). The collaborative relationship between two investigators is evident by an edge or link between the two nodes, and the weight (w_{i j}) of the edge (e_{i j}) is the number of research grants the two investigators (v_i and v _j) have collaborated on during the time period of interest. Figure 1 depicts two RCNs, where graph (a) is the RCN at UAMS prior to the CTSA from 2006 to 2009 (RCN_2006–2009) and graph (b) is the RCN after the CTSA from 2010 to 2012 (RCN_2010–2012). For visualization purpose, we only pick out the largest strongly connected components of the two RCNs. We note that both of the original RCNs contain isolated small clusters (i.e., groups that have strong collaborations internally but no connections to other parts of the RCN) and isolated individual nodes (i.e., investigators carried out the research independently).

Figure 1.

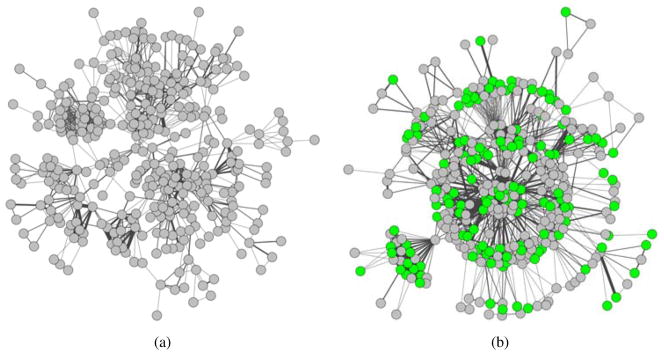
The research collaboration networks (RCNs) at UAMS, where graph (a) is the RCN prior to the CTSA (i.e., 2006 – 2009); and graph (b) shows the RCN after the CTSA from 2010 to 2012. (*The edge weights are visualized as thickened lines, which represent more collaborations between the two investigators. The nodes in green represent investigators who are supported by the CTSA.)

This weighting schema, however, is inappropriate to the situations where a smaller weight is preferred. For example, when calculating the characteristic path length of a network (i.e., the average (shortest) distance between all pairs of vertices), algorithms for finding shortest paths in a weighted graph favor smaller edge weight as the weight of an edge is considered as the cost to travel between two nodes. Hence, under the original weighting schema, shortest path algorithms will select the paths where the two investigators have less collaborations. Such results contradict the common sense that it is “shorter” and easier to reach a frequent collaborator than a one-time collaborator. Therefore, we use the reciprocal of the original edge weight (1/w_{i j}) as the new edge weight–namely the resistance factor–for edge e_{i j} where it is appropriate. In the rest of the paper, we denote the original weighting schema, where the edge weight is the number of collaborations between two investigators, as $w_{ij}^o$, and the revised weighting schema based on resistance factor as $w_{ij}^r(=1/w_{ij}^o)$.

2.3. “Small-world-ness” and the scale-free property

Small-world networks [14] and scale-free networks [15] are two important types of networks that are resilient to link failures. Watts and Strogatz coined the term “small-world” networks to categorize complex sparse real-life networks that have significantly high clustering coefficients than sparse random graphs yet have small degrees of separation between nodes. Small-world networks have been extensively studied in many domains [14, 16, 17, 18]. Within the context of research collaboration networks, a small-world network indicates the overall robustness of the collaborative relationships. Random deletion of a node in the RCN, e.g., an investigator leaving the institution, is unlikely to cause dramatic decreases in the overall collaborative research efforts.

In this study, we adopt a quantitative measure of the network’s “small-world-ness” S [9]. A network G is a small-world network [14] if it has greater clustering of nodes than an equivalent Erdős-Rényi graph[2] that has a similar small path length as G. The “small-world-ness” S measures the trade-off between high local clustering and short path length. Let G be the network of interest. Formally,

$${\gamma }_G=\frac{C_G}{C_{G-\mathit{Rand}}},\mathit{and}{\lambda }_G=\frac{L_G}{L_{G-\mathit{Rand}}},$$

where C_G and and C_G–Rand are the clustering coefficient of G and a corresponding E-R random network of G, respectively; and L_G and L_G–Rand are the mean shortest path length of G and the random graph, respectively. Then, the “small-world-ness” S of the network G is defined as

$$S=\frac{{\gamma }_G}{{\lambda }_G}.$$

A network is deemed as a “small-world” network if S > 1 [14].

There are two common ways of defining network clustering. In this study, we adopted the Watts and Strogatz definition [14] (see detail in the next section). For a graph with disconnected components, we compute the “small-world-ness” on the largest connected component (i.e., the subgraph with the most connected vertices). Moreover, we do not consider edge weights when calculating S, since there is not a meaningful way to generate comparable corresponding weighted E-R networks.

Another noteworthy model of complex networks is the scale-free network, where the network degree distribution follows a heavy-tailed power-law [15]. A power-law degree distribution suggests the relative commonness of nodes with a degree that greatly exceeds the average. Similar to the small-world property, the scale-free property strongly correlates with the network’s robustness. In this study, we tested the power-law degree distribution of our research collaboration networks according to the methods described in [10]. The goodness-of-fit between the data and the power-law can be computed and we can conclude that the power-law is a plausible hypothesis for the data if the resulting p-value is greater than 0.1. The p-value is used as a measure of the hypothesis that we are trying to verify, and high p-values are “good,” as noted in [10]. A good discussion of this interpretation of p-values can be found in [19].

2.4. Characteristics of research collaboration networks as evaluation metrics

Topological features of a network can be quantitatively measured as network characteristics such as the clustering coefficient and characteristic path length. These structural network characteristics are often used to benchmark or infer the functional aspects of the network. For example, the mean path length (characteristic path length) L of a network is often employed to measure the efficiency of information flow on a network.

The following are the network characteristics of our interest in analyzing research collaboration networks. Note that our RCNs are weighted undirected graph; therefore, we shall respect the edge weights if possible.

• Degree/strength: The degree of a vertex/node (v_i) – k_i – is the number of edges incident to v_i. The weighted degree (also called the strength) s_i of v_i is defined as s_i = Σ_j w_{i j}. Here w_{i j} denotes the weight of the edge (e_{i j}) between v_i and v _j, and we use the number of collaborations between the two investigators as the edge weight ( $w_{ij}=w_{ij}^o$).

• Characteristic path length: The characteristic path length (L) is the average shortest path length in a network [14], $L=\frac{1}{\mid V\mid }{\sum }_{v_i\in V}{L}_i$, where |V | is the cardinality of vertex set V, i.e., the number of vertices, and L_i is the average distance between vertex (v_i) and all other vertices in the network. The characteristic path length on a weighted graph is computed similarly, provided that path lengths are calculated with respect to the weights of the edges along the paths. Note that we use the resistant factor ( $w_{ij}=w_{ij}^r$) as the weighting schema for all shortest path related measures.

• Clustering coefficient: The clustering coefficient of a vertex expresses the chance of how likely its neighbors are also connected to one another. The (local) clustering coefficient is defined by Watts and Strogatz [14] as, $C_i=\frac{2E_i}{k_i(k_i-1)}$, where Ei is the number of connections between the neighbors of vertex v_i, and k_i is the degree of v_i. The global clustering coefficient C_G is the average of the local clustering coefficients of all vertices in the network: $C_G=\frac{1}{\mid V\mid }{\sum }_{v_i\in V}{C}_i$. A generalization of the clustering coefficient to weighted graphs was proposed by Barrat et al. [20], in which the weighted clustering coefficient of vertex v_i is defined as: $C_i^w=\frac{1}{s_i(k_i-1)}{\sum }_{j,h}\frac{(w_{ij}+w_{ih})}{2}{a}_{ij}{a}_{ih}{a}_{jh}$, where s_i and k_i are the strength and degree of v_i, respectively; w_{i j} is the weight of edge e_{i j} and a_{i j} is the element of the underlying binary adjacency matrix (i.e., a_{i j} is either 0 or 1 indicating whether v_i is connected with v _j). The weighted clustering coefficient of the network G is the average of weighted clustering coefficients of all vertices: $C_G^w=\frac{1}{\mid V\mid }{\sum }_{v_i\in V}{C}_i^w$. As the Barrat weighted clustering coefficient favors high edge weight (i.e., higher clustering coefficient value), we use the original weighting schema when calculating the weighted clustering coefficient ( $w_{ij}=w_{ij}^o$).

• Diversity: We propose a quantitative – diversity – measure to model the trend of cross-disciplinary collaborations in a RCN. We denote L_{S ->¬S} as the average distance from nodes in set S to all other nodes in the network: $L_{S->\neg S}=\frac{{\sum }_{i\in S;j\notin S}{L}_{i->j}}{\mid S\mid (\mid V\mid -\mid S\mid )}$, where |V | is the total number of nodes in the network, |S | is the number of nodes in set S, and L_i->j is the distance between node v_i and v _j. We define the diversity of a network D_G as the inverse of average L_{S ->¬S} for all S in the network:

  $$D_G={(\frac{1}{n}\sum _{k=1}^n{L}_{S_k->\neg S_k})}^{-1},$$

  where n is the number of distinct groups (a collection of nodes having the same property of certain kind) in the network. If we define each group as a discipline in the RCNs, the diversity can be interpreted as how easy an investigator from one discipline can reach another investigator of a different research field. Therefore, the higher the diversity value, the more diversified the collaborations are in the RCNs, as the average distance is shorter for an investigator to travel from one group to another. Note that the resistance factor as the weighting schema ( $w_{ij}=w_{ij}^r$) is used for calculating $D_G^w$ as $w_{ij}^r$ is employed in computing shortest paths.

2.5. Identify influential nodes in a research collaboration network

In social network analysis, the centrality measures of a vertex are often used to determine the relative importance of the node in the network. Within the context of research collaboration network, an investigator’s centrality measure can be interpreted as how influential or important the person is in the RCN of interest. There are various network centrality measures, where each measure defines the meaning of importance from a different perspective [2]. To identify influential nodes in a comprehensive manner, we investigate four widely-used network centrality measures: degree centrality, betweenness, closeness, and eigenvector centrality [21]. We briefly describe them below:

• Degree centrality is simply the degree of a vertex. Since RCNs are weighted graphs, we shall use the weighted degree (strength) when calculating degree centrality.

• Betweenness centrality of a vertex is defined as the fraction of all shortest paths in the network that pass through that vertex. Betweenness centrality on a weighted graph is defined similarly, given the shortest path length is the weighted shortest path length where the resistance factor based weighting schema is used, i.e., $w_{ij}=w_{ij}^o$. Betweenness centrality measures a node’s control of the communication between other nodes in the network [22]. Conceptually, in the RCNs, a node with a high betweenness centrality value can be interpreted as the investigator often acts as a bridge for other investigators in the research community.

• Closeness centrality of a vertex (i.e., local closeness centrality) is the inverse of the local characteristic path length of the vertex [22]. Closeness centrality on a weighted graph can be computed similarly, considering that the path lengths are calculated using the weighted definition (with resistance factor based weight schema). The closeness centrality value measures how fast information can flow from a node to all other nodes [23]; a node is more “central” if its closeness centrality value is higher.

• Eigenvector centrality measures the influence score of a vertex in the graph [24]. The random walk with restart (RWR) process that will be described in the next subsection essentially calculates the personalized pagerank score of each vertex, which is a variant of the eigenvector centrality measure. Calculating eigenvector centrality of a vertex in a weighted graph is straightforward and the original weighting schema $w_{ij}=w_{ij}^o$is used.

Using these centrality measures, we can rank an investigator’s relative influence (or importance, contribution) in the research community. However, the centrality measures can rarely make a consensus regarding the ranking orders of the nodes in the same network. Therefore, we propose to use rank aggregation techniques [11, 25, 12] that can combine multiple rankings of nodes (investigators) to generate a more convenient and concise ranking. There are basically two classes of rank aggregation methods: 1) score-based rank aggregation, where each object in the input ranking is associated with a score and the goal is to combine different scoring systems to produce one set of scores; and 2) order-based rank aggregation, where only the orders of objects produced by individual ranking methods are considered. Since the scores given by different centrality measures are diverse and it is difficult to choose a meaningful normalization process, we decide to use Borda count [25] system, which is an order-based voting system. The Borda count system gives each candidate certain points based on her position on each ballot, and the candidate with the most points is the winner. If we consider each centrality measure as a voter that gives a preference ranking of all investigators in the RCNs, the final ranking can be easily computed using the Borda count of each investigator.

2.6. Link prediction and collaboration recommendation model

Social networks including research collaboration networks are highly dynamic. They can grow and evolve rather quickly through edge additions and deletions, which evidences new interactions among social entities in the networks. The link prediction problem in social network analysis has drawn a considerable amount of attentions as it helps to understand how a complex social network evolves over time [26]. Recent surveys on this topic can be found in [27, 28]. In this study, we employ link prediction to discover missing links (overlooked collaborations) and the links that could appear in the future (new collaborations). Despite the conceptual differences, the same prediction model can fulfill both tasks.

We consider the link prediction problem in a weighted undirected graph G(V,E) in which no duplicate edges or self loops are allowed. One general approach to link prediction is to treat it as a recommendation (and ranking) problem. In this setting, the task is to find an algorithm that can rank a set of nodes with respect to a querying node (q_i), where the nodes that should have edges incident to q_i will have higher scores. Then the system would “recommend” a list of nodes to q_i as potentials to have new links according to the ranking. Such a system has a direct application in recommending new collaborations in research collaboration networks.

PageRank [29] and its variants such as Personalized PageRank [30] and Random Walks with Restarts (RWRs) [13] are effective methods for link prediction based on finding structure similarities between nodes in a network. Conceptually, the PageRank score of a node is the long-term probability that a random web surfer is at that node at a particular time step. For sufficiently long time, the probability distribution of the random walks on the graph is unique, that is, minor changes to the graph make the random walk transition matrix aperiodic and irreducible [31].

The Markov model represents the graph with a square transition matrix P whose element p_i->j is the probability of moving from state (node) i to state (node) j in one time step. The PageRank algorithm assumes that it is equally likely to follow any of the outgoing links from a node. In other words, p_i->j = 1/deg(i) where deg(i) is the out-degree of node v_i. However, the PageRank algorithm was originally defined on directed unweighted graphs. For an RCN, which is a weighted undirected graph, we make two necessary modifications to the construction of the transition matrix. First, we turn each undirected edge (e_{i j}) into two directed edges (e_i->j and e _j->i). Second, we take into account the weight of an edge p_i->j, which is w(i->j)/s(i) where w^(i->j) is the weight of the edge and s(i) is the strength of the node v_i, so that a random walker will be more likely to travel through an edge with a higher weight, under the premise that an investigator is more likely to work with an old long-turn collaborator. We also incorporate a restart probability c. With probability 1 − c the random walker jumps back to the seed node s and thus “restart”:

$$\begin{array}{l}E=\overrightarrow{e}{\overrightarrow{v}}^T,\\ P^{\prime }=cP+(1-c)E,\end{array}$$

where e⃗ = [1]_n×1 is a column vector of all ones, and v⃗ is the restart vector, where

$${\overrightarrow{v}}_i=\{\begin{array}{ll}1\hfill & \text{if}s=i,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

The unique stationary distribution ( $\overrightarrow{z_s}$) of the RWRs w.r.t. the seed node s can be found as the eigenvector with the largest eigenvalue (i.e., the construction of P′ guarantees the following equation has the largest eigenvalue as λ₁ = 1 [31]) of the following eigenvector problem:

$${P^{\prime }}^T\overrightarrow{z_s}={\lambda }_1\overrightarrow{z_s}.$$

Conceptually, the vector $\overrightarrow{z_s}$ (a.k.a. Personalized PageRank scores) gives us a probability distribution of walking from node v_s to all other nodes in the graph based on the network structure. Therefore, the similarity score of any two nodes v_i and v _j can be define as:

$$s_{ij}^{\mathit{RWR}}=z_{i->j}+z_{j->i},$$

where z_i->j is the probability to walk randomly from node v_i to node v _j. In an undirected graph, z_i->j = z _j->i as the adjacency matrix of the graph is symmetric. Based on these RWR scores, we can generate a ranking of all edges of interest, and recommend the top ranked edges as our prediction.

3. Results and Discussion

3.1. Characteristics of the research collaboration network at UAMS

We constructed a number of RCNs with varying time periods of interest to study the structure of an RCN from the short-term, medium-term, and long-term perspectives. Each RCN is composed based on the grants ³ that were awarded during a specific time period. We instantiated seven snapshot RCNs where each RCN covers one budget year from 2006 to 2012. We also created three aggregate RCNs: The first and second networks represent the RCN at UAMS prior to the CTSA from 2006 to 2009 (RCN_2006–2009) and after the award from 2010 to 2012 (RCN_2010–2012) respectively, and the third aggregate RCN covers all the research grants awarded since 2006 until 2012 (RCN_2006–2012). We eliminated all isolated single nodes, which are investigators who carried out research activities independently, from each network as those isolated individual nodes do not contribute to our study of collaborations.

Table 2 lists the network metrics we measured for the RCNs at UAMS. We included a few extra measures that are important but not formally defined in the previous section. We introduce these measures briefly as follows. The density d of a network is defined as the ratio of the number of edges over the maximum possible number of edges. It measures how “busy” the network is. For an undirected graph, $d=\frac{2\times \mid E\mid }{\mid V\mid \times (\mid V\mid -1)}$, where |E| is the number of edges and |V | is the number of vertices. An isolated component is a small subgraph that has no links to any nodes outside of that subgraph, and its count in a network is an important measure of connectedness (or segregation) of that network. The average number of new edges is measured as follows. We first compare each year’s RCN with the RCN in the previous year to identify all the nodes in both RCNs (i.e., investigators who had collaborative grants in both years). We then count the number of newly created edges for each of the identified nodes and take the average over all the nodes. Note that this metric is not applicable to RCN₂₀₀₆, RCN_2006–2009, and RCN_2006–2012 as those networks have no baseline data for comparison. The average number of new edges in RCN_2010–2012 is measured against the data in RCN_2006–2009. The transitivity [32] of a network, an alternative definition of network clustering coefficient, is expressed by

Table 2.

Network characteristics of the research collaboration network at the University of Arkansas for Medical Sciences from 2006 to 2012.

G = (V,E)						The largest connected component: Gl = (Vl, El)
RCN	|V|	|E|	density (d)	average # of new edges	# of isolated components	|Vl|	|El|	clustering coefficients			characteristic path length (Lgl )		diversity (Dgl )
								Cgl	$C_{g_l}^{w^o}$	$C_{g_l}^{w^t}$	Lgl	$L_{g_l}^{w^r}$
2006	184	279	0.017	N/A	51	22	54	0.763	0.764	0.725	2.303	2.216	0.392
2007	275	678	0.018	+1.577	44	68	185	0.788	0.796	0.710	4.661	4.537	0.206
2008	276	532	0.014	−0.097	48	88	231	0.658	0.673	0.654	4.784	4.419	0.168
2009	262	590	0.017	+0.343	41	124	418	0.729	0.737	0.789	5.840	5.239	0.147
2010	292	1,412	0.033	+10.803	31	214	1,351	0.796	0.810	0.773	3.365	2.718	0.232
2011	310	1,083	0.023	−10.013	35	207	959	0.773	0.783	0.752	3.769	3.440	0.240
2012	282	1,084	0.027	+0.300	32	149	643	0.757	0.767	0.727	3.409	3.007	0.255
2006 – 2009	487	1,318	0.011	N/A	55	339	1,183	0.639	0.654	0.660	5.084	3.537	0.133
2010 – 2012	429	2,008	0.022	+16.271	38	348	1,959	0.747	0.761	0.700	3.560	1.961	0.173
2006 – 2012	652	2,867	0.014	N/A	57	523	2,787	0.645	0.664	0.608	3.735	1.967	0.168

^*G = (V,E) is the original network excluding the isolated individual nodes, while G_l is a subgraph of the largest connected component excluding not only the isolated individual nodes but also the smaller disconnected components (components that do not have a link to G_l). |V | and |E| are the number of nodes and the number of edges in the corresponding network, respectively. The density d, the average number of new edges, and the number of isolated components are calculated on the original graph. The clustering coefficient, the characteristic path length, and the diversity are calculated on G_l as these measures are not that meaningful in graphs with disconnected subgraphs. Note that for the clustering coefficient measure we have three different approaches: 1) the unweighted Watts and Strogatz definition $C_g^{ws}$, 2) the Barrat’s generalization to weighted graph ${(C_g^{ws})}^w$, and 3) the transitivity definition $C_g^t(\mathit{unweighted})$. For the characteristic path length we presented measures for both the weighted and unweighted models of the same network.

$$C_g^t=\frac{\mathit{number}of\mathit{closed}\mathit{triples}}{\mathit{number}of\mathit{connected}\mathit{triples}of\mathit{vertices}}.$$

Therefore, the (global) clustering coefficient measure of a network has three versions in our study: the unweighted Watts and Strogatz definition $C_g^{ws}$, the Barrat’s generalization to weighted graph ${(C_g^{ws})}^w$, and the transitivity definition $C_g^t(\text{unweighted})$.

3.1.1. Temporal evolution of the research collaboration network at UAMS

Nagarajan et al. presented a baseline study [6] on research collaboration networks (RCNs) prior to the UAMS’ CTSA (from 2006 to 2009). Their study suggests that the RCNs at UAMS have “unique characteristics different from those of the established real-world networks.” For example, the networks were disconnected with mutually exclusive groups and few weakly connected clusters of staff within the same department.

In our study, as shown in Table 2, significant changes can be observed in UAMS’s RCN since the introduction of CTSA. By comparing RCN_2006–2009 with RCN_2010–2012, we see an evident increase in the number of edges, the weighed clustering coefficients, and the diversity measures; while a clear decrease manifests in the number of isolated components and the weighted characteristic path length. For the entire collaboration network, the number of edges increases from 1,318 in RCN_2006–2009 to 2,008 in RCN_2010–2012⁴, but the number of isolated components decreases from 55 (RCN_2006–2009) to 38 (RCN_2010–2012). Comparing the largest connected component of RCN_2006–2009 to that of RCN_2010–2012, all three clustering coefficients have increased after the CTSA award; in particular, the weighed clustering coefficient ( $C_{g_l}^{w^o}$) increases from 0.654 to 0.761. At the same time, the weighted characteristic path length (L) is substantially shortened from 3.537 and 1.961. The diversity of the largest component grows from 0.133 in RCN_2006–2009 to 0.173 in RCN_2010–2012.

Our measured network metrics indicate that the RCN at UAMS is moving towards a positive direction, that is, not only more collaborations but also more trans-disciplinary teamworks were generated between 2010 and 2012. The growth of the number of edges and average number of collaborators per grant (see Table 1) in RCN_2010–2012 reflects more collaborative research efforts were made at UAMS after the initiation of the CTSA, which coincides with the dramatic reduction of isolated components. The proposed diversity provides a concise quantitative measure of “interdisciplinary-ness.” The growth of diversity (from 0.133 in RCN_2006–2009 to 0.173 in RCN_2010–2012) suggests that the research community at UAMS is evolving towards more interdisciplinary collaborations. As the goal of CTSA is to incubate new multidisciplinary collaborations and high impact research across the spectrum of translational science, the revealed shifting suggests that the impact of CTSA is positive.

As the clustering coefficient (C) measures the degree of herding effect in a network (or network component), a large coefficient value implies that nodes tend to create more tightly knit groups, as shown in Figure 1. The characteristic path length (L) measures the average degree of separation between nodes in a network (or network component). Therefore, the shorter the length, the “easier” (or more likely) it becomes for an investigator to reach another researcher and form new collaborative research projects. The increase of C and decrease of L in the results are aligned with the finding in [6] that UAMS RCN is evolving towards a more robust small-world topology. Besides the observations of C and L, we also measured the “small-world-ness” of the three aggregate RCNs (RCN_2006–2009, RCN_2010–2012 and RCN_2006–2012). Our results confirm that the research collaboration network at UAMS is “small-world”. We will discuss the “small-world-ness” along with the scale-free property in detail in a later section.

We measured the clustering coefficient and the characteristic path length in both conventional model (unweighted edges) and our model (weighted edges), as presented in Table 2. Clearly, the clustering coefficient becomes larger and the characteristic path length is shorter in our weighted network model, which are consistent with the intuitions that the clustering effect shall be more evident with investigators who are already actively collaborating; and that more existing collaborations will create more opportunities (thus make it easier) for two separate researchers to establish new collaborations. In other words, the effects of collaboration in our weighted model can be recognized more easily and accurate.

The average number of new edges can be seen as a growth rate of newly secured collaborative grants. Its value is fairly stable across years with an interesting oscillation occurred in 2009–2011. There was a surge of new collaborative grants in 2010, that is, 10.803 new collaborations on average compared to the 2009 dataset. We believe it is a mixed effect of the CTSA award and the American Recovery and Reinvestment Act of 2009, which resulted in a large number of new grants funded that year. However, a significant drop immediately followed (i.e., −10.013 in 2010–2011), possibly due to the economic recession. Without network analysis of the RCNs, these novel observations would not be uncovered.

3.1.2. Impact of the CTSA program on the research collaboration network at UAMS

To examine the effectiveness of CTSA, we split nodes of RCN_2010–2012 into two disjoint groups, a CTSA-related group (denoted by +) which contains all the investigators either on the CTSA grant or supported by the CTSA and a non-CTSA group (denoted by −) which contains all the rest of investigators. We compared two network metrics, the average strength S̄ and the average shortest path length from a node to any other nodes in the same group, between the two groups. To understand how “fast” for an investigator in one group to establish a collaboration in general, we also calculated the average shortest path length from a node in one group to any other nodes (i.e., L̄^(+⇒±) and L̄ ^(−⇒±), ± denotes both groups). To assess the impact of CTSA, we used the CTSA-related group in RCN_2010–2012 as the hypothetical CTSA-related group in RCN_2006–2009 and calculated the same set of metrics for RCN_2006–2009. The results of those metrics are shown in Table 3.

Table 3.

Comparison of network metrics between CTSA-related group (+) and non-CTSA group (−)

	Average Strength		Average Shortest Path Length
RCN	S̄−	S̄+	L̄ (−)	L̄ (+)	L̄ (− ⇒±)	L̄ (+⇒±)
2006 – 2009	12.81	13.01	3.542	3.532	3.539	3.531
2010 – 2012	24.02	27.89	1.977	1.935	1.969	1.948

As shown in Table 3, the average strengths dramatically increase for both groups. Moreover, the average strength of the CTSA-related group (S̄ ⁺) is larger than that of the non-CTSA group (S̄ ⁻) in both RCNs and the difference between the two groups is enlarged after the inception of CTSA. Both intra-group (L̄ ⁽⁻⁾ and L̄ ⁽⁺⁾) and inter-group average shortest path lengths (L̄ ^(−⇒±) and L̄ ^(+⇒±)) are shortened significantly after the introduction of CTSA, which suggests CTSA is an important factor for promoting and catalyzing more collaborative research activities, not only for CTSA supported researchers but also for those not supported by CTSA.

3.1.3. Examination of “Small-world-ness” and the scale-free property

We measured the “small-world-ness” (S ) for the three aggregate RCNs (i.e., RCN_2006–2009, RCN_2009–2012, and RCN_2006–2012) and found that all the three networks meet the criterion of small-world network (i.e., S > 1). As the testing procedure involves generating a random graph, we bootstrapped the procedure 1,000 times to eliminate random fluctuation. The mean (avg(S )) and standard deviation (std(S )) of the measures are reported in Table 4 along with their minimum value (min(S )) and maximum value (max(S )) in the test. The averages of the S measures of the three aggregate networks are significantly higher than the “small-world” criterion, S > 1, as shown in Table 4. One interesting observation is that the S measures of RCN_2006–2009 appear to be more fluctuated than those of the other two RCNs, reflected by a much higher standard deviation. This may be attributed to the fact that RCN_2006–2009 has significantly less edges (see Table 2), which can cause more fluctuations to be generated in the testing procedure.

Table 4.

The “small-world-ness” (S ) of the research collaboration networks (RCN) at the University of Arkansas for Medical Sciences.

RCN	avg(S )	std(S )	min(S )	max(S )
2006 – 2009	23.873	8.158	12.995	74.142
2010 – 2012	17.413	1.311	13.800	22.399
2006 – 2012	24.845	3.036	19.811	49.017

Following the methods described by Clauset et al. in [10], we tested whether the degree distribution of the RCN at UAMS follows the power-law, and therefore is scale-free. We tested the power-law fitting for both unweighted and weighted (i.e., strength) degree distribution of the three aggregate RCNs. The p-values of all the power-law fitting experiments are not significant. Therefore, the RCN at UAMS is not scale-free.

Figure 2 shows the fitting of the degree distributions for the three aggregate RCNs. The top row of Figure 2 shows the fitting of the tails of the degree distributions. The best fitted power-law parameters can only cover a portion of the distribution’s tail, where the dotted green line shows the power-law fit starting at X_min = 1 while the dashed green line shows the power-law fit starting from the optimal X_min. The bottom row of Figure 2 shows the comparison of the fitting between the power-law distribution and the exponential distribution, where the dashed green line is the power-law fit and the dashed red curve is the exponential fit. As shown in Figure 2, it is not clear which hypothesis (power-law vs. exponential) can fit the degree distribution better.

Figure 2.

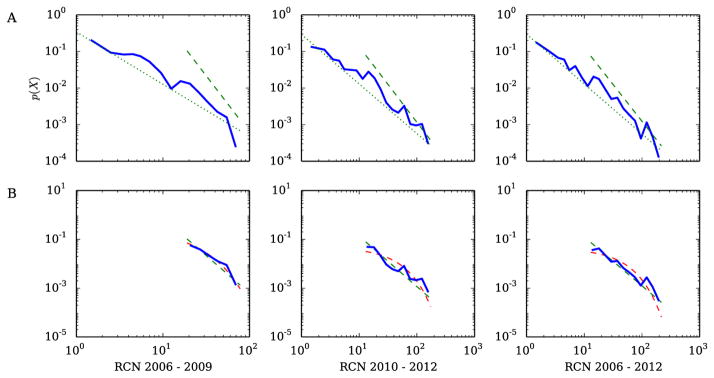
The power-law degree distribution plots for RCN_2006–2009 (X_min = 19, α = 3.083), RCN_2010–2012 (X_min = 13, α = 2.067), and RCN_2006–2012 (X_min = 13, α = 2.005).

3.2. Centrality leaders in the research collaboration network at UAMS

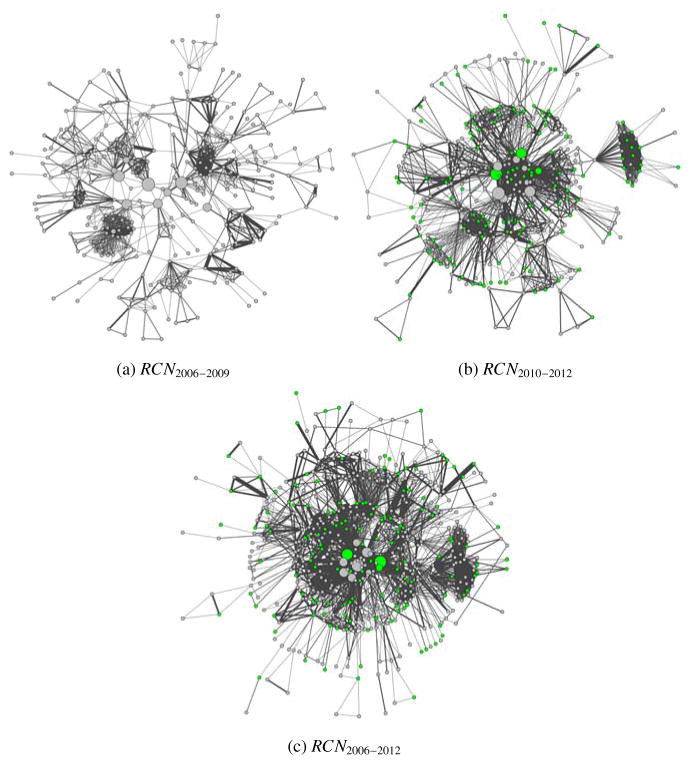
We use the proposed method to identify centrality leaders (i.e., influential nodes) in the three aggregate RCNs. Figure 3 visualizes the networks where the size of a node is set proportional to its ranking (i.e., the larger the node in size, the higher the investigator’s ranking) to depict the leader nodes. The networks shown in Figure 3 are plotted using a force-directed graph drawing algorithm–the Kamada-Kawai algorithm [33], where the positions of nodes are determined based on the spring forces proportional to the nodes’ graph theoretic distances. As shown in Figure 3, the identified centrality “leaders” are positioned in the center of the graphs, indicating that our method is consistent with the Kamada-Kawai algorithm.

Figure 3.

Visualization of the centrality leaders (i.e., influential nodes) identified in the RCNs at UAMS, where graph (a) is the RCN prior the CTSA award (2006 – 2009), graph (b) shows the RCN after the CTSA (2010 – 2012), and graph (c) presents the aggregate long-term network (2006 – 2012). *The relative sizes of nodes illustrate the consented centrality rankings. Green nodes represent investigators supported by the CTSA program.

The discovered centrality “leaders” are rather different from what we normally perceive in the context of organizational structure. For example, we found that some of the top ranked centrality “leaders” are neither the actual leaders of the university nor the leading investigators. A few top ranked investigators instead are biomedical informatics researchers or bio-statisticians, who appear on many different grants as “Co-Investigator.” In the context of collaboration network, researchers from these domains are the “leader” nodes as they do contribute more to the structure and efficiency of the network based on their network centrality scores. The ability to identify influential nodes in a RCN is important as these centrality “leaders” are often the bridges in the network as presented in Figure 3. Although a small-world network such as the RCN is robust to random failures, losing highly influential nodes could cause significant declines in terms of network efficiency. Thus, it is important for an organization to identify and protect the bridging nodes. For example, based on identified centrality “leaders”, the administration is considering different resource allocation strategies to maximize the possible outcomes of collaborative researches.

3.3. Link prediction based research collaboration recommendation

We benchmarked our link prediction models based on three widely used metrics: the area under the ROC Curve (AUC), the average precision at top k = {3,5} (AP@k), and the mean average precision at top k = {3,5} (MAP@k). An AUC score of 1.0 represents a perfect classifier/predictor, and a score of 0.5 is random guessing. The AP@k measure is derived from the Precision at k (P@k), i.e., how many of the top k nodes suggested by our algorithm to s actually receive links from s. However, the AP@k measure takes into account the ranking orders of the recommended nodes. The MAP@k for n nodes is simply the average of the AP@k of each node.

We performed two different types of prediction tasks: 1) per-user recommendations, where we recommend new collaborators to a specific investigator in the RCN; and 2) per-network recommendations, where a set of new collaborations are “prompt” to the overall collaboration network. The general procedures of benchmarking the two recommendation tasks are the same except that the MAP@k measure is only applicable to the per-user recommendation task as we want to measure how the model performs for all candidates on average. In either case, we first randomly select a set of edges as our target datasets. More specifically, in the per-user recommendation task, we first pick a pool of random nodes and then choose all the edges that incident to these nodes; while in the per-network task, we randomly select the set of edges from the network directly. For each dataset, we perform a 10-fold cross-validation. In each iteration we first choose 1/10 of the dataset as the test set, then remove all the edges in the network that exist in the test set, train the recommendation algorithm (i.e., calculate the RWR scores related to the test set) on the rest of the graph, and finally evaluate the method on the test set.

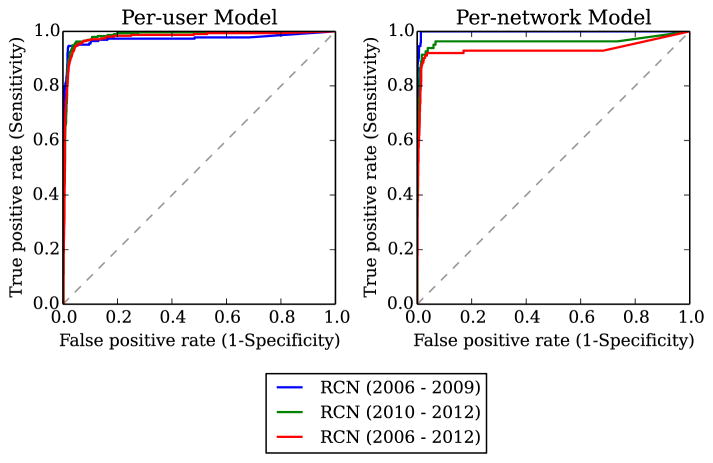
As shown in Table 5 and Figure 4, we can accurately identify missing links in RCNs. Especially in RCN_2006–2012, we can achieve a near optimal prediction model, reflected by AUC_{Per–U ser} = 0.990 and AUC_{Per–Network} = 0.954. The two testing approaches, per-user and per-network recommendations, provide us two complementary conceptual models for assessing collaboration recommendations and each has its own unique merit. The per-user model provides a more microscopic view of the recommendation problem, where it focuses on suggesting new collaborations to each investigator. On the contrary, the per-network model offers an eagle eye’s view over the entire collaboration network, and allows us to strategically allocate resources to catalyze important new edges in the network, therefore improving the overall network efficiency.

Table 5.

Performance measures of the link prediction model on UAMS’s research collaboration networks.

	Per-user Recommendation			Per-network Recommendation
RCN	AUC	MAP@3	MAP@5	AUC	AP@3	AP@5
2006 – 2009	0.977	1.660	1.761	0.838	0.572	0.529
2010 – 2012	0.976	1.593	1.678	0.974	0.906	0.825
2006– 2012	0.990	1.480	1.522	0.954	0.794	0.715

Figure 4.

The ROC curves for the two link prediction tasks, where the figure on the left shows the ROC curves for the per-user model and the figure on the right depicts the ROC curves for the per-network task.

4. Conclusion and Future Work

In this paper, we presented a set of network analysis methods that covers the full spectrum of a collaboration network study. We applied those methods to the research collaboration network at the University of Arkansas for Medical Sciences, a research institution with a Clinical and Translational Service Award (CTSA), to investigate the effectiveness of CTSA. Our analyses and quantitative measures suggest that the CTSA program has a positive effect in promoting research collaboration across disciplines inside the institution. Our analysis methods and findings can help not only researchers to improve the understanding of structural patterns and underlying generative force of collaboration networks, but also administration and leaderships of research institutions to strategically allocate resources and shape policies to attain an effective, trans-disciplinary collaboration environment.

Our study has spawned a few possible directions for future research on collaboration networks. One immediate study we would like to explore is to assess the effects of research environment changes on a collaboration network. For example, to foresee the impact of funding reduction, we can purposely remove certain edges from the network through simulation and measure the overall effects of such changes both qualitatively and quantitatively. Another direction we are interested in pursuing is the development of a hybrid network model that can combine collaborative relationships from multiple data sources (e.g., both collaborative grants and co-publications). We expect to use different sources to correlate collaborative activities and identify the roles of participants in the collaboration. We believe that such a hybrid model will be able to capture both short-term and long-term network dynamics and provide a more accurate and comprehensive abstraction of research collaborations.

Highlights.

• We model research collaborations as a weighted undirected graph.

• Research collaboration network is small-world but not scale-free.

• The Clinical & Translational Science Award has positive impacts on collaborations.

• Combining various centrality measures offers a concise ranking of influential nodes.

• Link prediction model can identify potentially successful collaborations.