Effects of airway tree asymmetry on the emergence and spatial persistence of ventilation defects

Abstract

Asymmetry and heterogeneity in the branching of the human bronchial tree are well documented, but their effects on bronchoconstriction and ventilation distribution in asthma are unclear. In a series of seminal studies, Venegas et al. have shown that bronchoconstriction may lead to self-organized patterns of patchy ventilation in a computational model that could explain areas of poor ventilation [ventilation defects (VDefs)] observed in positron emission tomography images during induced bronchoconstriction. To investigate effects of anatomic asymmetry on the emergence of VDefs we used the symmetric tree computational model that Venegas and Winkler developed using different trees, including an anatomic human airway tree provided by M. Tawhai (University of Auckland), a symmetric tree, and three trees with intermediate asymmetry (Venegas JG, Winkler T, Musch G, Vidal Melo MF, Layfield D, Tgavalekos N, Fischman AJ, Callahan RJ, Bellani G, Harris RS. Nature 434: 777–782, 2005 and Winkler T, Venegas JG. J Appl Physiol 103: 655–663, 2007). Ventilation patterns, lung resistance (R_L), lung elastance (E_L), and the entropy of the ventilation distribution were compared at different levels of airway smooth muscle activation. We found VDefs emerging in both symmetric and asymmetric trees, but VDef locations were largely persistent in asymmetric trees, and bronchoconstriction reached steady state sooner than in a symmetric tree. Interestingly, bronchoconstriction in the asymmetric tree resulted in lower R_L (∼%50) and greater E_L (∼%25). We found that VDefs were universally caused by airway instability, but asymmetry in airway branching led to local triggers for the self-organized patchiness in ventilation and resulted in persistent locations of VDefs. These findings help to explain the emergence and the persistence in location of VDefs found in imaging studies.

bronchoconstriction that occurs in asthma or during induced bronchoprovocation can lead to airway instability (2) resulting in different airway behaviors as some airways narrow and some other airways paradoxically dilate. Importantly, this behavior can be reproduced using a model of airway behavior that is fully symmetric in its anatomic and functional properties, yet produces markedly heterogeneous patchy patterns of ventilation, suggesting that airway instability and airway interdependence could be principal mechanisms for the emergence of areas of hypoventilation or gas trapping [ventilation defects (VDefs)] during bronchoconstriction (35). However, in a perfectly symmetric airway tree, interdependence among airways causes an unstable equilibrium state at each bifurcation of the tree. This model requires a perturbation to break the symmetry, triggering one airway to narrow relatively more than the other, thereby leading to asymmetric airflow. Venegas et al. (35) introduced small random variations in airway wall thickness to break the symmetry, leading to VDef formation that was entirely random in location. Yet in subjects with asthma the majority of VDefs are observed to be fairly persistent in their location after individual challenges even over time periods of days to months (13, 22).

The branching of human airway trees is bipodial but asymmetric. Pathological VDef formation occurs in lung diseases such as asthma (30), chronic obstructive pulmonary disease (21, 25), and cystic fibrosis (20) and is found to change with age in healthy elderly patients (28). However, it is unclear what effects branching asymmetry may have on bronchoconstriction and whether lung asymmetry is sufficient to reproduce persistent VDefs with airway narrowing. Several computational studies, including as demonstrated in single airway models (2, 19) and branching airway tree models (35, 38), have demonstrated that bronchoconstriction leads to a multistate solution in airway diameters and that airway closure and patchy ventilation were emergent phenomena that arose from the functional interactions of dynamic forces acting on the airway wall during bronchoconstriction (35). Strikingly, VDefs emerged in a symmetric tree that lacked the anatomic asymmetry of airway branching in humans (35, 36, 38, 39). These VDefs are random in location, which is inconsistent with imaging evidence to date that shows, while defects can change in location and size over long intervals, most are persistent and reappear in the same locations (13, 22). The reasons leading to this persistence are not understood.

We hypothesized that the asymmetric airway branching of the human lung affects airway behavior and lung function during bronchoconstriction, including the emergence of VDefs and their location. We also investigated the dependence of the formation of VDefs with varying levels of asymmetry in branching from a symmetric to an asymmetric tree of a human lung. We also quantified the heterogeneity and persistence of VDefs with increasing asymmetry and examined how lung asymmetry and VDef formation affected lung resistance and elastance from the complex impedance. Finally, we aimed to identify the difference between sister airways that predict differences in their behavior and, thus, the location of VDefs.

METHODS

Construction of Airway Trees

To investigate how anatomic asymmetry in terms of airway radii and lengths between daughter airways at branching points of the human airway tree contributes to lung function and spatial pattern of ventilation during constriction, five different airway trees were generated spanning in their degree of asymmetry from symmetric to an asymmetric tree based on human anatomy, which was provided by M. Tawhai, University of Auckland (33). Because that asymmetric tree served as a reference for other trees with intermediate degrees of asymmetry, we refer to it as the original or fully asymmetric tree. Briefly, the structure for the asymmetric human tree was generated using x-ray multidetector computed tomography (MDCT) imaging (33) to identify airway lengths and radii up to the eighth generation. Additionally, a volume-filling algorithm (33) was used to generate the distal airway generations maintaining daughter radius ratios and lengths consistent with published morphometric data (18). For this study, we used the airways from one-half of the Tawhai tree starting at the main bronchus corresponding to generation 1 and then spanning over 13 generations. We started at the main bronchus rather than the trachea to select airways surrounded by lung parenchyma. We chose the main bronchus that had fewer airways terminating, while maintaining the same number of generations as previously employed by Venegas et al. (35) and Winkler and Venegas (38), but using a more central section of airways compared with previous studies. The symmetric airway tree was created using airway radii and lengths of each generation equal to the mean radii and lengths of the same generation from the asymmetric tree. Although the symmetric airway tree had 4,096 terminal airways at generation 13, the asymmetric tree had fewer airways with terminal airways at generations 8 through 13 with a frequency distribution of 1, 5, 35, 112, 328, and 2,600 respectively. The fewer airways in the asymmetric tree meant the resistance of the asymmetric tree was slightly higher at 0.8476 cmH₂Ol⁻¹·s⁻¹ compared with 0.6418 cmH₂O for the symmetric tree. To avoid differences in total lung resistance, the airway radii of the symmetric tree were scaled by the factor 0.9338 calculated from (0.6418/0.8476)^0.25, following the fourth power law scaling of resistance, so that total lung resistance was identical without any loss of symmetry.

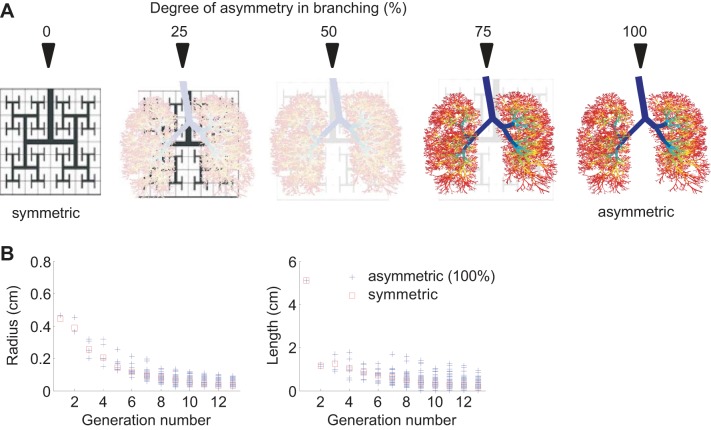
To use the same set of equations that was used for the symmetric tree of Venegas et al. (35) and Winkler and Venegas (38), the resistance of any airway with elements distal to a terminal airway was set to zero so that they became connectors to the compliance elements of the model without affecting the distribution of airflows. Intermediate asymmetric airway trees were constructed by linearly scaling the difference in radii and lengths between the symmetric and the original asymmetric tree, achieving in total five different trees with 0, 25, 50, 75, and 100% asymmetry. For example, 50% asymmetry means that, for each airway generation, the range in airway radii and lengths was 50% narrower relative to the range in the original asymmetric tree. The variation in radii and lengths of the original asymmetric tree can be observed at each generation in Fig. 1.

Fig. 1.

The symmetric tree and 3 intermediate airway trees with increasing degrees of asymmetry were generated by linear scaling of radius and length of each airway between the anatomically based asymmetric airway tree and the symmetric tree. Airway radius and length were distributed at each generation in the asymmetric tree (+) while they were identical in the symmetric tree (squares).

The total compliance in each airway tree was equivalent to a compliance of the respiratory system of 100 ml/cmH₂O scaled to the size of our reduced airway tree. Because the airway tree selected for our study corresponded to approximately one-half of normal lungs, we used for all trees a compliance of 50 ml/cmH₂O. In the symmetric lung, each terminal unit has a compliance that was equal to the total tree compliance divided by the number of terminating airways. Because the asymmetric airway tree had a smaller number of terminal airways than the other trees, a weighting vector was used to properly adjust the model's compliance units such that the asymmetric lung subtree would have equal compliances among its terminal units and the same total lung compliance as the symmetric lung. The adjustment resulted in a slight increase in compliance of each terminal unit of the asymmetric tree. However, we chose this method so that all airway trees with different degrees of asymmetry had equal pressure swings under the initial conditions of the models, so that the terminal units of all airway trees initially experienced the same relative tidal stretch and thus the same airway smooth muscle stretch during a single pressure swing.

Model of Bronchoconstriction

As described above, a model of bronchoconstriction that can explain the emergence of VDefs resulting from multistate airway constriction was previously described by Winkler and Venegas (38, 39). Briefly, the mechanics of the airway wall and tethering forces are modeled using the standard Lai-Fook equations relating parenchymal distortion to parenchymal tethering stress (23). The airway mechanics, including the smooth muscle in response to dynamic stretch, were empirically included as modeled by Anafi and Wilson (2) based on previous measurements of isometric force-length curves (14, 16, 32). Thus the airway wall of a given airway is stretched by the tethering forces and the transmural pressure difference, which change dynamically during the breathing cycle because of tidal expansion of the parenchyma associated with the tidal changes in the gas volume. The behavior of the forces experienced by each airway and the resulting distributions of pressure, flow, and volume along the airway tree were solved using Euler numerical integration with time steps of 10 ms over a time course of 600 breaths to determine the steady-state radii of airways (35, 38). In the model, the flow dynamics and distribution within the airway tree are determined by the input flow at the central airway opening and recursive equations for the network of resistances connected to the compliances of the terminal units. The breathing pattern consisted of a constant inspiratory flow and passive expiration with positive end-expiratory pressure = 5 cmH₂O, tidal volume = 600 ml, and a breathing frequency of 12 breaths/min. Ventilation maps for the lungs were produced from terminal unit ventilation organized two-dimensionally (2D) similar to Venegas et al. (35).

To explore the behavior of the different airway trees over a range of smooth muscle stimulations, we introduced a relative smooth muscle activation level (T_r), as was done previously (38), as the fraction of full activation airway smooth muscle generates (2, 17). We conducted simulations for relative levels ranging from T_r = 0.6, which corresponded to baseline tone, increasing to a maximal smooth muscle activation of T_r = 1.0 in steps of 0.05 corresponding roughly to exponentially increasing methacholine concentrations. Evolution and patterns of bronchoconstriction of airways were compared across different airway trees for each degree of asymmetry. As also was done previously (35, 38), the initial level of airway smooth muscle contraction of T_r = 0.6 corresponded to the predicted inner airway radius that coincided with in vivo measurements of individual airway baseline size during quiet breathing, reported by Brown et al. (5) and Brown and Mitzner (6).

Random perturbation.

In symmetric airway trees, random perturbations are necessary to disturb the unstable equilibrium state of perfect symmetry in airflow distribution throughout the branching network of airways, which would prevent any self-organized differentiation among different pathways. Thus, a random variation in airway wall thickness was added using 1% coefficient of variation in all airway trees for comparability. The effect of the random perturbations on VDefs was examined at airway smooth muscle contraction of T_r = 0.9 by running each airway tree through 10 simulations with different random perturbations.

Calculation of impedance.

The impedance of the airway tree for a given realization of airway radius distribution was calculated using a lumped element approach where the impedance of the airways was summed following the branching patterns using well-known serial and parallel network impedance relations. Airway resistance (R_a) for each branch was approximated using Poiseuille's flow given by

$${\mathrm{R}}_{\mathrm{a}}=\frac{8\mathrm{\eta }L}{\mathrm{\pi }{r}^4}$$ (1)

where η is the dynamic viscosity of humid air at 37°C, L is the length, and r is the radius of the airway. Each terminal unit was prescribed an elastance E_t to act functionally as the alveolar compartment accounting for parenchymal stretch, surface tension, and any gas compression (34). This neglects any contribution from airway wall compliance or any gas compression within the airways, but this effect is much smaller than the effect of the alveolar compartment. The impedance for a terminal airway (Z_t) was defined as

$${\mathrm{Z}}_{\mathrm{t}}={\mathrm{R}}_{\mathrm{a}}+i{\mathrm{X}}_{\mathrm{t}}={\mathrm{R}}_{\mathrm{a}}+i{\mathrm{I}}_{\mathrm{a}}\mathrm{\omega }-i\frac{{\mathrm{E}}_{\mathrm{t}}}{\mathrm{\omega }}$$ (2)

where X_t is the reactance of a terminal airway, ω is the angular frequency, and I_a is the inertance calculated as

$${\mathrm{I}}_{\mathrm{a}}=\frac{{\mathrm{\rho }}_{\mathrm{a}\mathrm{i}\mathrm{r}}L}{\mathrm{\pi }{r}^2}$$ (3)

with L and r of the terminal airway and ρ_air the air density. The airway impedance for a nonterminal airway (Z_a) was calculated as

$${\mathrm{Z}}_{\mathrm{a}}={\mathrm{R}}_{\mathrm{a}}+i{\mathrm{I}}_{\mathrm{a}}\mathrm{\omega }$$ (4)

The airway impedance of the entire airway tree could then be calculated numerically and further separated into real (resistance) and imaginary (reactance) parts. Because parallel pathways in a heterogeneous lung can lead to the product of reactances, the real part of the total impedance will have some dependence on the elastance and inertance, as was originally demonstrated in the two-compartment parallel lung the model of Otis et al. (27). We report here the resistance of the airway tree from the real part of the impedance as R_L6, the reactance as X_L6 at 6 Hz since this is a customary frequency used in the forced oscillation technique, and we calculated a dynamic elastance, E_L, by computing the impedance at breathing frequency (0.3 Hz), since the small contribution of inertance I_L at this frequency can be neglected giving

$${\mathrm{E}}_{\mathrm{L}}\mathrm{=}{\mathrm{\omega }}^{\mathrm{2}}{\mathrm{I}}_{\mathrm{L}}\mathrm{-}\mathrm{\omega }{\mathrm{X}}_{\mathrm{L}}\mathrm{=}\hspace{0.17em}\mathrm{\sim }\mathrm{-}\mathrm{2}\mathrm{\pi }\mathrm{\ast }\mathrm{0.3}\mathrm{\ast }{\mathrm{X}}_{\mathrm{L}}$$ (5)

Shannon Entropy

As an alternative to describe the overall effect of heterogeneity in bronchoconstriction as determined by the final steady-state airway geometry of our model, we quantified the Shannon entropy of the model using a simulated constant (DC) normalized airflow pushed through the resultant airway geometry. Mass conservation was held, assuming negligible gas compression, as the sum of the partial flows of each individual (ith) terminal airway was equal to the total flow through the main airway. The constant flow approach avoided potential effects of airflow asynchrony as would occur with periodic breathing or oscillation as described in other models of an airway tree or a bifurcation with asymmetric impedances (1, 11, 27). To determine the entropy, the probability distribution (p_i) was calculated from the relative flow of each terminal airway (using 256 bins) destined for alveoli. The Shannon entropy of flow (H) was then calculated as a spatial heterogeneity index of flow as

$$H=-{\displaystyle \sum p_i\log \left(p_i\right)}$$ (6)

At various levels of muscle activation T_r, we compared the resultant airway tree configurations, R_L6, X_L6, the 2D mapped ventilation patterns, and H.

Predicted Airway Behavior

We probed how initial structural and functional differences between the two sister airways at airway branching points affected the outcome in the airways constriction at the steady state. This was done by comparing several geometric and functional parameters of the airway tree with the final radii ratios of sister airways. We calculated the E_L value as the static value derived from a simple lumped element calculation of the parallel terminal elastances. We compared the geometric factor of the initial ratios of airway radius (r_i ratio) before constriction, as well as the initial functional ratios R_L6, E_t, and finally the time constant (T_c = R_L6/E_L) with the final ratio of airway radii of the bifurcating sister pair at steady state. For the functional parameters, R_L6, E_L, and T_c, we included not only the local effect of each sister airway but also the portion of the subtending lung distal to that airway. This was done at different levels of the airway tree to examine the behavior of central (generations 2–6), mid (generations 7–9), and distal (generations 10–13) airways. Initial parameter ratios, e.g., r_i for initial radius ratios before constriction, were plotted against the final radius ratios following constriction forming contingency plots, where each quadrant could be considered showing a different behavior, such as a sister airway being initially smaller will also be smaller or become larger during steady state of bronchoconstriction (Fig. 6). We then calculated the fraction of the ratios in the upper right and lower left quadrants of the 2 × 2 contingency squares, not including ratios of one, to determine the fraction of airways that exhibited initial airway asymmetry amplification, and we refer to it as the fraction of trending airways. This was similar for R_L6, E, and T_c ratio except that we counted the fraction when initially larger ratios (opposite quadrants) were associated with the sister airway with smaller final airway radius (lower right and upper left quadrants). The initial value of r_i, R_L6, E, and T_c for analysis was taken at breath 1 to allow the initialization procedure to propagate the perturbation in wall thickness into the airway tree. This was necessary since, at the very start of the simulation, the symmetric tree had indeed absolute symmetry without differences between sister airways. Once the symmetry was broken because of the random perturbation, the initial parameters would trend in the same manner as found in the asymmetric tree.

Fig. 6.

Sister pairs were analyzed by several anatomic and functional parameters to their final radius ratios (r_f ratio). These were to the initial ratios of initial radius size (r_i ratio in A), airway resistance from the airway and all distal contributions (R_L6 in A), elastance from distal contributions (E in A), and time constant (T_c in A) ratios. Initial conditions were compared in the asymmetric tree (A) and the symmetric tree (B) once some asymmetric structure could develop. In all plots, the central airways from generations 2–6 are colored in black, midgeneration airways 7–9 are colored in dark gray, and distal airways in generations 10–13 are colored in light gray. The predominance of sister pairs that landed in quadrants resulting from amplifying tendencies are calculated by the number of airways in these quadrants (upper right and lower left for the radius, for example) divided by the total number of airways. These data are plotted to the right of each 2 × 2 quadrant plot.

RESULTS

Relative Change in Airway Radius

Airway radii of the symmetric and different asymmetric airway trees with simulated bronchoconstriction at different levels of T_r were tracked since they narrowed in the model until steady-state conditions were reached. Starting from full dilation, all airways at all generations of the symmetric and the asymmetric trees narrowed homogeneously during the initial period of constriction. However, airway constriction was no longer homogenous when airways reached ∼40% of their initial radii in the symmetric and 45% in the fully asymmetric tree (T_r = 0.9). At this point there was a bifurcation between sister airway radii that occurred as the different trajectories show (Fig. 2). That differentiation was linked to preferential flow to one of the two sister airways. Some airways continued to narrow, whereas others reversed and began to dilate. This pattern, which we refer to in this work as ventilation bifurcations, repeated in each tree and was less variable at first in the symmetric tree. The symmetric tree ventilation bifurcations were smaller but occurred more often and took much longer to reach a steady-state condition compared with the asymmetric tree, and a larger fraction of airways was concentrated at larger radii as demonstrated in the histogram (Fig. 2). The asymmetric tree had more pronounced ventilation bifurcations at the onset and quickly reached more stable states, reaching a steady-state condition at ∼200 breaths. The distribution of relative airway sizes was slightly more uniform in the asymmetric case, having a SD of 0.32 compared with 0.13 for the symmetric case.

Fig. 2.

The relative change in airway radius of all airways for the symmetric and 100% asymmetric tree throughout the simulation at a relative smooth muscle activation level (T_r) = 0.9. The initial bifurcation in the behavior of airway radii may occur for both trees approximately after the same number of breaths, but the symmetric tree shows a greater number of bifurcation points over a greater number of breaths before equilibrium is reached. Histograms of the corresponding radii at the final breath are shown on right.

Lung Mechanics

R_L6, X_L6, and E_L were calculated for each breath to track lung function as the airways evolved to a steady state where airway radius and ventilation were no longer changing from breath to breath. During the initial stage (<20 breaths) with virtually homogenous bronchoconstriction (Fig. 2), R_L6 increased (Fig. 3) but then decreased after a peak. This peak occurred at the timing of first ventilation bifurcation in airway diameters (Fig. 2). The decline in R_L6 after the peak was slower in the symmetric (Fig. 3), which interestingly corresponded to a narrower airway diameter distribution compared with the wider and more rapid resolution to final configuration in the asymmetric tree (Fig. 2). The final airway resistance was also lower with increased asymmetry. The degree of asymmetry also affected X_L6, which exhibited similar patterns to R_L6 over the course of the simulation (Fig. 3). In addition to showing reactance at 6 Hz, we show the estimated elastance from E_L = −X_Lω at 0.3 Hz, since this reflects the stiffness of the lung at the breathing frequency. During the course of bronchoconstriction, E_L increased in all cases but was slower to increase in the symmetric lung. We observed that the increases in E_L corresponded to the early ventilation bifurcation. At steady state, unlike R_L6, E_L modestly increased with asymmetry.

Fig. 3.

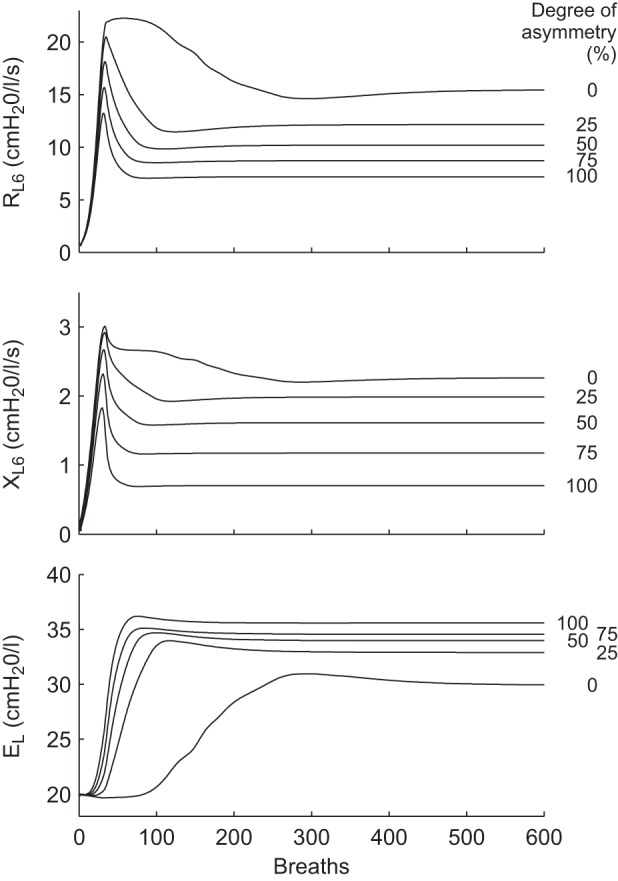
The evolution of resistance (R_L6) and reactance (X_L6) of the airway tree from the real part of the impedance and lung elastance at 6 Hz (E_L) for airway trees with various degrees of asymmetry in branching during the simulation of 600 breaths at T_r = 0.9. R_L6 increased to a peak at about 40 breaths followed by a decline. As the airway radii reached steady state, R_L6 was lowest in the most asymmetric lungs. X_L6 behavior was similar and also stabilized with the lowest X_L6 for the most asymmetric lungs. E_L showed similar behavior for all degrees of asymmetry; however, the symmetric lung maintained a lower E_L throughout the simulation.

We found that, at all levels of smooth muscle activation, the steady state of R_L6 and X_L6 was always lower with increasing asymmetry (Fig. 4). From the distributions of stationary airflows in terminal airways, we computed the entropy, H, which demonstrated interesting behavior (Fig. 4). Starting at T_r = 0.6, H of all trees increased with smooth muscle activation level to a peak followed by a descent, although this required high activation (T_r) for the symmetric model. Low values of H occurred with low levels of constriction and in particular occurred in the more symmetric airway trees, and, under these conditions, ventilation bifurcations and VDefs were not observed. Increasing levels of asymmetry caused a leftward shift of the peak in H, which appeared to correspond to the onset of ventilation bifurcations.

Fig. 4.

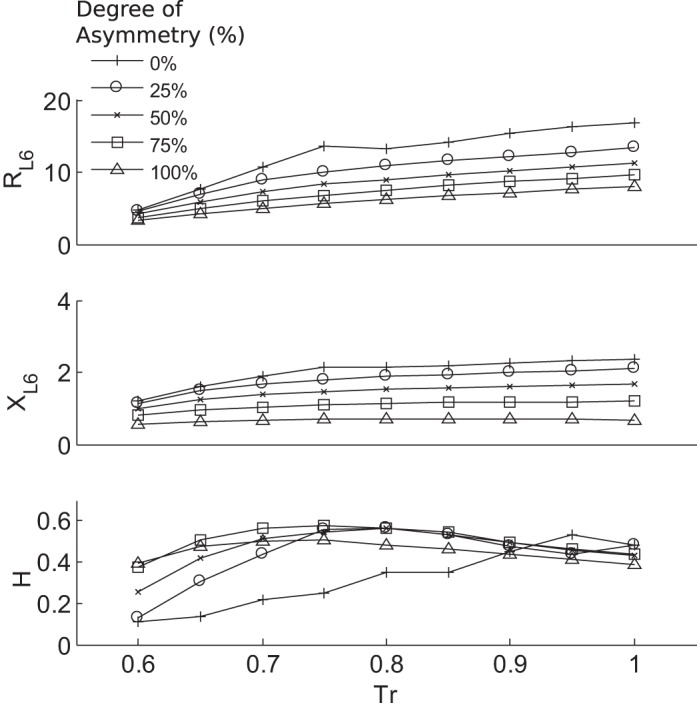
The R_L6, X_L6, and Shannon entropy of flow (H) for all airway trees at the end of the simulation (steady state) for different levels of airway smooth muscle activation T_r. Increasing T_r generally led to an increase in both the resistance and reactance at 6 Hz, which was more pronounced with decreasing asymmetry. Correspondingly, increasing asymmetry lowered resistance and reactance values for a given T_r value. H was normalized by the maximum possible entropy with all states occupied. H was found to reach maximum values that were for each degree of asymmetry at different T_r and corresponded to the emergence of ventilation defects.

Ventilation Defect Persistence

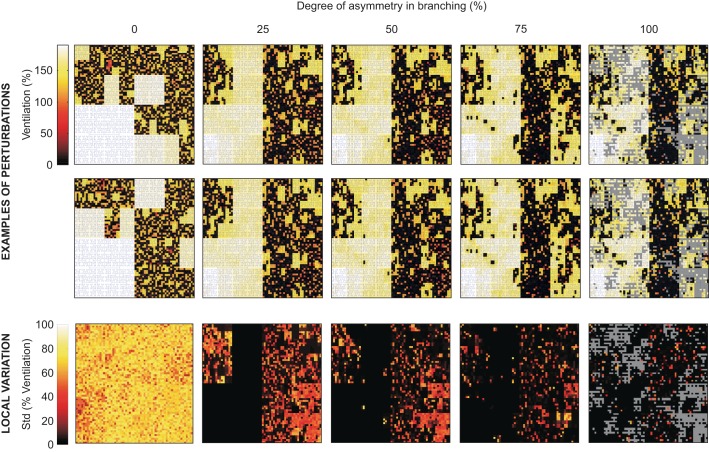
The ventilation maps are of the mean normalized ventilation at steady state, or volume of gas exchanged over one breath, in terminal units that are connected to the terminal airways. Following bronchoconstriction, areas of reduced ventilation appear to be more spread out and less concentrated spatially in the asymmetric tree compared with the symmetric tree (Fig. 5); however, within the defects themselves there was less variation in ventilation. This can be seen by a more checkerboard pattern of ventilation within the area of reduced ventilation in the symmetric tree.

Fig. 5.

Representative mean normalized ventilation maps (level of ventilation indicated by color) for 2 out of 10 different perturbations and maps of local variation in ventilation among the 10 perturbations. The degree of asymmetry in branching affected the variability in regional bronchoconstriction and, thus, in ventilation of each terminal unit that the different perturbations caused. The results represent steady-state bronchoconstriction at a relative smooth muscle stimulation of T_r = 0.9, and a schematic tree (blue) illustrates the connectivity among the terminal units within the airway tree. The local variation maps (row on bottom) show the SD of ventilation among the perturbations for each terminal unit of the model. Gray pixels in the ventilation map of the asymmetric trees indicate regions without terminal units at the 12th generation due to shorter pathways of the asymmetry airway tree. The asymmetric ventilation maps have a progressively lower SD among the 10 perturbations, whereas the symmetric map has a comparatively high SD illustrating that ventilation patterns were not persistent and therefore strongly affected by the perturbations. The mean of the SDs of ventilation from symmetric to most asymmetric was 65.2 (SD 10.4), 14.0 (SD 20.2), 8.8 (SD 16.7), 5.3 (SD 12.8), and 2.5 (SD 8.5)%.

The spatial persistency of ventilation heterogeneity was examined by changing the random perturbation in repeated simulations for each airway tree. In the symmetric tree, VDefs occurred in random locations, and the ventilation pattern was completely reordered. In contrast, in the asymmetric trees, VDefs were very persistent in location as the maps of the SD of ventilation across the repeated simulations demonstrate (Fig. 5, bottom).

Predicted airway behavior.

Because the location of VDefs was largely persistent in an asymmetric tree, we investigated several parameters that may affect the feedback mechanism and the interdependence among airways during bronchoconstriction. We mostly observed that, for a pair of sister airways, the airway with an initially smaller radius would have a proportionally even smaller radius during the steady state of bronchoconstriction at the end of the simulation, and sisters with larger airway radius would have the larger radius of the two sisters at the end of the simulation. This is the case when the initial airway asymmetry became amplified, and these are represented as points in the top right and lower left of the contingency square in the r_i ratio of Fig. 6A. Points in the other quadrants were initially smaller airways that dilated after the ventilation bifurcation, or initially larger airways that narrowed. For the asymmetric tree, and according to rank, we found that the most predominant association with final airway (r_f) radius ratios was r_i, along with T_c, and R_L6 having a similar result of nearly the same magnitude. The greatest fractions of these trending airways were airways in the distal generations for all associations. The central airways did have an increased association compared with mid- and distal-generation airways in R_L6 and T_c relative to r_i, indicated by the fraction of trending airways. The association of r_f with E was considerably less with central and midrange near 0.5, which would suggest zero dependence as from a random distribution. For the symmetric tree, the trend of r_f, R_L6, and T_c to r_i was similar to that observed in the asymmetric tree; however, because of the nature of the symmetric tree, E was perfectly symmetric and did not populate any quadrants.

DISCUSSION

We found that structural asymmetry in the airway tree of human lungs can strongly influence the emergence and location of VDefs and can lead to spatially persistent location of ventilation defect patterns. The formation of VDefs arose from feedback mechanics as modeled by Anafi and Wilson (2) and the interdependence among airways as demonstrated by Venegas and Winkler (35, 38), but the location of the defects was strongly determined by the structural heterogeneity of the branching airway tree. Additionally, the degree of airway branching asymmetry used here strongly influenced the lung mechanics. With increased asymmetry, at a given level of smooth muscle activation, R_L6 was lower while E_L was greater, implying that asymmetry leads to airway closure with loss of the compliance of affected terminal units, but the remaining terminal units become better ventilated via airways with lower resistance. We found that the final entropy at steady state was highest when lung conditions of airway smooth muscle activation and asymmetry produced ventilation patterns that were just on the verge of exhibiting ventilation bifurcation. Airway trees that produced homogeneous bronchoconstriction or high-level heterogeneous ventilation patterns and more aggressive ventilation bifurcation had lower entropy (Fig. 4).

Our findings are consistent with recent observations using hyperpolarized ³He magnetic resonance imaging that the spatial ventilation heterogeneity associated with VDefs tends to increase with the severity of asthma or increased inhaled methacholine (30). Furthermore, our findings are consistent with observations that the locations of VDefs are largely, but not completely, persistent even after long periods between imaging (12, 13, 22). We found most clearly that the VDefs were persistent in their locations in the asymmetric lung compared with the symmetric lung model (Fig. 5). This was despite the presence of small perturbations introduced in airway wall thickness to the symmetric tree to break the symmetry under unstable conditions. These variations randomized the VDefs formation in the symmetric tree but had no effect in the asymmetric trees. These small random perturbations were introduced in one parameter within the lung model but could have been introduced in other parameters to similarly break the symmetry, such as small heterogeneity in activation simulating distributed dose delivery or differences in tone or even differences that may occur with muscle content or wall stiffness associated with airway remodeling (7, 9, 15). It is also possible that differences in lung volume history may add to random variation within the lung that we did not model here. Regardless of the source of introduced variation to the initial conditions, it would be expected that increasingly large imposed perturbations of random or variable nature may reach a level that can overpower local geometric asymmetries in airway branching, which would make the locations of the VDefs in our model less spatially persistent in location.

In the symmetric airway tree, the mechanisms that led to the emergence of heterogeneous bronchoconstriction and a patchy distribution of VDefs are the interdependence of airways tethered by the parenchyma they inflate together with individual airway walls to stretch in a manner that is dependent on the amplitude of the tidal fluctuations they receive (37). We observed in our simulations that the emergence of VDefs occurred when R_L6 was at a maximum (Figs. 2 and 3). We believe this corresponds to a tipping point where some airways narrowed while others reversed direction and began to dilate as previously shown in the second figure by Winkler and Venegas (39). Also, as previously reported in vivo, during the early phase of bronchoconstriction, airway resistance increased to a peak value (4), reaching a tipping point that coincides in time with the onset of ventilation bifurcation. The ventilation distribution was virtually uniform up to this point, suggesting that structural differences in airway geometry have no substantial influence. Thereafter, the structural difference led to preferential locations for the formation of VDefs. We found that initial diameter differences in airway pairs and, to some extent, the downstream airway resistance and time constant differences between the pairs were reasonably good determinants of the ventilation bifurcation direction in that smaller airways were the ones that tended to narrow more, but not exclusively. This was stronger in smaller more distal airways than in the central airways (Fig. 6A). The fact that the structural differences play a significant role may mean that a defect can be persistent because of the presence of a pathologically affected airway, leading to the possibility of localized therapy. On the other hand, despite a wide variety in geometrical differences in daughter pairs in the asymmetric lung, the emergence of ventilation defects occurred virtually simultaneously in multiple airways, implying that the occurrence of VDefs with bronchoconstriction may not be prevented through controlling asymmetry at a single airway bifurcation, such as treatment of localized remodeling, and only their location would be affected.

However, a small fraction of airways did not obey this behavior, since differences in constriction between sister airway pairs were affected by both local (r_i) and more global (R_L6 and T_c) initial tendencies (Fig. 6). As such, an important limitation in our study was that it is limited to only the effects of the structural heterogeneity found in a representative healthy lung. Diseases that alter the lung structure or mechanical function locally such as airway remodeling in asthma may alter the preferential location of particular VDefs substantially, and, if treatable, this could decrease the sensitivity to the onset of VDef formation, but this remains to be studied.

Another limitation of our study is that the size and location of VDefs could be affected by changes in tidal volume, deep inspirations, or end-inspiratory volume that we did not study. Deep inspirations or increased end-inspiratory volume resulting in airway dilation in the model could recruit and reventilate some regions of the lung, altering the shape and location of VDefs. Venegas et al. demonstrated the possibility of such an effect in response to changes in tidal volume in a symmetric lung (35). However, asymmetry in airway branching may cause a sufficient structural bias preventing such changes in location. Also, we have assumed smooth muscle tone or compliance of the alveoli to be uniform throughout the lung; however, these variables are likely heterogeneous in location and time and history dependent, which could affect VDef location and size (29, 31). It is important to note that, although the asymmetric lung used in this study was based on an actual lung, it was not further characterized by measurements of impedance or asymmetric time constants T_c for the subject or for airway interdependence during bronchoconstriction. Some work suggests (3) that the real lung may be less asymmetric in function than the anatomically based asymmetric airway tree we used. That is because the T_c values are a function of both the resistance of the pathway from central to terminal airways and of the elastance of the terminal unit, and that could help to compensate or homogenize ventilation. Furthermore, the distribution of elastance between sister airways could be more or less symmetric than we have modeled, since we assumed identical terminal elastances at each terminal airway. Also, it is unclear if currently available anatomic data of asymmetric branching and different lengths of pathways from central to terminal airways include all characteristics that are relevant for feedback mechanisms within the lungs during bronchoconstriction. Although more needs to be done to probe mechanisms that could alter how and where VDefs occur, here we show that intrinsic heterogeneity in the pulmonary structure strongly governs both the location and persistence of VDefs.

Differences in the degree of asymmetry in the airway trees greatly influenced lung mechanics following airway smooth muscle activation as demonstrated by the differences in R_L6, X_L6, and E_L (Fig. 4). As expected, increasing smooth muscle activation led to increases in R_L6 irrespective of airway asymmetry, as is well established with inhaled histamine or methacholine (8). The fact that R_L6 was lower in the asymmetric lung at all activation levels was interesting. Structural heterogeneity appears to have provided an advantageous effect helping to maintain relatively lower airway resistance during bronchoconstriction. However, this came at the cost of increasing E_L with asymmetry, although this was a relatively smaller effect. E_L is usually reported from low-frequency reactance and increases in asthma with bronchoprovocation, which is thought to be the result of the loss of available alveoli because of excessive airway narrowing, thereby stiffening the lung (10, 24). Indeed, the increases in E_L corresponded well to the emergence of heterogeneity and VDefs. Gas compression and wall distension were neglected in our study since their effects are very small during tidal breathing (1). A sophisticated computational study from Amini and Kaczka showed for 6 Hz and 1 cmH₂O pressure amplitude, which are typically used for force oscillation measurements, that the net flow of both gas compression and wall distension was in the order of 1–2% of normalized flow magnitude (1). Whereas these effects would have an effect on our calculation of impedance, they are likely small, and stiffening of the airway wall during bronchoconstriction may reduce the effect of wall distension. In contrast to the global impedance parameters, the entropy of the terminal airflow distribution was calculated based on a constant normalized airflow to avoid flow asynchrony and frequency dependence. Thus our computation of entropy is not meant to quantify actual flow distribution, which would be time dependent, but describes the geometries' effect on DC flow. Flow asynchrony causing pendelluft may occur in the airway tree of the model during breathing and contribute to asymmetric tidal expansion of terminal units. However, flow asynchrony occurs in networks of airway impedances and is included in the global impedance parameters of the airway tree (1).

Interestingly, whereas E_L was very sensitive to the onset of airway closure given by the rise with constriction, the final E_L showed only a modest dependence on the degree of initial lung structural heterogeneity, indicating more similarity in the number of lost terminal airways compared with the differences in airway diameters evidenced by the resistance. This smaller dependence on E_L with the degree of asymmetry is in agreement with the similarity in H for activations greater than T_r = 0.7, possibly indicating that E_L could be good indexes of VDef heterogeneity, but imaging studies would be needed to examine this further. Indeed we observed that, for simulations using small values of T_r or trees with little or no asymmetry, the lung would bronchoconstrict, airways would evolve into a multitude of different airway diameters, and VDefs would develop as expected. Under these conditions, the value of H increased as either T_r or asymmetry increased. However, something interesting occurred at higher levels of either T_r or degrees of asymmetry. Here we found there were fewer regions of the lung with different amounts of flow (or states) as indicated by a decrease in H (Fig. 5). Thus, although H may be a good index of heterogeneity, heterogeneity does not always increase with muscle activation. This may be important, since it has recently been of great interest to quantify peripheral airway heterogeneity as a measure of peripheral airway closures, using such measures as the frequency dependence of R_L6 and nitrogen breath washout (26). However, we show that heterogeneity may in fact decline at high levels of airway constriction.

In summary, we found that ventilation defects emerged during bronchoconstriction in airway trees regardless of the degree of asymmetry. This demonstrates that previous results of characteristic airway behaviors governing emergence of VDefs using a symmetric airway tree (35) also apply to human airway trees with asymmetric airway branching. The simulated heterogeneous ventilation patterns generated here also agree with findings of imaging studies that show similar patterns in ventilation distribution. However, in contrast to a symmetric airway tree, our findings show that predetermined anatomic asymmetry and structural heterogeneity of the airway tree acts to initiate the emergence of VDefs with less muscle activation and that it results in high persistence of VDef location similar to reported persistency of the location of VDefs in vivo. Our results suggest that asymmetry in airway radii has a strong effect on airway behavior but is closely followed by functional asymmetry in resistances and time constants of different pathways of the airway tree. Our findings contribute to a better mechanistic understanding of bronchoconstriction in an asymmetric lung and to a better understanding of why imaging studies show a high degree of persistence in the location of ventilation defects.

GRANTS

This work was supported by a Natural Sciences and Engineering Research Council of Canada Strategic Operating Grant in partnership with an Atlantic Innovation Fund award from the Atlantic Canada Opportunities Agency, and by National Heart, Lung, and Blood Institute Grant R01HL087281. D. Leary is supported by a Canadian Thoracic Society studentship.

DISCLOSURES

Geoffrey Maksym has a 5% equity holding in shares in Thoracic Medical Systems Thorasys Inc. which develops a medical device for measuring respiratory impedance.

AUTHOR CONTRIBUTIONS

Author contributions: D.L., T.W., A.B., and G.N.M. conception and design of research; D.L., T.W., and A.B. performed experiments; D.L., T.W., and A.B. analyzed data; D.L., T.W., A.B., and G.N.M. interpreted results of experiments; D.L. prepared figures; D.L. drafted manuscript; D.L., T.W., A.B., and G.N.M. edited and revised manuscript; D.L., T.W., A.B., and G.N.M. approved final version of manuscript.