Normalization of neuronal responses in cortical area MT across signal strengths and motion directions

Abstract

Multiple visual stimuli are common in natural scenes, yet it remains unclear how multiple stimuli interact to influence neuronal responses. We investigated this question by manipulating relative signal strengths of two stimuli moving simultaneously within the receptive fields (RFs) of neurons in the extrastriate middle temporal (MT) cortex. Visual stimuli were overlapping random-dot patterns moving in two directions separated by 90°. We first varied the motion coherence of each random-dot pattern and characterized, across the direction tuning curve, the relationship between neuronal responses elicited by bidirectional stimuli and by the constituent motion components. The tuning curve for bidirectional stimuli showed response normalization and can be accounted for by a weighted sum of the responses to the motion components. Allowing nonlinear, multiplicative interaction between the two component responses significantly improved the data fit for some neurons, and the interaction mainly had a suppressive effect on the neuronal response. The weighting of the component responses was not fixed but dependent on relative signal strengths. When two stimulus components moved at different coherence levels, the response weight for the higher-coherence component was significantly greater than that for the lower-coherence component. We also varied relative luminance levels of two coherently moving stimuli and found that MT response weight for the higher-luminance component was also greater. These results suggest that competition between multiple stimuli within a neuron's RF depends on relative signal strengths of the stimuli and that multiplicative nonlinearity may play an important role in shaping the response tuning for multiple stimuli.

in natural visual scenes, multiple visual stimuli are commonly present in a given spatial region. The ability to extract information from a visual stimulus amidst other competing stimuli is crucial for correctly interpreting visual scenes. However, it is still unclear how multiple stimuli within neurons' receptive fields (RFs) interact to influence neuronal responses. For neurons in the extrastriate cortex that have larger RFs than those in the primary visual cortex, this question is even more prominent because larger RFs are more likely to encompass multiple stimuli. In this study we investigate how multiple, overlapping moving stimuli interact within the RFs of neurons in the motion-sensitive, extrastriate middle temporal (MT) cortex.

It has been well established that cortical area MT plays a crucial role in visual motion perception (Born and Bradley 2005) and in providing motion signals for guiding the initiation of smooth pursuit eye movements (Lisberger 2010). Most neurons in area MT are selective to motion directions (Albright 1984; Maunsell and Van Essen 1983). Previous studies using two separate stimuli moving in different directions within MT neurons' RFs have shown that neuronal response to bidirectional stimuli roughly follows the average of the responses to individual stimuli presented alone (Qian and Andersen 1994; Recanzone et al. 1997; Snowden et al. 1991; but see Krekelberg and van Wezel 2013). These results can be explained by the divisive normalization model in which each neuron computes a linear weighted sum of its inputs, divided by the summed activity of a pool of neurons excited by the visual stimuli (Heeger et al. 1996; Simoncelli and Heeger 1998). Using two stimuli moving in the same direction at different locations, Britten and Heuer (1999) have further shown that spatial summation within RFs of MT neurons follows a scaled version of weighted sum and divisive normalization. In these studies, simultaneously presented stimuli had the same signal strength.

To shed light on how multiple stimuli interact with each other, it is important to understand interactions between stimuli when they have different signal strengths. MT neurons may equally weight the responses elicited by component stimuli that have different signal strengths. Alternatively, MT neurons may weigh the stimulus component that has a higher signal strength more strongly. Heuer and Britten (2002) have shown that response normalization in area MT depends on the luminance contrast of visual stimuli: normalization is stronger when two Gabor stimuli presented in the RF both have a high contrast, and normalization is weaker when at least one of the two Gabor stimuli has a low contrast. These findings suggest that response weighting in MT can vary depending on the luminance contrast. However, how the response weighting in MT is governed by relative signal strengths remains unclear.

In the primary visual cortex, neuronal responses elicited by overlapping gratings that have different orientations can be accounted for by a weighted sum of the responses to individual gratings; moreover, the response weight is greater for the stimulus component that has a higher contrast (Busse et al. 2009; MacEvoy et al. 2009). These results can be explained by a contrast normalization model, in which the weight for the response to one grating is determined by the grating's contrast, normalized by the overall contrast of all gratings (Busse et al. 2009; Carandini et al. 1997). It is unknown whether the changes of response weights based on relative luminance contrasts also occur in the extrastriate cortex, and it remains unclear whether the scheme of weighting component responses based on relative signal strengths applies to other visual attributes.

In visual motion, the coherence of dynamic random-dot stimuli parametrically controls the strength of a motion signal, and neurons in area MT are sensitive to motion coherence (Britten et al. 1992, 1993). To investigate the rule governing the interaction/competition between multiple stimuli that have the same or different signal strengths, we manipulated the relative coherence levels of two overlapping, random-dot stimuli moving in different directions. We set out to test the hypothesis that stimulus competition depends on relative motion coherence of random-dot stimuli and favors the stimulus component that has the higher motion coherence. To test the generality of this hypothesis, we also varied signal strength by manipulating relative luminance levels of moving stimuli.

We found that, rather than weighting each stimulus component equally, MT neurons weighted the stimulus component that had a higher signal strength more strongly, regardless of whether the signal strength was defined by motion coherence or luminance contrast. In addition to the weighted linear summation, we also found evidence suggesting nonlinear interactions between stimulus components. The nonlinear interaction tends to have a suppressive effect on the neuronal response. Our results provide important constraints on neural models of encoding multiple visual stimuli and suggest a general rule of competition between multiple stimuli within neurons' RFs.

MATERIALS AND METHODS

Three adult male rhesus monkeys (Macaca mulatta) were used in the neurophysiological experiments. Experimental protocols were approved by local Institutional Animal Care and Use Committees and followed the NIH Guide for the Care and Use of Laboratory Animals. Procedures for surgical preparation and electrophysiological recording were routine and similar to those described previously (Huang et al. 2008; Huang and Lisberger 2009). During sterile surgery with the animal under isoflurane anesthesia, a head post and a recording cylinder were implanted to allow recording from neurons in cortical area MT. Eye position was monitored at 1,000 Hz using a video-based eye tracker (EyeLink; SR Research) for monkeys GE and BJ and the search coil method (Judge et al. 1980) for monkey RG.

For electrophysiological recordings from neurons in area MT, we lowered tungsten electrodes (1∼3 MΩ; FHC) into the posterior bank of the superior temporal sulcus. We identified area MT by its characteristically large portion of directionally selective neurons, small RFs relative to those of neighboring medial superior temporal cortex (area MST), and relatively low preferred speed (typically <40°/s) compared with that of MST neurons (Churchland et al. 2007; Nover et al. 2005). Electrical signals were amplified, and single units were identified with a real-time template matching system and an offline spike sorter (Plexon).

Visual stimuli and behavioral paradigm.

Stimulus presentation, the behavioral paradigm, and data acquisition were controlled by a real-time data acquisition program (https://sites.google.com/a/srscicomp.com/maestro/). Visual stimuli were presented on a 25-in. CRT monitor at a viewing distance of 63 cm. Monitor resolution was 1,024×768 pixels, and the refresh rate was 100 Hz. Visual stimuli were generated by a Linux workstation using an OpenGL application that communicated with an experimental control computer. The output of the video monitor was measured with a photometer (LS-110; Minolta) and was gamma corrected.

Visual stimuli were random-dot patterns, presented within a stationary, circular aperture that was 7.5° across. Each dot was a square of 2 pixels (0.08°) on a side. The dot density of a single random-dot pattern was 3.4 dots/deg². In the first two experiments investigating the effects of motion coherence, the luminance levels of the dots and the background were 15.3 and 1.9 cd/m², respectively. In the third experiment investigating the effects of the stimulus luminance, the luminance of the dots in each random-dot pattern was one of three values (2.5, 10, or 40 cd/m²), and the background was 0.2 cd/m². Under the three luminance conditions, the standard deviations of the luminance intensities that reflect the root mean square (RMS) contrasts (Kukkonen et al. 1992; Moulden et al. 1990; Peli 1990) were 0.34, 1.43, and 5.8 cd/m², respectively.

To generate a random-dot pattern moving at N% of motion coherence (after Britten et al. 1992; Newsome and Pare 1988), N% of the dots were selected to move coherently while the rest of the dots were repositioned randomly within the outer boundary of the stimulus. Random selections of signal and noise dots occurred at each monitor frame. Therefore, a given dot would switch back and forth between a signal dot and a noise dot as it traveled across the circular aperture. The lifetime of each dot was as long as the motion duration. All visual stimuli were presented in individual trials while the monkeys fixated within a 1.5° × 1.5° window of a spot of light to receive juice rewards. Visual stimuli were illuminated after the animal fixated for 200 ms. To separate the neuronal response to stimulus motion from that of the stimulus onset, visual stimuli remained stationary on the display for 200 ms before starting to move. In the first experiment, visual stimuli moved for 1,000 ms. We found essentially the same results when we analyzed the neuronal responses during the initial 500- or 300-ms motion periods. In the second and third experiments, we used shorter motion durations of 500 and 300 ms, respectively, to speed up data collection. The monkeys continued to fixate for 200 ms after the visual stimuli were turned off.

Experimental design.

We first characterized the direction selectivity of an isolated neuron by randomly interleaving trials of 30° × 27° random-dot patches moving at 10°/s in eight different directions at 45° steps. Directional tuning was evaluated online using Matlab (The MathWorks). We next characterized the speed tuning by interleaving 30° × 27° random-dot patches moving in the preferred direction (PD) of the neuron at one of eight different speeds, ranging from 1 to 128°/s, evenly spanning a log scale of speed. Next, we mapped the RF of the neuron by recording responses to a series of 5° × 5° patches of random dots that moved in the PD and at the preferred speed (PS) of the neuron. The location of the patch was varied randomly to tile the screen in 5° steps without overlap and to cover an area of 35° × 25°. The raw map of the RF was interpolated at an interval of 0.5°, and the location giving rise to the highest firing rate was taken as the center of the RF. In the following experiments, visual stimuli were centered on the RF.

In the first experiment, we set the levels of motion coherence of two superimposed random-dot patterns both at 100% or one at 100% and the other at 60%. The direction separation between the two random-dot patterns, referred to as two stimulus components, was fixed at 90°. Note that when a random-dot pattern moved at 60% coherence in a given direction, the visual stimuli were drastically different from a situation where 60% of the dots moved at 100% coherence and 40% of dots moved randomly. Because the random selections of signal and noise dots occurred at each monitor frame, a noise dot at one frame may have turned into a signal dot in the next frame and moved in the direction of the random-dot pattern. As a result, the noise dots did not appear to be separable from the random-dot pattern. When a random-dot pattern of 60% coherence was superimposed with a random-dot pattern of 100% coherence, the frame-to-frame noise dots of the 60% coherence pattern did not appear to interfere with the random-dot pattern of 100% coherence (see demos of visual stimuli at the URL given in the Endnote). Trials with different vector-averaged (VA) directions of the two stimulus components were randomly interleaved to characterize the response tuning to the bidirectional stimuli. The VA direction was typically varied at a step of 15°. Trials that contained unidirectional component stimuli presented alone were interleaved with the bidirectional stimuli.

In the second experiment, we used visual stimuli that contained two superimposed random-dot patterns, one moving in the PD of the neuron and the other moving in a direction that was 90° away from the PD. The motion coherence of the random-dot pattern moving in the PD (referred to as the PD component) was set at one of five levels, from 60 to 100% at 10% steps. The motion coherence of the orthogonal motion component was set at 100%. Trials of different levels of motion coherence were randomly interleaved. Also randomly interleaved were trials that presented the PD or the orthogonal motion component alone.

In the third experiment, we set the luminance of the stimulus component moving at the clockwise side of the two component directions at 40 cd/m² and the luminance of the other stimulus component at either 10 or 2.5 cd/m². We varied the VA direction of the bidirectional stimuli to characterize direction tuning curves. In all three experiments, the speeds of the two stimulus components were equal and were set within the range of 1.5–20°/s and closest to the preferred speeds of the recorded neurons. In the majority of the recording sessions, the stimulus speeds was set between 5 and 20°/s, with a median of 10°/s. The speed range was chosen to allow for better perceptual segmentation of the visual stimuli as guided by our pilot human psychophysics experiment.

Data analysis.

Response firing rate was calculated during the time interval of stimulus motion and averaged across repeated trials. We next fitted raw direction tuning curves using splines at a resolution of 1° and rotated the spline-fitted tuning curve elicited by the bidirectional stimuli to align the VA direction of 0° with the PD of each neuron. We normalized each neuron's responses by the neuron's maximum bidirectional response and averaged the aligned, normalized tuning curves across neurons.

To determine the impact of relative coherence levels of motion components on the response tuning curve, we computed the center of gravity (CG) of the aligned tuning curve as

$$CG\left(R\right)=\frac{{\displaystyle \sum \left[R\left(\theta \right)\hspace{0.17em}\cdot \vec{\theta }\right]}}{{\displaystyle \sum R\left(\theta \right)}},$$ (1)

where θ is the motion direction and R(θ) is the neuronal response to that direction. We calculated a center of gravity shift index (CGSI) to quantify the CG of the bidirectional responses in relation to the CGs of the corresponding component responses:

$$CGSI\left(x\right)=\frac{CG\left(R_x\right)-CG\left(R_{LC}\right)}{CG\left(R_{HC}\right)-CG\left(R_{LC}\right)},$$ (2)

where R_x refers to either the response tuning to the bidirectional stimuli or the averaged response tuning of the component responses; R_HC and R_LC refer to the response tuning curves elicited by the higher- and lower-coherence component, respectively. We took into account the circular nature of motion direction when calculating the difference between CGs in Eq. 2.

Model fits of bidirectional responses and evaluation of goodness of fit.

We fitted neuronal responses elicited by the bidirectional stimuli across the VA directions (in experiments 1 and 3) or multiple levels of motion coherence (in experiment 2) using several models (see results) by minimizing the sum of squared error. To evaluate the goodness of fit of a model, we computed the percentage of variance (PV) accounted for by each model fit as

$$PV=100\times \left(1-\frac{SSE}{SST}\right),$$ (3)

where SSE is the sum of squared errors between a model fit and the data, and SST is the sum of squared differences between the data and the mean of data (cf. Morgan et al. 2008). When occasionally SSE exceeded SST and gave rise to a negative PV, we forced the PV to be zero.

To evaluate whether adding a nonlinear interaction term to a linear weighted sum model significantly improved the goodness of fit, we used sequential F-tests (Draper and Smith 1998). The F ratio was calculated as

$$F\left(P_{NL}-P_L,\hspace{0.17em}N-P_{NL}\right)=\frac{\left(SS{R}_L-SS{R}_{NL}\right)/\left(P_{NL}-P_L\right)}{SS{R}_{NL}/\left(N-P_{NL}\right)},$$ (4)

where SSR_NL is the residual sum of squares from the fit using the nonlinear model that has P_NL parameters, SSR_L is the residual from the fit using the linear model that has P_L parameters, and N is the total number of data points. This test takes into consideration the difference in the number of parameters of the models to be compared.

RESULTS

To determine how multiple stimuli interact within the RFs of neurons, we investigated the rule that accounted for the relationship between the responses elicited by overlapping random-dot stimuli moving in different directions and those elicited by the constituent stimulus components. In the first two experiments, we varied relative levels of motion coherence of the stimulus components. In the third experiment, we varied relative luminance contrasts of the stimulus components. Our database comprised recordings from 224 single units in extrastriate area MT (128 from monkey GE, 88 from monkey BJ, and 8 from monkey RG). Among them, 141, 66, and 38 neurons were tested in the first, second, and third experiment, respectively.

Direction tuning of neuronal responses to bidirectional stimuli moving at the same or different levels of motion coherence.

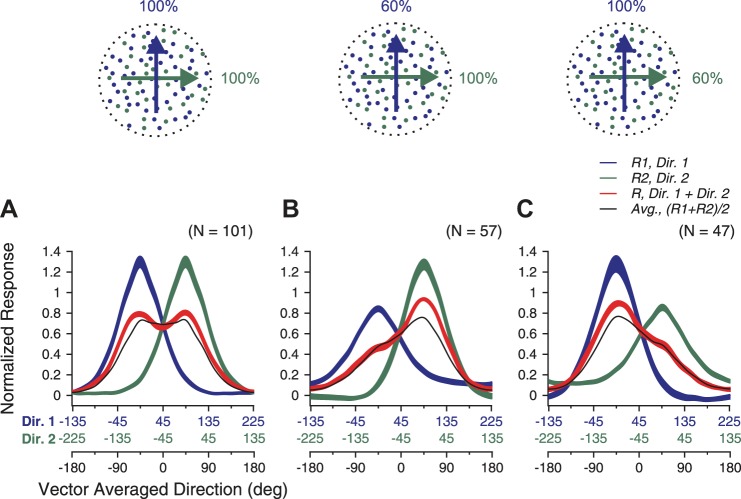
We first determined how direction tuning curves of MT neurons in response to the bidirectional stimuli varied with relative levels of motion coherence. The direction separation between the two motion components was 90°. To characterize the response tuning curve, we varied the VA direction of the two motion components to span 360°. We set the coherence levels of two motion components either both at 100% (referred to as the “equal-coherence condition”) or one at 100% and the other at 60% (referred to as the “different-coherence condition”) (illustrated in Fig. 1, A and B).

Fig. 1.

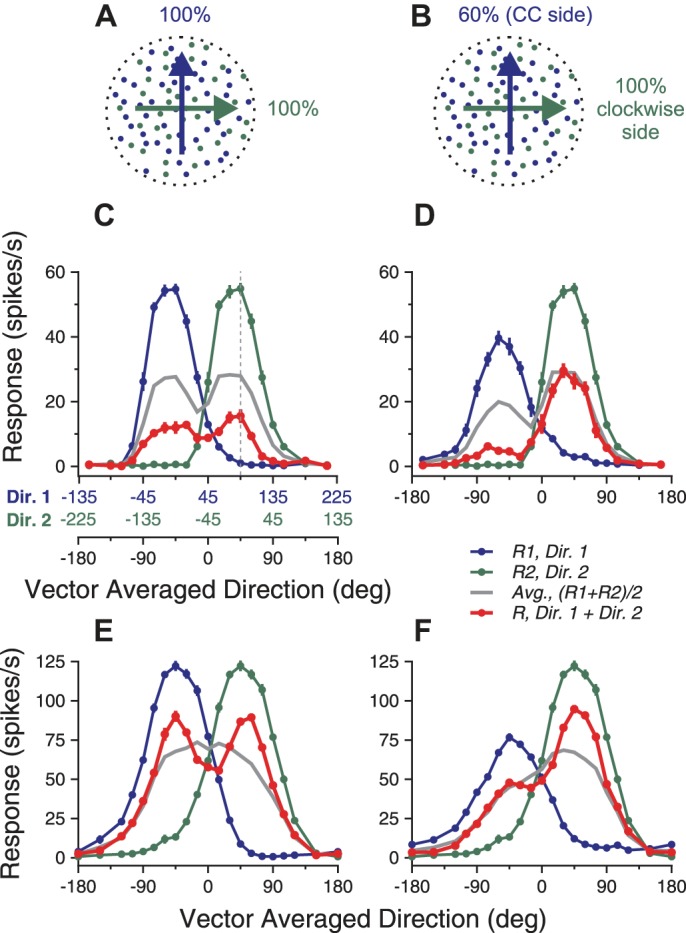
Visual stimuli and direction tuning curves of 2 example neurons elicited by bidirectional stimuli and the constituent unidirectional components. A and B: cartoon illustration of the visual stimuli. Blue and green dots indicate 2 achromatic random-dot patterns. The stimulus component shown in blue (direction 1, Dir. 1) moved at the counterclockwise (CC) side of the 2 component directions. The stimulus component shown in green (direction 2, Dir. 2) moved at the clockwise side of the 2 component directions. A: 2 motion components both moved at 100% coherence. B: the clockwise-side component moved at 100% coherence, whereas the CC-side component moved at 60% coherence. C and D: responses from 1 example neuron. E and F: responses from another example neuron. The abscissa in black refers to the vector-averaged (VA) direction of the bidirectional stimuli. The abscissas in blue and green (C) refer to Dir. 1 and 2, respectively, of the unidirectional stimulus components. The blue and green axes are shifted 90° relative to each other. VA direction of 0° is aligned with the preferred direction (PD) of the neuron. The dotted vertical line intersects with the bidirectional response at VA direction of 45° and the 2 component responses at directions of 90° (Dir. 1) and 0° (Dir. 2), respectively. Error bars indicate SE. See text for definitions.

Figure 1 shows the results from two example neurons. To visualize the relationship between the responses to the bidirectional stimuli and those evoked by the unidirectional stimulus components, we superimposed the response tuning curves evoked by the bidirectional stimuli and by the stimulus components. The blue and green curves show the direction tuning curves evoked by the stimulus components presented alone (Fig. 1). These two tuning curves were shifted by 90° relative to each other (note the color-coded component directions in the axis of abscissas). A vertical line at a given VA direction of the bidirectional stimuli intersects with the blue and green curves at response magnitudes corresponding to the responses elicited by the two component directions of the bidirectional stimuli (see the vertical dashed line in Fig. 1C).

When both stimulus components moved at 100% coherence, the tuning curves of the two example neurons to bidirectional stimuli were roughly symmetric (Fig. 1, C and E). When one stimulus component moved at 100% and the other moved at 60% coherence, the tuning curves showed a larger peak at the side where the component response elicited by the higher-coherence component was stronger than the other component response (Fig. 1, D and F). Although the average of the component responses also showed such bias toward the stronger component response elicited by the higher-coherence component (gray curves in Fig. 1, D and F), the observed bias of the bidirectional response was stronger than that predicted by the average of the component responses.

The two example neurons also showed some differences in their bidirectional responses. Under the equal-coherence condition, the bidirectional response of the first neuron was significantly less than the averaged component response across the whole direction tuning curve (Fig. 1C). In contrast, the second neuron roughly followed the average of the component responses when neither stimulus component moved near the PD of the neuron. When one stimulus component moved in a direction close to the PD (i.e., VA direction of ±45°), the bidirectional response was stronger than the average of the component responses. When the VA direction was near the PD (i.e., VA direction of 0°), the bidirectional response was weaker than the average of the component responses. As a result, the tuning curve showed two separate peaks, although the averaged component response only had a single peak (Fig. 1E).

Figure 2 shows the population-averaged tuning curves under the equal- and different-coherence conditions. Before averaging, the PD of the tuning curve for each neuron was aligned (see methods). When both stimulus components moved at 100% coherence, the population-averaged tuning curve had two symmetric peaks, located around ±45° at which one of the component directions was in the PD (Fig. 2A). The peak responses were significantly stronger than the average of the component responses (1-tailed paired t-test, P < 10⁻⁹). Moreover, the bidirectional response at the VA direction of the PD (i.e., 0°) was slightly weaker than the average of the component responses (1-tailed paired t-test, P < 0.02), reinforcing the appearance of two response peaks in the tuning curve.

Fig. 2.

Population-averaged tuning curves elicited by bidirectional stimuli and the unidirectional components. VA direction of 0° was aligned with the PD for each neuron, and response tuning curves were normalized by the maximum response elicited by the bidirectional stimuli before averaging. The widths of the red, blue, and green traces indicate SE. A: both motion components moved at 100% coherence. B: the clockwise-side component moved at 100% coherence, whereas the CC-side component moved at 60% coherence. C: the CC-side component moved at 100% coherence, whereas the clockwise-side component moved at 60% coherence.

When one stimulus component moved at 100% and the other moved at 60% coherence, the response tuning curve strongly favored the higher-coherence component. Figure 2B shows the population-averaged direction tuning curves when the higher-coherence component moved at the clockwise side of the two component directions. At directions where the component response elicited by the higher-coherence component was greater than that elicited by the lower-coherence component, the response to the bidirectional stimuli was strongly biased toward the response elicited by the higher-coherence component (Fig. 2B). When the higher-coherence component moved in the PD of the neuron (i.e., VA direction of 45°), the bidirectional response was significantly greater than the average of the two component responses (1-tailed paired t-test, P < 10⁻⁴). In contrast, at the other side of the tuning curve where the component response elicited by the lower-coherence component was stronger, the response to the bidirectional stimuli roughly followed the average of the component responses (Fig. 2B). We found similar results when the higher-coherence component moved at the counterclockwise side of the two component directions (Fig. 2C).

To quantify the bias of the response tuning curve elicited by bidirectional stimuli toward the response tuning elicited by the higher-coherence component, we computed the CG of the response tuning curve (see methods) and compared the CGs of the bidirectional responses with those of the component responses. Figure 3 shows the CGs of tuning curves obtained when the higher-coherence component moved at either the clockwise side (Fig. 3, A1 and A2) or the counterclockwise side (Fig. 3, B1 and B2) of the two component directions. The CG of the bidirectional responses shifted toward the CG of the component responses elicited by the higher-coherence component more than did the CG of the averaged component responses. To quantify the extent of this shift, we calculated a CGSI (see methods). A CGSI of >0.5 indicates that the CG is closer to that of the higher-coherence component than the lower-coherence component. The mean CGSI of 57 neurons shown in Fig. 3A1 (mean 0.76, SD 0.17) was significantly greater than 0.5 (1-tailed t-test, P < 10⁻¹⁶) and was also significantly greater than the mean CGSI of the averaged component responses (mean 0.67, SD 0.09; P = 1.8 × 10⁻⁵; Fig. 3A2). When the higher-coherence component moved at the counterclockwise side of the two component directions, the mean CGSI of 47 neurons was also significantly greater than the mean CGSI of the averaged component responses (P = 2.8 × 10⁻⁴).

Fig. 3.

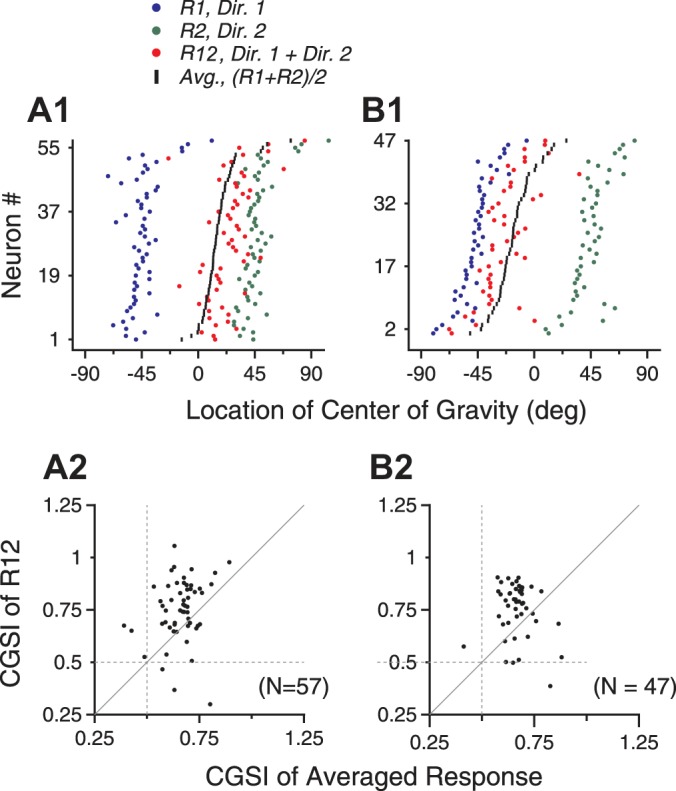
Center of gravity (CG) of the response tuning curve elicited by bidirectional stimuli when the stimulus components moved at different levels of coherence. A: the higher-coherence component moved at the clockwise side of the 2 component directions. B: the higher-coherence component moved at the CC side of the 2 component directions. A1 and B1: each row represents data from 1 neuron. The green and blue dots indicate the CGs of the response tuning curves elicited by the stimulus components moving at the clockwise and CC side of the 2 component directions, respectively. The red and black dots indicate the CGs of the response tuning curves elicited by the bidirectional stimuli and those of the averaged component responses, respectively. Rows were sorted on the basis of the CG of the averaged component responses. A2 and B2: scatter plots of the center of gravity shift index (CGSI) calculated on the basis of the bidirectional responses (ordinate) and the averaged component response (abscissa). One dot in A2 that had a CGSI for R₁₂ of 1.39 and a CGSI for the averaged responses of 0.85 is outside the axis scale and not shown.

Model fits of neuronal response tuning curves.

To determine the rule that accounts for the neuronal response tuning curves elicited by bidirectional stimuli moving at the same or different levels of coherence, we fitted the data using several models. First, we fit the responses elicited by bidirectional stimuli as a weighted sum of the responses elicited by the stimulus components presented alone, referred to as the linear weighted summation (LWS) model:

$$R_{{12}_{pred}}\left({\theta }_1,{\theta }_2\right)=w_1{R}_1\left({\theta }_1\right)+w_2{R}_2\left({\theta }_2\right)+c,$$ (5)

where θ₁ and θ₂ are the two component motion directions; R_{12_pred} is the tuning of the bidirectional response predicted by the model; R₁ and R₂ are the tuning curves of the component responses; w₁ and w₂ are the response weights for R₁ and R₂, respectively; and c is a constant. We fixed c to zero in all data fits, except when noted.

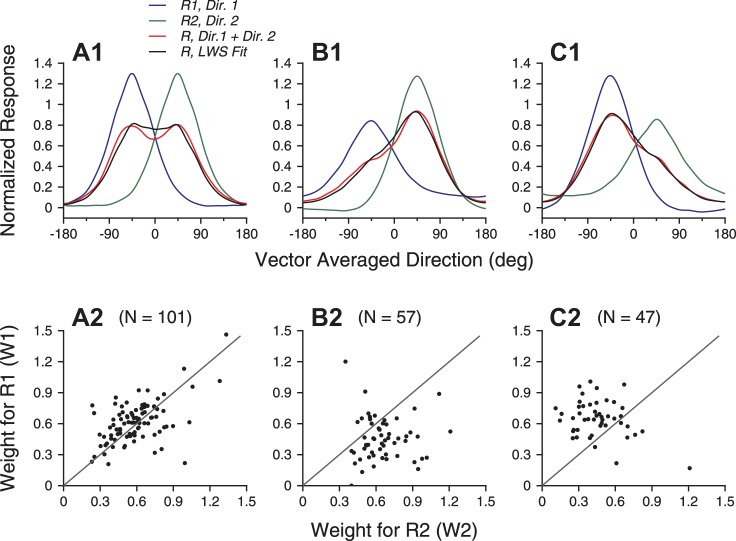
Figure 4 shows the model fits for the direction tuning curves of the two example neurons shown in Fig. 1. For the first example neuron, the LWS model provided good fits for the whole tuning curves, accounting for 93% of the response variance (see methods) when both stimulus components moved at 100% coherence (Fig. 4A) and 98% of the variance when one stimulus component moved at 100% and the other moved at 60% coherence (Fig. 4B). For the second example neuron, the LWS model accounted for 87% of the response variance under the equal-coherence condition (Fig. 4C) and 94% of the variance under the different-coherence condition (Fig. 4D). Note that the LWS model failed to capture the two response peaks in Fig. 4C and overestimated the responses near VA 0° in Fig. 4D.

Fig. 4.

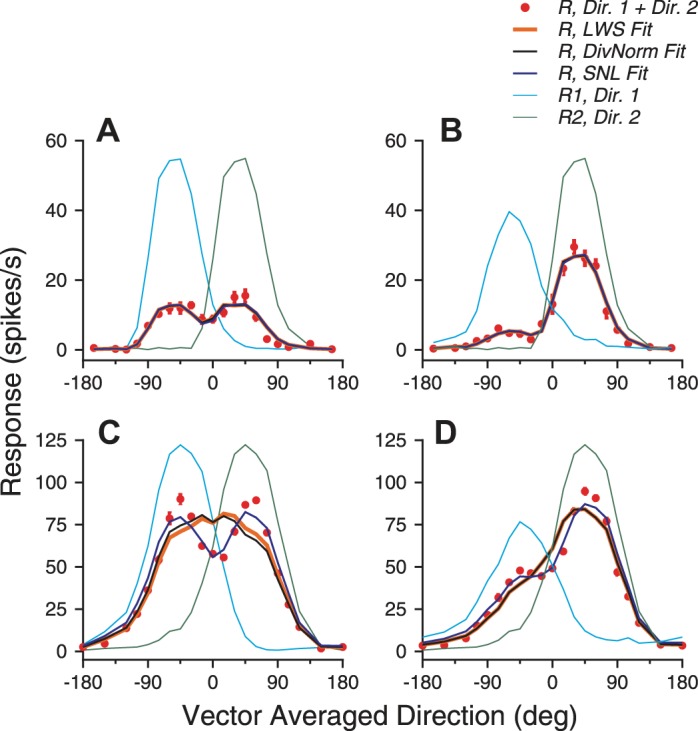
Model fits of the response tuning curves elicited by bidirectional stimuli of 2 example neurons. A and C: 2 motion components both moved at 100% coherence. B and D: the clockwise-side component moved at 100% coherence, and the CC-side component moved at 60% coherence. A and B: example neuron 1. All 3 models, linear weighted summation (LWS), simplified normalization (DivNorm), and summation plus nonlinear interaction (SNL), provided good fits. The fitting results of these models were almost identical, and therefore curves of different model fits are overlapping. C and D: example neuron 2. The LWS and DivNorm model fits are nearly identical in D. Error bars of the bidirectional responses indicate standard errors.

Across the neuron populations, the LWS model provided generally good fits of the data, accounting for >81% of the response variance (see Table 1). The model accounted for the population-averaged tuning curves elicited by the bidirectional stimuli well (Fig. 5, A1–C1), but with a caveat that the fits slightly overestimated the measured responses where the VA directions of the bidirectional stimuli were close to the neurons' PD. When two motion components moved at the same coherence, the mean weights w₁ and w₂ obtained using the LWS model were 0.61 (SD 0.2) and 0.58 (SD 0.2), respectively. The two means were not significantly different (N = 101, paired t-test, P > 0.1). The pooled mean weight across w₁ and w₂ was 0.6 (SD 0.2) and was significantly smaller than 1 (1-tailed t-test, P = 2.6 × 10⁻⁷³), indicating robust subadditive summation. Furthermore, the mean weight was also significantly greater than 0.5 (1-tailed t-test, P = 2.1 × 10⁻¹¹), indicating deviation from response averaging. Note that the response weights of the neurons in the population were distributed across a wide range (Fig. 5A2). For a given neuron, the bidirectional response can be closer to the weaker component response (e.g., Fig. 1C), the average of the component responses, or the stronger component response.

Table 1.

Percentage of variance accounted for by different models

Stimulus Configuration Motion Coherence			Models (Free Parameters)
Clockwise side	CC side	N	LWS (w1, w2)	SNL (w1, w2, b)	LWS_C (w1, w2, c)	SNL_C (w1, w2, b, c)	CohNorm (n, σ)	DivNorm (n, α)	NNL (n, α, b)
100%	100%	101	81.6 ± 16.6	88.4 ± 9.0	84.9 ± 12.4	90.4 ± 7.2	76.6 ± 20.1	78.7 ± 17.5	85.8 ± 10.2
100%	60%	57	85.2 ± 13.2	90.9 ± 8.1	87.7 ± 10.8	91.9 ± 7.7	83.0 ± 17.3	83.5 ± 17.9	88.9 ± 14.6
60%	100%	47	86.3 ± 10.4	89.5 ± 9.4	87.8 ± 9.7	90.9 ± 8.4	83.6 ± 17.0	83.6 ± 17.4	87.6 ± 14.8

Values are means ± SD of percentage of variance accounted for by different models (free parameters indicated in parentheses) for neurons tested in different coherence conditions.

CC, counterclockwise; N, no. of neurons.

See text for detailed descriptions of models and parameters.

Fig. 5.

LWS model fits of the population-averaged tuning curves and the response weights for the stimulus components. A: both motion components moved at 100% coherence. B: the motion component at the clockwise side of the 2 component directions moved at 100% coherence, and the CC-side component moved at 60% coherence. C: the CC-side component moved at 100% coherence, and the clockwise-side component moved at 60% coherence. A1–C1: LWS fits of the population-averaged tuning curves elicited by the bidirectional stimuli. A2–C2: response weights (w₁ and w₂) for the 2 stimulus components obtained using the LWS fits.

When two stimulus components moved at different levels of coherence, the response weights obtained from the LWS model fits were greater for the higher-coherence component than for the lower-coherence component. When the higher-coherence component moved at the clockwise side of the two component directions, the mean response weight for the higher-coherence component was 0.66 (SD 0.19), significantly greater than that for the lower-coherence component of 0.45 (SD 0.21, N = 57, 1-tailed paired t-test, P = 4.1 × 10⁻⁷; Fig. 5B2). When the higher-coherence component moved at the CC side of the two component directions, the mean response weight for the higher-coherence component was also significantly greater than that for the lower-coherence component (N = 47, P = 4.2 × 10⁻⁵; Fig. 5C2).

Although the LWS model could account for the responses elicited by the bidirectional stimuli reasonably well, the model failed to capture certain salient features of the direction tuning curves for some neurons (e.g., see Figs. 4C and 5A1). We next asked whether allowing nonlinear interactions between the responses evoked by the stimulus components helped to improve the data fit. We fitted the bidirectional responses using a linear weighted sum of the component responses plus a multiplicative interaction term between the component responses, referred to as the summation plus nonlinear interaction (SNL) model:

$$R_{{12}_{pred}}\left({\theta }_1,{\theta }_2\right)=w_1{R}_1\left({\theta }_1\right)+w_2{R}_2\left({\theta }_2\right)+b{R}_1\left({\theta }_1\right)R_2\left({\theta }_2\right)+c,$$ (6)

where b is a coefficient determining the sign and strength of the nonlinear interaction between the component responses, and c is a constant. We fixed c to zero in all data fits, except when noted.

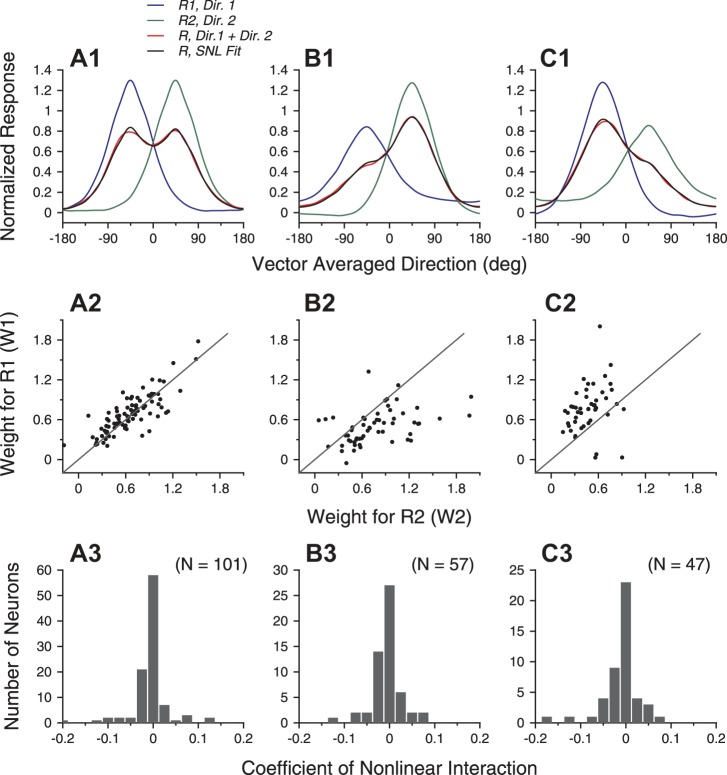
We found that the SNL model provided significantly better fits than the LWS model for 49 of 101 neurons under the equal-coherence condition (sequential F-test, P < 0.01) and better fits for 41 of 104 neurons under the different-coherence condition pooled across the two stimulus configurations (sequential F-test, P < 0.01; Fig. 6, A1 and B1). The improvement of the goodness of fit by the SNL model for one example neuron is illustrated in Fig. 4, C and D.

Fig. 6.

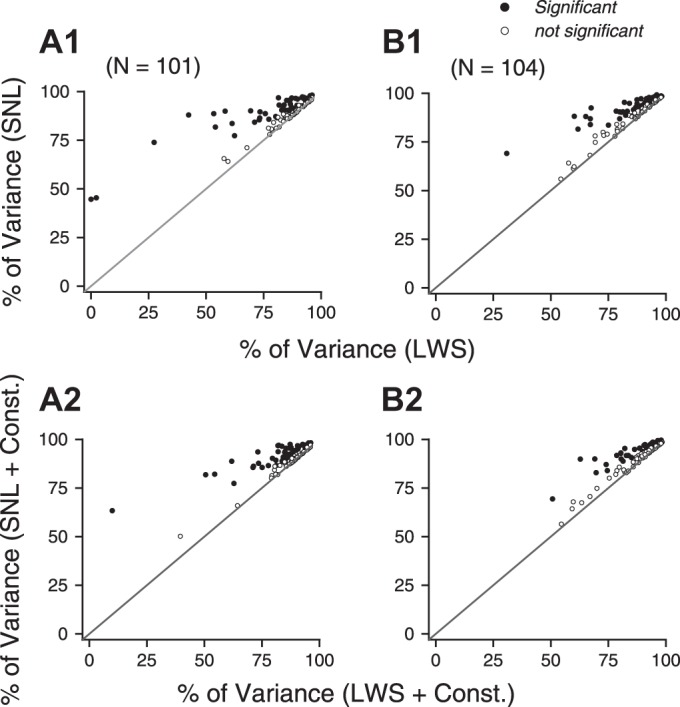
Comparison of the goodness of fit between the LWS and SNL models. A: both motion components moved at 100% coherence. B: one motion component moved at 100% coherence, and the other moved at 60% coherence. Data from the 2 stimulus configurations (i.e., the higher-coherence component moved at either the clockwise or CC side of the 2 component directions) were pooled together. A1 and B1: the constant c in the LWS and SNL model was fixed at 0. A2 and B2: the constant c in the LWS and SNL model was a free parameter.

The improvement of the data fit by using the SNL model could not be explained by simply adding a constant parameter in the LWS model. When we allowed the constant c in the LWS and SNL model (Eqs. 5 and 6) to vary freely, the SNL model with the constant term (referred to as the SNL_C model) again provided significantly better fits than the LWS model with the constant term (LWS_C) for 48 of 101 neurons under the equal-coherence condition and for 37 of 104 neurons under the different-coherence condition (sequential F-test, P < 0.01; Fig. 6, A2 and B2). The significance test took into consideration that the SNL (or SNL_C) model had one more free parameter than the LWS (or LWS_C) model. When we compared the goodness of fit between the LWS_C model and the SNL model, in which the two models had the same number of parameters, the goodness of fit of the SNL model was still significantly better than that of the LWS_C model under the equal- and different-coherence conditions (N = 101 and 104, respectively, 1-tailed paired t-test, P < 2 × 10⁻⁶). These results are consistent with the observation that the fitting error of the LWS model is not fixed, but rather varies with the stimulus directions and hence the component responses (see Fig. 5A1). The percentages of variance accounted for by the LWS and SNL models, with or without a constant term, are shown in Table 1.

Figure 7 shows the fitting results for the population data using the SNL model without the constant. The model fits captured population-averaged tuning curves, even where the LWS model overestimated the bi-directional responses (compare Fig. 5, A1–C1, with Fig. 7, A1–C1). From the SNL fits, we obtained weights w₁ and w₂ for the component responses (see Eq. 6). When the two stimulus components both moved at 100% coherence, the mean weight was 0.67 (SD 0.29, N = 202, pooled across w₁ and w₂; Fig. 7A2), which was significantly smaller than 1 (1-tailed t-test, P = 2.4 × 10⁻³⁹). The weights were also significantly greater than 0.5 (P = 2.1 × 10⁻¹⁴). When the two stimulus components moved at different coherence levels, the mean response weight was significantly larger for the higher-coherence component than for the lower-coherence component (Fig. 7, B2 and C2; P < 10⁻⁶). When the higher-coherence component moved at the clockwise side of the two component directions, the mean response weights for the higher- and lower-coherence components were 0.78 (SD 0.4) and 0.5 (SD 0.26, N = 57), respectively. When the higher-coherence component moved at the CC side, the mean response weights for the higher- and lower-coherence components were 0.77 (SD 0.35) and 0.48 (SD 0.2, N = 47), respectively.

Fig. 7.

SNL model fits of the population-averaged tuning curves and the response weights for the stimulus components. A: both motion components moved at 100% coherence. B: the clockwise-side component moved at 100% coherence, and the other motion component moved at 60% coherence. C: the CC-side component moved at 100% coherence, and the other motion component moved at 60% coherence. A1–C1: SNL fits of the population-averaged tuning curves elicited by the bidirectional stimuli. A2–C2: response weights for the 2 stimulus components obtained using the SNL fits. A3–C3: distribution of the nonlinear interaction coefficient of the SNL fits.

Importantly, the nonlinear multiplicative interaction between the component responses determined by the SNL fits tended to have a negative coefficient. Under the equal-coherence condition, SNL fits to the responses of 71 (of 101) neurons had negative nonlinear interaction coefficients (i.e., parameter b in Eq. 6). The mean coefficient was −0.016 (SD 0.09, N = 101), which was significantly negative (1-tailed t-test, P = 0.04). Under the two different-coherence conditions, the mean nonlinear interaction coefficients were also significantly negative (1-tailed t-test, P < 0.05). The distributions of the interaction coefficient are shown in Fig. 7, A3–C3.

Data fitting using both the LWS and SNL models showed subadditive summation and the response weights varied with the relative coherence levels of the motion components. We asked whether these results could be accounted for by a divisive normalization model (Carandini and Heeger 2012). We first fitted the data using a model after the “contrast normalization” model that was used to describe the responses of V1 neurons elicited by gratings with different luminance contrasts (Busse et al. 2009; Carandini et al. 1997). We referred to this model as the “coherence normalization” model (CohNorm):

$$R_{{12}_{pred}}\left({\theta }_1,{\theta }_2\right)=\frac{h_1^n}{{\left(\sqrt{h_1^2+h_2^2}\right)}^n+{\sigma }^n}{R}_1\left({\theta }_1\right)+\frac{h_2^n}{{\left(\sqrt{h_1^2+h_2^2}\right)}^n+{\sigma }^n}{R}_2\left({\theta }_2\right),$$ (7)

where h₁ and h₂ are the coherence levels of the two motion components, n is a positive exponent, and σ is a positive constant representing the semi-saturation coherence. The CohNorm model accounted for 76.6% of the response variance under the equal-coherence condition and 83% of the variance under the different-coherence conditions (Table 1). The median exponent n was 1.3 and 0.8 under the equal- and different-coherence condition, respectively.

In the divisive normalization model proposed by Heeger and colleagues, the response of a single neuron is determined by the linear input that the neuron receives, divisively normalized by the summed activity of a pool of neurons (Heeger 1992; Simoncelli and Heeger 1998; see Carandini and Heeger 2012 for a review). In the denominator of Eq. 7, the activity of the neuron pool elicited by the bidirectional stimuli is represented as proportional to the combined motion coherence of the two stimulus components

$${\left(\sqrt{h_1^2+h_2^2}\right)}^n$$

, as in the contrast normalization model. Since the signal strength (motion coherence or luminance contrast) has a positive value and the exponent n is also positive, any possible multiplicative terms between the signal strengths of the two stimulus components after expanding the term

$${\left(\sqrt{h_1^2+h_2^2}\right)}^n$$

would have only positive coefficients. However, as we have shown above, allowing a multiplicative interaction between the component responses provides a significantly better fit of the responses elicited by the bidirectional stimuli and the coefficient of the multiplicative interaction is often negative. Motivated by these observations, we used a modified normalization model to fit our data.

We represented the response of the neuron pool in the denominator evoked by the bidirectional stimuli as a weighted sum of the population responses evoked by each stimulus component plus a multiplicative interaction term between the component responses. We assumed that the population neural response evoked by a stimulus component was proportional to a power law transformation of the stimulus strength. The model has the form

$$R_{{12}_{pred}}\left({\theta }_1,{\theta }_2\right)=\frac{h_1^n}{p_1{h}_1^n+p_2{h}_2^n+\alpha h_1^n{h}_2^n}{R}_1\left({\theta }_1\right)+\frac{h_2^n}{p_1{h}_1^n+p_2{h}_2^n+\alpha h_1^n{h}_2^n}{R}_2\left({\theta }_2\right),$$ (8)

where h₁ and h₂ are the signal strengths of the two stimulus components, n is a positive exponent that transforms the signal strength into a measure of neural activity, p₁ and p₂ are two positive parameters governing the relative contribution of the population neural response evoked by each stimulus component to the population response evoked by the bidirectional stimuli, and α is the coefficient of the interaction term that can be positive or negative, which allows either a facilitatory or suppressive effect of the multiplicative interaction on the population response. The parameters p₁ and p₂ allow the response weights for the two stimulus components to have different values under the equal-coherence condition. Note that in experiment 1, h₁ and h₂ were fixed, and therefore the interaction term αh₁ⁿh₂ⁿ is essentially the same as a single constant. This normalization model fitted the bidirectional responses under the equal-coherence condition as well as the LWS model, accounting for on average 81.6% (SD 16.6, N = 101) of the variance.

We found that setting both p₁ and p₂ to 1 still provided good fits of the data. The simplified normalization model, referred to as the DivNorm model, can be expressed as

$$R_{{12}_{pred}}\left({\theta }_1,{\theta }_2\right)=\frac{h_1^n}{h_1^n+h_2^n+\alpha h_1^n{h}_2^n}{R}_1\left({\theta }_1\right)+\frac{h_2^n}{h_1^n+h_2^n+\alpha h_1^n{h}_2^n}{R}_2\left({\theta }_2\right)\mathrm{.}$$ (9)

Under the equal-coherence condition and when the motion coherence was 100% (i.e., one), the exponent n became irrelevant. The DivNorm model essentially had just one free parameter, α. Nevertheless, this one-parameter model accounted for on average 78.7% of the variance of the responses elicited by the bidirectional stimuli. The goodness of fit of the DivNorm model was slightly, yet significantly better than that of the CohNorm model (Table 1; 1-tailed paired t-test, P = 0.019). Under the different-coherence condition, both n and α were free parameters; the simplified model accounted for 83.5% of the response variance, which was not significantly different from that of the CohNorm model fits (Table 1).

Given that the SNL model provided a significantly better fit than the LWS model, we added a nonlinear interaction term to the DivNorm model. The resultant model is referred to as the normalization plus nonlinear interaction (NNL) model (Eq. 10). Again, the parameter b is a coefficient determining the sign and strength of the nonlinear interaction between the component responses of the neuron. The goodness of fit of the NNL model was better than the LWS and DivNorm models and was slightly worse than the SNL model (Table 1).

$$R_{{12}_{pred}}\left({\theta }_1,{\theta }_2\right)=\frac{h_1^n}{h_1^n+h_2^n+\alpha h_1^n{h}_2^n}{R}_1\left({\theta }_1\right)+\frac{h_2^n}{h_1^n+h_2^n+\alpha h_1^n{h}_2^n}{R}_2\left({\theta }_2\right)+b{R}_1\left({\theta }_1\right)R_2\left({\theta }_2\right)\mathrm{.}$$ (10)

For all the models, it was not necessary to vary the response weights as a function of the stimulus direction to account for the whole direction tuning curve. A fixed set of weights could well account for the bidirectional responses across motion directions, suggesting that the neural mechanism underlying the response weights can be invariant to the stimulus direction.

Relationship between bidirectional responses and the component responses across multiple levels of motion coherence.

To further understand the rule governing the responses elicited by multiple stimuli and how the response weights were determined, we examined the relationship between the bidirectional responses and the component responses across multiple levels of motion coherence. In this experiment, we set the direction of one stimulus component at the PD of the neuron (referred to as the PD component) and the other 90° away from the PD. We varied the motion coherence of the PD component from 60 to 100% and fixed the motion coherence of the orthogonal motion component at 100%.

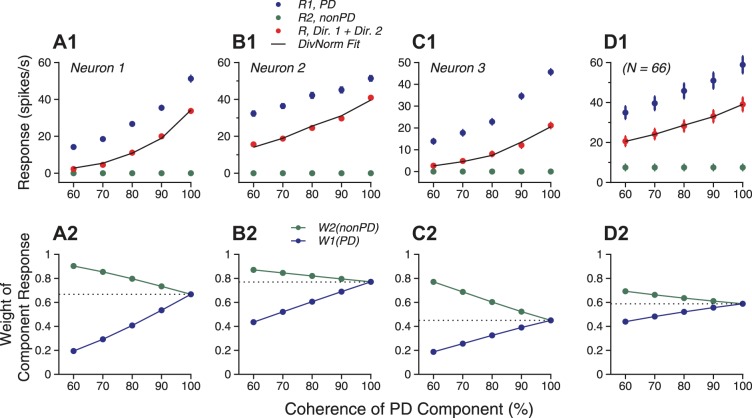
Figure 8 shows the results from three example neurons. As the coherence level of the PD component increased, the response to the bidirectional stimuli changed its magnitude relative to the component responses. Despite differences across individual neurons, a consistent trend was that the response to the PD component appeared to have an increasing contribution to the bidirectional response as the motion coherence of the PD component increased. This trend can also be seen from the population-averaged responses across 66 neurons (Fig. 8D1). In the LWS and SNL models, the response weights are fixed across stimulus conditions. It is therefore inappropriate to fit the results of this experiment using the LWS and SNL models. Instead, we fitted the responses using the normalization model, which allowed the response weights to vary with the motion coherence.

Fig. 8.

Responses of 3 example neurons and population-averaged responses elicited by the bidirectional stimuli as a function of the coherence level of the PD component (R₁). The coherence level of the orthogonal motion component (R₂) was fixed at 100%. A1–C1: firing rates of bidirectional responses and the corresponding component responses of 3 example neurons. D1: population-averaged responses. Error bars indicate SE. Solid lines are DivNorm model fits. A2–D2: corresponding to A1–D1, response weights for the 2 stimulus components obtained using the DivNorm model fits. The response weights in D2 were calculated on the basis of the population-averaged MT responses.

We found that MT responses to the bidirectional stimuli across multiple coherence levels could be well accounted for by the DivNorm model (Eq. 9), in which the response weight for a motion component is expressed as follows (Eqs. 11 and 12):

$$w_{PD}=\frac{h_{PD}^n}{h_{PD}^n+h_{orthogonal}^n+\alpha h_{PD}^n{h}_{orthogonal}^n}$$ (11)

$$w_{orthogonal}=\frac{h_{orthogonal}^n}{h_{PD}^n+h_{orthogonal}^n+\alpha h_{PD}^n{h}_{orthogonal}^n},$$ (12)

where w_PD and w_orthogonal are the response weights and h_PD and h_orthogonal are the motion coherence levels for the PD and orthogonal motion components, respectively. The DivNorm model provided excellent fits for the bidirectional responses of the three example neurons and the population averaged responses, accounting for greater than 98% of the response variance (Fig. 8, A1–D1). As the motion coherence of the PD component increased from 60 to 100%, the response weight for the PD component increased progressively (Fig. 8, A2–D2).

Across the population of 66 neurons, the DivNorm model provided good fits for the bidirectional responses as the motion coherence was varied. On average, the model accounted for 80.7% (SD 29.5) of the response variance. The population mean of the response weight for the PD component varied significantly as the motion coherence of the PD component changed (1-way ANOVA, F = 8.1, P = 3.1 × 10⁻⁶). The mean response weight for the PD component, averaged across the population of 66 neurons progressively increased from 0.39 to 0.60 as the motion coherence of the PD component increased from 60 to 100% (Fig. 9A). The median value of the exponent n of the DivNorm model fits was 1.04, suggesting a near-linear transformation between stimulus motion coherence and the magnitude of MT population response. Since different levels of motion coherence were randomly interleaved across trials, the change of the response weights occurred on the time scale of a single experimental trial. To determine how the response weight for the PD component changed with the motion coherence on a neuron-by-neuron basis, we fitted the response weights across five coherence levels for each neuron using linear regression. Figure 9B shows the distribution of the slope of the linear fit. The mean fitted slope was significantly positive (mean 0.51, SD 0.39; 1-tailed t-test, P = 4.2 × 10⁻¹⁶), indicating that the response weight for the PD component increased with its coherence.

Fig. 9.

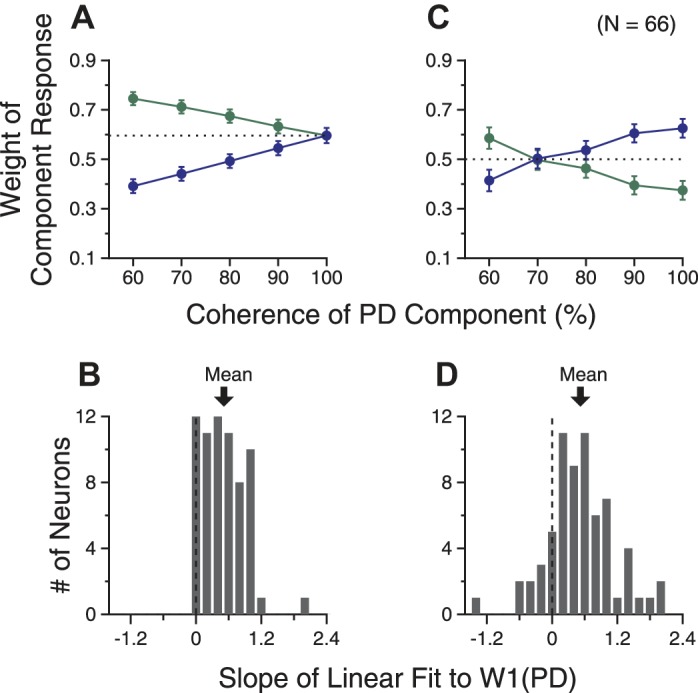
Response weights across multiple levels of motion coherence of a population of neurons. Results obtained using the DivNorm model fits are shown in A and B, whereas results calculated on the basis of the relative magnitudes of the bidirectional and the component responses (Eq. 13) are shown in C and D. A and C: averaged response weights as a function of the coherence level of the PD component. Error bars indicate SE. B and D: distribution of the slope of the linear fit of the response weights for the PD component across coherence levels.

For comparison, we also fitted the data using the CohNorm model (Eq. 7). The CohNorm model accounted for 72.1% (SD 36.0) of the response variance, significantly smaller than the mean of 80.7% of the DivNorm model (1-tailed paired t-test, P = 0.0015). When we allowed the DivNorm and CohNorm model to have an additional constant parameter that can be either positive or negative, as the parameter c in the LWS_C and SNL_C model (Eqs. 5 and 6), the variance accounted for by the DivNorm and CohNorm model increased to 87.3 and 82.3%, respectively. The variance accounted for by the DivNorm model was still significantly larger than that by the CohNorm model (1-tailed paired t-test, P = 0.0026).

The normalization model makes a specific assumption regarding how the response weights are determined by the relative levels of motion coherence (Eqs. 11 and 12). To verify whether the response weight for a stimulus component increased with its motion coherence, we used an additional approach to quantify the response weight that does not make any assumption regarding how the response weights change with the motion coherence. We calculated the response weight at each coherence level based on the relative magnitudes of the bidirectional response and the two component responses (Eq. 13):

$$R_{12}=\left(\frac{R_2-R_{12}}{R_2-R_1}\right)R_1+\left(\frac{R_{12}-R_1}{R_2-R_1}\right)R_2,$$ (13)

where R₁₂ is the bidirectional response, and R₁ and R₂ are the responses elicited by the PD and the orthogonal motion component, respectively. Therefore, the response weights are w_PD = (R₂ − R₁₂)/(R₂ − R₁) and w_orthogonal = (R₁₂ − R₁)/(R₂ − R₁). The response weights were determined by how close the bidirectional response was to one of the component responses, relative to the distance between the two component responses. If the bidirectional response was closer to one component response, that motion component had a higher weight than the other component. Note that the two response weights sum to 1. Since the right-hand side of Eq. 13 can be rearranged as

$$\frac{R_2{R}_1-R_{12}{R}_1+R_{12}{R}_2-R_1{R}_2}{R_2-R_1}=\frac{R_{12}(R_2-R_1)}{R_2-R_1}=R_{12},$$

Eq. 13 always holds as long as the two component responses R₁ and R₂ are not identical.

Figure 9C shows the averaged response weights across the neuron population obtained using Eq. 13. The mean weights for the PD component varied significantly as the motion coherence of the PD component changed (1-way ANOVA, F = 4.7, P = 0.001). The mean weight increased progressively from 0.41 to 0.63 as the motion coherence of the PD component increased from 60 to 100%, very similar to those obtained using the DivNorm model fits. We also fitted the response weights for the PD component across five coherence levels for each neuron using linear regression. The mean slope across the neuron population was 0.52, which was significantly positive (1-tailed t-test, P = 8.7 × 10⁻¹⁰; Fig. 9D) and almost the same as that obtained using the DivNorm model. These findings confirmed the results obtained using the DivNorm model, showing that the response weight for a stimulus component progressively increased with the coherence level of that stimulus component.

Direction tuning of neuronal responses to bidirectional stimuli moving at different luminance levels.

To test the generality that the response weights changed with the relative signal strengths, we next varied the luminance levels of the stimulus components and characterized the direction tuning curves elicited by the bidirectional stimuli. The luminance of the stimulus component moving at the clockwise side of the two component directions was 40 cd/m². The luminance of the stimulus component at the CC side was either 10 or 2.5 cd/m². Figure 10 shows the results from two example neurons. The tuning curve of the bidirectional response was biased toward the tuning curve of the higher-luminance component (i.e., the right side in the plot). The response bias was stronger when the luminance difference between the two stimulus components was larger (Fig. 10B). For these two neurons, the peak response elicited by the higher-luminance component was slightly weaker than that elicited by the lower-luminance component of 2.5 cd/m² (Fig. 10B). Nevertheless, this did not prevent the bidirectional response from showing a strong bias toward the response elicited by the higher-luminance component, suggesting that the response bias was not determined by the component responses of a single neuron. Across the neuron population, the mean peak firing rates to the stimulus components of 2.5, 10, and 40 cd/m² were 68.5 (N = 30), 72.1, and 75.8 Hz (N = 38), respectively, showing a modest increase with the luminance. The normalized and population-averaged tuning curve elicited by the bidirectional stimuli was also biased toward the response tuning elicited by the higher-luminance component (Fig. 11). The bias was stronger when the luminance difference between the two stimulus components was larger.

Fig. 10.

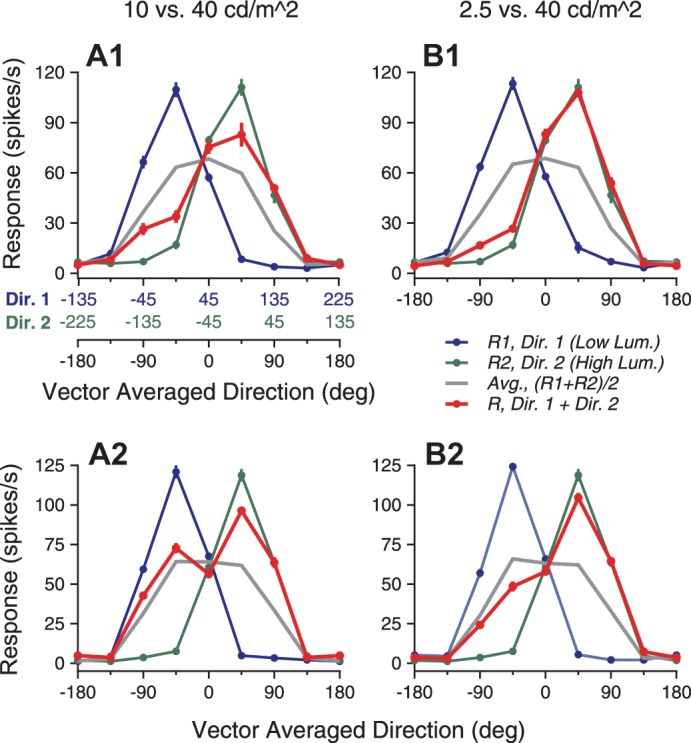
Direction tuning curves of 2 example neurons elicited by bidirectional stimuli and the stimulus components that had different luminance levels. The higher luminance of the 2 stimulus components was 40 cd/m². A1 and A2 (left) and B1 and B2 (right) show results when the lower luminance was 10 and 2.5 cd/m², respectively. The higher-luminance component always moved at the clockwise side of the 2 component directions. The convention of abscissas is the same as in Fig. 1. A1 and B1: response tuning curves of 1 example neuron. A2 and B2: responses of another example neuron. Lum., luminance.

Fig. 11.

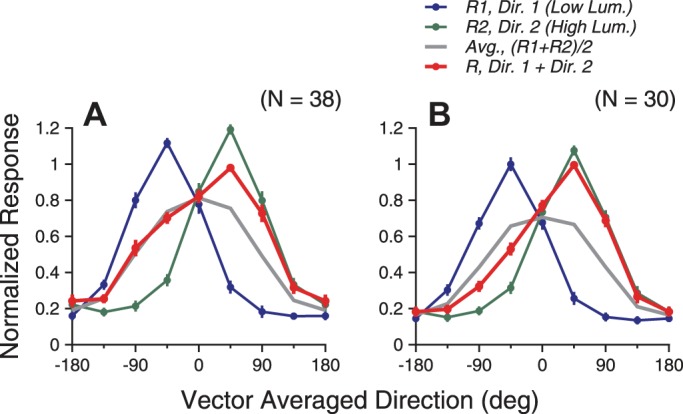
Population-averaged tuning curves elicited by bidirectional stimuli and the stimulus components that had different luminance levels. Before averaging, VA direction of 0° was aligned with the PD for each neuron and neuronal responses were normalized to the maximum bidirectional response. The higher luminance of the two stimulus components was 40 cd/m², and the higher-luminance component moved at the clockwise side of the 2 component directions. The lower luminance of the 2 stimulus components was 10 cd/m² in A and 2.5 cd/m² in B.

The tuning curves of neuronal responses elicited by the bidirectional stimuli were well accounted for by a weighted sum of the component responses (Fig. 12). The LWS model accounted for ≥91% of the variance for the two example neurons and the population-averaged response. The LWS model accounted for on average 93.0% (SD 6.6) of the variance when the lower luminance was 10 cd/m², and 94.2% (SD 4.8) when the lower luminance was 2.5 cd/m².

Fig. 12.

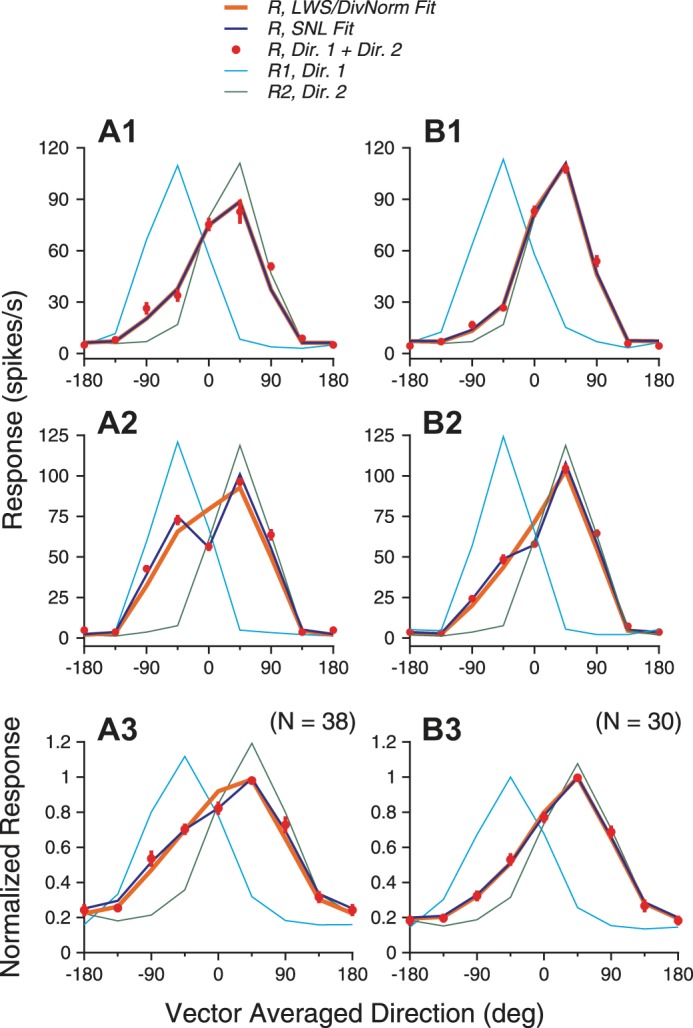
Model fits of response tuning curves elicited by bidirectional stimuli moving at different luminance levels. A1–A3 (left) and B1–B3 (right) show results when the luminance levels of the 2 stimulus components were 10 vs. 40 cd/m² and 2.5 vs. 40 cd/m², respectively. The DivNorm model fits gave the same results as the LWS fits. A1 and B1: example neuron 1. The 3 models, LWS, DivNorm, and SNL, provided almost identical fits. A2 and B2: example neuron 2. The SNL model provided better fits than the LWS or DivNorm models. Including response nonlinearity increased the variance accounted for from 91.0% (LWS/DivNorm) to 98.8% (SNL) when the lower luminance was 10 cd/m² and increased the variance from 96.8% (LWS/DivNorm) to 99.5% (SNL) when the lower luminance was 2.5 cd/m². A3 and B3: model fits of the population-averaged tuning curves. Error bars of the bidirectional responses indicate SE.

We also fitted the data using the DivNorm model, replacing motion coherence h in Eq. 9 with the luminance (L) of the stimulus component. The DivNorm model gave rise to almost identical fitting results as the LWS model, accounting for 92.9% (SD 6.8) of the response variance. We also fitted the data by replacing motion coherence h in the CohNorm model (Eq. 7) with the luminance L and obtained very similar fitting results as the DivNorm model.

Using the SNL model that allowed nonlinear interactions between the component responses improved the goodness of fit (e.g., Fig. 12, A2 and B2). On average, the SNL model accounted for 96.5% (SD 4.2) of the variance when the lower luminance was 10 cd/m², and 96.1% (SD 3.6) of the variance when the lower luminance was 2.5 cd/m².

The response weights for the higher-luminance component were significantly greater than those for the lower-luminance component (Fig. 13). With the use of the LWS fits, the median response weight for the higher-luminance component was 0.74, significantly different from that for the lower-luminance component of 0.39 (N = 38, signed-rank test, P = 9.8 × 10⁻⁸) when the luminance levels of the two stimulus components were 10 and 40 cd/m². As the luminance difference between the two motion components increased, the response weight for the higher-luminance component further increased and the weight for the lower-luminance component decreased. When the luminance levels of the stimulus components were 2.5 and 40 cd/m², the median response weight for the higher-luminance component was 0.86, significantly different from that for the lower-luminance component of 0.27 (N = 30, signed-rank test, P = 1.7 × 10⁻⁶). We found the same results when the response weights were obtained using the SNL fits (signed-rank test, P < 1.8 × 10⁻⁶). These results indicate that MT neurons weighted the component response elicited by the higher-luminance component more strongly. Again, a fixed set of response weights could account for the bidirectional responses across all stimulus directions when the two stimulus components differed in their luminance, suggesting that the neural mechanism underlying the response weights can be invariant to the stimulus direction.

Fig. 13.

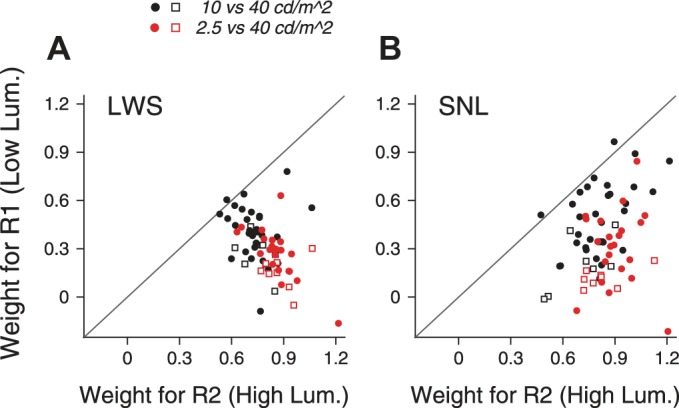
Response weights for the 2 motion components that had different luminance levels. A: response weights obtained using the LWS fits. B: response weights obtained using the SNL fits. When the lower luminance was 10 cd/m², the median response weights for the higher- and lower-luminance components obtained using the SNL fits were 0.79 and 0.43, respectively. When the lower luminance was 2.5 cd/m², the median response weights for the higher- and lower-luminance components were 0.87 and 0.23, respectively. Filled circles show results from monkey BJ; open squares show results from monkey RG.

DISCUSSION

We have examined how overlapping moving stimuli that have the same or different signal strengths interact within the RFs of neurons in the extrastriate area MT. Our principle finding is that, across signal strengths and motion directions, neuronal responses elicited by multiple stimuli moving in different directions can be well accounted for by a sublinearly weighted sum of the neuronal responses elicited by the stimulus components, plus a nonlinear interaction term between the component responses that typically has a suppressive effect on the neuronal response. Importantly, rather than always weight each stimulus component equally, MT neurons weight the stimulus component that has the higher signal strength more strongly, regardless of whether the signal strength is defined by motion coherence or luminance contrast.

Weighting component responses according to signal strengths.

Our results are consistent with previous findings made in V1 using oriented gratings and in the dorsal medial superior temporal area (MSTd) using multisensory stimuli. Responses of V1 neurons elicited by overlapping gratings follow a weighted sum of the component responses, and the response weight is stronger for the stimulus component that has a higher luminance contrast (Busse et al. 2009; MacEvoy et al. 2009). In MSTd, responses of multisensory neurons elicited by optical flow and vestibular self-motion cues also follow a weighted sum of the component responses, and the response weights change with the relative reliabilities of the visual and vestibular cues (Fetsch et al. 2011; Morgan et al. 2008). Our study provides new evidence supporting a general rule governing how neurons respond to multiple stimuli within their RFs. It appears that neurons weight the responses elicited by the constituent stimuli according to their signal strengths, weighting the stimulus component that has the higher signal strength more strongly. This scheme of selective weighting helps to make the stimulus that has the higher signal strength more salient and suppress the stimulus that has the weaker signal strength, implementing a type of stimulus competition useful for noise reduction and image segmentation.

When multiple stimuli are integrated to generate a single-valued behavioral output, weighting according to the signal strength would lead to a behavior that strongly favors the stimulus component having the higher signal strength. For multisensory integration, weighting multimodal cues according to their signal strengths gives rise to a perceived heading direction that is shifted toward the more reliable cue, and such a scheme may provide a near optimal solution for multisensory cue integration (Fetsch et al. 2011; Morgan et al. 2008). In the case of smooth pursuit (see Lisberger 2010 for a review), when two pursuit targets moving in different directions have the same luminance, the initiation of pursuit follows the vector-averaged direction of the two targets (Lisberger and Ferrera 1997). However, when two overlapping patches of moving random-dots have different levels of luminance, the initiation of pursuit is strongly biased toward the direction of the brighter random-dot patch, showing an effect of winner-take-all (Niu and Lisberger 2011). Our finding that the direction tuning curves of MT neurons elicited by overlapping stimuli are strongly biased toward the response elicited by the higher-luminance component provides a likely physiological basis for the pursuit behavior reported by Niu and Lisberger (2011). Since we have found that response weighting also depends on relative motion coherence, our results predict that when overlapping pursuit targets move at different levels of coherence, the initiation of pursuit should bias toward the direction of the higher-coherence component.

Divisive normalization and population neural response.

Response normalization in the extrastriate area MT has been suggested previously (Britten and Heuer, 1999; Heuer and Britten 2002; Lee and Maunsell 2009; Ni et al. 2012; Simoncelli and Heeger 1998). Our study using multiple stimuli with different signal strengths provides new constraints for models of response normalization. We have shown that in area MT the changes of response weights with relative signal strengths can be accounted for as the signal strengths of individual stimulus components divisively normalized by a combination of the signal strengths of all stimulus components. Our results are consistent with the findings that the changes of response weights in V1 with relative stimulus contrasts can be accounted for by a contrast normalization model (Busse et al. 2009; Carandini et al. 1997), and the changes of response weights of multisensory neurons in MSTd with relative reliabilities of visual and vestibular cues can also be explained by a divisive normalization model (Ohshiro et al. 2011).

For a given MT neuron, its response weights to two stimulus components are not determined by the single neuron's response magnitudes elicited by the stimulus components, but rather by the relative signal strengths of the stimulus components. For example, the response magnitude of an MT neuron elicited by a low-coherence stimulus component moving in the PD of the neuron is typically greater than the neuron's response elicited by a high-coherence component moving in the orthogonal direction. However, the neuron may still show a larger response weight for the high-coherence orthogonal component than the low-coherence PD component (e.g., see Fig. 8, A1 and C1). Moreover, the tuning curve of an MT neuron elicited by the bidirectional stimuli tends to show a strong bias toward the stimulus component that had a higher luminance contrast, even when the single neuron's peak responses elicited by the stimulus components with different luminance contrasts are similar (e.g., see Fig. 10).

In our data, the population-averaged response of MT neurons increases modestly with the stimulus luminance, which is consistent with previous reports of MT contrast response functions within a range of high luminance contrast (Cheng et al. 1994; Heuer and Britten 2002; Sclar et al. 1990). The population-averaged response of MT neurons also increases robustly with the motion coherence (Britten et al. 1992, 1993; and our results shown in Fig. 8D1). These findings are consistent with the idea that the response weight is determined by the activity of a population of neurons that reflects the signal strength of the visual stimuli.

In the normalization models proposed by Heeger (1992), Simoncelli and Heeger (1998), and Ohshiro et al. (2011), the linear inputs that a neuron receive are divisively normalized by the summed activity of a population of neurons, referred to as the normalization pool. Unlike those models, we did not directly compute the summed activity of a population of neurons as the denominator for normalization. Instead, we used a combination of the signal strengths of the stimulus components in the denominator to represent the population neural response. Our model is similar to the contrast normalization model (Busse et al. 2009; Carandini et al. 1997), with a notable difference. We used a linear combination of the power law-transformed signal strengths plus a multiplicative interaction term in the denominator to represent the activity of a population of neurons evoked by multiple, simultaneously presented stimuli. The denominator in our model does not reflect the “overall” signal strength of multiple stimuli. Our choice of the model was motivated by the success of the SNL model in describing MT neuronal responses elicited by bidirectional stimuli. Because the nonlinear interaction term can have either a facilitatory or suppressive effect on the population neural response, our DivNorm model has more flexibility in capturing the population neural response and provided a better goodness of fit than the CohNorm model when fitting the data obtained using stimuli with multiple levels of motion coherence.

The idea that the response weights are determined by the population neural responses makes a testable prediction: the response weight for a stimulus component should increase (or decrease) when the population neural response evoked by that stimulus component is enhanced (or suppressed). A recent study using optical imaging to record population neural responses from slices of rodent superior colliculus and dual-site electrical stimulations provided some support of this prediction (Vokoun et al. 2014).

Nonlinear interaction between component responses.

The success of the SNL and NNL model in fitting our data suggests that multiplicative interactions between the component responses may play an important role in shaping the response tuning for multiple stimuli. Because the product of component responses depends on the component directions, multiplicative nonlinearity can therefore exert a tuned effect on MT responses. We have found that the nonlinear interaction often has a suppressive effect on neuronal responses, and the suppression is most prominent when both component responses are strong. Multiplicative computation has been proposed in a variety of neural models and is thought to be important for sensory processing (Barlow and Levick 1965; Gabbiani et al. 2004; Pena and Konishi 2001; Sun and Frost 1998). Possible neural implementation of multiplicative computation has been demonstrated before (e.g., Gabbiani et al. 2002), although the neural mechanism underlying multiplication and how multiplication engages suppression are not yet clear.

The SNL model was previously used to fit the responses of multisensory neurons in MSTd (Morgan et al. 2008) and the responses of MT neurons that integrate velocity and disparity gradient cues of three-dimensional surface orientation (Sanada et al. 2012). Although the previous studies showed that the SNL model provided a better fit than the LWS model, the improvement was modest, explaining an additional 1% of the response variance for the MSTd data (Morgan et al. 2008) and significantly improved data fitting for only 14% of neurons for the MT data (Sanada et al. 2012). In our study, the benefit of the SNL model was the largest under the equal-coherence condition, explaining an additional 6% of the response variance and significantly improving the data fit for about half of the neurons. A possible explanation for the discrepancy between our results and the previous studies is that, in our study, both component responses can be strong when the VA direction is close to a neuron's PD under the equal-coherence condition, giving rise to a large product. It is also possible that the nature of the stimuli may contribute to the discrepancy: our stimuli are consistent with perceptual segmentation (Braddick et al. 2002), whereas in previous studies (Morgan et al. 2008; Sandada et al. 2012) different cues were integrated to form a single percept of heading direction or surface orientation, at least when different cues are congruent.

Tuned normalization and normalization pool.

It has been proposed that divisive normalization may be tuned to visual stimuli such that different stimuli may have different contributions to normalization (Carandini et al. 1997; Ni et al. 2012; Rust et al. 2006). In our data, it may seem that the population-averaged response tuning curves are consistent with the idea of tuned normalization: at some stimulus directions, the bidirectional response is closer to the stronger component response, and at other stimulus directions, the bidirectional response roughly follows the average of the component responses (e.g., see Fig. 2). However, our model fitting showed that using a weighted sum of the component responses with a fixed set of weights plus a nonlinear interaction term could well account for MT responses across different motion directions. To explain our data, it was not necessary to assume a mechanism that gives rise to different response weights at different stimulus directions. Our findings of fixed response weights across motion directions are consistent with the idea that the normalization pool includes neurons tuned to all motion directions, and therefore the neural activity of the normalization pool is invariant to the stimulus direction (Carandini et al. 1997; Simoncelli and Heeger 1998).

Consistent with previous reports (Ni et al. 2012; Qian and Andersen 1994), we have also found that the bidirectional responses of MT neurons are quite variable and can follow the average of the component responses, the stronger (or weaker) component response, or anywhere in between. This phenomenon can be explained by adding a parameter in the denominator of a normalization model that adjusts the relative contributions of different stimuli to normalization (see Eq. 2 in Ni et al. 2012; also see Carandini et al. 1997). However, we have found that the broad spectrum of the response weights across MT neurons can be explained by varying the sign and magnitude of the coefficient α of the nonlinear interaction term in the denominator (see our Eqs. 8–10). Although our results do not rule out tuned normalization, they suggest another possibility involving nonlinear interactions between the component responses to set the response weights differently across neurons.

Depending on the nature of visual stimuli, how multiple stimuli interact within neurons' RFs to influence neuronal responses may be more complicated than reported in this study. Krekelberg and van Wezel (2013) recorded responses of MT neurons using random-dot stimuli moving in opposite directions and found that the speed tuning curves of many MT neurons elicited by the bidirectional stimuli cannot be accounted for by a normalization model. It is possible that the interaction between stimulus components across motion speeds may differ from that across motion directions. Other factors such as adaptation (Patterson et al. 2014) and whether multiple stimuli give rise to integrated or segmented perception (Stoner and Albright 1992) may also influence the relationship between the responses elicited by multiple stimuli and the stimulus components. Understanding the neural computation underlying how multiple stimuli interact across a wide range of stimulus and perceptual conditions is likely to provide valuable insights into the operations of cortical circuits and sensory processing.

GRANTS

This research was supported by the University of Wisconsin-Madison and National Eye Institute Grant R01 EY022443.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at the institutional website of one of the authors, which at the time of publication they indicate is: http://www.neuro.wisc.edu/xhpub2014/. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

AUTHOR CONTRIBUTIONS

J.X., Y.N., and X.H. conception and design of research; J.X., Y.N., S.W., and X.H. performed experiments; J.X. and X.H. analyzed data; J.X. and X.H. interpreted results of experiments; J.X. and X.H. prepared figures; J.X., Y.N., S.W., and X.H. approved final version of manuscript; X.H. drafted manuscript; X.H. edited and revised manuscript.