Improved DTI registration allows voxel-based analysis that outperforms Tract-Based Spatial Statistics

Abstract

Tract-Based Spatial Statistics (TBSS) is a popular software pipeline to coregister sets of diffusion tensor Fractional Anisotropy (FA) images for performing voxel-wise comparisons. It is primarily defined by its skeleton projection step intended to reduce effects of local misregistration. A white matter “skeleton” is computed by morphological thinning of the inter-subject mean FA, and then all voxels are projected to the nearest location on this skeleton. Here we investigate several enhancements to the TBSS pipeline based on recent advances in registration for other modalities, principally based on groupwise registration with the ANTS-SyN algorithm. We validate these enhancements using simulation experiments with synthetically-modified images. When used with these enhancements, we discover that TBSS's skeleton projection step actually reduces algorithm accuracy, as the improved registration leaves fewer errors to warrant correction, and the effects of this projection's compromises become stronger than those of its benefits. In our experiments, our proposed pipeline without skeleton projection is more sensitive for detecting true changes and has greater specificity in resisting false positives from misregistration. We also present comparative results of the proposed and traditional methods, both with and without the skeleton projection step, on three real-life datasets: two comparing differing populations of Alzheimer's disease patients to matched controls, and one comparing progressive supranuclear palsy patients to matched controls. The proposed pipeline produces more plausible results according to each disease's pathophysiology.

Introduction

Diffusion Tensor Magnetic Resonance Images (DTI) measure directional water diffusion in each image voxel (Le Bihan et al., 1986). Because water primarily diffuses along white matter (WM) bundles, DTI can image WM structure, earning the attention of aging and dementia researchers (Carmichael and Lockhart, 2012; Stebbins and Murphy, 2009; Sullivan et al., 2006). Fractional Anisotropy (FA) is an important DTI-derived measure of per-voxel diffusion directionality strength (Pierpaoli and Basser, 1996), often employed as a proxy measure of WM integrity (Douaud et al., 2011; Jahanshad et al., 2013; Kohannim et al., 2012).

The most straightforward approach to calculate local image comparisons across subject groups is to coregister all subjects and perform statistical tests for groupwise differences in each coregistered voxel, a method known in analysis of structural MRI as Voxel-Based Morphometry (VBM). Originally designed to measure longitudinal gray-matter (GM) changes, VBM-style analysis or Voxel-based analysis (VBA) is highly sensitive to registration errors and may produce false positives in affected regions (Ashburner and Friston, 2000; Bookstein, 2001). For the particularly challenging application of coregistering DTI-FA images, Smith et al. introduced Tract-Based Spatial Statistics (TBSS), which attempts to reduce the effects of local misregistrations by projecting all FA voxels onto the nearest location on a “skeleton” approximating WM tract centers (Smith et al., 2006). TBSS has been widely adopted using the original authors' implementation provided in the FMRIB Software Library (FSL) (Jenkinson et al., 2012), although several recent studies have continued to use standard VBA instead of or in addition to TBSS (Chiang et al., 2011; Douaud et al., 2011; Kohannim et al., 2012).

Several recent publications have evaluated updating the TBSS processing pipeline with contemporary advancements in registration techniques. De Groot et al. investigated replacing TBSS's two-step registration-projection approach with a single registration step where performance metrics were constrained to the skeleton, and they demonstrated improved coregistration by this approach (De Groot et al., 2013). Keihaninejad et al. proposed groupwise registration for coregistering FA images to a custom-generated template, rather than by either coregistering all images to a standard template, or calculating the most representative subject, both of which are available in the standard TBSS implementation. These authors also developed and presented simulation experiments that evaluate the entire TBSS pipeline, rather than only the coregistration step, and used them to provide a region-based demonstration of their modifications' improved sensitivity and specificity of groupwise comparisons (Keihaninejad et al., 2012).

Although TBSS's skeleton projection was designed to compensate for local registration errors, it has been demonstrated using a series of simulated misregistration experiments that this process reduces the magnitude of such errors by at most 10% (Zalesky, 2011). Unfortunately, skeleton projection involves many compromises in return for these limited benefits. Voxels further from tract centers have decreased weighting in the average of voxels projected to that location (Smith et al., 2006), and detection of changes in such locations is consequently reduced. Furthermore, because each voxel is projected to the nearest skeleton location, regions centered between two skeleton points can be artificially split over multiple disparate anatomical locations (De Groot et al., 2013; Zalesky, 2011). These projections make results difficult to interpret because displayed findings may actually be driven by voxels elsewhere. These and other TBSS limitations are detailed in Zalesky (2011). White Matter Hyperintensities and other FA-reducing abnormalities, common in elderly subjects, are also particularly problematic because they can violate TBSS's assumption that local FA maxima are anatomical WM tract centers (Jones and Cercignani, 2010). TBSS also causes preferential sensitivity to detecting changes in diagonally-oriented tracts because skeletonized diagonal tracts are thicker in voxel-space than horizontal or vertical ones (Edden and Jones, 2011).

Because of these tradeoffs, we hypothesize that it may be desirable to omit skeleton projection if registration is improved to a point where they outweigh its benefits. While prior publications have examined limitations of TBSS (De Groot et al., 2013; Edden and Jones, 2011; Jones and Cercignani, 2010; Zalesky, 2011) and improved its coregistration (De Groot et al., 2013; Keihaninejad et al., 2012), to our knowledge no existing research has quantitatively evaluated effects of registration improvements on TBSS or tested whether such improvements remove the benefits of creating a skeleton space.

In this work, we propose substantial changes to multiple components of the popular TBSS software pipeline that incorporate advancements from other applications of VBA. We employ simulation experiments to test our proposed pipeline against the original TBSS pipeline included with FSL and validate its benefits. We then test each pipeline both with and without TBSS's definitive skeleton-projection step, and we test whether or not the sum of our proposed improvements renders its use more harmful than helpful. For this comparison and validation, we use synthetic data experiments from prior work (Keihaninejad et al., 2012), extended to provide quantitative measurements of sensitivity and speci-ficity. We also present the proposed pipelines' results for three different datasets: two comparing patients with clinically-diagnosed Alzheimer's disease (AD) to matched cognitively normal controls (CN), and one comparing patients with progressive supranuclear palsy (PSP) to CN.

Methods

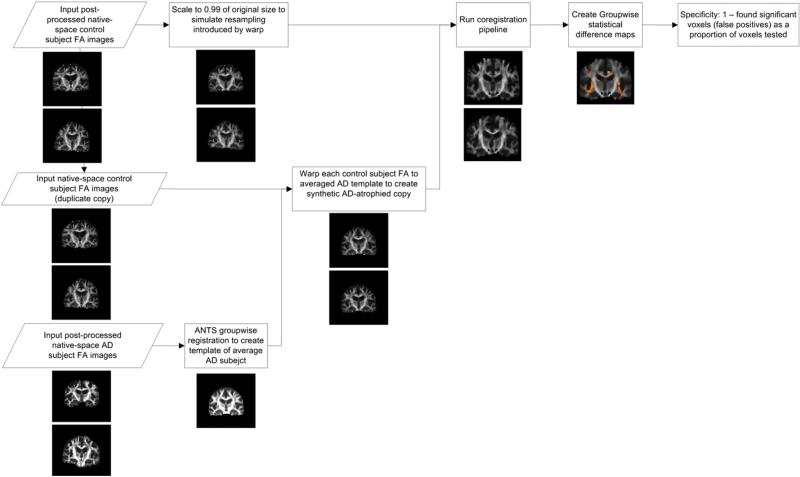
In this section, we describe each difference between the standard TBSS pipeline and our proposed ANTS-Groupwise pipeline (ANTS-GW), which we compare experimentally in this work. We provide a flowchart with the steps of the original TBSS in Fig. 1, and in Table 1 we present the differences between tested pipeline variants: FSL TBSS, ANTS-Groupwise (ANTS-GW) TBSS, FSL VBA, and ANTS-GW VBA. Those pipelines marked TBSS include the skeleton projection step, where those marked VBA do not. Unless otherwise specified, our tests of FSL TBSS and its components used FSL version 5.0 with the same parameters as in its included tbss_* series of scripts.

Fig. 1.

Steps of original FSL TBSS Pipeline, with example images.

Table 1.

Methodological differences between analysis pipelines.

Pipeline name/differences	1: Erosion kernel	2: Registration algorithm	3: Registration targets	4: Transforming to standard space	5: Masking of voxels	6: Skeleton projection
FSL TBSS	3 × 3 × 3	FNIRT	Most-representative subject	Affine registration (FLIRT)	Voxels in all subjects	Yes
ANTS-GW TBSS	3 × 3 × 1	ANTS SyN	ANTS groupwise Template	Nonlinear registration	Voxels in ≥ 50% of subjects	Yes
FSL VBA	3 × 3 × 3	FNIRT	Most-representative subject	Affine registration (FLIRT)	Voxels in all subjects	No
ANTS-GW VBA	3 × 3 × 1	ANTS SyN	ANTS groupwise Template	Nonlinear registration	Voxels in ≥ 50% of subjects	No

Preprocessing

Each diffusion image was acquired using 3 T scanners and corrected for subject motion and residual eddy current distortion by affine-registering each volume to the first (an undiffused) volume in the acquisition. FSL 4's Brain Extraction Tool (bet) program was used to exclude voxels outside the braincase, and diffusion tensors were fit for the remaining voxels using linear least squares optimization. FA images were calculated from the eigenvalues of the tensors without any modi-fications to reject negative eigenvalues (Jenkinson et al., 2012).

Difference 1: Erosion kernel

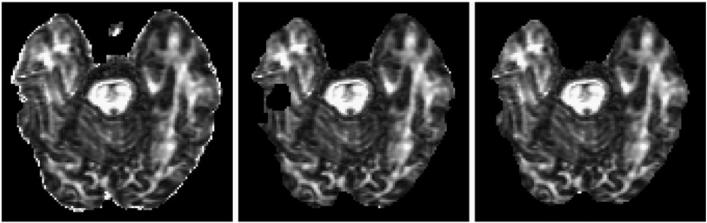
FSL TBSS and our proposed pipelines all operate on sets of FA images. For preprocessing, the standard implementation tbss_1_preproc performs binary erosion with a 3 × 3 × 3 voxel kernel. We hypothesize that this step was designed to remove the thin “halo” of bright voxels that typically surround the brain in FA images due to eddy current-induced distortions in cerebrospinal fluid (CSF) voxels (Bastin, 1999; Jones and Cercignani, 2010), but we noticed that in our data it commonly removed legitimate WM. The large slice thickness (2.7 mm) of our DTI acquisitions makes a 3 × 3 × 3 voxel kernel suboptimal, often removing much of the midbrain, brainstem, and parts of the temporal lobe. Although our acquisitions are nominally isotropic, because of zero-padding in k-space the voxels 1.35 × 1.25 × 2.7 mm are smaller in the x and y directions. In our modified pipelines, we replace this step with a 3 × 3 × 1 voxel intra-slice erosion. For our data, this mostly removes “halo” voxels while retaining more midbrain and temporal lobe structures. See Fig. 2. This change is made in the proposed ANTS-GW pipelines, while the FSL pipelines retain their original erosion step.

Fig. 2.

Left: Original unprocessed image showing “Halo” artifact around outside of brain Center: Standard FSL TBSS preprocessing applied, leaving “hole” in brain. Right: Proposed slicewise erosion applied, preserving “hole” location.

Difference 2: Registration algorithm

FSL TBSS uses the FSL's included linear and nonlinear registration algorithms: FLIRT and FNIRT respectively (Andersson et al., 2008; Jenkinson et al., 2002). Recently an independent analysis (Klein et al., 2009) compared these algorithms to Advanced Normalization Tools (ANTS) (Avants et al., 2008) and found the latter to give generally superior registration performance in a variety of T1-weighted MR registration tasks and metrics when compared to FNIRT and 13 other algorithms. Others have also found ANTS superior to FNIRT specifically for FA coregistration, and they presented arguments why the sum-of-squared-differences (SSD) metric used by FNIRT may introduce a statistical bias when used before voxel-based analysis (Tustison et al., 2014). Here, we test whether replacing the registration components of the TBSS pipeline with ANTS equivalents provides advantages. We used ANTS version 1.9.y with the cross-correlation cost function for all registrations in our proposed ANTS-GW pipelines, which we compared to the FSL pipelines using FLIRT/FNIRT. Both algorithms were used with their default settings and interpolation schemes unless otherwise specified.

Difference 3: Registration targets

Many strategies exist to coregister image sets to a common space. For example, each image may be pairwise-warped to a standard template space e.g. MNI, or to a study-specific template, or to a single chosen image within the set. The standard FSL TBSS pipeline includes all of these options, automatically choosing as a target in the latter case the image with the smallest average deformation to all others, i.e. the most representative subject (MRS).

For our proposed ANTS-GW pipelines, we extend the work of (Keihaninejad et al., 2012) by using a similar groupwise registration implementation to generate a study-specific template from all inputs in their native space. Groupwise registration iteratively coregisters image sets by alternating between registering each image to a shape-based mean of the inputs and recomputing this target as the mean over the coregistered set. The generated template has the same resolution and voxel space as the original inputs and can be used as a registration target for VBA or TBSS, rather than a standard template or MRS target. Creating a groupwise template also requires less computation than MRS, requiring O(n) pairwise registrations instead of O(n²).

For groupwise registration we use the buildtemplateparallel.sh script in the ANTS software package version 1.9.y (Avants and Gee, 2004; Avants et al., 2011) in place of the MRS algorithm in tbss_2_reg in FSL TBSS. We use the default of four nonlinear registration iterations, plus one initial iteration with rigid registration, because further iterations did not empirically provide additional visual clarity of the created templates. We compare this modified coregistration strategy in our ANTS-GW pipelines to the MRS algorithm in the traditional FSL pipelines.

Difference 4: Transforming to standard space

In FSL TBSS, the coregistration target is affine-aligned via FLIRT to an included FA template known as FMRIB58_FA_1mm. All coregistered images are then upsampled to this standard space for voxel-wise calculations. In our ANTS-GW pipelines, we use the ANTS-SyN algorithm to nonlinearly warp its groupwise template to FMRIB58_FA_1mm and similarly perform analyses in this space. We chose nonlinear registration, rather than affine alignment or simply remaining in the native coregistered voxel space, because it empirically provided the highest sensitivity and specificity in our simulations (slightly better than affine). While we hypothesize that improvements by affine alignment to the higher-resolution standard space are due to upsampling, the further gains by using nonlinear registration were very small, and so future experiments would be needed to confirm the significance of this particular choice. For space reasons we present these comparisons only in supplementary material. In all pipelines, the coregistration and upsampling to standard-space transformations for each image are combined before applying to prevent extra resampling.

Difference 5: Masking of voxels

In any VBA, one must determine a set of voxels to be analyzed. In FSL TBSS, this occurs during the tbss_3_postreg script, where voxels are only included if nonzero in all coregistered preprocessed subjects. This strategy is an accepted standard (Ashburner and Friston, 2000), but it allows a single outlier to exclude a voxel from comparison in all subjects. Because this step occurs after preprocessing, it strongly exacerbates the issue addressed in Difference 1, as superfluously-removed voxels in one subject are then removed from all subjects. As the size of the dataset n increases, the number of outliers tends to increase proportionally, and so superfluous removals are also proportional to n. In our experiments, this step frequently removed most of the brainstem and midbrain from analyses.

Prior VBM literature has described these issues as particularly problematic for atrophied brains (Ridgway et al., 2009), prevalent in all datasets in this work. Alternative masking options have been proposed for VBM-style analyses that include voxels if they are nonzero in at least some chosen proportion of subjects (Ridgway et al., 2009; Vemuri et al., 2008). We empirically evaluated a range of thresholds and determined that results were qualitatively identical in a range of 30–70%, and so chose 50% for our implementation. We employ this strategy in our proposed ANTS-GW pipelines, and we present a comparative example in Fig. 3. Quantitative analysis of this difference is also provided in supplementary material.

Fig. 3.

Top: Mean FA image of 60 subjects coregistered by the FSL TBSS pipeline and masked in its standard method of removing all voxels that are zero in at least one subject. Bottom: The same image, masked in the proposed method of removing only voxels that are zero in more than half of subjects. Note that “holes” in WM are prevented, and much more of the midbrain is left intact.

In tested VBA pipelines (those omitting skeletonization), we follow the standard set by other studies of additionally removing voxels where the mean FA across subjects is below 0.2, as this restricts analysis to mostly-WM regions (Chiang et al., 2011; Smith et al., 2006).

Difference 6: Skeleton projection

As we reviewed earlier, TBSS's definitive skeleton projection step requires many compromises in return for its limited compensation for registration errors. Thus we evaluate whether this step's cons outweigh its pros, particularly when used within pipelines that offer improved coregistration and thus have fewer errors to require compensation, by comparing pipelines that differ only by its inclusion or omission. In our experiments, pipelines that use skeleton projection are denoted by TBSS, where those that omit it are denoted by VBA, since without this step TBSS becomes essentially standard VBA. In the VBA pipelines, this skeletonization step is replaced with a Gaussian blur, which is standard in VBA to increase the Gaussianity of the data (Ashburner and Friston, 2000). For this we use the fslmaths program with a sigma of 1 mm. For TBSS pipelines' skeleton projection we use a skeleton threshold of 0.20 because empirically it produced skeletons that mostly include WM while mostly omitting GM. This value is also suggested by the original authors (Smith et al., 2006). We also examined additional variants where skeletonization was applied as a simple voxel mask without projection; these experiments are presented in the supplementary material.

Statistical calculations and correction for multiple comparisons

As in standard FSL TBSS, we use FSL's randomise for per-voxel statistical comparisons. For consistency with most related literature, we use the threshold-free cluster enhancement (TFCE) option for all analyses (Smith and Nichols, 2009). We use the defaults suggested in the standard FSL tbss_4_prestats script for randomise, with the exception of changing the -T2 parameter to -T in VBA pipelines, optimizing TFCE for 3D rather than 2D data. We report all results with a significance threshold of p < 0.05. Prior TBSS studies vary in whether results are reported with or without correction for multiple comparisons via Family-Wise Error (FWE) (Keihaninejad et al., 2012), so we explore and quantify the effects of this option by reporting our results in both ways.

Experiments

In this section we describe our experimental datasets and the designs of the simulation studies that provide the sensitivity and specificity metrics driving our major conclusions and the real-life data experiments on which we compare results with visual assessment.

Study subjects

Mayo AD–CN dataset

We identified a total of 30 AD subjects and 30 age-/sex-matched CN controls with DTI scans from the Mayo Clinic Study of Aging (MCSA) and Alzheimer's Disease Research Center (ADRC) studies (mean ± SD age 80.0 ± 5.1 years). MCSA is an epidemiological study of incidence, prevalence, and risk factors for Mild Cognitive Impairment (MCI) and dementia in the age 70–90 population of Rochester, Olmsted County, Minnesota (Petersen et al., 2010; Roberts et al., 2008). The ADRC study recruits and follows subjects initially seen as patients at the Mayo Clinic Behavioral Neurology practice. The criteria for normal subjects were: no cognitive complaints, normal neurological exam, no active psychiatric or neurological conditions, no psychoactive medications, and prior resolution of any previous neurological or psychiatric conditions, and the diagnosis of AD was made according to established criteria.

Scans of these subjects were performed on 3 T scanners manufactured by General Electric (Discovery MR750 and Signa HDxt models). The DTI acquisitions were a single-shot echo-planar (EPI) pulse sequence in the axial plane, with repetition time (TR) 8–11 s (depending on head size); in-plane matrix 128/128; FOV 35 cm; phase FOV 0.66 or 1.00, and 2.7 mm isotropic resolution. There were 41 diffusion directions with weighting (b) = 1000 s/mm² and 4–5 non-diffusion weighted T2 (b0) images.

ADNI AD–CN dataset

To cross-validate the experiments on an independent AD–CN dataset that was never used for tuning algorithm parameters, we also perform experiments using data from the Alzheimer's Disease Neuroimaging Initiative (ADNI), a longitudinal observational study of elderly individuals from 59 institutions with normal cognition, amnestic MCI, and AD (Jack et al., 2008). For up-to-date information, see www.adni-info.org. For our ADNI AD–CN dataset we identified 23 subjects with clinically-diagnosed AD and 23 age-/sex-matched CN (mean ± SD age of 74.5 ± 7.9 years) with usable DTI scans. These scans were also performed on 3 T scanners manufactured by General Electric (Discovery MR750, Signa HDx, and Signa HDxt models) using an axial EPI sequence. The TR was 9–14 s (depending on head size); the in-plane matrix 128/128; FOV 35 cm, and phase FOV 0.66 or 1.00. All scans had 41 diffusion directions with weighting (b) = 1000 s/mm², five non-diffusion weighted T2 (b0) images, and 2.7 mm isotropic resolution.

Mayo PSP–CN dataset

To validate our methodology on an independent group of patients with a different neurodegenerative disorder, and to compare the methods' abilities to distinguish these disorders, we identified 20 subjects diagnosed with PSP as part of a longitudinal imaging PSP study and 20 age-/sex-matched MCSA CN subjects (mean ± SD age of 68.7 ± 7.0 years). PSP subjects were identified from those recruited by the Department of Neurology, Mayo Clinic, Rochester, Minnesota who obtained a clinical diagnosis of probable PSP by a neurodegenerative expert (KAJ) of which 10 (50%) have now been pathologically confirmed and hence meet the criteria for definite PSP according to the established criteria (Litvan et al., 1996). Further details of this study are available in Josephs et al. (2013). The clinical scans of PSP subjects employed the same scanners as the Mayo AD–CN dataset with nearly the same parameters, but with some variation: the number of diffusion directions was either 37 or 41, and the resolution isotropically either 2.5 or 2.7 mm.

All studies were approved by their respective institutional review boards and all subjects or their surrogates provided informed consent compliant with HIPAA regulations. All scans used in our experiments were validated in-house by experts to confirm acceptable image quality and lack of significant confounding pathology.

Design of simulation experiments

Sensitivity experimental design

To quantify each method's sensitivity and specificity, we synthetically modified FA images to provide test cases with known ground truth. For sensitivity analysis, we employed the DTI scans of the 30 CN subjects from our Mayo AD–CN dataset. These scans were first preprocessed with a 3 × 3 × 1 erosion kernel to remove the “halo” artifact described previously, in order to allow registration with atlases that do not contain such an artifact (redundant further erosion was therefore disabled when using each pipeline).

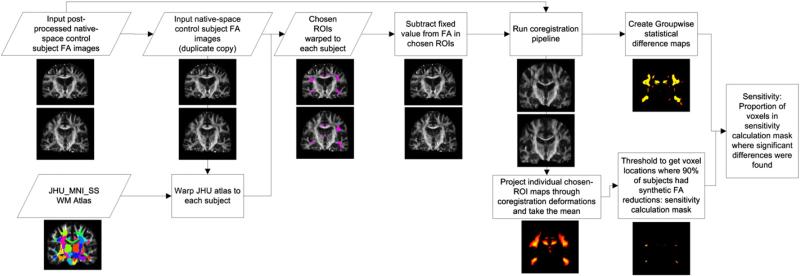
Our sensitivity experiments are designed to answer the following hypothetical question: For a comparison of 30 controls to 30 test subjects, if test subjects are identical to controls except for a known set of voxels where FA was synthetically reduced by a fixed value, what percentage of these voxels will be identified by each method as containing statistically significant group differences? In this way, we quantify each method's minimum detectable FA difference and compare these methods according to this sensitivity at each reduction level. We illustrate these experiments' design in Fig. 4.

Fig. 4.

Flowchart of steps in synthetic sensitivity analysis, where control subjects are compared to copies of themselves with FA synthetically reduced in a set of chosen ROIs, in order to quantify how well each method is able to detect these known change locations.

The design of these experiments is extended for quantitative analysis from prior work (Keihaninejad et al., 2012). We use the ANTS-SyN algorithm to calculate a nonlinear registration between the popular JHU_MNI_SS_FA WM atlas (Oishi et al., 2009) and each subject, resampling this atlas to each subject's native space using nearest-neighbor interpolation. We then subtract a known fixed value from each subject's FA in the following atlas-defined regions: uncinate fasciculus, inferior longitudinal fasciculus, superior longitudinal fasciculus, cingulum bundle, genu of the corpus callosum, splenium of the corpus callosum, fornix, posterior thalamic radiation, and inferior fronto-occipital. These regions were chosen because they frequently contain significant FA differences in TBSS-based comparisons of AD and control subjects (Keihaninejad et al., 2012). Finally, we use each pipeline variant (Table 1) to coregister and perform groupwise comparisons between the set of unmodified controls and their copies with synthetically-reduced FA values.

To quantify sensitivity, we take for each subject their map of voxels that were reduced according to the atlas, and we project these maps through the same set of deformations that were calculated to coregister their FA images, interpolating using nearest-neighbor. This process produces a map of which voxels in coregistered space correspond to those modified in their native space. We calculate the inter-subject mean of these maps, obtaining for each voxel the proportion of subjects whose FA was reduced in that location. For TBSS-based analyses, this changed-voxels map is then transformed by the same skeleton projection that was calculated for the input subjects. We present example slices of these maps in Fig. 10 in the Results section. Next, we threshold this map to remove voxels where FA differs in <90% of subject pairs, encoding the assumption that each method should detect significant FA reductions in every voxel where FA differs in ≥ 90% of subject pairs. Finally, we calculate each method's sensitivity: the percentage of these voxels in which significant FA reductions were detected between the control and the (synthetically-modified) test group.

Fig. 10.

Mean voxel locations where FA was synthetically reduced in selected ROIs by 0.05 in each subject during our sensitivity experiments, after coregistration transformations by each method. Sensitivity is calculated in voxels where at least 90% of subjects were changed (colored blue), as the proportion of these voxels where significant groupwise differences were observed. Note the more consistent localization of the fornix by ANTS-GW and the projection of voxels into the thalamus by TBSS skeletonization that were actually in the fornix or other nearby regions prior to this step.

We repeated these experiments with the chosen set of Regions of Interest (ROIs) reduced in each subject's FA images by the following amounts: 0.025, 0.05, 0.075, 0.10, 0.15, 0.20, 0.30, because empirically these provided good coverage of the range of sensitivities. Results are presented in the following section.

Specificity experimental design

Our specificity experiments are designed to answer the following hypothetical question: For a comparison of 30 control to 30 test subjects that have the same FA values in all anatomically-corresponding locations but differ only in the shape and voxel locations of these values due to disease-related atrophy, what fraction of voxels will be detected by each method as containing significant groupwise differences that are false-positives due to effects of misregistration and interpolation? For these experiments, we employ both the AD and CN subjects from our Mayo AD–CN dataset. As in the sensitivity experiments, these scans were first preprocessed with a 3 × 3 × 1 erosion kernel to remove the “halo” artifact, in order to allow registration with atlases that do not contain such an artifact (redundant further erosion was therefore disabled when using each pipeline). In this section we describe these experiments' design, also illustrated in Fig. 5.

Fig. 5.

Flowchart of steps in synthetic specificity analysis, where control subjects are compared to copies of themselves warped to resemble AD subjects, in order to quantify how well each method is able to avoid false positives from misregistrations caused by atrophy.

The design of these experiments is also extended for quantitative analysis from prior work (Keihaninejad et al., 2012). First, we employ the set of AD subjects to generate an AD-specific shape-averaged template brain via groupwise registration as described previously. We then calculate the nonlinear registration between each control subject and this AD template using ANTS-SyN, generating for each control subject a FA image with its same values projected to anatomical locations corresponding to a mean of our set of AD subjects, simulating the effect of AD-specific brain atrophy. To avoid the bias of comparing unmodified control subjects to corresponding subjects re-interpolated by warping, we perform the same trilinear interpolation on control subjects isotropically scaled by 0.99 of their original size. We then continue by running each software pipeline variant to compare these two groups: 1) 30 re-interpolated control subjects 2) the same 30 control subjects each nonlinearly coregistered to the mean of a set of shape-averaged age- and sex-matched AD subjects. Finally, we calculate the specificity value for each method as the percentage of the final analysis mask where FA values in the control group were statistically significantly higher than those in the synthetic atrophy group. We present these results in the following section.

Design of real-data experiments

AD vs. controls experiments

First, to validate and compare pipelines, we performed groupwise comparisons on our Mayo AD–CN dataset. Next, we use our independent ADNI AD–CN dataset, which was not used during the proposed method's development, for cross-validation. We used these datasets as inputs to each software pipeline variant (Table 1) and present these results in the following section.

PSP vs. controls experiment

To validate the methods on scans of subjects affected by a very different neurodegenerative pathology, we performed groupwise comparisons on our Mayo PSP–CN dataset as input to each software pipeline and present these results in the following section.

Results

Registration quality: Visual comparisons and coefficient of variation

In this section we present examples (Fig. 6) and visual indicators (Fig. 7) of the quality of inter-subject registration by each pipeline. All examples are from experiments more fully discussed later.

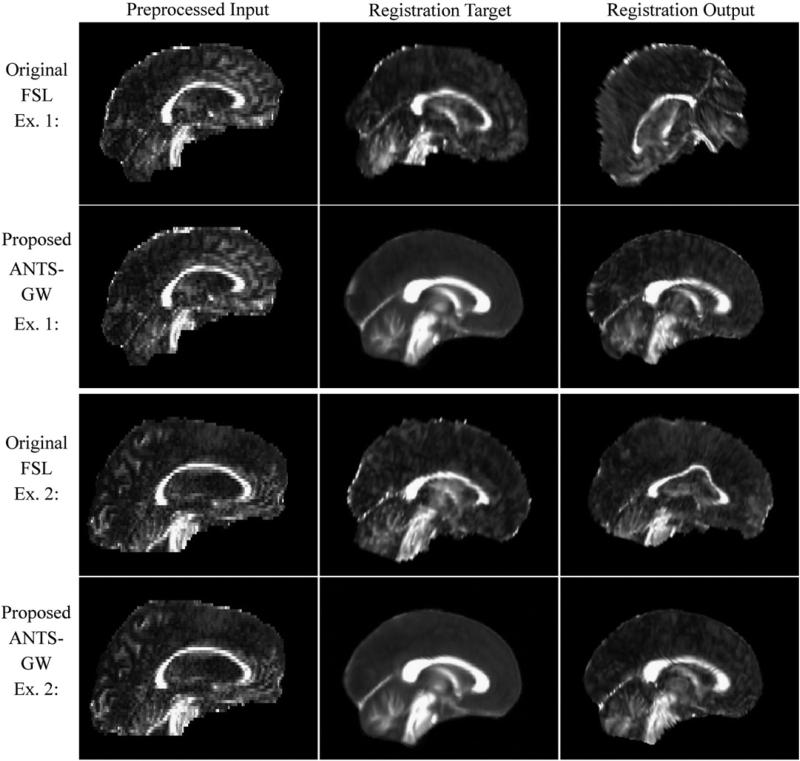
Fig. 6.

Two examples of misregistration in real data using the original FSL TBSS pipeline and corresponding registrations of the same inputs in the proposed ANTS-GW pipeline. The registration target is the most-representative subject in the original TBSS pipelines, and a study-specific template made by groupwise registration in the proposed pipelines. Example 1 (top) is taken from the real-data experiments with our Mayo PSP–CN dataset, and Example 2 (bottom) is from those with our Mayo AD–CN dataset.

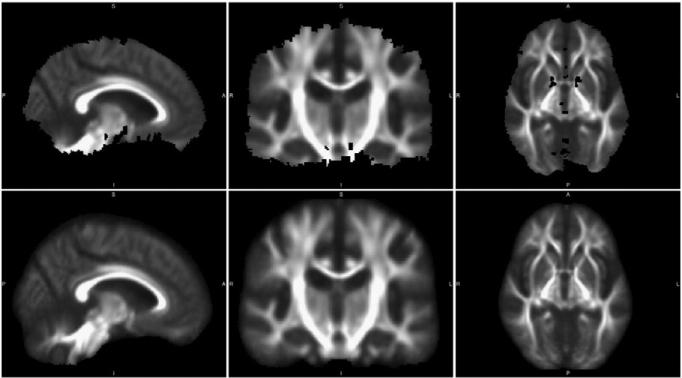
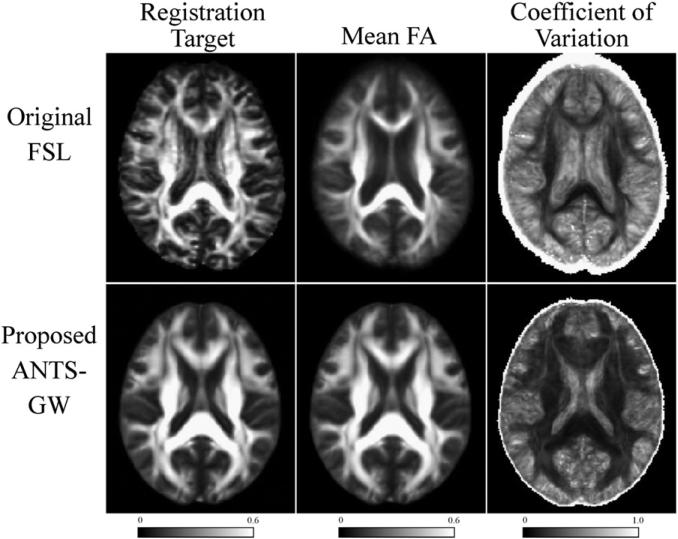
Fig. 7.

Comparison of registration targets (left), and mean (center) and coefficient of variation (right) of all control subjects in our Mayo AD–CN dataset, with original and proposed pipeline variants. The proposed pipeline shows more distinct tracts in the mean image, particularly in smaller tracts toward the cortical surface, and smaller variance in most locations, suggesting superior coregistration.

While lack of contrast in non-WM regions of FA images challenges any registration algorithm, the original FSL pipeline based on FLIRT and FNIRT occasionally made gross errors in both affine and nonlinear registration that were avoided by the ANTS-based pipelines (Fig. 6). Such gross affine registration errors (Fig. 6, top) occurred in two experiments, and the FSL-based pipelines were altered in these two experiments to use different flirt parameters to avoid them. More details are given in later sections. FSL-based pipelines very frequently gave relatively subtle errors in nonlinear registration (Fig. 6, bottom) in all tested datasets. Although alternative parameters to FNIRT might avoid such errors, to provide results with the unmodified software package we used those specified by the original authors in provided scripts designed for automated usage. An inspection of the subjects that experienced faulty registrations by FLIRT/FNIRT did not find any patterns or abnormalities to warrant their exclusion.

We present aggregated results of subject coregistration with each pipeline in Fig. 7 by calculating the mean and coefficient of variation (CV) across subjects. For this figure, we use CN scans from our Mayo AD–CN dataset to minimize confounding pathology. The mean FA image is the voxel-wise inter-subject mean of coregistered images, which is also used in these algorithms to determine the analysis mask. CV, the inter-subject standard deviation at each voxel divided by this mean, enables visualization of signal variability across images. In this figure, the ANTS-GW pipeline has increased visual clarity in the mean image and lower CV in WM regions with higher anatomical variability, such as the fornix and U-shaped fibers near the cortical surface, suggesting that its registration algorithms were more successful in aligning these regions. In the following subsections, we explore the effects of such registration differences on groupwise comparisons.

Sensitivity and specificity experimental results

Here we present the results of the sensitivity and specificity experiments with synthetically modified data described in the previous section. Each analysis pipeline was evaluated both with and without family-wise (FWE) statistical correction for multiple comparisons in order to simultaneously evaluate the effects of these corrections upon sensitivity and specificity. We first present the results without this correction (“uncorrected”) in Fig. 8, and with it enabled in Fig. 9. With FWE-correction applied, specificity is increased at a cost of reduced sensitivity. In this data, adding such correction had two major effects: specificity was increased to the ceiling for all methods, and sensitivity was decreased enough that all methods provided equal and zero sensitivity at ΔFA = 0.025.

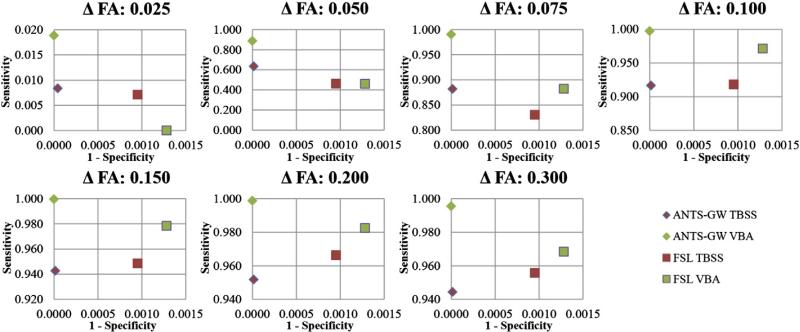
Fig. 8.

Receiver Operating Characteristic (ROC) curve plots of synthetic sensitivity and specificity experiments for each method using FWE-uncorrected statistics, which are frequently reported in the TBSS literature. Values near the top-left corner suggest superior results. Y axis scales vary. The proposed ANTS-GW VBA performs strongest in all tests.

Fig. 9.

Results of synthetic sensitivity experiments for each method with FWE-corrected statistics. Because specificity was perfect for all methods, we plot only sensitivity. We also omit the plot for ΔFA = 0.025 because all methods had zero sensitivity. Axis scales differ between rows. Higher values suggest superior results. The proposed ANTS-GW VBA pipeline achieves the highest sensitivity in all but the smallest FA reduction level.

Overall comparison of methods

Together, these experiments suggest that the proposed ANTS-GW VBA pipeline, which is based on groupwise registration using the ANTS registration software and omits the TBSS namesake skeleton projection step, has the highest sensitivity of all tested methods to detecting FA reductions across the entire tested range, with the exception of only one experiment among the fourteen performed. This pipeline also performed best in our specificity experiments, indicating a higher resistance to making false inferences due to misregistration errors than the other methods, although all methods' specificities experienced a ceiling effect under the added specificity of statistical FWE correction.

Testing skeleton projection

Focusing on comparisons between VBA and TBSS, i.e. whether or not TBSS's skeletonization step is beneficial, we see that when performed after ANTS-groupwise registration, the step reduced sensitivity in most experiments while providing no significant benefit to specificity. However, when performed after FSL-based registration as in the standard FSL TBSS pipeline, skeletonization provided increased specificity, perhaps by reducing the effects of misregistration. Its relationship to sensitivity depended on the magnitude of the FA differences: for subtle effects, skeletonization increased detection sensitivity, but this difference equalized and then reversed as the magnitude of the difference increased. Together, these experiments suggest that when used with the FSL-based coregistration pipeline, TBSS's skeletonization step is useful in some instances to reduce misregistration effects, but when used with the improved registration provided by our proposed ANTS-based approach, it is primarily detrimental.

Analyzing registration performance

Some of these results may be further explained using maps of voxel locations where the sensitivity experiments' synthetically-changed voxels in each subject were located after undergoing each coregistration pipeline (Fig. 10). In these maps, we see more consistent coregistration by the ANTS-GW pipelines. This is evidenced by a larger proportion of voxels with over 90% overlap (displayed in blue) of coregistered subjects' ROIs, especially in the fornix. These differences in coregistration quality offer one possible explanation for the higher sensitivity by the proposed methods in these regions. Furthermore, we see examples of skeletonization projecting voxels into anatomically different brain regions from where they originated, such as changed-voxels appearing in the thalamus even though no voxels in the thalamus were actually changed. Because corresponding VBA pipelines did not show significant differences in the thalamus, these misregistrations must have been introduced by the skeletonization process. This illustrates one of the TBSS limitations reviewed earlier in this work.

Additionally, the unmodified FSL-based pipelines experienced a severe affine misregistration of two synthetically-modified subjects in the ΔFA = 0.100 experiments. It was necessary to alter these pipelines so that flirt-based affine registration was performed using the -usesqform option to initialize the transforms from the files' headers, which prevented these errors. Visual inspection of these subjects showed no exclusionary criteria, and the unaltered pipeline did not have such errors in other ΔFA values. The ANTS-based pipelines had no such errors with these subjects. Only the FSL pipelines were altered in such a way in only the ΔFA = 0.100 experiments. Results for these pipelines without any modifications, thus including these erroneous registrations but preserving the same methodology across experiments, are plotted in supplementary material.

Comparing sensitivity in the fornix

In Table 2 we present the results of manually inspecting our sensitivity experiments' detections to determine whether any occurred in the fornix ROI. Because we synthetically reduced FA values in the fornix, among other ROIs, fornix detections are true positives and omissions are false negatives. The fornix is a region of particular interest to AD researchers because it is a primary WM connection to the hippocampus and has been detected as having reduced FA in most published DTI comparisons of AD and control patients (Keihaninejad et al., 2012). However, the fornix is a small, thin region surrounded by ventricles, and thus particularly prone to misregistration and partial volume averaging effects. Because of these difficulties, some groups choose to omit it from analysis despite its research importance (Nir et al., 2013). In Table 2, we see that the VBA pipelines omitting skeleton projection are more sensitive than their TBSS counterparts. After FWE correction, TBSS pipelines detected no fornix differences in any experiments, while the VBA pipelines succeed at detecting stronger FA differences. The fornix, however, remains a challenging ROI for all methods, and its relative insensitivity could be a target for future methodological improvement.

Table 2.

Fornix ROI detectability by each method in synthetic FA reduction sensitivity experiments. Note increased detection ability by the VBA-based pipelines.

Detection of synthetic FA reductions in the Fornix: Without FWE correction, p < 0.05
Method/Δ FA	0.025	0.050	0.075	0.100	0.150	0.200	0.300
FSL TBSS	No	No	No	No	Yes	Yes	Yes
FSL VBA	No	No	No	Yes	Yes	Yes	Yes
ANTS-GW TBSS	No	No	No	No	No	Yes	Yes
ANTS-GW VBA	No	No	No	Yes	Yes	Yes	Yes
Detection of synthetic FA reductions in the Fornix: With FWE Correction, p < 0.05
Method / Δ FA	0.025	0.050	0.075	0.100	0.150	0.200	0.300
FSL TBSS	No	No	No	No	No	No	No
FSL VBA	No	No	No	No	No	Yes	Yes
ANTS-GW TBSS	No	No	No	No	No	No	No
ANTS-GW VBA	No	No	No	No	No	Yes	Yes

AD vs. controls results

Here we present the results of our real-data experiments with AD–CN comparisons and show them in Fig. 11 (Mayo AD–CN dataset) and Fig. 12 (ADNI AD–CN dataset). With all methods, comparisons in the opposite direction (AD–Controls) in both datasets showed few if any isolated voxels of significance, none of which were significant after FWE correction (data not shown).

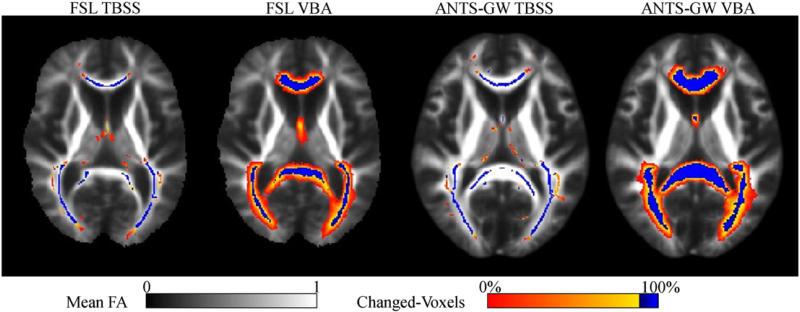
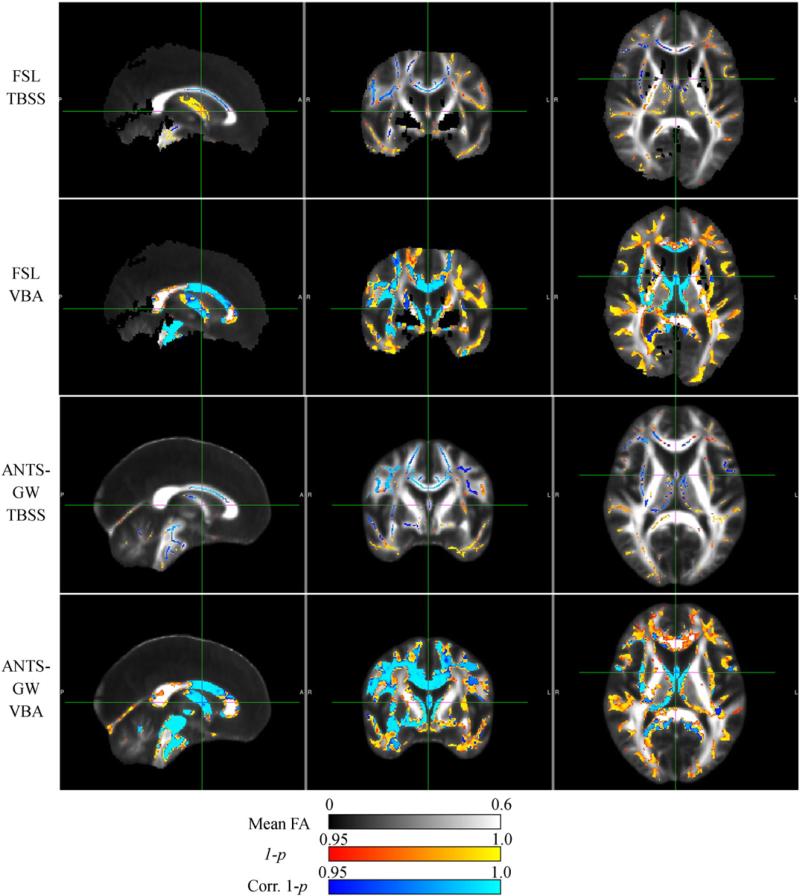
Fig. 11.

Results of each analysis pipeline computing significant FA reductions in 30 AD subjects versus 30 matched controls from Mayo Clinic data. Note reduced sensitivity in TBSS pipelines, and increased specificity in the ANTS-GW pipelines that prevents ventricle-boundary effects that appear to be caused by partial volume averaging.

Fig. 12.

Results of each analysis pipeline computing significant FA reductions in 23 AD subjects versus 23 matched controls from ADNI data. Note signal locational differences between TBSS and VBA methods, suggesting projection by TBSS into interpretability-confusing nearby locations, and increased symmetry in ANTS-GW VBA results.

In the Mayo AD–CN dataset (Fig. 11), VBA-based methods detected stronger differences particularly in the fornix, consistent with many similar studies (Keihaninejad et al., 2012). This result persists after FWE correction, unlike in TBSS-based methods. Both VBA methods appear more sensitive than their corresponding TBSS counterparts, with FSL-VBA appearing more sensitive than ANTS-GW. However, FSL-VBA also appears far less specific, including many strongly detected differences surrounding ventricle boundaries that we hypothesize to be a result of misregistration, partial volume averaging effects, susceptibility inhomogeneities, and/or confounding atrophy that were corrected by the additional step of skeleton projection in the FSL TBSS results. In the ANTS-GW pipelines, these regions do not pass FWE-corrected thresholds with or without skeleton projection, suggesting that their improved coregistration has removed these false positives without the need for that sensitivity-reducing step. Additionally, several regions of high-FA WM voxels were removed from consideration in the FSL pipelines that were retained with the proposed pipelines, although these incorrectly included CSF in the straight sinus/tentorium. These results particularly illustrate the harshness of FWE correction, which qualitatively changed the results from detecting significance in most WM regions to detected significance in only two focal ROIs.

In the ADNI dataset (Fig. 12), large regions of the midbrain and temporal lobe WM omitted by the FSL pipelines were included by the proposed ANTS-GW pipelines, although these also incorrectly included CSF in the straight sinus/tentorium. As in the previous dataset, the reduced capability of the TBSS pipelines to detect changes in the fornix resulted in this region's not surviving FWE-corrected thresholds. Examining the VBA pipelines' results with and without skeleton projection suggests that many of the FA differences detected by TBSS in peripheral WM actually occurred more centrally and these changes were mislead-ingly projected to these regions by skeletonization. The regions detected by VBA methods are similar to each other, but their spatial pattern in ANTS-GW VBA is much more symmetric and more strongly resembles the typical spatial distribution of age-related White Matter Hyperintensities (WMH) (Yoshita et al., 2006), suggesting a more plausible result because of the known correlation between WMH and reduced FA (Zhan et al., 2009). Locational inconsistencies of these regions with TBSS may also be explained by previously reported skeleton projection inaccuracies in the presence of WMH (Jones and Cercignani, 2010).

Comparing results in the two datasets, all methods generally showed a more aggressive pathology in the ADNI population than the Mayo Clinic population, agreeing with previous T1-based imaging comparisons between these groups (Whitwell et al., 2012a). Because our ADNI dataset contains relatively younger subjects, these results also agree with previous findings that differences between diagnostic groups decrease with age (Kantarci et al., 2010; Savva et al., 2009), possibly due to increased pathologic heterogeneity. These cross-dataset differences are particularly evident in the proposed ANTS-GW VBA method.

PSP vs. controls results

Here we describe the results of the real-data experiments with PSP vs. CN subjects and display them in Fig. 13. Like in the ΔFA = 0.100 sensitivity experiment, in these experiments, the FSL-based pipelines encountered a severe affine-misregistration of one PSP subject that required altering these pipelines so that flirt-based affine registration was performed using the -usesqform option, which prevented these errors. Visual inspection of this subject showed no exclusionary criteria, and the ANTS-based pipelines had no such errors. Results for these FSL pipelines without any modification, thus including these erroneous registrations, are presented in supplementary material.

Fig. 13.

Results of each analysis pipeline computing significant FA reductions in 20 PSP subjects versus 20 matched controls from Mayo Clinic data. Note the ANTS-GW pipelines' stronger detections in the midbrain, a definitive region for PSP, and improved specificity against detections along ventricle boundaries that appear to be caused by misregistrations and partial volume averaging.

With all methods, comparisons in the opposite direction (PSP– Controls) showed few if any isolated voxels of significance, none of which were significant after FWE correction (data not shown). In the presented comparisons, the FSL pipelines removed large portions of the midbrain and temporal lobes from consideration, which in the FSL TBSS pipeline was sufficient to prevent detecting significant FA reductions in most of the midbrain after FWE-correction, a region strongly implicated in this disease (Oba et al., 2005; Whitwell et al., 2012b). As a result, detections by the FSL TBSS method for CN-PSP subject differences were less differentiated from the previous comparisons of CN-AD subjects than those of the proposed methods. All pipelines detected large highly-significant reductions in FA surrounding the ventricles, particularly in the thalamus, which we hypothesize to be another instance of effects from misregistrations, susceptibility inhomogeneities, and partial volume averaging, like those in the FSL VBA pipeline's results in the AD–CN experiments. These regions have reduced significance in the ANTS-GW pipelines but mostly remain above thresholds, suggesting that while the ANTS-GW pipeline is an improvement over the FSL pipelines, future work could further improve DTI coregistration. Most of these regions were not eliminated by the skeleton projection step in either TBSS pipeline. Like in previous sections, the ANTS-GW pipelines incorrectly included CSF voxels in the straight sinus/tentorium that were omitted by the more conservative FSL pipelines.

Discussion and conclusions

Conclusions

In this work we present evidence that applying contemporary image coregistration improvements to DTI-FA images allows voxel-wise comparisons that are both more sensitive and more specific than the popular TBSS software pipeline, and that when used in combination with improved coregistration, TBSS's definitive skeleton projection step designed to compensate for misregistration errors is primarily detrimental to these metrics. We also present results of applying each method to three different datasets, on which the proposed improvements provide more plausible results according to disease pathophysiology. We suggest that future studies perform voxel-based analyses of DTI using groupwise registration based on ANTS or other well-performing nonlinear registration algorithms and omit the skeletonization step.

Limitations of current study

One limitation of the current study was the ceiling effect in the FWE-corrected specificity experiments, preventing specificity comparison between methods in this situation. While more general misregistration simulations could have been used, such as applying simple global deformations, these would not simulate the effects of atrophy, and such an evaluation of skeletonization has been previously published (Zalesky, 2011). In one attempt to improve the ceiling limitation for our experiments, we repeated them with an alternate design where each control subject was nonlinearly registered to a specific age and sex matched AD subject, rather than to a groupwise-averaged template of all AD subjects. While these deformations between individuals were generally much larger than the deformations to an averaged mean, the experiments experienced the same ceiling effect under FWE-correction. However, both registration pipelines preventing our simulated misregistrations from affecting FWE-corrected statistics provides further evidence that additional correction by skeletonization is not required. For further work, one might explore synthetic experiments using more sophisticated algorithms for atrophy simulation (Camara-Rey et al., 2006).

Another limitation occurs in our numerical comparisons of TBSS results vs. VBA results with FWE-correction. Because TBSS methods compute statistics over only skeleton voxels, fewer statistical comparisons occur in less-relevant voxels, and thus FWE-correction is less punitive. This potential bias may relatively increase the measured percentage sensitivity of FWE-corrected TBSS methods vs. VBA methods. However, because TBSS methods were less sensitive than VBA methods in a majority of our experiments, and the methods' sensitivities were also relatively similar with uncorrected statistics, we feel that these experiments support the conclusion that TBSS projection decreases sensitivity in most situations, although the magnitudes of that difference may be different than measured under FWE.

Future work

While this work suggests many promising directions for future studies, perhaps the most impactful would be a comparison of techniques for DTI coregistration. Here, we provide evidence that groupwise registration of FA images using the ANTS SyN algorithm is superior to the standard TBSS software pipeline's most-representative-subject-targeted registration using FLIRT and FNIRT. While our work combines with previous studies to suggest that groupwise registration is superior to the MRS approach (Keihaninejad et al., 2012), groupwise registration can be performed with any pairwise registration technique, and ANTS is only one such possibility. Although our experiments suggest that our proposed methods are an improvement, they could still be improved further. Of particular interest are DTI-specific registration algorithms based on pre-thresholded FA (Braskie et al., 2011), tensors (Keihaninejad et al., 2013; Zhang et al., 2010), Orientation Distribution Functions (Chiang et al., 2008), or tractography. One might also consider using ANTS or other non-DTI-specific registration algorithms with multiple channels in addition to FA, such as the undiffused “b0” volume, Mean Diffusion (MD), or Mode of Anisotropy (MO), similar to Park et al. (2003). Another option could be calculating inter-subject coregistration parameters between corresponding T1 volumes rather than DTI volumes directly, as advocated by Tustison et al. (2014). Registration improvements provided by such experiments could potentially increase sensitivity/specificity and improve ability to detect smaller FA changes particularly in areas with significant partial volume averaging such as the fornix.

Other possible directions include comparing an ANTS groupwise-registration-based VBM pipeline for T1 images against more standard implementations, possibly creating a unified pipeline for both DTI and T1 to allow more direct multimodal models or cross-modal comparisons. One could also investigate a voxel masking strategy that prevents false detections in CSF regions such as the straight sinus/tentorium seen in the proposed pipelines, without superfluously removing WM regions as in the FSL pipelines.