Abstract
Methods that integrate population-level sampling from multiple taxa into a single community-level analysis are an essential addition to the comparative phylogeographic toolkit. Detecting how species within communities have demographically tracked each other in space and time is important for understanding the effects of future climate and landscape changes and the resulting acceleration of extinctions, biological invasions, and potential surges in adaptive evolution. Here, we present a statistical framework for such an analysis based on hierarchical approximate Bayesian computation (hABC) with the goal of detecting concerted demographic histories across an ecological assemblage. Our method combines population genetic data sets from multiple taxa into a single analysis to estimate: 1) the proportion of a community sample that demographically expanded in a temporally clustered pulse and 2) when the pulse occurred. To validate the accuracy and utility of this new approach, we use simulation cross-validation experiments and subsequently analyze an empirical data set of 32 avian populations from Australia that are hypothesized to have expanded from smaller refugia populations in the late Pleistocene. The method can accommodate data set heterogeneity such as variability in effective population size, mutation rates, and sample sizes across species and exploits the statistical strength from the simultaneous analysis of multiple species. This hABC framework used in a multitaxa demographic context can increase our understanding of the impact of historical climate change by determining what proportion of the community responded in concert or independently and can be used with a wide variety of comparative phylogeographic data sets as biota-wide DNA barcoding data sets accumulate.
Keywords: comparative phylogeography, approximate Bayesian computation, historical demography, response to climate change
Introduction
Fluctuations in climate during the Quaternary resulted in widespread expansions and contractions of ice sheets, regional shifts in temperature and precipitation, and changes in sea levels and sea surface temperatures (Yu and Eicher 1998; Cutler et al. 2003; Pahnke et al. 2003). These fluctuations brought about profound changes in population sizes, species range distributions, and geographic patterns of genetic diversity in nearly all species (Graham et al. 1996; Comes and Kadereit 1998; Dynesius and Jansson 2000; Hewitt 2000, 2004; Davis and Shaw 2001; Hill et al. 2011). Characterizing the complex dynamics and aggregate demographic histories associated with expansions and contractions of large species assemblages is a daunting yet vital component of learning how climatic change can drive patterns of meta-community assembly in various regions (HilleRisLambers et al. 2012).
Despite the large number of phylogeographic studies examining species response to historical changes that have emerged since the field’s inception in the 1980s, there remains a pressing need for the integration of multispecies data sets within a cohesive statistical framework (Knowles 2009). Methods that use genetic data from whole assemblages can then be used to determine the community-level patterns of both individualistic and aggregate responses to climate cycles. Although community-level inference (Taberlet et al. 2002; Soltis et al. 2006; Drew and Barber 2012; Wood et al. 2012) from aggregate parameter estimates from each species and/or qualitative comparisons of phylogenetic trees or phylogeographic networks from each species can provide useful inferences about community responses to changes in climate and landscape (Sullivan et al. 2000; Soltis et al. 2006), a unified statistical framework that can pool information across species would be broadly beneficial.
In this study, we present a new and generally applicable multispecies population genetic method that is suitable for aggregate demographic histories of any community provided the availability of population-level sampling of single locus data across codistributed species. This general method can potentially make use of the plethora of data from nearly 25 years of phylogeographic studies (Hickerson et al. 2010) and mitochondrial DNA (mtDNA) barcode initiatives (17,505 chordate species; Ratnasingham and Hebert 2007, as of May 2014).
Under this strategy, this multitaxon statistical framework makes community-level inference while accommodating coalescent, mutational, and demographic variance associated with individual species and loci (Beaumont 2010; Morgan et al. 2011) and gains statistical strength from pooling data for a single analysis (Beaumont and Rannala 2004). Specifically, our multitaxon statistical framework uses hierarchical approximate Bayesian computation (hABC). Under complex models that make calculating the likelihood function difficult, ABC uses a comparison of observed to simulated summary statistics to sidestep the calculation of the likelihood function and develop approximate likelihoods for model choice and parameters (Sunnåker et al. 2013). hABC is an ABC extension of any hierarchical Bayesian model where multiple parameters are structured into multiple dependent levels whereby observable outcomes are modeled conditional on certain parameters, which themselves are given probabilistic specification in terms of higher level parameters, known as hyperparameters (Gelman et al. 2004). Hierarchical models are particularly useful when there are a number of quantities such as loci or populations, and it is unknown whether they should be parameterized the same way or independently (Beaumont 2010).
However, up to now, most hABC studies in a comparative phylogeographic context focused on studies of codivergence (Hickerson and Meyer 2008; Carnaval et al. 2009; Barber and Klicka 2010; Morgan et al. 2011) and local adaptation (Bazin et al. 2010). The method we introduce here is the first multispecies coalescent model-based method for the demographic inference of coordinated and/or independent multipopulation expansion histories, thereby allowing large-scale inferences relevant to questions about community assembly and variable responses to future climate changes.
The hABC Approach
Approximate Bayesian computation is particularly well suited to address the complexity of communities and natural populations where evaluation of the likelihood function is difficult (Csilléry et al. 2010). Often based on the rejection algorithm (Tavare et al. 1997; Pritchard et al. 1999), it involves the simulation of large numbers of data sets under different hypothesized scenarios with parameter values drawn from a prior. Simulated and observed data sets are reduced to summary statistics and then posterior probability distributions are approximated from the comparisons between the simulated and observed summary statistics. Although it has been used frequently in population and evolutionary genetics to estimate species-specific parameters such as effective population size and past demographic events such as growth, decline, and migration under complex demographic histories (Beaumont 2010), its application to community-wide dynamics is relatively recent (Hickerson et al. 2006) where it has been used to test for simultaneous divergence among sister taxa. Here, we infer community-wide dynamics based on a demographic history of concerted response. Our goal was to provide a tool to determine what proportion of a community responded simultaneously to a hypothesized historical event, such as a sea level change or expansion out of refugia, and to estimate the timing of the response.
We present an hABC scheme for detecting the presence and timing of multispecies coexpansion pulses at the time scale of the late Quaternary (table 1). We harness this approach to infer the proportion of a contemporary community that coexpanded simultaneously, as well as when that expansion occurred. Rather than compiling and qualitatively comparing a set of single-species inferences, this hABC method allows estimation of hyperparameters that quantify multispecies patterns, such as synchronicity in expansion time. By combining the data in a single hierarchical Bayesian analysis, we incorporate uncertainty in the amount of dependency among taxon-specific parameters, thereby allowing for both historical congruence and demographic independence across taxa (Beaumont 2010).
Table 1.
Hierarchical Approximate Bayesian Computation Procedure Outlined for Comparative Phylogeographic Inference of Concerted Demographic Response.
| Objectives |
|
| Draw hyperparameter value from prior | 1) For each data set of n taxa, draw a value of ζ representing ||nζ|| taxa that are coexpanding synchronously across n taxa |
| Draw taxon-specific parameter values from prior | 2) Draw an expansion time τa and for each ||1−nζ|| taxa expanding individualistically and a single τs from the prior for all ||nζ|| taxa that are coexpanding synchronously. Assign each of the n taxa an effective population size (N), expansion magnitude (ε), and mutation rate (u) drawn from taxon-specific priors |
| Simulate data for each taxon and calculate summary statistics | 3) Simulate data based on sample sizes, sequence lengths, and taxon-specific parameter values for all the n taxa using a coalescent simulation program |
| 4) Record parameter values and calculate summary statistics (number of haplotypes, haplotypic diversity, nucleotide diversity, and Tajima’s D) for each of the n taxa | |
| Calculate hypersummary statistics | 5) Calculate summary statistics for each set of n taxa based on the mean, variance, skewness, and kurtosis to compress multitaxon data set into Dj |
| 6) Repeat steps 1–5 for X iterations | |
| 7) Compute hypersummary statistics from the observed multitaxon data set D* | |
| Accept/Reject | 8) Accept Dj for 1,000 smallest Euclidean distances between simulated and observed∣Dj−D*∣ and record hyperparameter values ζ, E(τ), τs, and Var(τ)/E(τ). Reject the remaining |
| Estimation | 9) Fit local linear regression model to 1,000 accepted data sets and adjust hyperparameter values to obtain joint posterior probability estimates of E(τ), Var(τ)/E(τ),τs, and ζk |
First, we apply the hABC framework in extensive simulation experiments to validate the method and to examine the robustness of our model estimates and parameter estimation to different sizes of community samples and maximum expansion times. We introduce a model index hyperparameter of community congruence ζ, which ranges from complete simultaneous expansion (ζ = 1.0), where all n species expanded at the same time τs to complete random expansion (ζ = 0.0), where each of the n species expanded independently at times τi. For intermediate models, ζ is proportional to the number of species that coexpand synchronously with (1−ζ) being proportional to the number of species that expand individualistically at random times τi. All populations have a demographic model that consists of a contemporary effective size of Ni that is independently drawn from a uniform prior U(Nmin, Nmax), with every population instantaneously expanding from populations that are a fraction of their current size εi chosen from a uniform prior of expansion magnitudes U(εmin, εmax) at times τi or τs that have a uniform prior distribution of U(τmin, τmax) (fig. 1). Although each of the n taxa’s effective population size Ni and expansion magnitude εi are free to vary, the method allows estimating the following: 1) ζ, the proportion of the n taxa that synchronously expand; 2) E(τ), the mean expansion time of n taxa; 3) τs, the coexpansion time of the synchronous taxa; and 4) the dispersion index of all n expansion times, Var(τ)/E(τ).
Fig. 1.

Depiction of models of synchronous coexpansion (A; ζ = 1.0), partially synchronous coexpansion (B; ζ = 0.4), and asynchronous expansion (C; ζ = 0.0) all involving five populations. Each population has a contemporary effective population size of Ni from prior U(Nmin, Nmax) and expands instantaneously from a population εi the current size chosen from expansion magnitudes U(εmin, εmax) at times τi or τs from the uniform prior of U(τmin, τmax).
To demonstrate the method’s bias and accuracy given that the model is correct, we performed a series of cross-validation tests by simulating data sets having fixed values for the community congruence hyperparameter index ζ (pseudo-observed data sets [PODs]; Bertorelle et al. 2010) and subsequently estimating ζ, E(τ), τs, and Var(τ)/E(τ) using the ABC accept–reject method. To investigate the method’s performance when the model is incorrect (i.e., model generating the data differs from the model used for inference) and if such incorrect models could possibly be detected prior to applying our method, we simulated PODs from communities that differed from our coexpansion and random expansion community by including nonexpanding populations, declining populations, and multiple congruent pulses, and performed graphical checks using principal component analysis (PCA) given the PODs and data sampled from the hyperprior.
Finally, we apply this method to an empirical data set of 32 avian populations from Australia to determine how many bird species coexpanded simultaneously and the timing of any coexpansion. We validate our estimates with PODs using the sampling and species-specific prior distributions of these 32 avian populations and conduct graphical model checking of the prior and posterior predictive distributions. Thus, we verify that the model can generate the main features of the observed data. We then use PCA to help identify which of the 32 species coexpanded, followed by an hABC analysis on this subset to confirm species identification and validate the temporal coexpansion, and finally, to estimate when the coexpansion occurred.
Results
Cross-Validation of hABC Method
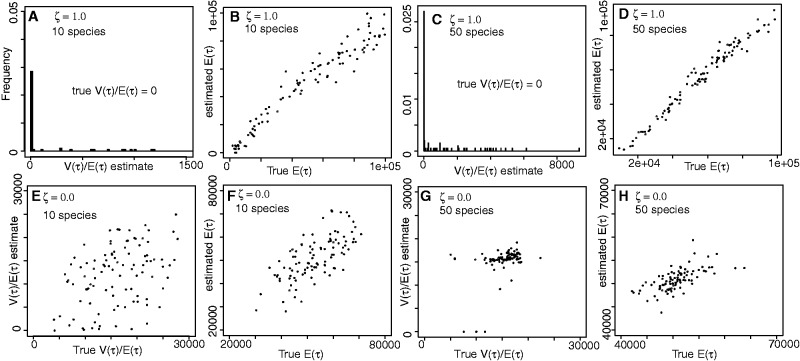
Sensitivity analyses to the size of the community (10 vs. 50 species) and the time frame (maximum expansion time τmax = 100,000 or 500,000 years before present) show that, as expected, the estimates of mean time E(τ) and dispersion index of time (Var(τ)/E(τ)) are substantially more accurate when a greater proportion of the taxa are coexpanding (fig. 2 and table 2). In addition, although the number of taxa sampled from a community (10 vs. 50) does have a strong effect on being able to test for synchronous or asynchronous coexpansion, the timeframe is much less so.
Fig. 2.
Simulation validation of the ABC estimator of the mean and dispersion index of the expansion times across 10 (panels A, B, E, and F) or 50 (panels C, D, G, and H) populations (E(τ) and Var(τ)/E(τ), respectively). Each joint estimate was made on a POD with parameter values randomly drawn from the priors Pr(τ) = U(1,000, 100,000) generations. Sets of PODs were drawn from histories with all populations expanding synchronously (ζ = 1.0; panels A–D) and asynchronously (ζ = 0.0; panels E–H). True value for Var(τ)/E(τ) = 0 when ζ = 1.0.
Table 2.
Comparison of Different Numbers of Species and Expansion Time Priors Indicates that Using Greater Numbers of Species Lowers the Error in Detecting Simultaneous Expansion.
| True Model (ζ) | Number of Species | τmax | Error Rate (majority) | Error Rate (Bayes factor threshold > 3) | Error Rate (Bayes factor threshold > 10) |
|---|---|---|---|---|---|
| 1 | 10 | 100,000 | 0.08 | 0.29 | 0.51 |
| 0 | 10 | 100,000 | 0.30 | 0.62 | 0.87 |
| 1 | 10 | 500,000 | 0.07 | 0.30 | 0.67 |
| 0 | 10 | 500,000 | 0.28 | 0.60 | 0.80 |
| 1 | 50 | 100,000 | 0.00 | 0.01 | 0.01 |
| 0 | 50 | 100,000 | 0.03 | 0.14 | 0.29 |
| 1 | 50 | 500,000 | 0.02 | 0.04 | 0.06 |
| 0 | 50 | 500,000 | 0.00 | 0.00 | 0.00 |
Note.—Error rates are calculated using either the majority of posterior samples or the Bayes Factor that compares the posterior weights of ζ = 0.0 and ζ = 1.0. Errors were determined from estimates of PODs generated under ζ = 0.0 and ζ = 1.0 for communities of 10 and 50 species and τmax of 100,000 and 500,000 generations.
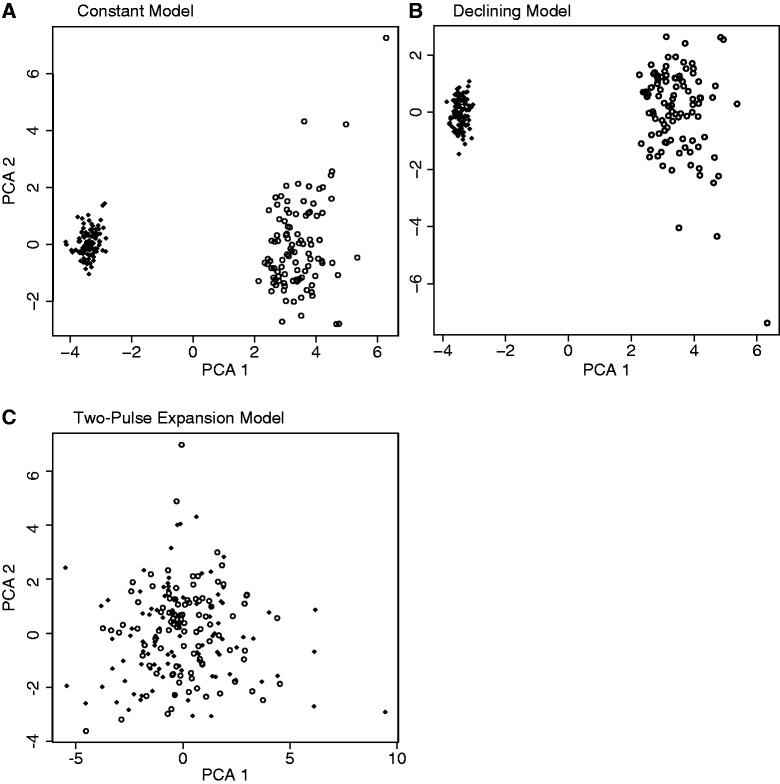
Model assumptions are an important component of all model-based methods (Csilléry et al. 2010), therefore we examined the behavior of three sets of PODs with key differences from the model used to generate prior samples contained in the reference table. These three sets of PODs were generated under the following three models: 1) “constant”—15 taxa expansion at the same time and 35 taxa with zero population growth; 2) “declining”—15 taxa expansion at the same time and 35 taxa declining to one-tenth their original size at random times; and 3) “two pulse”—15 taxa expansion at 30,000 generations before present and 35 taxa expansion at 90,000 generations before present. Using PCA, we compared data generated from each of these models to data generated from a model with 15 species coexpanding at a single time and 35 species expanding at independent times (i.e., ζ = 0.3) and expansion magnitudes εi drawn from the uniform prior U(εmin, εmax).
Using PCA as a graphical check to compare the PODs and data generated from the prior, we found that data generated from the constant and declining models can be detected with PCA to be a poor fit for hABC analysis under our coexpansion model (fig. 3A and B). In contrast, this PCA technique suggested that data generated from the two-pulse model were not found to be distinguishable from data generated from our single pulse ζ = 0.3 model (fig. 3C).
Fig. 3.
Projection of the summary statistics calculated from 100 PODs from constant, declining, and two-pulse models. (A) Constant: 15 species expanding congruently at 1,000–100,000 generations before present and 35 species not expanding (♦). (B) Declining: 15 species expanding congruently at 1,000–100,000 generations before present and 35 species declining at 1,000–100,000 generations before present (♦). (C) Two-pulse model that included 35 species expanding congruently at 30,000 generations before present and 15 species expanding congruently at 90,000 generations before present (♦); and 100 samples from the hyperprior (ο) of the expansion model where 15 species are expanding congruently at 1,000–100,000 generations before present and 35 are expanding at random times 1,000–100,000 generations before present onto the first two axes of a PCA.
Pleistocene Expansion Times in Australian Avian Populations
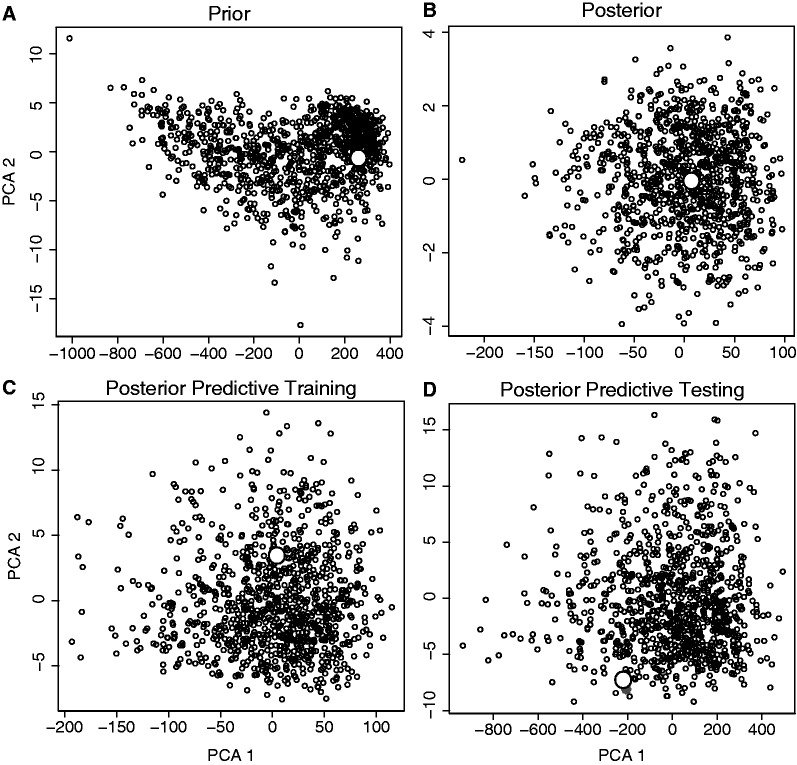
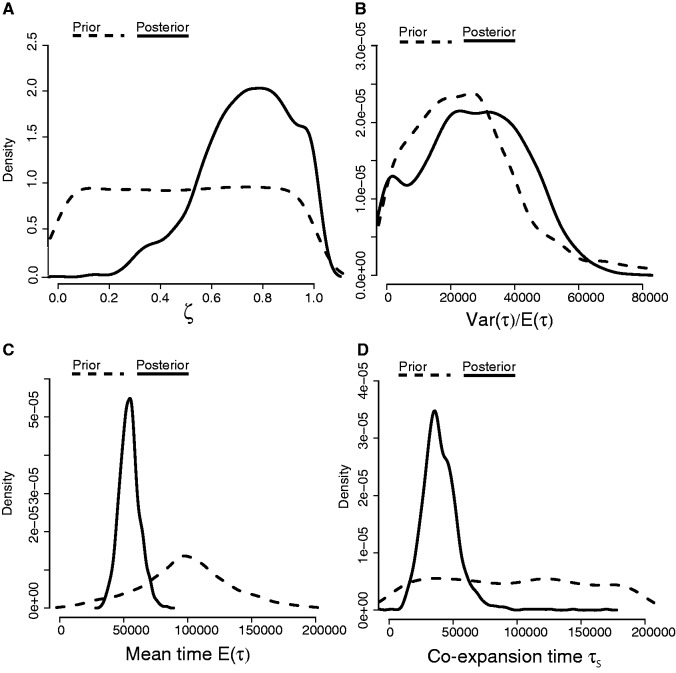
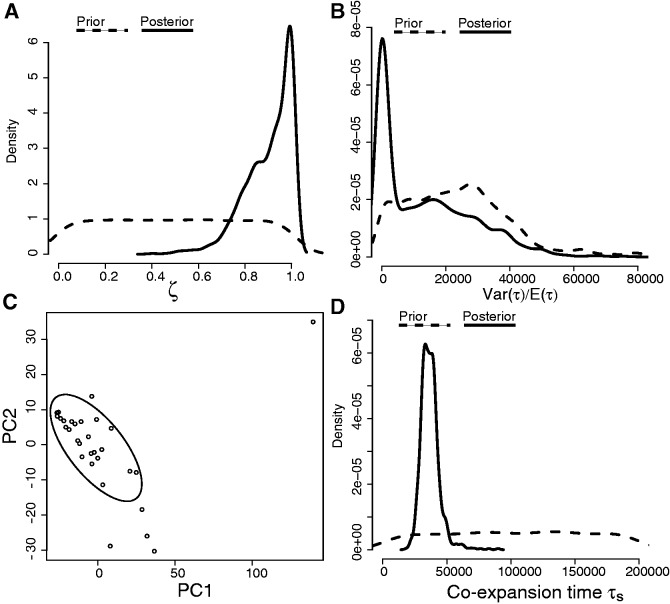
To demonstrate the method on an empirical data set, we applied this hABC method to data from 32 Australian bird populations. For this analysis, we specifically chose species in which all samples represented a monophyletic cluster lacking in genetic structure and putatively expanded from a single refugium. After using PCA to conduct graphical model checks of the prior and posterior predictive distributions to verify that the model can generate the main features of the observed data (fig. 4), we estimated ζ to be 0.8 (95% quantiles = 0.3–1.0; fig. 5A), thereby corresponding to an estimate of 26 of 32 populations temporally coexpanding (95% quantiles = 10–32). The mode for the mean expansion time E(τ) was 54,321 (95% quantiles = 38,918–71,287) and of the time of the coexpansion τs was 35,225 (95% quantiles = 18,963–67,545; fig. 5C and D).
Fig. 4.
Projection of the summary statistics calculated from 1,000 samples from the prior (A), posterior (B), and posterior predictive distributions (C and D) onto the first two axes of a PCA. The open circle is calculated from the observed Australian data collected from 32 avian populations. Panels (A–C) use the 16 original summary statistics used for the parameter estimates (mean, variance, skewness, and kurtosis of the number of haplotypes, haplotypic diversity, nucleotide diversity, and Tajima’s D) and panel (D) uses an alternative set of 8 summary statistics (mean, variance, skewness, and kurtosis of the number of segregating sites and Fu’s F). In panels (C) and (D), the 1,000 sets of accepted parameter values conditioned on the observed data to approximate the posterior were subsequently used to resimulate the data 1,000 times to obtain the posterior predictive distributions (Gelman et al. 2004; Cornuet et al. 2010).
Fig. 5.
Posterior estimates of model index of community congruence hyperparameter ζ (panel A) and parameter summaries time dispersion index Var(τ)/E(τ) (panel B), total mean expansion time E(τ), and coexpansion time τs (panels C and D) conditional on data from 32 Australian avian populations. The posterior of ζ with a mode between 0.7 and 0.8 and Var(τ)/E(τ) »0.0 indicates a mixed history that includes populations that expanded asynchronously and a synchronous pulse of coexpansion in a subset of the populations.
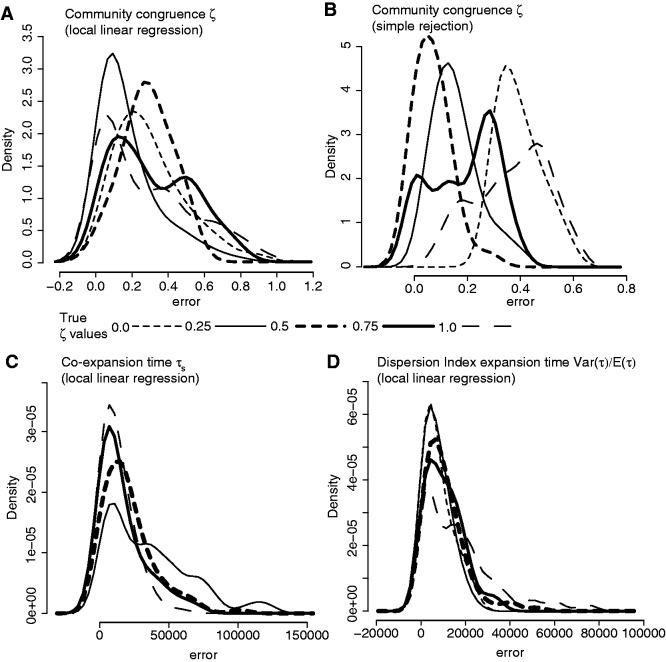
The hABC estimates of ζ, given five sets of 100 PODs each simulated from fixed values of ζ (0.0, 0.25, 0.5, 0.75, and 1.0), demonstrate that the method can detect the degree to which a community coexpanded at a single time, as well as estimate the expansion time and dispersion index of expansion times (fig. 6). For example, we simulated 100 PODs under the fixed value of ζ = 0.25, thereby yielding 8 taxa expanding synchronously at time τs and 24 taxa expanding at random times τi, with the expansion times drawn from priors Pr(τs) or Pr(τi) of U(1,000, 200,000) generations ago. Each estimate of ζ for each POD is based on 1,000 acceptances from a reference data table of 6.6 million simulations with ζ drawn from the discrete uniform hyperprior of Pr(ζ) = [0.0, 1/32, … , 31/32, 1.0]. In this case, the reference table consists of 200,000 data sets simulated from each of the 33 possible values of the hyperprior ζ ranging from 0 to a total of 32 populations expanding congruently with parameters for each population drawn from species-specific priors. The cross-validation PODs and error estimates demonstrate that the hABC method can potentially obtain accurate estimates of ζ, E(τ), τs, and Var(τ)/E(τ).
Fig. 6.
Error estimates from simulation validation of the hABC estimator of model index of community congruence ζ using local linear regression (panel A), simple rejection (panel B), τs coexpansion time (panel C), and Var(τ)/E(τ) time dispersion index of all expansion times (panel D). A set of 100 PODs was generated for five different levels of community congruence; true ζ = 1.0 where all species expanded in a synchronous pulse, true ζ = 0.0 where all species expanded randomly, and intermediate levels of synchronous and asynchronous expansion ζ = 0.25, 0.5, 0.75. Each set of 100 PODs was based on the sampling and priors of 32 Australian bird populations with expansion time randomly drawn from the prior Pr(τ) = U(1,000, 200,000).
As a heuristic approach to identify which 10–32 of the 32 avian populations coexpanded, we subsequently conducted an exploratory PCA. Specifically, we chose a cluster of 26 populations plotted on the first two components to identify a putative subset of populations that synchronously coexpanded (fig. 7C). We then assessed whether this subset of populations have data that are consistent with a history of temporal coexpansion by running an hABC analysis with a new reference table and observed summary statistic vector D regenerated from the subset of 26 populations corresponding to the PCA cluster. The estimates of ζ, Var(τ)/E(τ), and τs on this subset yield strong support for complete synchronous coexpansion (mode estimate of ζ = 0.95, fig. 7) and agree with the estimate of coexpansion time derived from the previous analysis (mode estimate of 32 populations τs= 35,225 vs. mode estimate of 26 populations τs= 33,465, τs 95% quantiles = 26,059–50,961; fig. 7).
Fig. 7.
Posterior estimates of hyperparameter ζ and parameter summaries τs and Var(τ)/E(τ) conditional on data from the subset of 26 Australian bird populations that were identified by the PCA to have synchronously coexpanded. The ABC posterior distributions indicate that these 26 populations expanded synchronously (panels A and B) approximately 33,000 years ago (panel D) during Marine Isotope Stage 3. Panel C depicts the first two principal components calculated from the 16 summary statistics calculated from the 32 Australian avian populations. The tightest cluster of 26 species was subsequently tested as a putative subset of species that synchronously coexpanded.
Discussion
The prevalence of shallow mtDNA genealogies found in many terrestrial and marine communities (Grant and Bowen 1998; Hewitt 2000) suggests that there may be widespread temporally and spatially shared responses of communities to Pleistocene environmental fluctuations such as sea level changes or glacial retreats. A statistical framework to test this hypothesis at the multispecies level will enable community-level inference for understudied groups and across whole biota. In contrast to previous applications of hABC to comparative phylogeographic data sets which sought to quantify support for models of vicariance or dispersal (Hickerson and Meyer 2008) or test for synchronous isolation (Huang et al. 2011), the method we present here enables quantifying the amount of temporal congruence in demographic coexpansion across species. Discerning whether species responded in concert or individualistically to historical changes in climate and landscape is important with respect to understanding the biogeographic dynamics of future climate changes, invasions, and extinction (Lavergne et al. 2010). Although we focus on comparative demographic inference, interpretations from this method could focus on demographic histories of matrilineages or selective sweeps accompanied by hitchhiking (Gillespie 2001; Bazin et al. 2006).
This general method and downstream extensions will be able to be deployed on the wealth of mtDNA, single-copy nuclear DNA, and chloroplast spacer regions that have become available for animals, plants, protists, and fungi over the last quarter of a century for phylogeographic (Soltis et al. 2006) and mtDNA studies (Ratnasingham and Hebert 2007), as well as newly available ancient DNA data (Ramakrishnan and Hadly 2009; Ho and Gilbert 2010; Lorenzen et al. 2011). Even if only a single genealogical sample is available from each animal species, the opportunity to sample this locus within communities across wide taxonomic breadth enables researchers to make regional-scale inferences of how whole assemblages responded to the cyclical climate changes of the Pleistocene, all while accounting for the variability associated with using a single locus per species.
The demographic model involves synchronous and asynchronous expansion where each taxon consists of a single panmictic population that is expanding. Although heterogeneity in sample size, sequence length, mutation model, and generation time, are incorporated into the simulations and taxon-specific parameters such as mutation rate and effective population sizes are allowed to freely and independently vary across taxa, we suggest that when applying this method, taxa/populations should be chosen that are likely to be panmictic. If taxa are found to have population structure, the data set can be divided into populations and each subset included separately in the analysis, although one should be cautious in cases where there are an unknown number of unsampled ghost populations that could cause distortions in inference (Heller et al. 2013). As with other model-based methods, it is important to perform model-checking procedures, such as posterior predictive checks and cross-validation simulation experiments, to determine whether parameters can be accurately estimated given the empirical data (Gelman et al. 2004; Csilléry et al. 2010).
To examine the robustness of our model estimation procedure, we quantified the impact of the prior on posterior distributions, parameter inference, and model choice (Gelman et al. 2004). We found that the timescale of the prior had little influence on the model choice or parameter estimation but that error rates for model choice were lower with 50 species compared with 10 species (table 2). To determine goodness-of-fit and examine whether misspecified models (i.e., when the actual model generating the data does not match the model used for inference) could be detected, we performed graphical model checking on PODs from constant, declining, and two-pulse models. We found that a PCA comparing summary statistics calculated from PODs generated from these alternative models and summary statistics calculated from data generated from random draws from the prior model used for inference (i.e., our expansion model) was effective for identifying cases of poor model fit for the constant and declining population models (fig. 3A and B) but not the two-pulse model (fig. 3C). However, in cases where the data are generated under a two-pulse model, one can first use our method to detect asynchronous coexpansion and subsequently explore running the framework on subsets of the data to identify multiple pulses of coexpansion (fig. 7).
To minimize bias introduced by violations of the assumption of panmictic populations (Navascués and Emerson 2009; Heller et al. 2013), we demonstrate the method on an avian assemblage from Australia, where species typically have high dispersal and consequently simplified patterns of population structure. In Australia, many common widespread species across the continent may have had assemblage-wide bottlenecks in response to widespread climatic events in the late Pleistocene (Barnosky et al. 2004), and our method suggests that a subset of populations potentially coexpanded 26,000–51,000 generations ago, coinciding with Marine Isotope Stage 3, a highly variable climatic period (Siddall and Rohling 2008).
Although hABC enabled the estimation of the number of species in the Australian data set that share congruent demographic dynamics, the identification of individual species by PCA shown here is heuristic, and there are likely to be other subsets that may also yield high posterior probability of synchronous coexpansion. Beyond such exploration with PCA, one could examine parameter estimates from individual species analysis using Bayesian skyline plots or mismatch distribution methods (Rogers and Harpending 1992; Kuhner et al. 1998; Schneider and Excoffier 1999; Ray et al. 2003; Excoffier 2004; Ho and Shapiro 2011). Whatever method is used to identify the individual species, the subset of congruent species can then be verified with an hABC analysis on the putative subset and with resulting parameter estimates of ζ ≈ 1.0 and Var(τ)/E(τ) ≈ 0 providing confirmation that the subset of species expanded synchronously, although competing models with alternate subsets may be unidentifiable given single locus mtDNA data.
We model an assemblage history that involves one synchronous expansion plus a group of asynchronous expansions, although future approaches could incorporate more than one synchronous expansion pulse and/or pulses or contraction pulses. The use of a more realistic model of population growth such as an exponential model may also improve inference, although our instantaneous model is likely to capture the effects of an exponential model (Rogers and Harpending 1992). Greater model complexity may also be accommodated by the incorporation of high throughput population genomic data obtained from next-generation sequencing technology.
Conclusion
We present a new hABC method for demographic inference and testing community response to climate change. This framework enables the estimation of the proportion of the present-day community that expanded in a single pulse in the past and will further aid in fitting predictive species distributional models of shared demographic and distributional changes (Lorenzen et al. 2011; Prunier et al. 2012). We test this method on an empirical data set of avian populations from Australia and demonstrate our ability to detect and estimate the timing of the expansion pulse. This method could help test macroecological hypotheses of community assembly (Weiher et al. 2011) and identify different responses by different ecological guilds or interacting species (Emerson and Gillespie 2008; Mikheyev et al. 2008; Stone et al. 2012). Overall, this approach can be extended to enable detecting forces underlying regional biodiversity patterns and provide a greater understanding of how changes in historical environmental features differentially affected species distributions (Hickerson et al. 2010; Emerson et al. 2011).
Materials and Methods
The hABC Model
Similar to the hierarchical Bayesian formulation of Ilves et al. (2010), which was used to estimate the proportion of taxon pairs that arose by way of colonization rather than “soft vicariance,” our objective here is to estimate the community congruence hyperparameter ζ, the proportion of n taxa that coexpanded in a single synchronous cluster. A flow chart of our method is outlined in table 1. The hierarchical structure of the model is such that the data D is conditional on species-specific parameters ϕ and τ, whereby the expansion time parameters τi for i = 1, 2, … , n species are conditional on ζ, whereas the other species-specific parameters ϕi (µi , Ni , and εi ; mutation rates, current effective population sizes, and expansion magnitudes, respectively) are assigned to i = 1, 2, … , n species independent of ζ. Under this scheme, the posterior distributions of the parameters given the data are π(ζ,τ|D)∝P(D|ζ,τ)π(τ|ζ)π(ζ), and π(ϕ|D)∝P(D|ϕ) with the joint hierarchical posterior distribution of the parameters given the data being π(ζ, τ, ϕ|D)∝P(D|ζ,τ,ϕ) = P(D|ϕ,τ)π(ϕ)π(τ|ζ)π(ζ). The community congruence hyperparameter ζ is then modeled, such that it can take k = n + 1 possible values ζ{0.0, 1/n, 2/n, … , n/n} that are assigned prior probabilities drawn from a discrete uniform distribution π(ζ). In this case, each model ζk within the vector {ζ0, … , ζ1} has equal prior probability, and the expansion time parameters τi are assigned to each of the n species conditional on ζ, π(τ|ζ).
Under the ABC scheme, this hierarchical Bayesian mixture model is used to simulate the data D in three steps: 1) generating the model ζk from π(ζ) with each ζ value having equal probability P(ζ0.0), … , P(ζ1.0); 2) generating the parameter vectors ϕk and τk from π(ϕ) and π(τ|ζ)π(ζ); and 3) generating the data D from P(D|ϕk,τk). By conditioning on the data D, this hierarchical ABC model then yields the approximate posterior probabilities of the focal hyperparameter ζ and parameter summaries E(τ),τs, and Var(τ)/E(τ), while allowing other taxon-specific parameters to be drawn independently for each taxon. For an analysis involving n taxa, these taxon-specific parameters ϕ include the n current effective population sizes {N1, … , Nn} drawn from a uniform prior P(Nk) = ∼U(Nmin, Nmax), the n expansion magnitudes {ε1, … , εn} drawn from a uniform prior P(εk) = ∼U(εmin, εmax), and the n mutation rates {µ1, … ,µn} that are in turn drawn from a uniform prior P(µk) = ∼U(µmin, µmax)µ with each locus-specific mean chosen according to the data and estimates based on the literature (table 3, Nabholz et al. 2008). With regard to each taxon’s expansion times τa = {τ1, … ,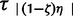 }, the ||(1−ζ)n||, independently expanding taxa are each independently and randomly assigned an expansion time from the uniform prior P(τa) = ∼ U(τmin,τmax), whereas the ||nζ|| taxa synchronously coexpanding are assigned a single τs that is randomly drawn from the same uniform ∼U(τmin, τmax) (||..|| notation specifies the integer nearest the number within).
}, the ||(1−ζ)n||, independently expanding taxa are each independently and randomly assigned an expansion time from the uniform prior P(τa) = ∼ U(τmin,τmax), whereas the ||nζ|| taxa synchronously coexpanding are assigned a single τs that is randomly drawn from the same uniform ∼U(τmin, τmax) (||..|| notation specifies the integer nearest the number within).
Table 3.
Summary and Sample Statistics for 32 Australian Birds Used in the hABC Analysis.
| Taxa | No. Samples | No. Base Pairs | Mutation Rate Prior (%/My) | Nucleotide Diversity | No. Haplotypes | Haplotypic Diversity | Tajima's D | P-Value Tajima's D | Reference |
|---|---|---|---|---|---|---|---|---|---|
| Gymnorhina tibicen clade A | 1,153 | 590 | 13–17 | 0.008110603 | 46 | 0.875974 | −0.0657334 | 0.557 | Baker et al. (2000) |
| Pomatostomus temporalis clade Aa | 84 | 399 | 13–17 | 0.010191312 | 21 | 0.849971 | −0.261851 | 0.477 | Edwards (1993) |
| Barnardius zonarius clade Aa | 11 | 1,036 | 0.6–1.0 | 0.000491502 | 3 | 0.472727 | −0.778153 | 0.311 | Joseph and Wilke (2006) |
| B. zonarius clade Ba | 70 | 1,036 | 0.6–1.0 | 0.00366875 | 13 | 0.701863 | −1.44079 | 0.056 | Joseph and Wilke (2006) |
| Malurus splendens clade Aa | 63 | 985 | 2.8–4.8 | 0.009792042 | 28 | 0.856631 | –0.304745 | 0.461 | Kearns et al. (2009) |
| Entomyzon cyanotis clade A | 6 | 1,032 | 2.8–4.8 | 0.055232558 | 4 | 0.8 | −1.52057 | 0.001 | Toon et al. (2010) |
| Platycercus elegans clade Aa | 82 | 935 | 0.6–1.0 | 0.00308655 | 28 | 0.841012 | −1.50608 | 0.054 | Joseph et al. (2008) |
| M. lambertii clade A | 63 | 969 | 2.8–4.8 | 0.007084969 | 39 | 0.950333 | −1.26882 | 0.084 | McLean et al. (2012) |
| Eopsaltria australis clade Aa | 53 | 1,002 | 2.8–4.8 | 0.001715967 | 18 | 0.716981 | −2.28436 | 0 | Pavlova et al. (2013) |
| E. australis clade Ca | 44 | 1,002 | 2.8–4.8 | 0.002325159 | 18 | 0.900634 | −1.15957 | 0.1 | Pavlova et al. (2013) |
| Cracticus quoyi clade Aa | 30 | 630 | 2.8–4.8 | 0.006871009 | 8 | 0.770115 | 1.05393 | 0.879 | Kearns et al. (2011) |
| Gliciphila melanops clade Aa | 27 | 865 | 2.8–4.8 | 0.005643745 | 18 | 0.94302 | −1.3094 | 0.092 | Dolman and Joseph (2012) |
| Cinclosoma cinnamomeum clade Aa | 18 | 884 | 2.8–4.8 | 0.006750362 | 13 | 0.901961 | −1.74447 | 0.025 | Toon et al. (2012) |
| Ci. cinnamomeum clade Ba | 9 | 884 | 2.8–4.8 | 0.006473102 | 8 | 0.972222 | −0.414598 | 0.399 | Toon et al. (2012) |
| M. leucopterus clade Aa | 34 | 1,007 | 2.8–4.8 | 0.00448793 | 18 | 0.932264 | −1.47934 | 0.051 | McLean et al. (2012) |
| Ptilonorhynchus violaceus clade Aa | 16 | 1,002 | 2.8–4.8 | 0.002170229 | 9 | 0.925 | −0.750111 | 0.235 | Nicholls and Austin (2005) |
| Pt. violaceus clade B | 78 | 1,002 | 2.8–4.8 | 0.004785263 | 47 | 0.968698 | −1.98111 | 0.003 | Nicholls and Austin (2005) |
| M. melanocephalus clade Aa | 14 | 467 | 2.8–4.8 | 0.000611808 | 3 | 0.274725 | −1.48074 | 0.138 | Lee and Edwards (2008) |
| M. melanocephalus clade Ba | 15 | 467 | 2.8–4.8 | 0.006322015 | 7 | 0.838095 | −0.490602 | 0.379 | Lee and Edwards (2008) |
| Biziura lobata clade Aa | 16 | 373 | 13–17 | 0.003024194 | 3 | 0.575 | 0.708323 | 0.783 | Guay et al. (2010) |
| Bi. lobata clade Ba | 135 | 373 | 13–17 | 0.002248703 | 8 | 0.413709 | −1.41781 | 0.047 | Guay et al. (2010) |
| C. nigrogularis clade Aa | 55 | 867 | 2.8–4.8 | 0.001648162 | 20 | 0.642424 | −2.42327 | 0 | Kearns et al. (2010) |
| Chalcites minutillus clade Aa | 48 | 1,497 | 2.0–4.0 | 0.004713327 | 27 | 0.953014 | −1.10275 | 0.147 | Joseph et al. (2011) |
| Anas gracilis clade A | 72 | 609 | 13–17 | 0.013997121 | 52 | 0.986307 | −1.05892 | 0.149 | Joseph et al. (2009) |
| Stipiturus malachurus clade Aa | 75 | 281 | 2.8–4.8 | 0.012100259 | 13 | 0.824144 | −0.711011 | 0.254 | Donnellan et al. (2009) |
| S. malachurus clade B | 4 | 281 | 2.8–4.8 | 0.044483986 | 2 | 0.5 | −0.858583 | 0.181 | Donnellan et al. (2009) |
| P. halli clade Aa | 20 | 403 | 13–17 | 0.002638109 | 6 | 0.573684 | −1.18349 | 0.115 | Lee and Edwards (2008) |
| P. halli clade Ba | 5 | 403 | 13–17 | 0.004472057 | 5 | 1 | −0.410175 | 0.526 | Lee and Edwards (2008) |
| Pezoporus wallicus clade Ba | 22 | 849 | 0.6–1.0 | 0.000504492 | 4 | 0.547619 | −0.849505 | 0.268 | Murphy et al. (2010) |
| Ch. basalis clade Aa | 21 | 1,689 | 2.0–4.0 | 0.001438751 | 14 | 0.938095 | −1.74716 | 0.022 | Joseph et al. (2002) |
| Ci. punctatum clade Aa | 11 | 884 | 2.8–4.8 | 0.002838338 | 8 | 0.890909 | −1.90258 | 0.012 | Toon et al. (2012) |
| Phylidonyris novaehollandiae clade Ba | 20 | 1,033 | 2.8–4.8 | 0.00462628 | 9 | 0.873684 | −1.44806 | 0.043 | Dolman and Joseph (2012) |
aSpecies were identified by the PCA as a possible coexpansion subset. Locus and taxon-specific avian mutation rate prior based on Nabholz et al. (2008).
Importantly, all n taxa experience an instantaneous expansion of magnitude εk at τs or τa= {τ1, … ,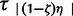 } generations in the past to reach their respective effective size Nk, such that each taxon’s effective population size at time τs or times τa= {τ1, … ,
} generations in the past to reach their respective effective size Nk, such that each taxon’s effective population size at time τs or times τa= {τ1, … ,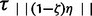 } is (εN)k < Nk as depicted in figure 1 under the three different hypothetical scenarios of ζ = 1.0, 0.4, and 0.0, respectively. As a practical way to estimate the hyperparameter model indicators for ζ0.0, … ,ζ1.0 from the data, we choose the hyperprior Pr(ζk) to be a simple discrete uniform prior P(ζk) ≡ 1/k to favor all models equally and where the posterior is proportional to the likelihood π(ζ,τ,ϕ|D)∝P(D|ζ,τ,ϕ) = P(D|ϕ,τ)π(ϕ)π(τ|ζ)π(ζ). In this case, there is one model ζk for each number of possible taxa coexpanding, such that if there are 100 taxa, then there are 101 models of ζk.
} is (εN)k < Nk as depicted in figure 1 under the three different hypothetical scenarios of ζ = 1.0, 0.4, and 0.0, respectively. As a practical way to estimate the hyperparameter model indicators for ζ0.0, … ,ζ1.0 from the data, we choose the hyperprior Pr(ζk) to be a simple discrete uniform prior P(ζk) ≡ 1/k to favor all models equally and where the posterior is proportional to the likelihood π(ζ,τ,ϕ|D)∝P(D|ζ,τ,ϕ) = P(D|ϕ,τ)π(ϕ)π(τ|ζ)π(ζ). In this case, there is one model ζk for each number of possible taxa coexpanding, such that if there are 100 taxa, then there are 101 models of ζk.
Using this hABC approach, we compress an observed multitaxon data set into a summary statistic vector (D*) and condition on D* to obtain π(ζ,τ,ϕ|D*), the approximate joint posterior probabilities of the expansion times τk (summarized by posterior estimates of E(τ), Var(τ)/E(τ)) and ζ, the proportion of the taxon assemblage that expanded synchronously. In this case, the data consist of a sample of multiple alleles from a single locus from each of n taxa assumed to be panmictic.
Multitaxa coalescent simulations were performed using a python script that combined single taxa simulations and summary statistics from Bayes Serial Simcoal (Anderson et al. 2005) into a single file and calculates the multispecies summary statistics. Python scripts for the simulations are available at https://github.com/UH-Bioinformatics/hBayeSSC (last accessed June 16, 2014).
Summary Statistics
Following our objectives of quantifying temporal patterns of coexpansion, we construct multispecies summary statistics that are based on four summary statistics that are known to be correlated with demographic expansion, including number of haplotypes, haplotypic diversity, nucleotide diversity, and Tajima’s D. To ensure that the summary statistic vector D, used for the ABC procedure, is independent of the ordering of the data configuration, and to reduce the dimensionality in D, we use the first four sample moments of these four summary statistics calculated on each of the four summary statistics across the n taxa. Specifically, we use the mean, variance, skewness, and kurtosis of each of these four summary statistics thereby yielding a vector D consisting of 16 order-independent multitaxa summary statistics. To initially explore the statistical behavior of the 16 components of D*, we simulated data from 50 taxa and a prior approximately U(1,000, 500,000) for τ under models ζ = 0.0 and ζ = 1.0. These conditions demonstrated the summary statistics to have differing distributions under these two models, a favorable condition for summary statistic selection in ABC (supplementary figs. S1 and S2, Supplementary Material online; Marin et al. 2012).
hABC Estimation
For obtaining the ABC joint posterior of ζk and the summaries of the n expansion times (E(τ), τs, Var(τ)/E(τ)), we use rejection sampling to identify the 10,000 closest Euclidean distances between D* and Di calculated from 2.0 × 106 random draws from each of the models P(ζk) = U(ζ0, … ζ1) with equal prior probability. After a second step of rejection sampling to identify the 1,000 closest Euclidean distances between D* and Di, we fit a local linear regression model to these posterior draws and applied this model to these remaining 1,000 acceptances to obtain an adjusted estimate of the joint posterior probability of E(τ), τs, Var(τ)/E(τ), and ζk using functions available from the R package abc.r (Csilléry et al. 2012). The local linear adjustment leads to improved estimation over estimates obtained by simple rejection sampling (fig. 6A and B). For ζk, we then back-transform the adjusted estimates to the closest value contained in the discrete uniform prior P(ζk) due to local linear regression leading to adjusted values of ζ that are not contained in the prior. For example, if the prior contains 0, 1/50 = 0.02, 2/50 = 0.04, … , 50/50 = 1, and the parameter value sampled in the posterior after the regression adjustment is 0.025, this value is set to 0.02 (1/50).
Simulation Cross-Validation of ABC Estimation
The development of novel ABC methods require careful examination of bias and accuracy, and especially in the case of using ABC for model estimation, these developments must go hand in hand with validating simulation experiments (Cook et al. 2006; Bertorelle et al. 2010; Cornuet et al. 2010; Csilléry et al. 2010; Robert et al. 2011). To this end, we first simulated 10-species and 50-species models, while varying the priors for expansion times using a P(τmin, τmax) of U(1,000, 100,000) and U(1,000, 500,000) generations. The sample configuration of the 10 and 50 species consisted of 40 sequences of 800 bp of single-locus mtDNA data and a fixed locus mutation rate of 8 × 10−5.
Initially, the prior distribution for ζ, P(ζ), only considered the two extreme values of ζ = 0.0 and ζ = 1.0, by simulating 500,000 prior draws from these two models. We then independently simulated 100 PODs (Bertorelle et al. 2010) from each of these two models and then used the ABC procedure to yield the 1,000 closest Euclidean distances between each PODs’ D* and Di calculated using the data generated from each of the 500,000 prior draws and used this to approximate the posterior probabilities of ζ = 0.0 and ζ = 1.0 for each estimate. Additionally, we used the Bayes Factor P(ζ = 0.0|D*)/P(ζ = 1.0|D*) ÷ P(ζ = 0.0)/P(ζ = 1.0) or P(ζ = 1.0|D*)/P(ζ = 0.0|D*) ÷ P(ζ = 1.0)/P(ζ = 0.0) (Kass and Raftery 1995) and the associated Jeffrey’s scale (Jeffreys 1961) to gauge one’s support for either history (ζ = 0.0 or ζ = 1.0). As an additional assessment, we estimated Var(τ)/E(τ) and E(τ) from 100 PODs conditional on ζ = 0.0 and ζ = 1.0, and either of the two numbers of populations (10 and 50) and priors for P(τ) = U(1,000, 100,000) and U(1,000, 500,000).
Detecting Poor Model Fit with Graphical Checks
We used the samples from the prior to check that our model priors could generate summary statistics similar to those calculated from PODs generated from alternative models (Cornuet et al. 2010). We performed a PCA using the “prcomp” function in R (R Development Core Team 2008) on the 16 multitaxa summary statistics from each of 100 PODs simulated from our hyperprior conditional on ζ = 0.4 given a history of 15 coexpanding taxa at 1,000–100,000 generations before present and 35 taxa expanding at independent times and 100 PODs generated from three alternative model priors: 1) constant—15 taxa coexpanding at 1,000–100,000 generations before present and 35 taxa not expanding; 2) declining—15 taxa coexpanding at 1,000–100,000 generations before present and 35 taxa declining at 1,000–100,000 generations before present; and 3) two pulse—35 taxa coexpanding at 30,000 generations before present and 15 taxa coexpanding at 90,000 generations before present. For the graphical checks, we specifically focused on PC1 and PC2 for comparison.
Pleistocene Expansion Times in Australian Avian Populations
We apply our method to a set of 32 avian populations distributed from across the Australian continent, most of which have been previously published and analyzed (table 3). Each population consists of a monophyletic cluster within which the population can be considered to be demographically panmictic. Each population putatively expanded from a single refugium during the Pleistocene, and our method attempts to discern if any of them coexpanded temporally without making any spatial assumptions or inferences. Following the general hierarchical ABC procedure, we simulated from the discrete uniform prior of P(ζk) = U(ζ0, … ,ζ1), with 200,000 simulations from each of the 33 coexpansion models, which ranged from 0 to 32 species coexpanding at time τs (total 6.6 million simulations). Following this hABC structure, τs and τa = {τ1, … ,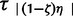 } are randomly drawn from the uniform prior P(τ) = U(1,000, 200,000). Likewise, the effective size Ni of each of the 32 contemporary populations is independently drawn from a species-specific uniform prior U(Nei_min, Nei_max) that instantaneously expands from an effective population εi its size at time τs or time τa = {τ1, … ,
} are randomly drawn from the uniform prior P(τ) = U(1,000, 200,000). Likewise, the effective size Ni of each of the 32 contemporary populations is independently drawn from a species-specific uniform prior U(Nei_min, Nei_max) that instantaneously expands from an effective population εi its size at time τs or time τa = {τ1, … ,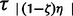 }. Mutation rates were drawn from a uniform prior distribution of U(µmin, µmax) that were based on previously reported locus and taxon-specific rates (table 3; Nabholz et al. 2008). After 6.6 × 106 simulated random draws from the prior, the ABC filter of 1,000 closest Euclidian distances between observed D*, and the 6.6 × 106 simulated values of Di are retained. Subsequently, we fit a local linear regression model to these posterior draws and apply this model to obtain an adjusted estimate of the joint posterior probability of ζk, E(τ),τs, and Var(τ)/E(τ). To further ascertain our ability to estimate the number of coexpanding populations, we estimated ζ, E(τ), τs, and Var(τ)/E(τ) from sets of 100 PODs that were drawn from ζ = 0.0, ζ = 0.25, ζ = 0.5, ζ = 0.75, and ζ = 1.0 and calculated the error as |(true value − estimated value)|.
}. Mutation rates were drawn from a uniform prior distribution of U(µmin, µmax) that were based on previously reported locus and taxon-specific rates (table 3; Nabholz et al. 2008). After 6.6 × 106 simulated random draws from the prior, the ABC filter of 1,000 closest Euclidian distances between observed D*, and the 6.6 × 106 simulated values of Di are retained. Subsequently, we fit a local linear regression model to these posterior draws and apply this model to obtain an adjusted estimate of the joint posterior probability of ζk, E(τ),τs, and Var(τ)/E(τ). To further ascertain our ability to estimate the number of coexpanding populations, we estimated ζ, E(τ), τs, and Var(τ)/E(τ) from sets of 100 PODs that were drawn from ζ = 0.0, ζ = 0.25, ζ = 0.5, ζ = 0.75, and ζ = 1.0 and calculated the error as |(true value − estimated value)|.
Model Checking of the Prior and Posterior Predictive Distributions
As a goodness-of-fit check to ascertain whether the model and our chosen priors can produce the main features of the observed data and to check for prior sampling efficiency (Hickerson et al. 2014), we deployed a PCA on prior and posterior samples of the 16 summary statistics. Initially, we used the first two principal components of the summary statistics calculated from 1,000 random draws from the simulated prior distribution and 1,000 samples from the hABC posterior to compare with these first two components from the 32 avian population samples (D*). Second, we sample from the posterior predictive distribution (Gelman et al. 2004) by simulating 1,000 data sets using parameters from the 1,000 posterior samples. To this end, we used the same 16 summary statistics, the mean, variance, skewness, and kurtosis of the number of haplotypes, haplotypic diversity, nucleotide diversity, and Tajima’s D (“training” set) as well as an alternative set (“testing” set) that included the mean, variance, skewness, and kurtosis of the number of segregating sites and Fu’s F and again projected the first two principal components of the corresponding observed summary statistics in both cases.
Selecting Taxa with Shared History
After the posterior estimate of ζ was obtained, given the observed D* from 32 avian population samples, we used a PCA on the summary statistics to aide in selecting and testing which 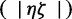 populations coexpanded synchronously. Specifically, we calculated the first two principal components of the summary statistics calculated from 32 avian population samples. After recalculating D* on a subset of populations that are closely clustered in the PCA, we then perform an hABC analysis to determine if this subset of populations plausibly coexpanded synchronously.
populations coexpanded synchronously. Specifically, we calculated the first two principal components of the summary statistics calculated from 32 avian population samples. After recalculating D* on a subset of populations that are closely clustered in the PCA, we then perform an hABC analysis to determine if this subset of populations plausibly coexpanded synchronously.
Supplementary Material
Supplementary figures S1 and S2 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
The authors thank the Australian Center for Ecological Synthesis working group on Reconstructing Effects of Past Climate Change, including A. Cooper, J. Soubrier, L. Joseph, and V. Thompson. They also thank the editor and two anonymous reviewers for their insightful comments and suggestions that helped us improve the manuscript. This work was supported by a Marie Curie International Incoming Fellowship within the 7th European Community Framework Programme, National Science Foundation, Division of Ocean Sciences (Award 1260169 to R.J. Toonen and B. Bowen) to Y.L.C. and by the National Science Foundation, Division of Environmental Biology (Awards 1253710 and 1343578) to M.J.H. Computational support was provided by the National Center for Research Resources (5P20RR016467-11) and the National Institute of General Medical Sciences (8 P20 GM 103466-11) from the National Institutes of Health. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575.
References
- Anderson CNK, Ramakrishnan U, Chan YL, Hadly EA. Serial SimCoal: a population genetics model for data from multiple populations and points in time. Bioinformatics. 2005;21:1733–1734. doi: 10.1093/bioinformatics/bti154. [DOI] [PubMed] [Google Scholar]
- Baker A, Mather P, Hughes J. Population genetic structure of Australian magpies: evidence for regional differences in juvenile dispersal behaviour. Heredity. 2000;85:167–176. doi: 10.1046/j.1365-2540.2000.00733.x. [DOI] [PubMed] [Google Scholar]
- Barber BR, Klicka J. Two pulses of diversification across the Isthmus of Tehuantepec in a montane Mexican bird fauna. Proc Biol Sci. 2010;277:2675–2681. doi: 10.1098/rspb.2010.0343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnosky A, Koch P, Feranec R. Assessing the causes of late Pleistocene extinctions on the continents. Science. 2004;306:70–75. doi: 10.1126/science.1101476. [DOI] [PubMed] [Google Scholar]
- Bazin E, Dawson KJ, Beaumont MA. Likelihood-free inference of population structure and local adaptation in a Bayesian hierarchical model. Genetics. 2010;185:587–602. doi: 10.1534/genetics.109.112391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazin E, Glemin S, Galtier N. Population size does not influence mitochondrial genetic diversity in animal. Science. 2006;312:570–572. doi: 10.1126/science.1122033. [DOI] [PubMed] [Google Scholar]
- Beaumont M. Approximate Bayesian computation in evolution and ecology. Annu Rev Ecol Evol Syst. 2010;41:379–406. [Google Scholar]
- Beaumont MA, Rannala B. The Bayesian revolution in genetics. Nat Rev Genet. 2004;5:251–261. doi: 10.1038/nrg1318. [DOI] [PubMed] [Google Scholar]
- Bertorelle G, Benazzo A, Mona S. ABC as a flexible framework to estimate demography over space and time: some cons, many pros. Mol Ecol. 2010;19:2609–2625. doi: 10.1111/j.1365-294X.2010.04690.x. [DOI] [PubMed] [Google Scholar]
- Carnaval A, Hickerson M, Haddad CFB, Rodrigues MT, Moritz C. Stability predicts genetic diversity in the Brazilian Atlantic forest hotspot. Science. 2009;323:785–789. doi: 10.1126/science.1166955. [DOI] [PubMed] [Google Scholar]
- Comes HP, Kadereit JW. The effect of Quaternary climatic changes on plant distribution and evolution. Trends Plant Sci. 1998;3:432–438. [Google Scholar]
- Cook SR, Gelman A, Rubin DB. Validation of software for Bayesian models using posterior quantiles. J Comput Graph Stat. 2006;15:675–692. [Google Scholar]
- Cornuet J-M, Ravigné V, Estoup A. Inference on population history and model checking using DNA sequence and micro-satellite data with the software DIYABC(v1.0) BMC Bioinformatics. 2010;11:401. doi: 10.1186/1471-2105-11-401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csilléry K, Blum MGB, Gaggiotti OE, Francois O. Approximate Bayesian computation (ABC) in practice. Trends Ecol Evol. 2010;25:410–418. doi: 10.1016/j.tree.2010.04.001. [DOI] [PubMed] [Google Scholar]
- Csilléry K, François O, Blum M. abc: an R package for approximate Bayesian computation (ABC) Methods Ecol Evol. 2012;3:475–479. doi: 10.1016/j.tree.2010.04.001. [DOI] [PubMed] [Google Scholar]
- Cutler KB, Edwards RL, Taylor FW, Cheng H, Adkins J, Gallup CD, Cutler PM, Burr GS, Bloom AL. Rapid sea-level fall and deep-ocean temperature change since the last interglacial period. Earth Planet Sci Lett. 2003;206:253–271. [Google Scholar]
- Davis MB, Shaw RG. Range shifts and adaptive responses to Quaternary climate change. Science. 2001;292:673–679. doi: 10.1126/science.292.5517.673. [DOI] [PubMed] [Google Scholar]
- Dolman G, Joseph L. A species assemblage approach to comparative phylogeography of birds in southern Australia. Ecol Evol. 2012;2:354–369. doi: 10.1002/ece3.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donnellan SCA, Armstrong JA, Pickett MC, Milne TC, Baulderstone JC. Systematic and conservation implications of mitochondrial DNA diversity in emu-wrens, Stipiturus (Aves: Maluridae) Emu. 2009;109:143–152. [Google Scholar]
- Drew JA, Barber PH. Comparative phylogeography in Fijian coral reef fishes: a multi-taxa approach towards marine reserve design. PLoS One. 2012;7:e47710. doi: 10.1371/journal.pone.0047710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dynesius M, Jansson R. Evolutionary consequences of changes in species’ geographical distributions driven by Milankovitch climate oscillations. Proc Natl Acad Sci U S A. 2000;97:9115–9120. doi: 10.1073/pnas.97.16.9115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards S. Mitochondrial gene genealogy and gene flow among island and mainland populations of a sedentary songbird, the grey-crowned babbler (Pomatostomus temporalis) Evolution. 1993;47:1118–1137. doi: 10.1111/j.1558-5646.1993.tb02140.x. [DOI] [PubMed] [Google Scholar]
- Emerson B, Gillespie R. Phylogenetic analysis of community assembly and structure over space and time. Trends Ecol Evol. 2008;23:619–630. doi: 10.1016/j.tree.2008.07.005. [DOI] [PubMed] [Google Scholar]
- Emerson BC, Cicconardi F, Fanciulli PP, Shaw PJA. Phylogeny, phylogeography, phylobetadiversity and the molecular analysis of biological communities. Philos Trans R Soc B Biol Sci. 2011;366:2391–2402. doi: 10.1098/rstb.2011.0057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L. Patterns of DNA sequence diversity and genetic structure after a range expansion: lessons from the infinite-island model. Mol Ecol. 2004;13:853–864. doi: 10.1046/j.1365-294x.2003.02004.x. [DOI] [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. 2004 Bayesian data analysis. Boca Raton (FL): Chapman & Hall/CRC. [Google Scholar]
- Gillespie JH. Is the population size of a species relevant to its evolution. Evolution. 2001;55:2161–2169. doi: 10.1111/j.0014-3820.2001.tb00732.x. [DOI] [PubMed] [Google Scholar]
- Graham RW, Lundelius EL, Jr, Graham MA, Schroeder EK, Toomey RS, III, Anderson E, Barnosky D, Burns JA, Churcher CS, Grayson DK, et al. Spatial response of mammals to late Quaternary environmental fluctuations. Science. 1996;272:1601–1606. doi: 10.1126/science.272.5268.1601. [DOI] [PubMed] [Google Scholar]
- Grant WS, Bowen BW. Shallow population histories in deep evolutionary lineages of marine fishes: insights from sardines and anchovies and lessons for conservation. J Hered. 1998;89:415–426. [Google Scholar]
- Guay P-J, Chesser RT, Mulder RA, Afton AD, Paton DC, McCracken KG. East–west genetic differentiation in Musk Ducks (Biziura lobata) of Australia suggests late Pleistocene divergence at the Nullarbor Plain. Conserv Genet. 2010;11:2105–2120. [Google Scholar]
- Heller R, Chikhi L, Siegismund H. The confounding effect of population structure on bayesian skyline plot inferences of demographic history. PLoS One. 2013;8:e62992. doi: 10.1371/journal.pone.0062992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hewitt G. The genetic legacy of the Quaternary ice ages. Nature. 2000;405:907–913. doi: 10.1038/35016000. [DOI] [PubMed] [Google Scholar]
- Hewitt GM. Genetic consequences of climatic oscillations in the Quaternary. Philos Trans R Soc Lond B Biol Sci. 2004;359:183. doi: 10.1098/rstb.2003.1388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickerson MJ, Carstens BC, Cavender-Bares J, Crandall KA, Graham CH, Johnson JB, Rissler L, Victoriano PF, Yoder AD. Phylogeography’s past, present, and future: 10 years after. Mol Phylogenet Evol. 2010;54:291–301. doi: 10.1016/j.ympev.2009.09.016. [DOI] [PubMed] [Google Scholar]
- Hickerson MJ, Meyer C. Testing comparative phylogeographic models of marine vicariance and dispersal using a hierarchical Bayesian approach. BMC Evol Biol. 2008;8:322. doi: 10.1186/1471-2148-8-322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickerson MJ, Stahl EA, Lessios HA. Test for simultaneous divergence using approximate Bayesian computation. Evolution. 2006;60:2435–2453. [PubMed] [Google Scholar]
- Hickerson MJ, Stone GN, Lohse K, Demos TC, Xie X, Landerer C, Takebayashi N. Recommendations for using msBayes to incorporate uncertainty in selecting an abc model prior: a response to Oaks et al. Evolution. 2014;68:284–294. doi: 10.1111/evo.12241. [DOI] [PubMed] [Google Scholar]
- Hill JK, Griffiths HM, Thomas CD. Climate change and evolutionary adaptations at species’ range margins. Annu Rev Entomol. 2011;56:143–159. doi: 10.1146/annurev-ento-120709-144746. [DOI] [PubMed] [Google Scholar]
- HilleRisLambers J, Adler PB, Harpole WS, Levine JM, Mayfield MM. Rethinking community assembly through the lens of coexistence theory. Annu Rev Ecol Evol Syst. 2012;43:227–248. [Google Scholar]
- Huang W, Takebayashi N, Qi Y, Hickerson MJ. MTML-msBayes: approximate Bayesian comparative phylogeographic inference from multiple taxa and multiple loci with rate heterogeneity. BMC Bioinformatics. 2011;12:1. doi: 10.1186/1471-2105-12-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho SYW, Gilbert MTP. Ancient mitogenomics. Mitochondrion. 2010;10:1–11. doi: 10.1016/j.mito.2009.09.005. [DOI] [PubMed] [Google Scholar]
- Ho SYW, Shapiro B. Skyline-plot methods for estimating demographic history from nucleotide sequences. Mol Ecol Resour. 2011;11:423–434. doi: 10.1111/j.1755-0998.2011.02988.x. [DOI] [PubMed] [Google Scholar]
- Ilves KL, Huang W, Wares JP, Hickerson MJ. Colonization and/or mitochondrial selective sweeps across the North Atlantic intertidal assemblage revealed by multi-taxa approximate Bayesian computation. Mol Ecol. 2010;19:4505–4519. doi: 10.1111/j.1365-294X.2010.04790.x. [DOI] [PubMed] [Google Scholar]
- Jeffreys H. Theory of probability. Oxford: Clarendon Press; 1961. [Google Scholar]
- Joseph L, Adcock GJ, Linde C, Omland KE, Heinsohn R, Terry Chesser R, Roshier D. A tangled tale of two teal: population history of the grey Anas gracilis and chestnut teal A. castanea of Australia. J Avian Biol. 2009;40:430–439. [Google Scholar]
- Joseph L, Dolman G, Donnellan S, Saint KM, Berg ML, Bennett ATD. Where and when does a ring start and end? Testing the ring-species hypothesis in a species complex of Australian parrots. Proc Biol Sci. 2008;275:2431–2440. doi: 10.1098/rspb.2008.0765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph L, Wilke T. Molecular resolution of population history, systematics and historical biogeography of the Australian ringneck parrots Barnardius: are we there yet? Emu. 2006;106:49. [Google Scholar]
- Joseph L, Wilke T, Alpers D. Reconciling genetic expectations from host specificity with historical population dynamics in an avian brood parasite, Horsfield’s Bronze-Cuckoo Chalcites basalis of Australia. Mol Ecol. 2002;11:829–837. doi: 10.1046/j.1365-294x.2002.01481.x. [DOI] [PubMed] [Google Scholar]
- Joseph L, Zeriga T, Adcock G, Langmore N. Phylogeography and taxonomy of the Little Bronze-Cuckoo (Chalcites minutillus) in Australia. Emu. 2011;111:113–119. [Google Scholar]
- Kass RE, Raftery AE. Bayes factors. J Amer Stat Assoc. 1995;90:773–795. [Google Scholar]
- Kearns AM, Joseph L, Cook LG. The impact of Pleistocene changes of climate and landscape on Australian birds: a test using the Pied Butcherbird (Cracticus nigrogularis) Emu. 2010;110:285. [Google Scholar]
- Kearns AM, Joseph L, Edwards SV, Double MC. Inferring the phylogeography and evolutionary history of the splendid fairy-wren Malurus splendens from mitochondrial DNA and spectrophotometry. J Avian Biol. 2009;40:7–17. [Google Scholar]
- Kearns AM, Joseph L, Omland KE, Cook LG. Testing the effect of transient Plio-Pleistocene barriers in monsoonal Australo-Papua: did mangrove habitats maintain genetic connectivity in the Black Butcherbird? Mol Ecol. 2011;20:5042–5059. doi: 10.1111/j.1365-294X.2011.05330.x. [DOI] [PubMed] [Google Scholar]
- Knowles LL. Statistical phylogeography. Annu Rev Ecol Evol Syst. 2009;40:593–612. [Google Scholar]
- Kuhner MK, Yamato J, Felsenstein J. Maximum likelihood estimation of population growth rates based on the coalescent. Genetics. 1998;149:429–434. doi: 10.1093/genetics/149.1.429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavergne S, Mouquet N, Thuiller W, Ronce O. Biodiversity and climate change: integrating evolutionary and ecological responses of species and communities. Annu Rev Ecol Evol Syst. 2010;41:321–350. [Google Scholar]
- Lee JY, Edwards SV. Divergence across Australia’s Carpentarian barrier: statistical phylogeography of the red-backed fairy wren (Malurus melanocephalus) Evolution. 2008;62:3117–3134. doi: 10.1111/j.1558-5646.2008.00543.x. [DOI] [PubMed] [Google Scholar]
- Lorenzen ED, Nogués-Bravo D, Orlando L, Weinstock J, Binladen J, Marske KA, Ugan A, Borregaard MK, Gilbert MTP, Nielsen R, et al. Species-specific responses of late Quaternary megafauna to climate and humans. Nature. 2011;479:359–364. doi: 10.1038/nature10574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marin J-M, Pillai N, Robert CP, Rousseau J. Relevant statistics for Bayesian model choice. J Royal Stat Soc Series B. 2013 Advance Access published December 9, 2013, doi: 10.1111/rssb.12056. [Google Scholar]
- McLean AJ, Toon A, Schmidt DJ, Joseph L, Hughes JM. Speciation in chestnut-shouldered fairy-wrens (Malurus spp.) and rapid phenotypic divergence in variegated fairy-wrens (Malurus lamberti): a multilocus approach. Mol Phylogenet Evol. 2012;63:668–678. doi: 10.1016/j.ympev.2012.02.016. [DOI] [PubMed] [Google Scholar]
- Mikheyev AS, Vo T, Mueller UG. Phylogeography of post-Pleistocene population expansion in a fungus-gardening ant and its microbial mutualists. Mol Ecol. 2008;17:4480–4488. doi: 10.1111/j.1365-294X.2008.03940.x. [DOI] [PubMed] [Google Scholar]
- Morgan K, O’Loughlin SM, Chen B, Linton Y-M, Thongwat D, Somboon P, Fong MY, Butlin R, Verity R, Prakash A, et al. Comparative phylogeography reveals a shared impact of pleistocene environmental change in shaping genetic diversity within nine Anopheles mosquito species across the Indo-Burma biodiversity hotspot. Mol Ecol. 2011;20:4533–4549. doi: 10.1111/j.1365-294X.2011.05268.x. [DOI] [PubMed] [Google Scholar]
- Murphy SA, Joseph L, Burbidge AH, Austin J. A cryptic and critically endangered species revealed by mitochondrial DNA analyses: the Western Ground Parrot. Conserv Genet. 2010;12:595–600. [Google Scholar]
- Nabholz B, Glémin S, Galtier N. Strong variations of mitochondrial mutation rate across mammals—the longevity hypothesis. Mol Biol Evol. 2008;25:120–130. doi: 10.1093/molbev/msm248. [DOI] [PubMed] [Google Scholar]
- Navascués M, Emerson BC. Elevated substitution rate estimates from ancient DNA: model violation and bias of Bayesian methods. Mol Ecol. 2009;18:4390–4397. doi: 10.1111/j.1365-294X.2009.04333.x. [DOI] [PubMed] [Google Scholar]
- Nicholls JA, Austin JJ. Phylogeography of an east Australian wet-forest bird, the satin bowerbird (Ptilonorhynchus violaceus), derived from mtDNA, and its relationship to morphology. Mol Ecol. 2005;14:1485–1496. doi: 10.1111/j.1365-294X.2005.02544.x. [DOI] [PubMed] [Google Scholar]
- Pahnke K, Zahn R, Elderfield H, Schulz M. 340,000-year centennial-scale marine record of Southern Hemisphere climatic oscillation. Science. 2003;301:948–952. doi: 10.1126/science.1084451. [DOI] [PubMed] [Google Scholar]
- Pavlova A, Amos JN, Joseph L, Loynes K, Austin JJ, Keogh JS, Stone GN, Nicholls JA, Sunnucks P. Perched at the mito-nuclear crossroads: divergent mitochondrial lineages correlate with environment in the face of ongoing nuclear gene flow in an Australian bird. Evolution. 2013;67:3412–3428. doi: 10.1111/evo.12107. [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Seielstad MT, Perez-Lezaun A, Feldman MW. Population growth of human Y chromosomes: a study of Y chromosome microsatellites. Mol Biol Evol. 1999;16:1791–1798. doi: 10.1093/oxfordjournals.molbev.a026091. [DOI] [PubMed] [Google Scholar]
- Prunier R, Holsinger KE, Carlson JE. The effect of historical legacy on adaptation: do closely related species respond to the environment in the same way? J Evol Biol. 2012;25:1636–1649. doi: 10.1111/j.1420-9101.2012.02548.x. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R: a language and environment for statistical computing. 2008 Vienna (Austria): R Foundation for Statistical Computing. [Google Scholar]
- Ramakrishnan U, Hadly EA. Using phylochronology to reveal cryptic population histories: review and synthesis of 29 ancient DNA studies. Mol Ecol. 2009;18:1310–1330. doi: 10.1111/j.1365-294X.2009.04092.x. [DOI] [PubMed] [Google Scholar]
- Ratnasingham S, Hebert P. BOLD: the Barcode of Life Data System ( www.barcodinglife.org) Mol Ecol Notes. 2007;7:355–364. doi: 10.1111/j.1471-8286.2007.01678.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray N, Currat M, Excoffier L. Intra-deme molecular diversity in spatially expanding populations. Mol Biol Evol. 2003;20:76–86. doi: 10.1093/molbev/msg009. [DOI] [PubMed] [Google Scholar]
- Robert CP, Cornuet J-M, Marin J-M, Pillai NS. Lack of confidence in approximate Bayesian computation model choice. Proc Natl Acad Sci. 2011;108:15112–15117. doi: 10.1073/pnas.1102900108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers AR, Harpending H. Population growth makes waves in the distribution of pairwise genetic differences. Mol Biol Evol. 1992;9:552–569. doi: 10.1093/oxfordjournals.molbev.a040727. [DOI] [PubMed] [Google Scholar]
- Schneider S, Excoffier L. Estimation of past demographic parameters from the distribution of pairwise differences when the mutation rates vary among sites: application to human mitochondrial DNA. Genetics. 1999;152:1079–1089. doi: 10.1093/genetics/152.3.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siddall M, Rohling E. Marine isotope stage 3 sea level fluctuations: data synthesis and new outlook. Rev Geophys. 2008;46:1–29. [Google Scholar]
- Soltis DE, Morris AB, McLachlan JS, Manos PS, Soltis PS. Comparative phylogeography of unglaciated eastern North America. Mol Ecol. 2006;15:4261–4293. doi: 10.1111/j.1365-294X.2006.03061.x. [DOI] [PubMed] [Google Scholar]
- Stone GN, Lohse K, Nicholls JA, Fuentes-Ultrilla P, Sinclair F, Schonrogge K, Csoka G, Melika G, Nieves-Aldrey J-L, Pujade-Villar J, et al. Reconstructing community assembly in time and space reveals enemy escape in a Western Palearctic insect community. Curr Biol. 2012;22:532–537. doi: 10.1016/j.cub.2012.01.059. [DOI] [PubMed] [Google Scholar]
- Sullivan J, Arellano E, Rogers DS. Comparative phylogeography of Mesoamerican highland rodents: concerted versus independent response to past climatic fluctuations. Am Nat. 2000;155:755–768. doi: 10.1086/303362. [DOI] [PubMed] [Google Scholar]
- Sunnåker M, Busetto AG, Numminen E, Corander J, Foll M, Dessimoz C. Approximate Bayesian computation. PLoS Comput Biol. 2013;9:e1002803. doi: 10.1371/journal.pcbi.1002803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taberlet P, Fumagalli L, Wust-Saucy AG, Cosson JF. Comparative phylogeography and postglacial colonization routes in Europe. Mol Ecol. 2002;7:453–464. doi: 10.1046/j.1365-294x.1998.00289.x. [DOI] [PubMed] [Google Scholar]
- Tavare S, Balding D, Griffiths R, Donnelly P. Inferring coalescence times from DNA sequence data. Genetics. 1997;145:505–518. doi: 10.1093/genetics/145.2.505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toon A, Austin JJ, Dolman G, Pedler L, Joseph L. Evolution of arid zone birds in Australia: leapfrog distribution patterns and mesic-arid connections in quail-thrush (Cinclosoma, Cinclosomatidae) Mol Phylogenet Evol. 2012;62:286–295. doi: 10.1016/j.ympev.2011.09.026. [DOI] [PubMed] [Google Scholar]
- Toon A, Hughes JM, Joseph L. Multilocus analysis of honeyeaters (Aves: Meliphagidae) highlights spatio-temporal heterogeneity in the influence of biogeographic barriers in the Australian monsoonal zone. Mol Ecol. 2010;19:2980–2994. doi: 10.1111/j.1365-294X.2010.04730.x. [DOI] [PubMed] [Google Scholar]
- Weiher E, Freund D, Bunton T, Stefanski A, Lee T, Bentivenga S. Advances, challenges and a developing synthesis of ecological community assembly theory. Philos Trans R Soc B Biol Sci. 2011;366:2403–2413. doi: 10.1098/rstb.2011.0056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood DA, Vandergast AG, Barr KR, Inman RD, Esque TC, Nussear KE, Fisher RN, Bode M. Comparative phylogeography reveals deep lineages and regional evolutionary hotspots in the Mojave and Sonoran Deserts. Divers Distrib. 2012;19:722–737. [Google Scholar]
- Yu Z, Eicher U. Abrupt climate oscillations during the last deglaciation in central North America. Science. 1998;282:2235–2238. doi: 10.1126/science.282.5397.2235. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.