Large scale affinity calculations of cyclodextrin host-guest complexes: Understanding the role of reorganization in the molecular recognition process

Abstract

Host-guest inclusion complexes are useful models for understanding the structural and energetic aspects of molecular recognition. Due to their small size relative to much larger protein-ligand complexes, converged results can be obtained rapidly for these systems thus offering the opportunity to more reliably study fundamental aspects of the thermodynamics of binding. In this work, we have performed a large scale binding affinity survey of 57 β-cyclodextrin (CD) host guest systems using the binding energy distribution analysis method (BEDAM) with implicit solvation (OPLS-AA/AGBNP2). Converged estimates of the standard binding free energies are obtained for these systems by employing techniques such as parallel Hamitionian replica exchange molecular dynamics, conformational reservoirs and multistate free energy estimators. Good agreement with experimental measurements is obtained in terms of both numerical accuracy and affinity rankings. Overall, average effective binding energies reproduce affinity rank ordering better than the calculated binding affinities, even though calculated binding free energies, which account for effects such as conformational strain and entropy loss upon binding, provide lower root mean square errors when compared to measurements. Interestingly, we find that binding free energies are superior rank order predictors for a large subset containing the most flexible guests. The results indicate that, while challenging, accurate modeling of reorganization effects can lead to ligand design models of superior predictive power for rank ordering relative to models based only on ligand-receptor interaction energies.

I Introduction

Molecular recognition plays a critical role in biological processes. Notable examples include protein-protein interactions occurring in signal transduction pathways and binding of substrates and inhibitors to target enzymes. Understanding the physical driving forces for or against binding and particularly the balance between enthalpic and entropic components is important in drug design applications.^1–3 The non-covalent association of two molecules into a complex is driven by hydrogen bonding and electrostatic and van der Waals interactions. These stabilizing forces are opposed by destabilizing effects due to the loss of conformational freedom, and conformational strain; desolvation of the protein and ligand may favor or oppose formation of the complex. Due to these complexities, the accurate prediction of binding affinities by computational means is still one of the most difficult challenges in molecular modeling.^4–7

Docking and scoring approaches^8–11 and related structure-based empirical techniques bypass many of these difficulties by emphasizing receptor-ligand interactions, which are the main driving force for binding. While successful in virtual screening applications, the usefulness of docking and scoring calculations for rank ordering of binding affinities and ligand optimization has been limited, likely because of the severe approximations made in the treatment of conformational flexibility and entropic effects.¹² The formation of ligand-receptor interactions is always accompanied by entropic losses and induced fit reorganization. So, while strong receptor-ligand interactions are prerequisites for good affinity, trends in binding affinities are often be determined by the balance between attractive receptor-ligand interactions and conformational reorganization effects.

Models incorporating reorganization free energy effects should in principle be able to provide improved computational tools for ligand design, and offer insights into important biological phenomena, such as mechanisms of drug resistance, where conformational flexibility plays a critical role.^{13, 14} Atomistic physics-based models of molecular recognition^{3, 15–30} include reorganization effects by considering the full free energy of the binding process.

However, the added benefits of physics-based models for calculating binding affinities over more approximate techniques like docking and scoring are uncertain and adoption in academic and industrial research continues to be low. While computational cost remains a relevant issue, poor reliability is often cited as the key barrier to adoption. After steady progress in the description of basic interatomic interactions, a growing awareness in the field is taking root about the remaining fundamental challenge of accurately modeling the entropic and conformational reorganization phenomena from first principles.^{31, 32} One of the aims of the present study is to examine the effects of conformational reorganization on binding.

Host-guest complexes provide an attractive alternative to protein-ligand systems for the study of general physical aspects of binding.^{19, 33–48} Due to their small size and simplicity, convergence of binding free energy estimates can be achieved for these systems at a relatively modest computational cost relative to protein-ligand systems. This computational ease also facilitates thorough statistical analysis, since a large number of absolute binding free energy calculations can be carried out and the global thermodynamic behavior of hosts with many guests can be characterized. In addition, structure-activity relationships are easier to tease out and trends in the enthalpic and entropic components for different groups of guests can be analyzed. Lastly, and very importantly, extensive high quality experimental binding affinity data in the form of calorimetric and spectroscopic measurements is available for host-guest systems. Data of this kind allows for direct comparisons between experiments and modeling prediction as illustrated for example by the recent SAMPL challenge to evaluate the current state of the art in free energy methods.^37–43. In contrast, protein-ligand binding data is most often available in the form of IC50 or EC50 inhibition constants, which are influenced by many, possibly unknown, factors in addition to the free energy of protein-ligand association.^49–51

Cyclodextrin (CD) host-guest complexes have been used as models for the study of molecular recognition phenomena.^{33, 52–54} CDs are employed in a variety of applications ranging from food and pharmaceutical preparations, to in-situ catalysis, and nanoengineering.^{55, 56} CDs are biological cyclic polymers of D-glucose molecules (typically with six, seven or eight monomers) formed through the degradation reaction of starch by cyclodextrin glucanotransferase (CGTase) enzyme via an intramolecular transglycosylation reaction.⁵⁷ The CD molecule is torus-shaped with a narrow opening laced with primary hydroxyls and a wider opening laced with secondary hydroxyls (Figure 1). The composition of the interior core is mainly hydrophobic. Due to its chemical nature, CD’s can coordinate with a variety of guests through either hydrophobic and/or polar interactions. The thermodynamics of CD host-guest complexation has been thoroughly studied experimentally; a comprehensive compilation of binding affinity data by Rekharsky and Inoue ⁵² is available. Studies by the Gilson lab ³³ used part of this set of thermodynamic data to evaluate the Mining Minima¹⁹ binding free energy model on a set of 15 host-guest CD complexes.³³

Figure 1.

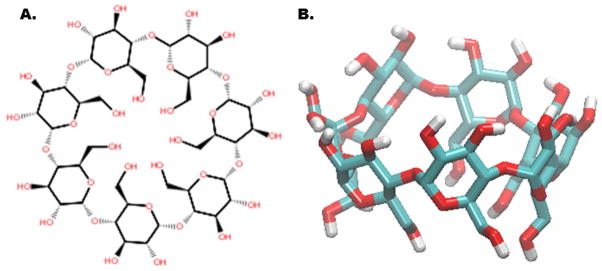
2D (A) and 3D (B) representation of β-cyclodextrin.

In this work, we employ the Binding Energy Distribution Analysis Method (BEDAM) ⁵⁸, a molecular dynamics-based absolute binding free energy method, to calculate standard binding free energies on a large set of β-CD host-guest systems, using the OPLS ^{59, 60} force field and the analytical generalized Born plus non-polar (AGBNP2) solvent model ^{61, 62}. BEDAM is based on a single direct alchemical coupling leg with implicit solvent (as opposed to two simulation legs as in the double decoupling method with explicit solvation^{17, 63}) and Hamiltonian replica exchange molecular dynamics for conformational sampling.⁵⁸ The Multiple Bennett Acceptance Ratio (MBAR) method⁶⁴ is employed to process the binding energy values of the conformational ensembles as a function of a coupling parameter (λ). The BEDAM approach has been used to model ligand binding affinities to protein receptors such as T4-lysozyme⁵⁸, FKBP12⁶⁵, HIV-RT⁶⁶ and others, as well as host-guest systems⁶⁷ as part of the SAMPL3 binding affinity challenge.

In this paper, we investigate the binding of β-CD to 57 different guests varying in size and chemical nature (Figure 2). For these calculations, we use a version of BEDAM which employs, in addition to parallel Hamiltionan replica exchange sampling, conformational reservoirs to further enhance sampling.⁶⁷ With these strategies convergence issues are reduced and the focus is shifted to evaluating the quality of the force field model and on examining trends in binding thermodynamics.

Figure 2.

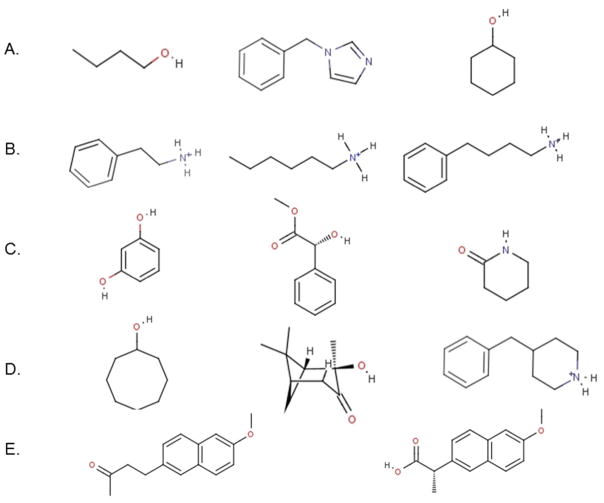
Chemical structures of 14 representative guests taken from the set of 57 guests investigated (see Supplementary Material for a complete list). Each row corresponds to a class of guest discussed in the text: (A) small guests with single functionalities well described by the model (this class comprises 17 members), (B) protonated amines (22 members) and (C) phenols, esters, and amides (6 members) with functionalities described less well by the model, (D) large and nominally rigid guests, and strong binders (10 members) believed to undergo complex reorganization upon binding, and (E) nabumetone and naproxen, which are correctly predicted as some of the strongest binders by the model.

We focus on comparing the relative performance of the full free energy model with models based only on the average binding energies in reproducing binding affinity rankings of this set of complexes. Similar to empirical approaches such as docking and scoring, and some MM/PBSA/GBSA implementations^{68, 69}, binding energies take mainly into account only the strength of host-guest interactions and neglect strain and entropic effects. We discuss the circumstances for which the full free energy model offers advantages in this respect.

II METHODS AND MATERIALS

A. Selection of host-guest systems

β-CD binding free energy data was obtained from a compilation of experimental studies by the Inoue and Rekharsky groups ^52–54. Complexes were selected from these sources if the chemical structure of the guest had less than 6 rotatable bonds, the binding affinity measurements were performed using microcalorimetry experiments and if the guests did not contain functional groups not explicitly parameterized for the AGBNP2 solvent model⁶²; guests with metals and sulfur were excluded. In general, the guests were selected in their R-stereoisomer conformation and at a pH value furthest away from the pKa to assist with the selection of the correct protonation state. We also included the 5 guests studied by Chen et al.³³

B. System preparation

Computations were performed for 57 host-guest systems in this study (Table S1 and S2). The molecular models were prepared using the Ligprep workflow as part of the Maestro program (Schrodinger inc.). Protonation states were assigned based on the experimental pH. Each initial conformation for the simulation was generated through the random placement of the guest in the host cavity.

C. BEDAM free energy protocol

The BEDAM method⁵⁸ is based on the formalism for the standard binding free energy $\mathrm{\Delta }{G}_b^{\circ }$ between a receptor A and ligand B using the following expression:

$$\mathrm{\Delta }{G}_b^{\circ }=-\mathit{kT}ln{C}^{\circ }{V}_{\mathit{site}}+\mathrm{\Delta }{G}_b$$ (1)

which follows without approximations, from a well-established statistical mechanics theory of association¹⁷, where β = 1/kT, C⁰ is the standard concentration for ligand molecules (set to C⁰ = 1M, or equivalently 1668 Å⁻³), V_site is the volume of the binding site and the binding free energy (ΔG_b) is defined below. In contrast to double decoupling methods in explicit solvation, in BEDAM, the receptor and ligand interact with the implicit solvent continuum. The binding energy

$$u(r_B,r_A)=V(r_B,r_A)-V(r_B)-V(r_A)$$ (2)

is defined for each conformation r = (r_B, r_A) of the complex as the difference between the effective potential energies with implicit solvation of the bound and separated conformations of the complex without conformational rearrangements.

BEDAM is based on biasing potentials of the form λu(r) yielding a family of λ-dependent hybrid potentials of the form

$$V_{\lambda }(r)=V_0(r)+\lambda \text{u}(\mathbf{r})$$ (3)

where

$$V_0(r)=V(r_B)+V(r_A)$$ (4)

is the effective potential in the decoupled state, when receptor and ligand are not interacting, and V₁ (r) is the effective potential in the coupled state, when receptor and ligand are fully interacting. The λ-dependent potential in Eq. (3) defines a transformation connecting the coupled and decoupled states through alchemical intermediate states in which receptor and ligand are partially interacting. A crucial aspect of the model is that at the end points and along the transformation, the ligand is confined within the chosen binding site volume (see below). The binding free energy (ΔG_b) in Eq. (1) is defined as the free energy difference between the λ = 0 and λ = 1 states.

Conformational sampling in BEDAM is enhanced by various advanced enhanced sampling strategies. A Hamiltonian replica exchange λ-hopping scheme is utilized to sample canonical distributions of structures at each λ-state. This implementation speeds convergence rates relative to simulating each λ state independently.⁵⁸ Conformational reservoirs of the λ=0 state^70–72 are also employed to accelerate the convergence of the BEDAM simulations.⁶⁷ The reservoirs are precomputed ensembles of the unbound host and guest from temperature Replica Exchange Molecular Dynamics (T-REMD).^{70, 71, 73} By using the reservoir, the BEDAM simulations can further explore conformational variability in the unbound state which may be necessary to capture multiple binding modes and/or the proper reorganization free energy during binding. To further improve convergence near λ=0, we also employed a modified a “soft-core” binding energy as implemented in our previous work.^65–67

We calculated the binding energy distributions and the standard binding free energies using the Multistate Bennett acceptance ratio estimator (MBAR).⁶⁴ For the MBAR analysis, we employed the code provided by John Chodera and Michael Shirts (http://alchemistry.org). Statistical uncertainties were obtained using block bootstrap analysis⁷⁴ with 100 blocks and 50 resampling trials for the last 3 ns of each BEDAM simulation. We also monitored the time evolution of several observables for each BEDAM simulation to ensure the convergence of each free energy simulation. This analysis is discussed in the Supplemental Information.

The conformational partitioning of the β-CD host-guest systems was based on the directionality of the guest’s polar functional group relative to the wider and the narrow rim on the β-CD (Figure 1). The directionality was determined by distance calculations involving the heavy atom of the polar group on the guest and each hydroxyl oxygen on the β-CD host. If the polar group of the guest was closer to the wider rim of the β-CD cavity, we referred to this conformation as an “up-state” binder. If the polar group of the guest was closer to the narrow rim, we referred to this conformation as a “down-state” binder. These binding modes were further characterized based on possible hydrogen bond interactions formed between the polar group and the hydroxyl oxygen. A hydrogen bond was formed between the guest and the host if the distance between the polar heavy atom on the guest and the hydroxyl oxygen on the host was less than 4.0 Å. The populations of different binding modes are described in the main text and are listed in Supplemental Table 3.

D. Thermodynamic decompositions

The binding free energy can be expressed as the sum of the reorganization free energy and the average binding energy¹⁶,

$$\mathrm{\Delta }{G}_b^{\circ }=\mathrm{\Delta }{E}_{\mathit{bind}}+\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$$ (5)

As illustrated in Figure 3, this decomposition corresponds to a hypothetical thermodynamic cycle in which the conformational ensembles of the unbound host (H) and guest (G) in solution are first reorganized to match those of the complex and in a subsequent step interactions between the host and guest are turned on. The first step corresponds to the reorganization free energy ( $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$) which can be further expressed as the sum of the intramolecular strain energies of the host and the guest, ΔE_strain, plus the change in conformational entropy $\mathrm{\Delta }{S}_{\mathit{conf}}^{\circ }$ upon binding:

$$\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }=\mathrm{\Delta }{E}_{\mathit{strain}}-T\mathrm{\Delta }{S}_{\mathit{conf}}^{\circ }$$ (6)

Figure 3.

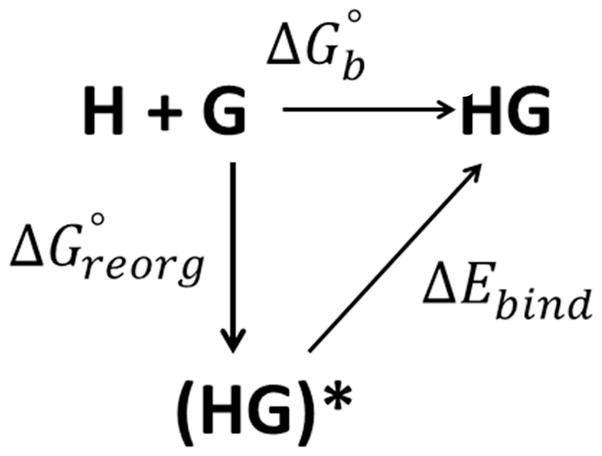
Thermodynamic cycle describing the binding of host-guest systems. H and G are the host and guest in the unbound state. (HG)* represents a state where the host and guest have been reorganized into their respective bound conformational ensembles with their interactions are turned off. HG represents the host+guest complex where the interactions between the host and the guest have been turned on.

ΔE_strain is the change in potential energy corresponding to the transformation of the conformational ensembles of the binding partners into the their respective bound conformation. $\mathrm{\Delta }{S}_{\mathit{conf}}^{\circ }$ measures the change in the number of accessible states of the system due to the formation of the complex and includes loss of translational, rotational, and vibrational freedom as well as reduction change in the number of the solution conformational states so as to be compatible with binding. $\mathrm{\Delta }{S}_{\mathit{conf}}^{\circ }$ is calculated as the difference between the reorganization and strain energy.

The average effective binding energy, ΔE_bind, which corresponds to turning on the interactions between the host and the guest in the bound state without conformational rearrangements, is an effective potential energy term which includes direct non-covalent interactions (electrostatic and van der Waals) as well as the net desolvation of the binding partners. ΔE_bind is computed from the average, 〈u〉_1, of the binding energy function in the ensemble of conformations of the complex in the coupled state (λ = 1). In the work, we use the term binding energy as shorthand for the “average effective binding energy”. The reorganization free energy ( $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$) is computed by difference from the computed binding free energy and the average binding energy:

$$\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }=\mathrm{\Delta }{G}_b^{\circ }-{\langle u\rangle }_1$$ (7)

An alternative thermodynamic decomposition is presented below in terms of compensating and energy/reorganization reinforcing components obtained by principal component analysis of average binding energies and reorganization free energies. The analysis was conducted with the prcomp() routine in R.⁷⁵ The main outcome of the principal component analysis are orthogonal axes, PC1 and PC2, in (ΔE_bind, $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$) space such that the projections PC1 and PC2 of (ΔE_bind, $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$) pairs along these axes are statistically uncorrelated; that is 〈δPC1δPC2〉_set = 0, where 〈…〉_set denotes an average over the 57 host-guest systems, and δPC1, δPC2 are deviations from the respective means.

E. Computational details

Binding free energies were obtained with the BEDAM method as described above using the OPLS-AA force field^{59, 60} and the AGBNP2^{61, 62} implicit solvent model. AGBNP2 includes an analytical pairwise descreening implementation of the Generalized Born model for the electrostatic term (G_el), a non-polar hydration free energy estimator for the non-electrostatic term (G_np), and a hydration correction term (G_hyd).

$$G_{\mathit{solvation}}=G_{el}+G_{np}+G_{\mathit{hyd}}$$ (8)

G_hyd accounts for first shell hydration effects not accounted for by linear dielectric screening, such as hydrogen bonding with solvent and water ordering in the receptor binding site. The hydration correction term is estimated using the analytical intermolecular hydrogen bond potential described by the following expression:

$$G_{\mathit{hyd}}={\sum }_{w}S(p_w)h_w$$ (9)

where S(p_w) is a switching function, based on the fraction p_w of solvent-occupied volume in the hydration site “w” of the first solvation shell of hydrogen bonding donor and acceptor groups of the solute and h_w is an empirical parameter that accounts for the water-solute interactions not accounted by the force field and solvation model. This correction parameter depends on the atom type of the solute (hydrogen bonding donor or acceptor or non-polar hydrogen). The sign of this component determines whether the interactions formed with the solvent are potentially favorable or unfavorable while its magnitude determines the strength of the excess interaction with water.

For this work, AGBNP2 parameterization was augmented to include two hydration sites for each glucose monomer pointing in, toward the buried interior of the β-CD host (Figure S1). The aim of these water sites is to model the effects of the expulsion of confined water molecules^{63, 76–82} from the cavity of the host upon binding of the guest. Based on preliminary results obtained from a training set of five guests previously studied in Chen et al.³³, the hydration strength of these water sites was set to h_w = 0.6 kcal/mol (See Supplemental Information).

The β-CD host-guest simulations were performed using the IMPACT program. ⁸³ Each system was equilibrated through energy minimization followed by thermalization at their respective experimental temperature. H-REMD simulations were conducted using 16 replicas at values of the coupling parameter λ set to 0.0, 0.001, 0.002, 0.004, 0.005, 0.006, 0.008, 0.01, 0.02, 0.04, 0.07, 0.1, 0.25, 0.5, 0.75, and 1.0. The binding site was defined as any conformation where the center of mass of the guest was within 6 Å from the center of mass of the host. No restriction on the ligand orientation was imposed. A flat bottom potential was utilized to restrict the guest to sample only the binding site volume. The volume of the binding site, V_site, can be expressed as the volume of a sphere with radius equal to the flat-bottom restraint potential tolerance above. In this work, V_site is approximately 904 ų and the standard state term, −kT ln C^∘V_site, is 0.36 kcal/mol.⁶⁷ Conformational reservoirs were obtained using temperature replica exchange with a series of 8 replicas between 300 and 600 K. Each T-REMD simulation was performed for 20 ns for each replica and frames from each trajectory were saved every 2 ps (10000 frames per trajectory). The 300 K temperature trajectories were subsequently used as the λ=0 conformational reservoir in the H-REMD simulation.

BEDAM simulations were performed for 5 ns per replica (80 ns cumulative simulation time for each complex) with a time step of 1.0 fs. Structures were saved every picosecond. The last 3 ns of data were used for analysis.

III RESULTS

BEDAM simulations were conducted for 57 β-CD host-guest inclusion complexes with a diverse set of organic molecules (Figure 2 and Figure 4) with some of the most common functional groups including aromatic, alcohols, protonated amines, amides, ketones, esters and ethers. In the following section, we characterize the structural and thermodynamic data collected from the BEDAM simulations to gain insights into the forces that guide binding in these small model systems.

Figure 4.

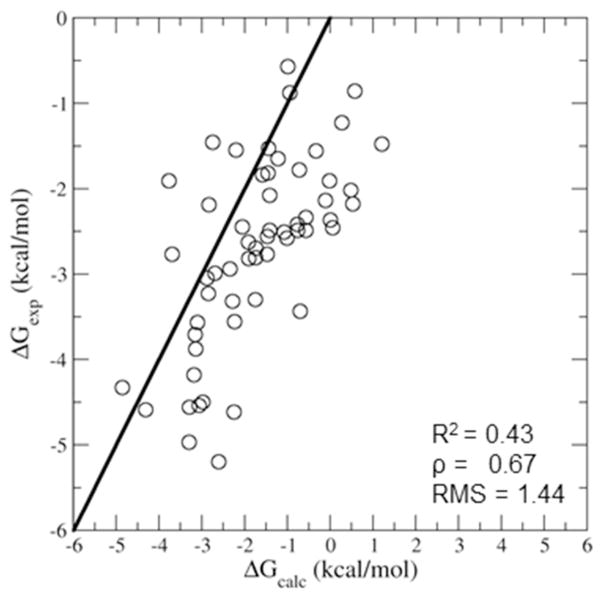
Comparison between the experimental and calculated binding affinities of the 57 β-CD host-guest complexes investigated. The x=y line is shown in black. The uncertainties for the experimental binding affinities generally range from 0.10 to 0.30 kcal/mol. The uncertainties for the calculated binding free energies range from 0.04 to 0.18 kcal/mol.

A. Binding Modes of β-CD host guest inclusion complexes

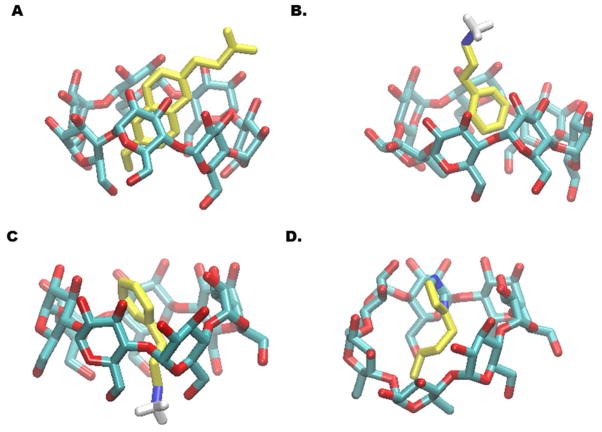
Absolute binding free energy approaches such as the BEDAM method allow us to investigate the interactions important in binding through the generation of ensembles of bound conformations. Generally, hydrophobic enclosure and the interaction of polar groups with pendant hydroxyls are the primary interactions driving the binding of the β-CD host guest systems. Hence, the hydrophobic and hydrophilic properties of the guest affect the binding mode and strength observed for each inclusion complex. The non-polar portion of the guest is typically located inside the cavity of the β-CD host as observed in the bound complex of β-CD+nabumetone (Figure 5A). In contrast, the polar portion of the guest typically protrudes into the solvent by pointing towards the secondary alcohols located on the wider rim of β-CD; this is also the most common binding mode for guests according to NMR studies.⁵² For instance, in the β-CD+nabumetone complex, the 1-butone group is sticking out of the β-CD through the wider rim while the more non-polar methyl ester group is pointed toward the narrow rim laced with primary alcohols. Hydrogen bonding interactions are also important for driving the binding of these β-CD complexes. For many polar guests, hydrogen bonds are formed between the polar atoms on the guest and the primary alcohols on the β-CD host. For β-CD+3-phenylpropylammonium, the most populated bound conformation (72% of the ensemble, Figure 5C) forms a h-bonding interaction between the charged amino group of the 3-phenylpropylammonium guest and the primary alcohols on the narrow rim of the β-CD. Some polar guests prefer to hydrogen bond with the secondary alcohols on the wider rim of the β-CD; this is observed for β-CD+1-butylimidizole (79% of the ensemble, Figure 5D).

Figure 5.

Binding modes of β-CD host-guest systems. Binding is driven by the hydrophobic enclosure of the non-polar group on the guest(A). Most guests are found in binding modes with their polar group sticking toward the primary (down-state) or secondary (up-state) alcohols. A majority of host-guest complexes found in the up-state conformation feature the guest’s polar group solvent exposed (B). This conformation is usually found in equilibrium with bound conformations where the guest is forming a hydrogen-bond in the down-state (C). However, some guests can be found with a hydrogen bond from the guest to the host in the up-state binding mode (D). The guests in these complexes are: nabumetone (A), 3-phenylpropylammonium (B/C)and 1-butylimidazole (D).

Enhanced conformational sampling protocols such as H-REMD as well as conformational reservoirs and soft-core potentials as implemented in the BEDAM approach are beneficial for the sampling of multiple binding modes that are relevant to the binding equilibrium and necessary for accurate binding affinity predictions. This is especially important for β-CD inclusion complexes which are relatively weak binders compared to the typical protein-ligand systems with more than one dominant mode for binding. We indeed often observe an equilibrium between two main binding modes of the guest inside the host cavity. In the first one mode, the guest has its polar functional group pointed towards the secondary alcohols; we refer to this conformation as the “up-state” binding mode (Figure 5B). In the second mode, the polar group points towards the primary alcohols; we refer to this conformation as the “down-state” binding mode (Figure 5C). Supplementary Table 3 includes the percentages of each binding mode in the ensemble as well as the percentage of time that a hydrogen bond forms in each respective binding mode. In a majority of β-CD host-guest systems, a hydrogen bond forms between the alcohols on the β-CD and the polar functional group on the guest in the down-state conformation. In the up-state conformation, the polar group of the guest prefers to be solvent exposed. This equilibrium is observed in guests containing amines and alcohols with longer alkyl chain such as R-hexanol. For example, the percentage of structures found in the down-state and up-state mode in the bound ensembles of R-2-hexanol+β-CD complex is 67% (64% forming h-bonds) and 33% respectively. In contrast, most guests containing ketone, imidazole and ester groups prefer to sample up-state conformations where the oxygen on the carbonyl group of the guest hydrogen bonds with the secondary alcohol on their wider rim (Figure 5D). The percentage of structures found in the down-state and up-state mode in the bound ensemble of 1-butylimidazole+β-CD complex is 21% and 79% (67% forming h-bonds) respectively. Smaller sized guests such as cyclic compounds and alkanols with shorter alkyl chains also prefer to sample the up-state binding h-bond mode, however, these guests can also form h-bonds with the oxygen atoms of the glycosidic linkage on the β-CD host. These dynamics are observed because smaller guests are more mobile in the host-cavity than larger guests.

B. Computed standard free energies of binding

The computed binding free energies are shown in Figure 4 compared to the corresponding experimental standard binding free energies. The calculated standard binding free energies range between 1.21 and −4.65 kcal/mol with an average of −1.73 kcal/mol. The corresponding experimental values are generally more favorable with an average binding affinity of −2.74 kcal/mol and ranging between −0.57 and −5.2 kcal/mol. The computed free energies are in reasonable agreement with the measurements (RMS_error = 1.44 kcal/mol and Spearman rank order coefficient ρ = 0.67). This level of agreement is consistent with the best models available^{33, 39} confirming that the model, force fields, and computational protocol we employed are sufficiently accurate to be used to study structural, energetic, and reorganization aspects of binding.

Naproxen and nabumetone (Figure 2E), with computed binding free energies of −4.85 and −4.31 kcal/mol, are predicted to be the strongest binders to β-CD in this set. These two guests are also among the strongest binders experimentally (measured binding free energies of −4.33 kcal/mol and −4.59, respectively). The calculations underpredict the strength of binding of 1R,2R,3S,5R-pinanediol, cyclooctanol, and 1R,2R,5R-2-hydroxy-3-pinanone (Figure 2D), which are the strongest binders experimentally.

In general, the computational model is found to be quite accurate (RMS_error = 0.74 kcal/mol and Spearman ρ= 0.84) for small aromatic and alkyl derivatives such as small linear, branched and cyclic alkanols, alkyl-ethers and alkyl-imidazoles (Figure 2A and Table S2B) comprising nearly a third of the overall set. The very good accuracy achieved for the latter class of compounds is in contrast to guests containing the alkyl-ammonium functionality such as hexylammonium (Figure 2B), whose binding free energies are often underestimated by more than 1 kcal/mol. This probably reflects difficulties in the model of accurately pinpointing the balance between electrostatic and desolvation effects of charged compounds such as these.⁸⁴ Alkyl-ammonium compounds, comprising 22 of the 57 guests, account for a large part of the deviations between computed and experimental affinities. Other problematic functional groups in this respect are phenols, anilines and amides (Figure 2C).

The binding free energies of guests with large or alkyl-substituted alkyl rings such as methylcyclohexanols, cycloheptanol, cyclooctanol, and the pinane derivatives mentioned above are also underestimated. As it is notoriously difficult to estimate accurately the relative free energies of rotameric states of complex cyclic compounds⁸⁵, this result suggests that, potentially, the energy model fails to properly model changes in rotameric states for these cyclic compounds.

C Thermodynamic decomposition

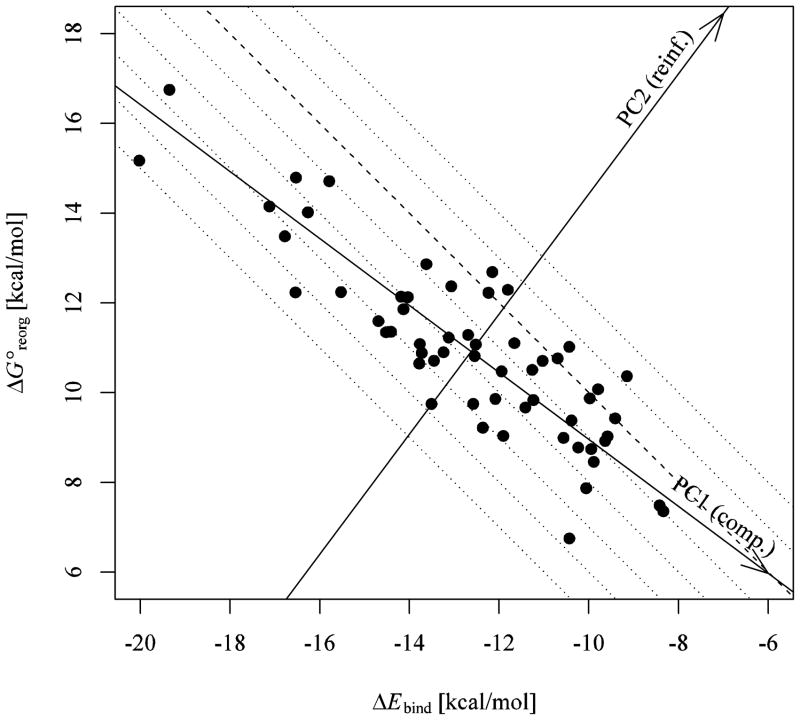
As illustrated in the Methods, the binding free energy is decomposed (see Figure 3, Figure 6 and Table S2A) into an average binding energy (ΔE_bind) component, which accounts for the effective energy of interactions between the host and the ligand in the bound state (λ=1), and a reorganization free energy term ( $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$), which measures collectively entropic losses and the intramolecular strain energies that oppose binding.¹⁶ The computed binding energies sample a range of values nearly one order of magnitude greater than the binding free energies from −20.02 to −8.33 kcal/mol with an average binding energy of −12.65 kcal/mol. The reorganization free energies are opposite in sign and sample a somewhat smaller range from 6.74 to 16.75 kcal/mol, with an average reorganization free energy of 10.92 kcal/mol.

Figure 6.

The reorganization free energies of the 57 host-guest complexes against the corresponding average binding energies. The dotted lines are loci of constant free energy of binding spaced in unitary increments. Starting from the dashed line at ${{\overline{\mathrm{\Delta }G}}^{\circ }}_{\text{b}}=0$, binding free energies decrease (become more favorable) towards the lower left corner of the plot and increase in the opposite direction. Also indicated are the axes corresponding to the first (PC1) and second (PC2) principal components of the data. The PC axes are centered on the mean point ( ${\overline{\mathrm{\Delta }E}}_{\text{bind}},{{\overline{\mathrm{\Delta }G}}^{\circ }}_{\text{reorg}}$). The uncertainties of the binding energies range from 0.04 to 0.56 kcal/mol. The uncertainties of the reorganization free energies range from 0.11 to 0.63 kcal/mol.

It is the compensation between binding energies and reorganization free energies which leads to computed binding free energies of significantly smaller magnitude which are commensurate with the experimental measurements. As evident from Figure 6, there is a strong and negative correlation between the two quantities (R² = 0.74 and ρ = −0.82). Compensation between binding energies and reorganization free energies, as well as related enthalpy/entropy compensation effects, are considered characteristic of the thermodynamics of non-covalent binding.^{2, 86–88} Based on the analysis below, for the 57 β-cyclodextrin host-guest complexes we observe on average as many as three quarters of a unit change of binding energy are lost to reorganization.

Also shown in Figure 6 are the PC1 and PC2 axes obtained by principal component analysis of the $\mathrm{\Delta }{E}_{\mathit{bind}}/\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$ data (see Methods). Along PC1, changes in ΔE_bind and $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$ have opposite signs (compensation), whereas along PC2 they vary in the same direction (reinforcement). The set of coordinates (PC1,PC2), obtained by projecting (ΔE_bind, $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$) pairs along the PC1 and PC2 axes, constitute an alternative representation of the binding energy/reorganization free energy data in terms of statistically uncorrelated variables (see Methods). As described in detail in the Supplementary Information, a linear relationship exists between these two representations, which, together with Eq. 5, lead to the following decomposition of the standard free energies of binding:

$$\mathrm{\Delta }{G}_b^{\circ }=\mathrm{\Delta }{G}_{\mathit{comp}}+\mathrm{\Delta }{G}_{\mathit{reinf}}$$ (10)

where ΔG_comp ≈ 0.2PC1 is the compensating component of the binding free energy, while ΔG_reinf ≈ 1.4PC2 is the corresponding reinforcement component. These relations indicated that a unitary change in PC2 causes a seven-fold greater variation in the binding free energy than a change in PC1 of the same magnitude. This behavior is consistent with the fact that the PC2 axis runs nearly parallel to the direction of greatest variation of binding free energy (see Figure 6), whereas the PC1 axis is nearly parallel to lines of constant binding free energy.

The binding affinity of a complex with a favorable ΔG_comp component can be interpreted as being influenced by a favorable host-guest interaction energy mostly offset by a reorganization free energy increase with proportion corresponding to the average compensation ratio of the set (roughly 75% based on the PC analysis). Conversely, ΔG_reinf describes deviations from this average compensating behavior by capturing effects that favor binding by simultaneously strengthening host-guest interactions and reducing reorganization losses. Unlike the ΔE_bind and $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$ components, which are highly correlated (i.e. complexes with large and favorable ΔE_bind tend to correspond to a large and unfavorable $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$), the ΔG_comp and ΔG_reinf components are uncorrelated so that, statistically, they occur independently from each other (i.e. a favorable ΔG_reinf component occurs equally likely in complexes with large or small ΔG_comp components).

It should be noted that the statistical PC analysis above, which is only capable of identifying how the binding thermodynamics of individual host-guest complexes compares with the average behavior of the set, does not directly offer a physical interpretation of compensation and reinforcement. However, as discussed below, we observed that experimental binding free energies of different classes of complexes display different patterns of correlations with the computed compensating and reinforcing components, potentially indicating a connection to molecular properties. A simple model of the compensation and reinforcement mechanism consistent with the observed thermodynamic signatures discussed below is presented in the Appendix.

The distributions of compensating and reinforcing components of the binding free energies of the 57 host-guest complexes are shown in Figure 7 (Table S4 in the Supplementary Information lists the corresponding values for each of the host-guest complexes investigated.) Relative variations of these quantities are more significant than their absolute scale. In this respect it is interesting to note that the range of variation of ΔG_reinf is nearly double that of ΔG_comp as measured by their standard deviations (0.64 kcal/mol and 1.17 kcal/mol, for ΔG_comp and ΔG_reinf, respectively). The greater variance of the reinforcing contribution indicates that differences in binding free energies among pairs of complexes are, on average, determined more by reinforcement mechanisms rather than compensation.

Figure 7.

Histogram of the compensating and, shaded, the reinforcing uncorrelated components of the binding free energy for the 57 host-guest systems. The uncertainty for the compensating component ranges from 0.10 to 0.83 kcal/mol. The uncertainty for the reinforcing component ranges from 0.11 to 0.84 kcal/mol.

D. Predictors of experimental rankings

In many structure-based ligand design applications, models of binding are employed not necessarily as quantitative tools, but rather as predictors of qualitative trends, such as rank-orders of binding affinities within congeneric series of ligands. In this section we explore the relative performance of quantities extracted from the calculations in reproducing trends in the measured binding affinities of the host-guest systems we investigated.

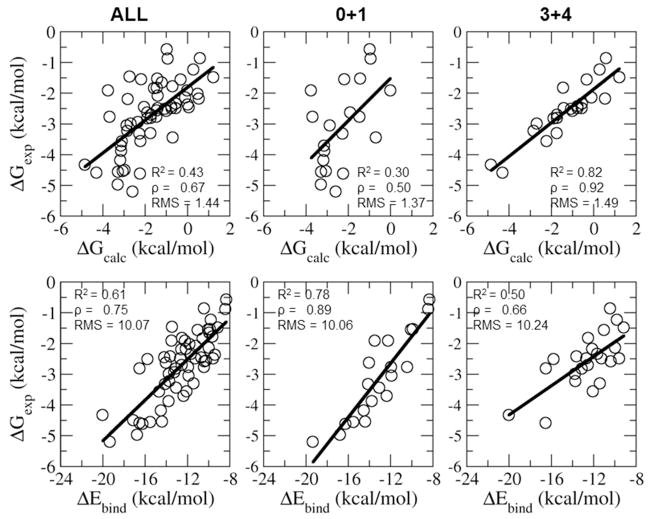
The computed binding free energies, with a Spearman rank-order correlation coefficient of ρ=0.68, are found to be reasonably good predictors of the relative binding strengths of the set of guests with respect to each other. The computed average binding energies, ΔE_bind lead to an even higher Spearman correlation coefficient of ρ = 0.75 (Figure 8) and are therefore, on average, better at reproducing relative ranks of guests compared to computed binding free energies. This is despite the fact that average binding energies are grossly inaccurate in a quantitative sense (computed average binding energies values range from −20 and −8 kcal/mol as compared to −5 to −0.5 kcal/mol for measured binding free energies).

Figure 8.

Comparison of the experimental and calculated binding free energies and experimental binding free energies and average binding energies for β-CD host-systems with guests with different numbers of rotatable bonds. The black line is the least squared fit line between the calculated and the experimental binding affinities.

While average binding energies are better overall predictors of rankings than computed free energies, it is notable that subsets of complexes exist where computed binding free energies are better predictors. Figure 8 displays the correlation between experimental binding free energies with computed binding free energies and average binding energies for complexes with rigid (0 to 1 rotatable bonds) and flexible guests (3 to 4 rotatable bonds). For rigid guests the binding energy is a better predictor of binding affinity rankings then computed binding free energies. However for flexible guests this behavior is reversed (ρ=0.66 for binding energies compared to ρ=0.92 for computed binding free energies), suggesting that modeled reorganization free energy losses, which are not included in the binding energy predictor and play a significant role in determining the rank ordering of binding, are sufficiently accurate for this subset of flexible guests to enable improved predictive accuracy using free energies as compared with only the binding energy component.

The interplay between energetic and reorganization driving forces is particularly noticeable for the subset of flexible guests with moderate binding affinity (−4 < ΔG_exp < −2) (Figure 9). The computed binding free energies reproduce very well the trends in the experimental affinities for this subset (ρ=0.93, p-value < 1e-4). In contrast, the binding energy and reorganization free energy components are each alone very poorly correlated to the experimental affinities (ρ=0.34 and 0.21, respectively) (Figure 9).

Figure 9.

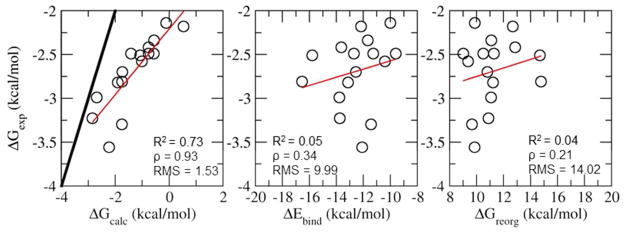
Comparison of the experimental binding free energies versus the calculated binding affinity, binding energy and the reorganization free energy for the 16 β-CD host-systems with guests with 3 or 4 rotatable bonds with moderate binding affinity (−2 < ΔG_exp < −4). The black line is the x=y line. The red line is the least squared fit line between the calculated and the experimental binding affinities.

Understanding the cause of the difference of performance of predictors for these two classes of guests would be very valuable for developing guidelines to suggest when it is feasible to adopt approximate models of binding in lieu of full free energy models in ligand design applications. The results above suggest that when the binding partners exhibit considerable flexibility, free energy models allow for superior predictive power than models based only on interaction energies. Clearly, most of the information needed to accurately rank rigid guests with our model is contained in the average binding energy values, whereas for flexible guests useful information is shared among both the energetic and reorganization components and, consequently, the full free energy model is better equipped to describe them.

The direct statistical quantification of this effect in terms of binding energies and reorganization free energies is confounded by the fact that these two quantities are strongly correlated (see above) and therefore contain related information. That is for example we find that the experimental affinities of any subset of complexes correlate to some extent with both, binding energy and reorganization components, if they correlate to any one of them. This is indeed problematic when comparing the thermodynamic trends for the rigid and flexible guests. One would expect that flexible guests would reorganize more than rigid guests; however their distributions are quite similar. More useful insights are obtained by analyzing the data in terms of the compensating and reinforcing components, which, by construction, contain orthogonal information. We find that experimental binding free energies for the complexes with rigid guests correlate almost exclusively with the compensating component ΔG_comp (correlation coefficient R² = 0.72 relative to ΔG_comp and R² = 0.0024 for ΔG_reinf). In contrast, the experimental binding free energies for the flexible guests correlate to both compensating and reinforcing components (R² = 0.35 for ΔG_comp and R² = 0.71 for ΔG_reinf), indicating that the combination of these two independent sources of information is responsible for the better performance of the free energy model for the set of flexible guests.

This hypothesis is further confirmed by analysis of variance (ANOVA) tests (see Supplementary Material) of single variable versus bilinear regression models of the experimental free energies using as predictors both ΔG_comp and ΔG_reinf, or only one of the two. These tests show that for complexes with flexible guests a bilinear model incorporating ΔG_comp and ΔG_reinf is significantly superior to linear models based only on ΔG_comp or ΔG_reinf alone. In contrast, for rigid guests adding the ΔG_reinf variable does not improve by a statistically significant amount a regression model based only on ΔG_comp.

It is interesting to note that the observed lack of significance of the reinforcing component for rigid guests relative to flexible guests does not appear to be due to obvious differences in magnitude and variability of reinforcing effects; for example, the standard deviations of ΔG_reinf differ by only few percentage points between the rigid and flexible subsets. It is therefore tempting to hypothesize that, while compensating and reinforcing effects are present throughout the systems investigated, our free energy model fails to correctly capture reinforcing effects for some of the complexes with rigid guests, but is successful for the set of 23 flexible guests. This point is elaborated further below.

IV DISCUSSION

In this work, we investigated the binding thermodynamics of 57 β-CD host guest systems using the BEDAM free energy protocol. Perhaps one of the main conclusions of this work is that atomistic free energy models of this kind can be deployed on this large scale allowing the survey of a large variety of chemical functionalities and topologies, and draw insights about general trends. Large scale surveys of solvation free energy predictions have long been used as validation benchmarks for force fields and free energy protocols.^89–94 The present work is one of the first attempts to compare side by side binding affinity data and rigorous binding free energy predictions on a large scale.

Binding equilibria probes intramolecular interactions in more direct ways than vacuum to water transfer free energies. Binding processes probe the relative preference of chemical groups to interact with water and with each other; something that is of a direct relevance for the modeling of molecular recognition processes in solution. For example, it is feasible, as we have done here, to investigate ionic interactions, which are problematic for hydration free energy studies due to experimental and modeling limitations. Furthermore, large sets of high quality experimental binding affinity data are available for host-guest systems such as the ones studied here, covering many different chemical functional groups. Due partly to difficulties in obtaining hydration free energy data of sufficient quality, a recent SAMPL challenge aimed at evaluating the current state of the art in free energy methods has focused on the prediction of host-guest binding free energies.³⁸ We expect that large scale binding free energy surveys will find increasing use in validation experiments of this kind.

Dehydration of the interior of beta-cyclodextrin is believed to be one of the primary driving forces towards binding.⁹⁵ This effect is based on the idea that water molecules are unfavorably restricted (entropically and enthalpically relative to bulk water) within the hydrophobic binding site of the host. Upon ligand binding, these water molecules are released from the binding cavity into the bulk, resulting in a free energy gain. Hydration effects such as these are quite challenging to model.^{81, 82, 96} In this work, we are using an implicit solvent model with hydration sites in the host-cavity of β-CD to model the effects of water expulsion. Specifically, the AGBNP2 parameterization was augmented to include two sites for each glucose monomer pointing in toward the buried interior of the β-CD host (Supplemental Information Figure S1A and S1B). The aim of these hydration sites is to model the effects of releasing confined water molecules upon binding of the guest. A positive free energy factor of 0.6 kcal/mol is associated with each fully water-occupied hydration site. In the bound state, most guests will occupy these positions which will result in no energetic penalty. In the unbound state however, most of these water sites will not be occupied by solute atom resulting in a maximum free energy factor of +7.0 kcal/mol (14 hydrogen bond sites * +0.6 kcal/mol) in favor of the bound state (although it is often significantly smaller than this maximum due to partially occupancy in the bound state by host atoms, especially in distorted conformations). Including the effects of expulsion of enclosed water molecules leads to a more realistic model that can mimic phenomena typically not described by implicit solvent representations.

Computational predictions were found to be in reasonable quantitative agreement with measured affinities. The accuracy of predictions (RMSD=1.44 kcal/mol) is comparable to high-quality recent hydration free energy studies ^90–94 and binding free energy calculations of host guest systems.^{33, 48} The particularly good accuracy for small guests (RMSD=0.74 kcal/mol, see Supplementary Material) containing alkyl, aromatic, alkanol, alkyl-ether and alkyl-imidazole functionalities adds to our confidence of the fundamental soundness of the computational model. Derivatives built around the same simple scaffoldings and containing functional groups such as ammonium, phenols, and aromatic amines, were predicted less well, suggesting that these would benefit from reparameterization of force field and/or solvation parameters. Conversely, compounds with complex topologies such as those with single and condensed alkyl rings, appear problematic even when in combination with functionalities that are modeled correctly in simpler compounds, suggesting that conformational reorganization processes exist for these complexes that are not completely captured by the model (see discussion below).

Thermodynamic decomposition shows that the binding free energies are the result of a large compensation between favorable binding energies, which measure the strength of net interactions between the host and the guest, and unfavorable reorganization free energies, which measures conformational entropy losses as well as strain energies.^{2, 16, 86} We generally observed small strain energies for these host-guest complexes (Table S5), indicating that reorganization free energies are dominated by entropic contributions. Compensation between binding energies and entropic losses has been observed in modeling studies of binding of cyclodextrins³³ and other host-guest systems^{19, 67} as well as protein-ligand systems⁶⁵. The related enthalpy-entropy compensation effect has been observed and discussed in many contexts.^{87, 97} It has been rationalized in terms of the greater entropic and energetic strain costs necessary to form stronger and specific receptor-ligand interactions. Doubts have been raised concerning the physical insights obtainable from entropy/enthalpy information^{98, 99} and the usefulness of basing ligand design choices on this information.⁸⁸

In the present application, thermodynamic decomposition of binding free energies into average binding energies and reorganization free energies has been useful in gaining insights into the thermodynamics of binding of these systems. The first observation is that both energetic and reorganization effects are important, as quantitative agreement with the magnitude of measured affinities is obtained only by considering them together. On the other hand, experimental affinity rank orders for the entire set are reproduced by considering only average binding energy values. Based on this observation it can be concluded that for these small molecular systems binding is primarily driven by receptor-ligand interactions. That is guests capable of forming, say, stronger van der Waals interactions with the host are also likely to display stronger binding affinity. The increase of the interaction strength tends however to overestimate the effect on the binding affinity because this is opposed by a concomitant increase in the reorganization free energy that, because it is often of smaller magnitude, tends to dampen the effect rather than reverse it. However, as discussed below, important exceptions to this general trend for the more flexible guests have been found, which have provided further insights into the behavior of these systems and the performance of the free energy model we employed.

Whereas the affinity rank order of rigid guests were reproduced by the binding energies, the rankings of flexible guests were found to be poorly correlated to binding energies or reorganization free energies individually, and that only their combination into binding free energy scores accurately reproduced the measurements. Clearly, mutual information contained in both components is helpful for flexible guests.

The significance of this effect is crystallized by the results shown in Figure 9 for the 16 flexible guests with moderate affinity. Trends in measured binding affinities for this set are practically uncorrelated to binding energies scores alone. For example 4-phenylbutylammonium, the guest with the strongest binding affinity (−3.56 kcal/mol) in this set, has a moderate binding energy score of −12.08 kcal/mol, exceeded by more than half of the guests in the set. Despite this, the binding free energy score, which includes the reorganization free energy component, accurately predicts that 4-phenylbutylammonium is among the three best binders of the set. While in this case the improved prediction is due to a low reorganization free energy, in general, as shown in Figure 9, reorganization free energy scores alone are also unhelpful in picking trends in binding affinities. Clearly the considerably improved rank order predictions for flexible guests hinge on the capability of the free energy model to capture the balance between the strength of host-guest interactions and the opposing reorganization losses, which vary considerably from average values.

Understanding this interplay is complicated by the fact that energetic and reorganization effects do not occur independently. As discussed above these are, in fact, highly correlated so that it has proven difficult to disentangle the information contained in one, the other, or their combination. We found indications that the quality of binding free energy predictions is not strongly tied to the ability of the model to reproduce energetic and reorganization effects, but rather to the ability of the model to describe compensating and reinforcing effects. This conclusion derives from the observation that for the classes of complexes well represented by the free energy model (those with small and flexible guests) information from compensating and reinforcing components together explain variations in binding affinities better than either of the two components individually. In contrast, the affinities of larger and nominally rigid guests correlate almost exclusively with the compensating component, ΔG_comp, with the reinforcing component appearing to simply add “noise” to the predictions.

The results suggest that energy/reorganization reinforcing effects connected with conformational induced fit processes are better captured for flexible guests, where conformational rearrangements mostly involve simple rotations of alkyl chains. On the other hand, guests containing large cycloalkyl and condensed alkyl rings such cycloheptanol and octanol and the pinane derivatives discussed above, while nominally classified as rigid based on the count of rotatable bonds, are suspected to undergo cooperative conformational rearrangements of the ring to bind to β-CD, perhaps also in combination with specific rearrangements of the host, which are not modeled sufficiently accurately by the force field.

Based on these observations, we conclude that the model we employed accurately describes compensating effects common to the rigid and flexible guests. We speculate that these are due to compensating processes involving local energetic strain and restrictions to vibrational and rotational motion occurring upon binding.^{2, 100} In contrast, effects due to complex conformational changes upon binding^{23, 24, 31, 101} and redistribution of population among multiple binding modes lead to energy/reorganization reinforcement. The latter effects are more difficult to model because they involve capturing the remodeling of the conformational landscapes of the binding partners rather than only the strength of interatomic interactions.

While most complexes display a combination of both compensating and reinforcing behaviors, analysis of guest modifications leading to nearly “pure” compensating or reinforcing behavior confirms the hypothesis that compensation follows the formation of specific host-guest interactions whereas reinforcement is caused by a population redistribution among conformational macrostates. The hydrogen-to-methyl substitution on the ammonium group of phenethylammonium (see N-methylphenethylammonium and phenethylammonium in Tables S2A and S4 in Supplemental Section) is an example of a purely compensating modification resulting in a 2.9 kcal/mol energetic gain, 75% of which is canceled by a compensating reorganization penalty of 2.2 kcal/mol. The methyl substitution results in an energetic gain as a result of an increase in the number and strength of the hydrogen bonds formed between the host and the guest in the down-state conformation; this down-state conformation is compensated by a substantial reorganization penalty. In contrast, the significant gain in affinity corresponding to the ortho-to-para isomerization of methoxyphenethyammonium is, according to our model, largely due to energy/reorganization reinforcement (see the 2-methoxyphenethylammonium and 4-methoxyphenethylammonium entries in Tables S2A and S4 in Supplemental Information). That is, the para isomer is favored over the ortho isomer both in terms of energetic gain and reduced reorganization penalty. This is consistent with the poorer fit and more restricted motion of the ortho isomer in the host cavity, and with the ability of the para-isomer to sample both down-state and up-state binding modes (Table S3).

Implications for computational drug design

In the field of structure-based drug design, the accurate prediction of protein-ligand binding affinities remains very challenging. Molecular modeling, almost exclusively in the form of virtual screening applications, has been proven useful in lead identification. Methods such as docking and scoring and MM/PBSA/GBSA^{18, 102} are commonly used for predicting affinity rankings, although often they capture only differences in interaction energies and neglect entropic and reorganization effects. For congeneric series of ligands sharing the same binding mode where the binding energy is correlated with the experimental binding affinities, these methods can sometimes successfully predict experimental rank ordering.¹⁰ Yet, in cases involving larger, flexible ligands and receptors, possibly undergoing conformational reorganization and capable of binding in multiple modes, entropic and reorganization effects play a greater role.

In this work, we have demonstrated that accounting for the full free energy of binding, including entropic effects explicitly, provides a significant advantage in predicting the rank ordering of binding affinities for a large set of flexible guests. We found that accurate predictions for this class of guests stem from information from both compensating as well as energy/reorganization reinforcing processes. Binding energy-based predictors predominantly capture only energy/reorganization compensation effects and are therefore not as capable at describing the affinities of this class of guests. However, energy/reorganization reinforcement processes, which likely often involve population redistribution among multiple conformational states upon binding, are more difficult to model. Difficulties arise both because of slow equilibration among conformational states in rugged energy landscapes (something we sought to overcome in this work), but also, and more importantly, because conformational populations and their responses to binding can be very sensitive to force field inaccuracies. This is in contrast to effects due to specific ligand-receptor interactions, which can be related to a specific binding mode of the complexed state, but often lead only to expected binding energy and compensation signatures.

This assessment points to a major challenge for free energy simulations as applied to ligand design.¹⁰³ Energy/reorganization reinforcing processes, which are the most likely to lead to large affinity enhancements and can lead to the discovery of candidates with new binding modalities, are unfortunately also the processes that are the most difficult to model accurately.

V Conclusions

In this paper, we present results from a large scale survey studying the binding of 57 β-CD host-guest systems using the BEDAM algorithm to calculate absolute binding free energies. For this large set we have observed that generally accurate binding affinity predictions can be obtained. Difficulties are noted for some functional groups, which could benefit from tuning of interaction and solvation parameters, and for some cycloalkyl guests which likely undergo complex conformational rearrangements upon binding in ways that are not fully captured by our model.

Statistical analysis has revealed that the successes as well as the failures of the free energy model have hinged in part on the level of description of effects that lead to energy/reorganization free energy compensation versus those that lead to reinforcement. We have identified classes of flexible guests (with more than three rotatable bonds) for which modeled reinforcements effects provide a more accurate description of measured affinities than compensation effects alone.

While improvements of energy models and conformational sampling tools are needed to improve the accuracy of free energy models so as to make them robustly applicable to complex biological systems, the promising results obtained here have offered insights on aspects of physics-based atomistic free energy models with the potential to provide significant advances in drug design applications over simplified approaches based only on interaction energy scoring.

Appendix

A simple physical model of compensation and reinforcement

Consider the ligand-receptor system depicted in Figure 10, consisting of a ligand, L, receptor, R, and complex RL with internal degrees of freedom x_L, x_R, and x_RL of dimensionality n_L, n_R, and n_RL=n_L+n_R+6, respectively. The 6 additional degrees of freedom of the complex correspond to the position and orientation of the ligand relative to receptor. All of these degrees of freedom are assumed to follow a harmonic potential of the general form

Figure 10.

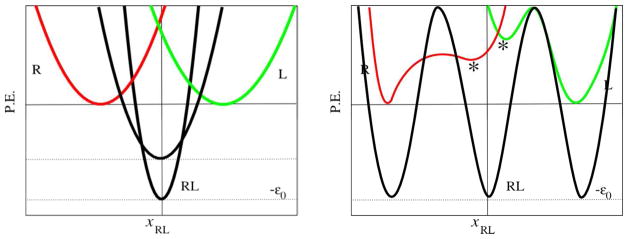
Illustration of the potential energy landscapes of receptor (red) and ligand (green) in the unbound state, and of their complex (black). The left panel shows two representative potential energy landscapes for the complex, one in which the well-depth (ligand-receptor interaction energy) is large and accompanied by a concomitantly large reduction of flexibility, and another one characterized by a smaller energy gain and smaller reduction of flexibility. The right panel illustrates a more general case with multiple equivalent binding modes of the complex and multiple macrostates of the receptor and ligand in the unbound state, only some of which (denoted by a “*”) are compatible with binding.

$$U(x)=\frac{{\text{k}}_f}{2}{(x-x_0)}^2$$ (11)

where (x − x₀)² is a square distance in n-dimensional space and k_f is a generalized force constant. The latter can be equivalently interpreted as an actual spring constant or the inverse of the variance of a multivariate Gaussian distribution over a set of collective variables.

From the expression of the binding constant^{16, 17}

$$K_b=C^{\circ }\frac{Z_{RL}}{Z_R{Z}_L}$$ (12)

where C^∘ is the standard state concentration and Z_s is the internal configurational partition function of species s, and extending the integration of the external degrees of freedom of the ligand for Z_RL to infinity (assuming a negligible contribution from the integration of the Gaussian function outside the binding site volume), we obtain

$$K_b=e^{{\epsilon }_0/kT}\left[C^{\circ }{\left(\frac{2\pi kT}{{\text{k}}_t}\right)}^{3/2}\right]\left[{\left(\frac{2\pi kT}{{\text{k}}_{\theta }}\right)}^{3/2}\right]\left[{\left(\frac{{\text{k}}_L^u}{{\text{k}}_L^b}\right)}^{n_L/2}\right]\left[{\left(\frac{{\text{k}}_R^u}{{\text{k}}_R^b}\right)}^{n_R/2}\right]$$ (13)

where ε₀ is the magnitude of the well depth of the complex relative to the sum of those of the receptor and ligand (see Figure 10), k_t and k_θ are the generalized force constants for the translational and rotational degrees of freedom of the ligand, respectively, ${\text{k}}_L^u$ and ${\text{k}}_L^b$ are the generalized force constants for the internal degrees of freedom of the ligand in the unbound and bound states, respectively, and ${\text{k}}_R^u$ and ${\text{k}}_R^b$ are similarly defined for the receptor. The standard binding free energy is $\mathrm{\Delta }{G}_b^{\circ }=-\mathit{kT}ln{K}_b$.

Let us now hypothesize that the internal degrees of freedom of the receptor and ligand are more restrained in the complexed state than in the unbound state, that is we assume that the ratios ${\tau }_L={\text{k}}_L^b/{\text{k}}_L^u$ and ${\tau }_R={\text{k}}_R^b/{\text{k}}_R^u$ are greater than one. For simplicity we also make the assumption that the degree of reduction of flexibility is the same for ligand and receptor, that is τ_L =τ_R =τ.

Further, we hypothesize that a one-to-one monotonic relationship τ=τ(ε₀) exists between the ligand-receptor interaction energy ε₀ and the change in flexibility of the ligand and receptor upon binding (flexibility metric (τ)). Specifically, we hypothesize that flexibility is decreased with increasing interaction energy (as depicted in Figure 10) in such a way that the binding energy and reorganization free energy contributions to the binding free energy compensate and result in a linear relationship between binding free energy and binding energy:

$$\mathrm{\Delta }{G}_b^{\circ }=\alpha \mathrm{\Delta }{E}_{\mathit{bind}}$$ (14)

as seen for the average behavior observed for the host-guest systems studied (where we measured a linear coefficient of α ≈ 0.25). By computation from the partition of the complex Z_RL or by direct application of the equipartition theorem, the average binding energy is

$$\mathrm{\Delta }{E}_b=-{\epsilon }_0+\frac{kT}{2}(n_L+n_R+6)=-{\epsilon }_0+\frac{n_{RL}kT}{2}.$$ (15)

By substituting this expression in Eq. (14) and applying the hypotheses so far formulated, we obtain

$$\tau ({\epsilon }_0)=e^{\alpha n_{RL}/(n_R+n_L)}{e}^{2(1-\alpha ){\epsilon }_0/[kT(n_R+n_L)]}$$ (16)

which establishes that, for a strict linear relationship between binding free energy and binding energy to occur, the rate of reduction of the variances of internal coordinates must increases exponentially with the increase of the magnitude of the ligand-receptor energy per degree of freedom, ε₀/(n_R + n_L), of the binding partners.

The simple illustrative model above formulates a mechanistic hypothesis for the source of the compensating contribution ΔG_comp extracted from the host-guest data and discussed in the main text of the paper. The formation of specific host-guest interactions (such as a hydrogen bond) is accompanied by a reduction of flexibility and increased unfavorable reorganization of the atoms involved. The two effects are on average tied by a relationship, such as the one derived above, such that only a fraction of the gain in host-guest interaction energy translates into increased binding affinity.

Now consider the case in which the observed binding constant is the results from the contribution of multiple binding modes (Figure 10, right panel). It can be generally shown¹⁶ that in this case the binding constant can be expressed as the sum of the binding constants corresponding to each binding mode i:

$$K_b={\sum }_i{K}_b(i)$$ (17)

where K_b(i) is assumed to be given Eq. 13 with binding mode-dependent parameters ε₀(i), ${\text{k}}_L^b(i)$, etc. as assumed above and obeying the compensation relationship (Eq. 16). By following the same arguments as sketched out above, it is straightforward to show that the binding constant of each mode scales as K_b (i) ∝ exp[αε₀(i)/kT], thereby showing that the overall binding constant is dominated by the mode with the greatest interaction energy and, consequently, the same conclusions reached above for the case of a single binding mode apply.

If, on the contrary, N_m binding modes of similar interaction energy ε₀(i) ≈ ε₀ contribute approximately equally, it is straightforward to show that the overall binding free energy is given approximately by

$$\mathrm{\Delta }{G}_b^{\circ }=\mathrm{\Delta }{G}_b^{\circ }(1)-\mathit{kT}ln{N}_{\text{m}}$$

where $\mathrm{\Delta }{G}_b^{\circ }(1)$ is the binding free energy corresponding to one of the equivalent binding modes.

In addition to multiple binding modes, the binding partners may undergo conformational reorganization to adapt to one or multiple binding modes of the complex (Figure 10, right panel). This effect can be captured by a parameter p* representing the population of the binding-competent macrostate in the unbound state:

$$\mathrm{\Delta }{G}_b^{\circ }=\mathrm{\Delta }{G}_b^{\circ }(1)-\mathit{kT}ln{N}_{\text{m}}-\mathit{kT}ln{p}^{\ast }$$

Based on the arguments above we have established that the binding free energy to a typical binding mode $\mathrm{\Delta }{G}_b^{\circ }(1)$ is proportional to the average binding energy ΔE_b(1) of that mode (which, given the assumption of equivalency of the binding modes is equal to the overall average binding energy ΔE_bind) with proportionality coefficient α. We can therefore tentatively identify this term with the compensating contribution ΔG_comp.

The remainder, −kT ln N_m −kT ln p*, captures the effect of multiple contributing binding modes and the population of the binding-competent macrostate in the unbound state which, can be hypothesized to be not statistically correlated with the properties of the individual binding modes of the complex. After all, it is not obvious why the strength of a binding mode should be related to the number of such modes, or to the behavior of the binding partners when they are not interacting. In conclusion, given that, by definition, the compensating and reinforcing component are statistically uncorrelated, it is reasonable to identify the conformational redistribution term −kT ln N_m −kT ln p* with the reinforcement component ΔG_reinf extracted from the host-guest data and discussed in the main text.