The Need for Double-Sampling Designs in Survival Studies: An Application to Monitor PEPFAR

Summary

In 2007, there were 33.2 million people around the world living with HIV/AIDS (UNAIDS/WHO, 2007). In May 2003, the U.S. President announced a global program, known as the President’s Emergency Plan for AIDS Relief (PEPFAR), to address this epidemic. We seek to estimate patient mortality in PEPFAR in an effort to monitor and evaluate this program. This effort, however, is hampered by loss to follow-up that occurs at very high rates. As a consequence, standard survival data and analysis on observed nondropout data are generally biased, and provide no objective evidence to correct the potential bias. In this article, we apply double-sampling designs and methodology to PEPFAR data, and we obtain substantially different and more plausible estimates compared with standard methods (1-year mortality estimate of 9.6% compared to 1.7%). The results indicate that a double-sampling design is critical in providing objective evidence of possible nonignorable dropout and, thus, in obtaining accurate data in PEPFAR. Moreover, we show the need for appropriate analysis methods coupled with double-sampling designs.

1. Introduction

According to the Joint United Nations Programme on HIV/AIDS (UNAIDS) and World Health Organization (WHO) statistics, in 2007 there were 33.2 million people around the world living with HIV/AIDS (UNAIDS/WHO, 2007). Almost 23 million of these live in sub-Saharan Africa. In May 2003, the U.S. President announced a global program, known as the United States President’s Emergency Plan for AIDS Relief (PEPFAR), to address this epidemic, primarily in Africa. In response to this initiative, the U.S. Congress passed the United States Leadership Against HIV/AIDS, Tuberculosis, and Malaria Act of 2003. Under this act, $15 billion were allocated over 5 years (2004–2008). The act calls for an evaluation of the PEPFAR program, which screens, treats, and follows HIV patients over time.

A key component of the evaluation of the impact of PEPFAR-supported programs on the HIV epidemic is the estimation of survival for patients under their care. As these are usually outpatient care and treatment programs that monitor mortality passively, a major obstacle for their appropriate monitoring and evaluation is patient loss to follow-up, which occurs at rates as high as 59% (van Oosterhout et al., 2005). Moreover, there is some evidence that standard analytic methods produce biased results in the sense that the individuals lost to follow-up (“dropouts”) are generally sicker than those who stay in the study (Touloumi et al., 2002; Wu, 2007). Thus, estimates derived from passively monitored programs may seriously underestimate patient mortality (Antiretroviral Therapy in Lower Income Countries Collaboration and ART Cohort Collaboration groups, 2006) even after adjusting for covariates measured prior to dropout.

Of course, methods based solely on such passive monitoring can be enriched through sensitivity analysis (e.g., Rosenbaum and Rubin, 1984; Scharfstein et al., 2001), or joint parametric modeling of survival and dropout (e.g., De Gruttola and Tu, 1994). Such methods, however, cannot provide additional objective evidence of nonignorable dropout (i.e., different survival between dropouts and nondropouts) after conditioning on the observed (possibly longitudinal) covariates (for an analogous argument, see, e.g., Scharfstein et al., 2001, points (b) and (c), p. 406). The important role of double sampling is that it does provide such objective evidence (e.g., Glynn, Laird, and Rubin, 1993; Hirano, Imbens, and Rubin, 2001; Scharfstein et al., 2001), although the way to extract this evidence can be challenging with survival data (Frangakis and Rubin, 2001, FR01 henceforth).

“Double sampling” is a design-based method first introduced in survey research (Neyman, 1938). It aims to address this issue of nonignorable dropout by allocating resources to intensively pursue and find a sample of observed dropouts. Baker, Wax, and Patterson (1993) and FR01 both addressed analysis of double sampling in the context of survival data. In particular, FR01 showed that a bias arises when standard double-sampling methods are used with survival data; FR01 also derived the empirical maximum likelihood estimator (MLE) based on minimal data requirements without covariates.

In this article, we apply the double-sampling design to survival data from one of the PEPFAR-funded sites in western Kenya, with appropriate extensions to allow for covariates in the design and analysis. We show that we obtain substantially different and more plausible estimates of patient mortality rates when using the double-sampled data appropriately. The results indicate that a double-sampling design is critical for accurate data in PEPFAR and providing objective evidence for possible nonignorable dropout, and that special methods are critical for appropriate analyses of such data to monitor and evaluate PEPFAR.

2. Design and Data

Data were assembled by one of us (CY, Principal Investigator of the Regional Data Center in East Africa¹) for a study cohort of 8977 adults who entered the PEPFAR program in western Kenya between January 1, 2005 and January 31, 2007. The care and treatment program and the patient double-sampling (“outreach”) efforts are described in detail elsewhere (Wools-Kaloustian et al., 2006; Einterz et al., 2007).

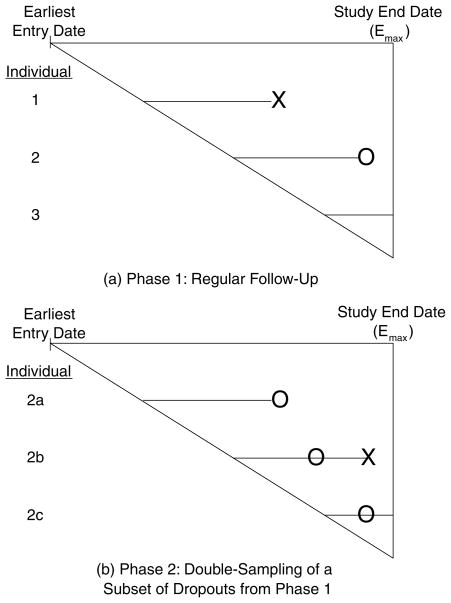
The design of our study has two possible “phases” of follow-up for each individual, each phase corresponding to different intensities of follow-up effort. Figure 1 depicts these two phases: the diagonal line of the triangle allows visualization of the different entry date of each individual; and the vertical line represents the common date of analysis, which we label “study end date. “ For an individual who enters the study, the follow-up effort in the first phase is at a regular level, meaning we record data from either regularly scheduled follow-up visits or from finding the alive status with relatively simple effort (e.g., a relative calling in). In this phase, an individual is either observed to die (individual 1 in Figure 1), or observed to remain alive until the end of study (individual 3), or else observed to drop out (lost to follow-up) before death or end of study (individual 2).

Figure 1.

The two phases of double sampling with survival data (X denotes death and O denotes dropout).

In the second phase, we consider the observed dropouts from the first phase. From among these dropouts, the design selects a subset to be double sampled (individuals 2b and 2c in Figure 1). This selection can be based on stratification variables. The individuals double sampled in the second phase are then pursued intensively (e.g., including tracking them even to their house at remote regions of the country using maps) and are observed either to die (individual 2b) or to remain alive until the end of the study (individual 2c).

The study in Kenya follows a protocol of deciding when to double sample patients lost to follow-up according to antiretroviral treatment (ART) start status. If the patient has been on ART for less than 3 months, then double-sampling efforts start 1 day past the missed visit. For patients on ART more than 3 months, double sampling begins 7 days past a missed visit. Finally, for patients not on ART, double sampling begins 28 days past a missed visit. The team conducting the double sampling consists of HIV-infected patients. This team first tries to contact the person by telephone and, if necessary, performs a home visit often in remote areas. In this manner, the patient’s vital status is ascertained. Best attempts were made to follow this protocol schedule for all patients, although due to a variety of reasons, deviations from protocol were inevitable. Main reasons included: distance—some patients travel far from their homes to seek care because of the stigma surrounding the disease; self-return—some patients returned to the clinic before attempts at double sampling were started; and no locator information—for some patients, no locator information was available either due to patient refusal or due to logistical issues. We adjust for covariates predictive of dropout, as described in Section 4.3. Within levels of the covariates, we assume double sampling is random. This assumption cannot be checked with the observed data.

3. Framework, Goals, and Assumptions

Here we describe the general framework and goal of our study. To best address the problem, it is important to consider two types of data—observed data and potentially observable data. Observed data are those that we actually measure in our study design. Potential data (Neyman, 1923; Rubin, 1974, 1978) are those that would be observed under different designs, and the collection of such data describes inherent characteristics of an individual.

Potential Data

• T_i = survival time

• R_i = potential dropout status if the study were to continue indefinitely under phase 1 follow-up (=1 if no dropout)

• L_i = potential time to dropout if the study were to continue indefinitely under phase 1 follow-up (<T_i for R_i = 0; defined to equal T_i for R_i = 1),

We assume the study individuals are a random sample from a larger cohort.

Goal

Our target estimand is the survival function for the entire larger cohort, S(t) = P(T > t).

Observed Data

• E_i = entry date

• E_max = study end date (common across individuals i)

• C_i = time between study entry and end, namely, administrative censoring time (E_max − E_i)

• Z_i = a function of covariates (gender, baseline CD4 count, baseline WHO stage, indicator of urban versus rural clinic, and ART start status)

• $R_i^{\text{obs}}=1-(1-R_i)·I(L_i<C_i)$, observed dropout status (=1 if observed nondropout)

• S_i = indicator for being selected for and recovered (or found) by double sampling (if $R_i^{\text{obs}}=0$)

• X_i = min{T_i, C_i} (if $R_i^{\text{obs}}=1$, or $R_i^{\text{obs}}=0$ and S_i = 1)

• Δ_i = indicator for whether survival time is shorter than the administrative censoring time (if $R_i^{\text{obs}}=1$ , or $R_i^{\text{obs}}=0$ and S_i = 1)

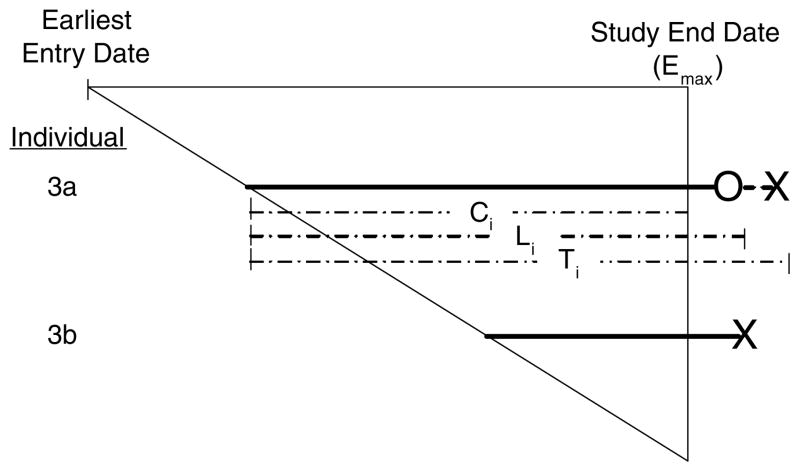
It is important to note that the observed nondropouts from the first phase ( $R_i^{\text{obs}}=1$) are actually a mixture of true dropouts (R_i = 1) and true nondropouts (R_i = 0). Referring to Figure 2, within our observed study period, both individuals 3a and 3b represent observed nondropouts. However, if we had continued phase 1 follow-up beyond the study end date, we would have seen individual 3a dropping out eventually before dying (R_i = 0), whereas individual 3b would have died on-study without dropping out (R_i = 1).

Figure 2.

Observed nondropouts ( $R_i^{\text{obs}}=1$) are a mixture of true dropouts (R_i = 1) and true nondropouts (R_i = 0) (X denotes death and O denotes dropout).

More generally, the potential dropout behavior expressed by R and L, although missing for those who are administratively censored, is central for characterizing the objective dropout behavior of individuals, that is, separately from the effects that a particular length of phase 1 follow-up has on observed data.

Having such an objective characterization of dropout behavior, we now consider two plausible assumptions that allow estimation of the cohort survival function.

Assumption A1

Conditional on the set of observed covariates, entry time (and equivalently, administrative censoring time) is independent of survival time and of potential dropout status. We can express this as: C_i ⊥ (T_i, R_i, L_i) | Z_i, because entry times E_i = E_max − C_i.

We note that Assumption A1 includes the typical conditional independence assumption from survival analysis, C_i ⊥ T_i |Z_i. Moreover, Assumption A1 is plausible if, conditional on observed covariates such as gender, baseline CD4 count, baseline WHO stage, clinic type, and treatment status, we assume no secular trends in survival or true dropout behavior during the study period. Such an assumption could not be expressed in terms of observed data, because the observed dropout status depends not only on individual characteristics but also on when the individual entered the study and when the study ends.

Assumption A2

Among observed dropouts, the observed covariates Z_i include the variables involved in the selection and successful recovery of those to be double sampled. We can express this by stating that, among observed dropouts and after we condition on Z_i, selection for and recovery by double sampling is independent of survival and entry times, or equivalently, $S_i\perp (T_i,C_i)\mid (R_i^{\text{obs}}=0,Z_i)$, because entry times E_i = E_max − C_i.

Because the typical survival data (X_i, Δ_i) are functions of (T_i, C_i), it is an immediate implication of A2 that, conditional on the observed covariates, selection for and recovery by double sampling is independent of (X_i, Δ_i): $S_i\perp (X_i,{\mathrm{\Delta }}_i)\mid (R_i^{\text{obs}}=0,Z_i)$.

4. Methods

4.1 Based on the Design Principles

Consider first the case where Assumptions A1 and A2 are plausible with no covariates. After double sampling, we observe the typical survival data (X_i, Δ_i) for the nondropouts ( $R_i^{\text{obs}}=1$), and for the double-sampled dropouts (S_i = 1). For these data, the only remaining reason for missing T_i is due to administrative censoring C_i. It is thus tempting to estimate the two Kaplan–Meier curves (Kaplan and Meier, 1958) separately within strata defined by $R_i^{\text{obs}}=1$ and S_i = 1, and combine their estimates to obtain the cohort survival function. Such an approach, however, is generally biased because, as FR01 showed, under A1 and A2, a dependence is induced between administrative censoring C_i and survival times T_i when one conditions on the observed stratum of nondropouts or on the observed stratum of double-sampled dropouts. This dependence arises because the observed nondropouts are a mixture of true dropouts and true nondropouts as discussed in Section 3. Nevertheless, FR01 showed that one can use even the reduced data $\{R_i^{\text{obs}},S_i\}\cup \{(X_i,{\mathrm{\Delta }}_i):R_i^{\text{obs}}=1\text{or}{S}_i=1\}$ to produce a nonparametric MLE that, under A1 and A2, is consistent for the cohort survival function. This MLE is obtained by first estimating the stratified crude hazard functions separately for nondropouts and double-sampled dropouts, and then synthesizing these estimators to the hazard function of the original cohort.

In our study, we have measured covariates predictive of dropout and thus wish to incorporate them to make Assumptions A1 and A2 more plausible. For the analysis, we consider the reduced data

$${\mathcal{D}}^{\text{redu}}=\{Z_i,R_i^{\text{obs}},S_i\}\cup \{(X_i,{\mathrm{\Delta }}_i):R_i^{\text{obs}}=1\text{or}{S}_i=1\},$$

and their likelihood function conditionally on the covariate Z_i:

$$L(\theta ;{\mathcal{D}}^{\text{redu}})=\prod _{i}P{(X_i,{\mathrm{\Delta }}_i,R_i^{\text{obs}}=1\mid Z_i,\kappa )}^{R_i^{\text{obs}}}\times P{\left(X_i,{\mathrm{\Delta }}_i,R_i^{\text{obs}}=0\mid S_i=1,Z_i,\theta \right)}^{(1-R_i^{\text{obs}})S_i}\times P{\left(R_i^{\text{obs}}=0\mid S_i=0,Z_i,\kappa \right)}^{(1-R_i^{\text{obs}})(1-S_i)}.$$ (1)

In the above, θ is the vector of parameters governing the inherent characteristics of the population of interest, that is, the joint distribution of (T, L, R, E, Z). Then, based on (1) and Assumptions A1 and A2, we obtain the MLE for the full cohort survival function S(t), which is a consistent and robust estimator for the cohort survival function S(t) = P(T > t).

To derive this MLE, we note three key observations:

1. The “net” hazard function within a covariate stratum z, defined as ${\lambda }_z^{\text{net}}(t)\equiv {lim}_{\epsilon \to 0}\{P(t\le T<t+\epsilon \mid T\ge t,Z=z)/\epsilon \}$, equals the crude hazard function in stratum z, defined as ${\lambda }_z^{\text{crd}}(t)\equiv {lim}_{\epsilon \to 0}\{P(t\le T<t+\epsilon \mid X\ge t,Z=z)/\epsilon \}$, because administrative censoring and survival times are assumed independent conditional on observed covariates (Assumption A1).

2. The crude hazard function ${\lambda }_z^{\text{crd}}(t)$ in stratum z can be expressed as the weighted average ${\sum }_{g=0,1}{w}_{g\mid z}(t){\lambda }_{g,z}^{\text{crd}}(t)$, where ${\lambda }_{g,z}^{\text{crd}}(t)$ is the crude hazard within R^obs = g, Z = z, for g = 0, 1; and the weights w_g|z(t) ≡ P(R^obs = g |X ≥ t, Z = z) are the proportions of individuals with observed dropout status g within the risk set X ≥ t and stratum z. The above expression does not depend on Assumptions A1 and A2.

3. The crude hazard function ${\lambda }_{g=0,z}^{\text{crd}}(t)$ for observed dropouts R^obs = 0 within stratum z equals the crude hazard function ${\lambda }_{s=1,z}^{\text{crd}}(t)$ of the double-sampled dropouts S = 1 within stratum z, by Assumption A2.

Using these relations, we obtain that, under A1 and A2, the nonparametric MLE of S(t) from (1) is given by a weighted combination of the within-stratum estimated survival curves, using

$$\begin{array}{l}\widehat{S}(t)\equiv \sum _z{\widehat{p}}_z{\widehat{S}}_z(t),\text{where}{\widehat{p}}_z\text{are}\text{the}\text{observed}\text{proportions}\text{of}\text{strata}z,\\ {\widehat{S}}_z(t)=exp\left\{-{\int }_0^t{\widehat{\lambda }}_z^{\text{net}}(t)dt\right\}\\ =exp\left\{-{\int }_0^t{\widehat{\lambda }}_z^{\text{crd}}(t)dt\right\}\text{by}\text{observation}(\mathrm{i}),\text{and}\\ {\widehat{\lambda }}_z^{\text{crd}}(t)=\sum _{g=0,1}{\widehat{w}}_{g\mid z}(t){\widehat{\lambda }}_{g\mid z}^{\text{crd}}(t)\text{by}\text{observations}(\text{ii})\text{and}(\text{iii}),\end{array}$$ (2)

and where, in the last expression, ${\widehat{\lambda }}_{g=1\mid z}^{\text{crd}}(t)$ is the Nelson estimator of ${\lambda }_{g=1\mid z}^{\text{crd}}(t)$ based on {(X_i, Δ_i): $R_i^{\text{obs}}=1$} from the non-dropouts; ${\widehat{\lambda }}_{g=0\mid z}^{\text{crd}}(t)$ is the Nelson estimator of ${\lambda }_{g=0\mid z}^{\text{crd}}(t)$ based on {(X_i, Δ_i) : S_i = 1} from the double-sampled dropouts, as allowed by observation (iii); and ŵ_g|z(t) is the empirical estimator of w_g|z(t) based on D_redu.

We have derived the standard errors for the above estimators, based on the theory of FR01 and the delta method, and have developed an R program for the computations that we can provide to interested readers.

4.2 Comparison with Other Methods

We compared results obtained using the above method with other methods, which we describe in this section. With each of these other methods, we calculate an overall survival estimate as a weighted average of survival estimates within covariate strata. Below we describe these methods as applied within covariate strata.

1. No double sampling. This method uses a Kaplan–Meier estimator (within covariate strata) applied to the data observed from only the phase 1 follow-up, without using the double-sampling data from phase 2. This method cannot differentiate between dropout and administrative censoring (i.e., observed dropouts are considered censored at the time of dropout), and reflects the analysis one could conduct without the double-sampling design. Such an analysis is biased if there are unmeasured reasons for dropout relating to health, and therefore to survival.

2. Ignoring distinction between nondropouts and double-sampled dropouts. This method uses the Kaplan–Meier estimator (within covariate strata) applied to the data (X, Δ) from the nondropouts in phase 1 plus from the double-sampled dropouts from phase 2. However, this method makes no distinction between the two groups. As discussed in FR01, such an analysis seems typical in implicit uses of double sampling, but is not generally appropriate because only a subset of the observed dropouts (R^obs = 0) are double sampled.

3. Stratifying Kaplan–Meier estimators on observed dropout groups. This method first obtains separate Kaplan–Meier estimators (within covariate strata) within the observed nondropouts and within the double-sampled dropouts, and then combines these estimates with weights according to the proportion of dropouts. Formally, the estimator of this method is of the form (1 − p̂_z)KM_1,z + p̂_zKM_0,z, where p̂_z are as in (2), KM_1,z is the Kaplan–Meier estimator among observed non-dropouts (R^obs = 1) in covariate stratum z, and KM_0,z is the Kaplan–Meier estimator among double-sampled dropouts (R^obs = 0 and S = 1) in covariate stratum z. FR01 showed that under Assumptions A1 and A2, such an analysis is generally biased because of the dependence that is induced between survival and administrative censoring times when one stratifies on the observed dropout groups as discussed in Section 4.1.

4. Based on the design principles. This is the nonparametric MLE Ŝ_z(t) described in Section 4.1, based on the explicit design principles of Section 3.

Each of the above methods is applied first within strata of covariates, and then the within-strata estimators are combined to estimate the cohort survival function.

4.3 Stratification on Factors Predictive of Discontinuation

It is generally good practice, especially with standard methods that cannot otherwise distinguish between dropout and administrative censoring, to first stratify on factors that are predictive of discontinuation from follow-up (which we define here as the earlier of dropout or administrative censoring). This practice attempts to make independence of such discontinuation and survival times within covariate strata more plausible. In our analysis, we first use a Cox proportional hazards model (Cox, 1972) to identify factors predictive of such discontinuation. We include the following as predictive factors, Z*: gender, baseline CD4 count, baseline WHO stage, indicator of urban versus rural clinic, and ART start status. Then we take the linear predictor (Z*β̂) from this model as a continuous score, and we let Z be the quintiles of Z* β̂, with higher quintiles corresponding to increasing hazard of discontinuation. We use these quintiles as our covariate strata for all of the above methods.

Here, we report standard errors based on (i) treating the transformation Z* β̂ as fixed and its discretization to quintiles as a design choice; for this standard error, we reflect uncertainty only in the estimation of quintile-specific survival curves, S_Z(t); and (ii) 100 bootstraps of the combined processes described in Sections 4.3 and 4.2.

5. Results

During the 2-year period from January 1, 2005 to January 31, 2007, we observed a total of 230 deaths, 124 of which were ascertained by double-sampling efforts. The cumulative observed dropout rate was 39%. Of the 3528 dropouts, 1143 (32%) were pursued by double-sampling efforts and 621 (18%) were recovered (or found) by double-sampling efforts. The survival data (X, Δ) were obtained for these 621. Reasons for incomplete ascertainment via double-sampling efforts are described in Section 2.

The most important predictors of discontinuation in the Cox proportional hazards model were the baseline WHO stage with a hazard ratio of 1.03 (95% CI: 1.01, 1.06) and male gender with a hazard ratio of 1.06 (95% CI: 1.02, 1.11).

Table 1 shows mortality (100% – survival) estimates at 1 year from study entry. The Q1–Q5 columns correspond to the quintiles of linear predictors from the Cox proportional hazards model of time to discontinuation (dropout or administrative censoring) on gender, baseline CD4 count, baseline WHO stage, urban clinic indicator, and ART start status as described in Section 4.3. The column “overall” is a weighted average of the stratified survival estimates for the different methods described in Section 4.

Table 1.

Mortality estimates % (SE) at 1 year from study entry, by quintiles of linear predictor of time to discontinuation. Methods 1–4 correspond to those of Section 4.2, and the quintiles Q1–Q5 are described in Section 4.3.

Method	Q1	Q2	Q3	Q4	Q5	Overall
Without double sampling
(1) No double sampling	0.8	0.8	1.8	1.3	3.6	1.7
	(0.3)	(0.3)	(0.4)	(0.3)	(0.6)	(0.2)a	(0.3)b
With double sampling
(2) Ignoring dropout group distinction	1.6	1.2	3.5	2.2	5.4	2.8
	(0.3)	(0.3)	(0.5)	(0.4)	(0.6)	(0.2)a	(0.3)b
(3) Stratifying KM on observed dropout groups
Nondropout	1.0	1.1	2.4	1.6	5.3
	(0.3)	(0.3)	(0.5)	(0.4)	(0.8)
Dropout	13.4	8.6	23.2	18.7	31.5
	(3.5)	(3.1)	(3.7)	(4.2)	(4.4)
Combined	5.6	3.8	11.3	8.0	16.6	8.9
	(1.3)	(1.2)	(1.6)	(1.6)	(2.0)	(0.7)a	(1.1)b
(4) Based on the design principles of Section 1	6.3	4.0	12.1	8.8	17.6	9.6
	(1.5)	(1.2)	(1.8)	(1.8)	(2.1)	(0.8)a	(1.2)b

^aStandard errors treating the discretized covariate Z as fixed.

^bStandard errors based on 100 bootstraps of the combined processes of Sections 4.3 and 4.2. Bold values indicate overall estimates.

Within each method, there is a general pattern of increasing mortality estimates for strata with increasing hazard of discontinuation (Q1 → Q5). Furthermore, the overall estimates of 1-year mortality increase as we progress from method 1 (least appropriate) through method 4 (most appropriate). The method that uses no double-sampling data (method 1) gives an overall mortality estimate of 1.7%, whereas the method that is explicitly developed based on the design (method 4) provides an overall mortality estimate of 9.6%.

6. Discussion

The results suggest two important points, regarding the need for double-sampling data and the analysis with such data. First note that the method that ignores the data obtained from double sampling yields substantially lower estimates than the remaining three methods, which do incorporate data obtained via double sampling. This relative ordering of the methods implies that individuals who drop out are sicker than the others in dimensions and degrees not measured by the covariates, but captured by the double sampling. The magnitude of the implied bias of the first method is alarming and indicates that double sampling is an essential design component for PEPFAR in providing objective evidence of possible nonignorable dropout and accurate data. Second, even with double-sampling data, the difference of results among the various methods of analysis suggests that using an appropriate method is important for the accuracy of the results.

Also important is the observation that within each method, there exists a pattern of increasing mortality estimates for increasing quintiles of predicted hazard for discontinuation. Although this is a relationship described through the observed covariates, the fact that this relationship does not level off at the higher quintiles suggests that there is an underlying more fundamental relationship between discontinuation and survival. Such a more fundamental relationship would expectedly extend to dimensions and degrees not directly captured by the covariates. This is another, indirect, way of understanding the severe bias of the method that does not use double-sampling data.

In this article, we have addressed the problem of loss to follow-up from a simple double-sampling design that allocates the same efforts to find individuals selected for double sampling. It will be important next to study prospectively properties of different double-sampling designs: (1) how many individuals to double sample and (2) what profiles of dropouts to double sample with higher probability.

In summary, this article provides evidence that double-sampling designs and methods are critical for accurate and more objective monitoring of passive follow-up programs such as PEPFAR.