Bayesian adaptive designs in single ascending dose trials in healthy volunteers

Abstract

Aim

Recent publications indicate a strong interest in applying Bayesian adaptive designs in first time in humans (FTIH) studies outside of oncology. The objective of the present work was to assess the performance of a new approach that includes Bayesian adaptive design in single ascending dose (SAD) trials conducted in healthy volunteers, in comparison with a more traditional approach.

Methods

A trial simulation approach was used and seven different scenarios of dose–response were tested.

Results

The new approach provided less biased estimates of maximum tolerated dose (MTD). In all scenarios, the number of subjects needed to define a MTD was lower with the new approach than with the traditional approach. With respect to duration of the trials, the two approaches were comparable. In all scenarios, the number of subjects exposed to a dose greater than the actual MTD was lower with the new approach than with the traditional approach.

Conclusions

The new approach with Bayesian adaptive design shows a very good performance in the estimation of MTD and in reducing the total number of healthy subjects. It also reduces the number of subjects exposed to doses greater than the actual MTD.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Bayesian adaptive designs in phase 1 oncology trials have been used for more than two decades.

• Outside of oncology, these model-based approaches are very rarely used in phase 1 studies.

• Recent publications indicate an interest to find better and more efficient approaches in the conduct of single ascending dose trials.

WHAT THIS STUDY ADDS

• An approach with Bayesian adaptive design shows a very good performance in the estimation of maximum tolerated dose (MTD) and in reducing the total number of healthy subjects.

• This approach reduces the number of subjects exposed to doses greater than the actual MTD.

Introduction

Bayesian adaptive trial designs for first time in humans (FTIH) studies and especially the continual reassessment method (CRM) have been used for more than two decades in the development of therapies for oncological indications [1,2]. Surprisingly, these model-based designs have not been adopted for early clinical studies in other therapeutic areas. Recent publications indicate a willingness to explore application of these approaches to FTIH studies outside of oncology. Perlstein et al. [3] have evaluated a series of agile designs in FTIH trials in healthy volunteers using simulation techniques and found that this type of approach can increase the efficiency of study conduct. In another publication, Chu et al. [4] also used simulation to explore 15 various designs of a FTIH trial. They reported that three of the designs would offer greater efficiency in assessing safety, whereas pharmacokinetic parameters and dose proportionality were well characterized with all the designs. These two publications indicate an interest in finding new and improved ways to conduct FTIH studies in healthy volunteers, increasing efficiency and quality in the estimates of the actual maximum tolerated dose (MTD) without jeopardizing the safety of the volunteers.

The objective of the present work was to assess the performance of a new approach to healthy volunteer single ascending dose (SAD) trials that includes a Bayesian adaptive element. As the primary objective of SAD trials is safety and tolerability, the present work was limited to the assessment of safety and more precisely the occurrence or absence of a dose limiting event (DLE). A DLE can be defined as an adverse event or laboratory abnormality that would preclude a second drug administration at the same dose level in a given subject [5].

Endpoints used in the assessments explored three aspects of trial design and outcomes. Firstly, the quality of the study outcome was examined with a focus on the variance and bias in the estimate of MTD. Secondly, the efficiency of study conduct (defined here as the number of subjects and the duration of trials) was investigated, reflecting a desire to minimize the total number of subjects and the overall duration of the study, whilst maintaining a high quality of results. And last but not least, a safety component of study design was explored with the intention of reducing the number of subjects exposed to doses greater than the MTD, since SAD trials must always minimize the risk to each volunteer.

The new approach was compared with a traditional approach that is commonly used in pharmaceutical companies. The latter was used as a benchmark in the present work.

In addition to the inclusion of Bayesian adaptive methodology, the new approach includes other features that are summarized in Table 1, explained in more detail in the method section and commented on in the discussion. The effectiveness of various trial designs and procedures were evaluated by means of simulation.

Table 1.

Key features of the new and the traditional approaches

	Traditional approach	New approach
Definition of MTD	Dose level below the dose at which ≥3/6 subjects had a DLE	MTD is the dose at which P(DLE) = 30%
Dose escalation	Three-fold increase initially then two-fold increase	Bayesian technique using a logistic regression model and maximum of three-fold increase
Cohort size	Six subjects on active treatment and two subjects on placebo (6A + 2P)	3A + 1P initially, then 3A + 1P or 6A + 2P based on results and switching rule
Number of dose levels	Nine possible dose levels assuming the use of a solid formulation with limited number of strengths defined before study start	Fifteen possible dose levels, assuming the use a solid formulation with multiple strengths or even better, of extemporaneous formulations, so the next cohort of subjects can receive a dose level close to the one recommended by the model.

Methods

Simulation methodology was used to evaluate the performance of the new approach in comparison with the traditional approach. The assumptions used in the simulations were chosen to reflect typical practice in SAD trials [6].

Study designs and assumptions used in the simulations

The traditional approach (benchmark)

Each cohort was assumed to be composed of eight healthy subjects with six receiving active treatment and two receiving a placebo. The cohort size was the same at each dose level. The possible dose levels were defined as 0, 1, 3, 9, 25, 50, 100, 200 and 400 mg, with a typical three-fold increase at the initial low dose levels, followed by a two-fold increase at higher dose levels, based on standard practice in FTIH studies [6]. The dose escalation was stopped when the maximum dose level (400 mg) was received by one cohort or when three or more of the six subjects on active treatment experienced a DLE. When dose escalation was stopped under these circumstances, this dose level was defined as the minimum intolerated dose (MID) and the MTD was taken to be the previously administered dose level, following the definitions by Cutler et al. [7]. The authors acknowledge the diversity in the definitions (MID, MTD, stopping rule) used in phase 1 trials. For example, the dose escalation stopping rule of two out of six is sometimes used in FTIH studies. The rule of three out of six adopted in the present work is typical and, compared with two out of six, less prone to stopping the trial erroneously because of a chance finding. The definitions by Cutler et al. [7] selected in the present work emerged from a symposium that gathered investigators and representatives from industry, academia and health authorities and are considered more representative of the practice in traditional phase 1 trials.

The new approach with Bayesian adaptive trial design

This methodology is derived from the classical CRM method [8] which is well described in the literature. It is based on a model that characterizes the relationship between the dose and the occurrence of DLE [9], rules to select the next dose level and several stopping rules.

Logistic regression was used to describe the dose–response curve. More specifically, let P be the probability of observing a DLE in a subject who received a dose level dose_i:

(1)

where a, the intercept and b, the slope, are the parameters to be estimated with a Bayesian approach. Based on the definition most commonly used in the literature [3,10–12] and also to ensure a better comparability with the traditional approach, the MTD was defined as the dose at which P(DLE) = 30%. In practice, this criterion of 30% can be modified and any change of such a threshold will not affect the procedure [3,10]. Based on equation (1), the MTD is calculated from the model parameters as MTD = [log(0.3/0.7) – a]/b.

The initial number of subjects per cohort was limited to four (three subjects receiving active treatment and one subject receiving placebo). The main purpose of adaptive dose level selection was to distribute the subjects among the most informative dose levels, that is dose levels close to the MTD. Dose levels were selected among the following set of candidates, in our example 0, 1, 3, 6, 9, 20, 25, 40, 50, 75, 100, 150, 200, 300 and 400 mg. The selection of the next dose level was guided by the data from previous dose levels and the model. Using all the observed proportions of DLEs at each tested dose level (accumulated data), a logistic regression model is fitted and the parameters of the model are estimated. For each sample obtained from the Markov Chain Monte Carlo (MCMC) algorithm, the probability of experiencing a DLE is obtained. The minimum value where this probability is greater or equal to 30% is flagged with value 1 (0, otherwise). The mean value is then calculated through the MCMC estimations and this mean value represents the probability of being the MTD for each dose level. The dose level to be given to the next cohort was determined by the posterior probabilities of each dose level to be the MTD. This next dose level was the candidate with the largest probability among the set to be the MTD. Based on safety considerations, the maximum increase to the next dose level was limited to three-fold.

Using this escalation process, two stages can be identified in the MTD search. At first, three-fold increases are generated until the first DLEs are reported. Then, the model tries to gain precision about the estimation of MTD and the next dose level selected may be lower or the same as the previously tested dose level. In the latter case, the size of a cohort was increased from four to eight subjects (a switching rule).

Four stopping rules were used. The trial was stopped when (rule 1) the estimation of MTD was precise enough and this was implemented as robust coefficient of variation [13] of MTD, RCV(MTD) ≤30%, when (rule 2) there was a high probability that MTD is higher than the maximum possible dose (e.g. 400 mg in our example) and this was implemented as P(P(DLE at 400 mg) ≤30%) ≥80% and 400 mg tested at least once, when (rule 3) two consecutive doses were at the same level and the next predicted dose level would be the same and when (rule 4) a maximum number of planned cohorts was reached. A maximum of 16 cohorts was chosen for this method to ensure a comparable maximum number of subjects (64) for both approaches if the switching condition was not fulfilled with the Bayesian adaptive design.

When a trial was stopped because RCV(MTD) was ≤30% (rule #1) or because the same dose level was repeated (rule #3), the MTD was considered as defined. When a trial was stopped because the whole dose range did not include the MTD (rule #2) or because the maximum number of cohorts was reached (rule #4), the MTD was considered as not obtainable. When it could be obtained, the MTD was defined as the mean of the posterior distribution of the MTDs in each trial. The posterior distribution was estimated by MCMC simulations, taking account of the priors and the information from the data. In order to keep draws from the posterior distribution after convergence, a burn in period was set to 5000.

Simulations

Simulations were performed by calling WinBUGS [14–16] via the BRUGS package [17] from R2.4.1 [18]. For each scenario and approach, 5000 simulations of FTIH trials were performed. For both approaches, P(DLE) for subjects on placebo was considered as 5% and this number was based on the experience of the authors in the conduct of clinical studies. For the relationship between P(DLE) and dose, seven different types of response curves (called scenarios), from very shallow to very steep, were tested (Figure 1). The duration of the trial was defined as the number of weeks from first dose administration until the decision to stop the study. This calculation assumed weekly dose escalations.

Figure 1.

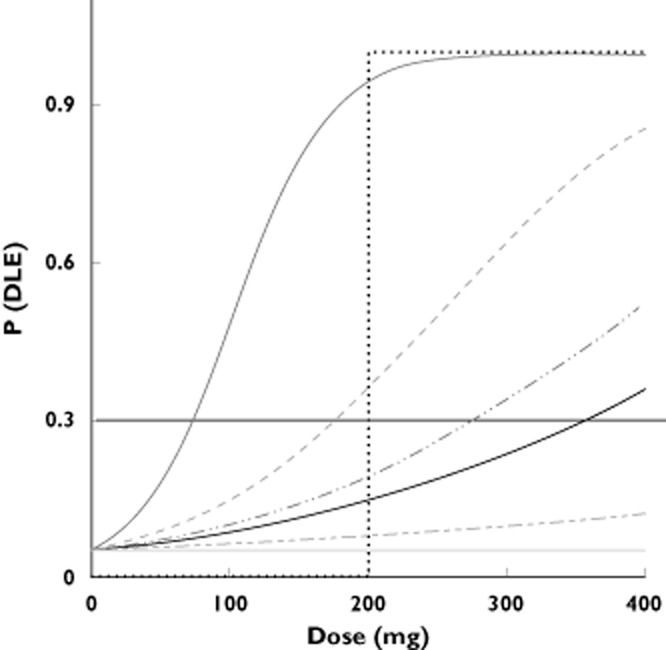
P(DLE) as a function of dose for the seven dose–response scenarios. The title of each scenario gives P(DLE) at the maximum dose of 400 mg. The horizontal line at P(DLE) = 30% gives the MTD for each scenario. () scenario 7: Abrupt at 200 mg, () scenario 6: Pr(DLE) 100%, () scenario 5: Pr(DLE) 85%, () scenario 4: Pr(DLE) 52%, (—) scenario 3: Pr(DLE) 35%, () scenario 2: Pr(DLE)12%, () scenario 1: Flat 5%

Due to the use of the Bayesian adaptive method, some prior information (so called ‘priors’) had to be defined in order to estimate the parameters of the model (the intercept and the slope). The prior distribution chosen for the intercept was a normal distribution with a mean of –3 and a variance equal to 4. For the slope, the prior selected was a truncated normal distribution to allow only positive values. The mean and the variance were selected to represent a mean (± SD) MTD of 208 ± 157 mg. The prior probability distribution of the MTD is presented in Table 2. The MTD distribution is equally spread in the range of possible doses (0 to 400 mg). Further, the MTD has a 32% probability to exceed the maximum possible dose (400 mg). As the MTD distribution is relatively uniform, the priors used during the simulations can be considered as relatively non-informative. The same priors were used for all the scenarios.

Table 2.

Prior probability distribution of the MTD

MTD range	Prior probability of the MTD*
<10 mg	15.3%
Between 10 and 100 mg	14.2%
Between 100 and 200 mg	17.0%
Between 200 and 400 mg	21.1%
>400 mg	32.4%

^*Probabilities obtained from 100 simulations.

To measure the quality in the estimates of the MTD, median prediction error (MPE) and root median squared prediction error (RMSE) are reported. MPE is a measure of the bias whereas RMSE incorporates both the variance and the bias of the estimator [19,20].

Results

The results of the 5000 simulations for each of the seven scenarios selected and the two methods (i.e. 70 000 FTIH trials) are summarized in Table 3. The percentages of trials stopped due to each of the four stopping rules used in the new approach are presented in Table 4. The results are presented in three sections addressing the quality of the estimates of MTD, the efficiency of the study conduct and the safety of the subjects.

Table 3.

Main results from simulations of 5000 trials in each approach for each of the seven scenarios of dose–response relationship

Scenario	Actual MTD* (mg)	Approach	% of trials where MTD was obtained†	MTD (mg) Median‡ (2.5–97.5th percentiles)	MPE§ (%)	RMSE§ (%)	Duration of trials¶ (weeks) Mean (95% CI)	Number of subjects (mean value) (with a dose ≥ actual MTD/total number of subjects)
1 Flat 5%	NA	Traditional	2%	9 (0–50)**	NA	NA	7.94 (7.92, 7.95)	0 / 64
		New	6%	463 (158–835)**	NA	NA	7.32 (7.31, 7.34)	0 / 31.4
2 Pr(DLE)12%	867	Traditional	6%	20 (0–50)**	−98	98	7.89 (7.87, 7.90)	0 / 64
		New	18%	463 (204–924)**	−47	47	7.54 (7.52, 7.57)	0 / 33.5
3 Pr(DLE)35%	356	Traditional	37%	200 (3–200)	−44	44	7.82 (7.80, 7.85)	8 / 63.9
		New	77%	363 (185–676)	+2	19	7.99 (7.95, 8.00)	5.3 / 37.6
4 Pr(DLE)52%	277	Traditional	74%	200 (50–200)	−28	28	7.79 (7.77, 7.81)	7.8 / 63.8
		New	94%	295 (156–500)	+6	21	8.03 (8.00, 8.06)	4.3 / 38.6
5 Pr(DLE)85%	178	Traditional	100%	200 (50–200)	+12	12	7.46 (7.44, 7.49)	14.8 / 62.8
		New	99%	200 (118–336)	+12	18	7.82 (7.79, 7.85)	7.9 / 37.9
6 Pr(DLE)100%	73	Traditional	100%	50 (9–100)	−32	32	6.17 (6.15, 6.20)	13.4 / 53.3
		New	100%	91 (61–139)	+25	25	7.81 (7.78, 7.85)	12.2 / 39.5
7 Abrupt at 200 mg	199	Traditional	100%	100 (100–100)	−50	50	7 (7–7)	8 / 56
		New	100%	154 (154–154)	−23	23	7 (7–7)	3 / 32

^*MTD is defined as the dose at which P(DLE) = 30%.

^†See definitions in the Methods section.

^‡Median value from the trials where MTD was obtained.

^§MPE = median prediction error and RMSE = root median squared prediction error and both are expressed in % of actual MTD.

^¶Mean value from 5000 trials.

^**These numbers should be interpreted with caution as the percentage of trials where MTD was obtained was small.

NA: not applicable as the dose–response is flat at 5%, hence there is no actual MTD.

Table 4.

Percentage of trials stopped due to each of the four stopping rules used in the new approach

Scenario	Reason for stopping	% (out of the 5000 trials simulations)
1 Flat 5%	Rule 1 RCV(MTD)*	2
	Rule 2 MTD > 400 mg*	94
	Rule 3 Three repetitions*	4
2 Pr(DLE)12%	Rule 1 RCV(MTD)*	9
	Rule 2 MTD > 400 mg*	82
	Rule 3 Three repetitions*	9
3 Pr(DLE)35%	Rule 1 RCV(MTD)*	50
	Rule 2 MTD > 400 mg*	23
	Rule 3 Three repetitions*	28
4 Pr(DLE)52%	Rule 1 RCV(MTD)*	67
	Rule 2 MTD > 400 mg*	6
	Rule 3 Three repetitions*	28
5 Pr(DLE)85%	Rule 1 RCV(MTD)*	75
	Rule 2 MTD > 400 mg*	0.02
	Rule 3 Three repetitions*	25
6 Pr(DLE)100%	Rule 1 RCV(MTD)*	72
	Rule 2 MTD > 400 mg*	0
	Rule 3 Three repetitions*	28
7 Abrupt at 200 mg	Rule 1 RCV(MTD)*	100

^*A precise description of the rule is provided in the text (Methods section). Stopping rule 4 was never used.

Quality of MTD estimates

Using the new approach, a MTD was reached in a very large proportion of the trials with two exceptions: when an actual MTD did not exist (scenario 1) and when the actual MTD was larger than the maximum tested dose level of 400 mg (scenario 2). A MTD does not exist in scenario 1 and, in a satisfactory manner, the results of the simulations showed that the MTD was not estimated in 98% and 94% of the studies with the traditional and new approach, respectively. In the small percentage of trials where MTD was erroneously estimated, the median value of the MTD with the new approach (463 mg) was larger than the maximum dose tested in the study (400 mg). Therefore the overall impact on the MTD decision (i.e. MTD > 400 mg) was minimal. Conversely, with the traditional approach, the median MTD value (9 mg) was a relatively low value within the range tested and the impact of a wrong MTD decision with this approach would be more serious. The same comment also applies to scenario 2 (true MTD > 400 mg) where the number of trials in which the MTD was erroneously obtained was higher than with scenario 1.

The estimated MTD values were closer to the actual values with the new approach compared with the benchmark in all but scenario 5 where the MPE was the same (+12%).

Efficiency of study conduct

The total number of subjects exposed in the various scenarios and the duration of the trials as a result of the simulations are presented in Table 3. In all scenarios, the total numbers of subjects exposed were lower with the new approach than with the traditional design (Table 3). The simulations indicated a typical exposure of 30–40 subjects to the test drug in the case of the proposed new approach vs. some 50–65 subjects for the traditional approach. The two approaches appeared comparable with respect to the estimated duration of the trial with the duration similar across all scenarios (Table 3).

Safety of subjects

The number of subjects exposed to a dose greater than or equal to the actual MTD was used as a metric to assess which of the two approaches would result in the least risk for the participating healthy volunteers. The outcome of the simulations is presented in Table 3 and indicates an advantage in favour of the new approach with the number of subjects exposed to a dose ≥ the actual MTD lower than that resulting from the traditional methodology in all the scenarios examined.

Discussion

The present work is part of a general initiative to improve the way FTIH trials are designed and conducted. Based on a survey of 105 FTIH studies, Buoen et al. [6] concluded that ‘phase 1 dose escalation trials are still conservative and seem to be based more on habit and preferences than experimental and scientific rationale’ and they encouraged the scientific community to optimize these trials in healthy volunteers with statistical methodologies. The present work can be seen as a direct response to their recommendation as the new approach includes a Bayesian adaptive design component and other features indicated in Table 1 that were expected to increase the quality and efficiency of the conduct of FTIH trials in healthy volunteers.

The quality of MTD estimation was superior with the proposed new Bayesian approach. The MPE was lower in all the scenarios examined with the exception of one scenario (scenario 5), where the MPE was equally low at +12% for both approaches. Other published simulation studies concerning adaptive designs in SAD trials in healthy volunteers [3,4] did not assess the bias and precision of the MTD estimation so a comparison is not possible. It should be noted that the traditional approach led to a MPE of about 30% or more in all scenarios, with the exception of the low number in scenario 5. These results highlight an important weakness of the traditional methodology and hence, fully support the use of the new approach.

With respect to the efficiency in the conduct of SAD trials, the results of simulations revealed that the duration of the trials with both approaches are comparable. This result is important as previous research with the CRM indicated that this approach would lead to longer phase 1 trials [21]. The cohort size of three subjects receiving the active treatment was initially proposed by Goodman et al. as a modification of the classical CRM in order to decrease the duration of phase 1 trials [22]. It should be noted that the dose stopping and switching rules have also a direct impact on the estimated duration of the study. In our simulation work, several variations of these rules were tested until a satisfactory set of rules could be defined, taking into account outcomes across all the scenarios. In the present work, an assumption of a weekly dose escalation was used for both approaches. When potential adverse effects of the drug are expected to occur within 48 h after drug administration, two dose escalations within a week can also be envisaged and the use of a small cohort of four subjects (three on active and one on placebo) should facilitate the operational implementation.

With regard to the total number of subjects needed to complete the study, the results of the simulations show a marked advantage in favour of the new Bayesian approach with less biased estimates of MTD being obtained with fewer subjects using this methodology. The recruitment of healthy volunteers in clinical pharmacology studies is not usually a rate limiting step so the reduced number of subjects with the new approach provides the potential to reduce the costs of FTIH studies.

This simulation exercise revealed that the number of subjects receiving a dose ≥ the actual MTD is lower with the new approach than with the traditional methodology in all the cases examined. This is a very important result as it should reassure clinical investigators (who are accountable in terms of individual safety of the healthy volunteers) and members of the Investigational Review Boards (who are charged with assessing and judging the ethical aspects of each individual clinical trial) that the implementation of this new approach actually increases safety by decreasing the risk of an undesirable event at the level of the individual subject participating in the trial. Administering dose levels that are toxic was also a concern with the CRM in the field of oncology and our modifications of the classical CRM are consistent with previous research work [23,24]. In the present work, the switching rule and the cohort size of three subjects on active treatment also diminish the risk of dose level ≥ the MTD and increase the probability to administer informative dose levels.

The new approach includes Bayesian adaptive methodology, a model-based technique to select the most appropriate next dose level and the number of healthy volunteers to be included in the next treatment cohort. Only a few Bayesian methods in FTIH studies in the literature use flexible numbers of subjects and stopping rules [12,25]. The Bayesian method presented in this manuscript is novel because it combines a flexible number of cohorts and a flexible number of subjects per cohort with simple empirical stopping rules to increase performance and facilitate implementation. Furthermore, the stopping rule based on RCV is innovative and permits halting of the trial on the basis of the precision of the estimated MTD. This novel Bayesian adaptive method is the result of a close and synergistic interaction between statisticians and clinical pharmacologists, with a common goal to strike a balance between the use of robust stopping rules and the practical aspects of the conduct of a SAD trial.

The main component of the proposed new approach is the use of a Bayesian adaptive method with efficient stopping rules. Another important element in this new approach is to use dose levels recommended by the model. This is achieved with multiple strengths of tablets or more simply with extemporaneous formulations. The use of such extemporaneous formulations in early clinical drug development is a re-emerging trend in pharmaceutical companies, essentially to save resources and time in formulation development [26]. Extemporaneous formulations (e.g. suspension, powder in a capsule) can be prepared at the appropriate strength shortly before dosing and offer more flexibility in the dose levels that can be studied in the next cohort of subjects. This is in contrast with the traditional way of conducting SAD trials using tablets with limited number of strengths defined and prepared before the start of the study and offering no or limited flexibility during study conduct to adjust precisely the dose level based on emerging results. Our recommendation is to use a combination of flexible dose levels and a Bayesian adaptive approach to improve further the quality of results from SAD trials.

As presented in Table 1, the new approach combines several features including dose escalation using a Bayesian technique, a smaller cohort size at initial dose levels and a greater number of possible dose levels. The superior performance of the new approach results from the combination of these various features and should not be attributed to any single element such as the Bayesian methodology. The purpose of the present work was to assess the performance of the new approach as a whole, not to quantify the contribution of each element on the selected endpoints. The novelty in the new approach is not with a single element but much more in the integration of several features that could be synergistic, such as the use of extemporaneous formulations that offer the flexibility to use precisely the dose recommended by the logistic regression model and the Bayesian adaptive method.

This difference in the number of possible dose levels between the two approaches helps to reduce the bias in the MTD estimates but does not help the new approach do better than the traditional approach in terms of number of subjects and duration of the trials. For example, if the new approach was not effective in selecting informative dose levels, the greater number of possible dose levels with the new approach could easily result in a larger number of tested dose levels and as a consequence, in larger numbers of subjects and longer trial durations.

The two approaches do not use the same definition of MTD. With the new approach, the MTD is the dose level at which P(DLE) = 30% whereas in the traditional approach, the MTD is the dose level below the MID [7]. The MTD definition in the traditional approach implies that the estimated MTD is associated with a P(DLE) < 50%. Assuming that the dose level below MID corresponds to two subjects out of six with a DLE, then the corresponding P(DLE) is 33%. This leads to the realization that the two definitions should provide MTDs that are not so far apart. The new approach uses a more scientific definition of MTD as the estimated MTD is associated with a predefined probability of DLE (30%), is the same across all the trials and scenarios, and is not dependent on the possible dose levels. For these reasons, the actual MTD used in the simulations can only be based on the definition used with the new approach. The authors acknowledge that the comparison would be simpler if the two approaches would use the same definition of MTD.

In general, for the simulation work presented in this manuscript, there are several values (related to the rules and priors) and rules that were selected on the basis of the broad experience of several of the authors in the field of Bayesian statistics and clinical trials. Additional research is necessary to optimize and refine these rules and selection of these values.

The present work focused on SAD trials with a parallel group design where each volunteer can receive only one dose level. Other designs where each volunteer receives more than one dose level (e.g. three dose levels with a sufficient wash out between each dose level) are used in SAD trials and are called dose escalation with crossover designs or leap frog designs [6,27]. The performance of the Bayesian adaptive approach with crossover designs is of great interest and further research work should be conducted to explore an area where improvements are also possible.

As the primary objective of SAD trials is safety and tolerability, the present work was focused on the assessment of safety and more precisely the occurrence of DLE. Secondary objectives in SAD trials include pharmacodynamics and pharmacokinetics. When the pharmacodynamic marker or biomarker used in healthy volunteers in the SAD trial is considered relevant to the design of the next trial, usually the multiple ascending dose (MAD) trial, it is important in the SAD trial to characterize well the dose or drug concentration–pharmacodynamic response relationship. Further research work in the application of Bayesian adaptive designs in SAD trials with the goal to characterize the dose–pharmacodynamic response relationship is also required. In the meantime, a pragmatic approach would consist of a contingency to supplement the existing cohorts, if required, with one or two additional cohorts of four subjects at appropriate dose levels that would bridge the gaps in the exposure–pharmacodynamic response relationship established on the basis of the initial dose levels selected to study safety. Another opportunity to improve the understanding of the dose–response relationship is to study the dose–concentration-effect (PK/PD) relationship by including all the information from the time courses of the drug effect and drug concentration in blood or plasma.

The Bayesian adaptive methodology has been used for decades in clinical trials and in that sense, the general statistical methodology used in this work is not new, although there are some important statistical elements (e.g. innovative stopping rules and a switching rule which allows changing the sample size per cohort) that have not been described elsewhere in the literature. The proposal to use this methodology in FTIM SAD trials in healthy volunteers (outside of oncology) is new, as well as the results from trial simulations that demonstrate the expected added value.

A SAD trial is a key component in every drug development programme as it generates important information about pharmacologic properties, dose levels and dosing intervals that can be used in subsequent trials. Although SAD trials have been around for decades and the designs and conduct of these studies are well defined and established, there is still room for improvement. The present simulation work has shown that with a new approach that includes a Bayesian adaptive design, significant improvements are possible in the quality of the estimates of the MTD and in reducing the total number of subjects. Last but not least, the new approach should decrease the number of subjects exposed to doses ≥ the MTD, representing an improvement to the safety of the subjects participating in SAD trials.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare ClinBAY had financial support from F. Hoffmann-La Roche Ltd for the submitted work. The authors declare no other financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted work.