A BAYESIAN INTEGRATION MODEL OF HIGH-THROUGHPUT PROTEOMICS AND METABOLOMICS DATA FOR IMPROVED EARLY DETECTION OF MICROBIAL INFECTIONS

Abstract

High-throughput (HTP) technologies offer the capability to evaluate the genome, proteome, and metabolome of an organism at a global scale. This opens up new opportunities to define complex signatures of disease that involve signals from multiple types of biomolecules. However, integrating these data types is difficult due to the heterogeneity of the data. We present a Bayesian approach to integration that uses posterior probabilities to assign class memberships to samples using individual and multiple data sources; these probabilities are based on lower-level likelihood functions derived from standard statistical learning algorithms. We demonstrate this approach on microbial infections of mice, where the bronchial alveolar lavage fluid was analyzed by three HTP technologies, two proteomic and one metabolomic. We demonstrate that integration of the three datasets improves classification accuracy to ~89% from the best individual dataset at ~83%. In addition, we present a new visualization tool called Visual Integration for Bayesian Evaluation (VIBE) that allows the user to observe classification accuracies at the class level and evaluate classification accuracies on any subset of available data types based on the posterior probability models defined for the individual and integrated data.

1. Introduction

Developing molecular markers of disease is a subject of intense interest, however knowing a priori the appropriate analytical methods to target the correct biomolecules is challenging. With recent advances in high-throughput (HTP) experimental methods, the need for statistical methods to integrate data of different types to provide biological models that can be used to make predictions about the underlying systems has become paramount. Integrating the data from multiple technologies into an interpretable form, to identify either a diagnostic pattern or the underlying molecular response, requires developing statistical methods that can mange the differences in formats, resolutions, and data sizes from the different instruments. The promise of data fusion or data integration is that different types of data about a system can be integrated to give biological models that are more complete and accurate than those obtained by using any of the individual data sources, i.e. the whole is greater than the sum of its parts. Data integration requires a number of choices to be made: e.g., the biological question to be asked, the input data that will enable that question to be answered, and the learning model.

Despite the obvious importance of fusing HTP biological data, the heterogeneity of the data (widely varying size, scale, specificity and format) presents many challenges. To date, most methods for biological data fusion use a combination of experimental data (e.g., gene expression measurements) and predictive information (e.g., sequence homology). The most common methods use kernel fusion, such as a support vector machine (SVM), or Bayesian integration approaches [1–11]. The success of these methods depends on the data from different streams being independent enough to improve elucidation of the underlying system. For example, Lu et al. [10] showed that the predictive potential of their integrative model was reached after integrating the top few data types; many other kinds of data examined did not add any value to the model. Therefore it is important to have a way to evaluate the contribution of each type of input data to the final model.

We present a Bayesian integration strategy that uses statistical learning algorithms, such as partial least squares discriminant analysis (PLS-DA) [12], to build initial likelihood probability models which are then transformed into the posterior probability models of interest, in particular, the probability of class membership given the sample and data stream [13]. In addition, the Bayesian model can be used directly to integrate disparate data types using posterior probabilities. We demonstrate that the integration of datasets can increase the classification accuracy of the model, although integration of pairs of datasets does not always improve classification accuracy. We also present a visualization tool, Visual Integration for Bayesian Evaluation (VIBE), which allows the user to easily determine the class for which each dataset holds the most power, and allows the user to investigate different combinations of the datasets in an automated fashion.

One area of particular interest for data integration is early detection of exposure to pathogens. We present a mouse aerosol exposure experiment for which both proteomic and metabolomic biosignatures were collected. In this experiment mice were exposed to one of three organisms, Pseudomonas aeruginosa, Francisella novicida, and Francisella tularensis subsp. novicida, an avirulent mutant of F. novicida. The mice were evaluated at 4 and 24 hour time points to determine if markers of exposure were present at a pre-symptomatic state. F. novicida infection in mice serves as a model of human infection with the category A pathogen, F. tularensis subsp. tularensis [14]. In mice the disease course with aerosol exposure to F. novicida is fatal, with necrosis in the lungs as a typical pathology, whereas P. aeruginosa infection results in a distinct pneumonia. The goal of this study was to determine if integration of the HTP proteomic and metabolomic data can more accurately predict the infection class than any data source individually.

2. Sample Preparation and Analysis Methods

2.1. Pathogen Exposure

Young male mice (C57/BL) were subjected to aerosol exposure to initiate infection with one of three organisms (Table 1): virulent strains of F. novicida (FTN) and P. aeruginosa (PA), and an avirulent F. novicida (MGLA) containing a mutation to the transcriptional regulator gene mglA. The C57/BL mice were obtained from Jackson Labs (Bar Harbor, ME), exposed to one of the above pathogens using Intox snout-only restraining tubs (In-Tox Products LLC, Moriarty, NM), and sacrificed at one of three time points. This resulted in seven classes of interest shown in Table 1: (1) Control at times 0, 4 and 24 Hrs, (2) PA at 4 Hrs, (3) PA at 24 Hrs, (4) FTN at 4 Hrs, (5) FTN at 24 Hrs, (6) MGLA at 4 Hrs, and (7) MGLA at 24 Hrs. The study was conducted using an experimental design to limit effects of exposure time or order prior to sample collection.

Table 1.

Pathogen Exposure Experiment.

	0 Hrs	4 Hrs	24 Hrs
Controla	n = 4	n = 4	n = 4
PAb		n = 4	n = 4
FTNb		n = 4	n = 4
MGLAb		n = 4	n = 4

^aControl animals were exposed to phosphate buffered saline.

^bPA = P. aeruginosa, FTN = F. novicida (wild-type) and MGLA = F. novicida mglA⁻.

Bronchial alveolar lavage fluid (BALF) was collected from each animal and subjected to three HTP analytical methods: Matrix Assisted Laser Desorption/Ionization (MALDI) mass spectroscopy (MS) to evaluate large proteins, accurate mass and time tag (AMT) proteomics on an Orbitrap mass spectrometer to evaluate protein fragments, and nuclear magnetic resonance (NMR) spectroscopy to evaluate metabolites.

2.2. MALDI Mass Spectrometry

The MS analysis of purified proteins was performed using an Autoflex II MALDI tandem time-of-flight mass spectrometer equipped with a HIMAS^™ detector (Bruker Daltonics, Billerica MA). Raw data was processed using available functions in the vendor software, which allows for spectral recalibration and alignment. Peaks are extracted using an automated peak detection algorithm that creates a list of peak locations (m/z) and associated intensity values from the mass spectrum of each sample [15]. The full sets of spectra (all technical replicates from all experimental replicates) are aligned for each peak, identifying its location (or non existence) over all replicates [16]. The code to perform this processing runs in MatLab® Version R2008a. Replicate peak identifications within a sample class were averaged and subjected to an occurrence filter of 60% [17], which resulted in a final dataset of peak intensities for 51 locations. Due to the variability of peak intensities and missing data, MALDI data are commonly converted to binary values. Thus, the final dataset consisted of 51 locations marked with presence/absence over the 36 samples.

2.3. AMT-based Proteomics

MS analysis was also performed on protein fragments (peptides) using an LTQ-Orbitrap^™ mass spectrometer (Thermo Electron Corp., Waltham, MA) with nanoelectrospray ionization. Orbitrap^™ spectra were collected from 400–2000 m/z at a resolution of 100k and analyzed using the accurate mass and elution time (AMT) tag approach [18]. Briefly, the theoretical mass and the observed normalized elution time (NET) of peptides identified by LC MS/MS have been used previously to construct a reference database of murine AMT tags [19]. Features from the LC MS analyses (i.e., m/z peaks deconvolved of isotopic and charge state effects and then correlated by mass and NET) were matched to AMT tags to identify peptides, using a tolerance of +/−6 ppm for mass and 0.025% for the LC NET. The mass deisotoping and alignment process was performed using Decon2LS, and the matching process was performed using VIPER [20].

Peptide abundance data was further processed to remove peptides identified with low confidence. First, a uniqueness filter of a SLiC score of 0.5 with DELSLiC of 0.2 was applied to the data [21]. All peptides were then filtered using an occurrence filter that required peptides to have been observed in at least one exposure class for at least 75% of the samples. After filtering, the missing observations for the remaining 2023 non-redundant peptides were imputed using a tiered strategy, where if a peptide was observed in more than 50% of the samples of a particular class the missing values were imputed as the mean of the observed values, otherwise it was imputed as ½ of the minimum observed abundance for that peptide. Thus, the final reduced dataset consisted of the 36 samples with measured or imputed abundance values for 2023 peptides.

2.4. Proton (¹H) NMR

NMR analysis of metabolites was performed by adding 200 μL of D₂0 containing 0.4 mM trimethylsilylpropionic-2,2,3,3,-d₄ acid (internal reference) to 400 mL of each BALF sample and recording a one-dimensional ¹H NMR spectrum on a Varian Unity-600 NMR spectrometer (Varian Inc., Palo Alto, CA) at 10°C. The data were collected with a sweep width of 8000 Hz, 32k of data points, a delay of 3.0 s, and 4096 transients, and processed with Felix 97 software (Accelrys, San Diego, CA). After converting the Varian free-induction decay data into Felix format, the data were adopidized with a square sinebell function prior to Fourier transformation into the frequency domain. The spectral files were then imported to Chenomx NMR Suite 5.0 software (Chenomx Inc, Alberta, Canada) for baseline correction, normalization, and binning using 0.01 ppm bins. This resulted in a final dataset that consisted of 324 bins. A large fraction of these bins had considerable variability and were further processed by a Kruskal-Wallis test across the seven exposure classes defined in Table 1 [20]. A bin inclusion p-value of 0.01 was selected, which resulted in a final reduced dataset of measured intensity values for 27 bins for the 36 samples.

3. Statistical Methods

3.1. Statistical Learning Algorithms

Bayesian integration is based on the ability to define probability models for independent sources of data. We used partial least squares discriminant analysis (PLS-DA) [12] to evaluate the Orbitrap and NMR datasets. The MALDI data is in a binary format, not well suited to PLS-DA, thus, a spectral fingerprinting approach called degree of association was used [17]. Additionally, leave-one-out cross-validation (LOOCV) was used to assure that the probabilities obtained for a specific sample were independent from the training data [23].

3.1.1. Partial Least Squares– Discriminant Analysis (PLS-DA)

The primary goal of PLS [24] is to build a linear model between a set of independent variables and a predictor variable (e.g., exposure and time). In general, PLS produces factor scores that are linear combinations of the original variables in such a manner that the factor score variables are uncorrelated. PLS-DA is used for categorical variables, such as the binned NMR and proteomics values in this analysis. PLS-DA was run in MatLab® Version R2008a using Version 4.2 of the PLS_Toolbox© from Eigenvector Research. PLS-DA gives a number nominally between zero and one that is associated with the likelihood that the sample i (s_i) from dataset Q belongs to event k, P(s_i,D_Q|E_k), where Q∈[O,N] for the Orbitrap and NMR datasets, respectively and k=1,…,7 (classes associated with Table 1). The LOOCV allows these likelihood values to deviate outside of the zero-to-one boundary of probability values, therefore a piecewise function was used to assure that appropriate probability values were obtained.

$$P(s_i,D_Q\mid E_k)=\{\begin{array}{l}0\text{if}{\mathit{PLS}}_{\mathit{LOOCV}}(s_i,D_Q\mid E_k)<0\hfill \\ 1\text{if}{\mathit{PLS}}_{\mathit{LOOCV}}(s_i,D_Q\mid E_k)>1\hfill \\ {\mathit{PLS}}_{\mathit{LOOCV}}(s_i,D_Q\mid E_k)\text{otherwise}\hfill \end{array}$$ (1)

3.1.2. Degree of Association

Degree of Association is a statistical algorithm that returns a probability associated with the similarity of a MALDI reference library and the spectra of interest [17]. In particular, the null hypothesis (H_O) that a specific sample is from class k (e.g., FTN at 4 hours) is considered versus the alternative that the specific sample is not from class k. Assuming H_O, the sample under consideration can be described by the probability of observing peak i (p_i). These probabilities are compared to the reference fingerprint of class k based on the set of peaks that differ and those that are in common between the sample fingerprint and the reference fingerprint:

$$da(k)=P(s_i,D_M\mid E_k)=1-\prod _{i\in A^C}{p}_i\left[\prod _{i\in A}(1-p_i)\right]$$ (2)

where A is the fingerprint peaks that are not observed in the sample and A^C is the complement, i.e., observed peaks. The code to compute the Degree of Association runs in MatLab® Version R2008a. The result of the model is the likelihood that that the sample is in the modeled class based on LOOCV.

3.2. Bayesian Statistics, Integration, and Classification

Bayesian statistics is an attractive approach for making probabilistic inferences from biological data because all data are defined as random variables, allowing the removal of nuisance parameters via integration or summation [13]. Let ϑ denote the set of unknown parameters and let y_obs denote the observed data, e.g., resulting from an experimental technique like NMR. The likelihood function is defined as the probability of the observed data given the unknown parameters:

$$L(\vartheta ;y_{\mathit{obs}})=P(y_{\mathit{obs}}\mid \vartheta ).$$

Thus, the joint probability distribution of ϑ and y_obs is defined as:

$$\begin{array}{c}\mathit{Joint}=\mathit{Likelihood}\ast \mathit{Priors}\\ P(y_{\mathit{obs}},\vartheta )=L(\vartheta ;y_{\mathit{obs}})P(\vartheta )=P(Y_{\mathit{obs}}\mid \vartheta )P(\vartheta ).\end{array}$$

The Bayesian inference is made by obtaining and inspecting the posterior distributions of the unknown quantities of interest. These posterior distributions are obtained from Bayes theorem:

$$P(\vartheta \mid y_{\mathit{obs}})=\frac{P(y_{\mathit{obs}},\vartheta )}{P(y_{\mathit{obs}})},$$

where P(y_obs) is computed by integrating over ϑ in the joint distribution. Suppose the unknown parameter is of n dimension, ϑ = (ϑ₁,…,ϑ_n). Those parameter components that are not of immediate interest, but necessary to the model, must be integrated out from the joint distribution to provide a proper inference on the unknown variable of interest.

For our experiment, the probabilities obtained in Eqs. (1) and (2) are the likelihood of observing sample i (s_i) associated with dataset Q given a specific exposure/time class (Table 1). However, in predicting an exposure/time class, the posterior probability is the one of primary interest:

$$P(E_k\mid s_i,D_Q)=\frac{P(s_i,D_Q\mid E_k)P(E_k)}{{\displaystyle \sum _{k=1}^{NG}}P(s_i,D_Q\mid E_k)P(E_k)},Q\in [0,\mathrm{N},\mathrm{M}]$$ (3)

where NG is the number of classes, seven for our mouse infection experiment. Thus, for each sample a set of NG probabilities are obtained which sum to one. Class membership is assigned to the class that has maximum probability:

$$s_i\in E_k\text{where}\mathrm{k}=\underset{\mathrm{k}=1}{\overset{\text{NG}}{max}}\left(P(E_k\mid s_i,D_Q)\right).$$ (4)

Bayes formula can also be used to integrate and extract posterior probabilities for multiple data streams. Under the assumption that each data stream is independent but shares a common sample source, then the integrated likelihood is the product of the individual likelihoods:

$$P(s_i,D_1,\dots ,D_{NQ}\mid E_k)=P(s_i,D_1\mid E_k)\ast P(s_i,D_2\mid E_k)\ast \dots P(s_i,D_{NQ}\mid E_k),$$

where NQ is the number of data streams. Given that the datasets share common samples, the datasets likely have some correlation; however, since the end goal is classification this assumption simplifies the integration step and the visualization tool can be used to assess the accuracy of the model and the probability of a particular sample is

$$P(E_k\mid s_i,D_1,\cdots ,D_{NQ})=\frac{\left[{\displaystyle \prod _{Q=1}^{NQ}}P(s_i,D_Q\mid E_k)\right]P(E_k)}{{\displaystyle \sum _{k=1}^{NG}}\left[{\displaystyle \prod _{Q=1}^{NQ}}P(s_i,D_Q\mid E_k)\right]P(E_k)}.$$ (5)

For our experiment, the maximum of NQ was three, however any subset of data streams can be analyzed. For our experiment, the prior probabilities P(E_k) were set to be equal (1/NG). Classification of the integrated data is performed in an analogous manner to Eq. (4).

4. Results and Discussion

In our pathogen exposure experiment, three data sources representing the proteomic and metabolomic profiles were collected, each of varying size and content. For example, the Orbitrap data has multivariate form of n = 36 samples by 2023 abundance values, while the MALDI data is in the form of 36 samples by 51 binary values. To transform the three datasets into a common form, we first used statistical learning algorithms, PLS-DA (Section 3.1.1) and Degree of Association (Section 3.1.2), to transform these datasets into probability metrics associated with class membership using Eqs. (1) and (2). The second step consisted of using Bayesian statistics to modify these probability models into the posterior form associated with the probability of observing a specific class given the observed data (Eq. (3)). This posterior probability model was then used directly to perform classification on individual datasets (Eq. (4)) and the product of sets of probability models used to compute integrated posterior probability models (Eq. (5)). This process is described in Figure 1 with respect to the pathogen exposure experiment and is easily generalizable.

Figure 1.

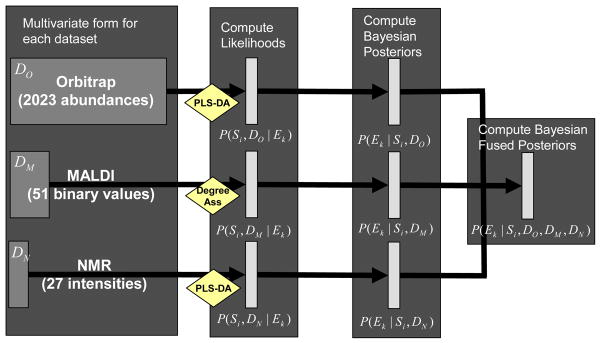
Standard analysis pipeline to obtain integrated posterior probabilities across the heterogeneous data types.

We describe the results for the individual and integrated datasets with respect to classification accuracy (CA). CA is simply measured as the number of correctly classified observations (#TP) divided by the total number of samples: (CA = #TP/n). Samples were classified into whichever class they fell with maximum probability (Eq. (4)). We observed that the individual data source with the highest LOOCV CA was the AMT-based Orbitrap data, with on overall CA of ~83.3%. Second was the MALDI data with an overall CA of ~75%, followed by the NMR data at ~61.1%. Integration of the three datasets increased the overall CA of the model to ~89%. The results broken down by class are given in Table 2.

Table 2.

Overall class accuracy results for each class using LOOCV.

	NMR	MALDI	Orbitrap	Integrated
Control	75%	75%	92%	100%
PA – 4	75%	100%	100%	100%
PA – 24	50%	75%	50%	50%
FTN – 4	50%	75%	75%	100%
FTN – 24	75%	25%	75%	100%
MGLA – 4	75%	100%	75%	75%
MGLA – 24	0%	75%	100%	75%
Total	61.1%	61.1%	83.3%	89.0%

We were interested not simply in the CA values for each dataset, but also in which samples were misclassified into which classes, as well as which dataset offered the most advantage to the integration. To explore these questions we developed a visualization tool in MatLab® Version R2008a called Visual Integration for Bayesian Evaluation (VIBE) that ingests the posterior probability models from Eq. (3), computes the CA and performs the integration. VIBE plots the CA matrices, where the x-axis is the true class and the y-axis is the predicted class, and the color indicates the fraction of samples that were classified into specific classes (see Figure 2). For example, we observed that the NMR data misclassified a few samples into the P. aeruginosa class at 24 hours and the F. novicida class at 4 hours, and the MALDI data misclassified control samples into the P. aeruginosa and the F. novicida mutant (MGLA) 4 hour classes. The visualization allows the user to observe these apparent differences, which presumably allow the integrated probabilities to attain the correct classification and point out both correlated and orthogonal structures between the datasets at the classification level. Thus, in this manner the complementary or overlapping nature of specific datasets can be explored. In addition, VIBE computes the posterior probability of each dataset in the integrated model (below the integrated CA plot), which gives a rough measure of the contribution of each dataset.

Figure 2.

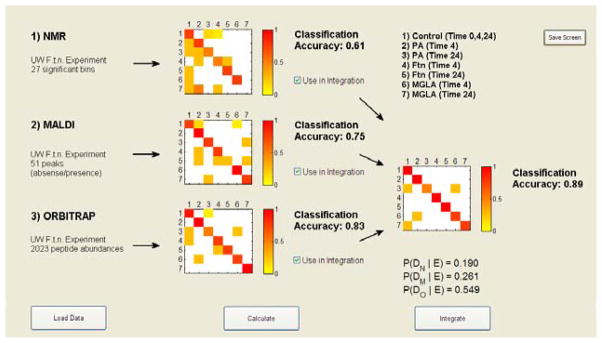
VIBE screenshot of the integrated classification and accuracy calculation over the Orbitrap, MALDI, and NMR datasets.

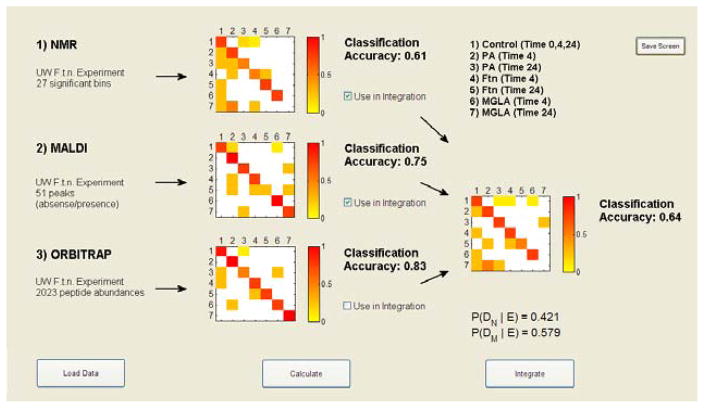
It is not always the case that integration improves the CA of a system. For example, the overall CA drops to ~64% when using only the NMR and MALDI data to perform the integration (Figure 3), and to ~81% when integrating only NMR and Orbitrap data. These values are lower than individual CAs for MALDI and Orbitrap, respectively. However, we do see an increase in CA to ~86% when the MALDI and Orbitrap data are combined. Thus, it appears that the NMR data does not complement the MALDI and Orbitrap datasets as we might have expected, but instead validates misclassifications and, in some cases, changes correct classifications to incorrect ones.

Figure 3.

VIBE visualization of the integrated classification and accuracy calculation over two datasets: NMR and MALDI.

Observations from the CA plots, such as the lack of correct classifications of the MGLA (24h) by NMR could be used to derive prior probabilities that would account for these biases. The small sample size of the data used here is not adequate to derive completely disjoint training and testing data, but with an additional independent experiment such priors could be validated. Nonetheless, the observations in the CA plots give significant insight into the potential biomarkers of infection; future work would include methods to identify which biomolecules are working cooperatively across datasets to improve the classification accuracy of the model. They also yield insight into which datasets may not be adequately independent for the model in Eq. (5).

In evaluating the CA plots in VIBE, we also observed that many of the misclassifications in each dataset remain misclassified in the integrated model (see Figure 3). This suggests that the probabilities associated with these misclassifications are relatively strong and only with all three datasets can many of the probabilities be pushed toward a maximum value for the correct class. The MGLA at 24 hours is a good example. This class is completely misclassified using only the NMR dataset, correctly classified 3 out of 4 times using only the MALDI dataset, and correctly classified in all cases using only the Orbitrap dataset. In the integrated model using just NMR and MALDI data, samples from this class were never correctly classified, however, for the integrated model with all three datasets this class is correctly classified 3 out of 4 times. This type of exploration allows users to evaluate the data in both the context of the individual data sources as well as in the integrated model, and draw new hypotheses. For instance, one may infer that a biomarker of late exposure to the mutant strain of F. novicida is a protein and not a metabolite.

5. Conclusions

Data integration is a key challenge associated with the availability of HTP technologies that are being used to simultaneously measure various types of biomolecules. The Bayesian integration approach presented offers flexibility to tackle this challenge, by allowing any appropriate statistical learning algorithm to be used to derive the likelihood values associated with samples originating from common classes. The posterior probability models associated with each dataset yield a natural means to perform classification and can be directly integrated. Here we undertake a problem associated with metabolic and proteomic profiles associated with HTP techniques applied to a mouse infection model. The derived posterior probability models are integrated into a visualization tool, VIBE, which allows the user to explore multiple combinations of the data and evaluate specific class accuracies in the context of each dataset. This type of exploratory analysis is helpful in defining appropriate prior probabilities that could be added to the model for classes associated with specific types of HTP platforms. Future work includes deriving these priors and testing the model on an independently derived sister experiment, as well as using the defined biosignatures of the model to determine the suite of biomolecules relevant to each class separation.