From normal to anomalous diffusion in comb-like structures in three dimensions

Abstract

Diffusion in a comb-like structure, formed by a main cylindrical tube with identical periodic dead ends of cylindrical shape, occurs slower than that in the same system without dead ends. The reason is that the particle, entering a dead end, interrupts its propagation along the tube axis. The slowdown becomes stronger and stronger as the dead end length increases, since the particle spends more and more time in the dead ends. In the limiting case of infinitely long dead ends, diffusion becomes anomalous with the exponent equal to 1/2. We develop a formalism which allows us to study the mean square displacement of the particle along the tube axis in such systems. The formalism is applicable for an arbitrary dead end length, including the case of anomalous diffusion in a tube with infinitely long dead ends. In particular, we demonstrate how intermediate anomalous diffusion arises when the dead ends are long enough.

I. INTRODUCTION

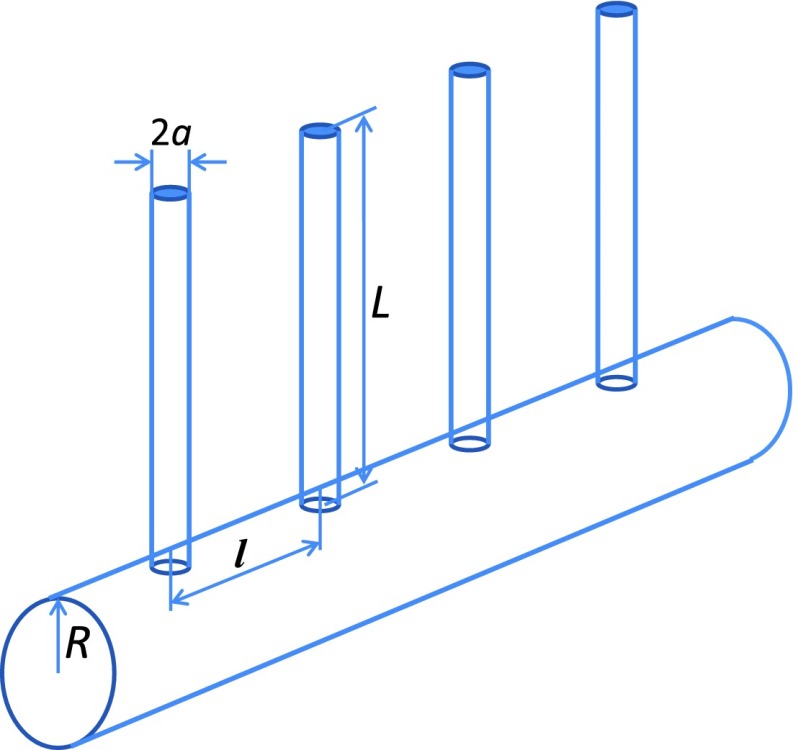
The model of a particle diffusing in a tube with dead ends is widely used in studies of linear porous media.^1–3 Examples of transport in such systems include transport in dendrites,⁴ extra-cellular diffusion in brain tissue,⁵ diffusion of water and other substances in muscles,⁶ etc. An analytical theory of diffusion in tubes with periodic dead ends formed by identical cavities connected to the main tube by narrow necks has been developed in Ref. 3(a)). The focus of the present study is on a special case of such a tube, where the dead ends are periodic thin cylinders. This is the so-called comb-like structure schematically shown in Fig. 1. The mean square displacement ⟨x²(t)⟩ of a particle diffusing in such a structure has qualitatively different long-time behavior depending on whether the dead end length is finite or infinite. When the length is finite ⟨x²(t)⟩|_t→∞ ∝ t, while when the length is infinite ⟨x²(t)⟩|_t→∞ ∝ t^1/2. Thus, at a finite dead end length we deal with normal effective diffusion, whereas when this length is infinite, the diffusion is anomalous.^7–10

FIG. 1.

Schematic representation of a comb-like structure formed by a main cylindrical tube of radius R and periodic narrow cylindrical dead ends of radius a and length L, separated by distance l.

When the dead ends are long enough, the particle is “unaware” of their finiteness at intermediate times. As a result, anomalous-like diffusion naturally arises during the transient behavior to the effective normal diffusion at long times. Such transient behavior can be misinterpreted as anomalous diffusion.¹¹ Intermediate anomalous diffusion in cells and other complex environments has been discussed recently.^7–11

Diffusion and random walk in comb-like structures have been studied by many authors (see, for example, the books by Weiss¹² and Redner¹³ and references therein). A distinctive feature of the present study is that we develop a formalism which allows us to derive an expression for the Laplace transform of the mean square displacement ⟨x²(t)⟩, which is applicable for an arbitrary comb tooth length. This is done in Sec. II. Inverting this transform numerically, one can obtain the mean square displacement over the entire range of time. In Sec. III, we use this transform to analyze the behavior of ⟨x²(t)⟩ at short and long times. In addition, we demonstrate intermediate anomalous subdiffusion, ⟨x²(t)⟩ ∝ t^1/2, during the transition to the effective normal diffusion at long times. The obtained results are summarized and some concluding remarks are made in Sec. IV.

II. GENERAL THEORY

Consider a point particle diffusing in a comb-like structure schematically shown in Fig. 1. The structure is formed by a main cylindrical tube of radius R and periodic thin cylindrical dead ends of radius a and length L, separated by distance l. The cylinders are thin in the sense that their radius a is much smaller than both the period l and the main tube radius R, a ≪ l, R. The dead end length L can be arbitrary, L ⩾ 0. The case of L = 0 corresponds to a purely cylindrical tube with no dead ends. The particle propagates along the tube axis only when it is in the main tube. Entering a dead end, the particle interrupts its propagation. Later it returns, and the propagation continues. Particle transitions between the main tube and the dead ends can be described as transitions between mobile (m) and immobile (de) states by the kinetic scheme

$$m\rightleftarrows \mathit{de}$$ (2.1)

We assume that the particle starts in the main tube and choose its starting position along the tube axis as the origin. Consider those realizations of the particle trajectory, for which the cumulative time spent by the particle in the mobile state is equal to t_m, t_m ⩽ t, where t is the total observation time. The particle propagator due to such realizations is the free propagator for time t_m,

$$G_0(x,t_m)=\frac{1}{\sqrt{4\pi D_0{t}_m}}{e}^{-x^2/\left(4D_0{t}_m\right)},$$ (2.2)

where D₀ is the particle diffusivity in a cylindrical tube with no dead ends. Time t_m is a random variable. Denoting the probability density for this time, conditional on that the total observation time is t, by φ(t_m|t), we can write the particle propagator for time t, G(x, t), as the averaged propagator G₀(x, t_m),

$$G(x,t)={\int }_0^t{G}_0(x,t_m)\phi \left(t_m|t\right)d{t}_m.$$ (2.3)

Both propagators satisfy the same initial condition,

$$G(x,t=0)=G_0(x,t_m=0)=\delta \left(x\right).$$ (2.4)

We use the propagator in Eq. (2.3) to find the mean square displacement of the particle,

$$\begin{array}{ccc}\hfill ⟨x^2\left(t\right)⟩& =& {\int }_{-\infty }^{\infty }{x}^{2}G(x,t)dx\hfill \\ & =& {\int }_0^t\left[{\int }_{-\infty }^{\infty }{x}^2{G}_0(x,t_m)dx\right]\phi \left(t_m|t\right)d{t}_m.\hfill \end{array}$$ (2.5)

Since

$${\int }_{-\infty }^{\infty }{x}^2{G}_0(x,t_m)dx=2D_0{t}_m,$$ (2.6)

we obtain

$$⟨x^2\left(t\right)⟩=2D_0⟨t_m\left(t\right)⟩,$$ (2.7)

where ⟨t_m(t)⟩ is the mean cumulative time spent by the particle in the mobile state

$$⟨t_m\left(t\right)⟩={\int }_0^t{t}_m\phi \left(t_m|t\right)d{t}_m.$$ (2.8)

Introducing the fraction of time spent by the particle in the mobile state, f_m(t),

$$f_m\left(t\right)=\frac{⟨t_m\left(t\right)⟩}{t},$$ (2.9)

we can write the mean square displacement in Eq. (2.7) as

$$⟨x^2\left(t\right)⟩=2D_{0}t{f}_m\left(t\right).$$ (2.10)

As t → ∞, f_m(t) tends to its equilibrium value $f_m^{eq}$. If $f_m^{eq}\ne 0$, Eq. (2.10) leads to

$$⟨x^2\left(t\right)⟩=2D_{eff}t,t\to \infty ,$$ (2.11)

where D_eff is the effective diffusion coefficient given by

$$D_{eff}=D_0{f}_m^{eq}.$$ (2.12)

It can be shown^3(a) that

$$f_m^{eq}=\frac{V_m}{V_m+V_{de}},$$ (2.13)

where V_m is the volume of the main tube per one dead end, and V_de is the dead end volume,

$$V_m=\pi R^{2}l,V_{de}=\pi a^{2}L.$$ (2.14)

Diffusion is normal when L is finite, and, as a consequence, both $f_m^{eq}$ and D_eff are finite. The situation changes dramatically when L is infinite, and hence V_de is infinite. In this case, both $f_m^{eq}$ and D_eff vanish. If f_m(t) tends to zero at long times as 1/t^β, β < 1, Eq. (2.10) leads to ⟨x²(t)⟩|_{t → ∞} ∝ t^α, where α = 1 − β < 1. Thus, in such a case we deal with anomalous subdiffusion.

After the Laplace transformation ($f\left(t\right)\to \widehat{f}\left(s\right)={\int }_0^{\infty }{e}^{-st}f\left(t\right)dt$, where $\widehat{f}\left(s\right)$ is the Laplace transform of function f(t), and s is the Laplace parameter), Eq. (2.7) takes the form

$$⟨{\widehat{x}}^2\left(s\right)⟩=2D_0⟨{\widehat{t}}_m\left(s\right)⟩,$$ (2.15)

where $⟨{\widehat{t}}_m\left(s\right)⟩$ is the Laplace transform of the mean cumulative residence time ⟨t_m(t)⟩,

$$⟨{\widehat{t}}_m\left(s\right)⟩={\int }_0^{\infty }{e}^{-st}⟨t_m\left(t\right)⟩dt.$$ (2.16)

In our analysis, we exploit the fact that there is a simple relation between $⟨{\widehat{t}}_m\left(s\right)⟩$ and the double Laplace transform of the conditional probability density φ(t_m|t) defined by

$$\begin{array}{ccc}\hfill \widehat{\phi }\left(\sigma ,s\right)& =& {\int }_0^{\infty }{e}^{-st}dt{\int }_0^t{e}^{-\sigma t_m}\phi \left(t_m|t\right)d{t}_m\hfill \\ & =& {\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\sigma t_m-st}\phi \left(t_m|t\right)d{t}_{m}dt.\hfill \end{array}$$ (2.17)

Taking advantage of the small-σ expansion of $\widehat{\phi }\left(\sigma ,s\right)$, one can check that the relation between $⟨{\widehat{t}}_m\left(s\right)⟩$ and $\widehat{\phi }\left(\sigma ,s\right)$ is given by

$$⟨{\widehat{t}}_m\left(s\right)⟩=-{\left.\frac{\partial \widehat{\phi }\left(\sigma ,s\right)}{\partial \sigma }\right|}_{\sigma =0}.$$ (2.18)

As shown below, the double Laplace transform $\widehat{\phi }\left(\sigma ,s\right)$ can be easily found, and then used to obtain $⟨{\widehat{t}}_m\left(s\right)⟩$ by the above equation.

To find $\widehat{\phi }\left(\sigma ,s\right)$, we introduce the probability densities for the particle lifetimes in the mobile state and in the dead ends, w_i(t), and corresponding survival probabilities in the two states, S_i(t), i = m, de,

$$S_i\left(t\right)={\int }_t^{\infty }{w}_i\left(t^{\prime }\right)d{t}^{\prime }=1-{\int }_0^t{w}_i\left(t^{\prime }\right)d{t}^{\prime },i=m,de.$$ (2.19)

We use these survival probabilities and probability densities to write a linear integral equation for the conditional probability density φ(t_m|t),

$$\begin{array}{ccc}\hfill \phi \left(t_m|t\right)& =& S_m\left(t\right)\delta (t_m-t)+w_m\left(t_m\right)S_{de}(t-t_m)\hfill \\ & & +{\int }_0^t{w}_m\left(t^{\prime }\right)d{t}^{\prime }{\int }_0^{t-t^{\prime }}{w}_{de}\left(t^{″}\right)\phi \left(t_m-t^{\prime }|t-t^{\prime }-t^{″}\right)d{t}^{″}.\hfill \end{array}$$ (2.20)

The first term on the right-hand side of this equation represents those realizations of the particle trajectory, which do not enter a dead end and spend all the time in the main tube. For such trajectories we have t_m = t. The second term represents trajectories which spend time t_m in the main tube, then enter a dead end, and never return to the main tube. The third term is due to realizations that escape from the main tube and come back at least once.

After the double Laplace transformation, Eq. (2.20) takes the form

$$\begin{array}{ccc}\hfill \widehat{\phi }\left(\sigma ,s\right)& =& {\widehat{S}}_m(s+\sigma )+{\widehat{w}}_m(s+\sigma ){\widehat{S}}_{de}\left(s\right)\hfill \\ & & +{\widehat{w}}_m(s+\sigma ){\widehat{w}}_{de}\left(s\right)\widehat{\phi }\left(\sigma ,s\right).\hfill \end{array}$$ (2.21)

Solving this equation we obtain

$$\widehat{\phi }\left(\sigma ,s\right)=\frac{{\widehat{S}}_m(s+\sigma )+{\widehat{w}}_m(s+\sigma ){\widehat{S}}_{de}\left(s\right)}{1-{\widehat{w}}_m(s+\sigma ){\widehat{w}}_{de}\left(s\right)}.$$ (2.22)

Finally, we take advantage of the relation between ${\widehat{S}}_i\left(s\right)$ and ${\widehat{w}}_i\left(s\right)$, which follow from Eq. (2.19),

$${\widehat{S}}_i\left(s\right)=\frac{1}{s}\left(1-{\widehat{w}}_i\left(s\right)\right),i=m,de.$$ (2.23)

This allows us to write Eq. (2.22) as

$$\widehat{\phi }\left(\sigma ,s\right)=\frac{s\left(1-{\widehat{w}}_m(s+\sigma ){\widehat{w}}_{de}\left(s\right)\right)+\sigma {\widehat{w}}_m(s+\sigma )\left(1-{\widehat{w}}_{de}\left(s\right)\right)}{s(s+\sigma )\left(1-{\widehat{w}}_m(s+\sigma ){\widehat{w}}_{de}\left(s\right)\right)}.$$ (2.24)

Substituting this expression for $\widehat{\phi }\left(\sigma ,s\right)$ into Eq. (2.18), we arrive at

$$⟨{\widehat{t}}_m\left(s\right)⟩=\frac{1-{\widehat{w}}_m\left(s\right)}{s^2\left(1-{\widehat{w}}_m\left(s\right){\widehat{w}}_{de}\left(s\right)\right)}.$$ (2.25)

To finish the derivation, it remains to specify the probability densities of the particle lifetimes in the two states, w_m(t) and w_de(t). We begin with the former. For a particle diffusing in the main tube, entry into a dead end may be considered as trapping by the dead end entrance. Then, for the particle in the main tube, the boundary conditions on the tube wall are non-uniform: absorbing on the disks of radius a forming the dead end entrances and reflecting on the rest of the tube wall. One can approximately describe trapping by such non-uniform boundary using boundary homogenization, which is the replacement of the initial non-uniform boundary by an effective uniformly absorbing boundary with correctly chosen effective trapping rate. (One can learn more about boundary homogenization in papers cited in Ref. 14, and references therein.) Since the disk surface fraction is small, a²/(Rl) ≪ 1, the effective trapping rate of the boundary, κ, is given by¹⁴

$$\kappa =\frac{4D_{0}a}{2\pi Rl}=\frac{2D_{0}a}{\pi Rl}.$$ (2.26)

This is in fact a linearized version of the Berg-Purcell-Shoup-Szabo formula^15,16 for the effective trapping rate by a patchy surface.

The trapping rate in Eq. (2.26) is very low in the sense that the radial relaxation time, τ_rel, is much shorter than the trapping time, τ_tr, found assuming uniform distribution of the particle over the main tube cross section. To show this, we note that τ_rel ∝ R²/D₀, while ${\tau }_{tr}^{-1}=2\kappa /R\propto D_{0}a/\left(R^{2}l\right)$. So, the ratio of the two times is

$$\frac{{\tau }_{rel}}{{\tau }_{tr}}\propto \frac{a}{l}\ll 1.$$ (2.27)

Since τ_rel ≪ τ_tr, the particle survival probability in the mobile state decays as a single exponential, $S_m\left(t\right)=e^{-k_{m}t}$, where the rate constant k_m is given by

$$k_m=\frac{1}{{\tau }_{tr}}=\frac{2\kappa }{R}=\frac{4D_{0}a}{V_m}.$$ (2.28)

Respectively, the probability density for the particle lifetime in the main cylindrical part of the tube is

$$w_m\left(t\right)=-\frac{d{S}_m\left(t\right)}{dt}=k_m{e}^{-k_{m}t}.$$ (2.29)

The Laplace transform of w_m(t) has the form

$${\widehat{w}}_m\left(s\right)=\frac{k_m}{s+k_m}.$$ (2.30)

Substituting this transform into Eq. (2.25), we arrive at

$$⟨{\widehat{t}}_m\left(s\right)⟩=\frac{1}{s\left[s+k_m\left(1-{\widehat{w}}_{de}\left(s\right)\right)\right]}.$$ (2.31)

Finally, the Laplace transform of the probability density of the particle lifetime in the dead end can be found using the results obtained in Ref. 3(a)), where the escape from a dead end of a more general shape is considered. For a cylindrical dead end of length L and radius a, ${\widehat{w}}_{de}\left(s\right)$ is given by

$${\widehat{w}}_{de}\left(s\right)=\frac{{\kappa }_{de}}{{\kappa }_{de}+\sqrt{s{D}_{de}}\tanh \left(L\sqrt{s/D_{de}}\right)},$$ (2.32)

where D_de is the particle diffusivity in the dead end, which may differ from the diffusivity D₀ in the main tube, and parameter κ_de is¹⁷

$${\kappa }_{de}=\frac{4D_0}{\pi a}.$$ (2.33)

The case of L = 0 corresponds to the tube without dead ends. In this case, according to Eq. (2.32), we have ${\widehat{w}}_{de}\left(s\right)=1$. Substituting this into Eq. (2.31), we obtain $⟨{\widehat{t}}_m\left(s\right)⟩=1/s^2$. Inverting this Laplace transform we find that ⟨t_m(t)⟩ = t, as it must be in the absence of dead ends, since the particle spends all time in the mobile state. For infinitely long dead ends, Eq. (2.32) simplifies and takes the form

$${\widehat{w}}_{de}\left(s\right){|}_{L=\infty }=\frac{{\kappa }_{de}}{{\kappa }_{de}+\sqrt{s{D}_{de}}}.$$ (2.34)

The expressions in Eqs. (2.15), (2.31), and (2.32) allow us to find the Laplace transform of the mean square displacement, $⟨{\widehat{x}}^2\left(s\right)⟩$, at arbitrary length L of the dead ends. In Sec. III, we use these expressions to study the long-time behavior of ⟨x²(t)⟩ as a function of L.

III. APPLICATION OF THE THEORY

Having in hand the Laplace transform $⟨{\widehat{x}}^2\left(s\right)⟩$, one can obtain the mean square displacement over the entire range of time by inverting the transform numerically. In addition, one can use asymptotic behavior of $⟨{\widehat{x}}^2\left(s\right)⟩$ at large and small values of the Laplace parameter to find the short- and long-time behavior of ⟨x²(t)⟩, respectively. As s → ∞, ${\widehat{w}}_{de}\left(s\right)\to 0$, and Eq. (2.31) reduces to

$$⟨{\widehat{t}}_m\left(s\right)⟩\approx \frac{1}{s^2}-\frac{k_m}{s^3},s\to \infty .$$ (3.1)

Inverting this Laplace transform we find the short-time behavior of ⟨t_m(t)⟩,

$$⟨t_m\left(t\right)⟩\approx t-k_m\frac{t^2}{2},t\to 0.$$ (3.2)

Then the fraction of time spent by the particle in the main tube, Eq. (2.9), and the mean square displacement, Eq. (2.10), at short times, respectively, are

$$f_m\left(t\right)\approx 1-\frac{1}{2}{k}_{m}t,t\to 0,$$ (3.3)

$$⟨x^2\left(t\right)⟩\approx 2D_{0}t-D_0{k}_m{t}^2,t\to 0.$$ (3.4)

The relations in Eqs. (3.2)–(3.4) are universal in the sense that they are independent of the dead end length L, assuming that L ≠ 0. This is quite natural since the particle, starting in the main tube, is unaware of the dead end length at short times. However, the long-time behaviors of ⟨t_m(t)⟩, f_m(t), and ⟨x²(t)⟩ are not universal. Moreover, they are qualitatively different depending on whether the dead ends are of finite or infinite length. Therefore, below we analyze the two cases separately starting with the latter one.

A. Infinitely long dead ends

When the dead ends are infinitely long, we find the Laplace transform of ⟨t_m(t)⟩ by substituting into Eq. (2.31) the expression for ${\widehat{w}}_{de}\left(s\right){|}_{L=\infty }$ given in Eq. (2.34). This leads to

$$⟨{\widehat{t}}_m\left(s\right)⟩=\frac{{\kappa }_{de}+\sqrt{D_{de}s}}{s\left(k_m\sqrt{D_{de}s}+{\kappa }_{de}s+\sqrt{D_{de}}{s}^{3/2}\right)}.$$ (3.5)

The leading term of the small-s asymptotic behavior of $⟨{\widehat{t}}_m\left(s\right)⟩$ is

$$⟨{\widehat{t}}_m\left(s\right)⟩\approx \frac{{\kappa }_{de}}{k_m\sqrt{D_{de}}{s}^{3/2}},s\to 0.$$ (3.6)

Inverting this Laplace transform we find the long-time behavior of ⟨t_m(t)⟩,

$$⟨t_m\left(t\right)⟩\approx \frac{2{\kappa }_{de}}{\sqrt{\pi D_{de}}{k}_m}\sqrt{t},t\to \infty .$$ (3.7)

The long-time behavior of f_m(t) and ⟨x²(t)⟩ can be respectively found by substituting ⟨t_m(t)⟩ given in Eq. (3.7) into Eqs. (2.9) and (2.10). The results are

$$f_m\left(t\right)\approx \frac{2{\kappa }_{de}}{k_m\sqrt{\pi D_{de}t}},t\to \infty$$ (3.8)

and

$$⟨x^2\left(t\right)⟩\approx \frac{2D_0{\kappa }_{de}}{\sqrt{\pi D_{de}}{k}_m}\sqrt{t},t\to \infty .$$ (3.9)

Using Eqs. (2.28) and (2.33), we can write the long-time behaviors of f_m(t) and ⟨x²(t)⟩ given in Eqs. (3.8) and (3.9) in terms of the geometric parameters of the system, volume V_m = πR²l and the area of the dead end entrance, A_de = πa²,

$$f_m\left(t\right)\approx \frac{2V_m}{A_{de}\sqrt{\pi D_{de}t}},t\to \infty$$ (3.10)

and

$$⟨x^2\left(t\right)⟩\approx \frac{2D_0{V}_m}{A_{de}}\sqrt{\frac{t}{\pi D_{de}}},t\to \infty .$$ (3.11)

The expressions in Eqs. (3.9) and (3.11) show that in comb-like structures with infinitely long dead ends diffusion is anomalous with the exponent α = 1/2. This is a consequence of the fact that the fraction of time spent by the particle in the main tube (mobile state) tends to zero at long times as 1/t^1/2, Eqs. (3.8) and (3.10). Thus, in comb-like structures with infinitely long teeth the exponents α and β are equal to each other, α = β = 1/2. The range of applicability of the asymptotic results discussed above is given by

$$t\gg \frac{{\kappa }_{de}^2}{k_m^2{D}_{de}}=\frac{V_m^2}{A_{de}^2{D}_{de}}.$$ (3.12)

This inequality follows from the requirement that the small-s expansion of the Laplace transform of ⟨t_m(t)⟩, Eq. (3.5), is determined by its leading term, Eq. (3.6).

Finally, we define function α(t), which can be interpreted as a time-dependent analog of the exponent α,

$$\alpha \left(t\right)=\frac{d\ln ⟨x^2\left(t\right)⟩}{d\ln t}=1+\frac{d\ln f_m\left(t\right)}{d\ln t},$$ (3.13)

where the second equality follows from the first one and Eq. (2.10). According to Eq. (3.3), and Eqs. (3.8) and (3.10) liming values of this function are

$$\begin{array}{c}\hfill \alpha \left(t\right)\approx \left\{\begin{array}{cc}\hfill 1,& \hfill t\to 0\\ \hfill 1/2,& \hfill t\to \infty \end{array}\right..\end{array}$$ (3.14)

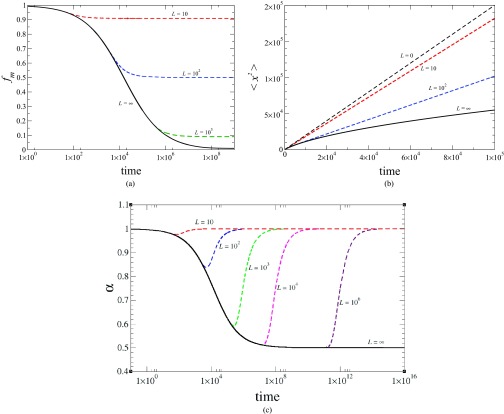
Solid lines in Fig. 2 show the time dependences f_m(t), ⟨x²(t)⟩, and α(t) obtained by numerically inverting the Laplace transforms $⟨{\widehat{t}}_m\left(s\right)⟩$, Eq. (3.5), and $s⟨{\widehat{t}}_m\left(s\right)⟩$. The curves were drawn assuming that R = l = 1, a = 0.1, and D₀ = D_de = 1. In the rest of this section, we discuss how the dependences f_m(t), ⟨x²(t)⟩, and α(t) are modified when the dead ends are of finite length, and how they are affected by the difference in the diffusivities D₀ and D_de.

FIG. 2.

The time dependences of the fraction of time spent by the particle in the main tube, f_m(t), panel (a), the mean square displacement, ⟨x²(t)⟩, panel (b), and function α(t), panel (c), defined in Eqs. (2.7), (2.9), and (3.13), respectively. Solid curves show the dependences for the tube with infinitely long dead ends, L = ∞, while the dashed lines show these dependences for tubes with dead ends of a finite length L. The values of L are given near the curves. The dependences are obtained by numerically inverting the Laplace transforms $⟨{\widehat{t}}_m\left(s\right)⟩$ and $s⟨{\widehat{t}}_m\left(s\right)⟩$, where $⟨{\widehat{t}}_m\left(s\right)⟩$ is given by Eq. (3.5) for L = ∞, and by Eq. (3.15) for L ≠ ∞, assuming that the other parameters are R = l = 1, a = 0.1, and D₀ = D_de = 1.

B. Dead ends of finite length

When the dead end length is finite, the Laplace transform of the probability density of the particle lifetime in the dead end is given by Eq. (2.32). Substituting this transform into Eq. (2.31), we arrive at

$$⟨{\widehat{t}}_m\left(s\right)⟩=\frac{{\kappa }_{de}+\sqrt{D_{de}s}\tanh \left(L\sqrt{s/D_{de}}\right)}{s\left[k_m\sqrt{D_{de}s}\tanh \left(L\sqrt{s/D_{de}}\right)+{\kappa }_{de}s+\sqrt{D_{de}}{s}^{3/2}\tanh \left(L\sqrt{s/D_{de}}\right)\right]}.$$ (3.15)

As s → 0, this Laplace transform reduces to

$$⟨{\widehat{t}}_m\left(s\right)⟩\approx \frac{1}{s^2}{f}_m^{eq},s\to 0,$$ (3.16)

where $f_m^{eq}={\kappa }_{de}/\left(k_{m}L+{\kappa }_{de}\right)$, which leads to the expression in Eq. (2.13) after we substitute here the expressions for k_m and κ_de given in Eqs. (2.28) and (2.33). Respectively, the long-time asymptotic behavior of the mean cumulative residence time spent by the particle in the mobile state is

$$⟨t_m\left(t\right)⟩\approx f_m^{eq}t,t\to \infty .$$ (3.17)

As discussed earlier this leads to the mean square displacement in Eq. (2.11) with D_eff in Eq. (2.12). It can be shown that the range of applicability of the long-time behavior of the expression for ⟨t_m(t)⟩ in Eq. (3.17) is determined by the inequality

$$t\gg \left[⟨{\tau }_{de}⟩+L^2/\left(3D_{de}\right)\right]f_m^{eq},$$ (3.18)

where ⟨τ_de⟩ is the mean particle lifetime in the dead end^3(a)

$$⟨{\tau }_{de}⟩=\frac{\pi aL}{4D_0}.$$ (3.19)

According to Eqs. (2.11) and (3.4), function α(t), defined in Eq. (3.13), is equal to unity in both limiting cases of t → 0 and t → ∞. In between, α(t) first decreases, reaches a minimum, and then increases coming back to unity. Initial decrease of α(t) is identical to that in the case of infinitely long dead ends, since the particle is unaware of the finiteness of the dead end length. The larger is the dead end length, the longer function α(t) is close to its counterpart in the case of infinitely long dead ends. For sufficiently long dead ends α(t) reaches the limiting value 1/2 and stays at this value for some time before it starts increasing to come back to unity at longer times. This is an example of intermediate anomalous diffusion which arises as a part of the transient regime to the effective normal diffusion. As follows from the inequalities given in Eqs. (3.12) and (3.18), this happens when the characteristic time in the right-hand side of the latter inequality significantly exceeds its counterpart in the former inequality,

$$\left(⟨{\tau }_{de}⟩+\frac{L^2}{3D_{de}}\right)f_m^{eq}\gg \frac{V_m^2}{A_{de}^2{D}_{de}}.$$ (3.20)

Using Eqs. (2.13), (2.14), and (3.19), it can be shown that the above inequality is fulfilled when V_de ≫ V_m.

We illustrate how the finiteness of the dead end length affects the dependences f_m(t) and α(t) in panels (a) and (c) of Fig. 2 by showing these dependences for several values of L (the dashed curves). The dependences ⟨x²(t)⟩ for some of these values of L are shown in panel (b) of Fig. 2. One can see that as the dead end length increases, $f_m^{eq}$ and D_eff decrease, while α(t) stays close to its counterpart for a tube with infinitely long dead ends, α(t)|_{L = ∞}, for longer and longer times. For sufficiently long dead ends, α(t) approaches the limiting value α = 1/2, corresponding to anomalous diffusion, before it starts increasing to reach its long-time asymptotic value α = 1. This is an example of the so-called intermediate anomalous subdiffusion.^7–11

Concluding this section, we discuss how the difference between the diffusivities D₀ and D_de affects the dependencies f_m(t), ⟨x²(t)⟩, and α(t). To do this, we consider these dependences as functions of D_de at a fixed value of D₀. First, we note that the increase of D_de accelerates the transition of functions f_m(t) and α(t) to their long-time asymptotic behaviors, and diminishes the rate of growth of the mean square displacement, ⟨x²(t)⟩, with time. As D_de decreases, the transition to the long-time behavior slows down. In the limiting case of D_de = 0, the particle never enters the dead ends. Formally, it follows from Eq. (2.32). Indeed, when D_de = 0, according to this equation ${\widehat{w}}_{de}\left(s\right)=1$ and, hence, w_de(t) = δ(t). As a consequence, in this limiting case α(t) = f_m(t) = 1 and ⟨x²(t)⟩ = 2D₀t, as it must be for a particle diffusing in a tube with no dead ends.

IV. CONCLUDING REMARKS

This paper is devoted to diffusion of point particles in three-dimensional comb-like structures (Fig. 1). We develop a formalism that allows us to analyze the problem for the comb teeth of an arbitrary length. A distinctive feature of the formalism is that it focuses on the cumulative time t_m(t) spent by a diffusing particle in the main tube conditional on that the total observation time is t, t_m ⩽ t. This conditional cumulative residence time is important because the particle propagates along the tube axis only during this time.

The key relation in our analysis is the linear integral equation for the conditional probability density of time t_m(t), φ(t_m|t), Eq. (2.20). Solving this equation in the Laplace space, we find the double Laplace transform of the conditional probability density, $\widehat{\phi }\left(\sigma ,s\right)$, given in Eq. (2.24). This transform can be used to find the Laplace transform of an arbitrary moment of time t_m(t),

$$⟨t_m^n\left(t\right)⟩={\int }_0^t{t}_m^n\phi \left(t_m|t\right)d{t}_m,n=0,1,2,....$$ (4.1)

The relation between $⟨{\widehat{t}}_m^n\left(s\right)⟩$ and $\widehat{\phi }\left(\sigma ,s\right)$ has the form

$$⟨{\widehat{t}}_m^n\left(s\right)⟩={\int }_0^{\infty }{e}^{-st}⟨t_m^n\left(t\right)⟩dt={\left(-1\right)}^n{\left.\frac{{\partial }^n\widehat{\phi }\left(\sigma ,s\right)}{\partial {\sigma }^n}\right|}_{\sigma =0},$$ (4.2)

which is a generalization of the relation in Eq. (2.18) for the first moment. Since our main quantity of interest is the mean square displacement of the particle along the tube axis, we need only the first moment ⟨t_m(t)⟩, Eq. (2.7), whose Laplace transform in its final form is given in Eq. (3.15).

The formalism is used to study the dependence of the mean square displacement ⟨x²(t)⟩ on the tooth length L, assuming that the particle starts in the main tube. After some relaxation time, ⟨x²(t)⟩ approaches its asymptotic long-time behavior which is qualitatively different depending on whether L is finite or infinite. When L is finite, the diffusion at long times is normal and ⟨x²(t)⟩ is given by Eq. (2.11). However, the situation is qualitatively different when L is infinite. Here the diffusion at long times is anomalous with the exponent α = 1/2, and ⟨x²(t)⟩ is given by Eq. (3.11).

The difference in the long-time behavior of ⟨x²(t)⟩ can be rationalized using function f_m(t) defined in Eq. (2.9), which is the fraction of time spent by the particle in the mobile state. When L is finite this fraction tends to a finite limit given in Eq. (2.13), whereas when L is infinite, it tends to zero. For sufficiently large L, the relaxation time, required for the fraction to reach its long-time asymptotic value, may significantly exceed the relaxation time to the asymptotic behavior of the system with infinitely long teeth. In such a case, intermediate anomalous diffusion is observed, as illustrated in Fig. 2(c).

Finally, we note that this paper supplements our recent work¹¹ in which we show that transient behavior to the normal diffusion at long times can be misinterpreted as anomalous diffusion. Here we demonstrate how intermediate anomalous diffusion arises in comb-like structures when the comb teeth are long enough.

In this paper, we consider diffusion of point particles, i.e., we assume that the particle radius is small enough and, therefore, can be neglected. Finiteness of the particle radius leads to new effects. First of all, this is the exclude volume effect due to the fact that the particle center cannot approach the tube wall at a distance smaller than particle radius. As a consequence, the volume available for the center of the particle is smaller than the total volume of the system. Importantly, a particle of finite size “sees” a smaller dead end entrance than a point particle. The particle does not enter dead ends, when its radius exceeds that of the dead ends.^3(b) In addition, a finite size particle “feels” hydrodynamic interaction with the tube walls. All these effects are beyond the scope of this paper that focuses on diffusion of point particles. However, they may play an important role when the particle radius is comparable with that of the dead ends.^3(b)