Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jul 1.
Published in final edited form as: J Immunol Methods. 2014 Apr 12;409:54–61. doi: 10.1016/j.jim.2014.04.002

Setting objective thresholds for rare event detection in flow cytometry

Adam J Richards a,b,c,*, Janet Staats b,c,d, Jennifer Enzor b,c,d, Katherine McKinnon e, Jacob Frelinger f, Thomas N Denny c,g, Kent J Weinhold b,c,d, Cliburn Chan a,b,c
PMCID: PMC4138273  NIHMSID: NIHMS594212  PMID: 24727143

Abstract

The accurate identification of rare antigen-specific cytokine positive cells from peripheral blood mononuclear cells (PBMC) after antigenic stimulation in an intracellular staining (ICS) flow cytometry assay is challenging, as cytokine positive events may be fairly diffusely distributed and lack an obvious separation from the negative population. Traditionally, the approach by flow operators has been to manually set a positivity threshold to partition events into cytokine-positive and cytokine-negative. This approach suffers from subjectivity and inconsistency across different flow operators. The use of statistical clustering methods does not remove the need to find an objective threshold between between positive and negative events since consistent identification of rare event subsets is highly challenging for automated algorithms, especially when there is distributional overlap between the positive and negative events (“smear”). We present a new approach, based on the Fβ measure, that is similar to manual thresholding in providing a hard cutoff, but has the advantage of being determined objectively. The performance of this algorithm is compared with results obtained by expert visual gating. Several ICS data sets from the External Quality Assurance Program Oversight Laboratory (EQAPOL) proficiency program were used to make the comparisons. We first show that visually determined thresholds are difficult to reproduce and pose a problem when comparing results across operators or laboratories, as well as problems that occur with the use of commonly employed clustering algorithms. In contrast, a single parameterization for the Fβ method performs consistently across different centers, samples, and instruments because it optimizes the precision/recall tradeoff by using both negative and positive controls.

Keywords: ICS, Standardization, Reproducibility, Rare events, Positivity, Automated analysis

1. Introduction

The classification of events as positive and negative based on the setting of a threshold has traditionally been a fundamental requirement in many flow cytometry (FCM) applications, particularly in the case when positive and negative populations overlap (Maecker and Trotter, 2006). In the context of HIV monitoring, intracellular staining (ICS) assays are often employed to track functionally active antigen-specific cells that may be exceedingly rare. The current practice in most laboratories is to set a positivity threshold for each effector function (e.g. cytokine expression) by visual comparison of negative and test/positive control data, designating events that fall above the threshold as positive. However, there is no objective method for threshold determination in the FCM community and this represents a roadblock to harmonizing ICS analyses across laboratories (Maecker et al., 2005, 2010). Visual threshold determination is problematic due to its subjectivity, but also because there is poor scalability to large panels.

There is sometimes substantive overlap between the positively and negatively stimulated samples in terms of target cell subsets and it becomes necessary to either set a threshold based on expert opinion or ‘tune’ the algorithm or model to enable discovery of the rare events in the case of automated methods. A number of potentially viable methods to detect rare events are available through the use of clustering (Finak et al., 2009; Hahne et al., 2009; Lo et al., 2009; Pyne et al., 2009; Cron et al., 2013). An important initiative called FlowCAP (Aghaeepour et al., 2013) exists to critically evaluate the numerous methods available for automated analysis in flow cytometry. If the target population is reasonably separable from the negative events then the use of automated methods like clustering is ideal and it eliminates the need to find a threshold. The main issue with clustering methods and model-based methods in general is that of data masking, where the target population is identified as events in the tail of the negative event population rather than as a separate population. These clustering methods are also unsupervised which creates the additional challenge of labeling clusters as positive — in this case, the availability of an objective threshold can be helpful in separating positive from negative clusters.

The method we propose here provides an objective means of separating biologically meaningful categories of events that are difficult to consistently resolve with clustering. Our method essentially sets a threshold by optimizing the precision–recall trade-off through the use of both positive and negative controls (Calvelli et al., 1993; Nicholson et al., 1996) as the use of negative controls alone cannot control for false discoveries. This approach to the automatic assignment of thresholds is one-dimensional. However, the F-score threshold can serve as a generator for methods that combine univariate thresholds to identify high-dimensional cell subsets (Roederer et al., 2011; Aghaeepour et al., 2012) or as a filter for events of interest before further exploratory analysis with unsupervised algorithms (Qiu et al., 2011).

In this work, we first illustrate common scenarios where thresholding methods based on negative controls alone perform poorly. Then we compare several commonly employed clustering algorithms and discuss each method's suitability in the context of rare event detection. Finally, we compare Fβ thresholds to expert visual gating, optimized using back-gating, by making use of data from the multi-center proficiency study, EQAPOL

2. Methods

2.1. Data sets

Two 11-color data sets (11C-EQAPOL-1, 11C-EQAPOL-2) with explicit positive (SEB) stimulations were used in this study as well as a 4-color data set (4C-EQAPOL) without an explicit positively stimulated control. Negative controls for the 11-color data included co-stimulatory monoclonal antibodies (mAbs) anti-CD28 and anti-CD49d together with both Brefeldin A (BRF) and monensin, while the negative control for the 4C-EQAPOL panel used only dimethylsulfoxide (DMSO) (no Costim) and BRF. The 11C-EQAPOL-1 data were used to demonstrate the difficulties encountered with an endogenous background response, where the 11C-EQAPOL-2 data provided a data set with a more typical response. All three panels were developed as part of the External Quality Assurance Program Oversight Laboratory (EQAPOL) proficiency program. The lymphocyte subsets for these three data sets are available through http://duke.edu/∼ccc14/papers/fscore.

2.2. Sample preparation and ICS assay

Normal human donors were leukapheresed in accordance with Duke University's Institutional Review Board and informed consent was obtained prior to sample collection (Jaimes et al., 2011). Sample preparation and staining were performed as previously described for the 4-color (Jaimes et al., 2011) and 11-color ICS assays (Ottinger et al., 2008; Snyder et al., 2011).

2.3. Manual gating

Gating for each data set was performed by highly trained operators in accordance with our established standard operating procedure and the process included extensive back-gating to both maximize signal and minimize noise. Uniform gates were applied within each donor. In Section 3.2 the manual gates and thresholds (see Fig. 2) from two independent experts were used to infer a range for the value of β, the principal tunable parameter in the Fβ method. In Fig. 3, manual gates and thresholds from two independent labs who participated in the EQAPOL 4-color ICS EP1 Program were used.

Fig. 2.

Fig. 2

Open in a new tab

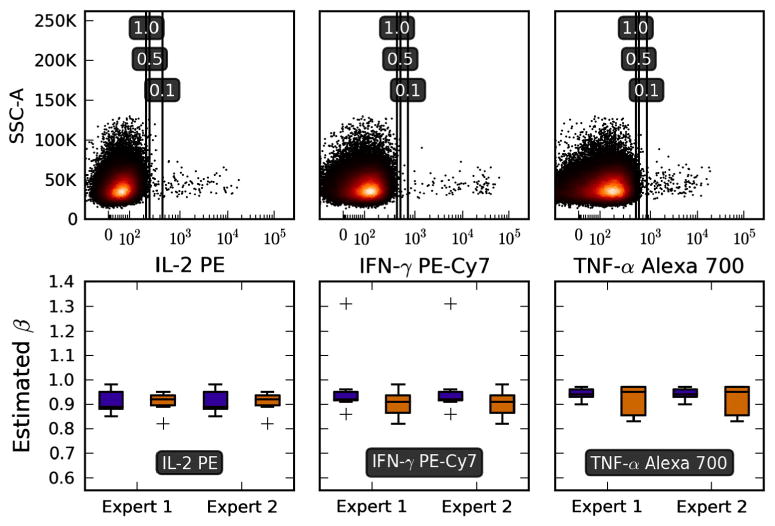
Choosing a reasonable β. The top panels show data from samples stimulated with CMV pp65 peptide pools, for three different cytokines. Positivity thresholds shown in the plot were calculated from the SEB positive and Brefeldin negative controls (not shown). As β increases (number in black rectangles), the threshold moves to the left resulting in larger cytokine percentages. We can estimate the value of β corresponding to manual thresholding by finding the value of β at which the manual and automated percentages overlap. Two expert flow operators from independent laboratories manually set positivity thresholds on data samples from normal donors treated with identical stimulation conditions, and we show the corresponding estimated β values as box-and-whiskers plots. The blue boxes are CD3+CD4+ and the orange boxes are CD3+CD8+ subsets. The ‘+’ symbols indicate outliers. The data set used here was 11C-EQAPOL-2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 3.

Fig. 3

Open in a new tab

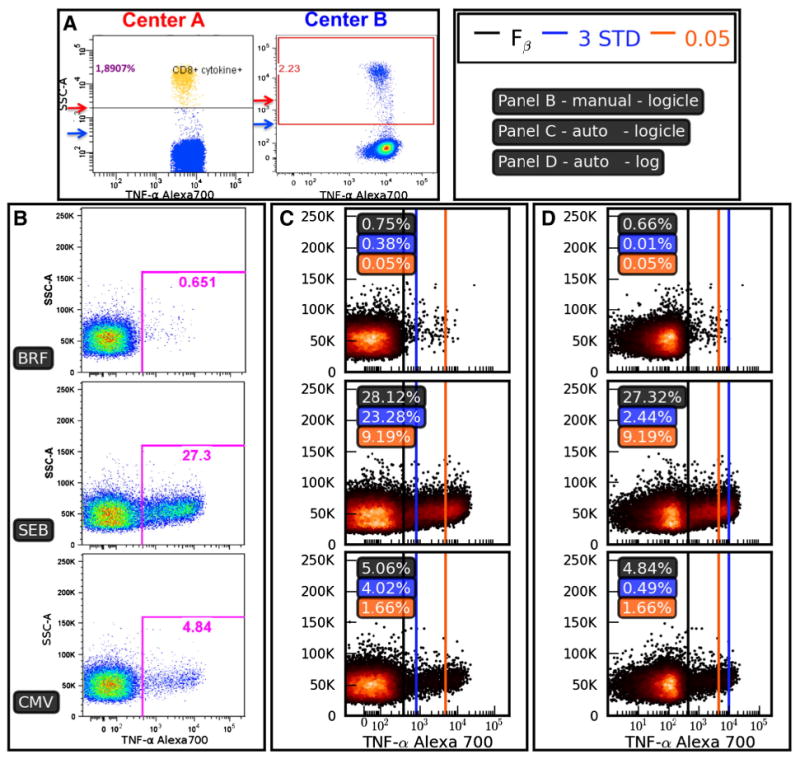
Inconsistencies in thresholding methods. Panel A: Two centers participating in the EQAPOL program evaluated the same sample using a common protocol to quantify the frequency of CD8+ cytokine positive events. Note that Center B places the threshold much closer to the negative population than Center A. Panels B–D show the setting of positivity thresholds for a sample from a donor with an endogenous CD4+ response that can be characterized by a high background even for the BRF-only negative control. Panel B shows thresholds set using manual analysis, while Panels C and D compare three different automated methods for setting the positivity threshold on the same data. Panel B: Results of manual threshold setting based on negative (BRF) and positive (SEB) controls. Panel C: Thresholds are calculated and drawn based on data that have been transformed using a biexponential (logicle) transformation. The ‘3 STD’ method sets the threshold at three standard deviations from the mean (blue line), the ‘0.05’ method sets the threshold at the 99.95% percentile (orange line), and the Fβ thresholding algorithm sets a threshold (black line) according to the methods described in this manuscript (β = 0.9). The ‘3 STD’ and Fβ methods give reasonable thresholds here, while the ‘0.05’ method excludes most of the positive response. Panel D: The data and thresholding methods are identical to Panel C, except that a logarithmic transformation has been applied. The dramatic shift of the blue line between Panels C and D shows the sensitivity to distributional assumptions that come with the ‘3 STD’ method. The data set used in Panels B–D was 11C-EQAPOL-1.

2.4. Automated analyses

All automated data analyses were carried out using the Python programming language (http://python.org). In addition, all figures in this manuscript were produced using the Python library matplotlib (Hunter, 2007). The basic subsets for all samples were found by manual gating and exported from Flowjo as FCS files. The subsets were then imported into the Python environment using the Python package py-fcm (http://code.google.com/p/py-fcm). The axis scaling for event plots that used a biexponential transform was configured for visual clarity (Parks et al., 2006). All plotted events use a biexponential transformation unless otherwise stated with the biexponential parameters (w = 0.5, D = 4.5, T = 262144). The calculation of an Fβ determined threshold is detailed in Section 3.1. The parameters for the positivity thresholding method were optimized in Section 3.2.

In Section 4.2, there are a number of clustering algorithms that were applied to discover cytokine subsets. These methods were realized through the use of py-fcm along with the machine learning package scikit-learn (Pedregosa et al., 2011). The parameters were tuned by hand using a basic grid search approach. We also constrained each method to a single best set of parameters that work for all three stimulations. We provide in the supplemental materials (http://duke.edu/∼ccc14/papers/fscore) a description of these methods and all necessary code required to reproduce the results and accompanying figure.

3. Calculation

3.1. F-score as a tool to identify positivity thresholds

The F-score or F-measure (van Rijsbergen, 1979) is widely used in information retrieval and statistics to measure the accuracy of a test (Jensen et al., 2006). The F-score balances precision and recall. Precision is defined as TPTP+FP and recall as TPTP+FN, where true positive (TP), false positive (FP), and false negative (FN) events are defined with respect to a known standard. In more general terms, precision summarizes the relevancy of a subset of events classified as positive and recall summarizes how many events we are missing. The traditional F-score is simply the harmonic mean of precision and recall. In the biomedical literature, precision is synonymous with positive predictive value and recall is the same as sensitivity. A more flexible variant of the F-score can be defined as

Fβ=(1+β2)×(precision×recall)(β2×precision)+recall. (1)

In Eq. (1), increasing the value of β gives a larger weight to recall; conversely decreasing the value of β gives a larger weight to precision. In terms of the assay, large values of β will draw a threshold close to the ‘negative’ event population and as smaller values of β are used, thresholds tend to move away from the negative population. For a given value of β, a natural choice of threshold is the value that maximizes the Fβ function.

The calculation of precision and recall requires the binary classification counts of the number of TP, FP, and FN events. Since the correct classification of events is not available in general, we use an empirical estimate of these values based on a comparison of normalized histograms (probability density) representing the negative and positive control samples (see Fig. 1). The number of bins in the histogram is automatically set to N, where N is the largest event count from the positive and negative files. In addition we transform the histogram through the use of a sliding window smoothing function (aperture = 10).

Fig. 1.

Fig. 1

Open in a new tab

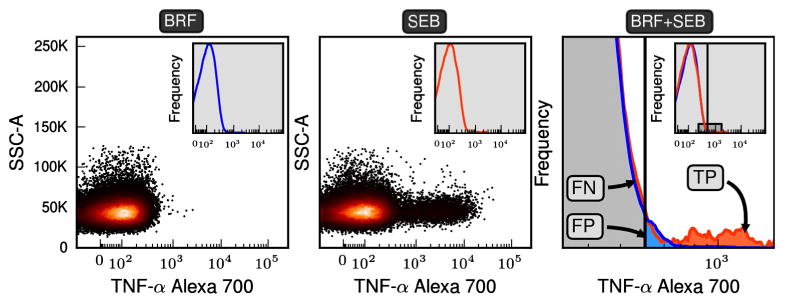
Specifying classification regions. The scatter plots of the first two panels are the fluorescent intensities for the gated events for TNF-α. To specify the classification regions needed for the Fβ method a negatively stimulated and a positively stimulated control are transformed into probability density functions (pdfs) (see insets of the first two panels). The pdf for positive (SEB) and negative (BRF) samples are overlaid in the third panel, where frequency is on the y-axis. The third plot expands the region shown in the inset. An arbitrary threshold is shown and events falling to the left and right of the threshold are classified as negative and positive respectively. Because we assume that the negative and positive samples are representative of their true populations we can define true positive, false positive, and false negative regions of event space. In the Fβ method a range of thresholds are searched until a threshold is found that optimizes the desired precision–recall trade-off specified by β. The CD3+CD8+ subset of 11C-EQAPOL-2 was used in this figure and the non-default parameters of β = 1.0 and θ = 3.0 were used to ensure all regions were easily visible.

For any given threshold, we define the TP events to be from the region to the right of the threshold where the positive control distribution has a higher density than the negative control distribution. FP events are in the area to the right as well but come from the tail of the negative histogram. FN events are the events in the negative histogram to the left of the threshold where the positive control distribution has a higher density than the negative control distribution. For clarity see Fig. 1.

When there is little difference between the negative and test sample distributions, random noise effects can result in shifts in the F-score threshold. In practice, we are only interested in the TP events where the density of the positive control sample is significantly higher than the density of the negative control sample, and not in small differences in regions where the density of both samples is equivalent. We can achieve this by modifying the definition of TP such that a region is only considered TP if the density of the positive sample is greater than θ times the negative density, where θ is a number larger than 1. As such, we introduce a parameter, θ, that biases the algorithm to detect differences only in regions where the negative sample has a low density. The default value of θ = 2.0 identifies regions where the positive sample density is at least twice that of the negative sample, and is analogous to a low-pass filter in signal processing.

3.2. Establishing parameters for ICS analysis

The β parameter establishes the desired level of weight given to precision or recall and the positivity threshold is set accordingly. Since the trade-off between precision and recall depends on the experimental context and goal of the analysis, there is no single default value of β that will work for all possible analysis scenarios. For example, diagnostic and screening assays will likely require different criteria for thresholding. However, it is convenient to have a default value for β that can be used for ICS analysis. The top panels in Fig. 2 help illustrate how changes in β affect threshold positioning. The bottom panels establish a default range of values for β that generate thresholds similar to experienced flow operators. This was done by reverse-engineering of the values of β from carefully back–gated thresholds set by expert operators at two centers (Duke and NCI flow cores). For each donor in the analysis, we plotted the percent of cytokines discovered via the Fβ method over a range of values for β and given this line we extrapolated the approximate value of β used by flow operators.

The bottom panels of Fig. 2 show that the values of β inferred from manually gated results are generally between 0.8 and 1.0. It is for this reason that we suggest 0.8 as a conservative default value for β. Of important note is that the value of β is dependent on the value of θ being 2.0. This same default parameter setting works consistently across data samples for two 11-color data sets acquired at our institution, as well as for 4-color data sets that came from a large number of other flow cores (see Section 4.3).

The value of β has meaning outside the context of flow cytometry. Precision is the ability of a classifier not to label something as positive that is truly negative. Recall is the ability to obtain all of the positive samples. A value of β = 0.8 specifies a threshold that slightly favors precision. In our approach the value β is defined before classification in the same way that the traditional α = 0.05 is used for p-value interpretations. These values exist as a guide for interpretation. Although β is appropriate in this study it may be that different experimental contexts (e.g. diagnostic versus screening assays) require a more or less conservative value.

4. Results and discussion

4.1. Using positive and negative controls for rare event detection

Positivity thresholds using a percentile cutoff based on the negative control sample alone can control false positive rates effectively and provide high precision. However, use of a negative control only allows one to minimize noise — it tells us little about how much signal we can detect. An alternative statistical approach to automate positivity thresholding based on negative controls only is to set the threshold at the mean plus a fixed number of standard distributions. This has the same limitations as using a percentile cut-off, and in addition, also has distributional assumptions that may not be met (symmetrical distribution, approximately normal etc.). Under standard practices, positive and negative controls are used to visually determine thresholds (Maecker et al., 2005); however these methods have limited reproducibility due to their subjectivity.

The mentioned negative control only methods are shown in Fig. 3 and we contrast them with thresholds derived from the Fβ and manual methods. Both the Fβ and manual methods shown in Fig. 3 use positive and negative controls. From these comparisons we note that thresholds set using a fixed number of standard deviations are highly sensitive to the choice of transformation applied (log versus biexponential), while thresholds set using percentile cut-offs can result in obvious signals being missed when there is a high background present. We also observe from the figure that Fβ method is not overly sensitive to the choice of transformation and is resilient to endogenous background responses.

4.2. Using clustering to automate rare subset discovery

Automated methods have the advantages of being able to handle large volumes of data and they can effectively work in higher dimensional space. However, with the convenience of automation comes the burden of parameter estimation. Using the same data that was used in Fig. 3 we applied four commonly used clustering algorithms and plot the results in Fig. 4. The K-means and Gaussian Mixture Model (GMM) are examples of parametric approaches that may be used in the automated analyses of flow cytometry data. Some of the most commonly used automated approaches are based on parametric models (Chan et al., 2008; Lo et al., 2009; Aghaeepour et al., 2011; Geo and Sealfon, 2012). For this example, in terms of estimating the cytokine percentages K-means and GMMs produce very comparable results. Mean shift and spectral clustering on the other hand are non-parametric methods that differ in both algorithm and result. There is clearly potential for the use of spectral clustering in FCM (Zare et al., 2010), however, it is very difficult to come up with a single set of parameter values that works across a large set of samples with different stimulations let alone instruments and laboratories. It is interesting that only the mean shift algorithm was able to detect the events from the endogenous response in the BRF stimulated sample.

Fig. 4.

Fig. 4

Open in a new tab

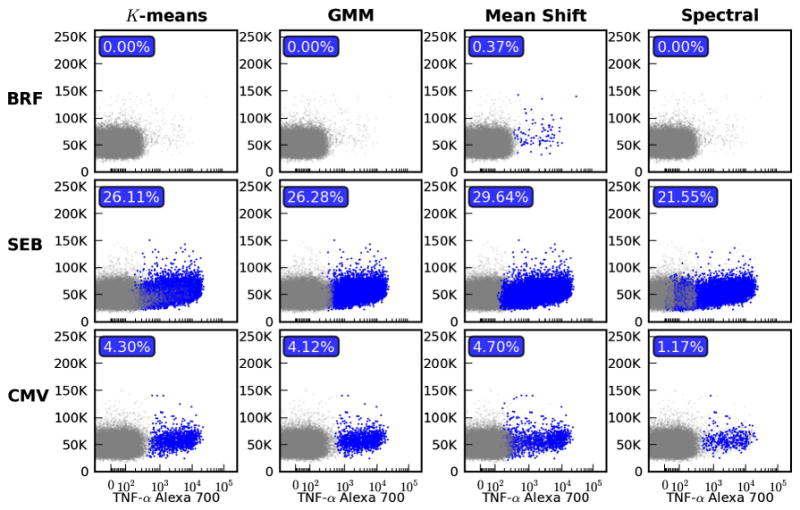
Using clustering to automate rare subset discovery. The donor and stimulated samples used in Fig. 3 are analyzed here using four different clustering methods. Each column represents a different algorithm: K-means, Gaussian Mixture Model (GMM), mean shift and spectral clustering. For each separate model all parameters were tuned to provide a single set of parameters for the three stimulations that yielded the best results. Within each subplot all clusters with a centroid that fell above the 99th percentile of the BRF stimulated sample are highlighted in blue and counted as positive in the calculation of percentage. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

For all the methods, events from a cluster were designated as positive if the centroid fell above the 99th percentile of the BRF stimulated sample. It is due to this constraint that clusters with irregular shapes are not consistently classified. This problem is the case with spectral clustering whether we use a mean or median with respect to the cutoff, which explains the lower percentages. The problem of selecting a proper heuristic for the threshold of ‘positive’ is not a small one and it is amplified as we move to new panels and instruments. Another shortcoming of these clustering methods is that they do not share data across stimulations. Take for example the case where there is a strong response from a SEB stimulated sample, but only a handful of events are present in the CMV sample. It is unlikely that these events will be picked up as an individual cluster, given the patterns observed in Fig. 4.

4.3. Application to a multi-center study

There have been many efforts to harmonize or standardize FCM assays across laboratories so as to improve reproducibility and reduce intra- and inter-laboratory variability. While the importance of protocol standardization with respect to data manipulation and instrument setup is evident (Perfetto et al., 2006; Maecker et al., 2010), standardization of data analysis is also necessary. We have described an automated method that aims to increase reproducibility over traditionally used manual methods for separating cytokine-positive from cytokine-negative events in ICS studies (Maecker et al., 2005). The method determines thresholds that optimize the trade-off between recall and precision, and is simple, robust and fast.

From the 4C-EQAPOL-1 data set we analyzed nine separate FCM centers to determine IFN-γ + IL-2 percentages for both CD3+CD4+ and CD3+CD8+ lymphocytes. The stimulations were masked in the study so we used the highest and lowest ranked samples, based on the mean of the top 1% of events, as the positive and negative controls respectively. In order to ensure discriminatory effectiveness, the Fβ method requires a minimal positive response. As a quality control for positive response, the value of the maximum Fβ score can be used where maximal Fβ < 0.5 values should be flagged.

The manual results shown in Fig. 5 were carried out by the same operator to control for potential differences. The three centers shown in the figure are reasonably similar when we compare the manual versus Fβ approaches. The Fβ method appears to be slightly more conservative in general, because the percentages are often slightly smaller than those of manual approaches. This is likely due to the fact that we use a single conservative value for β where operators generally have some variation in their preference for precision or recall (see Fig. 2). Manual approaches have the additional advantage of being able to back-gate to optimize the threshold, but even so the observed differences are well within reason. The results for the other centers are very similar and can be viewed along with the other supplemental materials (http://duke.edu/∼ccc14/papers/fscore). Also, a small Python library is available through the supplemental website as an implementation of the Fβ method described here.

Fig. 5.

Fig. 5

Open in a new tab

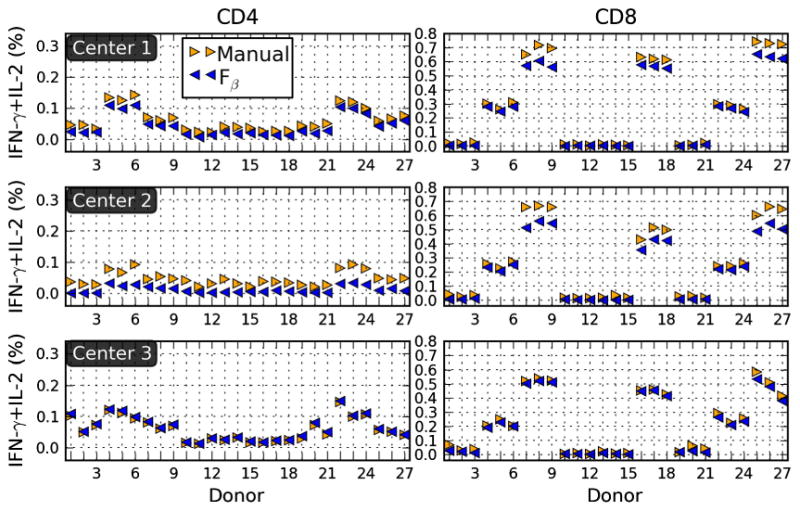
Application to EQAPOL. Cytokine percentages for three centers participating in the EQAPOL program found using and manual methods are summarized in the panels. The data set for this example is from 4C-EQAPOL.

5. Conclusions

Automated threshold determination using the Fβ method provides a potential solution to the longstanding challenge of finding a reasonably objective way to set positivity thresholds in FCM in the context of overlapping positive and negative populations. As we have shown, threshold determination works even for the discrimination of extremely rare cell populations, which is critical since thresholds are often used to detect cell frequencies of 0.1% or lower. The Fβ method can identify thresholds that are optimal with respect to a specified precision–recall trade-off, and eliminates the issue of subjectivity (reproducibility) that manual methods must deal with.

The Fβ method is not a drop-in replacement for clustering approaches since practical applications require the comparison of relatively pure cell subset populations (e.g. CD3+CD8+ T lymphocytes) across multiple samples. In most rare event search scenarios (e.g. extremely rare cytokines or tetramer positive antigen-specific events) a practical hybrid approach would be to use clustering in place of gating to extract well-defined populations such as CD3+CD8+ lymphocytes, and threshold determination to define negative and positive cytokine+ or tetramer+ events within that CD3+CD8+ population. Since the Fβ threshold is determined purely from the data for a given value of β, this algorithm provides an objective and consistent basis for identifying thresholds that will reduce the variability of flow cytometric analysis, be of benefit to automation efforts, and in general contribute to the harmonization of inter-laboratory results.

Acknowledgments

This research was partially supported by NIH grants RC1AI086032-01 and 5P30-AI064518-05 (The Duke Center for AIDS Research), and the EQAPOL contract HHSN272201000045C.

References

  1. Aghaeepour N, Nikolic R, Hoos HH, Brinkman RR. Rapid cell population identification in flow cytometry data. Cytometry A. 2011;79:6. doi: 10.1002/cyto.a.21007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aghaeepour N, Chattopadhyay PK, Ganesan A, O'Neill K, Zare H, Jalali A, Hoos HH, Roederer M, Brinkman RR. Early immunologic correlates of HIV protection can be identified from computational analysis of complex multivariate T-cell flow cytometry assays. Bioinformatics. 2012;28:1009. doi: 10.1093/bioinformatics/bts082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Aghaeepour N, Finak G, Consortium F, Consortium D, Hoos H, Mosmann TR, Brinkman R, Gottardo R, Scheuermann RH. Critical assessment of automated flow cytometry data analysis techniques. Nat Methods. 2013;10:228. doi: 10.1038/nmeth.2365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Calvelli T, Denny TN, Paxton H, Gelman R, Kagan J. Guideline for flow cytometric immunophenotyping: a report from the National Institute of Allergy and Infectious Diseases, Division of AIDS. Cytometry. 1993;14:702. doi: 10.1002/cyto.990140703. [DOI] [PubMed] [Google Scholar]
  5. Chan C, Feng F, Ottinger J, Foster D, West M, Kepler TB. Statistical mixture modeling for cell subtype identification in flow cytometry. Cytometry A. 2008;73:693. doi: 10.1002/cyto.a.20583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cron A, Gouttefangeas C, Frelinger J, Lin L, Singh SK, Britten CM, Welters MJP, van der Burg SH, West M, Chan C. Hierarchical modeling for rare event detection and cell subset alignment across flow cytometry samples. PLoS Comput Biol. 2013;9:e1003130. doi: 10.1371/journal.pcbi.1003130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Finak G, Bashashati A, Brinkman R, Gottardo R. Merging mixture components for cell population identification in flow cytometry. Adv Bioinformatics. 2009;2009:247646. doi: 10.1155/2009/247646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Geo Y, Sealfon SC. flowPeaks: a fast unsupervised clustering for flow cytometry data via K-means and density peak finding. Bioinformatics. 2012;28:2052. doi: 10.1093/bioinformatics/bts300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hahne F, LeMeur N, Brinkman RR, Ellis B, Haaland P, Sarkar D, Spidlen J, Strain E, Gentleman R. flowCore: a Bioconductor package for high throughput flow cytometry. BMC Bioinformatics. 2009;10:106. doi: 10.1186/1471-2105-10-106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hunter JD. Matplotlib: a 2D graphics environment. Comput Sci Eng. 2007;9:90. [Google Scholar]
  11. Jaimes MC, Maecker HT, Yan M, Maino VC, Hanley MB, Greer A, Darden JM, D'Souza MP. Quality assurance of intracellular cytokine staining assays: analysis of multiple rounds of proficiency testing. J Immunol Methods. 2011;363:143. doi: 10.1016/j.jim.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Jensen LJ, Saric J, Bork P. Literature mining for the biologist: from information retrieval to biological discovery. Nat Rev Genet. 2006;7:119. doi: 10.1038/nrg1768. [DOI] [PubMed] [Google Scholar]
  13. Lo H, Hahne F, Brinkman RR, Gottardo R. flowClust: a Bioconductor package for automated gating of flow cytometry data. BMC Bioinformatics. 2009;10:145. doi: 10.1186/1471-2105-10-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Maecker HT, Trotter J. Flow cytometry controls, instrument setup, and the determination of positivity. Cytometry A. 2006;69:1037. doi: 10.1002/cyto.a.20333. [DOI] [PubMed] [Google Scholar]
  15. Maecker HT, Rinfret A, D'Souza P, Darden J, Roig E, Landry C, Hayes P, Birungi J, Anzala O, Garcia M, Harari A, Frank I, Baydo R, Baker M, Holbrook J, Ottinger J, Lamoreaux L, Epling LC, Sinclair E, Suni MA, Punt K, Calarota S, El-Bahi S, Alter G, Maila H, Kuta E, Cox J, Gray C, Altfeld M, Nougarede N, Boyer J, Tussey L, Tobery T, Bredt B, Roederer M, Koup R, Maino VC, Weinhold K, Pantaleo G, Gilmour J, Horton H, Sekaly RP. Standardization of cytokine flow cytometry assays. BMC Immunol. 2005;6:13. doi: 10.1186/1471-2172-6-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Maecker T, McCoy P, Consortium FHI, Amos M, Elliott J, Gaigalas A, Wang L, Aranda R, Banchereau J, Boshoff C, Braun J, Korin Y, Reed E, Cho J, Hafler D, Davis M, Fathman G, Robinson W, Denny T, Weinhold K, Desai B, Diamond B, Gregersen P, Meglio PD, Nestle F, Peakman M, Villanova F, Ferbas J, Field E, Kantor A, Kawabata T, Komocsar W, Lotze M, Nepom J, Ochs H, O'Lone R, Phippard D, Plevy S, Rich S, Roederer M, Rotrosen D, Yeh JH. A model for harmonizing flow cytometry in clinical trials. Nat Immunol. 2010;11:975. doi: 10.1038/ni1110-975. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Nicholson J, Kidd P, Mandy F, Livnat D, Kagan J. Three-color supplement to the NIAID DAIDS guideline for flow cytometric immunophenotyping. Cytometry. 1996;26:227. doi: 10.1002/(SICI)1097-0320(19960915)26:3<227::AID-CYTO8>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
  18. Online supplemental materials for setting objective thresholds for rare event detection in flow cytometry. [accessed March 2014]; doi: 10.1016/j.jim.2014.04.002. http://duke.edu/∼ccc14/papers/fscore. [DOI] [PMC free article] [PubMed]
  19. Ottinger JS, Mensali N, Enzor J, Weinhold AK, Weinhold KJ. A simplified method to optimize reagents for an 11-color (13-marker) polychromatic intracellular staining (ICS) panel. Cytometry B. 2008;74:363. [Google Scholar]
  20. Parks DR, Roederer M, Moore WA. A new “Logicle” display method avoids deceptive effects of logarithmic scaling for low signals and compensated data. Cytometry A. 2006;69:541. doi: 10.1002/cyto.a.20258. [DOI] [PubMed] [Google Scholar]
  21. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E. Scikit-learn: machine learning in Python. J Mach Learn Res. 2011;12:2825. [Google Scholar]
  22. Perfetto S, Ambrozak D, Nguyen R, Chattopadhyay P, Roederer M. Quality assurance for polychromatic flow cytometry. Nat Protoc. 2006;1:1522. doi: 10.1038/nprot.2006.250. [DOI] [PubMed] [Google Scholar]
  23. py-fcm — a Python library for flow cytometry. [accessed March 2014]; http://code.google.com/p/py-fcm.
  24. Pyne S, Hu X, Wang K, Rossin E, Lin TI, Maier LM, Baecher-Allan C, McLachlan GJ, Tamayo P, Hafler DA, Jager PLD, Mesirov JP. Automated high-dimensional flow cytometric data analysis. Proc Natl Acad Sci U S A. 2009;106:8519. doi: 10.1073/pnas.0903028106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Python programming language — official website. [accessed March 2014]; http://python.org.
  26. Qiu P, Simonds EF, Bendall SC, Gibbs KD, Bruggner RV, Linderman MD, Sachs K, Nolan GP, Plevritis SK. Extracting a cellular hierarchy from high-dimensional cytometry data with SPADE. Nat Biotechnol. 2011;29:886. doi: 10.1038/nbt.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Roederer M, Nozzi JL, Nason MC. SPICE: exploration and analysis of post-cytometric complex multivariate datasets. Cytometry A. 2011;79:167. doi: 10.1002/cyto.a.21015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Snyder LD, Medinas R, Chan C, Sparks S, Davis WA, Palmer SM, Weinhold KJ. Polyfunctional cytomegalovirus-specific immunity in lung transplant recipients receiving valganciclovir prophylaxis. Am J Transplant. 2011;11:553. doi: 10.1111/j.1600-6143.2010.03405.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. van Rijsbergen CJ. Information Retrieval. Butterworth 1979 [Google Scholar]
  30. Zare H, Shooshtari P, Gupta A, Brinkman RR. Data reduction for spectral clustering to analyze high throughput flow cytometry data. BMC Bioinformatics. 2010;11:403. doi: 10.1186/1471-2105-11-403. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES