Blood flows and metabolic components of the cardiome

Abstract

This is a plan for the first stage of The Cardiome Project. The cardiome is the representation, in quantitative, testable form, of the functioning of the normal heart and its responses to intervention. The goal is to integrate the efforts of many years into a comprehensive understandable scheme. Past efforts have spanned the fields of transport within blood vessels, the distributions of regional coronary blood flows, permeation processes through capillary and cell walls, mediated cell membrane transport, extra- and intracellular diffusion, cardiac electrophysiology, the uptake and metabolism of the prime substrates (fatty acid and glucose), the metabolism of the purine nucleosides and nucleotides (mainly adenosine and ATP), the regulation of the ionic currents and of excitation–contraction coupling and finally the regulation of contraction. The central theme is to define the coronary flows and metabolic components of a computer model that will become a part of a three-dimensional heart with appropriate fibre shortening and volume ejection. The components are: (a) coronary flow distributions with appropriate heterogeneity, (b) metabolism of the substrates for energy production, (c) ATP, PCr and energy metabolism and (d) calcium metabolism as it relates to excitation–contraction coupling. The modeling should provide: (1) appropriate responses to regional ischemia induced by constriction of a coronary artery, including tissue contractility loss and aneurysmal dilation of the ischemic region; (2) physiological responses to rate changes such as treppe and changes in metabolic demand and (3) changes in local metabolic needs secondary to changes in the site of pacing stimulation and shortening inactivation or stretch activation of contraction.

1. Introduction

The Cardiome Project is focused on developing a computational, interactive model of the physiologically normal working heart. It is a part of the Physiome Project, an international effort to organize and integrate the functioning of an organism, ultimately the human. The Physiome Project was endorsed at an international conference in St. Petersburg in July 1997, “On Designing the Physiome Project”, by the International Union of Physiological Sciences and is targeted now by units within agencies of the U.S. government such as the National Institutes of Health, the National Science Foundation and by organizations of academia and industry such as AIMBE (American Institute of Medical and Biological Engineering). The cardiome, our specific target, is one of the eight fields selected at the St. Petersburg meeting to demonstrate the practicality and utility of the approach. While the focus of this essay is on the cardiome, a quantitative description of cardiac function, the setting for such a project and the rationale for undertaking it now, is in genomics, the proteome and the need to integrate molecular and cell biology into an understanding of the functions of intact organisms. Proteins function differently in isolation than in propinquity to neighboring proteins, as one sees with channels (Santana et al., 1998) or with G-protein mediated receptor responses.

1.1. The genome

The Genome Project is the predecessor to the Physiome Project. This project, under which the sequencing of the human genome will be finished by about the year 2002, exemplifies a strategy of cooperation, dedication and goal setting that has made a great stride in the understanding of biology, fostering new qualitative and quantitative approaches in the biological sciences. The genome of each organism is more or less exact and reproducible; the structure is linear and expressible in a 4 letter alphabet and is finite. Thus, the Genome Project is rather cleanly defined. Yet predictions of phenotypic responses from genomic interventions can seldom be made. Changes in protein expression are not the same as pharmaceutical intervention. The identification of each gene and the amino acid sequences of its associated proteins forces us to recognize that we don't understand how these proteins function as parts of organized cells, tissues and organisms. Physiological phenotyping of organisms can follow after protein structuring and characterization, if a bottom up approach is taken. However, a lesson from the geneticists is that most of the genes identified so far have been pinpointed from the top down, identifying the locus by association with other genes and with expressed sequence tags. Secondly, the naive idea of ‘one gene, one protein’ has now been replaced by ‘one gene, several proteins following post transcriptional modifications occurring at different stages of development’.

From the therapeutic point of view, there is not yet a large role for direct genomic intervention, though there is a growing industrial production of human proteins by yeast and E. coli. Pharmaceutical intervention, like genomic intervention, is not precisely predictable of function: side effects are common and interactions with the effects of other drugs put patients at risk. Accurate prediction will require having a comprehensive grasp of the workings of cells, tissues and whole intact organisms and information on the short and long term regulation of physiology from gross system behavior (e.g. blood pressure) to modulation of protein expression.

1.2. The morphome

The ‘morphome’ derives from genome and environment to provide the machinery for function. It is the quantitative representation of structure from molecule to organism. The Proteome is the part coming directly from the gene: it includes the amino acid sequence of each protein, the structure of the protein, its physico–chemical description, its location (cytosolic, free, integral transmembrane proteins, etc.) and its variant forms following proteolysis, glycosylation, phosphorylation or more complex processes of slicing and splicing (Wilkins et al., 1997). Indirectly, through proteins which may be expressed only at specific stages of embryogenesis, materials from the environment (ions, substrates) are used to form multimolecular structures (membranes, organelles, cytoskeleton) at the cellular and then at tissue and organ level. The morphome includes tissue composition, material and chemical properties and anatomic structure of the organism. The Proteome is more difficult to define as a finite task than is the genome, because protein sequences do not yet predict form (the protein-folding problem) or location or function in precise terms. The 20-letter alphabet (the amino acids) is explicit, but, if the cystic fibrosis transporter protein is a good example, there are many isoforms (perhaps 100) which function adequately and some others which do not.

Yet more difficult, more subject to variability, is the description of the structures of cells, tissues, organs and organisms. Even so, useful results at the whole human level have been achieved in the Visible Human Project (National Library of Medicine, http://www.nlm.nih.gov/research/visible/visible_human.html). The Physiome Project will bring the Visible Human to life.

1.3. The physiome

The physiome is ‘the quantitative description of the physiological dynamics and functional behavior of the intact organism’ (Bassingthwaighte, 1992; Marmarelis et al., 1994). The goal of the Physiome Project is to systematize current and future biophysical, biochemical and physiological knowledge into a framework where it can be used for prediction of functional behavior, in the spirit envisioned by Boyd and Noble (1993). The project consists of two parts: (1) the databasing of biological information for rapid retrieval and (2) the systematic organization of that information into descriptive schema of interactions, quantitative descriptions of interrelationships, and eventually computational models of integrated systems with appropriate short and long-term dynamical behavior (Bassingthwaighte, 1995). The databases must go beyond itemizing information on the genome, protein sequences and structure and protein behavior in solution. Whether they be standard databases or highly flexible relational or object-oriented databases, they must be designed for retaining data of high variability and questionable reproducibility on all aspects of patho-physiologic functions from protein kinetics, the nature of the ‘milieu interieur’ of cells, tissues and organs and the elements of intracellular, humoral and neural regulation. Such items make up multi-component systems. If one can specify their relationships by equations and determine values for specific parameters then one can build quantitative mathematical models. Via integrative functional models one should be able to predict the expected behavior of a system, test prediction against observation and when prediction fails, define which undiscovered information is needed. The integrated models may then allow choosing which drugs to design and which genetic manipulations to attempt.

Models come in different forms. A primitive form of model is a diagram suggesting associations between elements of the system. Such diagrams help to see the general nature of a system, and convey an overview, but are not predictive. A second, more explicit level of modeling is provided by schema of relationships which give the direction of influences or driving forces or fluxes. Lacking specific values for parameters, this schematic stage still does not allow quantitative prediction: it designates pathways, but not the traffic along them. A third stage is modeling using sets of equations. Given the rate constants, amounts, material properties, etc. the model can be used to predict the responses to stimuli or changes in conditions.

Since highly complex systems are not intuitively understandable, the more comprehensive mathematical models should be designed so that an explorer begins with a simple version and can use it as the entry into the deeper, more complete and complex versions. Imagine a model of the heart: how does it respond to the constriction of a specific coronary artery, to the compression of the aorta or to sympathetic nerve stimulation? Only a rather comprehensive model can give correct responses to all of these questions. If the model were adequate for such tasks, then the explorer might be yet more demanding, asking for not only the short-term acute responses, but also the long-term responses. Guyton's model of the cardiovascular-renal regulation of blood pressure (Guyton et al., 1972) exhibited both short and long-term regulation that gave fairly realistic descriptions of whole animal responses even though it was not based on events at the molecular level.

A fully constructed model is to the explorer much like the real system in the sense that an understanding of its behavior is not immediately intuitive, but requires observation and probing by experimentation. Cause and effect relationships can be explored within such a model, if it is constructed to allow ‘experimental’ intervention by the explorer. Models are hypothesized predictors of responses, merely ‘working hypotheses’. They are therefore testable by experiment; they serve as the vehicle for the design of the critical experiment, the one that will disprove the model. As Thomas Henry Huxley recommended when discussing Darwin's theory of evolution (Huxley, 1997), maintain your ‘thaetige skepsis’ or ‘active doubt’, a phrase he took from Goethe. Active doubt means not bland acceptance, but careful consideration and persistent conscious skepticism with respect to any model. Models are all wrong, inexact or incomplete and will probably be so forever, but remain as the strongest form of the working hypothesis.

The models need to be usable by learners and teachers. Most models will be constructed so that they cover very few hierarchical levels. There will be difficulty in predicting organism-level adaptive behavior without bringing all the pieces together, so strategies will have to be developed by which the behavior of pieces of the system can be represented at the higher levels, even while maintaining the capability of adjusting those pieces at their deeper levels. Small parts of the Physiome are in use for diagnosis, therapy and aid in drug design. The capability for prediction is of high economic benefit: predictors of the effects of intervention will save hundreds of millions of dollars per year by improved drug design, target specificity in pharmaceutical and genomic therapies and eventually in disease prevention.

1.4. The cardiome project

The cardiome is the description, in quantitative, testable form, of the functioning of the normal heart and its responses to intervention. It will prove helpful in integrating results from many years' efforts into a comprehensive understandable scheme. These efforts have spanned the fields of transport within blood vessels, the distributions of regional coronary blood flows, permeation processes through capillary and cell walls, mediated cell membrane transport, diffusion, electrophysiology, metabolism of the prime substrates (fatty acid and glucose) and studies of metabolism of the purine nucleosides and nucleotides (mainly adenosine and ATP).

The overall Cardiome Project is a large-scale multidisciplinary, multiuniversity effort (Bassingthwaighte, 1997). It involves physicians, computer scientists, pharmacologists, electrophysiologists and biomedical engineers working together to develop a model of the human heart. A model heart put together through the collaborative efforts of Hunter, Smaill, Noble, Winslow, McCulloch and others provides fully quantitative descriptions of the electrical currents and ion pump, of the spread of electrical activity across a finite element representation of the fibre directions in the myocardium and the cardiac contraction itself. The beginnings of this were presented by Glass et al. (1991) and Noble (1995). We at the University of Washington have since the early 1970s been putting together whole organ models describing transport and exchange of substrates and to account for the spatial distribution of the coronary arteries, the regional myocardial blood flows, the uptake and metabolism of glucose, fatty acids and oxygen used for the energy to form ATP, which is in turn used to fuel the work of contraction and ion pumping. In order to link the metabolism with the finite element representations of the mechanics of contraction we will collaborate with Peter Hunter at Auckland University, New Zealand, Andrew McCulloch at UC San Diego and Theo Arts at Maastricht University, Maastricht, The Netherlands. The ionic currents in the Hunter–McCulloch model use the equations either of Denis Noble (Oxford University, UK) or of Yoram Rudy (Case Western Reserve University). Rai Winslow (Johns Hopkins University) used these models for ionic currents to derive the spread of excitation throughout the three-dimensional cardiac structure.

To model the chemico–mechanical conversion of high energy phosphate for contraction we have begun a collaboration with Amir Landesberg and Samuel Sideman, at Technion University, Haifa and with Martin Kushmerick, Michael Regnier and Albert Gordon at the University of Washington. The fatty acid metabolism studies are a continuation of work in collaboration with Ger van der Vusse, Rob Reneman, and Jan Glatz at Maastricht University and James Caldwell at the University of Washington. The glucose studies are a continuation of a collaboration with Claudio Cobelli and Paolo Vicini at The University of Padua which, like most of the others above, is formalized through their participation in the activities of our National Simulation Resource at the University of Washington. Other collaborations are developing too. Our group at the University of Washington is too small to maintain adequate expertise in more than a relatively narrow aspect of the program. Sharing the effort, as has proven effective in sequencing the genome for H. influenzae, is the only way to reach the goal expeditiously.

2. Design of the Cardiome Project

In order to provide a demonstration of the utility of modeling we would like to have a functional version of the Cardiome developed within three years to the level where it is useful for predicting responses to blockage of coronary arteries, to pharmaceutical agents used for blocking channels or pumps (e.g. digitalis in cardiac failure) and to metabolic stimuli or exercise. It will require many additional steps of subsequent development to account for intracellular regulatory processes, so our planned initial result can only be regarded as a primitive beginning.

The goal is to develop an integrated synthesis of cardiac metabolic, electrical and mechanical events into a visualizable form that can be seen by the public to represent cardiac mechanics in health and disease and can be used by investigators as a stepping stone for developing insight into the complex metabolic and biophysical interrelationships that are the basis for cardiac function. Within this context we define four linked modules which, along with two modules already well developed by others for the electrophysiology and the mechanics, describe cardiac function. The six modules are as shown in Fig. 1:

Fig. 1.

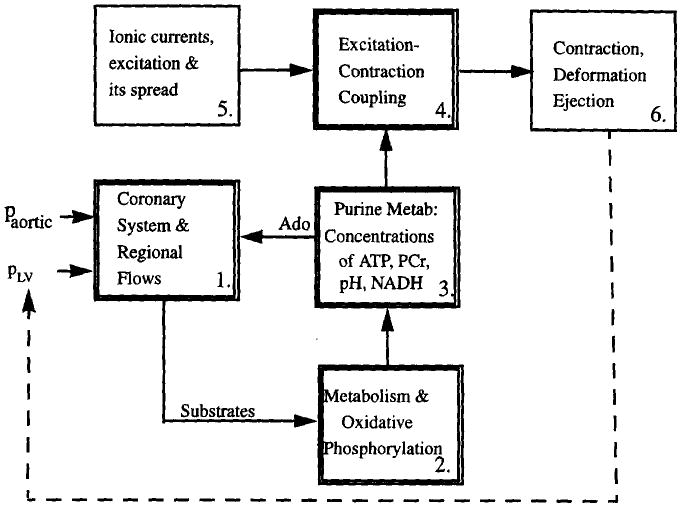
Overall diagram of the cardiome model components.

1. Coronary artery anatomic localization and regional myocardial flows, providing substrate and oxygen delivery.

2. Metabolism of the substrates for energy metabolism, fatty acid and glucose, the tricarboxylic acid cycle and oxidative phosphorylation.

3. Purine nucleoside and purine nucleotide metabolism, describing the formation of ATP and the regulation of its degradation to adenosine in endothelial cells and myocytes and its effects on coronary vascular resistance.

4. Excitation–contraction coupling (ECC), calcium release and reuptake and the relationships between these and the strength and extent of sarcomere shortening.

5. The electrical currents and their spread across the myocardium: these are described by either the Luo–Rudy model (Luo and Rudy, 1994a,b; Shaw and Rudy, 1995; Rudy and Shaw, 1997) or the Noble–DiFrancesco model (DiFrancesco and Noble, 1985; Ch'en et al., 1997).

6. The three-dimensional finite element representation of the contracting heart has been brought to an advanced stage by Peter Hunter and his group at University of Auckland, New Zealand (Hunter et al., 1988; Hunter and Arts, 1997) and Andrew McCulloch and his group at U.C. San Diego (see McCulloch et al., 1997). It is into their three-dimensional finite element reconstructions of the mechanically contracting heart that we will put our components describing the physiological responses.

The major inputs to the model will be: aortic blood pressure, hematocrit, pO₂, pCO₂, heart rate, concentrations of palmitate, lactate, acetate, glucose, pyruvate, pH, Na⁺, Ca²⁺, K⁺, Cl⁻, PO₄, HCO₃, Mg²⁺. To take this through the first stage gross simplifications must be made, so we will temporarily omit incorporating: (1) mechanico–electrical feedback, (2) systolic compression of intramyocardial coronary arteries and veins, (3) regulation of intracellular enzymes by secondary processes, (4) vascular and tissue remodeling, (5) protein metabolism, (6) systemic influences on total body vascular resistance, (7) changes in cardiac pool sizes of glycogen and di- and triphosphoglycerides and many other features. Any list of omissions should be nearly infinite; these are merely the more obvious ones. These, and others found to be critical, will be the subject of later modifications.

The overall schema (Fig. 1) is centered around the fluxes of ATP, ADP/Pi and H⁺ in module 3, linking the other modules in the regulation in the functioning heart. Module 4 for the excitation–contraction coupling now exists only as a purely empirical relationship without adaptability or regulatory control, or any link to ATP. The other modules, for coronary flow distribution and substrate and oxygen delivery to tissue, for substrate utilization and oxidative phosphorylation, and for purine metabolism are new undertakings. We will focus initially on the single sarcomere level modules and their interactions with one another. Periodically, we will incorporate each module into the integrated whole organ model for testing there. Each stage remains archived through our source code control system to preserve all previous versions. As information from experiments is gathered, or inconsistencies recognized from the behavior of the whole organ model, improvements will be made in the sarcomere modules. To give users prompt responses computational efficiency is critical. Periodic reviews to improve speed will be essential in a large long-range project like this.

2.1. Module 1. Coronary system and regional flow distributions

Intramyocardial flow distributions are remarkably heterogeneous (Yipintsoi et al., 1973; Bassingthwaighte et al., 1990), showing a range of 6 to 10-fold in normal hearts in awake or anesthetized animals. This is explained by the fractal self-similar branching of the coronary arteries (Bassingthwaighte et al., 1989). Anatomic data from van Bavel and Spaan (1992) and Kassab et al. (1993) serve as a more realistic basis for network reconstructions than we achieved earlier (van Beek et al., 1989). Network reconstructions developed by Daniel Beard exhibit appropriate pressure distributions, regional flow heterogeneities and fractal spatial correlations in flows, and the same power law form (∼1/t³) for the washout time course as is observed (Bassingthwaighte and Beard, 1995).

The next stages concern the delivery of substrates and oxygen. The mechanism for glucose delivery to myocytes is through the interendothelial clefts and from the interstitium via a transporter across the cell membrane (Kuikka et al., 1986). Fatty acid transport is more complex because it binds tightly to albumin; it does not traverse the clefts, but must be stripped off the albumin before being translocated (reviewed by van der Vusse et al., 1988). The inhibition of tracer palmitate permeability by high albumin concentration was explained by Bassingthwaighte et al. (1989) in a model for the fatty acid translocation. In a further refinement, Caldwell et al. (1994) found in exercising dogs that the regional density of fatty acid transporters in the heart is proportional to the regional flows.

The noninvasive measurement of regional myocardial blood flow (MBF) and oxygen consumption (MRO₂) using positron emission tomography (PET) that we have developed in the past two years contributes directly to the Cardiome Project and leads to an important simplification. The most direct measure of oxidative tissue metabolism is the conversion rate of oxygen to water via mitochondrial respiration. A sequence of cardiac images obtained at two-second intervals after single-breath inhalation of ¹⁵O-oxygen (Li et al., 1997) gives, in each region of interest, the time-activity curves of the sum of the ¹⁵O-oxygen and its product, ¹⁵O-water. Their relative amounts can be distinguished by kinetic modeling (Fig. 2) because the mean transit time for water produced in the tissue is much longer than that for untransformed oxygen, most of which is in the form of oxyhemoglobin within the red blood cells. Consequently, the extraction of ¹⁵O-oxygen can be estimated and used to calculate the steady-state oxygen consumption within each region of interest, ROI. The model (Fig. 2) accounts for intravascular convection, penetration of capillary and parenchymal cell barriers, the metabolism to ¹⁵O-water in parenchymal cells and ¹⁵O-water transport into the venous effluent. Nonlinear binding of oxygen to hemoglobin in erythrocytes and to myoglobin in myocytes is explicitly incorporated in the model. This model is more accurate and much easier to use than the linear model by Deussen and Bassingthwaighte (1996) because the local volumes of distribution for oxygen are calculated automatically from oxygen supply and demand at steady state.

Fig. 2.

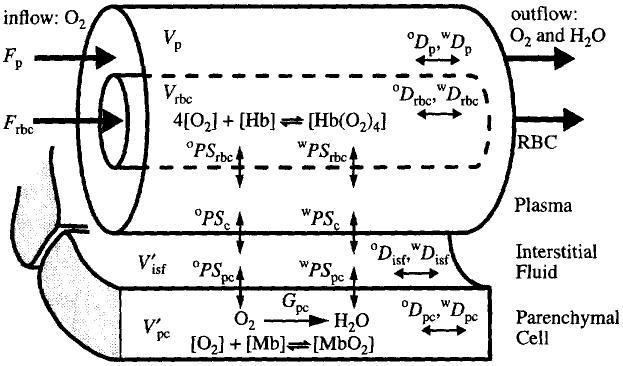
Dual capillary-tissue model for ¹⁵O-oxygen transport and metabolism into ¹⁵O-water. The four concentric regions are red blood cells (rbc), plasma (p), interstitial fluid (isf) and parenchymal cells (pc). The symbols used are F for flow, ml min⁻¹ g⁻¹; V for anatomical volumes and V′ for volumes of distribution, ml g⁻¹; PS for permeability-surface area product, ml min⁻¹ g⁻¹; G for the first-order consumption rate, ml min⁻¹ g⁻¹ and D for the axial dispersion coefficient, cm² s⁻¹. The superscripts ‘o’ and ‘w’ denote oxygen and water, respectively.

With this PET method we were able to study the correlation between regional myocardial blood flow and oxygen consumption in vivo. Our results from a limited number of experiments showed that the regional oxygen consumptions were approximately proportional to the regional flows as measured by the microsphere technique (Yipintsoi et al., 1973; Bassingthwaighte et al., 1990) (Fig. 3). These results support the generality that flows, transport conductance for substrate (Caldwell et al., 1994) and oxygen consumption are regionally matched. This strong evidence for proportional regional requirements will simplify the overall modeling project if we find that there is regional matching with ATP usage.

Fig. 3.

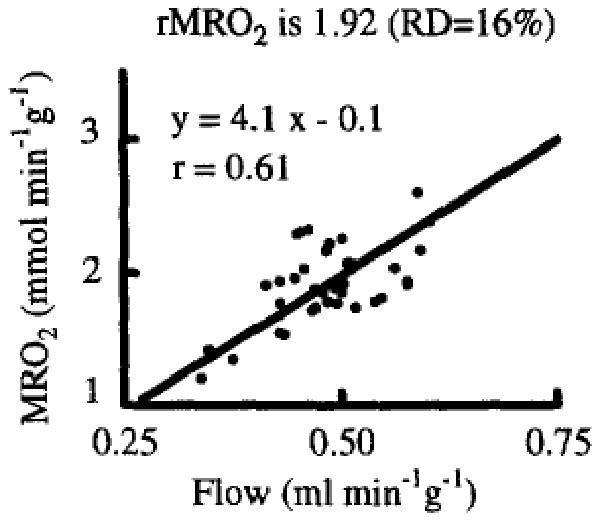
Correlation between blood flow (rMBF) and oxygen consumption (rMRO₂) in regions of interest (0.9 ± 0.3 g) of the LV myocardium of a closed-chest dog (from Li et al., 1996).

The methods for using models to determine the parameters of transport and metabolism are discussed by Bassingthwaighte and Goresky (1984), Kuikka et al. (1986) and in a book by Bassingthwaighte et al. (1998). Optimized parameter adjustment can be accomplished manually under XSIM, a graphical user-friendly interface developed by King et al. in our group, or by using automated optimization, e.g. by a steepest descent technique modified from that of Bronikowski et al. (1980) with our sensitivity function based approach (Chan et al., 1993). As a standard technique for evaluating the error and bias in estimates, we use Monte Carlo assessment of the effects of adding noise to simulate ‘pseudo data’ from model solutions.

A satisfactory first definition for regional substrate delivery therefore provides for the fluxes by flow and transmembrane transport of oxygen, the substrates and the metabolites, including lactate and CO₂. The oxygen model diagrammed in Fig. 2 is of the same general form as for these other solutes, all of which can be metabolized, but the others are more complex because they need specialized transporters, e.g. for fatty acid and for adenosine.

2.2. Module 2. Metabolism and oxidative phosphorylation in mitochondria

Module 2, ‘metabolism and oxidative phosphorylation’, outlined in Fig. 4, contains the detailed enzymatic reaction network for Glycolysis, TCA cycle, oxidative phosphorylation and acyl CoA mobilization from fatty acids and pyruvate. General overviews of cardiac metabolism are given by Randle and Tubbs (1979) and Bassingthwaighte (1991). Mitochondria, which comprise one-third of myocyte volume, are well dispersed among and closely apposed to bundles of myofilaments.

Fig. 4.

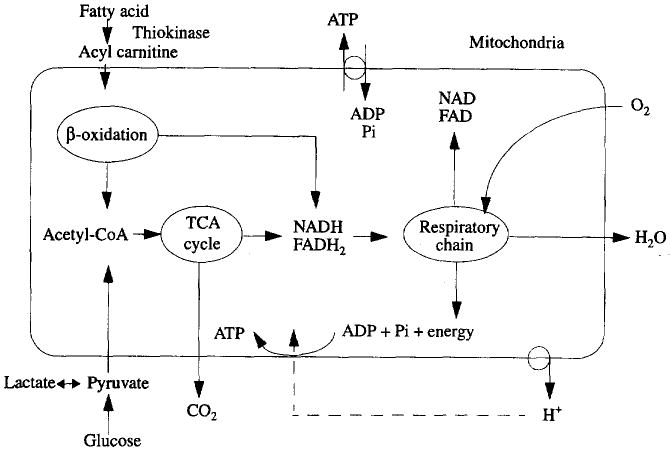
Summary of oxidative phosphorylation in mitochondria. Fats, pyruvate and other reduced carbon chains enter TCA cycle as acetyl-CoA to form NADH and FADH₂. NADH is the carrier of energy from glycolysis, P-oxidation of fatty acid and reactions in the TCA cycle. FADH₂ is produced during oxidation involving succinate, α-glycerophosphate and acyl-CoA. The free energy of NADH and FADH₂ is used to transport protons out of mitochondria, producing H⁺ gradient. H⁺ moves back into mitochondria driving ATP synthesis to convert ADP and P_i into ATP. NADH and FADH₂ go through respiratory chain (or electron transport chain) to provide energy for ATP synthesis.

The heart uses substrates principally for energy production. The main substrate is fatty acid, supporting about two-thirds of the caloric needs; the range of estimation is very wide, from 35 to 95%, which reflects the ability of the myocyte to shift fuels under different circumstances. The remainder of energy comes from glucose, lactate and amino acids. Glucose also provides pyruvate and lactate needed to maintain the constituents of the TCA cycle. Amino acids maintain intracellular proteins and enzymes and support transport reactions, exemplified by the role of camitine in the transfer of fatty acids across the mitochondrial membrane. The overall processes of substrate metabolism include: delivery by flow into capillaries; transport across the capillary walls and across the sarcolemma of myocyte; diffusion and reaction in the cytosol; transport across the mitochondrial inner membrane; intramitochondrial reactions; breakdown of 2-carbon fragments into CO₂ and water through the TCA cycle; the reactions of the electron transport chain and the production of ATP from ADP, coupled to the electron transfer chain and to other reactions in the glycolytic series. For fatty acids, Chatham et al. (1995) provide data on TCA fluxes of 2-carbon fragments and the shifts between oxidative and anaerobic metabolism.

For fatty acid metabolism, the thiokinase reaction requires one ATP-to-AMP reaction per free fatty acid, β-oxidation produces one molecule of FADH₂ and one molecule of NADH per 2-carbon fragment (total eight 2-carbon fragments from palmitate) and yields 35 molecules of ATP (one NADH yields 3 ATP, one FADH₂ yields 2 ATP). Each acetate molecule gives a total of 12 molecules of ATP in TCA and respiratory chain. So the total ATP generation per palmitate is 8 × 12 + 5 × 7 − 2= 129 molecules of ATP.

In glucose metabolism, for every molecule of glucose, 4 molecules of ATP are produced in anaerobic (2 ATP) and aerobic (2 ATP) glycolysis and 32 molecules of ATP are produced in TCA and respiratory chain by oxidation of NADH and FADH₂ (for every molecule of glucose, 6 molecules of NADH and 2 molecules of FADH₂ are formed in the TCA cycle; 2 molecules of NADH are formed during aerobic glycolysis and 2 molecules of NADH are formed during pyruvate oxidation). To relate ATP generation to oxygen utilization, for glucose, 6 ATP per O₂; for palmitate, 5.6 ATP per O₂. So the oxygen cost per ATP is similar with fatty acid versus glucose during aerobic metabolism. Module 2 can therefore in its most elementary form for the normal physiological state be represented by the stoichiometric conversion of substrate and oxygen to ATP, with proportional usage the same everywhere.

Through the supply/demand imbalance the cardiac contractile performance influences and indirectly governs the blood flow and oxygen delivery in normal physiological states. The rate of carbon flux through TCA cycle is reduced when the O₂ supply is low, inducing a shift away from aerobic fatty acid metabolism toward glycolysis and lactate production. With anaerobic metabolism there is no ATP formed from palmitate (actually a net loss due to diacylglycerophosphate production) and only 2 ATP are formed per glucose used, in glycolysis. The costs are in lactic acid production, whose metabolism must be included (Achs and Garfinkel, 1977). The shift from aerobic metabolism to glycolysis is probably more a function of pO₂, pH and NADH levels than of substrate availability.

To develop this part of the model we need values for the various biochemical constants for the enzymes; Selkov has developed an enzyme database for the metabolic pathways (Selkov et al., 1996, 1997). This module is complex, but simplified versions have been worked out, for example by Magnus and Keizer (1997). Theirs has the explicit advantage of incorporating the influences of Ca²⁺ on the transformations within the mitochondrion. Selkov has such a model himself.

2.3. Module 3. ATP and adenosine metabolism and release

The ‘purine metabolism’ module contains the kinetic reactions for myocardial phosphoenergetics (Fig. 5). Purine, as both ATP and adenosine, is an important biochemical regulator for the cardiac muscle mechanics. This key to understanding the energetics was extensively studied experimentally and computationally by the late Keith Kroll (Kroll and Stepp, 1996; Kroll et al., 1997; Kroll and Bassingthwaighte, 1997). Based on experimental measurements on rabbit heart and subsequent comparison with the simulation from this kinetic model, he showed that an energy imbalance, represented in the term Δr_ATP in Fig. 5, arises in the underperfused heart and that the intracellular free energy loss is minimized by losing adenosine and AMP from the cell. Further study (Gustafson and Kroll, 1998) suggests also that the enzyme 5′-nucleotidase is down-regulated when PCr and ATP decrease and P_i increases.

Fig. 5.

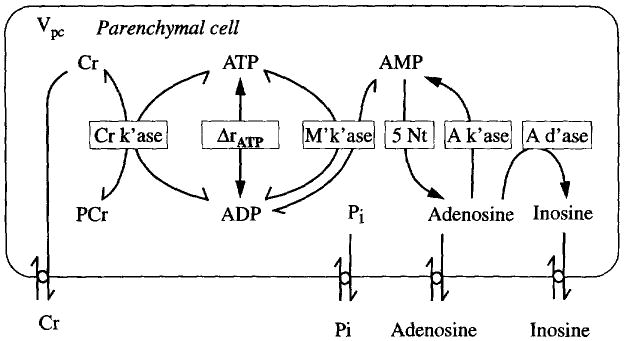
The kinetic model for purine metabolism and phosphoenergetics. Five enzymes are involved. This picture is also the computer window appearance for this module. The hierarchical design of our computer model is as follows: when clicking on the modules in the Fig. 1, the more detailed kinetic networks appear. A further click on the buttons in this diagram brings up details of the mechanism. For example, Fig. 6 comes up when the Cr k'ase button is clicked. M'k'ase is myokinase, A k'ase is adenosine kinase, A d'ase is adenosine deaminase. Parenchymal cell in this case is myocyte.

The descriptive element, Δr_ATP, must be replaced by the appropriate reactions for formation and degradation of ATP. The former are in the ‘oxidative phosphorylation’ module and the latter in the modules for ‘contraction’ and for the ion pumps, included in ‘ionic currents’ and ‘ECC’. All modules are tested for adherence to mass balance; for this module the test is to set the membrane permeabilities to zero for all forms of creatine, phosphate and purine base while running model solution for conditions that degrade ATP and PCr and to see whether or not their totals remain constant; such constancy is a minimal requirement, without which the model is invalid. There is never a proof of validity, but when many tests against observed data are satisfied one gains confidence in such a model as a working hypothesis.

The computer simulation program we developed for this uses mouse clicks to bring out deeper features. A click on the button ‘Cr k'ase’ in Fig. 5 pops up a new window to show the underlying mechanics for the enzyme, as shown in Fig. 6. Clicking on the rate constants reveals their values the rate constants reveals their values and allows one to change them. This style will be used in the other modules.

Fig. 6.

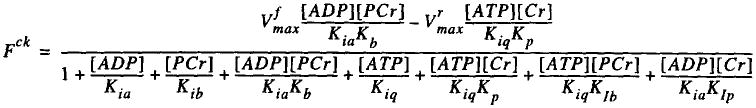
Picture of the equation which appears when the button labelled Cr k'ase in Fig. 5 is clicked. F^ck is the flux through the creatine kinase reaction; the K's are binding constants and the V_max's the maximum reaction rates; clicking on the parameters in this expression allows them to be adjusted for the specific cells and species being modeled. The concentrations, in square brackets, are the variables involved in the flux, ADP + PCr ↔ ATP + Cr.

2.4. Module 4. Excitation–contraction coupling

Our earliest model of excitation–contraction coupling (Bassingthwaighte and Reuter, 1972) included the kinetics of the slow inward calcium current reported formally in the Beeler and Reuter (1977) model of the action potential. It was timely as a step in integrated modeling and it incorporated the concepts of that time on how calcium cycling in the myocyte served as the key factor in the governance: trigger Ca²⁺ current, calcium release from the SR, calcium–troponin binding, contractile filament shortening and reuptake of calcium by the sarcoplasmic reticulum, SR. A more modem view is provided for example by Bers (1991) in an excellent monograph. Module 4 requires information from the ionic currents (module 5). Initially we will not use the detailed time course of the currents, but to speed computation will use the total net quantities of each ion transferred during the action potential to determine the concentrations within the cytosol. These are the quantities that need to be removed by the pumps and exchanges during the remainder of the cardiac cycle during any steady state. These will determine the ATP usage for ionic balance.

The ATP used for cross-bridge shortening is influenced by the tension and the time course of the shortening velocity in the sarcomere (Blei et al., 1993; Landesberg and Sideman, 1994a,b; McFarland et al., 1994; Chase and Kushmerick, 1995; Regnier et al., 1995, 1997; Wiseman and Kushmerick, 1995; Landesberg, 1996; Landesberg et al., 1996). Because local Ca²⁺ and early systolic pre-ejection phase shortening cause a shift from the strongly to the weakly bound form of ATP–myosin, this reduces the amount of ATP required during a contraction. Consequently our modeling needs to take this level of detail into account when it comes to examining the relationship between local flows, local metabolism and contractile function, especially in situations such as prolonged ventricular pacing where remodeling occurs (Arts et al., 1994, 1995), thinning the ventricular wall at sites of early activation and causing hypertrophy in late activated regions. Since there is potential benefit in using pacing as an inhibitor of outflow tract obstruction in hypertrophic subaortic stenosis, for example, testing this approach in a model of an intact heart may be one way to use the modeling in defining therapy, as considered by van Bilsen and Chien (1993). Since one can obtain individual cardiac structural descriptions from MR and regional physiological information from PET and ultrasound, this could evolve to a stage, as it has for repairing knees, where the modeling is key to designing or choosing the therapeutic intervention.

The myosin ATP form and Ca²⁺ influence the patterns of deformation through the ventricle; the ventricular structure has been precisely detailed in two dog hearts (LeGrice et al., 1995, 1997) with fiber directions over the whole ventricle and fibre sheets and bundles between which the vessels are positioned. Passive material properties are presented by Smaill and Hunter (1991). These have been integrated into whole heart mechanical models (module 6) by our collaborators (Hunter et al., 1988; McCulloch et al., 1989, 1997; McCulloch and Omens, 1991; Bovendeerd et al., 1992; Hunter and Arts, 1997) and it is with these model structures and the ionic current module 5, that we will integrate our modules 1 to 4.

3. Summary

The goal, to develop a functioning three-dimensional computational model of the excitation, metabolism and contraction of the heart within three years, is one of the beginnings for the Cardiome Project. Our first stage will not provide highly accurate prediction of physiological behavior in general, but will be focussed so that it is adequate for at least three specific purposes: response to regional flow reduction, response to heart rate changes and response to increased metabolic drive. We would like to make the model visualizable by three-dimensional viewing, with cross-sectional and transparency viewing approaches, illustrate the fiber directions, the arteries, the deformation with contraction and images of regional functions such as oxygen consumption, pre-ejection strain or lactate concentration. The display techniques developed by Hunter et al. and by McCulloch et al. would be excellent for such demonstration and teaching purposes, and should be attractive enough for public display.