Abstract
Fine structures of spatial profiles were computed from existing records of cat and chinchilla auditory-nerve fibers on the basis of their characteristic frequencies and cochlear maps. The spatial fine structures of characteristic-frequency thresholds and of “spontaneous” and driven firing rates were mutually correlated, implying the presence of sensitivity fluctuations due to spatial irregularities of presynaptic structures or processes of the inner hair cells and their input. These findings suggest that activity that appears spontaneous is not actually spontaneous and may indicate irregularities of tonotopic mapping in cochlear mechanics.
Keywords: auditory-nerve fibers, cochlea, inner hair cells, organ of Corti, spatial irregularities
Introduction
The mammalian cochlea is famously known for the traveling waves that propagate on its basilar membrane (BM; von Békésy, 1947; Rhode, 1971; Cooper and Rhode, 1996; Russell and Nilsen, 1997; Rhode and Recio, 2000; Ren, 2002; Fisher et al., 2012; Temchin et al., 2012; for review, see Robles and Ruggero, 2001). However, there is also evidence of other forms of cochlear vibration. In humans, hearing thresholds include fine structures as a function of frequency (Elliott, 1958; van den Brink, 1970; Thomas, 1975) and, in cats, average rates of responses to tones of auditory-nerve fibers (ANFs) include fluctuations as a function of characteristic frequency (CF) that can be interpreted as spatial fine structures (Kim and Molnar, 1979; Kim et al., 1990). The present investigation was undertaken to search for comparable spatial fluctuations in responses to tones of chinchilla ANFs (Ruggero et al., 1996; Temchin et al., 2008a,b; Temchin and Ruggero, 2010). We did find spatial fine structures in driven responses of chinchilla ANFs but, unexpectedly, we also uncovered correlated spatial irregularities in spontaneous-activity rates (SRs) and CF thresholds in both cat and chinchilla. The mutual correlations, implying the presence of sensitivity fluctuations due to spatial irregularities of presynaptic structures or processes of the inner hair cells (IHCs) and/or their input, suggest that “spontaneous” activity is not actually spontaneous, and may indicate irregularities of tonotopic mapping in cochlear mechanics.
Materials and Methods
The present work is based on data gathered in previous investigations on chinchilla ANFs (Ruggero et al., 1996; Temchin et al., 2008a,b; Temchin and Ruggero, 2010) and cat ANFs (Liberman, 1978; Kim and Molnar, 1979). Chinchilla ANF data were locally available in digital form. ANF data for four cats raised in a quiet environment (Liberman, 1978) were provided by M. C. Liberman in digital form (all chinchillas were males; the chamber-raised cats included two males and two females; sex of other cats is unknown). CFs were converted into distances using CF-distance maps for “standard” cat and chinchilla cochleae of 25 and 20 mm, respectively (Liberman, 1982; Müller et al., 2010). CFs for chinchilla ANFs were determined from third-order polynomial equations fitted to the tips of frequency-threshold tuning curves (Temchin et al., 2008a). This procedure circumvented possible artifactual effects of the logarithmic spacing of frequencies in frequency-threshold tuning curves that might influence the computation of spatial profiles.
Raw data consisted of CFs, SRs, average rates of responses to tones, and CF thresholds of ANFs. Spatial profiles with 0.1 mm resolution were obtained, as exemplified in Figure 2, by subtracting running averages computed over 2.5 mm bands from averages computed within 0.1 mm bands. The main analyses of the spatial profiles were carried out with unfiltered data but, additionally, after zero-phase shift low-pass filtering (second-order Butterworth filters with corner spatial frequencies of 2 or 5 mm−1). The similarity between spatial profiles was assessed by computing the crosscorrelograms of the profiles, series of Pearson product-moment correlation coefficients as a function of relative lag. The significance (p) of the correlations coefficient (r) at zero lag (the linear correlation coefficient) was assessed for two-sided distributions using two alternative procedures, described below.
Figure 2.
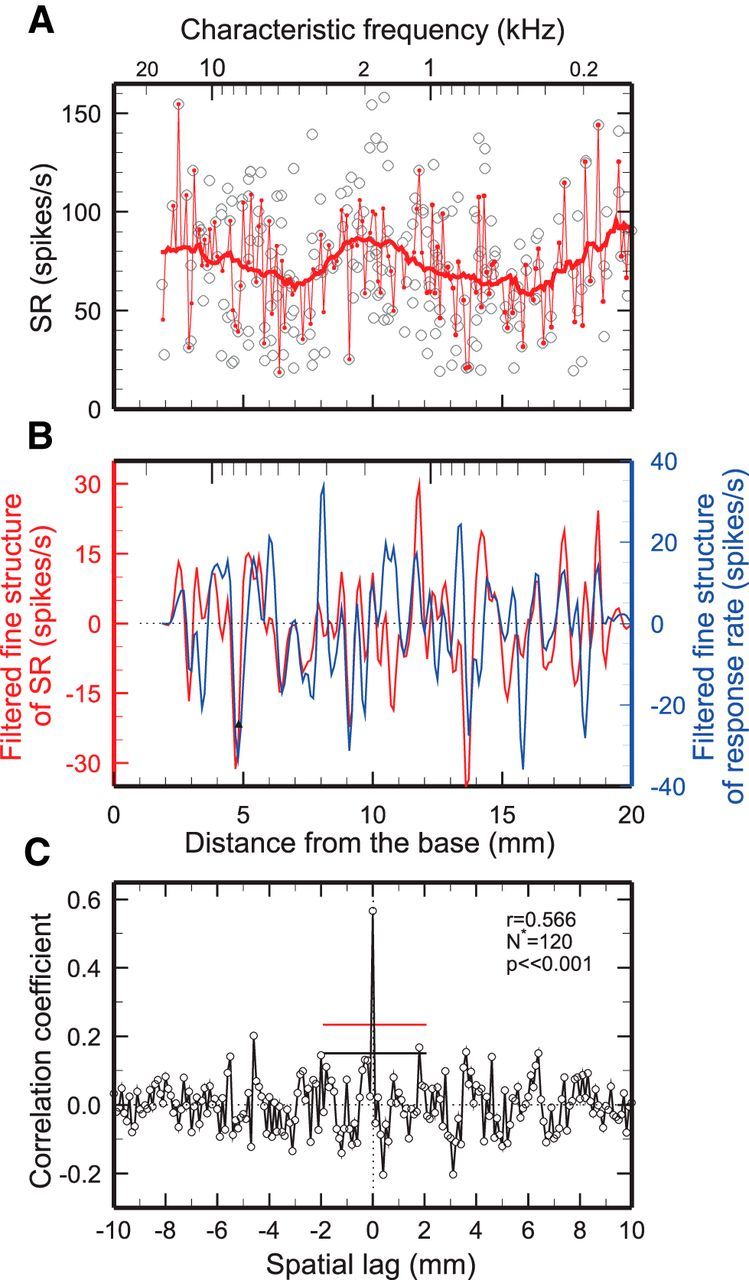
Similarity of spatial irregularities of SR and rate of responses to tones in chinchilla. A, Open symbols indicate SRs of 285 ANFs with SRs >18 spikes/s pooled from 35 chinchillas, plotted against cochlear distance. Thick and thin red traces are running averages computed respectively over 2.5 or 0.1 mm bands. B, Red trace, Spatial irregularity of SRs, computed as the difference between the thin and thick traces of A and low-pass filtered (corner frequency, 2 mm−1). Blue trace, Spatial irregularity of responses to tones (100 Hz, 70 dB SPL) for the same ANFs represented in A and B (Temchin et al., 2012) computed and filtered in the same manner as for SR. C, Crosscorrelogram between the unfiltered spatial irregularities of SR and response rate. At zero lag, r = 0.566, p ≪ 0.001, N* = 120. Flat red and black lines indicate the zero-lag 99% confidence limits computed, respectively, on the assumption that correlation coefficients are normally distributed and by bootstrap resampling (see Materials and Methods).
In one procedure, the significance of the correlation coefficient at zero lag was determined with a t test carried out on the assumption (empirically confirmed) that the crosscorrelogram coefficients were normally distributed. To circumvent the effects of autocorrelations, both inherent (Bartlett, 1935) and introduced by filtering, the numbers of degrees of freedom were estimated from autocorrelograms of the spatial profiles (computed using Matlab function xcorr.m) and the following equation (Eq. 1): N* = N/Σ(1 + 2rjrj* + 2rjrj* + …), where N is the number of paired observations, N* is the number of degrees of freedom, j is the lag, rj are the autocorrelation coefficients for one of the spatial profiles, and rj* are the autocorrelation coefficients for the other spatial profile (Bartlett, 1935; Dawdy and Matalas, 1964; Yevdjevich, 1964; Pyper and Peterman, 1998). For the present application, the summation was carried out over N terms, closely approximating an asymptote for N*.
In a second procedure, the significance of the correlations coefficient at zero lag was assessed using a bootstrap resampling computation (Efron and Tibshirani, 1993; Davison and Hinkley, 1997). This consisted of repeated random shuffling of the data for the two variables before computing their fine structures and their crosscorrelation. The frequency distribution of the zero-lag correlation coefficients after 100,000 shuffles, which was always Gaussian, was compared with the measured zero-lag coefficient to determine its probability.
The frequency spectra of spatial profiles and crosscorrelograms were determined by Fourier transformation of windowed data using the Matlab function fft.m. The windowing function (tukeywin.m of Matlab) consisted of onset and offset ramps (shaped, respectively, like the second and first half-periods of a raised cosine), each lasting for 7.5% of the waveform span, and a central segment with constant amplitude, lasting for 85% of the span. The instantaneous frequencies of the spatial profiles were estimated by computing their Hilbert transforms (Matlab function hilbert.m; the instantaneous spatial frequency of a waveform is the spatial derivative of the phase of its Hilbert transform;Oppenheim and Schafer, 1999). Additionally, spatial quasiperiods were estimated by measuring the spacing between peaks and troughs with amplitudes >25% of the overall waveform rms.
Results
Correlated spatial irregularities of SRs, rates of responses to tones, and CF thresholds
Fluctuations as a function of CF were first noted in running averages of ANF responses to tones measured in single cats (Kim and Molnar, 1979; Kim et al., 1990). Such fluctuations, which motivated the present investigation, are evident in Figure 1A, which shows spatial profiles of responses to 1000 Hz tones presented at 20, 45, and 70 dB SPL for ANFs with SRs >15/s in cat TRF98 (reproduced from Kim and Molnar, 1979, their Figs. 3A, 4A, 5A). The profiles reach maxima in the apical half of the cochlea, near the 1 kHz characteristic place (as expected, given the single-peak spatial envelopes of BM traveling waves), but also exhibit local maxima in the basal region. Spatial profiles of rates of responses to low-frequency (100–1000 Hz) tones of ANFs pooled across many chinchillas (Fig. 1B) also include apical and basal maxima (Temchin et al., 2012) and irregular fluctuations with peaks and troughs at places that vary little as a function of stimulus frequency. The fact that the spatial irregularities are sufficiently stable to persist after averaging across many chinchillas suggests that they reflect cochlear features with distributions that scale according to percentage cochlear length (rather than absolute distances). Such scaling has been proposed for anatomical features of cat and chinchilla cochleae (Bohne and Carr, 1979; Liberman, 1982).
Figure 1.
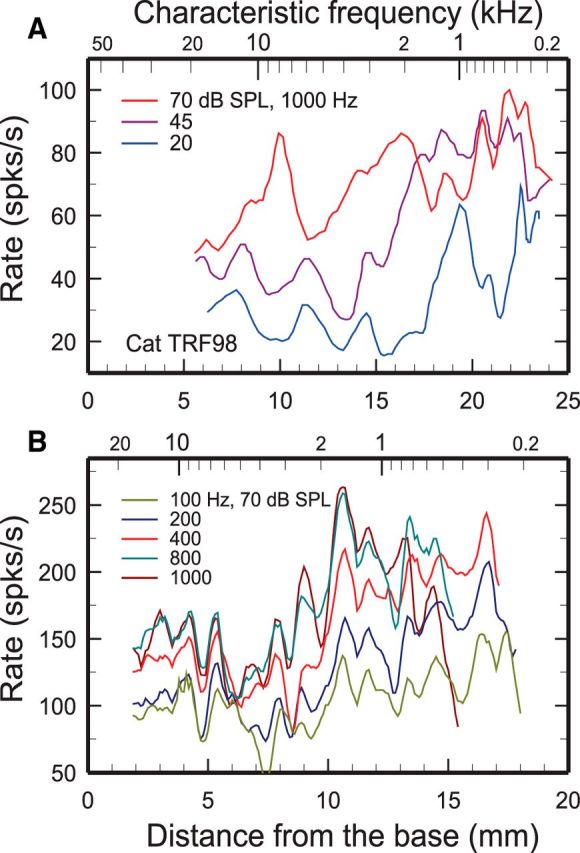
Spatial profiles of ANF rates of response to low-frequency tones in cat and chinchilla. A, Running averages of rates of response to 1 s, 1 kHz tones of 119 ANFs with SRs >15/s in one cat (legend indicates levels). The upper and lower abscissa scales, respectively, indicate CFs and the corresponding distances derived from a cochlear map for cats (Liberman, 1982; data from Kim and Molnar, 1979, their Figs. 5A, 4A, 3A, cat TRF98). B, Average rates of responses to 5 100 ms tones presented at 70 dB SPL (legend indicates frequencies) in 227–311 ANFs with SRs >18/s pooled across 33–36 chinchillas (Temchin and Ruggero, 2010). Trends were extracted from individual raw data by computing average rates within 0.1 mm bands and low-pass filtered (corner frequency, 2 mm−1; see Materials and Methods). The upper and lower abscissa scales, respectively, indicate CFs and the corresponding distances, derived from a cochlear map for chinchillas (Müller et al., 2010).
Figure 3.
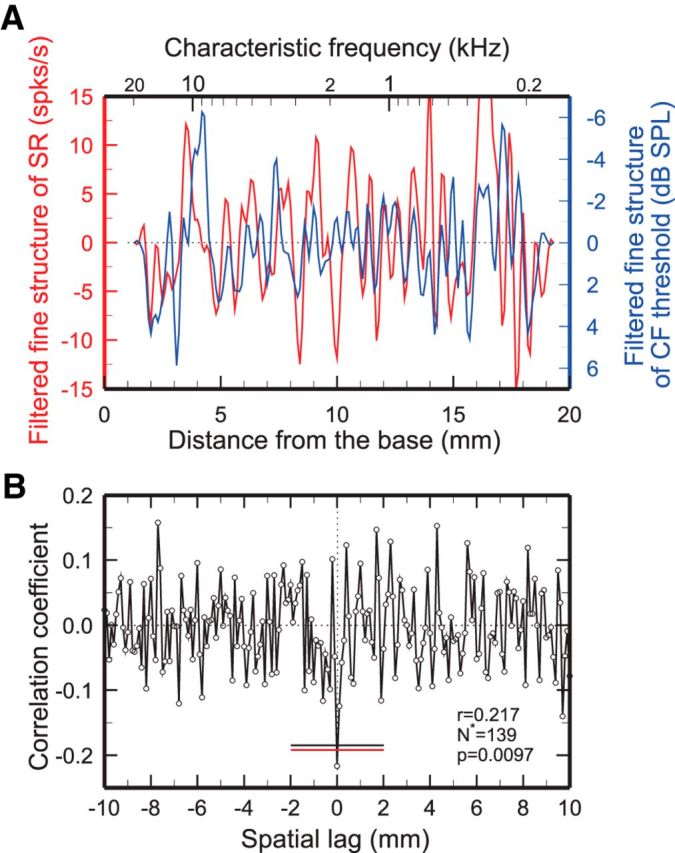
Similarity of CF-threshold and SR spatial irregularities of chinchilla ANFs. A, Average spatial irregularities of low-pass filtered (corner frequency, 2 mm−1) SR and CF thresholds computed from 2250 ANFs with SRs >18/s pooled across 190 chinchillas. B, Crosscorrelogram of the unfiltered spatial irregularities. The irregularities are significantly and negatively correlated at zero lag: r = −0.217; p = 0.0097; N* = 139. Flat red and black lines indicate the zero-lag 99% confidence limits computed, respectively, on the assumption that correlation coefficients are normally distributed and by bootstrap resampling (see Materials and Methods).
Figure 4.
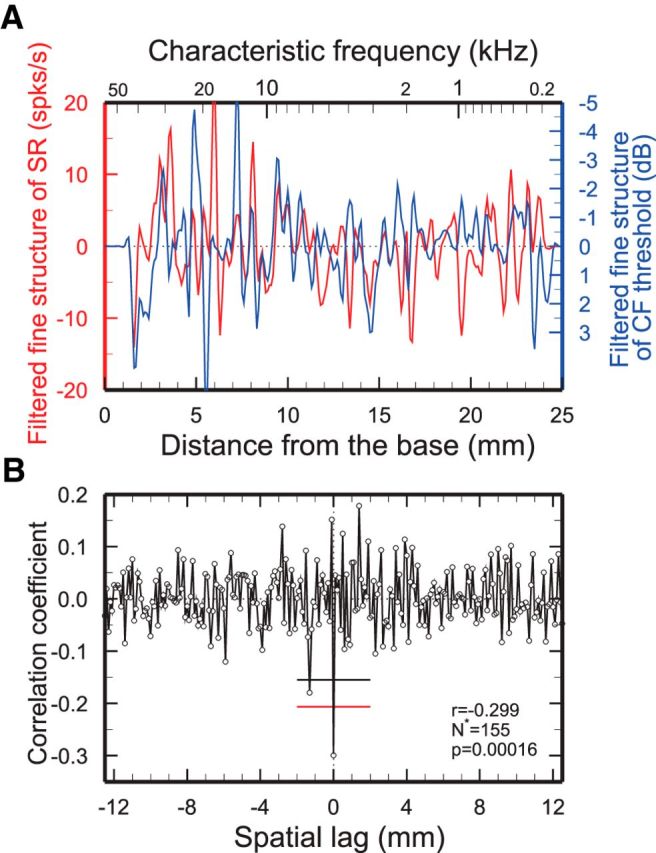
Similarity of CF-threshold and SR spatial irregularities of cat ANFs. A, Average low-pass filtered (corner frequency, 2 mm−1) spatial irregularities of SR and CF thresholds (blue and red traces, respectively) computed from 612 ANFs with SRs >18/s pooled across four cats (MCL93–MCL96). B, Crosscorrelogram between the unfiltered SR and CF-threshold irregularities. The irregularities are significantly and negatively correlated at zero lag: r = −0.30, p ≪ 0.001, N* = 155. Flat red and black lines indicate the zero-lag 99% confidence limits computed, respectively, on the assumption that correlation coefficients are normally distributed and by bootstrap resampling (see Materials and Methods).
Figure 2 illustrates how spatial fine structures were extracted from ANF data. Figure 2A shows SRs (open symbols) of 285 ANFs with SRs >18 spikes/s recorded in 35 chinchillas, plotted against distance from the cochlear base determined from CFs according to the CF-distance map of Müller et al. (2010). Thick and thin traces, respectively, indicate SR averages computed over 2.5 and 0.1 mm intervals, respectively, with 0.1 mm resolution. Subtracting the former from the latter isolates the SR spatial irregularities. Spatial irregularities of rates of responses to 100 Hz, 70 dB tones of the same ANFs were estimated similarly. Figure 2B allows for a comparison of the low-pass filtered (corner frequency, 2 mm−1) spatial irregularities of SRs and of rates of responses to tones. There are many coincidences between the peaks and troughs of the two spatial profiles.
Reasoning that similarity between the spatial irregularities of different cochlear properties implies that the latter are not fortuitous and that they reflect an underlying common origin, the present analyses rely centrally on establishing correlations between spatial profiles of various ANF properties. The correlations between pairs of spatial profiles are studied using crosscorrelograms, which consist of Pearson product-moment correlation coefficients as a function of relative lag. Figure 2C shows the crosscorrelogram between the unfiltered spatial profiles of SR and of rates of response to 100 Hz tones (illustrated in Fig. 2B after filtering). The maximal correlation coefficient occurs at zero lag, indicating that the response-rate and SR irregularities are positively correlated and perfectly aligned as functions of distance. The statistical significance of the zero-lag correlation coefficient was determined on the assumption that the crosscorrelogram coefficients were normally distributed (which was empirically confirmed) or by bootstrap resampling, i.e., constructing a frequency distribution of the zero-lag coefficients of 100,000 crosscorrelograms computed after repeated random shuffling of the values of the two variables (see Materials and Methods). The value p indicates the probability that the zero-lag correlation coefficient r results from random sampling from the frequency distribution, which was always Gaussian.
At zero lag, r = 0.566 (p ≪ 0.001, N* = 120). The horizontal red and black lines in Figure 2C (as well as Figs. 3B, 4B) indicate 99% confidence limits at zero lag computed, respectively, on the assumption of normal distribution of correlation coefficients and by bootstrap resampling (see Materials and Methods). Significant positive correlations at zero lag were also obtained (data not shown) with profiles low-pass filtered at 5 mm−1 (r = 0.479, p < 0.0031, N* = 36) and at 2 mm−1 (Fig. 2B, fine structures; r = 0.405, p = 0.013, N* = 35). The spectra of the SR and response-rate spatial irregularities are complex and include multiple peaks throughout the frequency range (data not shown). The significant correlations between the spatial irregularities of SR and of rates of responses to low-frequency tones despite averaging across many individuals imply that their link is general and robust. These correlations suggest that “SRs” are related to cochlear sensitivity and that they are not really spontaneous.
If SRs are not spontaneous, the fine structures of their spatial profiles should be negatively correlated with those of CF thresholds. Since CF thresholds and SRs of ANFs with SRs <18/s are strongly negatively correlated in ANFs of both cat and chinchilla (Liberman, 1978; Temchin et al., 2008b), presumably due to synaptic factors, it is important to ascertain whether possible negative correlations between the fine structures of SR and CF-threshold spatial irregularities reflect solely fluctuations in the local mix of SRs or additional presynaptic factors. For this purpose, the irregularities of response rates (Fig. 2), SRs (Figs. 2–4), and CF thresholds (Figs. 3, 4) were computed from ANFs with SRs >18/s, which have uniformly low thresholds despite great SR variations in both cat and chinchilla (Liberman, 1978; Temchin et al., 2008b). The “raw” SRs and CF thresholds of 2250 individual chinchilla ANFs with SRs >18/s (data not shown) were very weakly correlated (r = −0.05, p = 0.018, N = 2250). In contrast, as shown in Figure 3A, the (low-pass filtered; 2 mm−1) SR and CF-threshold irregularities extracted from the same ANFs include several coincident troughs and peaks, consistent with mutually correlated processes. Figure 3B shows the crosscorrelogram of unfiltered SR and CF-threshold irregularities, which includes a negative peak at zero lag (r = −0.217, p = 0.0097, N* = 139). After low-pass filtering with corner frequencies of 5 and 2 mm−1 (data not shown), the irregularities also yielded significant negative correlation coefficients: r = −0.18 (p = 0.032, N* = 140) and −0.32 (p = 0.027, N* = 46), respectively.
CF-threshold irregularities and their crosscorrelograms with SR have wide-band power spectra, including multiple peaks (data not shown), with the largest between 0.31 and 3 mm−1 (quasiperiods of 3.2 and 0.33 mm, respectively). We explored the quasiperiodicity of the CF-threshold spatial irregularity profiles (Fig. 3A) by measuring the spacing between peaks and troughs exceeding a quarter of the rms and by computing spatial frequencies using Hilbert transforms (see Materials and Methods). These analyses revealed no evidence of a systematic variation of frequency or quasiperiodicity with position.
In cat, as in chinchilla, the “raw” SRs and CF thresholds of 612 ANFs with SRs >18/s (pooled from four individuals) were poorly correlated (data not shown; r = −0.075, p = 0.066, N = 612). However, as shown in Figure 4, the unfiltered spatial irregularities extracted from the same SRs and CF thresholds are negatively correlated at zero lag (r = −0.30, p ≪ 0.001, N* = 155). After low-pass filtering with corner frequencies of 2 and 5 mm−1, the irregularities also yielded strong and significant correlation coefficients (data not shown): r = −0.68 (p ≪ 0.001, N* = 52) and −0.73 (p ≪ 0.001, N* = 120), respectively. The power spectra of the CF-threshold irregularities (data not shown) and the cross-power spectra include multiple peaks, the largest in the range 0.48–2.1 mm−1 (quasiperiods of 2.1 and 0.5 mm, respectively). As for chinchillas, neither the spacing between peaks and troughs nor a Hilbert transform of the CF-threshold spatial irregularity profile of cat ANFs (Fig. 4A) revealed any evidence of a systematic variation of spatial frequency with position.
Discussion
Summary of findings
First, in both cats and chinchillas, average rates of ANF responses to tones have spatial fine-structure profiles (Fig. 1). Second, in chinchillas, the spatial fine structures of ANF responses to tones are significantly and positively correlated with spatial SR irregularities (Fig. 2). Third, in both cats and chinchillas, spatial SR irregularities of ANFs with high spontaneous activity are significantly negatively correlated with CF-threshold irregularities (Figs. 3, 4).
Validity and limitations of the finding of spatial irregularities
The validity of the finding of spatial irregularities in cat and chinchilla cochleae depends largely on the statistical significance of the correlations between pairs of spatial fine structures, specifically the zero-lag Pearson product-moment correlations of the crosscorrelograms. Since statistical significance depends on the number of degrees of freedom, a crucial concern is the existence of autocorrelations, which reduce the numbers of degrees of freedom relative to the numbers of paired observations. We partly addressed this concern by computing the effective number of degrees of freedom according to Equation 1 (Dawdy and Matalas, 1964; Yevdjevich, 1964), previously used in crosscorrelation analyses of other autocorrelated data (Pyper and Peterman, 1998; Fox et al., 2000; MacKenzie and Schiedek, 2007).
The main limitation of the present study is that correlated fine structures of spatial irregularities were demonstrated from data pooled across individuals (four cats or many chinchillas). As a result, the only pointers to what the spatial irregularities might look like in individual cochleae are the ANF responses to single tones in individual cats (Kim and Molnar, 1979; Kim et al., 1990).
Origin of spatial irregularities
To the extent that the mutual correlations of the fine structures of ANF properties are evident in both cat and chinchilla ANFs with high SRs, they appear to have presynaptic origins, either intrinsic to the IHCs (e.g., variations in synaptic structures or processes) or extrinsic (i.e., the vibrations that stimulate their stereocilia). One interpretation is that the spatial irregularities arise from counterparts in the cochlear CF-distance tonotopic map. A similar conjecture was put forth by Pat Wilson (Wilson, 1980a) in the context of otoacoustic emissions: “… irregularity superimposed upon the normal tonotopic relationship … might be expected to give a stronger summed response … where the frequency–position slope is lower than average” (Wilson and Sutton, 1981; Sutton and Wilson, 1983; Strube, 1989), as strikingly exemplified in the cochlear foveae of echolating bats (Kössl and Vater, 1985; Vater et al., 1985). Irregularities of tonotopic maps might arise in cochlear dynamics (e.g., from ripples generated by superposition of traveling waves; Shera and Cooper, 2013), or from structural features, such as outer hair cell (OHC) packing density, with higher-density regions producing enhanced amplification.
Irregularities of CF thresholds in chinchillas as possible counterparts of the fine structure of hearing thresholds in humans
The spatial irregularities of CF threshold in cat and chinchilla are reminiscent of the fine structure of hearing thresholds in humans (Elliott, 1958; van den Brink, 1970; Thomas, 1975; Kemp, 1979; Wilson, 1980b). However, the fluctuations of CF thresholds in cat and chinchilla are irregular, in contrast to the fairly periodic fine structures of hearing thresholds in humans (Kemp, 1979; Schloth, 1983; Zwicker and Schloth, 1984). The troughs of hearing-threshold fine structures in humans often coincide with the frequencies of spontaneous otoacoustic emissions. In chinchilla, spontaneous otoacoustic emissions typically have frequencies of >5 kHz and are separated by frequency intervals corresponding to spatial multiples of 0.25 mm (Long et al., 2000). Thus, high-frequency hearing thresholds might have spatial periodicity of ∼0.25 mm. Such periodicity is approximately consistent with theoretical estimates by Christopher Shera (personal communication) that predict fine-structure periods in the chinchilla cochlea of ∼0.4 mm for the 10 kHz place or 1.2 mm for the 1 kHz place (Shera et al., 2010, their Fig. 10). We did detect CF-threshold irregularities with a quasiperiod of 0.3 mm in chinchilla ANFs, but we found no evidence for a systematic variation of quasiperiodicities as a function of place or CF.
Tentative conclusions
The correlated spatial irregularities of ANF properties (SR and response sensitivity) in cat and chinchilla suggest the existence of presynaptic cochlear irregularities, either in the IHCs themselves or in the mechanical input to their stereocilia. We speculate that so-called SRs contain a significant component driven by subthreshold vibrations caused by either uncontrolled environmental noise or internal cochlear noise (possibly Brownian motion). Cochlear vibrations at subthreshold stimulus levels would be consistent with ANF phase locking at stimulus levels lower than rate thresholds (Johnson, 1980), BM responses to subthreshold CF tones (Narayan et al., 1998; Ruggero et al., 2000), and spontaneous BM vibrations at the CF (Nuttall et al., 1997). Subthreshold cochlear vibrations might conceivably arise from frequency-tuned spontaneous oscillations of OHC stereocilia [analogous to those of hair bundles in the bullfrog sacculus (Martin et al., 2003) or the tokay gecko's basilar papilla (Gelfand et al., 2010)], which might feed back onto BM vibrations or forward into vibrations of IHC stereocilia. Finally, one important caveat: although there is evidence for spatial irregularities in the organ of Corti, nothing is known of possible counterparts in BM vibrations.
Footnotes
This work was supported by National Institutes of Health Grant R01-DC000419. We thank Charlie Liberman for sharing with us data that he collected >35 years ago; Karolina Charaziak, Mary Ann Cheatham, James Dewey, Sumitrajit Dhar, Tina Grieco-Calub, Jungmee Lee, Luis Robles, Christopher Shera, and Jonathan Siegel for helpful comments on earlier versions of this manuscript; Sumitrajit Dhar and Julia Lee for advice on statistics; and Jonathan Siegel for suggesting possible irregularities in cochlear maps as the source of the irregularities of apparent auditory-nerve fiber density.
The authors declare no competing financial interests.
References
- Bartlett MS. Some aspects of the time-correlation problem in regard to tests of significance. J Roy Statist Soc. 1935;98:536–543. doi: 10.2307/2342284. [DOI] [Google Scholar]
- Bohne BA, Carr CD. Location of structurally similar areas in chinchilla cochleas of different lengths. J Acoust Soc Am. 1979;66:411–414. doi: 10.1121/1.383092. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Fast travelling waves, slow travelling waves and their interactions in experimental studies of apical cochlear mechanics. Audit Neurosci. 1996;2:289–299. [Google Scholar]
- Davison A, Hinkley D. Bootstrap methods and their application. Cambridge, UK: Cambridge UP; 1997. [Google Scholar]
- Dawdy DR, Matalas NC. Statistical and probability analysis of hydrologic data, part III: analysis of variance, covariance and time series. In: Chow VT, editor. Handbook of applied hydrology, a compendium of water-resources technology. New York: McGraw-Hill; 1964. pp. 8.68–68.90. [Google Scholar]
- Efron B, Tibshirani R. An Introduction to the bootstrap. New York: Chapman and Hall; 1993. [Google Scholar]
- Elliott E. A ripple effect in the audiogram. Nature. 1958;181:1076. doi: 10.1038/1811076a0. [DOI] [PubMed] [Google Scholar]
- Fisher JA, Nin F, Reichenbach T, Uthaiah RC, Hudspeth AJ. The spatial pattern of cochlear amplification. Neuron. 2012;76:989–997. doi: 10.1016/j.neuron.2012.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox CJ, Planque BP, Darby CD. Synchrony in the recruitment time-series of plaice (Pleuronectes platessa L) around the United Kingdom and the influence of sea temperature. J Sea Res. 2000;44:159–168. doi: 10.1016/S1385-1101(00)00039-3. [DOI] [Google Scholar]
- Gelfand M, Piro O, Magnasco MO, Hudspeth AJ. Interactions between hair cells shape spontaneous otoacoustic emissions in a model of the tokay gecko's cochlea. PLoS One. 2010;5:e11116. doi: 10.1371/journal.pone.0011116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DH. The relationship between spike rate and synchrony in responses of auditory-nerve fibers to single tones. J Acoust Soc Am. 1980;68:1115–1122. doi: 10.1121/1.384982. [DOI] [PubMed] [Google Scholar]
- Kemp DT. The evoked cochlear mechanical response and the auditory microstructure—evidence for a new element in cochlear mechanics. Scand Audiol Suppl. 1979;9:35–47. [PubMed] [Google Scholar]
- Kim DO, Molnar CE. A population study of cochlear nerve fibers: comparison of spatial distributions of average-rate and phase-locking measures of responses to single tones. J Neurophysiol. 1979;42:16–30. doi: 10.1152/jn.1979.42.1.16. [DOI] [PubMed] [Google Scholar]
- Kim DO, Chang SO, Sirianni JG. A population study of auditory-nerve fibers in unanesthetized decerebrate cats: response to pure tones. J Acoust Soc Am. 1990;87:1648–1655. doi: 10.1121/1.399412. [DOI] [PubMed] [Google Scholar]
- Kössl M, Vater M. The cochlear frequency map of the mustache bat, Pteronotus parnellii. J Comp Physiol A. 1985;157:687–697. doi: 10.1007/BF01351362. [DOI] [PubMed] [Google Scholar]
- Liberman MC. Auditory-nerve response from cats raised in a low-noise chamber. J Acoust Soc Am. 1978;63:442–455. doi: 10.1121/1.381736. [DOI] [PubMed] [Google Scholar]
- Liberman MC. The cochlear frequency map for the cat—labeling auditory-nerve fibers of known characteristic frequency. J Acoust Soc Am. 1982;72:1441–1449. doi: 10.1121/1.388677. [DOI] [PubMed] [Google Scholar]
- Long GR, Shaffer LA, Dhar S, Talmadge CL. Cross species comparison of otoacoustic fine structure. In: Wada H, Takasaka T, Ikeda K, Ohyama K, Koike T, editors. Recent developments in auditory mechanics. Singapore: World Scientific; 2000. pp. 367–373. [Google Scholar]
- MacKenzie BR, Schiedek D. Long-term sea surface temperature baselines—time series, spatial covariation and implications for biological processes. J Marine Systems. 2007;68:405–420. doi: 10.1016/j.jmarsys.2007.01.003. [DOI] [Google Scholar]
- Martin P, Bozovic D, Choe Y, Hudspeth AJ. Spontaneous oscillation by hair bundles of the bullfrog's sacculus. J Neurosci. 2003;23:4533–4548. doi: 10.1523/JNEUROSCI.23-11-04533.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller M, Hoidis S, Smolders JW. A physiological frequency-position map of the chinchilla cochlea. Hear Res. 2010;268:184–193. doi: 10.1016/j.heares.2010.05.021. [DOI] [PubMed] [Google Scholar]
- Narayan SS, Temchin AN, Recio A, Ruggero MA. Frequency tuning of basilar membrane and auditory nerve fibers in the same cochleae. Science. 1998;282:1882–1884. doi: 10.1126/science.282.5395.1882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuttall AL, Guo M, Ren T, Dolan DF. Basilar membrane velocity noise. Hear Res. 1997;114:35–42. doi: 10.1016/S0378-5955(97)00147-0. [DOI] [PubMed] [Google Scholar]
- Oppenheim AV, Schafer RW. Discrete-time signal processing. 2nd edition. Upper Saddle River, NJ: Prentice Hall; 1999. [Google Scholar]
- Pyper BJ, Peterman RM. Comparison of methods to account for autocorrelation in correlation analyses of fish data. Can J Fish Aquat Sci. 1998;55:2127–2140. doi: 10.1139/f98-104. [DOI] [Google Scholar]
- Ren T. Longitudinal pattern of basilar membrane vibration in the sensitive cochlea. Proc Natl Acad Sci U S A. 2002;99:17101–17106. doi: 10.1073/pnas.262663699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhode WS. Observations of the vibration of the basilar membrane in squirrel monkeys using the Mossbauer technique. J Acoust Soc Am. 1971;49(Suppl 2):1218–1231. doi: 10.1121/1.1912485. [DOI] [PubMed] [Google Scholar]
- Rhode WS, Recio A. Study of mechanical motions in the basal region of the chinchilla cochlea. J Acoust Soc Am. 2000;107:3317–3332. doi: 10.1121/1.429404. [DOI] [PubMed] [Google Scholar]
- Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. 2001;81:1305–1352. doi: 10.1152/physrev.2001.81.3.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC, Shivapuja BG, Temchin AN. Auditory-nerve responses to low-frequency tones: intensity dependence. Audit Neurosci. 1996;2:159–185. [Google Scholar]
- Ruggero MA, Narayan SS, Temchin AN, Recio A. Mechanical bases of frequency tuning and neural excitation at the base of the cochlea: comparison of basilar-membrane vibrations and auditory-nerve-fiber responses in chinchilla. Proc Natl Acad Sci U S A. 2000;97:11744–11750. doi: 10.1073/pnas.97.22.11744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell IJ, Nilsen KE. The location of the cochlear amplifier: spatial representation of a single tone on the guinea pig basilar membrane. Proc Natl Acad Sci U S A. 1997;94:2660–2664. doi: 10.1073/pnas.94.6.2660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schloth E. Relation between spectral composition of spontaneous oto-acoustic emissions and fine structure of threshold in quiet. Acustica. 1983;53:250–256. [Google Scholar]
- Shera CA, Cooper NP. Basilar-membrane interference patterns from multiple internal reflection of cochlear traveling waves. J Acoust Soc Am. 2013;133:2224–2239. doi: 10.1121/1.4792129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera CA, Guinan JJ, Jr, Oxenham AJ. Otoacoustic estimation of cochlear tuning: validation in the chinchilla. J Assoc Res Otolaryngol. 2010;11:343–365. doi: 10.1007/s10162-010-0217-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strube HW. Evoked otoacoustic emissions as cochlear Bragg reflections. Hear Res. 1989;38:35–45. doi: 10.1016/0378-5955(89)90126-3. [DOI] [PubMed] [Google Scholar]
- Sutton GJ, Wilson JP. Modelling cochlear echoes: the influence of irregularities in frequency mapping on summed cochlear activity. In: de Boer E, Viergever MA, editors. Mechanics of hearing. Delft: Delft UP; 1983. pp. 83–90. [Google Scholar]
- Temchin AN, Ruggero MA. Phase-locked responses to tones of chinchilla auditory nerve fibers: implications for apical cochlear mechanics. J Assoc Res Otolaryngol. 2010;11:297–318. doi: 10.1007/s10162-009-0197-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temchin AN, Rich NC, Ruggero MA. Threshold tuning curves of chinchilla auditory-nerve fibers. I. Dependence on characteristic frequency and relation to the magnitudes of cochlear vibrations. J Neurophysiol. 2008a;100:2889–2898. doi: 10.1152/jn.90637.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temchin AN, Rich NC, Ruggero MA. Threshold tuning curves of chinchilla auditory nerve fibers. II. Dependence on spontaneous activity and relation to cochlear nonlinearity. J Neurophysiol. 2008b;100:2899–2906. doi: 10.1152/jn.90639.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temchin AN, Recio-Spinoso A, Cai H, Ruggero MA. Traveling waves on the organ of Corti of the chinchilla cochlea: spatial trajectories of inner hair cell depolarization inferred from responses of auditory-nerve fibers. J Neurosci. 2012;32:10522–10529. doi: 10.1523/JNEUROSCI.1138-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas IB. Microstructure of the pure-tone threshold. J Acoust Soc Am. 1975;57:S26–S27. doi: 10.1121/1.1995148. [DOI] [Google Scholar]
- van den Brink G. Experiments on binaural diplacusis and tone perception. In: Plomp R, Smoorenburg GF, editors. Frequency analysis and periodicity detection in hearing. Leiden: A. W. Sijthoff; 1970. pp. 362–372. [Google Scholar]
- Vater M, Feng AS, Betz M. An HRP-study of the frequency-place map of the horseshoe bat cochlea: morphological correlates of the sharp tuning to a narrow frequency band. J Comp Physiol. 1985;157:671–686. doi: 10.1007/BF01351361. [DOI] [PubMed] [Google Scholar]
- von Békésy G. The variation of phase along the basilar membrane with sinusoidal vibrations. J Acoust Soc Am. 1947;19:452–460. doi: 10.1121/1.1916502. [DOI] [Google Scholar]
- Wilson JP. Model for cochlear echoes and tinnitus based on an observed electrical correlate. Hear Res. 1980a;2:527–532. doi: 10.1016/0378-5955(80)90090-8. [DOI] [PubMed] [Google Scholar]
- Wilson JP. Evidence for a cochlear origin for acoustic re-emissions, threshold fine-structure and tonal tinnitus. Hear Res. 1980b;2:233–252. doi: 10.1016/0378-5955(80)90060-X. [DOI] [PubMed] [Google Scholar]
- Wilson JP, Sutton GJ. Acoustic correlates of tonal tinnitus. In: Evered D, Collins GM, editors. Tinnitus. London: Pitman; 1981. pp. 82–100. [DOI] [PubMed] [Google Scholar]
- Yevdjevich VM. Statistical and probability analysis of hydrologic data, part II: Regression and correlation analysis. In: Chow VT, editor. Handbook of applied hydrology. New York: McGraw-Hill; 1964. pp. 8.43–48.67. [Google Scholar]
- Zwicker E, Schloth E. Interrelation of different oto-acoustic emissions. J Acoust Soc Am. 1984;75:1148–1154. doi: 10.1121/1.390763. [DOI] [PubMed] [Google Scholar]


