Skull Retrieval for Craniosynostosis Using Sparse Logistic Regression Models

Abstract

Craniosynostosis is the premature fusion of the bones of the calvaria resulting in abnormal skull shapes that can be associated with increased intracranial pressure. While craniosynostoses of multiple different types can be easily diagnosed, quantifying the severity of the abnormality is much more subjective and not a standard part of clinical practice. For this purpose we have developed a severity-based retrieval system that uses a logistic regression approach to quantify the severity of the abnormality of each of three types of craniosynostoses. We compare several different sparse feature selection techniques: L₁ regularized logistic regression, fused lasso, and clustering lasso (cLasso). We evaluate our methodology in three ways: 1) for classification of normal vs. abnormal skulls, 2) for comparing pre-operative to post-operative skulls, and 3) for retrieving skulls in order of abnormality severity as compared with the ordering of a craniofacial expert.

1 Introduction and Motivation

This work is focused on retrieval of CT images for patients with craniosynostosis, a common congenital condition in which one or more of the fibrous sutures in an infant’s calvaria fuse prematurely, resulting in restricted skull and brain growth. Because the brain cannot expand perpendicular to the fused suture, it redirects growth in the direction of the open sutures, resulting in abnormal head shape and in some cases, facial features. Craniosynostosis results in head deformity that can be severe if it is not corrected surgically. This condition may result in increased intracranial pressure on the brain and is correlated with developmental delays, although the cause of such delays is not currently known [11]. It is estimated that the fusion of any one or more sutures occurs in approximately 1 in 2, 000 live births [7]. In clinical practice, craniosynostosis is diagnosed by a physician on the basis of head shape and confirmatory CT scan.

Automatic analysis of CT scans, including a measure of shape deformation, would be of great help to both doctors and medical researchers. In our previous work, we built a system that automatically generates a shape representation called the cranial image (CI) [4] from the CT image of a patient’s skull. The cranial images are used as shape features to distinguish between skulls of patients with different types of craniosynostosis. We also proposed using logistic regression and three variations of the logistic regression model for classifying different types of craniosynostosis: L₁ regularized logistic regression [2], the fused lasso [9] and the clustering lasso (cLasso) [1], which is a variation of L₁ logistic regression. These models avoid overfitting of the regression model, and they also could select subsets of features from the cranial image that represent skull regions associated with the distinctive shape differences related to different suture fusions (e.g., sagittal vs metopic suture fusion).

It is important to note that clinicians do not need to rely on a quantitative model to make the diagnosis of craniosynostosis. However, there is a lack of criteria to quantify the severity of the abnormality for research purposes. For example, when estimating the relative effects of different surgical methods on cranial shape (i.e., pre-, post-surgery change), quantitative measurement is essential. For this reason, we have developed a system to retrieve CT images based on quantification of the severity of the abnormality of the 3D skull shape. Given an enlarged data set containing pre-operative and post-operative CT scans of subjects with three classes of craniosynostosis (coronal, metopic and sagittal) plus a set of scans from similar-age control subjects, we conducted a set of experiments in classification, quantification and retrieval using the three logistic regression methods proposed in [1]. Different sparse logistic regression models are compared in terms of misclassification on whether a skull has craniosynostosis or not. Then we show our retrieval results using the best model for our data -cLasso. Abnormality of the skulls of the same patient before a surgery and after a surgery is compared using the quantification criteria as well.

The rest of the paper is organized as follows. Section 2 summarizes the related literature, Section 3 gives an overview of the framework of our approach for abnormality quantification, Section 4 describes the details on how logistic regression models are used for quantification, and Section 5 shows the experimental results of our work.

2 Related literature

Calvarial (skull) abnormalities are frequently associated with severely impaired central nervous system functions due to brain abnormalities, increased intracranial pressure and abnormal build-up of cerebrospinal fluid. In [3], Shapiro et al. introduced several different craniofacial descriptors that have been used in studies of two craniofacial disorders: 22q11.2 deletion syndrome (a genetic disorder) and deformational plagiocephaly/brachycephaly. They provided feature extraction tools for the study of craniofacial anatomy from 3D mesh data obtained from the 3dMD active stereo photogrammetry system. These tools produce quantitative representations (descriptors) of the 3D data that can be used to summarize the 3D shape as pertains to the condition being studied and the question being asked. This work is different from the current study in that it analyzed the shape of the midface and back of the head, while our work focuses on the shape of the skull.

There are some previous studies on examining the specific skull shapes of patients. Previously, we proposed the cluster lasso [1], a logistic regression model, for classification of three types of craniosynostoses: coronal, metopic and sagittal. Lin et al. [4] developed symbolic shape descriptors to classify skull deformities caused by metopic and sagittal synostoses. Ruiz-Correa et al. [5] used a set of scaphocephaly severity indices (SSIs) for predicting and quantifying head-and skull-shape deformity in children diagnosed with isolated sagittal synostosis (ISS).

The study differs from previous work in that it focuses on the task of skull retrieval, while our previous work focused on classifying different types of craniosynostoses. Another difference is that the current work fits a regression model based on abnormal shapes versus normal ones, while in our previous work we were merely comparing different types of abnormal shape and could therefore not quantify severity with respect to normal. Other efforts mentioned above differ from our approach in that they were not fully automatic and therefore required human interaction for selecting planes and landmarks from the skull for the purpose of extracting shape features.

3 Skull Retrieval Pipeline

3.1 System Design

A system was built for skull retrieval according to shape abnormality severity. With an input of 3D CT volume data of random pose, our system first extracts the skull and performs pose normalization, so that it is symmetric with respect to the right and left sides. Then, surface points are extracted that are evenly spaced all over the skull. After that, a shape feature called the cranial image [4] is calculated by computing pairwise distances of these points. Last, a method is proposed to quantify skull abnormality severity using the shape feature.

3.2 Surface Points Extraction

The first step of this module is to locate a base plane on the skull based on two important landmarks: the nasion and the opisthion. The base plane goes through these two biological landmarks, and is perpendicular to the symmetry plane that separates the right and left sides.

The nasion is the intersection of the frontal and two nasal bones of the human skull [8]. Its manifestation on the visible surface of the face is a distinctly depressed area directly between the eyes, just superior to the bridge of the nose. The opisthion is the mid-point of the posterior margin of the foramen magnum on the occipital bone [8]. The two points were chosen because of their locations at the front and back of the head, and because they are stable during the human growth process The nasion and opisthion are detected as follows. First, the plane of symmetry of the left and right sides of the skull on which the landmarks are expected to be is extracted. Then, the tip of the nose is located as the point with the smallest horizontal value. The nasion is located as the point closest to the tip of the nose, which is above it and which has a zero curvature in the vertical direction. The opisthion is located as the point in the left part of the outline, which has the closest distance to the nasion of all points below the nasion.

Our shape measure is based on the distances between points on the surface of the skull, so the second step is to extract a set of planes from which surface points are located. These planes are parallel to the base plane. The top plane of the skull is a plane that has intersection with the skull and which is parallel to the base plane but has the furthest distance to the base plane. Our system can extract any plane that is parallel to the base plane and located between the base plane and the top plane of the skull, based on the ratio of its distance to these two planes. Multiple planes may be selected with equal distances among them. In the rest of our experiments, 10 planes that are evenly distributed across the whole skull were used to provide a rich 3D shape descriptor.

In the third step of this module, N points are evenly extracted along the outlines of the planes from the previous step. N is chosen by the user, and N = 100 in our experiments.

3.3 Cranial Image Generation

Our shape feature is a N × N pairwise distance matrix among the surface points from the previous step. The number at position (i, j) of the matrix represents the distance between point number i and point number j (the last module of in Fig. 1). The matrix is symmetric. Such a shape feature is a rich representation of the skull shape, and its dimension is usually very high (over 10⁴).

Fig. 1.

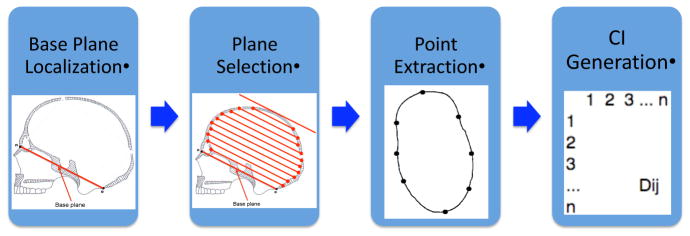
Surface points extraction: the first three modules are the three steps for extracting surface points; the last image is the distance matrix generated from the surface points.

3.4 Abnormality Quantification

The task of the system is to retrieve CT images by their skull shape abnormality severity. To rank the CT images, a qualification criterion for shape abnormality is needed. Based on our previous work [1], sparse logistic regression models have been effectively used to fit our data with the high dimensional shape features (CI). We use these models to generate quantification scores that represent the severity of the abnormality.

4 Sparse Logistic Regression Models for Abnormality Quantification

4.1 Sparse Logistic Regression Models

In our previous work, we explored logistic regression and three sparse logistic regression models for the purpose of classifying three different types of craniosynostosis. They can be summarized as follows.

Logistic Regression

Logistic regression is a workhorse in machine learning that uses a generalized linear model for binomial regression. In logistic regression model, the probability of being classified as one class is a linear function of the features.

$$p(y\mid \mathbf{x},\mathbf{w})=\frac{1}{1+\mathit{exp}(-y({\mathbf{w}}^T\mathbf{x}+w_0))}$$ (1)

where vector x contains the feature values of a data sample; y is its class label (for example, y = 1 refers to coronal and y = −1 refers to non-coronal), w contains the coefficients for x, and w₀ is the intercept. Furthermore, w₀ and w are model parameters, and p(y|x, w) is the probability that a data sample belongs to a certain class.

We can estimate the optimal parameters w₀ and w that minimize the following loss function:

$$l(w_0,\mathbf{w})=\sum _{i=1}^{n}log(1+exp)(-y_i({\mathbf{w}}^T{\mathbf{x}}_{\mathbf{i}}+w_0))$$ (2)

$$\{w_0,\mathbf{w}\}=\underset{w_0,\mathbf{w}}{min}l(w_0,\mathbf{w})$$ (3)

where y_i is the actual class label of a data sample x_i.

L₁ Regularized Logistic Regression

Due to the high-dimensionality of the data (i.e. a large number of features and a modest size of samples), learning the unregularized logistic regression [3] will result in overfitting. To avoid overfitting, L₁ regularization is usually applied to induce sparsity in the solution w such that many of the coefficients in w are set to exactly zero. L₁ regularization [2] has been rigorously proven to be effective in selecting relevant features when there are exponentially many irrelevant ones [6]. The log-likelihood of L₁ regularized logistic regression is as follows.

$$l(w_0,\mathbf{w})=\sum _{i=1}^{n}log(1+exp(-y_i({\mathbf{w}}^T{\mathbf{x}}_{\mathbf{i}}+w_0)))+\lambda \sum _{i=1}^m\mid w_i\mid$$ (4)

where λ is a regularization parameter for the L₁-norm of the coefficients.

Fused Lasso

One problem with L₁ regularization is that when features are highly correlated, it arbitrarily chooses one of many correlated features. Some variations of L₁ regularization can better exploit the underlying structure of our feature data. Specifically, the fused lasso induces bias from prior knowledge such that correlated feature groups will be assigned similar weights. In this work, the fused lasso [9] places a constraint on the weights of the features that are geographically related - sharing the same or neighboring surface points.

The loss function of the fused lasso with induced bias is,

$$l(w_0,\mathbf{w})=\sum _{i=1}^{n}log(1+exp(-y_i({\mathbf{w}}^T{\mathbf{x}}_{\mathbf{i}}+w_0)))+\lambda \sum _{i=1}^m\mid w_i\mid +\mu \sum _{\{w_i,w_j\}\in M}\mid w_i-w_j\mid$$ (5)

where μ is a regularization parameter for the new penalty term. M is a set that contains all pairs of features that are neighbors, whose endpoints are the same or next to each other. In equation [5], $\lambda {\sum }_{i=1}^m\mid w_i\mid$ penalizes large feature weights, and μΣ_{wiwj}∈M |w_i − w_j| penalizes large weight differences between correlated features.

Clustering Lasso

As mentioned before, L₁ regularized logistic regression tends to assign different weights to highly correlated features. When features are highly correlated, it arbitrarily chooses one of them and assigns a non-zero weight only to it. The fused lasso is one way to avoid this problem by placing constraints on the weight differences based on prior knowledge. However, this requires the model to know ahead of time the right grouping of the features. An alternative to using such prior knowledge, is to penalize the weight differences of correlated features.

The clustering lasso (or cLasso) is a new form of regularized logistic regression we recently proposed in [1]. The model for the clustering lasso is:

$$p(y\mid \mathbf{x},\mathbf{w},{\mathbf{w}}^{\mathbf{c}})=\frac{1}{1+\mathit{exp}(-y({\mathbf{w}}^T\mathbf{x}+{\mathbf{w}}^{\mathbf{c}T}\mathbf{c}+w_0))}$$ (6)

where x contains the feature values of a data sample; y is its class label (for example, y = 1 refers to sagittal and y = −1 refers to non-sagittal); c are the cluster centers of x; w contains the coefficients for x; w^c contains the coefficients for c; and w₀ is the intercept. Furthermore, w₀, w and w^c are model parameters, while p(y|x, w, w^c) is the probability that a data sample belongs to a certain class.

The loss function for the cLasso is

$$l(w_0,\mathbf{w},{\mathbf{w}}^{\mathbf{c}})=\sum _{i=1}^{n}log(1+exp(-y_i({\mathbf{w}}^T{\mathbf{x}}_{\mathbf{i}}+{\mathbf{w}}^{\mathbf{c}T}{\mathbf{c}}_{\mathbf{i}}+w_0)))+\lambda \sum _{i=1}^m\mid w_i\mid +\nu \sum _{i=1}^k\mid w_i^c\mid$$ (7)

where c_i (i ∈ [1, k]) is the centroid of a group of features {x_i1, x_i2, …, x_ik} (its feature value is their average); $w_i^c$ is the weight for c_i; and ν is the regularization parameter for the weights of the cluster centers.

This loss function is designed to cluster the features based on their correlation, and penalize their shared weights ( $w_i^c$) and individual weights (w_i1, w_i2, …, w_ik) respectively. When ν is small and λ is large, individual weights are penalized, and features tend to be split into groups based on their correlation and to share the same weights. When λ is large enough, this model is equivalent to the model of L₁ regularized logistic regression (equation [4]).

Parameter $w_i^c$ encourages correlated features to share the same weight, and w_i allows unique features to be used. Therefore, the cLasso is equivalent to using only shared weights ( $w_i^c$) when each centroid c_i (i ∈ [1, k]) is computed as a weighted average with the weights determined by (w_i1, w_i2, …, w_ik).

4.2 Abnormality Quantification

Using the models to fit to the data, the predicted probability of a sample data set x being a certain class p(y = 1|x, w) can be viewed as a quantification measure of skull abnormality. However, the use of the sigmoid function $P(t)=\frac{1}{1+e^{-t}}$ in computing the probability does not work well as a quantification criteria. Because a regression model that fits the data well tends to assign a value close to 1 to all positive instances, the quantification results are too similar. Instead, we use the linear function of the features before taking the sigmoid function to obtain the probability. The second option produces a better quantification measure, because the linear function differentiates abnormal skulls better, even when they are classified as the same class.

For the logistic regression, lasso and fused lasso models, the quantification scores are

$$S(\mathbf{x})=-y({\mathbf{w}}^T\mathbf{x}+w_0)$$ (8)

For the clustering Lasso, the quantification score is

$$S(\mathbf{x})=-y({\mathbf{w}}^T\mathbf{x}+{\mathbf{w}}^{\mathbf{c}T}+w_0)$$ (9)

5 Experiments

The experiments were designed to show the ability of our system to retrieve CT images based on skull shape abnormality of different types of craniosynostosis. As a measurement for performance, we also provide phenotype prediction accuracy by comparing our prediction with the groundtruth diagnoses of the doctors. Cranial images were generated using our system with 10 planes and 10 points on each plane. Logistic regression, L₁ regularized logistic regression, the fused lasso and the cLasso were compared in terms of phenotype prediction accuracy, while the quantification measure of cLasso is used as the ranking criterion in our system. Implementation of L₁ regularized logistic regression is from the authors of [6], and implementation of the fused lasso is the machine learning package SLEP [10]. In our previous work, we did a thorough study on choosing regularization parameter λ, μ and ν in equations 4, 5 and 7 for the sparse logistic regression models. We continue to use these parameters.

5.1 Medical data

Our system was tested on 3D CT images of children’s heads from hospitals in four different cities in the US. There are different types of craniosynostosis depending on the affected suture; the sagittal suture is between the parietal bones, metopic between the frontal bones, coronal between the frontal and parietal bones, and lambdoid between the parietal and occipital bones. Our study is focused on three types of synostosis - sagittal, metopic, and coronal. In total we examined approximately 200 CT image volumes, each comprising a stack of image slices (approximately 150 slices per volume). About half the data are controls (normal skulls), and the other half have one of the three types of craniosynostosis. Fig. 2 shows some examples of slices from the CT image stacks for all four classes.

Fig. 2.

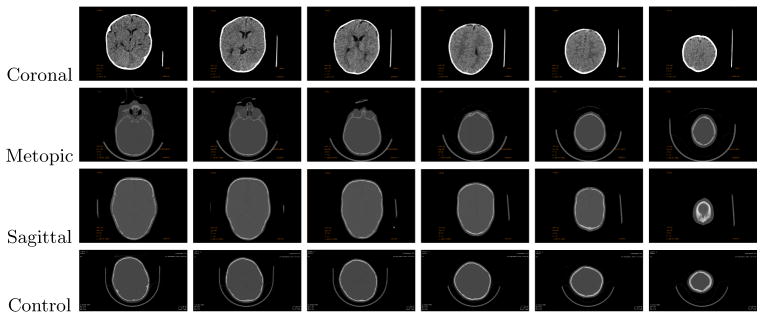
Examples of CT image slices

5.2 Evaluation on Classification

In the first part of our experiment, we evaluate our approach based on its prediction of whether a skull is abnormal or not, meaning the misclassification rate of each class. Classification results using the four different models are shown in Table 1. The results of logistic regression substantiates the overfitting problem with the large number of features it uses. The misclassification rate greatly improves when regularization is used in the logistic regression model. Specifically, the clustering lasso exhibits the best results on average. The misclassification rate of the coronal class is higher than the other two classes. This is because the coronal class is the most similar to the controls of all three classes. Its shape deformation is not immediately obvious as the deformation of the sagittal and metopic classes, as can be observed from Figure 2. This is consistent with the results from [1].

Table 1.

Misclassification rates using multiple planes for three types of craniasynostosis versus controlled skulls. Four different logistic regression models are used for comparison. Classo performs the best on all three types.

Misclassification Rate	Coronal vs Control	Metopic vs Control	Sagittal vs Control
Logistic regression	37.5%	36.25%	30%
L1 regression	26.3%	8.75%	8.75%
Fused lasso	16.3%	21.3%	8.75%
Clustering lasso	14.1%	7.5%	8.75%

5.3 Abnormality Quantification of Pre- and Post-Operative Skulls

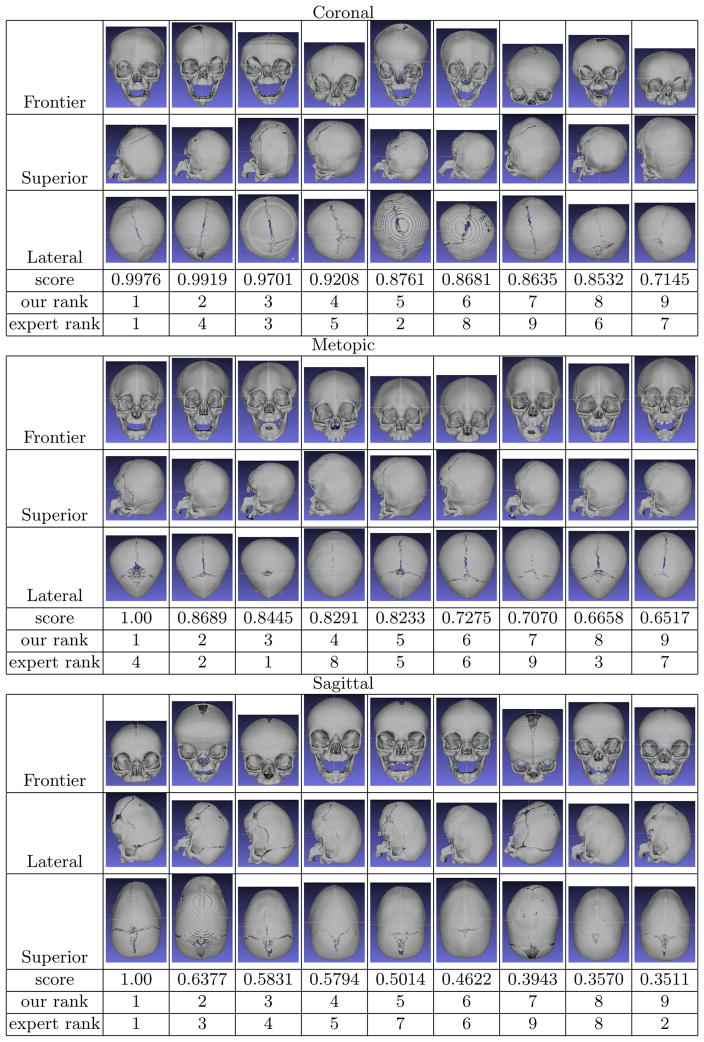
Besides testing our quantification measure on the CT images of patients when they are diagnosed, we also tested it on their CT scans two years after skull surgery was performed. Although the skull abnormality is corrected with surgery, it tends to relapse toward the original deformity with time. Our quantitative severity measure provides an objective measure for the comparison. Fig. 3 shows the comparison results for a set of pre-operative and post-operative skulls. The pair of skulls in each column are from the same patient. The abnormality reduction after surgery is according to our scoring method. This shows that the surgeries resulted in improvement in all cases even after two years of growth.

Fig. 3.

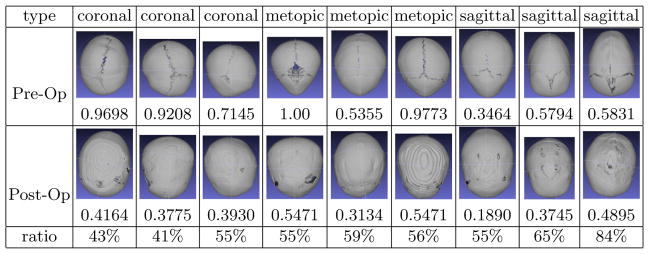
Quantification comparison of pre-operative and post-operative skulls: these images are the superior views of nine skulls (for each symptom type). Under the images are their severity scores. The upper row contains pre-operative skulls, and the bottom row are the post-operative skulls of the same subjects as the pre-op ones above it. A subject is normal if the score is ≤ 0. The larger a number is, the more abnormal it is.

5.4 Evaluation of Skull Retrieval

There is no gold standard for evaluating the quantification results, because an objective judgement of severity of craniosynostosis in the form of a medical test does not exist. Medical experts are accustomed to providing diagnoses but have no scoring criteria. In fact, our work was motivated by the need for severity quantification in medical research. However, we were able to have a craniofacial expert rank a subset of the skulls for each type of abnormality for our comparisons.

Based on the quantification measure using the clustering lasso, each skull was assigned a value that represents the degree of severity of the craniosynostosis type to which it belongs (coronal, metopic or sagittal). The results for these skulls in each class are shown in Fig. 4. (The numbers are normalized from −1 to 1; 0 to 1 means a subject is abnormal, and −1 to 0 means a subject is a control.) This result provides a useful measurement for physicians and researchers to quantify the severity of individual cases with different types of craniosynostosis. Our results correlate well with expert measures. Most of the orderings are only slightly permuted from the expert’s ranking. This is because some of the severity scores are very similar in themselves, so any of them can be ranked before the others in a subjective ordering. There are several exceptions on which our system and the expert disagree in an obvious way, such as No. 4 in the metopic group and No. 9 in the sagittal group in Fig. 4. Discussion with the expert disclosed that different parts of the skull were being weighted differently by the system and the expert. For example for No. 4 in the metopic group, the expert ranked it last because his focus, the pointy shape at the front, is not obvious in the skull. However, our system ranked it higher because its global shape is more similar to a typical metopic skull. This discovery reversely inspired the expert to notice certain shape features that he had previously ignored. The expert also told us that our quantification captured some shape features that could not be observed from the three standard views by doctors. This is evidence that our system would be helpful for clinicians to make more accurate diagnoses.

Fig. 4.

Quantification results: nine skulls are shown for each type of synostosis (coronal, metopic, and sagittal) from three different views. They are ordered by the severity scores produced by our system for the craniosynostosis type to which they belong. Under the images are their severity scores, their ranks by our system (ordered 1–9, with 1 being most severe), and expert ranks for comparison.

6 Conclusions

In this work, we built a system that performed skull analysis and severity based retrieval for patients with craniosynostosis. The system was tested with four different logistic regression models: logistic regression, L₁ regularized logistic regression, the fused lasso and the clustering lasso on classifying abnormal skulls from normal ones. The cLasso model was used for quantification of skull shape abnormality. Our experimental results validate the model, both by the error rate on the classification task and by comparison with expert ranks on the retrieval task. This retrieval system provides a convenient tool that can help medical researchers to quantify craniosynostosis for research studies. For example, the methods reported here would facilitate studies of the effects of different surgical methods on cranial shape, associations between severity of cranial deformation and subsequent neurodevelopmental outcomes and the relation of severity to genetic processes.