EXACT DISTRIBUTIONS OF INTRACLASS CORRELATION AND CRONBACH’S ALPHA WITH GAUSSIAN DATA AND GENERAL COVARIANCE

Abstract

Intraclass correlation and Cronbach’s alpha are widely used to describe reliability of tests and measurements. Even with Gaussian data, exact distributions are known only for compound symmetric covariance (equal variances and equal correlations). Recently, large sample Gaussian approximations were derived for the distribution functions.

New exact results allow calculating the exact distribution function and other properties of intraclass correlation and Cronbach’s alpha, for Gaussian data with any covariance pattern, not just compound symmetry. Probabilities are computed in terms of the distribution function of a weighted sum of independent chi-square random variables.

New F approximations for the distribution functions of intraclass correlation and Cronbach’s alpha are much simpler and faster to compute than the exact forms. Assuming the covariance matrix is known, the approximations typically provide sufficient accuracy, even with as few as ten observations.

Either the exact or approximate distributions may be used to create confidence intervals around an estimate of reliability. Monte Carlo simulations led to a number of conclusions. Correctly assuming that the covariance matrix is compound symmetric leads to accurate confidence intervals, as was expected from previously known results. However, assuming and estimating a general covariance matrix produces somewhat optimistically narrow confidence intervals with 10 observations. Increasing sample size to 100 gives essentially unbiased coverage. Incorrectly assuming compound symmetry leads to pessimistically large confidence intervals, with pessimism increasing with sample size. In contrast, incorrectly assuming general covariance introduces only a modest optimistic bias in small samples. Hence the new methods seem preferable for creating confidence intervals, except when compound symmetry definitely holds.

1. Introduction

1.1. Motivation

Estimates of interrater reliability are often of interest in behavioral and medical research. As an example, consider a study in which each of five physicians used X-ray images (from CT scans) to measure the volume of the hippocampus (a region of the brain). Each physician measured the volume for each of twenty subjects. The scientist sought to evaluate inter-physician reliability. This led to a wish to compute estimates of reliability and confidence intervals for the estimates. The intraclass correlation coefficient and Cronbach’s alpha, which are one-to-one functions of each other, provide appropriate indexes of reliability. The disparities in training and experience among physicians makes it seem unlikely that equal variances and equal correlations (compound symmetry) occur in this setting.

The exact, small sample, distributions of the estimates of intraclass correlation and Cronbach’s alpha are known only for Gaussian data with compound symmetric covariance. However, as for the example just described, it may be invalid to assume equal variances and equal covariances across raters and time. Only a large sample approximation is available for covariance matrices that are not compound symmetric.

1.2. Literature Review

Cronbach (1951) defined coefficient alpha, ρ_α, a lower bound of the reliability of a test. Subsequently, Kristof (1963) and Feldt (1965) independently derived the exact distribution of a sample estimate, ${\widehat{\rho }}_{\alpha }$, assuming Gaussian data and compound symmetric covariance. Exact calculations require specifying the common variance and correlation. Recently, van Zyl, Neudecker, and Nel (2000) derived a large sample approximation of the distribution of ${\widehat{\rho }}_{\alpha }$ for Gaussian data with a general covariance matrix. Approximate calculations require specifying the population covariance matrix. The results all extend to estimates of the intraclass correlation, due to the one-to-one relationship between the two measures of reliability.

1.3. Overview of New Results

Section 2 contains exact and approximate expressions for the distribution functions of estimates of both intraclass correlation and Cronbach’s alpha. A theorem in Section 2.2 provides the key result. It allows computing each distribution function in terms of the probability that a weighted sum of independent chi-square random variables is less than zero. A simple F approximation is derived and provides a much simpler algorithm than the one required to compute exact probabilities.

Section 3 contains three kinds of numerical evaluations of the new results. The first involves verifying the accuracy of the exact forms. The second centers on comparing the existing Gaussian approximation to the new exact result and the new F approximation. The third contains an evaluation of the coverage accuracy of confidence intervals based on an estimated covariance matrix.

2. Analytic Results

2.1. Notation

A scalar variable will be indicated by lower case, such as x; a vector (dimension n × 1, always a column) by bold lower case, such as x; an n × p matrix by bold upper case, X; and its transpose by X’. For example, 1_n indicates an n × 1 vector of 1’s. If X = [x₁ x₂ … x_p], then the stacking of the columns into an n · p × 1 will be indicated by vec(X), with the first column at the top, followed by the second, etc. The Kronecker product is defined as X ⊗ Y = {x_ij · Y}. For an n × 1 vector x, the n × n matrix with all zero elements off the diagonal and x_i as the (i, i) element will be written Dg(x). As needed, a scalar, vector or matrix is described as constant, random, or a realization of a random scalar, vector or matrix.

Properties of Gaussian variables will be used throughout (Arnold, Chapter 3, 1981). All parameters are assumed finite. A scalar variable, y, will be indicated to follow a Gaussian distribution, with expected value, the mean, ε(y) = μ and variance, ν(y) = ε(y²) − [ε(y)]² = σ², by writing y ~ N (μ, σ²). An n × 1 vector will be indicated to follow a Gaussian distribution, with n × 1 mean vector ε(y)= μ and n × n covariance matrix ν(y) = ε(yy’ − εy)[ε(y)]’ = Σ, by writing y ~ N_n(μ, ∑).

Interest in this paper centers on an n × p matrix of data, Y, for which the rows form a set of independent and identically distributed Gaussian vectors. This may be indicated symbolically as [row_i(Y)]’ ~ N_p (μ, Σ), assuming independent and identically distributed rows. Throughout this paper, Σ represents a p × p, symmetric, and positive definite population covariance matrix. The spectral decomposition allows writing Σ = V_ΣDg(λ_Σ)V’_Σ, with positive eigenvalues {λ_Σ,j}. Corresponding eigenvectors are the columns of V_Σ, which is p × p, of full rank, and orthonormal (V’_ΣV_Σ = I_p). Furthermore, if F_Σ = V_ΣDg(λ_Σ)^1/2 then Σ = F_ΣF’_Σ.

Johnson, Kotz, and Balakrishnan (1994, 1995) gave detailed treatments of the chi-square and F distributions. Writing X ~ χ²(ν) indicates that X follows a central chi-square distribution, with ν degrees of freedom. If X₁ ~ χ²(ν₁) X₂ ~ χ²(ν₂) then writing (X₁/ν₁)(X₂/ν₂) ~ F(ν₁, ν₂) indicates that the radio follows a central F distribution, with numerator degrees of freedom ν₁ and denominator degrees of freedom ν₂. The distribution function of a central F will be indicated as F_F(f;ν1, ν2), with corresponding qth quantile $f=F_F^{-1}(q;{\nu }_1,{\nu }_2)$. The identity $F_F^{-1}(q;{\nu }_1,{\nu }_2)=1∕F_F^{-1}(1-q;{\nu }_2,{\nu }_1)$ is useful.

2.2. Known Results

A covariance matrix may be described as compound symmetric if all variances are equal and all correlations are equal. If so, and σ² is the common variance while ρ_I is the common correlation, Σ = σ²[ρ_I1_p1’_p − (1 − ρ_I)I_p]. The matrix has two distinct eigenvalues. The first is τ₁ = σ²[1 + (p − 1)ρ_I], with corresponding eigenvector ${\mathbf{v}}_0=1_p∕\sqrt{p}$. The second is τ₂ = σ²(1 − ρ_I), which has multiplicity p − 1 and corresponding eigenvectors any matrix V_⊥, of dimension p × (p − 1), such that V’_⊥ V_⊥ =I_p−1 and V’_⊥ 1_p = 0_p−1. Without loss of generality, V_⊥ may be taken to be the orthogonal polynomial trend coefficients (normalized to unit length). Requiring 0 < σ² < ∞ and −(p − 1)⁻¹ < ρI < 1 ensures finite and positiv definite Σ. See Morrison (1990, p. 289) for additional detail.

In practice, caluculations are based on $\widehat{\Sigma }={\mathbf{Y}}^{\prime }[{\mathbf{I}}_n-1_n{1}_n^{\prime }∕n]\mathbf{Y}∕\nu$, with ν = n − 1 > p assumed throughout. In turn, this leads to the estimated intraclass correlation coefficient,

$${\widehat{\rho }}_{\mathrm{I}}=\frac{[1_p^{\prime }\widehat{\Sigma }{1}_p-\mathrm{tr}(\widehat{\Sigma }\left)\right]∕\left[p\right(p-1\left)\right]}{\mathrm{tr}\left(\widehat{\Sigma }\right)∕p},$$ (1)

with $-{(p-1)}^{-1}<{\widehat{\rho }}_{\mathrm{I}}<1$. Similarly, the estimate of Cronbach’s α is

$${\widehat{\rho }}_{\alpha }=\frac{p}{(p-1)}\left[1-\mathrm{tr}\left(\widehat{\Sigma }\right)∕1_p^{\prime }\widehat{\Sigma }{1}_p\right],$$ (2)

with $-\infty <{\widehat{\rho }}_{\alpha }<1$. Estimated Cronbach’s α is a one-to-one function of estimated intraclass correlation:

$${\widehat{\rho }}_{\alpha }=\frac{p{\widehat{\rho }}_{\mathrm{I}}}{1+(p-1){\widehat{\rho }}_{\mathrm{I}}}.$$ (3)

Replacing $\widehat{\Sigma }$ with Σ gives the population values. If Σ is compound symmetric, then ρ_I is the common correlation, with ${\widehat{\rho }}_{\mathrm{I}}$ the maximum likelihood estimate (with Gaussian data).

To avoid confusion it may help to describe ρ_I as the intraclass correlation if Σ is compound symmetric, and as the generalized intraclass correlation if Σ is not compound symmetric. The two situations have different analytic properties, including different maximum likelihood estimates of Σ. Under compound symmetry, ρ_I equals the average population correlation, and ${\widehat{\rho }}_{\mathrm{I}}$ is the corresponding maximum likelihood estimate. In contrast, without compound symmetry, typically ρ_I will not equal the average correlation and ${\widehat{\rho }}_{\mathrm{I}}$ will not be the maximum likelihood estimate of the average correlation. See Morrison (1990, p. 250) for some additional detail.

2.3. New Exact Distributions and Related Properties

Theorem 1. With multivariate Gaussian data, the cumulative distribution function of the estimate of intraclass correlation exactly equals the probability that a particular weighted sum of independent central chi-square random variables is less than zero. A parallel statement holds for Cronbach’s α.

In particular, consider observing the n × p random matrix Y with independent and identically distributed rows such that [row_i(Y)]’ ~ N_p(μ, Σ), with Σ = F_ΣF’_Σ, a p × p, symmetric, and positive definite matrix. Recall that the corresponding estimate is $\widehat{\Sigma }$, with ν = n − 1 > p degrees of freedom. Let r_I indicate a particular quantile of ${\widehat{\rho }}_{\mathrm{I}}$, with −(p − 1)⁻¹ < r_I < 1, and let r_α indicate a particular quantile of ${\widehat{\rho }}_{\alpha }$, with −∞ < r_α < 1. In addition, define the following one-to-one functions of the quantiles:

$$x_{\mathrm{I}}=\left[\right(p-1)r_{\mathrm{I}}+1]$$ (4)

$$x_{\alpha }={[1-r_{\alpha }(p-1)∕p]}^{-1}.$$ (5)

For c ∈ {α, I}, also define

$$D\left(x_c\right)=1_p^{\prime }\left(\nu \widehat{\Sigma }\right)1_p-x_c\mathrm{tr}\left(\nu \widehat{\Sigma }\right).$$ (6)

The assumptions just stated suffice to allow proving the following results.

The Matrix F’_Σ(1_p1’_p − x_cI_p)F_Σ is a p × p, symmetric full rank, with one strictly positive eigenvalue, λ_2c,1, and p − 1 strictly negative eigenvalues, {λ_2c,2, …, λ_2c,p}. Most importantly,

$$\begin{array}{cc}\hfill \mathrm{Pr}\{{\widehat{\rho }}_c\le r_c\}& =\mathrm{Pr}\left\{D\right(x_c)\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{{\lambda }_{2c,1}{X}_{c1}-\sum _{j=2}^p\mid {\lambda }_{2c,j}\mid X_{\mathit{cj}}\le 0\right\},\hfill \end{array}$$ (7)

with X_cj ~ χ²(ν), independently of X_cj, if j ≠ j’.

Proof. See Propositions 1–4 and their proofs in the appendix.

Corollary 1

The previously known exact results for compound symmetry are special cases of the theorem results.

1. If Σ has compound symmetry then the proofs of Propositions 1–4 lead to simple forms of the required eigenvalues. In turn, $D\left(x_c\right)=\left[{\tau }_1\right(p-x_c\left)\right]X_{c1}-\left({\tau }_2{x}_c\right){\sum }_{j=2}^p{X}_{\mathit{cj}}$ and

$$\begin{array}{cc}\hfill \mathrm{Pr}\{{\widehat{\rho }}_c\le r_c\}& =F_F\left[\frac{{\tau }_2{x}_c(p-1)}{{\tau }_1(p-x_c)};\nu ,\nu (p-1)\right]\hfill \\ \hfill & =1-F_F\left[\frac{{\tau }_1(p-x_c)}{{\tau }_2{x}_c(p-1)};\nu (p-1),\nu \right].\hfill \end{array}$$ (8)

2. If Σ has compound symmetry and q ∈ [0, 1] then

$$q=F_F\left[{\tau }_2\right(p-1)x_c∕[{\tau }_1(p-x_c)];\nu ,\nu (p-1\left)\right].$$

Solving for x_c gives

$$x_c={\tau }_{1}p∕\left[{\tau }_2(p-1)F_F^{-1}[1-q;\nu (p-1),\nu ]+{\tau }_1\right],$$

with corresponding qth quantiles

$$r_{\alpha }=1-F_F^{-1}[1-q;\nu (p-1),\nu ]{\tau }_2∕{\tau }_1$$ (9)

and

$$r_{\mathrm{I}}=\frac{1-F_F^{-1}[1-q;\nu (p-1),\nu ]{\tau }_2∕{\tau }_1}{1+(p-1)F_F^{-1}[1-q;\nu (p-1),\nu ]{\tau }_2∕{\tau }_1}.$$ (10)

3. If Σ has compound symmetry, an exact confidence interval can be computed as follows. Let $f_L=F_F^{-1}[{\alpha }_L;\nu (p-1),\nu ]$ and $f_U=F_F^{-1}[1-{\alpha }_U;\nu (p-1),\nu ]$. For ρ_α, a confidence interval size 1 − α_L − α_U < 1, with 0 ≤ α_L < 1 and 0 ≤ α_U < 1, is given by

$$1-{\alpha }_L={\alpha }_U=\mathrm{Pr}\left\{1-(1-{\widehat{\rho }}_{\alpha })f_L^{-1}\le {\rho }_{\alpha }\le 1-(1-{\widehat{\rho }}_{\alpha })f_U^{-1}\right\}.$$ (11)

Similarly, if ${\widehat{\tau }}_1∕{\widehat{\tau }}_2=[1+(p-1\left){\widehat{\rho }}_{\mathrm{I}}\right]∕(1-{\widehat{\rho }}_{\mathrm{I}})$, then for ρI it follows that

$$1-{\alpha }_L-{\alpha }_U=\mathrm{Pr}\left\{\frac{f_L{\widehat{\tau }}_1∕{\widehat{\tau }}_2-1}{f_L{\widehat{\tau }}_1∕{\widehat{\tau }}_2-1+p}\le {\rho }_{\mathrm{I}}\le \frac{f_U{\widehat{\tau }}_1∕{\widehat{\tau }}_2-1}{f_U{\widehat{\tau }}_1∕{\widehat{\tau }}_2-1+p}\right\}.$$ (12)

Part 1 is proven in the appendix. The result coincides with the previously known form, as do 2 and 3, which follow easily from 1.

Corollary 2

The moment, characteristic, and cumulant generating functions, as well as all cumulants and the first two moments of D(x_c), have simple closed forms. In particular, with $\mathrm{i}=\sqrt{-1}$, the characteristic function is (Johnson & Kotz, 1970, equation 15, p. 152)

$${\varphi }_{D\left(x_c\right)}(t;\Sigma )=\prod _{j=1}^p{(1-2\mathrm{i}t{\lambda }_{2c,j})}^{-\nu ∕2}.$$ (13)

The moment generating function is the same function with t replacing it and the cumulant generating function is the logarithm of the moment generating function. The mth cumulant is (Johnson & Kotz, 1970, equation 20, p. 153)

$${\kappa }_{D\left(x_c\right)}\left(m\right)=2^{m-1}(m-1)!\nu \sum _{j=1}^p{\lambda }_{2c,j}^m.$$ (14)

The first cumulant is the mean,

$${\kappa }_{D\left(x_c\right)}\left(1\right)=\epsilon \left[D\right(x_c\left)\right]=\nu \sum _{j=1}^p{\lambda }_{2c,j},$$ (15)

and the second cumulant is the variance,

$${\kappa }_{D\left(x_c\right)}\left(2\right)=\mathcal{V}\left[D\right(x_c\left)\right]=2\nu \sum _{j=1}^p{\lambda }_{2c,j}^2.$$ (16)

Corollary 3

Davies’ algorithm (1980) allows computing the exact distribution function of estimates of intraclass correlation and Cronbach’s alpha.

The algorithm computes the distribution function of a weighted sum of independent chi-squares with any combination of positive and negative weights, by numerical inversion of the characteristic function.

2.4. An F Approximation for the Distribution Function

Davies’ algorithm can be computationally intensive. Therefore an approximation was derived for the distribution function of D(x_c), based on Satterthwaite’s method (Mathai & Provost, 1992). The approximation matches the first two moments of

$$Q=\sum _{j=2}^p\mid {\lambda }_{2c,j}\mid X_j$$ (17)

to Q_* = λ_* X_* with X_* ~ χ²(ν_*). The constants that define the approximation are

$${\lambda }_{\ast }=\sum _{j=2}^p{\lambda }_{2c,j}^2/\sum _{j=2}^p\mid {\lambda }_{2c,j}\mid$$ (18)

and

$${\nu }_{\ast }=\nu {\left(\sum _{j=2}^p\mid {\lambda }_{2c,j}\mid \right)}^2/\sum _{j=2}^p{\lambda }_{2c,j}^2.$$ (19)

Assuming Q ≈ Q_* allows writing

$$\begin{array}{cc}\hfill \mathrm{Pr}\{{\widehat{\rho }}_c\le r_c\}& \approx \mathrm{Pr}\{{\lambda }_{2c,1}{X}_1-{\lambda }_{\ast }{X}_{\ast }\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\frac{X_1∕\nu }{X_{\ast }∕{\nu }_{\ast }}\le \frac{{\nu }_{\ast }{\lambda }_{\ast }}{\nu {\lambda }_{2c,1}}\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\frac{X_1∕\nu }{X_{\ast }∕{\nu }_{\ast }}\ne \sum _{j=2}^p\mid {\lambda }_{2c,j}\mid ∕{\lambda }_{2c,1}\right\}\hfill \\ \hfill & =F_F\left(\sum _{j=2}^p\mid {\lambda }_{2c,j}\mid /{\lambda }_{2c,1};\nu ,{\nu }_{\ast }\right).\hfill \end{array}$$ (20)

Note that both the exact distribution and the approximate F distribution depend only on the eigenvalues of A_2c, which are functions of Σ and r_c. The approximation reduces to the exact result in the special case of compound symmetry.

2.5. Proposals for Approximating Confidence Limits with General Covariance

Two different methods for approximating confidence limits with general covariance have some appeal. For a confidence level of 1 − α_L − α_U, the simplest method is to merely replace Σ by $\widehat{\Sigma }$ and find the values of r_cL and r_cU that satisfy the equation $1-{\alpha }_L-{\alpha }_U=\mathrm{Pr}\{r_{\mathit{cL}}\le {\widehat{\rho }}_c\le r_{\mathit{cU}}\}$. This first approach is based on approximate quantiles. Alternately, the relationship between the forms of the exact quantiles and confidence bounds under compound symmetry leads to suggesting a simple modification in the context of the F approximation. The confidence limit differs from the quantile by replacing an F quantile with the reciprocal of the opposite tail quantile. In the context of numerically inverting the approximate distribution function, this corresponds to replacing

$$F_F\left(\sum _{j=2}^p\mid {\widehat{\lambda }}_{2c,j}\mid /{\widehat{\lambda }}_{2c,1};\nu ,{\nu }_{\ast }\right)\text{by}1-F_F\left({\widehat{\lambda }}_{2c,1}/\sum _{j=2}^p\mid {\widehat{\lambda }}_{2c,j}\mid ;\nu ,{\nu }_{\ast }\right).$$

The second approach may be described as being based on approximate confidence limits.

3. Numerical Evaluations

3.1. Check Exact Results with Simulations

Given a critical value, r_c, and Σ calculation of the exact distribution function required the following steps.

1. Use Cholesky decomposition to compute F_Σ such that Σ = F_ΣF’_Σ.

2. Compute x_c as either xI = [(p − 1)rI + 1] or x_α = [1 − r_α(p − 1)/p]⁻¹.

3. Compute A_1c = (1_p1’_p − x_cI_p).

4. Compute the eigenvalues of A_2c = F’_ΣA_1cFΣ.

5. Apply Davies’ algorithm to compute Pr{D(x_c) ≤ 0}, based on equation 7.

Computer simulations allowed checking the accuracy of the calculations of exact probabilities. All such simulations used ν = 9 and p = 4. Using SAS/IML® (SAS Institute, 1999), 100,000 random samples were generated from a multivariate normal distribution. Twelve distinct choices for Σ, assumed known, were created by combining one of four correlation matrices with one of three variance patterns. One correlation matrix had all correlations equal to ρ 0.5 (all off-diagonal elements were 0.5). The other three correlation matrices were autoregressive = of order 1, indicated AR(1), which implies the j, j’ element was ρ^|j−j’|, with ρ ∈ {0.2, 0.5, 0.8}. The variance pattern, ${\left[{\sigma }_1^2{\sigma }_2^2{\sigma }_3^2{\sigma }_4^2\right]}^{\prime }$, was [1 1 1]’, [1 2 3 4]’, or [4 3 2 1]’. The observed probability that the estimate of Cronbach’s alpha was less than the critical value of r_α = 0.70 was tabulated from the 100,000 replications. Each observed probability was compared to the corresponding exact probability computed with Davies’ algorithm. In all cases the exact probability was contained within the 95% confidence interval around the observed probability. The confidence intervals were based on a Gaussian approximation.

3.2. Evaluation of the F Approximation

Calculation of the F approximation for the distribution function began with computing the eigenvalues of A_2c, as described in the opening paragraph of Section 3.1. Then equations 19 and 20 were used to complete the calculation.

The F approximation was computed for all cases considered in Section 3.1, again assuming Σ known (see Table 1). As stated in Corollary 1, the approximation gives the exact probability with compound symmetry. More notably, at least for the cases considered in Table 1, the approximation achieves three to four digits of accuracy.

TABLE 1.

$\{{\widehat{\rho }}_{\alpha }\le 0.70\}$ with Σ Known and ν = 9

Correlation	ρ	$[{\sigma }_1^2$	${\sigma }_2^2$	${\sigma }_3^2$	${{\sigma }_4^2]}^{\prime }$	Exact	F Approx.
equal	0.5	[1	1	1	1]’	0.2689	0.2689
AR(1)	0.5	[1	1	1	1]’	0.5628	0.5631
AR(1)	0.2	[1	1	1	1]’	0.9442	0.9440
AR(1)	0.8	[1	1	1	1]’	0.0430	0.0429
equal	0.5	[1	2	3	4]’	0.4697	0.4705
AR(1)	0.5	[4	3	2	1]’	0.7139	0.7135

Table 2 illustrates the behavior of the approximation for a range of quantiles with ν 9, p = 3, AR(1) with ρ = 0.5, and ${\left[{\sigma }_1^2{\sigma }_2^2{\sigma }_3^2{\sigma }_4^2\right]}^{\prime }={\left[123\right]}^{\prime }$. For the case considered, the approximation is accurate even at the extremes of the distribution.

TABLE 2.

$\{{\widehat{\rho }}_{\alpha }\le r_{\alpha }\}$ with Σ Known, AR(1) Correlation with ρ = 0.5 and ${\left[{\sigma }_1^2{\sigma }_2^2{\sigma }_3^2\right]}^{\prime }={\left[123\right]}^{\prime }$

rα	Exact	F Approx.
0.10	0.0614	0.0614
0.20	0.0899	0.0900
0.30	0.1349	0.1353
0.40	0.2072	0.2079
0.50	0.3231	0.3242
0.60	0.5010	0.5020
0.70	0.7367	0.7361
0.80	0.9418	0.9391
0.90	0.9992	0.9989

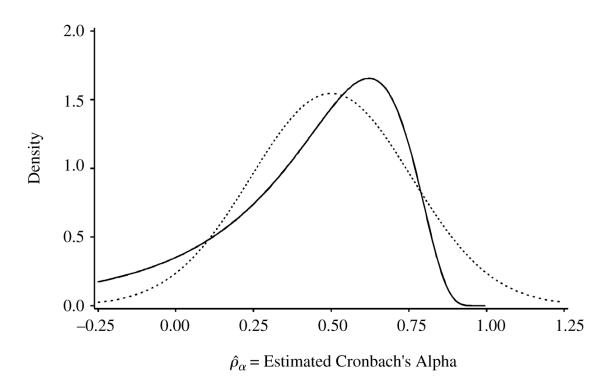
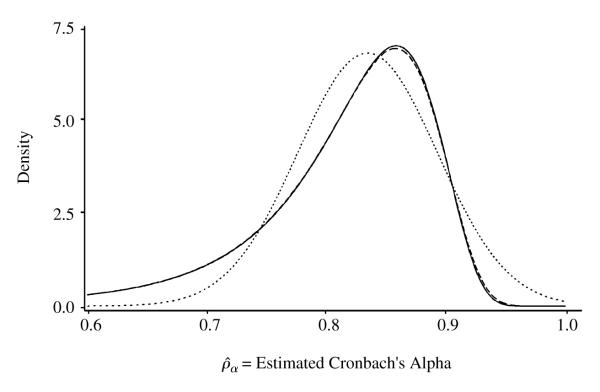
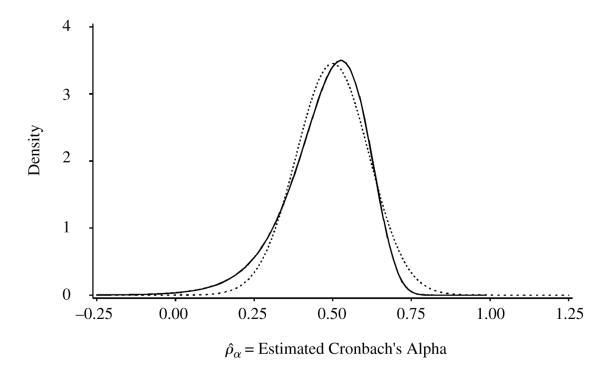
Figures 1–4 display the exact density function of Cronbach’s alpha, the F approximate density, and the Gaussian approximate density due to van Zyl et al. (2000). The exact and F approximation densities were computed as numerical derivatives of the corresponding distribution functions. In Figures 1 (ν = 9) and 2 (ν = 49), which differ only due to sample size, the exact density and the F approximate density coincide exactly because both are based on compound symmetry. Figures 3 (ν = 9) and 4 (ν = 49), which differ only due to sample size, are based on an AR(1) correlation pattern with heterogeneity of variance. In Figure 3, the exact and F approximate densities differ only slightly (by less than 10% in ordinate values) for only a subset of the domain. In Figure 4, the exact and F approximate densities are indistinguishable at the resolution of the plot.

Figure 1.

Density of ${\widehat{\rho }}_{\alpha }$ for ν = 9. Solid line for exact and F approximate, dotted line for Gaussian approximate, for p = 4 and compound symmetry with ρ = 0.20, σ² = 1.

Figure 4.

Density of ${\widehat{\rho }}_{\alpha }$ for ν = 49. Solid line for exact and F approximate, dotted line for Gaussian approximate, for p = 4, AR(1) with ρ = 0.80 and ${\left[{\sigma }_1^2{\sigma }_2^2{\sigma }_3^2{\sigma }_4^2\right]}^{\prime }={\left[1234\right]}^{\prime }$.

Figure 3.

Density of ${\widehat{\rho }}_{\alpha }$ for ν = 9. Solid line for exact, dashed line for F approximate, and dotted line for Gaussian approximate, for p = 4, AR(1) with ρ = 0.80 and ${\left[{\sigma }_1^2{\sigma }_2^2{\sigma }_3^2{\sigma }_4^2\right]}^{\prime }={\left[1234\right]}^{\prime }$.

Two overall conclusions seem apparent. First, the Gaussian approximation may deviate substantially from the exact result, including nonzero probabilities for values of Cronbach’s α greater than 1.0 (which are impossible). Second, the F approximation is nearly always indistinguishable from the exact result, except for some small differences in the right half of Figure 3. These results agree with those in Tables 1 and 2.

3.3. Confidence Intervals from Estimated Σ

All research to this point has assumed that the true covariance matrix is known. In practice, the covariance matrix can only be estimated. This leads to the desire to compute confidence intervals based on an estimated Σ. Four distinct methods for computing confidence intervals are defined by making two choices. The first choice is to assume either compound symmetry or general covariance. The second choice is to compute estimated quantiles or estimated confidence limits.

Assuming general covariance led to difficulties with finding lower quantiles of the unbounded random variable ${\widehat{\rho }}_{\alpha }$. Hence all calculations were conducted in terms of the intraclass correlation coefficient, which has a finite range, (−(p − 1)⁻¹, 1), while the range of ${\widehat{\rho }}_{\alpha }$ is unbounded, (−∞, 1). The change ensured stable convergence.

When assuming compound symmetry, equation 1 was used to compute ${\widehat{\rho }}_{\mathrm{I}}$. In turn, ${\widehat{\tau }}_2∕{\widehat{\tau }}_1=(1-{\widehat{\rho }}_{\mathrm{I}})∕[1+(p-1\left){\widehat{\rho }}_{\mathrm{I}}\right]$ was computed. The quantile approach values were computed by replacing τ₂/τ₁ with ${\widehat{\tau }}_2∕{\widehat{\tau }}_1$ in equation 10. The confidence limits approach values were computed by replacing τ₂/τ₁ with ${\widehat{\tau }}_1∕{\widehat{\tau }}_2$ in equation 12.

Assuming general covariance requires an iterative process to compute quantiles or approximate confidence limits. The corresponding method assuming compound symmetry provided the starting value. The associated approximate distribution function value was computed next. This was done by computing the eigenvalues of A_2c, as described in the opening paragraph of Section 3.1, but with $\widehat{\Sigma }$ replacing Σ, and then using equations 19 and 20. A simple bisection algorithm was applied to numerically invert the process and find a particular quantile. As described in Section 2.5, the confidence interval approach differs only by replacing the calculation of

$$F_F\left(\sum _{j=2}^p\mid {\widehat{\lambda }}_{2c,j}\mid ∕{\widehat{\lambda }}_{2c,1};\nu ,{\nu }_{\ast }\right)$$

with the calculation of

$$1-F_F\left({\widehat{\lambda }}_{2c,1}∕\sum _{j=2}^p\mid {\widehat{\lambda }}_{2c,j}\mid ;\nu ,{\nu }_{\ast }\right).$$

Simulations were used to estimate the coverage probability, which is the number of times a confidence interval contains the true value of the parameter, ρ_α, when estimating Σ. In all cases p = 4, with 500,000 samples from a multivariate normal distribution. One of four covariance matrices were used. Two were compound symmetric (see Table 3) with constant variance of ${\sigma }_j^2=1$ and ρ ∈ {0.2, 0.8}. Two (see Table 4) used ${\left[{\sigma }_1^2{\sigma }_2^2{\sigma }_3^2{\sigma }_4^2\right]}^{\prime }={\left[1234\right]}^{\prime }$ with an AR(1) correlation matrix and ρ ∈ {0.2, 0.8}.

Table 3.

Estimated Coverage Probability of Confidence Interval for ρ_α with Compound Symmetry and All ${\sigma }_j^2=1$

		95% CI for Coverage of ρα
		Assume Compound Symmetry		Assume General Σ
ρ	ν+ 1	Quantiles	Conf. Limits	Quantiles	Conf. Limits
0.2	10	(0.929, 0.930)	(0.949, 0.950)	(0.919, 0.921)	(0.936, 0.937)
	50	(0.946, 0.947)	(0.949, 0.950)	(0.944, 0.945)	(0.948, 0.949)
	100	(0.948, 0.949)	(0.949, 0.950)	(0.946, 0.948)	(0.949, 0.950)
	200	(0.948, 0.949)	(0.949, 0.951)	(0.948, 0.950)	(0.949, 0.950)
0.8	10	(0.929, 0.930)	(0.950, 0.951)	(0.919, 0.920)	(0.936, 0.937)
	50	(0.946, 0.947)	(0.949, 0.951)	(0.943, 0.945)	(0.948, 0.949)
	100	(0.948, 0.949)	(0.949, 0.950)	(0.947, 0.949)	(0.948, 0.950)
	200	(0.948, 0.949)	(0.949, 0.950)	(0.948, 0.949)	(0.949, 0.950)

Table 4.

Estimated Coverage Probability of Confidence Interval for ρ_α with AR(1) Correlation and ${\left[{\sigma }_1^2{\sigma }_2^2{\sigma }_3^2{\sigma }_4^2\right]}^{\prime }={\left[1234\right]}^{\prime }$

		95% CI for Coverage of ρα
		Assume Compound Symmetry		Assume General Σ
ρ	ν+ 1	Quantiles	Conf. Limits	Quantiles	Conf. Limits
0.2	10	(0.952, 0.953)	(0.973, 0.974)	(0.929, 0.930)	(0.934, 0.935)
	50	(0.970, 0.971)	(0.974, 0.975)	(0.946, 0.947)	(0.946, 0.948)
	100	(0.972, 0.973)	(0.974, 0.975)	(0.948, 0.950)	(0.948, 0.949)
	200	(0.973, 0.974)	(0.974, 0.975)	(0.949, 0.950)	(0.948, 0.949)
0.8	10	(0.978, 0.979)	(0.992, 0.993)	(0.932, 0.934)	(0.932, 0.934)
	50	(0.993, 0.993)	(0.995, 0.996)	(0.946, 0.948)	(0.946, 0.947)
	100	(0.994, 0.995)	(0.995, 0.996)	(0.948, 0.949)	(0.948, 0.949)
	200	(0.995, 0.995)	(0.995, 0.996)	(0.949, 0.950)	(0.949, 0.950)

The coverage probability was estimated by tabulating the fraction of times the estimated confidence interval contained the true value of ρ_α. Results in Tables 3 and 4 followed consistent patterns. Overall, estimating the covariance matrix introduced bias in confidence interval coverage, with the nature of the bias varying with the underlying assumption.

Naturally, if the assumption of compound symmetry holds in the population, confidence intervals based on the exact method worked perfectly. In contrast, the quantile based approximation gave accurate confidence intervals in large samples and optimistically narrow confidence intervals in small samples. Of course, the quantile approach would never be used in practice if compound symmetry were known to hold. However, the results give some guidance as to the sources of inaccuracy in the general covariance setting.

When general covariance is assumed regardless of the underlying covariance matrix, both methods generated optimistically narrow intervals in small samples, with the approximate confidence limit approach generating slightly less bias. In larger samples, assuming general covariance works very well with either method.

A very different picture arose from assuming compound symmetry when the assumption was false. Violation of the assumption led to consistently wide confidence intervals, independent of sample size for the approximate confidence limit approach. The quantile approach also always gave pessimistically wide intervals, although with somewhat less bias in small samples.

4. Conclusions

The new results provide a wide range of properties of estimates of intraclass correlation and Cronbach’s alpha with Gaussian data and general covariance. In addition, Davies’ algorithm provides precise numerical calculation of probabilities and densities.

The new F approximation, based on assuming general covariance, provides the best combination of accuracy and convenience, for both known and estimated Σ. In comparison to the Gaussian approximation, the new F approximation provides substantially greater accuracy, especially in small samples.

The one-to-one relationship between estimates of intraclass correlation and Cronbach’s alpha has two practical implications. First, all of the conclusions from the simulations about estimates of Cronbach’s alpha also apply to estimates of intraclass correlation. Second, the bounded nature of the intraclass correlation, leads to preferring calculations based on the intraclass correlation, even when interest centers on Cronbach’s alpha.

Not surprisingly, assuming general covariance provides much greater accuracy than that obtained when wrongly assuming that compound symmetry holds. Equally important, assuming general covariance in the presence of compound symmetry has only a small effect on confidence interval accuracy, and then only in small samples. Hence any substantial doubt about the validity of the compound symmetry assumption should lead to assuming general covariance and using the new results.

A number of avenues have appeal for future research. An improved approximation for confidence intervals based on estimated Σ in very small samples merits attention. Methods for comparing two or more estimates of reliability, and associated sample size formulas, would be valuable. It would be useful to know the impact of allowing missing data. Finally, the robustness of the probability calculations to the violation of the assumption of Gaussian variables holds great interest.

Free software which implements the new methods may be found at http://www.bios.unc.edu/~muller. Distribution function and confidence interval algorithms are implemented as collections of SAS/IML modules (SAS Institute, 1999).

Figure 2.

Density of ${\widehat{\rho }}_{\alpha }$ for ν = 49. Solid line for exact and F approximate, dotted line for Gaussian approximate, for p = 4 and compound symmetry with ρ = 0.20, σ² = 1.

Appendix. Definitions and Properties of Matrix Normal and Wishart Matrices

Arnold (1981, pp. 310–311) provided a general notation for a Gaussian data matrix. It is used because it helps simplify the proof of Theorem 1. In particular, an n × p matrix, Y, will be indicated to follow a matrix normal distribution, with n × p mean matrix, M, n × n row structure, Ξ, p × p column structure, Σ, by writing Y ~ N_n,p(M, Ξ, Σ). Equivalently, vec(Y) ~ N_n·p[vec(M), Σ ⊗ Ξ], or vec(Y’) ~ N_n·p[vec(M’), Ξ ⊗ Σ. Both Ξ and Σ are required to be symmetric and positive symmetric and semi-definite.

A reproductive property of a matrix normal will be used repeatedly. For constants A, (n_* × n), B (p × p_*), and C (n_* × p_*), it follows that AYB + C ~ N_n*,p* (AMB + C, AΞA’ B’ΣB), Either the original or transformed distribution may be singular, depending on the combination of ranks of A, B, Ξ and Σ.

Following Arnold (1981, pp. 314–323), if Y ~ N_n,p(M, I, Σ), then Y’Y is described as following a Wishart distribution, written Y’Y ~ W_p(n, Σ, M’M). Many variations occur, depending on the relative sizes of p and n, as well as the ranks of Σ and M. If M = 0 then write W_p(n, Σ) to indicate a central Wishart.

Proof of Theorem 1

The following assumptions suffice to prove Theorem 1. The n × p random matrix Y has independent and identically distributed rows such that [row_i (Y)]’ ~ N_p(μ, Σ), with Σ = F_ΣF’_Σ, a p × p, symmetric, and positive definite matrix. The corresponding estimate is $\widehat{\Sigma }$. The functions x_I = [(p−1)r_I+1] and x_α = [1−r_α(p−1)/p]⁻¹ are functions of −(p−1)⁻¹ < r_I < 1 and −∞ < r_α < 1, while for $c\in \{\alpha ,\mathrm{I}\},D\left(x_c\right)=1_p^{\prime }\left(\nu \widehat{\Sigma }\right)1_p-x_c\mathrm{tr}\left(\nu \widehat{\Sigma }\right)$ (see equations 4–6).

The assumptions have the following immediate implications. With ν = n − 1 > p, the estimated covariance matrix, $\widehat{\Sigma }$, is such that $\nu \widehat{\Sigma }\sim {\mathcal{W}}_p(\nu ,\Sigma )$. A lemma in Glueck and Muller (1998) ensures that for any such $\widehat{\Sigma }$ there exists a ν × p matrix Y₀ ~ N_ν,p(0, I_ν, Σ) with ${\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0=\nu \widehat{\Sigma }$. The spectral decomposition allows writing Σ = V_ΣDg(λ_Σ)V’_Σ, with V_ΣV’_Σ = V’_ΣV_Σ = I_p. Also F_Σ = V_ΣDg(λ_Σ)^1/2 and Σ = F_ΣF’_Σ. The matrices V_Σ, Dg(λ_Σ) and F_Σ are p × p and full rank.

Proposition 1

Let V₁ = [v₀ V_⊥ ], with v₀ = 1_p p^−1/2. Also let V_⊥ be a p × (p − 1) matrix such that V’_⊥V_⊥ = I_p−1 and V’_⊥1_p = 0_p−1. For c ∈ {α, I}, A_1c = (1_p1’_p − x_cI_p) is p × p, symmetric and full rank, with one positive eigenvalue (p − x_c) and p − 1 negative eigenvalues of −x_c. Corresponding orthonormal eigenvectors are v₀ and V_⊥. Also A_1c = V₁Dg[(p − x_c), −x_c1_p−1]V’₁, with V’₁V₁ = I_p.

Proof of Proposition 1

A_1c is a difference of p × p matrices and A’_1c = (1_p1’_p − x_cI_p)’ = A_1c. The fact that V’₁V₁ = I_p follows from the definitions of v₀ and V_⊥. It is easy to directly verify that A_1cv₀ = (p − x_c)v₀ and that A_1cV_⊥ = −x_cV_⊥, which proves the eigenvalue and eigenvector properties. The restriction −(p − 1)⁻¹ < r_I < 1 ensures (p − x_I) > 0 and x_I > 0. It also implies −∞ < r_α < 1, which ensures (p − x_α) > 0 and x_α > 0.

Proposition 2

For c ∈ {α, I}, A_2c = F’_ΣA_1cF_Σ is p × p, symmetric full rank, with one strictly positive eigenvalue, λ_2c,1, and p − 1 strictly negative eigenvalues, {λ_2c,2, … , λ_2c,p}.

Proof of Proposition 2

As a product of full rank p × p matrices, A_2c is p × p and full rank. Also A’_2c = (F’_ΣA_1cF_Σ)’ = A_2c. Hence the spectral decomposition may be written A_2c = V_2cDg(λ_2c)V’_2c. If $\mathbf{T}={\mathbf{F}}_{\Sigma }^{-1}{\mathbf{V}}_1$ then

$$\begin{array}{cc}\hfill {\mathbf{T}}^{\prime }{\mathbf{A}}_{2c}\mathbf{T}& ={\mathbf{T}}^{\prime }\left({\mathbf{F}}_{\Sigma }^{\prime }{\mathbf{A}}_{1c}{\mathbf{F}}_{\Sigma }\right)\mathbf{T}\hfill \\ \hfill & ={\left({\mathbf{F}}_{\Sigma }^{-1}{\mathbf{V}}_1\right)}^{\prime }\left[\right({\mathbf{F}}_{\Sigma }^{\prime }{\mathbf{V}}_1\left)\mathrm{Dg}\right[(p-x_c),x_c{1}_{p-1}\left]\right({\mathbf{V}}_1^{\prime }{\mathbf{F}}_{\Sigma }\left)\right({\mathbf{F}}_{\Sigma }^{-1}{\mathbf{V}}_1)\hfill \\ \hfill & =\mathrm{Dg}\left[\right(p-x_c),-x_c{1}_{p-1}].\hfill \end{array}$$ (A21)

This demonstrates that A_2c and Dg[(p−x_c), −x_c1_p−1] are congruent. Consequently Sylvester’s Law of Inertia (Lancaster, 1969, p. 90) allows concluding that A_2c has one positive and p − 1 negative eigenvalues.

Proposition 3

$\mathrm{Pr}\{{\widehat{\rho }}_c\le r_c\}=\mathrm{Pr}\left\{D\right(x_c)\le 0\}$.

Proof of Proposition 3

$$\begin{array}{cc}\hfill \mathrm{Pr}\{{\widehat{\rho }}_{\mathrm{I}}\le r_{\mathrm{I}}\}& =\mathrm{Pr}\left\{\frac{[1_p^{\prime }\widehat{\Sigma }{1}_p-\mathrm{tr}(\widehat{\Sigma }\left)\right]∕\left[p\right(p-1\left)\right]}{\mathrm{tr}\left(\widehat{\Sigma }\right)∕p}\le r_1\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{1_p^{\prime }\widehat{\Sigma }{1}_p∕\mathrm{tr}\left(\widehat{\Sigma }\right)-1\le (p-1)r_{\mathrm{I}}\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\left(\nu 1_p^{\prime }\widehat{\Sigma }{1}_p\right)∕\left[\nu \mathrm{tr}\right(\widehat{\Sigma }\left)\right]\le x_{\mathrm{I}}\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{1_p^{\prime }{\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0{1}_p-x_{\mathrm{I}}\mathrm{tr}\left({\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0\right)\le 0\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{D\right(x_{\mathrm{I}})\le 0\},\hfill \end{array}$$ (A22)

and

$$\begin{array}{cc}\hfill \mathrm{Pr}\{{\widehat{\rho }}_{\alpha }\le r_{\alpha }\}& =\mathrm{Pr}\left\{[1-\mathrm{tr}(\widehat{\Sigma })∕1_p^{\prime }(\widehat{\Sigma }\left)1_p\right]p∕(p-1)\le r_{\alpha }\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{-\left[\nu \mathrm{tr}\right(\widehat{\Sigma }\left)\right]∕\left(\nu 1_p^{\prime }\widehat{\Sigma }{1}_p\right)\le \left[r_{\alpha }\right(p-1)∕p-1]\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{1_p^{\prime }{\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0{1}_p{x}_{\alpha }^{-1}-\mathrm{tr}\left({\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0\right)\le 0\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{1_p^{\prime }{\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0{1}_p-x_{\alpha }\mathrm{tr}\left({\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0\right)\le 0\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{D\right(x_{\alpha })\le 0\}.\hfill \end{array}$$ (A23)

Proposition 4

$D\left(x_c\right)={\lambda }_{2c,1}{X}_{c1}-{\sum }_{j=2}^p\mid {\lambda }_{2c,j}\mid X_{\mathit{cj}}$, with X_cj ~ χ²(ν), independently of X_cj’ if j ≠ j’.

Proof of Proposition 4

The fact that tr(AB) =tr(BA), when the matrices conform, allows writing

$$\begin{array}{cc}\hfill \mathrm{Pr}\left\{D\right(x_c)\le 0\}& =\mathrm{Pr}\{1_p^{\prime }{\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0{1}_p-x_c\mathrm{tr}({\mathbf{Y}}_0^{\prime }{\mathbf{Y}}_0)\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\mathrm{tr}\right({\mathbf{Y}}_0{1}_p{1}_p^{\prime }{\mathbf{Y}}_0^{\prime })-x_c\mathrm{tr}({\mathbf{Y}}_0{\mathbf{Y}}_0^{\prime })\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\mathrm{tr}\right[{\mathbf{Y}}_0(1_p{1}_p^{\prime }-x_c{\mathbf{I}}_p){\mathbf{Y}}_0^{\prime }]\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\mathrm{tr}\right({\mathbf{Y}}_0{\mathbf{A}}_{1c}{\mathbf{Y}}_0^{\prime })\le 0\}.\hfill \end{array}$$ (A24)

If Z₁ ~ N_ν,p(0, I_ν, I_p) then Y₀ = Z₁F’_Σ. Note that Z₁ = {z_{1,i j}} is a collection of independent standard Gaussian variables. With V_2c the orthonormal eigenvectors of A_2c, define Z_2c = Z₁V_2c, with Z_2c ~ N_ν,p(0, I_ν, I_p). Therefore

$$\begin{array}{cc}\hfill \mathrm{Pr}\left\{D\right(x_c)\le 0\}& =\mathrm{Pr}\left\{\mathrm{tr}\right[{\mathbf{Z}}_1\left({\mathbf{F}}_{\Sigma }^{\prime }{\mathbf{A}}_{1c}{\mathbf{F}}_{\Sigma }\right){\mathbf{Z}}_1^{\prime }]\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\mathrm{tr}\right[{\mathbf{Z}}_1\left({\mathbf{V}}_{2c}\mathrm{Dg}\right({\lambda }_{2c}\left){\mathbf{V}}_{2c}^{\prime }\right){\mathbf{Z}}_1^{\prime }]\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\mathrm{tr}\right[{\mathbf{Z}}_{2c}\mathrm{Dg}\left({\lambda }_{2c}\right){\mathbf{Z}}_{2c}^{\prime }]\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\mathrm{tr}\right[{\mathbf{Z}}_{2c}^{\prime }{\mathbf{Z}}_{2c}\mathrm{Dg}\left({\lambda }_{2c}\right)]\le 0\}.\hfill \end{array}$$ (A25)

A diagonal element of Z’_2cZ_2c is z’_2c,jz_2c,j, with z_2c,j the (ν × 1) column j of Z_2c. Using the fact that postmultiplying by a diagonal matrix scales the columns allows writing

$$\begin{array}{cc}\hfill \mathrm{PR}\left\{D\right(x_c)\le 0\}& =\mathrm{Pr}\left\{\mathrm{tr}\right[{\mathbf{Z}}_{2c}^{\prime }{\mathbf{Z}}_{2c}\mathrm{Dg}\left({\lambda }_{2c}\right)]\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\sum _{j=1}^p{\lambda }_{2c,j}{\mathbf{z}}_{2c,j}^{\prime }{\mathbf{z}}_{2c,j}\le 0\right\}.\hfill \end{array}$$ (A26)

The independent standard Gaussian nature of the elements of Z_2c allows concluding that

$$X_{\mathit{cj}}={\mathbf{z}}_{2c,j}^{\prime }{\mathbf{z}}_{2c,j}\sim {\chi }^2\left(\nu \right),$$ (A27)

with X_cj independent of X_cj’ if j ≠ j’. Without loss of generality, assume that λ_2c,1 is the single positive eigenvalue of A_2c. The proof is completed by splitting the summation:

$$\mathrm{Pr}\left\{D\right(x_c)\le 0\}=\mathrm{Pr}\left\{{\lambda }_{2c,1}{X}_{c1}-\sum _{j=2}^p\mid {\lambda }_{2c,j}\mid X_{\mathit{cj}}\le 0\right\}.$$ (A28)

Proof of Corollary 1

If Σ is compound symmetric then the eigenvectors of A_1c and Σ coincide, which implies V’₁V_Σ = V’_ΣV₁ = I_p. In turn,

$$\begin{array}{cc}\hfill {\mathbf{A}}_{2c}& ={\mathbf{F}}_{\Sigma }^{\prime }{\mathbf{A}}_{1c}{\mathbf{F}}_{\Sigma }\hfill \\ \hfill & ={\left[{\mathbf{V}}_{\Sigma }\mathrm{Dg}{\left({\lambda }_{\Sigma }\right)}^{1∕2}\right]}^{\prime }\left[{\mathbf{V}}_1\right[(p-x_c),-x_c{1}_{p-1}\left]{\mathbf{V}}_1^{\prime }\right]\left[{\mathbf{V}}_{\Sigma }\mathrm{Dg}{\left({\lambda }_{\Sigma }\right)}^{1∕2}\right]\hfill \\ \hfill & =\mathrm{Dg}{\left({\lambda }_{\Sigma }\right)}^{1∕2}\mathrm{Dg}\left[\right(p-x_c),-x_c{1}_{p-1}]\mathrm{Dg}{\left({\lambda }_{\Sigma }\right)}^{1∕2}\hfill \\ \hfill & =\mathrm{Dg}{[{\tau }_1,{\tau }_2{1}_{p-1}]}^{1∕2}\mathrm{Dg}\left[\right(p-x_c),-x_c{1}_{p-1}]\mathrm{Dg}{[{\tau }_1,{\tau }_2{1}_{p-1}]}^{1∕2}\hfill \\ \hfill & =\mathrm{Dg}\left[{\tau }_1\right(p-x_c),-{\tau }_2{x}_c{1}_{p-1}].\hfill \end{array}$$ (A29)

If $X_{c+}={\sum }_{j=2}^p{X}_{\mathit{cj}}$ then X_c+ ~ χ²[ν(p − 1)]. Furthermore

$$\begin{array}{cc}\hfill \mathrm{Pr}\left\{D\right(x_c)\le 0\}& =\mathrm{Pr}\left\{{\tau }_1(p-x_c)X_{c1}-{\tau }_2{x}_c\sum _{j=2}^p{X}_{\mathit{cj}}\le 0\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{{\tau }_1\right(p-x_c)X_{c1}-{\tau }_2{x}_c{X}_{c+}\le 0\}\hfill \\ \hfill & =\mathrm{Pr}\left\{\frac{X_{c1}∕\nu }{X_{c+}∕\left[\nu \right(p-1\left)\right]}\le \frac{{\tau }_2(p-1)x_c}{{\tau }_1(p-x_c)}\right\}\hfill \\ \hfill & =F_F\left[\frac{{\tau }_2(p-1)x_c}{{\tau }_1(p-x_c)};\nu ,\nu (p-1)\right]\hfill \\ \hfill & =1-F_F\left[\frac{{\tau }_1}{{\tau }_2}\frac{(p-x_c)}{(p-1)x_c};\nu (p-1),\nu \right].\hfill \end{array}$$ (A30)

Note the identity $F_F^{-1}[q;\nu ,\nu (p-1\left)\right]=1∕F_F^{-1}[1-q;\nu (p-1),\nu ]$.