Variability in Cadence During Forced Cycling Predicts Motor Improvement in Individuals With Parkinson’s Disease

Abstract

Variability in severity and progression of Parkinson’s disease symptoms makes it challenging to design therapy interventions that provide maximal benefit. Previous studies showed that forced cycling, at greater pedaling rates, results in greater improvements in motor function than voluntary cycling. The precise mechanism for differences in function following exercise is unknown. We examined the complexity of biomechanical and physiological features of forced and voluntary cycling and correlated these features to improvements in motor function as measured by the Unified Parkinson’s Disease Rating Scale (UPDRS). Heart rate, cadence, and power were analyzed using entropy signal processing techniques. Pattern variability in heart rate and power were greater in the voluntary group when compared to forced group. In contrast, variability in cadence was higher during forced cycling. UPDRS Motor III scores predicted from the pattern variability data were highly correlated to measured scores in the forced group. This study shows how time series analysis methods of biomechanical and physiological parameters of exercise can be used to predict improvements in motor function. This knowledge will be important in the development of optimal exercise-based rehabilitation programs for Parkinson’s disease.

I. Introduction

Parkinson’s disease (PD), which affects nearly 1.5 million Americans [1], is a progressive neurological disorder that is characterized by the loss of dopaminergic neurons in the brainstem. As PD progresses, the combined motor (e.g., tremor, bradykinesia, rigidity, posture, and gait disorders) and nonmotor symptoms (e.g., cognitive deficits, depression) often lead to decreased independence and increased reliance on others for activities of daily living. Dopaminergic drugs (e.g., levodopa) reduce tremor, bradykinesia, and rigidity symptoms but do not slow down the progression of the disease. As medication dose levels increases over time, motor fluctuations and dyskinesia often develop. Furthermore, these medications are costly and can cause side effects such as nausea, orthostatic hypotension, and drowsiness [2]. There is a need for additional therapies that improve motor function. Exercise and movement therapies have been shown to benefit individuals with PD but there is little consensus on the optimal mode or intensity [3]–[5].

We previously developed a novel approach to increase exercise intensity in individuals with PD called forced exercise [6]. This approach used a stationary tandem bicycle and an able-bodied cyclist to assist individuals with PD to pedal at a cadence [revolutions per minute (rpm)] between 80–90 rpm. This cadence was roughly 30% faster than they were able to pedal on their own at a self-selected rate that was determined during baseline evaluation. Crank-based powermeters (Schoberer Rad Meßtechnik [SRM]) measured the work of the individuals with PD during each exercise session. Forced exercise results in a significant improvement in motor symptoms as measured with the Unified Parkinson’s Disease Rating Scale (UPDRS) Motor III. This clinical scale evaluates the degree of tremor, bradykinesia, rigidity, and posture/gait difficulties in individuals with PD. However, individuals that cycled on a single stationary ergometer at similar aerobic intensity, but at a self-selected pedaling rate (voluntary exercise) showed no change in UPDRS Motor III scores.

The goal of this study was to examine the complexity of biomechanical and physiological features of forced and voluntary cycling and to relate these features to improvements in motor function as measured by the UPDRS Motor III scale. We hypothesize that temporal variability or lack of predictability in cadence during forced cycling can be used to accurately predict resulting improvements in UPDRS Motor III scores.

Subject and trainer data (power, heart rate, and cadence), collected previously from exercise training sessions using a stationary tandem bicycle in our previous study [6], were examined using sophisticated signal processing techniques: approximate entropy (ApEn), sample entropy (SampEn), and spectral entropy (SpecEn). ApEn is a “regularity statistic” that quantifies the unpredictability of temporal fluctuations in a time series such as an instantaneous heart rate time series, HR(i). The presence of repetitive temporal patterns in a time series renders it more predictable than a time series in which such patterns are absent. ApEn quantifies the likelihood that “similar” patterns of observations will not be followed by additional “similar” observations. A time series containing many repetitive patterns has a relatively small ApEn; a less predictable (i.e., more random or less time-correlated) time series will have a greater ApEn. SampEn is a modification of ApEn [7] that removes the potential bias in ApEn [8], eliminates self-matches in the computation, reduces computational complexity, and can be applied to short time series data. Both ApEn and SampEn quantify the predictability (or regularity) in a time series, and are useful in quantifying differences in health and disease [7]–[11]; whereas SpecEn quantifies the distribution of frequency content in a time series.

More sophisticated analysis of the exercise performance variables across groups and throughout exercise sessions will aid in identifying and quantifying time and frequency domain features that may be responsible for the improved motor performance observed after forced exercise. Our previous studies showed that behavioral effects of forced and voluntary exercise were dramatically different [6]. A precise understanding of specific and differentiating characteristics between forced and voluntary exercise will provide important guidance in the development of more cost and time effective methods of delivering forced exercise than tandem cycling, such as motorized single bikes that will not require a trainer [12].

II. Materials and Methods

A. Forced and Voluntary Cycling Data Collection

Ten individuals with idiopathic Parkinson’s disease were assigned to one of two groups: forced (tandem) or voluntary (single) cycling. Both groups completed 24 1-h exercise sessions (three per week) over an eight-week period. In the forced cycling group, the PD subject was assisted by an able-bodied cyclist and Certified Personal Trainer riding on the front of a stationary tandem bike. The trainer had the objective of maintaining bike operation at an accelerated cadence rate between 80 and 90 rpm. The voluntary cycling group pedaled a stationary single bike (SRM indoor trainer, Jülich, Germany) at a self-selected cadence of roughly 60 rpm. The pedal cadence and power performed by the subject and the trainer on the tandem and on the single bicycle were measured using SRM powermeters. A Polar heart rate monitor (Polar Electro, Lake Success, NY, USA) was used to collect heart rate data. Heart rate (HR), cadence, and power variables were averaged for 20–24 sessions per subject. In order to examine the raw data for single (voluntary) and tandem (forced) rider exercise tests, the mean and standard deviation of the “heart rate,” “power,” and “cadence” signals for all tests were calculated. Approximately 20 or more data sets for each person were collected for exercise sessions across the eight-week intervention. Additional methodological details and photos of the tandem setup can be found in Ridgel et al. 2009 [6]. The Cleveland Clinic Institutional Review Board approved this project.

B. Motor Function Assessment

The Unified Parkinson’s Disease Rating Scale (UPDRS) Part III motor exam was administered while individuals were “off” anti-Parkinsonian medication for 12 h. Assessments were performed prior to and after completion of the eight week exercise intervention. The difference in UPDRS Motor III scores between these two time periods was calculated and was used in the model (described below). A positive score represents improvement while a negative score indicates worsening of motor symptoms.

C. Biomechanical and Physiological Feature Analysis

Three main parameters approximate entropy (ApEn), sample entropy (SampEn), and spectral entropy (SpecEn) for “heart rate,” “power,” and “cadence” signals were computed in all data sets for each person. These parameters were used to quantify complexity in terms of both temporal and frequency domain patterns of variability. The values for ApEn and SampEn computed for the dataset are approximately the same, so further analysis focused on the ApEn computations. The mean of these parameters for all exercise sessions were computed for the single (voluntary) and tandem (forced) groups.

Approximate entropy (ApEn) was used to quantify the degree of temporal regularity or predictability in the time series data for power, heart rate, and cadence. The algorithm for computing ApEn has been published elsewhere [8], [9]. Here, we provide a brief summary of the calculations, as applied to a time series of instantaneous heart rate measurements, HR(i). Given a sequence S_N, consisting of N instantaneous heart rate measurements HR(1), HR(2),…, HR(N), and a time delay τ=1, we chose values for two input parameters, m and r, to compute the approximate entropy, ApEn(S_N, m, r), of the time series. The parameter m specifies the pattern length, and the parameter r defines the criterion of similarity. We denoted a subsequence (or pattern) of m heart rate measurements, beginning at measurement i within S_N, by the vector p_m(i). Two patterns, p_m(i) and p_m(j), are similar if the difference between any pair of corresponding measurements in the patterns is less than the tolerance r, i.e., if

$$\mid HR(i+k)-HR(j+k)\mid <r\text{for}0\le k<m.$$

Now consider the set P_m of all patterns of length m [i.e., p_m(1), p_m(2),…, p_m(N − m + 1)], within S_N. We now defined

$$C_{im}(r)=\frac{n_{im}(r)}{N-m+1}$$

where n_im(r) is the number of patterns in P_m that are similar to p_m(i) (given the similarity criterion r). The quantity C_im(r) is the fraction of patterns of length m that resemble the pattern of the same length that begins at interval i. We can calculate C_im(r) for each pattern in P_m, and we define C_m(r) as the mean of these C_im(r) values. The quantity C_m(r) expresses the prevalence of repetitive patterns of length m in S_N. Finally, we define the ApEn of S_N, for patterns of length m and similarity criterion r, as

$$\mathit{ApEn}(S_N,m,r)=ln\left[\frac{C_m(r)}{C_{m+1}(r)}\right].$$

Note, ApEn(S_N, m, r) is the natural logarithm of the relative prevalence of repetitive patterns of length m compared with those of length m + 1.

ApEn estimates the logarithmic likelihood that the next intervals after each of the patterns will differ (i.e., that the similarity of the patterns is mere coincidence and lacks predictive value). Smaller values of ApEn imply a greater likelihood that similar patterns of measurements will be followed by additional similar measurements. If the time series is highly irregular, the occurrence of similar patterns will not be predictive for the following measurements, and ApEn will be relatively large. It should be noted that ApEn has significant weaknesses, notably its strong dependence on sequence length and its poor self-consistency (i.e., the observation that ApEn for one data set is larger than ApEn for another for a given choice of m and r, does not necessarily, hold true for other choices of m and r).

Sample entropy (SampEn) was used to quantify the complexity of a time series using a measure of predictability that is very similar to ApEn. Spectral entropy (SpecEn) was used to measure the complexity of time series data in the frequency domain and was used to quantify frequency domain variability in power by computing the power-spectral-density (PSD) of the time series. The PSD was normalized to produce a probability-like density function and transformed with the Shannon function as follows.

1. Compute the power spectral density (PSD) of the signal, P(f).

2. Normalize the power spectrum

   $$Q(f)=\frac{P(f)}{\sum P(f)}.$$
3. Compute the Shannon function

   $$H(f)=Q(f)log\left(\frac{1}{Q(f)}\right).$$
4. Compute the spectral entropy (SpecEn)

   $$\mathit{SpecEn}=\sum \frac{H(f)}{log(N)}$$

   where N is the number of data points.

Statistical analysis, including linear regression, logistic regression and computation of the odds ratio, was used to investigate the relationship between the measures of exercise variability and the exercise related change in motor performance as measured by UPDRS Motor III scores. The data in Tables I and II were used to develop a multiple linear regression model (MLR) and apply logistic regression to determine the odds ratio for achieving a positive change in the UPDRS Motor III scores in each group. Each regression model has four independent variables: ApEn (heart-rate), ApEn (power), ApEn (cadence), and SpecEn (power), and one dependent variable: UPDRS score. The data was analyzed in two ways: first two separate MLR models were built, one model for the single sessions and one model for the tandem sessions (Table III) and then the data were combined into a single dataset and a single MLR model was built (Table IV). The residual values in Tables III and IV, and the predicted UPDRS values in Fig. 1 were obtained from MLR modeling using the “regress” function in MATLAB. The odds ratio is the ratio of the odds of an event occurring in one group to the odds of it occurring in another group. It is also used to refer to sample-based estimates of this ratio. The predicted UPDRS Motor III scores were obtained using MLR as described above. A Pearson product-moment correlation coefficient was computed to assess the relationship between the real and predicted values of UPDRS motor III scores.

TABLE I.

Mean and Variance for Power, Heart Rate, and Cadence Signals

Patient ID	Group	UPDRS changea	Heart rate		Power		Cadence
			Meanb	Stdev	Meanb	Stdev	Meanb	Stdev
1	Single	+9	100.86	3.24	42.07	9.27	58.35	6.95
2	Single	0	116.20	2.46	73.77	7.01	43.60	2.80
3	Single	−4.5	124.84	6.55	105.26	22.81	75.72	6.81
4	Single	−10	110.43	2.96	41.36	5.42	57.38	3.94
5	Single	−15	156.10	3.92	72.83	9.27	69.27	3.91
MEAN		−4.1	121.68		67.05		60.86
6	Tandem	+23	113.86	4.16	45.81	14.45	86.64	1.83
7	Tandem	+23	119.54	4.93	24.46	13.64	85.67	2.80
8	Tandem	+17	121.67	4.41	63.30	16.00	84.72	1.73
9	Tandem	+11.5	122.51	7.51	50.63	24.45	80.49	2.70
10	Tandem	+8.5	108.94	4.37	68.07	16.80	85.31	1.99
MEAN		16.6	117.30		50.45		84.56

^apositive change in UPDRS represents improvements in motor function

^bmean values were calculated over 20–24 exercise sessions per patient

TABLE II.

ApEn and SpecEn for Power, Heart Rate, and Cadence Signals

Patient ID	Group	UPDRS change	Power (ApEn)	Heart rate (ApEn)	Cadence (ApEn)	Power (SpecEn)
1	Single	+9	0.1379	0.4017	0.2048	0.1053
2	Single	0	0.2292	0.5366	0.5653	0.0782
3	Single	−4.5	0.2600	0.0924	0.1658	0.0854
4	Single	−10	0.4080	0.6235	0.4417	0.0913
5	Single	−15	0.2024	0.2974	0.5128	0.0843
MEAN		−4.1	0.2475	0.3903	0.3780	0.0889
6	Tandem	+23	0.0563	0.1932	1.0540	0.1072
7	Tandem	+23	0.0450	0.0961	1.0411	0.2190
8	Tandem	+17	0.0347	0.1997	1.2030	0.1050
9	Tandem	+11.5	0.0106	0.0878	0.7739	0.1663
10	Tandem	+8.5	0.0133	0.1498	0.9850	0.0990
MEAN		16.6	0.0319	0.1453	1.011	0.1393

TABLE III.

Regression Analysis Results for Single and Tandem Rider Tests

Patient ID	Group	UPDRS change	Residuals	P	P/(1-P) Odds Ratio	Exp(P/(1-P))
1	Single	+9	−0.7792	0.9999	1.7662e+004	Inf
2	Single	0	5.9906	0.0025	2.5021e−003	1.0025
3	Single	−4.5	3.3679	0.0004	3.8283e−004	1.0004
4	Single	−10	−2.7698	0.0007	7.2440e−004	1.0007
5	Single	−15	−4.9959	0.0000	4.5213e−005	1.0000
MEAN		−4.1	0.1627	0.2007	-	-
6	Tandem	+23	−0.2864	1.0000	1.2976e+010	Inf
7	Tandem	+23	−0.0502	1.0000	1.0246e+010	Inf
8	Tandem	+17	0.7353	1.0000	1.1579e+007	Inf
9	Tandem	+11.5	0.2011	1.0000	8.0734e+004	Inf
10	Tandem	+8.5	−0.6965	0.9999	9.8624e+003	Inf
MEAN		16.6	−0.0193	1.0	-	-

TABLE IV.

Combined Single and Tandem Rider Data Regression Analysis Results

Patient ID	Group	UPDRS change	Residuals	P	P/(1-P) Odds Ratio	Exp(P/(1-P))
1	Single	+9	5.6618	0.9657	2.8167e+001	1.7095e+012
2	Single	0	0.2101	0.4477	8.1054e−001	2.2491e+000
3	Single	−4.5	5.3617	0.0001	5.2132e−005	1.0001e+000
4	Single	−10	−0.0317	0.0000	4.6864e−005	1.0000e+000
5	Single	−15	−13.7226	0.2180	2.7877e−001	1.3215e+000
MEAN		−4.1	−0.5041	0.3263	-	-
6	Tandem	+23	10.3048	1.0000	3.2618e+005	Inf
7	Tandem	+23	1.0756	1.0000	3.3239e+009	Inf
8	Tandem	+17	1.9278	1.0000	3.5137e+006	Inf
9	Tandem	+11.5	−5.7279	1.0000	3.0337e+007	Inf
10	Tandem	+8.5	−5.0596	1.0000	7.7419e+005	Inf
MEAN		16.6	0.5041	1.0	-	-

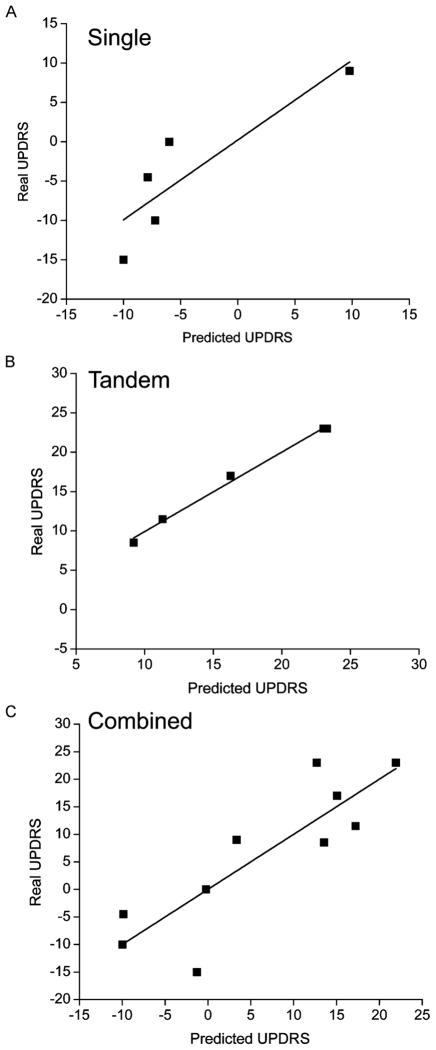
Fig. 1.

Real (measured) versus predicted UPDRS values. (A) Single (voluntary) exercise data. (B) Tandem (forced) data. (C) Combined single and tandem data. A multiple linear regression model was used to calculate predicted values of UPDRS. The model more accurately predicted UPDRS Motor III scores in the tandem (forced) group than in the single (voluntary) group. The combined model was inaccurate in predicting scores in both groups.

Dependent variables (e.g., heart rate, power, cadence, power ApEn, heart rate ApEn, cadence ApEn, power SpecEn) were compared between single and tandem groups using a one-way ANOVA (SPSS, Inc., ver. 18). Significance was set at P ≤ 0.05.

III. Results

There were no significant differences in heart rate and power between the two groups (Table I). However, the pedaling cadence showed a significant difference (F_1,8 = 17.8, P = 0.003) between the raw values in voluntary (60.8 ± 12.3 rpm) and forced (84.5 ± 2.4 rpm) groups. Cadence for the forced exercise sessions was higher than the voluntary sessions with less variability as quantified by the standard deviation.

For “SpecEn,” only the power signals are distinguishable between the single and tandem groups. Comparison of each variable shows clear differences. ApEn for the power in the single sessions (0.247 ± 0.10) is significantly greater (F_1,8 = 22.2, P = 0.002) than the ApEn for the power in the tandem sessions (0.032 ± 0.02). ApEn for the heart rate in single sessions (0.390 ± 0.09) is also significantly greater (F_1,8 = 6.51, P = 0.034) than the ApEn for the heart rate in the tandem group (0.145 ± 0.02). This suggests that the power and heart rate signals in the voluntary (single) group have greater variability (are less predictable) than the signals in forced (tandem) group. The results for the cadence signal are opposite; that is, the cadence signals for the single group (0.378 ± 0.18) show less variability (are more predictable) and are significantly less (F_1,8 = 35.05, P < 0.0001) than the cadence signals for tandem sessions (1.01 ± 0.15). Spectral entropy of the power (SpecEn) in the tandem group (0.139 ± 0.05) showed slightly greater, but not significant, variability (F_1,8 = 4.48, P = 0.67) than in the single sessions (0.089 ± 0.01).

Predicted values of UDPRS, using MLR analysis, are plotted against real (measured) values in Fig. 1. Four out of the five individuals who completed single (voluntary) sessions showed no improvement or worsening of UPDRS Motor III scores while one individual showed a slight improvement [Fig. 1(a)]. The MLR model is less accurate in individuals whose scores worsened. All participants who completed forced exercise sessions showed improvement in the UPDRS Motor III scores [Fig. 1(b)] and the model shows a more accurate prediction in this group. The combined model results in greater differences between the predicted and real scores for most subjects [Fig. 1(c)].

There was no significant correlation between the real and predicted UPDRS Motor III scores in the voluntary exercise (single) group (Fig. 2(a), r = 0.875, N = 5, P = 0.052). However, there was positive and significant correlation in the forced exercise (tandem) group (Fig. 2(b), r = 0.997, N = 5, P < 0.001). When the two groups were combined, there was also a significant and positive correlation between real and predicted UPDRS values (Fig. 2(c), r = 0.858, N = 10, P = 0.001).

Fig. 2.

Correlation analysis of real (measured) versus predicted UPDRS values. (A) Single (voluntary) exercise data. (B) Tandem (forced) data. (C) Combined single and tandem data. There was a positive and significant correlation of the real and predicted UPDRS Motor III scores in the tandem group but no correlation in the single group. Combined scores maintained a significant correlation between real and predicted scores.

IV. Discussion

Although many studies have documented the benefits of exercise, it is unclear what elements (i.e., dosage, intensity, intervention type) constitute an optimal exercise intervention for PD. Each individual with PD has different symptoms and capabilities that make it challenging to design a single rehabilitation program that is optimal for all. Furthermore, progression of the disease often requires reassessments and changes to rehabilitation programs.

This study reveals that pattern irregularity in HR and power is greater in the single sessions when compared to the tandem sessions, indicating that the trainer provides a “stabilizing” influence on the patient’s exercise intensity, while maintaining elevated cadence. The single PD rider has a tendency to introduce greater variability (less regular patterns) in power output, inducing greater fluctuations in HR, when compared to tandem PD riders. In contrast, the cadence signal shows greater variability during the tandem sessions. This variability is likely due to the inability of individuals with PD to maintain a constant high-speed pedal cadence. Furthermore, variability was also introduced when the able-bodied trainer was required to increase or decrease pedal speed to maintain the desired cadence. The single PD riders rode at a self-selected cadence and thus showed lower variability during exercise bouts.

This supports our hypothesis that temporal variability or lack of predictability (not quantified by conventional statistical parameters such as variance or coefficient of variation) in cadence during forced exercise can be used to accurately predict resulting improvements in UPDRS Motor III scores. Lastly, predicted UPDRS Motor III scores are highly correlated to measured scores in the tandem sessions. These data provide insight into how times series analysis methods can be applied to uncover potential features in the measured variables and how this information can be used to correlate exercise parameters with improved motor function.

A. Changes in the Complexity of Motor Output With PD

Typically, researchers use the mean and standard deviation or standard error of the mean to define variability in a dataset. These measures provide a description of the magnitude of the variability around a central point. However, the presence of certain patterns or shifts in patterns can often provide primary insight into health status or motor performance [13], [14]. Assessment of irregularities of serial data using entropy statistics has been shown to reveal subtle disruptions in movement patterns prior to changes in mean and variance.

Previous work has postulated that aging and disease are accompanied by reduction in the complexity of physiological and behavioral control [15], [16]. This loss of complexity can reduced the body’s ability to adapt to physiological stress. For example, Vaillancourt et al. [17] examined the ApEn of hand tremor during a grip force task in individuals with PD and healthy age-matched controls. They showed that tremor is less variable in PD than healthy controls and that there was a negative correlation between variability of tremor and severity of the disease, as measured by the UPDRS Motor III. This suggests that progression of PD results in decreased variability of motor output. In light of these findings, it is possible that exercise or movement training, that emphasizes complex and variable movements, could promote motor improvement in PD.

B. Role of Intensity and Complexity of Exercise in Improvements

Few other studies have correlated the biomechanics of exercise with improved function in PD. Abe et al. examined rotational velocities and relative phase during leg pedaling in individuals with PD and were able to divide their subjects into groups using cluster analysis [18], [19]. Each group showed distinctive clinical features, specifically the probability of freezing of gait.

Several studies have described how activity-dependent neuroplasticity of the motor cortex and basal ganglia could be affected by the intensity and complexity of motor training and exercise [20]–[27]. Body weight supported treadmill training (BWSTT) has been used to increase intensity of exercise by allowing individuals to walk faster than they are able over-ground. This paradigm uses a harness to support a small percentage of the body weight. After 24 sessions of BWSTT, subjects showed improved walking performance and UPDRS Motor III scores [24], [27], [28]. Furthermore, Fisher et al. documented lengthening of the cortical silent period using transcranial magnetic stimulation (TMS) after BWSTT but not after standard physical therapy [21]. The authors suggested that improvements after BWSTT was due to the fact that it allowed higher treadmill speed compared to walking without body weight support. These findings support the idea of dose-dependent benefits of exercise and suggest that high-intensity exercise can normalize corticomotor excitability in early PD.

In animal models of PD, high intensity treadmill running resulted in gait and balance improvements, as well as partial recovery of dopaminergic neurons after injection of the neurotoxin, MPTP [20], [26], [29], [30]. Animals that exercised on a running wheel at their own pace or those that did not exercise did not show similar improvements. In addition, Petzinger suggested that intensive treadmill running resulted in different neuroplastic changes within the basal ganglia between lesioned and nonlesioned animals [29]. Despite these promising studies, there is still much to be learned about the specific exercise parameters that can maximize motor improvement in PD.

C. Implications for Neurorehabilitation

Although high-intensity exercise can improve motor function in PD and animal models of PD, the mechanisms of this improvement are unclear. Understanding of potential mechanisms will be important in the development of additional rehabilitation paradigms that could benefit these individuals. It is possible that changes in proprioceptive input during a bout of tandem cycling provide complex and variable sensory feedback that increases cortical activation [3].

Accurate voluntary movements require somatosensory input from the periphery. Peripheral receptors, such as joint receptors, golgi tendon organs, muscle spindles, and cutaneous receptors, send feedback information from the limbs to the motor cortex. Several studies have identified proprioceptive impairment in PD, specifically in muscle spindle responses, load sensitivity, and kinesthesia [31]–[34]. However, levodopa does not appear to improve kinesthetic deficits in PD [35], [36] and has been associated with suppression of sensitivity to joint position [37]. Therefore, deficits in peripheral afferent input or in the cortical response to that input could affect motor output in individuals with PD.

During leg cycling, there are a number of proprioceptive signals including hip and knee joint angle, muscle length and force, as well as cutaneous input from the bottom of the foot [38]. Improvements in motor function and mobility after bouts of cycling in individuals with PD could be due to increases in afferent input to the cortex. Snijders et al. described a case in which an individual with PD presented with severe freezing of gait but was able to ride a bicycle [39], [40]. They suggested that forces transferred from the rotating pedals to the individual’s feet might provide tactile cues that trigger appropriate rhythmic movements to overcome freezing of gait. This suggests that activation of proprioceptors with a high frequency but variable pattern may be important for motor improvements in PD. Future studies should assess the role of proprioceptive input in motor improvements after forced cycling by altering or removing that input.

Nomenclature

UPDRS

Unified Parkinson’s Disease Rating Scale

Stdev

Standard deviation

ApEn

Approximate entropy

SpecEn

Spectral entropy

SampEn

Sample entropy

P

Probability of a 1 (the proportion of 1 s, the mean of Y)

P/(1 − P)

Odds ratio

EXPP/(1 − P)

Exponent of the odds ratio

RPM

Revolutions per minute

PSD

Power spectral density

SRM

Schoberer Rad Meßtechnik

BWSTT

Body weight supported treadmill training

Biographies

Angela L. Ridgel received the Ph.D. degree in biomedical sciences from Marshall University, Huntington, WV, USA. She completed her postdoctoral training in neurobiology at Case Western Reserve University, Cleveland, OH, USA, and in biomedical engineering at the Cleveland Clinic, Cleveland, OH, USA.

She is an Assistant Professor in Exercise Science at Kent State University, Kent, OH, USA. For the last nine years, she has been interested in how aging and neurological disorders limits movement in humans. Her laboratory examines the effects of exercise and motor rehabilitation therapies on motor function, cognition, and balance in Parkinson’s disease. She is currently funded through a NIH R21 grant.

Hassan Mohammadi Abdar (S’12) received the B.S. degree in electronic engineering and the M.S. degree in control engineering from K. N. Toosi University of Technology, Tehran, Iran. He is currently working toward the Ph.D. degree in systems and control engineering at Case Western Reserve University, Cleveland, OH, USA.

He has worked in industry for eight years in the area of embedded systems, industrial automation, and signal processing. He has been working on several research projects in the field of microgrid systems, grid-tie inverter, signal processing, and serial data communication at Case Western Reserve University.

Jay L. Alberts is the Director of the Cleveland Clinic Concussion Center and holder of the “Edward F. and Barbara A. Bell Family Endowed Chair.” He is Associate Staff in the Department of Biomedical Engineering and the Center for Neurological Restoration. He also holds appointments at the Functional Electrical Stimulation Center at the Louis Stokes VA Medical Center and in the Department of Biomedical Engineering at Case Western Reserve University. His research is focused on the role of the basal ganglia in movement control and the role of surgical and behavioral interventions on cognitive and motor performance.

Fred M. Discenzo received two B.S. degrees in mathematics, the M.S. degree in polymer physics, and the Ph.D. degree in systems and control engineering from Case Western Reserve University, Cleveland, OH, USA.

He is the Manager of Rockwell Automation’s Advanced Technology Laboratory, Cleveland, OH, USA, and is a Rockwell Automation Fellow. He currently holds over 60 U.S. patents and has published many papers spanning artificial intelligence, machinery diagnostics, sensors, control, power scavenging, and artificial neural networks.

Dr. Discenzo represents Rockwell Automation on various university/industry advisory committees, he serves on multiple conference committees, and is a board member of the Machinery Failure Prevention Technology (MFPT) Society.

Kenneth A. Loparo (F’99) is the Nord Professor of Engineering in the Case School of Engineering, Case Western Reserve University, Cleveland, OH, USA. He has academic appointments in the Departments of Biomedical Engineering, Electrical Engineering and Computer Science, and Mechanical and Aerospace Engineering. His research interests include stability and control of nonlinear and stochastic systems; nonlinear filtering with applications to monitoring, fault detection, diagnosis and reconfigurable control; information theory aspects of stochastic and quantized systems with applications to adaptive and dual control; the design of digital control systems; and advanced signal processing techniques for monitoring and tracking of physiological behavior.