Abstract
Objective
To establish a simple two-compartment model for glomerular filtration rate (GFR) and renal plasma flow (RPF) estimations by dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI).
Materials and Methods
A total of eight New Zealand white rabbits were included in DCE-MRI. The two-compartment model was modified with the impulse residue function in this study. First, the reliability of GFR measurement of the proposed model was compared with other published models in Monte Carlo simulation at different noise levels. Then, functional parameters were estimated in six healthy rabbits to test the feasibility of the new model. Moreover, in order to investigate its validity of GFR estimation, two rabbits underwent acute ischemia surgical procedure in unilateral kidney before DCE-MRI, and pixel-wise measurements were implemented to detect the cortical GFR alterations between normal and abnormal kidneys.
Results
The lowest variability of GFR and RPF measurements were found in the proposed model in the comparison. Mean GFR was 3.03±1.1 ml/min and mean RPF was 2.64±0.5 ml/g/min in normal animals, which were in good agreement with the published values. Moreover, large GFR decline was found in dysfunction kidneys comparing to the contralateral control group.
Conclusion
Results in our study demonstrate that measurement of renal kinetic parameters based on the proposed model is feasible and it has the ability to discriminate GFR changes in healthy and diseased kidneys.
Introduction
Glomerular filtration rate (GFR) is the most critical functional parameter of the kidney [1], [2]. Inulin clearance is widely considered the gold standard in quantification of GFR. However, it is not routinely being used in the clinical setting, since it requires multiple blood and urine samples over a period of several hours and could not obtain single-kidney GFR. Traditional radioactive labeled methods are invasive and result in radiation burden. Therefore, it is important to establish a simple new method for quantitative measurements of GFR to monitor renal function.
Recently, on the basis of dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI), functional parameters could be estimated in a wide range of applications including breast imaging [3], brain imaging [4], and abdominal imaging [5]. In order to overcome some mentioned limitations of GFR measurement, several compartment models based on DCE-MRI have been proposed. Patlak-Rutland method was introduced to evaluate glomerular filtration rate, neglecting the outflow of contrast agent from the tubular compartment [6]. Under this assumption, it was often applied to the whole kidney to ensure the tracer stays in the region of interest (ROI) [7], [8], which, however, could not directly reflect GFR since the glomerular filtration predominantly exist in renal cortex [9]–[12].
Subsequently, a two-compartment model with constant dispersion of contrast agent and the consideration of outflow was proposed [13]. However, lacking of accurate tubule parameters estimation was supported and underestimated GFR was found. Later, a similar model was employed to measure GFR in patients by using the whole kidney ROI, which was just simplified by ignoring the dispersion effect in the original two-compartment model [14]. Then, a separable compartment model, of which the time delay of contrast was assumed to be zero [15], provided estimated parameters which were analogues to those of the original two-compartment model [13].
Besides these models, three-compartment models were also proposed for GFR estimations [16], [17]. Nevertheless, the variability of GFR measurement was more pronounced than that of two-compartment models [18]. In addition, the assessment of GFR was sensitive to the segmentation of cortex and medulla, which may result in an unstable measurement [19]. The increase of compartment number would result in an expense of system complexity, and a simple cortical compartment model is alternative because the glomerular filtration occurs in the cortex. We borrowed Zhang et al's idea of using impulse residue function to improve the robustness in GFR measurements [17], and combine it into a two-compartment model.
In this study, a modified two-compartment model was proposed by introducing the impulse residue function to obtain effective estimations of GFR and renal plasma flow (RPF) from DCE-MRI. The advantage of the new model in GFR or RPF measurements over other published models was investigated in Monte Carlo simulation under different noise levels. Then, quantitative estimations were performed in healthy rabbits by using our new model. Furthermore, the proposed model was employed to measure GFR changes in rabbits with unilateral ischaemic acute kidney injury (AKI) to test its validity. Pixel-wise calculation was performed and the cortical GFR results were compared with its contralateral kidney. The major focus of this study was put on the sufficient robustness in kinetic parameters estimation and the ability to discriminate healthy and diseased kidneys.
Materials and Methods
Animals
This study was approved by the Ethics Committee on animal care and use of Peking University First Hospital (Ethic number: 10/235). Eight male New Zealand white rabbits (weighing from 2.9 kg to 3.5 kg) underwent this experiment (n = 6 for normal kidney experiment; n = 2 for dysfunction kidney experiment). All the rabbits were housed in individual cages at room temperature, and free fed with standard feed and tap water, and stopped 12 hours before experiments. Before DCE-MRI, pentobarbital sodium (0.5 ml/kg body mass) was injected through the marginal ear vein with a 24-gauge catheter for anesthetization. All the animals were placed in a supine position in a fixed device to limit abdominal motion during scans. Heart rate was continuously monitored by using a photopulse sensor of the MR scanner during acquisitions.
In the experiment of dysfunction kidneys, two rabbits (2.9 kg and 3.3 kg) were implemented a unilateral renal ligation surgery procedure after anesthetization. After a midline incision, the aorta of left kidney was clamped for 45 minutes to induce ischaemic acute kidney injury. The right kidney was normal and regarded as the control group. After surgery, we sew up the incision with sewing wires and give analgesic treatment to minimize suffering. The animals' body temperature was maintained about 38° by using a hotplate during surgery and exposed to an infrared light in the box before MR scans. Two days later, the DCE-MRI experiment was implemented. These two injured rabbits (acute ischemia in the left kidney) were scanned together with all the other six normal rabbits.
MRI
The abdomen dynamic images were acquired on a whole body 3.0 T MR scanner (Signa Excite; GE Medical Systems, Milwaukee, WI, USA) with TORSOPA coil. Before each DCE-MRI scan, T1 measurement was conducted firstly with a three-dimensional spoiled gradient-recalled echo sequence. T1 mapping was measured by using variable flip angles method [20], and the imaging parameters are as follows: TR = 6.2 msec, TE = 2.9 msec, flip angle = [3], [9], [20]°, slices = 16, slice thickness = 4.0 mm, matrix = 256×256, FOV = 200×200 mm2. Then, DCE-MRI scans were performed by a three-dimensional fast spoiled gradient recalled echo sequence with the following parameters: TR = 3.3 msec, TE = 1.3 msec, flip angle = 15°, FOV = 160×160 mm2, ASSET = 2, acquisition matrix was 128×128 and interpolated to 256×256, slice thickness = 4.0 mm, slice number = 16, bandwidth was 488 Hz/pixel, and acquisition time was 3.0 s/frame. Five precontrast frames were obtained before bolus injection, then, an administration of 0.05 mmol/kg of Gd-DTPA (Omniscan; GE Healthcare Ireland, IDA Business Park, Carrigtohill, Co.Cork) was performed with a venous cannula at a rate of 2 ml/s. 5 ml of saline was immediately flushed in and totally 100 frames were obtained in about five minutes.
Data Analysis
Renal parenchyma and the aorta were automatically segmented from the surrounding tissue with a Level-Set framework [21]. The parameters used in segmentation were: alpha = 0.04, a parameter that controls the weight of smoothing item of the image features; and iteration was set to 60, such values were sufficient for detection of kidney outline in this experiment. Afterwards, dynamic images of the segmented regions were registrated to reduce motion [22]. Then, a slice which covering the largest possible parenchyma during corticomedullary phase was used for cortical ROI drawing to obtain the tissue signal intensity curves. The size of ROIs for all the kidneys was 590 pixels in average. The arterial input function (AIF) was determined by drawing ROI in the slice that a branch of renal artery was obviously seen, that is, the ROI was placed within the aorta distal to the branch of the renal artery. To improve the robustness of AIF and reduce the inflow artifacts, one more slice above was also selected for averaging. A 3×3 pixel size ROI was used. Furthermore, the tail of the AIF was fit to a biexponential decay to reduce respiratory motion related noise [23].
Then, signal intensity curves were converted into gadolinium concentrations with the T1 values from T1 mapping [23], under the assumption that a linear relationship between relaxation rate changes and [Gd] concentrations according to the following equation:
 |
(1) |
where, 1/T1pre and 1/T1post are the contrast relaxation rates before and after bolus injection. r1 is the specific T1 relaxivity at physiological temperatures in plasma (4.1 L s−1 mmole−1) [24], [25].
The New Compartment Model
The proposed model in this study describes two compartments: the intrarenal arteries and glomerular vessels (A) and the renal tubules in cortex (T), with tracer flowing from compartment A into compartment T, shown in Fig. 1. The concentration in descending aorta is expressed as the arterial input A0(t), and the concentration in cortex, Ccortex(t) is contributed by the retention in compartment A and T over time. The arterial input A0(t) is converted into plasma concentration Ap(t) by dividing by (1-Hct), where Hct = 0.45 is the hematocrit for rabbits.
Figure 1. Schematic diagram of the modified two-compartment model with impulse residue function for glomerular filtration.
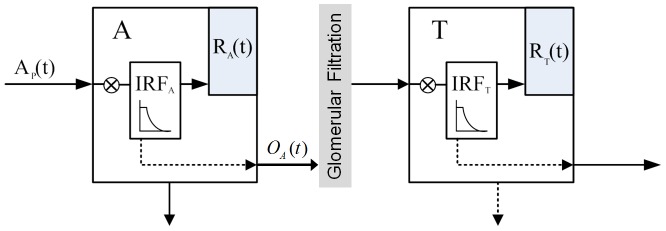
A is the vascular compartment includes intrarenal arteries and glomerular vessels, and T is the tubules compartment. The retention function RA and RT in compartment A and T (represented in solid arrow within the box) are the convolution of the input and each impulse residue function. Dashed lines denote the outflow of each compartment and the outflow of compartment A partially flows into compartment T.
While contrast passes through the kidney, an administration of impulse residue function (IRF) can be useful to describe the characteristics of contrast agent distribution in each compartment [26]. In our study, considering the dispersion effect and transit time of contrast, piecewise-exponential impulse residue function is introduced to determine its response to the idealized bolus injection. For an ideal instantaneous unit bolus injection, it is actually a time-enhancement function [27]. The contrast is considered to be a bolus injection into the kidney and equals 1 (t<τi), then an exponential fall with constant rate mi starts when the contrast is washing out (t>τi), and the parameter τi is the minimal transit time:
 |
(2) |
where the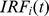 
is the impulse residue function and i represents A and T.
With the proposed model (Fig. 1), the residue amount of contrast in each compartment after a bolus injection is presented as such a convolution of the input and its corresponding impulse residue function:
 |
(3) |
where 
express the convolution, RPF is the renal plasma flow, GFR is the glomerular filtration rate, and Ci(t) is the contrast concentration in each compartment.
In renal system, we defined the retention function RA and RT to illustrate the changes of contrast for each compartment after the convolution of IRFi. We assumed the unit input for compartment A is 1, then the retention function of A equals IRFA(t), however, the unit input changes in compartment T. Because the input for T is from the output of compartment A, the retention function for T is the convolution of OA(t) and IRFT(t), then equation 3 becomes:
 |
(4) |
where
 |
 |
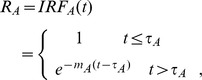is the unit input and then cortical retention function written as: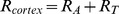 
.
The mean transit time (MTT) was defined as the area under the retention curves according to the equation: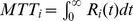 
.
Thus, the amount of contrast remained in cortex region is given by:
 |
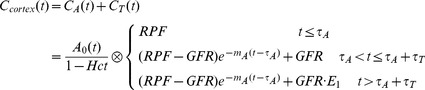(5) |
where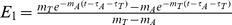 
, Ccortex(t) is the concentration in cortex. Parameters were fitted by using the nonlinear least-squares algorithm.
Monte Carlo Simulation
To evaluate the reliability of the new model compared with other published models in estimating GFR in rabbit kidney, Monte Carlo simulations were conducted. Artificial aortic input function used in this simulation was obtained by smoothing an AIF curve with temporal resolution of 3 second. Smoothing was carried out by a gamma variante function [28].
Totally six compartmental models were included with the same preset GFR values in this simulation: Patlak-Rutland method (GFR = 3.0 ml/min, va = 2.4), PR [6]; a two- compartment model (GFR = 3.0 ml/min, kout = 0.08, fa = 0.2, d = 0.42), 2CD [13]; a simplified two-compartment model (GFR = 3.0 ml/min, kout = 0.08, fa = 0.2), 2C [14]; a separable compartment model (GFR = 3.0 ml/min, Tt = 1/kout = 12.5, Vp = fa = 0.2, Tp = d = 0.42), SP [15]; a three-compartment model (GFR = 3.0 ml/min, RPF = 3.0 ml/g/min, fp = 0.18, wa_c = 0.2, wa_m = 0.08, wp = 0.18), 3C [16]; and the proposed two compartment model with impulse residue function in this study(GFR = 3.0 ml/min, RPF = 3.0 ml/g/min, mA = 0.2, τA = 3.2 s, mT = 0.1) and τT was assumed to be 0, 2C-IRF. Then, the tissue curves were generated from their corresponding initial parameters and the artificial AIF. Considering the impact of noise in DCE-MRI scans, different levels of noise were reintroduced to each concentration curve in Monte Carlo simulation. Guassian noise with zero mean and SD equals to 2%, 3%, 5%, 10%, and 15% of the mean magnitude of each gadolinium concentration curve were used. These noise were generated by using randn(1,N) function in Matlab and be added to construct noisy tissue curves. All these models were used to fit its corresponding noisy data for which true values of these parameters were known. 2000 Monte Carlo trials were conducted, and the variability of each fitted parameter was obtained. In order to assess the variability of the estimated parameter, the coefficient of variation (CV) was used according to the equation: CV = SD/mean. The bias in estimated parameters can be given by the difference between mean value of 2000 simulations and the actual values.
In-vivo Experiment
After testing the reliability and bias of the proposed model in parameters estimation and comparing the precision of GFR measurement with other published models, the extracted concentration curves from DCE-MRI data were used for the measurements of kinetic parameters with 2C-IRF model in normal rabbit kidneys. Nonlinear least squares fitting was implemented with all the data sets by using Levenberg-Marquardt algorithm. To assess the goodness of fit, coefficient of determination, denoted R2, was also calculated.
Acute kidney injury causes significant renal dysfunction in terms of decreased glomerular filtration rate [29]. In order to investigate the validity of the proposed model to detect GFR alterations in such an abnormal condition, pixel-wise calculation of GFR were measured with the dysfunction kidney, as well as the contralateral kidney. To further quantify the cortical mean GFR in the abnormal kidneys, two-certified radiologists with at least 5 years of experience in renal DCE MR imaging, who were blinded to the experiment, draw the cortical ROI on the T1-weighted images and the mean GFR values from its corresponding mapping image were obtained.
Histology
Kidneys in dysfunction experiment were fixed in 10% neutral buffered formalin and embedded in paraffin for light microscopic study. Kidneys were sectioned into 3-µm slides and stained for histology with hematoxylin-eosin. One experienced pathologist, who was blind to which experimental group the samples belonged, reviewed histological findings.
Statistical Analysis
Results of the quantitative measurements are expressed as mean 
SD. Paired t-test was performed and a P value<0.05 was considered statistically significant. Coefficient of determination (R2) is calculated to assess the goodness of fit. All analysis are implemented in Matlab (MathWorks, Natick, MA).
Results
Monte Carlo Simulation
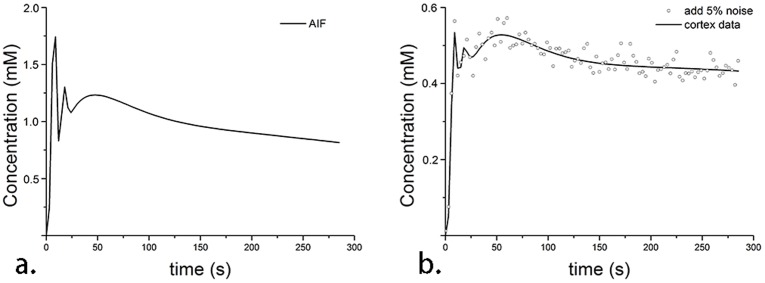
In Monte Carlo simulation, the artificial AIF is shown in Fig. 2a, and 2%, 3%, 5%, 10% and 15% noise were reintroduced into the concentration curves at all the time points, shown in Fig. 2b with 5% noise for instance.
Figure 2. Concentration curves in Monte Carlo simulation for a.) the artificial AIF and b.) the tissue curve which is generated with the known initial parameters and added with 5% level noise.
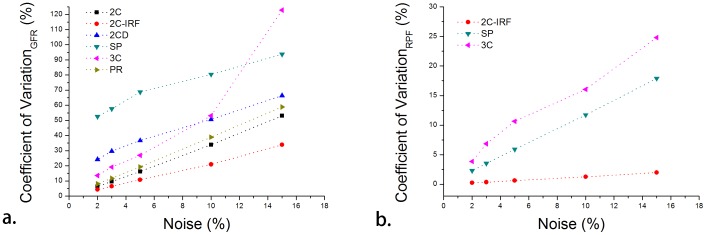
Compared with other five published models, the smallest CV values of estimated GFR were found in 2C-IRF model, seen in Fig. 3a. Higher variability was found in the other compartment models in GFR estimate and pronounced impact existed in 3C model when noise level was above 5%. The bias of estimated GFR was 0.01%–4.0% for 2C-IRF, 0.2–11.3% for 2C, 2.6%–9.8% for 2CD, 8.4%–14.7% for SP, 1.1%–17.1% for 3C, and 0.2%–1.7% for PR. For RPF Monte Carlo simulation, smallest CV values were also found in 2C-IRF model, ranging from 0.2% to 2.0%, seen in Fig. 3b. The other models have a bigger variability of more than 10% when the noise level is above 5%. The bias of estimated RPF of 2C-IRF model was 0.05% to 0.3%, much lower than those of other models.
Figure 3. Monte Carlo simulation results for each compartment model in estimating a.) GFR and b.) RPF, only three models could extract RPF.
Lowest variability of estimated GFR and RPF (red dotted line) are found in the proposed two-compartment model at 2%, 3%, 5%, 10% and 15% noise, respectively.
The estimated GFR and RPF results are robust under noise conditions by using 2C-IRF model. Small variability of estimated RPF was found with CV values ranging from 0.2% to 2.0%, while CV values of GFR were 4.2% to 10.8% under 10% noise. The bias of the estimated GFR, RPF from the new model was low with a range of 0.0%–0.6% for different noise levels, excluding one larger bias of 4.0% for GFR at 15% noise level.
In-vivo Experiment
In this study, all the rabbits were analyzed with the 2C-IRF model for kinetic parameter estimations. A segmentation result is shown in Fig. 4a. After registration, cortical ROI was manually drawn (shown in Fig. 4b) and slice that with branch of renal artery (white arrow in Fig. 4c) was selected for aortic ROI drawing. Representative concentration curves derived from corresponding ROIs are shown in Fig. 4d.
Figure 4. A representative image from DCE-MRI acquisition.
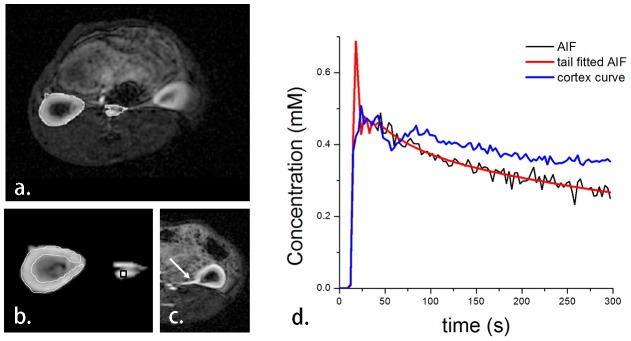
a.) showing the region of interest after segmentation; b.) the manually drawn cortical ROI (white line); c.) the image in which a branch of renal artery is clearly seen is used for aortic ROI drawing; and d.) the concentration curves of each corresponding ROI. The original aortic input function (black line) fits its tail with a biexponential method (shown in red line). The blue line is the cortical concentration curve.
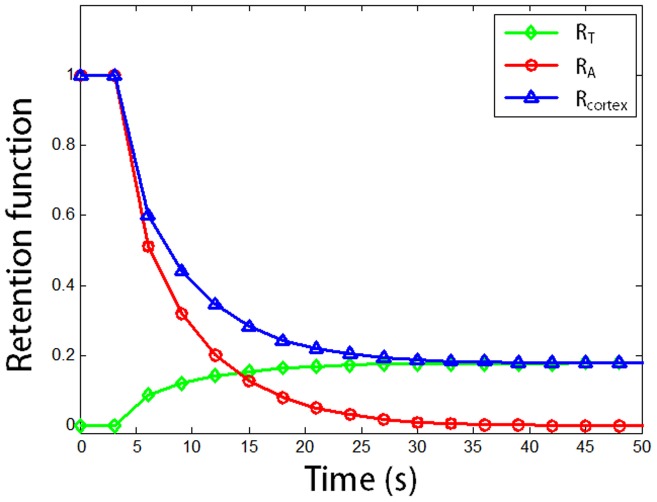
Estimation results of all the kidneys are listed in Table 1. GFR obtained from the new model was 3.03±1.1 ml/min, RPF was 2.64±0.5 ml/g/min, vascular mean transit time MTTA was 5.6±0.6 s, tubule mean transit time MTTT was 15.1±8.8 s and the mean transit time of the kidney MTTK was 20.7±8.7 s in average. No significant differences were found for GFR, RPF, MTTA, MTTT or MTTK when comparing the left and right kidney groups (p>0.05 for all). Satisfactory goodness of fit was found for all the cases, with R2 ranged from 0.81 to 0.97. Typical retention curves are shown in Fig. 5.
Table 1. Estimated parameters of normal kidneys using the proposed two-compartment model and goodness of fit for the nonlinear fitting.
| Num. | GFR | RPF | τA | MTTA | MTTT | MTTK | R2 |
| (ml/min) | (ml/g/min) | (s) | (s) | (s) | (s) | ||
| 1_L | 3.25 | 2.85 | 2.96 | 5.51 | 13.15 | 18.66 | 0.95 |
| 2_L | 3.44 | 2.65 | 2.76 | 4.95 | 25.47 | 30.42 | 0.88 |
| 3_L | 3.85 | 2.15 | 1.85 | 5.91 | 20.81 | 26.72 | 0.97 |
| 4_L | 2.92 | 3.71 | 3.77 | 6.52 | 10.07 | 16.59 | 0.94 |
| 5_L | 1.08 | 2.07 | 1.85 | 4.80 | 6.35 | 11.15 | 0.95 |
| 6_L | 2.42 | 3.12 | 1.06 | 5.62 | 3.95 | 9.57 | 0.81 |
| mean | 2.83 | 2.76 | 2.37 | 5.55 | 13.3 | 18.85 | 0.92 |
| (±SD) | 0.98 | 0.61 | 0.97 | 0.63 | 8.37 | 8.32 | 0.06 |
| 1_R | 3.58 | 2.55 | 2.61 | 5.20 | 16.15 | 21.35 | 0.94 |
| 2_R | 3.69 | 2.40 | 2.48 | 4.70 | 30.66 | 35.36 | 0.83 |
| 3_R | 3.77 | 2.10 | 1.67 | 6.40 | 23.35 | 29.75 | 0.97 |
| 4_R | 4.87 | 3.04 | 3.19 | 5.92 | 19.42 | 25.34 | 0.94 |
| 5_R | 0.94 | 2.19 | 1.98 | 5.17 | 5.36 | 10.53 | 0.96 |
| 6_R | 2.59 | 2.85 | 1.20 | 6.36 | 6.90 | 13.26 | 0.82 |
| mean | 3.24 | 2.52 | 2.19 | 5.63 | 16.97 | 22.60 | 0.91 |
| (±SD) | 1.33 | 0.37 | 0.71 | 0.70 | 9.70 | 9.55 | 0.06 |
Note: L represents the left kidney and R represents the right kidney in normal rabbits.
Figure 5. Typical retention function curves for vascular compartment (RA, red), tubule compartment (RT, green) and the cortex region (Rcortex, blue).
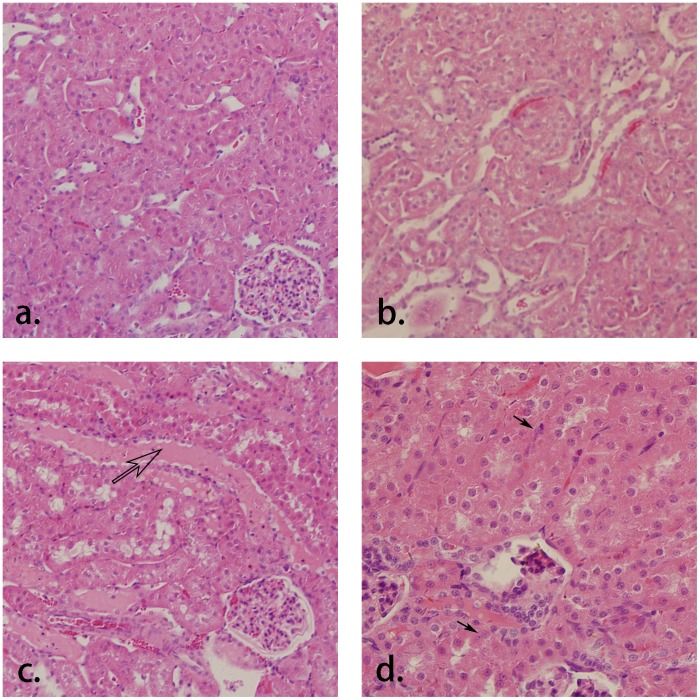
In dysfunction kidney experiments, large decrease of GFR was found in the cortical region of the left kidneys, shown in Fig. 6b, while the right kidneys (control group, Fig. 6a) remain normal. Pixel-wise calculation was implemented and the GFR mapping shows the differences between the dysfunction kidney and the contralateral normal kidney, which are in good concordance with the cortical mean values that listed in Table 2. The changes of the kidney with acute injury are particularly visible on histology compared to the normal kidney (Fig. 7a). Histological findings show main tubular dilatation (Fig. 7b), cast deposition (open arrow, Fig. 7c) and cell necrosis (black arrow, Fig.7d) in the injured kidney.
Figure 6. GFR mapping of a.) the normal kidney (right kidney) and b.) the acute ischemia kidney (left kidney) by using the new model.
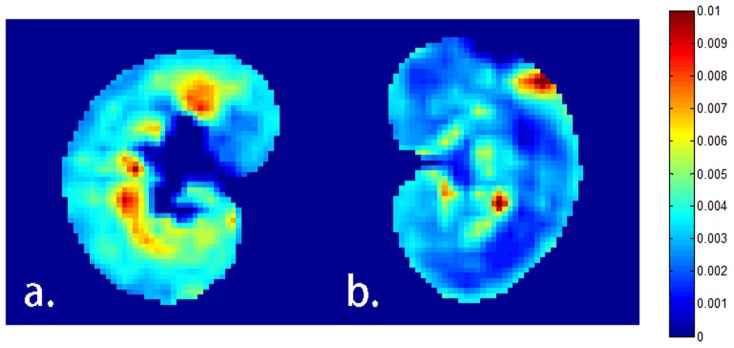
The left kidney of the rabbit is under surgical ligation for totally 45 minutes, and lower GFR values are clearly observed in the cortex and outer stripes of the outer medulla regions while corresponding regions are high in the control group.
Table 2. Pixel-wise estimation of GFR for dysfunction kidneys by using the proposed two-compartment model.
| Cortical | Region | |
| Kidneys | pixel GFR | mean GFR |
| (ml/min) | (ml/min) | |
| Injury 1. | 0.0037 | 2.27a |
| Control 1. | 0.0080 | 4.55 |
| Injury 2. | 0.0042 | 2.78a |
| Control 2. | 0.0068 | 4.73 |
pronounced reduction was found compared to the control group.
Figure 7. Histology sections of a.) the normal kidney (H&E, ×100) and the acute ischemia kidney with histological findings of b.) tubular dilatation (×100), c.) cast deposition (open arrow, ×100) and d.) cell necrosis (black arrow, ×200).
Discussion
In present study, a modified two-compartment model with impulse residue function is implemented, and Monte Carlo simulation results indicate the reliability of the proposed model in parameters estimates. The main result of this study is that the GFR and RPF measurements are in close agreement with literature results in rabbits. Moreover, the new model is valid in detecting GFR alterations in diseased kidneys. The GFR value of normal kidneys in our study is 3.03±1.1 ml/min (n = 6), which is comparable to a mean value of 2.9±1.0 ml/min measured in rabbits using a deconvolution method [30] and model derived GFR of 2.3±1.0 ml/min with original two-compartment model and 2.8±1.2 ml/min with Patlak-Rutland method reported in rabbits study (n = 10) [13]. Here, GFR results of each compartment model for in-vivo experiments are presented in Table 3. The close agreement with literature results for the proposed model is found.
Table 3. Estimated results of GFR for each two-compartmental model.
| n = 6 | 2C-IRF | 2CD | 2C | SP | PR |
| GFR(ml/min) | 3.03 | 1.29 | 1.55 | 1.80 | 0.84 |
| (±SD) | 1.1 | 0.7 | 1.1 | 0.6 | 0.5 |
Moreover, the RPF measured in this study is 2.64±0.5 ml/g/min, which is in close agreement with literature reports [22], [30]–[33], shown in Table 4. Our results resemble the renal perfusion reported in rabbits and larger than the deconvolution method (Hermoye L et al.). The perfusion results in rats (Zimmer F et al., 4.16±1.24 ml/g/min based on arterial spin labeling method and 5.42±0.85 ml/g/min based on DCE method) are larger than the results in our study (2.64±0.5 ml/g/min), this discrepancy underscores physiological differences across species. The close agreement with literature and the valid assessments of discriminating healthy and dysfunction kidneys indicate that the proposed 2C-IRF model provides a useful method for quantitative measurements in kidneys, and the difference in accuracy is relevant. Our results show that the new model is feasible and not only achieves reliable measurements of renal function, but also be capable in detecting of GFR alterations in dysfunction kidneys.
Table 4. RPF values in literature studies.
| Authors | year | ml/g/min | method |
| Ott CE et al. [31] | 1979 | 3.2±0.3 (n = 13) | inulin clearance |
| Hermoye L et al.* a [30] | 2004 | 1.3±0.4 (n = 6) | deconvolution |
| Winter JD et al. [22] | 2011 | 3.28±0.59 (n = 5) | ASL* c based |
| 2.98±0.60 (n = 6) | DCE* d based | ||
| Zhang Y et al. [32] | 2012 | 3.20±0.67 (n = 9) | ASL based |
| Zimmer F et al.* b [33] | 2013 | 4.16±1.24 (n = 6) | ASL based |
| 5.42±0.85 (n = 6) | DCE based |
Unit is ml/g/min.
*aunit converted to ml/g/min with 1 g/ml density.
*brat models were used in RPF measurements. Five of the six rats had a unilateral ischaemic AKI and total seven healthy kidneys were included in the calculation of mean RPF.
*carterial spin labeling (ASL) MRI.
*ddynamic contrast-enhanced (DCE) MRI.
Using the predefined impulse residue function, which considers the transit time and dispersion effect of contrast agent in kidney, our new model could characterize the distribution of contrast and elucidate physiological meaning better, as well as improves the model reliability with reduced bias in measurements of parameters. A similar use of impulse residue function approach has been reported [17]. However, in order to increase the accuracy of the estimated parameters, they introduced more compartments, which results in the expense of system complexity.
In this study, the smallest variability of estimated GFR and RPF is found in 2C-IRF model, which illustrates that it is not sensitive to noise and sufficiently robust in GFR or RPF measurements from DCE-MRI. Usually, deconvolution method is clinically used to determine renal transit time, however, it continues to exhibit noise in the deconvolved curves. By using the impulse residue function in our model, the vascular mean transit time is 5.6±0.6 s, which is similar to the result (6.8±1.7 s) in a previous study [30], and we also generated the tubule mean transit time (15.1±8.8 s) and kidney mean transit time (20.7±8.7 s).
In DCE-MRI scans, administration of gadolinium contrast is usually used to enhance the signal. Gd contrast agents are rapidly cleared with a half-life of about 2 h in normal kidneys, however, it would exceed in patient with dysfunction kidneys. Thus, the retained and subsequent retention of Gd contrast would activate illness known as the nephrogenic systemic fibrosis (NSF) disease [34], [35]. Researchers demonstrated Gd contrast possibly plays the triggering role in the development of NSF [36]. Thus, higher dose of Gd contrast would more easily lead to NSF disease. In our study, low dose of contrast about 0.05 mmol/kg was used and this may reduce the risk of NSF.
There are several limitations in our study. First, the population of the dysfunction kidneys is small. Second, the arterial input function may be affected by the inflow effects in the aorta. Last, the validity of the new model should be tested in human kidneys before clinical utility.
In conclusion, our new model with the introduction of impulse residue function is feasible and suitable to estimate important renal functional parameters, and has the ability to discriminate GFR changes in healthy and diseased kidneys.
Supporting Information
ARRIVE Checklist.
(DOC)
Funding Statement
The authors have no support or funding to report.
References
- 1. Hayashi T, Nitta K, Hatano M, Nakauchi M, Nihei H (1999) The serum cystatin C concentration measured by particle-enhanced immunonephelometry is well correlated with inulin clearance in patients with various types of glomerulonephritis. Nephron 82: 90–92. [DOI] [PubMed] [Google Scholar]
- 2. Craig AJ, Britten A, Heenan SD, Irwin AG (2011) Significant differences when using MDRD for GFR estimation compared to radionuclide measured clearance. Eur Radiol 21: 2211–2217. [DOI] [PubMed] [Google Scholar]
- 3. Fluckiger JU, Schabel MC, Dibella EV (2012) The effect of temporal sampling on quantitative pharmacokinetic and three-time-point analysis of breast DCE-MRI. Magn Reson Imaging 30: 934–943. [DOI] [PubMed] [Google Scholar]
- 4. Pauliah M, Saxena V, Haris M, Husain N, Rathore RK, et al. (2007) Improved T(1)-weighted dynamic contrast-enhanced MRI to probe microvascularity and heterogeneity of human glioma. Magn Reson Imaging 25: 1292–1299. [DOI] [PubMed] [Google Scholar]
- 5. Khalifa F, Abou El-Ghar M, Abdollahi B, Frieboes HB, El-Diasty T, et al. (2013) A comprehensive non-invasive framework for automated evaluation of acute renal transplant rejection using DCE-MRI. NMR Biomed 26: 1460–1470 doi:10.1002/nbm.2977 [DOI] [PubMed] [Google Scholar]
- 6. Hackstein N, Heckrodt J, Rau WS (2003) Measurement of single-kidney glomerular filtration rate using a contrast-enhanced dynamic gradient-echo sequence and the Rutland-Patlak plot technique. J Magn Reson Imaging 18: 714–725. [DOI] [PubMed] [Google Scholar]
- 7. Hackstein N, Bauer J, Hauck EW, Ludwig M, Krämer HJ, et al. (2003) Measuring single-kidney glomerular filtration rate on single-detector helical CT using a two-point Patlak plot technique in patients with increased interstitial space. AJR Am J Roentgenol 181: 147–156. [DOI] [PubMed] [Google Scholar]
- 8. Tsushima Y, Blomley MJ, Kusano S, Endo K (1999) Use of contrast-enhanced computed tomography to measure clearance per unit renal volume: a novel measurement of renal function and fractional vascular volume. Am J Kidney Dis 33: 754–760. [DOI] [PubMed] [Google Scholar]
- 9. Wolf GL (1999) Using enhanced computed tomography to measure renal function and fractional vascular volume. Am J Kidney Dis 33: 804–806. [DOI] [PubMed] [Google Scholar]
- 10. Krier JD, Ritman EL, Bajzer Z, Romero JC, Lerman A, et al. (2001) Noninvasive measurement of concurrent single-kidney perfusion, glomerular filtration, and tubular function. Am J Physiol Renal Physiol 281: F630–F638. [DOI] [PubMed] [Google Scholar]
- 11. Laurent D, Poirier K, Wasvary J, Rudin M (2002) Effect of essential hypertension on kidney function as measured in rat by dynamic MRI. Magn Reson Med 47: 127–134. [DOI] [PubMed] [Google Scholar]
- 12. Miles KA, Leggett DA, Bennett GA (1999) CT derived Patlak images of the human kidney. Br J Radiol 72: 153–158. [DOI] [PubMed] [Google Scholar]
- 13. Annet L, Hermoye L, Peeters F, Jamar F, Dehoux JP, et al. (2004) Glomerular filtration rate: assessment with dynamic contrast-enhanced MRI and a cortical- compartment model in the rabbit kidney. J Magn Reson Imaging 20: 843–849. [DOI] [PubMed] [Google Scholar]
- 14. Buckley DL, Shurrab AE, Cheung CM, Jones AP, Mamtora H, et al. (2006) Measurement of single kidney function using dynamic contrast-enhanced MRI: comparison of two models in human subjects. J Magn Reson Imaging 24: 1117–1123. [DOI] [PubMed] [Google Scholar]
- 15. Sourbron SP, Michaely HJ, Reiser MF, Schoenberg SO (2008) MRI-measurement of perfusion and glomerular filtration in the human kidney with a separable compartment model. Invest Radiol 43: 40–48. [DOI] [PubMed] [Google Scholar]
- 16. Lee VS, Rusinek H, Bokacheva L, Huang AJ, Oesingmann N, et al. (2007) Renal function measurements from MR renography and a simplified multicompartmental model. Am J Physiol Renal Physiol 292: F1548–F1559. [DOI] [PubMed] [Google Scholar]
- 17. Zhang JL, Rusinek H, Bokacheva L, Lerman LO, Chen Q, et al. (2008) Functional assessment of the kidney from magnetic resonance and computed tomography renography: impulse retention approach to a multicompartment model. Magn Reson Med 59: 278–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Bokacheva L, Rusinek H, Zhang JL, Chen Q, Lee VS (2009) Estimates of glomerular filtration rate from MR renography and tracer kinetic models. J Magn Reson Imaging 29: 371–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Rusinek H, Boykov Y, Kaur M, Wong S, Bokacheva L, et al. (2007) Performance of an automated segmentation algorithm for 3D MR renography. Magn Reson Med 57: 1159–1167. [DOI] [PubMed] [Google Scholar]
- 20. Cheng HL, Wright GA (2006) Rapid high-resolution T(1) mapping by variable flip angles: accurate and precise measurements in the presenceof radiofrequency field inhomogeneity. Magn Reson Med 55: 566–574. [DOI] [PubMed] [Google Scholar]
- 21. Vese LA, Chan TF (2002) A multiphase level set framework for image segmentation using the Mumford and Shah model. Int J Comput Vis 50: 271–293. [Google Scholar]
- 22. Lv D, Zhuang J, Chen H, Wang J, Xu Y, et al. (2008) Dynamic Contrast-Enhanced Magnetic Resonance Images of the Kidney. IEEE Eng Med Biol Mag 27: 36–41. [DOI] [PubMed] [Google Scholar]
- 23. Winter JD, St Lawrence KS, Cheng HL (2011) Quantification of renal perfusion: comparison of arterial spin labeling and dynamic contrast-enhanced MRI. J Magn Reson Imaging 34: 608–615. [DOI] [PubMed] [Google Scholar]
- 24. Peeters F, Annet L, Hermoye L, Van Beers BE (2004) Inflow correction of hepatic perfusion measurements using T1-weighted, fast gradient-echo, contrast- enhanced MRI. Magn Reson Med 51: 710–717. [DOI] [PubMed] [Google Scholar]
- 25. Shuter B, Wang SC, Roche J, Briggs G, Pope JM (1998) Relaxivity of Gd-EOB-DTPA in the normal and biliary obstructed guinea pig. J Magn Reson Imaging 8: 853–861. [DOI] [PubMed] [Google Scholar]
- 26. Miles KA, Griffiths MR (2003) Perfusion CT: a worthwhile enhancement? Br J Radiol 76: 220–231. [DOI] [PubMed] [Google Scholar]
- 27. Lawson RS (1999) Application of mathematical methods in dynamic nuclear medicine studies. Phys Med Biol 44: 57–98. [DOI] [PubMed] [Google Scholar]
- 28. de Priester JA, den Boer JA, Christiaans MH, Kessels AG, Giele EL, et al. (2003) Automated quantitative evaluation of diseased and nondiseased renal transplants with MR renography. J Magn Reson Imaging 17: 95–103. [DOI] [PubMed] [Google Scholar]
- 29. Joyce M, Kelly C, Winter D, Chen G, Leahy A, et al. (2001) Pravastatin, a 3-hydroxy-3-methylglutaryl coenzyme A reductase inhibitor, attenuates renal injury in an experimental model of ischemia-reperfusion. J Surg Res 101: 79–84. [DOI] [PubMed] [Google Scholar]
- 30. Hermoye L, Annet L, Lemmerling P, Peeters F, Jamar F, et al. (2004) Calculation of the renal perfusion and glomerular filtration rate from the renal impulse response obtained with MRI. Magn Reson Med 51: 1017–1025. [DOI] [PubMed] [Google Scholar]
- 31. Ott CE, Vari RC (1979) Renal autoregulation of blood flow and filtration rate in the rabbit. Am J Physiol 237: F479–F482. [DOI] [PubMed] [Google Scholar]
- 32. Zhang Y, Wang J, Yang X, Wang X, Zhang J, et al. (2012) The serial effect of iodinated contrast media on renal hemodynamics and oxygenation as evaluated by ASL and BOLD MRI. Contrast Media Mol Imaging 7: 418–425. [DOI] [PubMed] [Google Scholar]
- 33. Zimmer F, Zöllner FG, Hoeger S, Klotz S, Tsagogiorgas C, et al. (2013) Quantitative renal perfusion measurements in a rat model of acute kidney injury at 3T: testing inter- and intramethodical significance of ASL and DCE-MRI. PLoS One 8: e53849 doi: 10.1371/journal.pone.0053849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Sadowski EA, Bennett LK, Chan MR, Wentland AL, Garrett AL, et al. (2007) Nephrogenic systemic fibrosis: risk factors and incidence estimation. Radiology 243: 148–157. [DOI] [PubMed] [Google Scholar]
- 35. Kuo PH (2008) NSF-active and NSF-inert species of gadolinium: mechanistic and clinical implications. AJR Am J Roentgenol 191: 1861–1863. [DOI] [PubMed] [Google Scholar]
- 36. Grobner T (2006) Gadolinium—a specific trigger for the development of nephrogenic fibrosing dermopathy and nephrogenic systemic fibrosis? Nephrol Dial Transplant 21: 1104–1108. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
ARRIVE Checklist.
(DOC)