Abstract
Bisection tasks are used in research on normal space and time perception and to assess the perceptual distortions accompanying neurological disorders. Several variants of the bisection task are used, which often yield inconsistent results, prompting the question of which variant is most dependable and which results are to be trusted. We addressed this question using theoretical and experimental approaches. Theoretical performance in bisection tasks is derived from a general model of psychophysical performance that includes sensory components and decisional processes. The model predicts how performance should differ across variants of the task, even when the sensory component is fixed. To test these predictions, data were collected in a within-subjects study with several variants of a spatial bisection task, including a two-response variant in which observers indicated whether a line was transected to the right or left of the midpoint, a three-response variant (which included the additional option to respond “midpoint”), and a paired-comparison variant of the three-response format. The data supported the model predictions, revealing that estimated bisection points were least dependable with the two-response variant, because this format confounds perceptual and decisional influences. Only the three-response paired-comparison format can separate out these influences. Implications for research in basic and clinical fields are discussed.
Keywords: Bisection task, Landmark task, Method of single stimuli, Single-presentation method, Two-alternative forced-choice, Response bias, Indecision
Measuring the perceptual midpoint along some physical dimension is theoretically important in basic perception science, but it is also clinically useful. For instance, several psychiatric or neurological disorders are accompanied by impaired time processing and a distorted perception of temporal duration or time continuity (e.g., Lee et al., 2009); similarly, neurological conditions such as hemianopia and spatial neglect often involve unilateral visual-field defects accompanied by anomalies of space perception (e.g., Schuett, Dauner, & Zihl, 2011), and midline marking is actually used for diagnosing neglect (Schenkenberg, Bradford, & Ajax, 1980). This article focuses on measurement of the spatial midpoint, although the situation in measurements of the temporal midpoint is analogous. The spatial perceptual midpoint is measured in one of two ways:
with the bisection task—a subjective, free-viewing, free-response task in which observers manually or ocularly transect a line at what they perceive to be its midpoint; or
with Milner's landmark task (Milner, Brechmann, & Pagliarini, 1992)—an objective, generally short-presentation task in which a series of identical lines, each pretransected by a bar at a different point, are displayed one at a time, and observers judge for each line (i) whether the transecting bar is to the left or the right of what they perceive to be the midpoint of the line, or (ii) which of the two segments of the transected line is longer (or shorter). It should be noted that the temporal analogue of the landmark task is instead dubbed the temporal bisection task (in which observers are requested to indicate whether each of a set of presentation durations is closer to designated short or long durations that have previously been presented).
Empirical research has shown that bisection and landmark tasks generally yield different results, even in within-subjects studies (e.g., Cavézian, Valadao, Hurwitz, Saoud, & Danckert, 2012; Harvey, Krämer-McCaffery, Dow, Murphy, & Gilchrist, 2002; Harvey & Olk, 2004; Luh, 1995). This has prompted some researchers to suggest that different strategies and neural networks govern performance in each task, a reasonable notion, on consideration of a fundamental difference between the tasks: The bisection task directly asks observers to indicate where they perceive the midpoint to be; and in contrast, the landmark task prevents observers from reporting the location(s) at which they perceive the transecting bar to be at the midpoint by forcing them to give instead a “left” or a “right” response. It is hardly contentious that informed “left”/“right” responses cannot be given when the transecting bar is at the perceptual midpoint. Thus, the landmark task only gathers indirect data whose interpretation rests on the assumption that observers evenly give “left” and “right” responses when they perceive the transecting bar to be at the midpoint. This assumption is explicitly built into some models of performance in the analogous temporal bisection task (see Wearden & Ferrara, 1995), but empirical evidence discussed next shows that the assumption is untenable.
Morgan, Dillenburger, Raphael, and Solomon (2012) used a modified form of the landmark task to illustrate the empirical consequences of alternative strategies that observers may use to respond when undecided—that is, when they cannot tell whether the displayed stimulus is on the right or the left of the midpoint. The net effect is that the estimated perceptual midpoint is artifactually shifted in either direction by a meaningful, and potentially large, amount. Such response bias, defined as unbalanced “left”/“right” responses when undecided,1 produces analogous shifts in many other psychophysical tasks (see, e.g., Alcalá-Quintana & García-Pérez, 2011; García-Pérez & Alcalá-Quintana, 2010a, 2010b, 2011a, 2011b, 2012a, 2012b), and other accounts describe shifts due to what we will define later as decisional bias (see, e.g., Schneider, 2011; Schneider & Komlos, 2008). These findings cast doubts on the validity of estimates of the perceptual midpoint obtained with the landmark task. Specifically, any observed shifts could be spurious consequences of nonperceptual biases in the absence of true perceptual distortions, but, on the other hand, a lack of observed shifts could also be a spurious consequence of nonperceptual biases countering true perceptual distortions. Bisiach, Ricci, Lualdi, and Colombo (1998) proposed a method to eliminate the influence of response bias from estimates obtained with the landmark task, but comments on it will be deferred to the “Discussion” section. Analogous considerations have led to questioning the interpretability of results obtained with the temporal bisection task (e.g., Allan, 2002; Raslear, 1985).
The landmark task is an instance of what used to be called the method of single stimuli (MSS), to stress the fact that a single stimulus is presented in each trial for the observer to make a categorical judgment on. Because this judgment is typically binary (e.g., left vs. right, in the landmark task) this method is also frequently dubbed single-presentation, two-alternative forced choice. In a theoretical analysis of the task, García-Pérez and Alcalá-Quintana (2013) showed that MSS has inherent and inevitable shortcomings that make it unsuitable for the investigation of perceptual processes. The theoretical analysis also showed that these problems can be partly alleviated with a slight amendment of the MSS task, and that the problems can be completely solved with a paired-comparison task including three response options. The goal of this article is to test these theoretical results in a within-subjects study using three alternative formats for the landmark task. All observers also carried out a manual bisection task in a computer-administered form that involved the same stimulus used in the landmark tasks. Before describing our experiments and the results, the next two sections will outline the model of psychophysical performance that motivates this research, provide mathematical expressions for the theoretical psychometric functions that should describe the data, and present the predictions of performance across the variants of the landmark task that will be tested in this study.
The indecision model of psychophysical judgments
The indecision model in signal detection theory (SDT) is built on the fact that categorical or comparative judgments along bipolar continua always render three qualitative outcomes. In paired-comparison tasks involving stimuli A and B, the outcomes are “A weaker than B,” “A stronger than B,” or “A indistinguishable from B”; in the landmark task (under MSS), the outcomes are “bar to the left of the midpoint,” “bar to the right of the midpoint,” or “bar seemingly at the midpoint.” The usual format with which these tasks are administered does not allow for reporting the intermediate judgment (i.e., “bar seemingly at the midpoint”), despite the interest in estimating the physical position at which this judgment is maximally prevalent; instead, observers are forced to give left/right responses. The model described next highlights the undesirable implications of this practice.
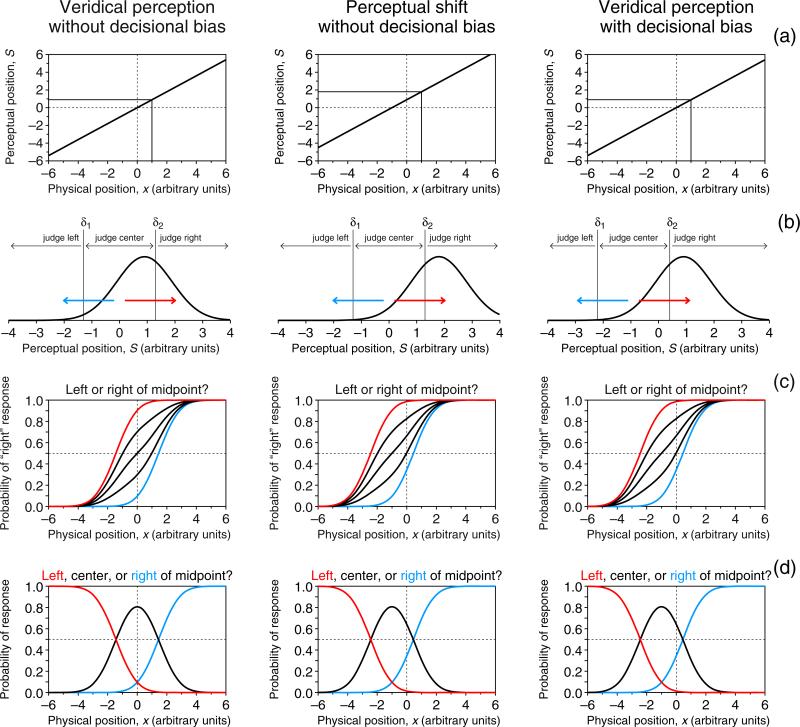
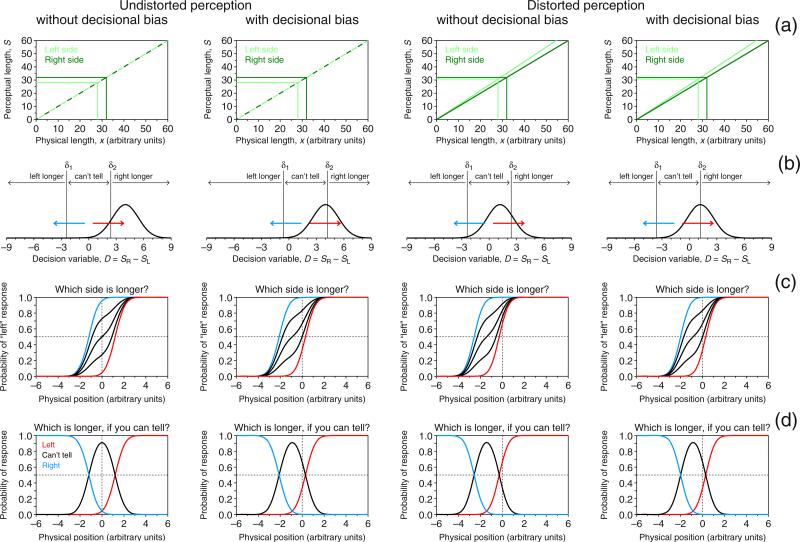
The indecision model includes a psychophysical function relating mean sensory effects to the relevant physical dimension of a stimulus (Fig. 1a) and a decision space mapping continuous sensory states onto judgments (Fig. 1b). Each column in Fig. 1 depicts a different scenario. For the landmark task, the psychophysical function μ maps physical space onto perceptual space. Without loss of generality, this function is assumed to be linear in this illustration; that is,
| (1) |
where α = 0 (left and right panels in Fig. 1a) makes the function go through the origin, so that physical position 0 (the physical midpoint) maps onto perceptual position 0 (the perceptual midpoint). In contrast, α ≠ 0 (center panel in Fig. 1a) renders μ(0) = α, so that the perceptual midpoint occurs at the physical position μ−1(0) = −α/β. This creates a true perceptual shift, caused by whatever pushes μ away from the origin.
Fig. 1.
Indecision model and predictions on observed performance in two variants of the landmark task under three scenarios (columns). a Psychophysical functions μ mapping physical space onto perceptual space. The function has the form of Eq. 1, with α = 0 and β = 0.9 (left and right columns), so that the perceptual midpoint and physical midpoint match (i.e., the zero crossing of μ is at x = −α/β = 0), or with α = 0.9 and β = 0.9 (center column), so that the perceptual midpoint is not at the physical midpoint (i.e., the zero crossing of μ is at x = −α/β = −1). b Distributions of perceptual position (curve) given by Eq. 2 for a configuration in which the transecting bar is at x = 1, yielding the mean perceptual position indicated by the solid lines in row a. Also shown is the decision space with boundaries at S = δ1 and S = δ2, which partitions the continuum into intervals associated with the judgments indicated at the top. Judgments are not affected by decisional bias if δ1 = −δ2 (left and center columns, where δ1 = −1.3 and δ2 = 1.3); otherwise (right column, where δ1 = −2.2 and δ2 = 0.4), a decisional bias is involved whereby the strength of evidence, |δ1|, required for a “left” judgment differs from (is larger than, in this illustration) the strength of evidence, |δ2|, required for a “right” judgment. c Ranges of psychometric functions Ψ (probability of “right” response as a function of position of the transecting bar) that could be observed when observers are asked to report a “left”/“right” judgment. The mathematical form of Ψ is given by Eq. 3. If observers invariably report “center” judgments as “right” responses (i.e., ξ = 1; red arrows in row b), Ψ as plotted in red obtains; if they always report “center” judgments as “left” responses (ξ = 0; blue arrows in row b), Ψ as plotted in blue obtains; the black curves plot the resultant Ψs for intermediate cases (left to right, ξ = .75, .5, and .25). Of all these functions, only the 50 % point on the one for which ξ = .5 reflects the true perceptual midpoint, provided that the observer does not have any decisional bias. d Psychometric functions arising in a ternary variant of the landmark task, whose mathematical forms are given by Eqs. 4. Each curve represents the probability of the response printed with the same color in the upper part of the panel. response bias no longer affects these psychometric functions, because “center” judgments are reported separately (black curves); however, decisional bias (right column) displaces the ensemble just as a true perceptual shift (center column) does. Color is available only in the online version
The psychophysical function gives the mean sensory effect S (here, perceived position) elicited by a stimulus at position x, but, across trials, the perceived position of a transecting bar at physical position x is in SDT a unit-variance2 normal random variable with a density
| (2) |
Figure 1b shows this distribution for a stimulus at x = 1 along with the decision space that partitions the continuum of perceived positions into three regions delimited by vertical lines at S = δ1 and S = δ2: a region of large negative values yielding judgments of “left of the midpoint,” a region of large positive values yielding judgments of “right of the midpoint,” and a region of values around zero yielding judgments of “at the midpoint.” The region (δ1, δ2) is Fechner's (1860/1966) interval of uncertainty and reflects the resolution with which observers can judge that transection occurs away from the midpoint. Then, the probabilities of “left,” “center,” and “right” judgments are, respectively, Prob(S < δ1), Prob(δ1 < S < δ2), and Prob(S > δ2). Note that δ1 = −δ2 in the left and center panels of Fig. 1b, implying that the interval of uncertainty is centered. In contrast, the interval is off-center in the right panel of Fig. 1b, yielding what is referred to as decisional bias: The strength of evidence requested to make a “left” judgment differs from that requested to make a “right” judgment.
Although observers make judgments with these three outcomes, the conventional response format forces them to mis-report “center” judgments as “left” or “right” responses. This two-response variant of the landmark task will be referred to as MSS-2R hereafter. In these cases, and for one reason or another, observers may have a response bias, giving “right” responses with probability ξ and “left” responses with probability 1 − ξ. The psychometric function for “right” responses in MSS-2R is thus
| (3) |
where Φ is the unit-normal cumulative distribution function. The form and location of the resultant psychometric function thus varies with α, β, δ1, δ2, and ξ. As is shown in the left panel of Fig. 1c, mere response bias (i.e., ξ ≠ .5) masquerades as a perceptual shift: When α = 0 (i.e., no perceptual shift) and δ1 = −δ2 (i.e., no decisional bias), an observer with ξ = 0 always gives “left” responses for “center” judgments (blue arrow in the left panel of the electronic version of Fig. 1b; all subsequent color references to figures refer to the versions obtainable online), and the resultant psychometric function is shifted to the right (blue curve in the left panel of Fig. 1c), so that its 50 % point does not reflect the true perceptual midpoint at x = 0; at the other extreme, an observer with ξ = 1 always gives “right” responses for “center” judgments (red arrow in the left panel of Fig. 1b), the resultant psychometric function is shifted to the left (red curve in the left panel of Fig. 1c), and its 50 % point also does not reflect the true perceptual midpoint; finally, observers with intermediate values of ξ give a potentially unbalanced mixture of “left” and “right” responses for “center” judgments that reflect smaller shifts of the psychometric function (black curves in the left panel of Fig. 1c). The observer can only be claimed to be unbiased when ξ = .5, so that the 50 % point on the resultant psychometric function (central black curve in the left panel of Fig. 1c) reflects the true perceptual midpoint. These shifts caused by response bias occur also under the conditions illustrated in the center and right columns of Fig. 1, and across the board, the three panels of Fig. 1c show that the left/right response format cannot separate perceptual shifts from artifactual shifts caused by response bias or decisional bias. In the absence of true perceptual shifts, response bias can displace the psychometric function anywhere from well below to well above the physical midpoint (left panel in Fig. 1c), and decisional bias can displace the psychometric function even further (right panel in Fig. 1c). True perceptual shifts, on the other hand, can be spuriously inflated, reduced, eliminated, or even inverted by either response bias (center panel in Fig. 1c) or decisional bias (not illustrated in Fig. 1). In other words, the 50 % point on the psychometric function for the MSS-2R task is uninterpretable, because there is no way to determine whether its location has been affected by response or decisional biases.
It is paradoxical that a design aimed at estimating the perceptual midpoint prevents observers from reporting judgments of perceived midpoint, forcing them to misreport such judgments as “left” or “right” responses, at random. The conventional binary format can be replaced with a ternary format with “left,” “center,” and “right” as response options. To our knowledge, a “center” response option in the landmark task has been used only once, for a different purpose: Olk, Wee, and Kingstone (2004) used it to confirm Marshall and Halligan's (1989) surmise that, as compared to normal controls, neglect patients have a broader “indifference zone,” defined as the range of positions at which a transecting bar appears subjectively to be at the midpoint. But Olk et al. did not consider the implications for estimates of the perceptual midpoint obtained under the left/right format. This may explain why the benefits of including a “center” response option in the landmark task have not been appreciated, and also why the inadvisable left/right format continues to be massively used.
Inclusion of a “center” response option provides a separate category for the judgment of the utmost interest. This three-response variant of the landmark task will be referred to as MSS-3R here. The main advantage of this format is that it removes response bias entirely: Observers no longer exert bias when guessing “left” or “right” responses for “center” judgments. Formally, the psychometric functions for “right” and “center” responses in the ternary task are, respectively,
| (4a) |
| (4b) |
(see Fig. 1d), whereas the psychometric function for “left” responses is simply 1 − ΨMSS-3R − ϒMSS-3R. The peak of ϒMSS-3R (i.e., the physical position at which “center” responses prevail) reveals the true perceptual midpoint in the absence of decisional bias (left and center panels in Fig. 1d), but decisional bias alters the location of this peak to give the appearance of a nonexistent perceptual shift (right panel in Fig. 1d). Thus, the three-response format only removes response bias; the effects of decisional bias cannot be removed under any variant of MSS. As we will show next, paired-comparison tasks with the ternary response format separate out decisional bias and allow for identifying true perceptual shifts.
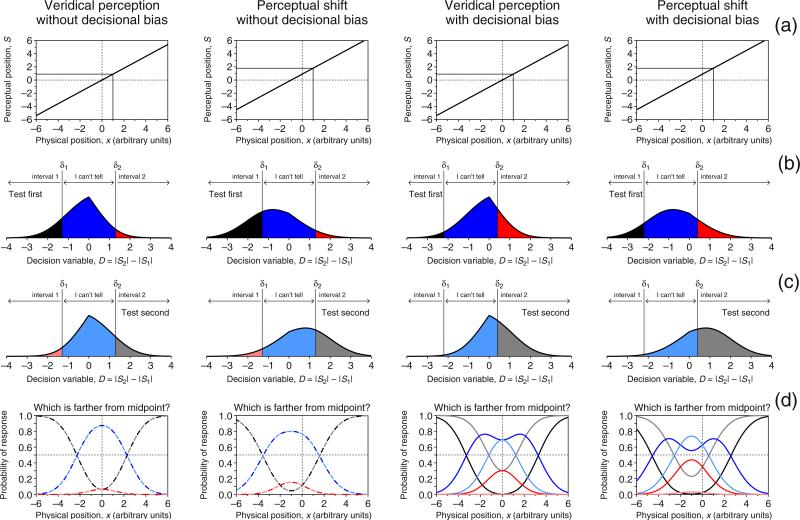
A paired-comparison variant of the landmark task displays two configurations (two transected lines). Under the ternary format, observers report in which of the configurations the transecting bar is farther from (or closer to) the midpoint, with “I can't tell” as the third response option. One of these configurations (the so-called standard) is always transected at the midpoint, whereas the other (the so-called test) is transected at an arbitrary position that varies across trials. The order of presentation (in successive temporal displays) or spatial arrangement (in simultaneous spatial displays) of the standard and test is randomized across trials.
Figure 2 shows the indecision model for a paired-comparison task with the ternary response format (henceforth, the PC-3R task) under scenarios encompassing perceptual shifts and decisional bias. The psychophysical function (Fig. 2a) is the same as in Fig. 1, because it reflects a mapping of physical space onto perceptual space that precedes and is independent of the task. In the PC-3R task, observers are assumed to compare the absolute offsets perceived in the first and second intervals (with sequential presentations) and to report the interval in which the offset was larger, or that they could not tell a difference. Thus, the decision variable D is the difference between the absolute offsets |S1| and |S2| perceived in the first and second intervals, and thus, the difference between the absolute values of random normal variables with densities given by Eq. 2. The distribution of such variables is derived in Appendix A and illustrated in Figs. 2b and c. The use of a difference variable in decision space requires separate consideration of cases in which the test is presented first (Fig. 2b) or second (Fig. 2c). The direction in which the difference is computed only affects verbal descriptions of the decision process, and we will assume without loss of generality that D = |S2| − |S1|, as is shown in Figs. 2b and c.
Fig. 2.
Indecision model and predictions for a paired-comparison variant of the ternary landmark task under four scenarios (columns). a Psychophysical functions μ, identical to those in Fig. 1a and reflecting either veridical perception (first and third columns) or a perceptual shift (second and fourth columns). b Distributions of the decision variable given by Eq. A5 for a pair in which the test configuration is presented in the first interval with the transecting bar at x = 1, whereas the standard configuration is presented in the second interval and transected at the physical midpoint (x = 0). Also shown is the decision space with boundaries at D = δ1 and D = δ2, analogous to that in Fig. 1b. Here, judgments are also not affected by decisional bias if δ1 = −δ2 (first and second columns), and are affected by them otherwise (third and fourth columns). (c) Analogous to row b, but for the case in which the test configuration is displayed after the standard. (d) Psychometric functions for each type of response according to order of presentation. Psychometric functions for correct responses (“Interval 1” responses when the test is presented first, and “Interval 2” responses when the test is presented second) are shown in black/gray; psychometric functions for incorrect responses (“Interval 2” responses when the test is presented first and “Interval 1” responses when the test is presented second) are shown in red/pale red; psychometric functions for “I can't tell” responses (under both orders of presentation) are shown in blue/pale blue. The psychometric functions do not differ across presentation orders if there is no decisional bias (first and second columns), and they do differ if there is decisional bias (third and fourth columns). In either case, the ensemble of psychometric functions has a vertical axis of bilateral symmetry at the true perceptual midpoint—that is, at the zero crossing of μ in row a. Color is available only in the online version
When the test is presented first (or second), a correct “Interval 1” (or “Interval 2”) decision is made if D < δ1 (or D > δ2), which occurs with the probability indicated by the shaded black (gray) areas in Fig. 2b (2c), and this probability varies with test position, as is shown by the black (gray) curves in Fig. 2d (plotted with a dashed trace when one of the curves would occlude the other); on the other hand, an incorrect “Interval 2” (“Interval 1”) decision is made if D > δ2 (D < δ1), which occurs with the probability indicated by the shaded red (pale red) areas in Fig. 2b (2c), and this probability also varies with test position, as is shown by the red (pale red) curves in Fig. 2d; finally, an “I can't tell” judgment occurs if δ1 < D < δ2, with the probability indicated by the shaded blue (pale blue) areas in Fig. 2b (2c), and this probability varies with test position as well, as is shown by the blue (pale blue) curves in Fig. 2d. Formally, the psychometric functions Ψi and ϒi—respectively describing the probability of a correct response and an “I can't tell” response when the test stimulus at position x is displayed in interval i—are given by
| (5a) |
| (5b) |
| (5c) |
| (5d) |
with F being given by Eq. A6 in Appendix A.
As compared to Figs. 1c and d for the MSS variants of the task, Fig. 2d reveals how PC-3R separates perceptual shifts from decisional bias: The psychometric functions are identical across presentation orders in the absence of decisional bias (first and second columns in Fig. 2), but they vary across presentation orders if decisional bias is present (third and fourth columns in Fig. 2); on the other hand, the ensemble of psychometric functions has an axis of bilateral symmetry at the physical midpoint in the absence of a perceptual shift (i.e., when α = 0 in the psychophysical function μ; first and third columns in Fig. 2), but the axis of symmetry moves to μ−1(0) = −α/β if there is a true perceptual shift (i.e., when α ≠ 0; second and fourth columns of Fig. 2). Paired-comparison tasks with the ternary format thus allow for separating decisional bias from perceptual shifts while entirely removing response biases, since the “I can't tell” response option prevents observers from guessing when undecided.
It is useful to note that the conventional probability of a correct response in the implied 2AFC task with aggregated data across presentation orders (i.e., the probability that observers will respond “Interval 1” when the test was in the first interval, and “Interval 2” when the test was in the second) is
| (6) |
and the probability of an “I can't tell” response is
| (7) |
with the probability of an incorrect response being 1 − Ψ2AFC − ϒ2AFC. It should be stressed that fitting psychometric functions to data aggregated across presentation orders is highly unadvisable (Alcalá-Quintana & García-Pérez, 2011; García-Pérez & Alcalá-Quintana, 2010b, 2011b; Ulrich & Vorberg, 2009). Although aggregated data will not be used to fit psychometric functions here, it is nevertheless convenient to look at plots of aggregated data and average psychometric functions, if only because such plots involve twice as much data as separate plots for each presentation order, and thus, less noise.
Predictions to be tested
Figures 1 and 2 showed model-based psychometric functions describing performance across variants of the landmark task. The characteristics of these psychometric functions allow empirical tests of the underlying model, and these are described next, in two separate blocks.
The first block comprises aspects of performance explicitly represented in the psychometric functions themselves and their parameters. The model is expected to describe empirical performance on each task through suitable parameters estimated separately with data from each task. But more importantly, the model is also expected to describe performance in all tasks with common values for parameters α and β in the psychophysical function μ. The reason is that the empirical study reported in this article used the same type of stimuli and viewing conditions in all tasks, and hence, the sensory mapping described by the psychophysical function in Eq. 1 should not vary across tasks. At the same time, decisional aspects may vary across tasks, because each task requests a decision that is subject to different requirements. Fitting the model separately to data from each task is nevertheless expected to produce different estimates of α and β, partly because of sampling error, but also, and more importantly, because of the unidentifiability of models for MSS versions of the task (see Fig. 1). Fitting the model jointly to data from all tasks solves the unidentifiability and should permit accounting for the data with common sensory parameters and potentially different decisional parameters across tasks.
The second block of predictions comprises implicit characteristics that give rise to conventional performance measures—namely, the bisection point (BP) and the difference limen (DL). Both performance measures are typically extracted by fitting arbitrary psychometric functions to data, and these can also be extracted from the model-based psychometric functions to be fitted here. These performance measures are likely to vary across variants of the landmark task as a result of the decisional aspects of each task. Consider Fig. 1 again. In MSS-3R (Fig. 1d), the BP is defined as the peak of the psychometric function for “center” responses, and it can be at the physical midpoint (left panel in Fig. 1d) or displaced away from it as a result of a perceptual shift (when α ≠ 0 and δ1 = −δ2; center panel), a decisional bias (when α = 0 and δ1 ≠ −δ2; right panel), or both (when α ≠ 0 and δ1 ≠ −δ2; not shown in Fig. 1d). Indeed, maximizing Eq. 4b shows that the BP in the MSS-3R task is given by
| (8) |
explicitly showing that the empirical BP intermixes sensory and decisional aspects inextricably, so that only when δ1 = −δ2 (i.e., no decisional bias) will the BP reflect the true perceptual midpoint at −α/β. In contrast, the DL, defined as the distance between the 75 % and 25 % points on the psychometric function for “right” responses, is unaffected by perceptual shifts or decisional biases and is only determined by the slope parameter β of the psychophysical function μ. Specifically, from Eq. 4a,
| (9) |
In other words, MSS-3R is suitable for estimating the DL but not the BP.
Identical scenarios concerning perceptual shifts or decisional biases have different effects in the MSS-2R task. The mathematical form of Eq. 3 does not allow for obtaining closed-form expressions for BPMSS-2R and DLMSS-2R. Yet, a comparison of Figs. 1c and d reveals some properties when δ1 and δ2 have the same values in MSS-2R and MSS-3R tasks. Specifically, BPMSS-2R, defined as the 50 % point on the psychometric function (see the crossings at .5 of the curves in each panel of Fig. 1c) can be anywhere between the two 50 % points on the MSS-3R psychometric function for “center” responses (see the crossings at .5 of the black curve in each panel Fig. 1d), and only when ξ = .5 (central black curve in each panel of Fig. 1d) will the BPs in both tasks coincide. On the other hand, DLMSS-2R, defined also as the distance between the 75 % and 25 % points on the psychometric function, will equal DLMSS-3R only if ξ = 0 (blue curve in each panel of Fig. 1c) or ξ = 1 (red curve in each panel of Fig. 1c), and it will be larger for intermediate values of ξ. In other words, MSS-2R is unsuitable for estimating the BP or the DL.
As for the PC-3R task (newly introduced in this study), Fig. 2 showed that the BP is given by the location of the axis of bilateral symmetry, and that this is a genuine estimate of the true bisection point, whether in the presence or the absence of decisional bias. Although a closed-form expression for the BP cannot be derived from Eqs. 5, it can be easily seen numerically that the vertical axis of bilateral symmetry lies at BPPC-3R = −α/β, matching what the BP would be under MSS variants for an observer with infinite resolution (i.e., δ1 = δ2 = 0). The DL, on the other hand, does not manifest as a specific aspect of the shape of PC-3R psychometric functions. However, because the true DL is only determined by the slope β of the psychophysical function μ, it will be defined here also through Eq. 9 above, with the value of β being estimated from PC-3R data.
In sum, BPPC-3R is a dependable estimate of the true BP, whereas BPMSS-2R and BPMSS-3R are affected by decisional biases that may bring those estimates away from one another or from BPPC-3R. Note that the model does not predict that BPMSS-2R and BPMSS-3R will differ from one another or that they will differ from BPPC-3R: They all may, indeed, be identical under the model when δ1 = −δ2 and ξ = .5. What the model shows is only that BPMSS-2R and BPMSS-3R are uninterpretable, because the values of δ1, δ2, and ξ cannot be estimated from isolated MSS data. On the other hand, DLPC-3R is a dependable estimate of the true DL, and it should match the estimate DLMSS-3R within sampling error, whereas DLMSS-2R is expected to be equal to or larger than either of them.
Method
Observers
Seven experienced psychophysical observers and six paid volunteers (age range: 24–76) with normal or corrected-to-normal vision participated in the study. Observers signed an informed consent form prior to their participation, and the study was approved by the local institutional review board.
Apparatus and stimuli
Stimuli were displayed at 60 Hz on a SAMSUNG SyncMaster 192N LCD monitor (flat screen size: 37.5 cm horizontally, 30 cm vertically). All experimental events were controlled by MATLAB scripts, and responses were collected via the computer keyboard.
The image area had 1,280 × 1,024 pixels and subtended 28.07 × 22.62 deg of visual angle at the viewing distance of 75 cm. Horizontal lines and transecting bars were displayed in black on a gray background that covered the entire screen except for a banner at the top with text reminding the observer of the question to be answered and the response options (which differed across variants of the landmark task). The horizontal line was 203 pixels (5.95 cm; 4.45 deg) long and 3 pixels (0.09 cm; 0.07 deg) wide; the transecting bars were vertical lines 21 pixels (0.59 cm; 0.46 deg) long and also 3 pixels (0.09 cm; 0.07 deg) wide, and were vertically centered on the horizontal line at a position that varied across trials with 1-pixel (0.03 cm; 0.02 deg) resolution.
Procedure
In the bisection task, the horizontal line was displayed at the center of the screen with the transecting bar at a random location between five and ten pixels away (in either direction) from the physical midpoint. Observers were asked to place the vertical bar at the location that they perceived to be the midpoint of the horizontal bar. For this purpose they used designated keys that moved the bar left or right in steps of one pixel per stroke. Free viewing was used and observers could make corrections before hitting another key to enter their final setting. Each observer made ten consecutive settings, in half of which the initial position of the bar was on the left (or the right) of the midpoint.
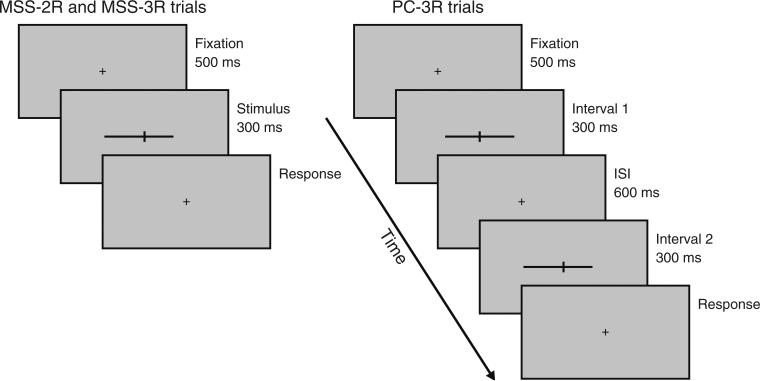
Under all variants of the landmark task, a black fixation cross was presented at the center of the image area throughout the session. The fixation cross consisted of horizontal and vertical arms one pixel wide and five pixels long. MSS variants of the landmark task displayed the stimulus configuration (horizontal line and transecting bar) directly on the fixation cross, which was thus occluded by the stimulus. To prevent fixation from acting as a clue to the midpoint of the line, the center of the transecting bar was always presented where the center of the fixation cross had been displayed, and the horizontal line was displayed with a lateral shift to attain the desired transecting offset. In the MSS-2R task, observers were asked to indicate whether the vertical bar was located on the right or on the left of what they perceived to be the midpoint of the horizontal line; observers who asked what they should do if they judged the vertical bar to be at the midpoint were instructed to make their best guess. In the MSS-3R task, observers were asked to report whether the vertical bar was on the left, on the right, or at the midpoint of the horizontal bar. Trials were self-initiated, as the next trial did not start until observers had hit the key that entered their response to the preceding trial. The session was also self-initiated. Trials consisted of a get-ready period of 500 ms, followed by a beep that immediately preceded the 300-ms stimulus presentation (see a schematic diagram of MSS trial timing in Fig. 3).
Fig. 3.
Schematic diagram of trial timings in method-of-single-stimuli (MSS) and paired-comparison (PC) variants of the landmark task. The fixation cross and the stimuli are not drawn to scale. In the MSS variants (left side), the actual transecting position in each trial was dictated by the applicable staircase, and the response requested could be binary (in MSS-2R) or ternary (in MSS-3R). In the PC-3R task (right side), in which a ternary response was requested, the interval in which the standard configuration transected at the center was presented (Interval 1 in this illustration), and the locations at which the test configuration in the other interval was transected were dictated by the applicable staircase in that trial
In the PC-3R task, two configurations were sequentially shown at the same location on the monitor as in the MSS tasks. Observers were asked to indicate which of the two presentations had displayed the vertical bar farther from the midpoint of the horizontal line. Trials were also self-initiated, and their timing was as follows (see the schematic diagram in Fig. 3): a get-ready period of 500 ms, followed by a beep and by one of the stimulus configurations displayed for 300 ms, an interstimulus interval (ISI) of 600 ms, and another beep followed by the other stimulus configuration, displayed for another 300 ms. One of the intervals displayed the transecting bar at the midpoint (standard configuration); the other displayed the transecting bar at an arbitrary position (test configuration). The order of presentation of the test and standard was randomized across trials.
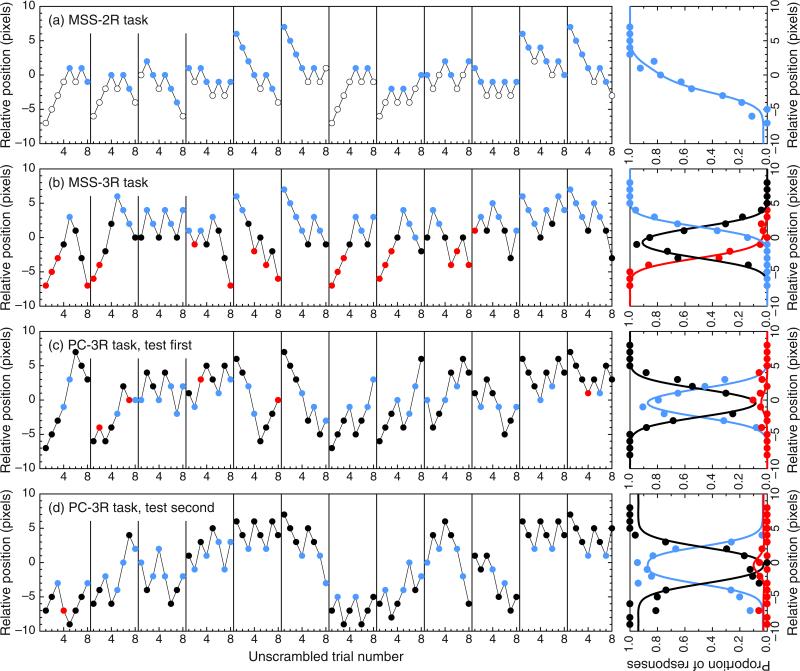
Data under the MSS variants (MSS-2R and MSS-3R) were collected in two consecutive sessions of 144 trials each, preceded by a practice session of at least 30 trials; data under the PC-3R task were collected in three consecutive sessions of 192 trials each, also preceded by a practice session of at least 36 trials. In each trial, the transecting location relative to the midpoint of the line was determined by adaptive methods optimized for efficient and accurate estimation of monotonic or nonmonotonic psychometric functions (García-Pérez, 2014; García-Pérez & Alcalá-Quintana, 2005). In the MSS variants, the 144 trials in each session arose from 18 eight-trial, randomly interwoven adaptive staircases, with three staircases starting at each of six levels (i.e., the position of the transecting bar on the first trial along the staircase: −7, −6, 0, 1, 6, and 7 pixels away from the physical midpoint of the horizontal line; negative values indicate leftward locations). Under the MSS-2R task, a “left” (vs. “right”) response shifted the transecting bar two pixels to the right (vs. the left) for the next trial along that staircase (which was not necessarily the next trial in the session); under the MSS-3R task, “left” and “right” responses had these same effects, whereas “center” responses shifted the transecting bar four pixels away from its current position in a direction decided at random with equiprobability. Trials under the PC-3R task arose from 24 eight-trial, randomly interwoven staircases, with four staircases starting at each of the initial levels used for the MSS variants. The 24 staircases represented two otherwise identical sets of 12, differing in that the test stimulus was displayed in the first interval in one of the sets, whereas it was displayed in the second interval in the other. Figure 4 shows sample tracks of actual staircases in each of the three tasks, along with psychometric functions fitted to the data gathered with them.
Fig. 4.
Tracks from sample staircases used to collect data from Observer 1 (left panels) and psychometric functions fitted to the data (right panels). Only a subset of 12 staircases is plotted for the MSS-2R task (a), the MSS-3R task (b), and the PC-3R task with the test presented in either the first interval (c) or the second interval (d). The binned data used to fit the psychometric functions in the right column come from the total number of staircases used in each case. The major color conventions are as in Figs. 1 and 2, except that the use of pale/dark shades has been altered to enhance visibility. Color is available only in the online version
Data collection within each session proceeded at the observer's pace, since only a response to the current trial triggered the next trial (thus allowing observers to take breaks, if necessary). A key was also enabled for observers to decline responding to the current trial if they had missed it for any reason (e.g., a blink or a lapse of attention), but observers were instructed to use this key only in such events, and not as a means to give themselves a second chance with the stimulus. Trials thus discarded were repeated when the staircase that they belonged to was reselected by the random interweaving process.
Data processing and parameter estimation
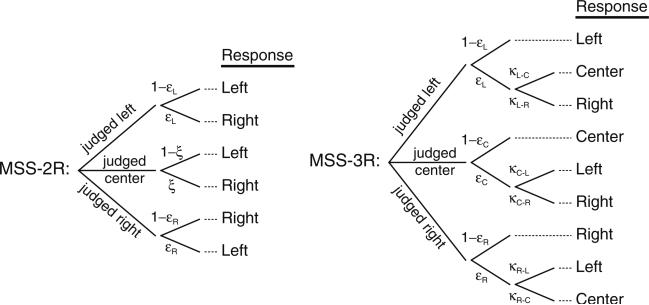
The means and standard deviation of each observer's ten settings in the bisection task were computed. On the other hand, the model-based psychometric functions presented above were fitted separately to the data from each observer in each variant of the landmark task, as follows. Because the model is unidentifiable in MSS versions of the task (see Fig. 1), the constraints δ2 ≥ 0 and δ1 = −δ2 were imposed, whose consequence was that a fitted MSS-2R curve with its 50 % point away from x = 0 was forced in order to indicate a perceptual shift (i.e., α ≠ 0 in Eq. 1). Thus, Eq. 3 was fitted to the data from the MSS-2R task under the above constraints, with α, β, δ2, and ξ as free parameters. Similarly, Eqs. 4 were fitted to the data from the MSS-3R task, also under the above constraints, with α, β, and δ2 as free parameters, because ξ is not involved in the corresponding model. The PC-3R task makes the model fully identifiable and allows for estimation of all free parameters (α, β, δ1, and δ2) upon fitting the psychometric functions in Eqs. 5 to PC-3R data. In all cases, maximum-likelihood estimates of the applicable parameters were obtained using the NAG subroutine e04jyf (Numerical Algorithms Group, 1999), which allows constrained optimization, although only the natural constraints β > 0 and δ1 ≤ δ2 were additionally imposed, where applicable. For simplicity, the preceding description has omitted that the fitted psychometric functions were in all cases extended to include lapse parameters, to account for empirical evidence of response errors. Such extension is described in Appendix B.
Performance measures (BP and DL) were computed from the fitted psychometric functions as discussed above, which implies that the lapse parameters were excluded from all computations, because they only had the instrumental goal of removing bias from estimates of the remaining parameters (see García-Pérez & Alcalá-Quintana, 2012b; van Eijk, Kohlrausch, Juola, & van de Par, 2008).
Parameter estimates were also sought for each observer under a joint fit to data from the three variants of the landmark task, which implemented the constraint that parameters α and β had common values across tasks (since they reflect task-independent perceptual processes), whereas parameters δ1 and δ2 varied freely across tasks. We had two reasons for the latter decision. First, evidence from other areas has indicated that observers push their resolution limit according to the difficulties that they experience with each particular task (see García-Pérez & Alcalá-Quintana, 2012b). Secondly, parameters δ1 and δ2 are incommensurate across the MSS and PC tasks, since they reflect the resolution to tell a given offset from zero in MSS tasks (see the horizontal axis in Fig. 1b), whereas they reflect the resolution to tell a difference of offsets from zero in PC tasks (see the horizontal axes in Figs. 2b and c). For the joint fit, no additional constraints on δ1 and δ2 were imposed on the models for MSS tasks, and the model for the MSS-2R task also included the parameter ξ. Other options for a joint fit (and their outcomes) are discussed at the end of the “Results” section.
The agreement among parameter estimates (α and β) or performance measures (BP and DL) across variants of the landmark task was evaluated pairwise through the concordance correlation coefficient ρc (Lin, 1989; Lin, Hedayat, Sinha, & Yang, 2002), which ranges from −1 to 1 and is defined as
| (10) |
where X and Y are the two variables whose concordance is assessed. In general, |ρc | ≤ |rxy|, because ρc measures scatter around the identity line, whereas rxy measures scatter around an arbitrary line described by the data. As we discussed earlier, differences in the estimates of α, β, and the BP across tasks may or may not be observed contingent on the values of the remaining model parameters, and therefore these differences were statistically assessed with Bradley and Blackwood's (1989) simultaneous test for equality of means and variances, which has been shown to be more efficient and robust to violations than are separate tests for means and variances conducted with a Bonferroni correction (García-Pérez, 2013). On the other hand, the model predicts that the DL estimates from MSS-3R and PC-3R tasks should be similar, whereas DL estimates from the MSS-2R task should not be smaller than either of the other two. This was assessed pairwise across tasks using paired-samples t tests.
Results
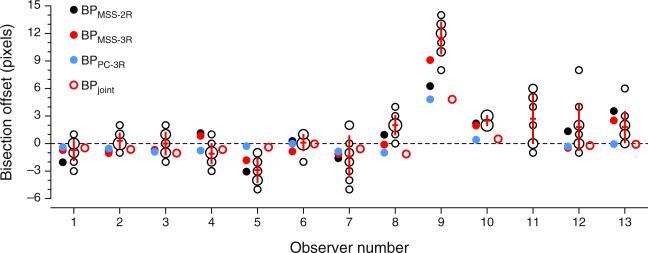
Figure 5 shows the bisection results for each observer. Despite the allowance of unlimited time to scan the configuration and make adjustments, some observers were not accurate at estimating the midpoint, although most of them made settings that were on average within three pixels of the physical midpoint. These results reflect each observer's best estimate of the midpoint under free-viewing conditions, and therefore the true reality that landmark tasks might be expected to estimate. It should nevertheless be kept in mind that the landmark task was in all variants carried out under meaningfully different conditions: Presentations were short (300 ms, with only enough time to get an overall impression of the configuration) and under fixation (so that the endpoints of the horizontal line were only visible peripherally). A close match between bisection and landmark results is probably not feasible, due to these differences in viewing conditions. (In anticipation of the results to be presented later, color circles in Fig. 5 give BP estimates from each variant of the landmark task; see the inset.)
Fig. 5.
Results for 13 observers. The central bundle of open circles indicates the bisection settings at the corresponding offsets (negative ordinates indicate positions to the left of the physical midpoint, and the horizontal dashed line indicates the physical midpoint); the radius of each circle indicates the number of settings at that particular offset. The superimposed cross-like red sketches indicate the average settings (horizontal segment) and the width of the interval spanning ±1 SD from the average. Color circles on the left for each observer indicate the bisection points (BPs) estimated separately from each variant of the landmark task; the colored ring on the right indicates the BP estimated through the joint fit of the model to data from all variants (see the inset). The results for Observer 11 in the landmark tasks are omitted (see Appendix C). Observers 1–7 were experienced, and the remaining observers were inexperienced paid volunteers. Color is available only in the online version
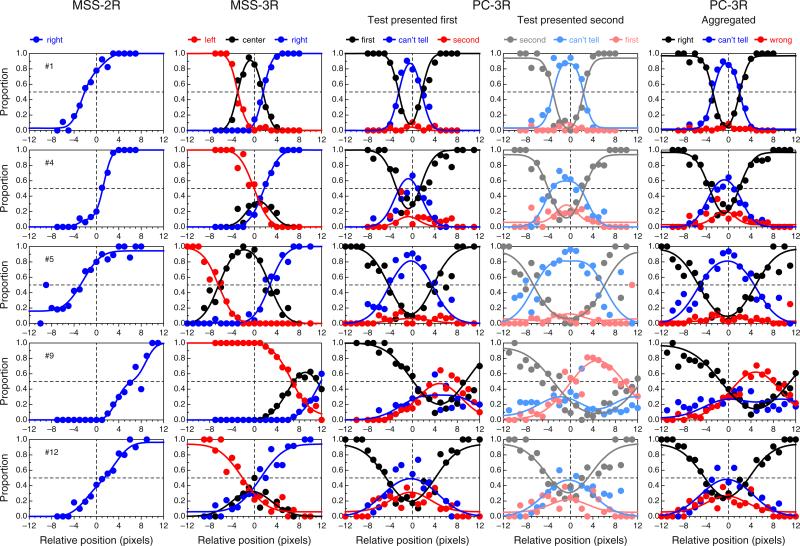
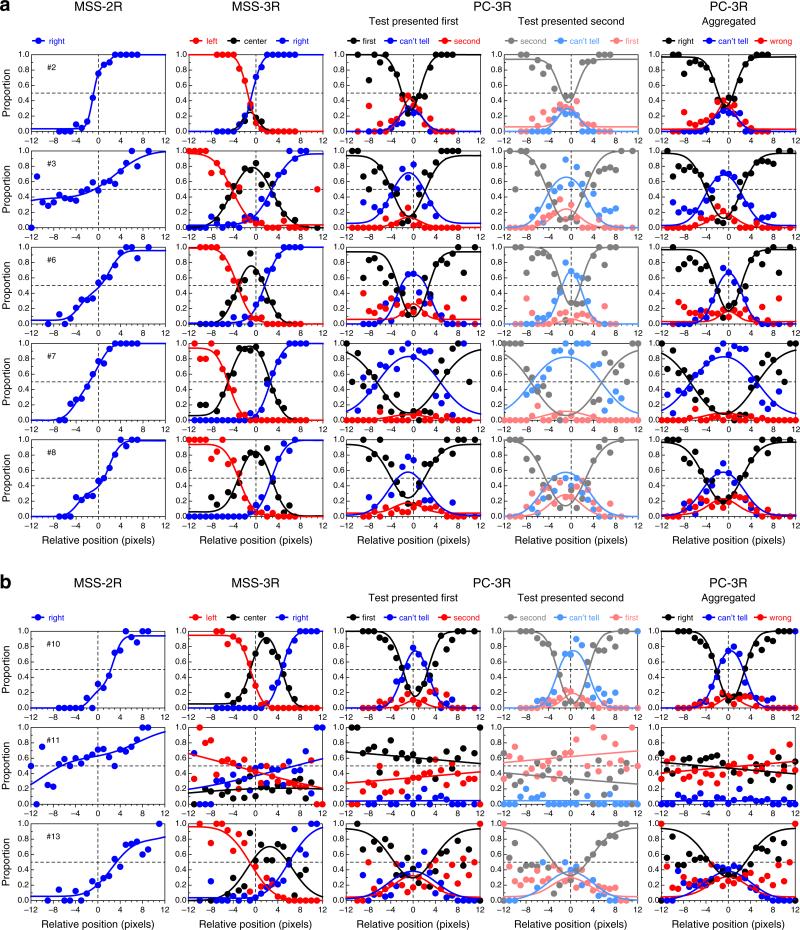
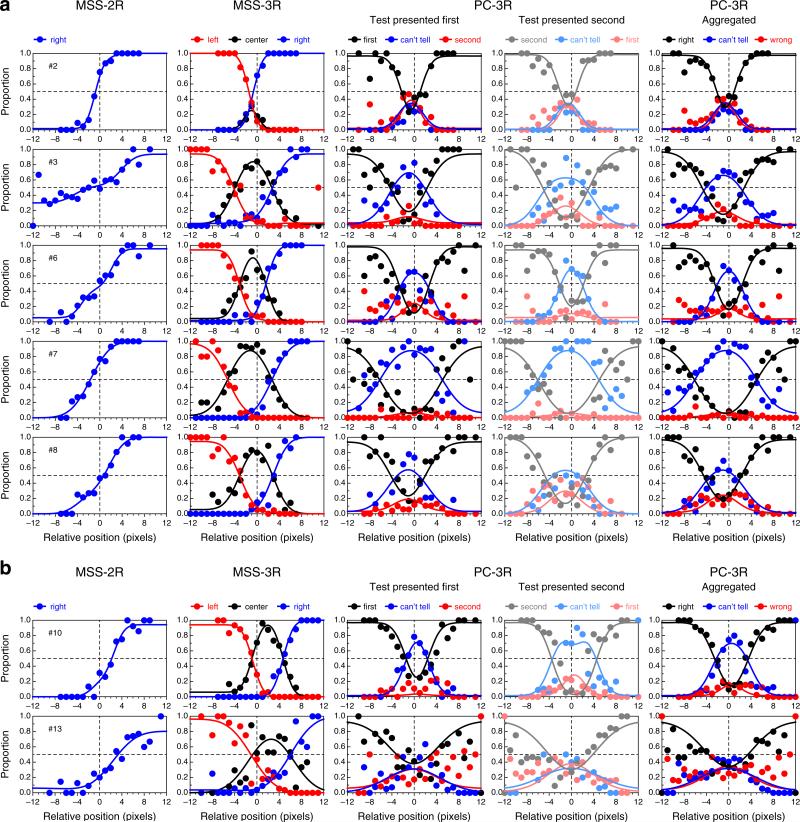
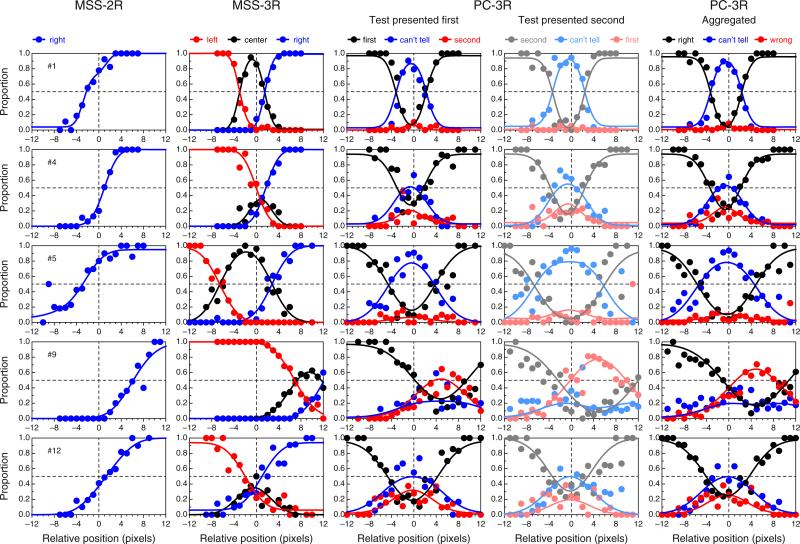
Figure 6 shows data and fitted psychometric functions for a subset of the observers in each variant of the landmark task, revealing a broad diversity of patterns within and across tasks (the results for the remaining observers are displayed and discussed in Appendix C). These psychometric functions were fitted separately to data from each task, and the fit seems adequate in all cases, although data are relatively more noisy for some observers than for others in some variants of the task. The data also reveal clear differences in the BPs across tasks for some observers. Specifically, the estimated BP is generally closer to the physical midpoint under the PC-3R task than under either MSS version (see also Fig. 5). The fact that psychometric functions in the PC-3R task also differed slightly across presentation orders (as is expected when decisional bias is present; see Fig. 2) suggests that estimates of the BP from the MSS versions of the task may also have been affected by decisional bias, and in a way that cannot be separated out from true perceptual shifts (see Fig. 1). Recall that the model fitted to data from MSS tasks assumed no decisional bias (i.e., δ1 = −δ2) and, hence, construes psychometric functions that are laterally displaced from the physical midpoint (x = 0) as evidence of a perceptual shift. As a result, parameter α is estimated to lie away from zero.
Fig. 6.
Data and fitted psychometric functions in each variant of the landmark task for five representative observers (rows). The rightmost column plots aggregated data across the two presentation orders in the PC-3R task, and also the average of the psychometric functions fitted for each separate order. The color conventions are as in Figs. 1 and 2, including the use of paler shades for the subset of trials in which the test was presented second (fourth column). Color is available only in the online version
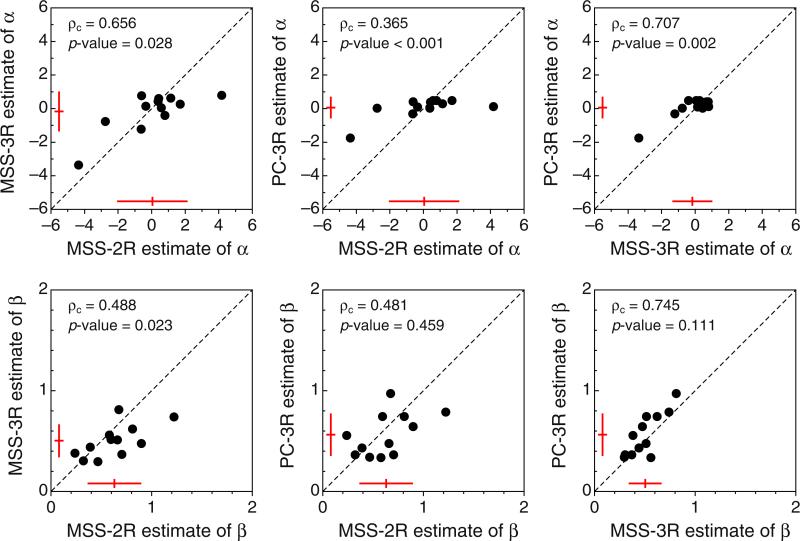
Figure 7 shows scatterplots of the estimates of α and β across tasks, revealing that these estimates differed meaningfully: Data points are not generally packed around the identity line, and ρc is accordingly low or moderate. As we discussed above, this is partly due to sampling error, but it is also caused by the assumption of lack of decisional bias made upon fitting the model to MSS data. Interestingly, the PC-3R task (which permits separating out sensory and decisional determinants of performance; see Fig. 2) renders estimates of α that are closer to zero than are their counterparts from MSS variants (see the red sketches in the panels on the top row of Fig. 7), suggesting that the constraint needed to fit the model to MSS data has overemphasized perceptual shifts in one direction or the other. The Bradley–Blackwood (1989) test for estimates of α was significant for all pairwise comparisons. On the other hand, estimates of β are more similar across tasks (bottom row of Fig. 7), and equality of means and variances was only rejected by the Bradley–Blackwood test in the comparison of estimates from the MSS-2R and MSS-3R tasks (left panel). Although this significant effect is not a necessary model outcome, it is expected when the interval of uncertainty is relatively broad and response bias is not extreme, so that the psychometric function turns out flatter in the MSS-2R task than in the MSS-3R task (see the earlier discussion of model psychometric functions in Figs. 1c and d).
Fig. 7.
Scatterplots of estimated α (top row) and estimated β (bottom row) across variants of the landmark task. Estimates from Observer 11 are excluded (see Appendix C). The inset at the top left of each panel shows the value of the concordance correlation coefficient ρc and the p value associated with the Bradley–Blackwood (1989) test for equality of means and variances. The sketches near the bottom and left axes in each panel indicate the mean and standard deviation of the data along the corresponding dimension. Color is available only in the online version
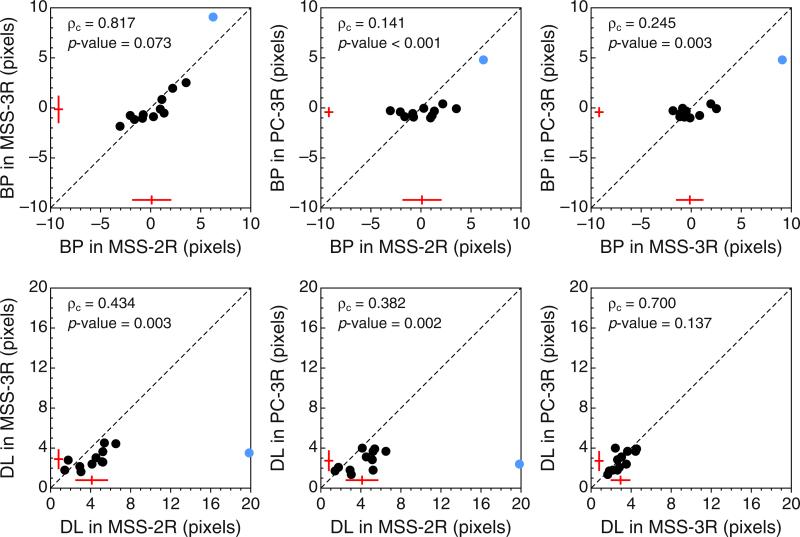
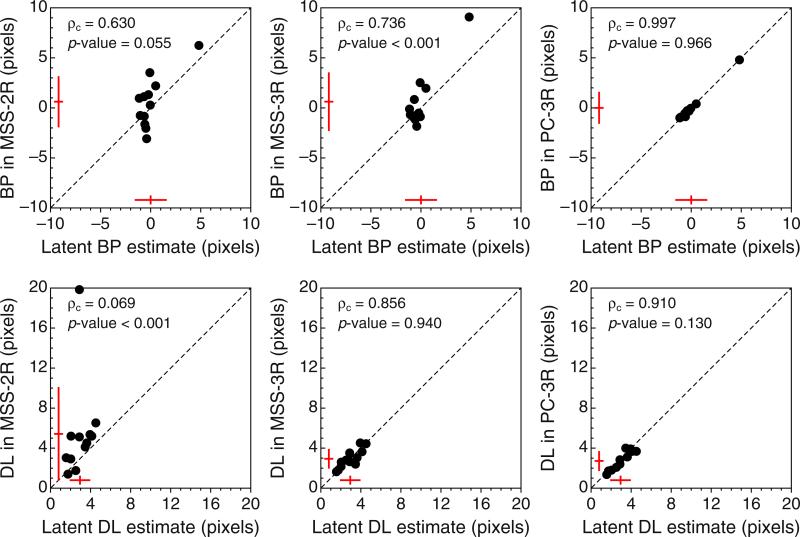
Since estimates of BP and DL are mostly (though not only) determined by estimates of α and β, Fig. 8 shows the implications via scatterplots of estimates of BP and DL across tasks. As can be seen in the top row of Fig. 8, estimates of BPPC-3R are closer to the physical midpoint than are estimates obtained with MSS variants of the task, provided that the stray data point plotted in blue is disregarded. This data point comes from Observer 9, whose consistent shift is clearly apparent in Fig. 5 and in the fourth row in Fig. 6. The value of ρc, the p value associated with the Bradley–Blackwood test, and the sketches of the distributions plotted in each panel excluded this stray data point in order to prevent contaminating these summary measures with an outlier, but note that this exclusion is inconsequential as far as model expectations are concerned: The model does not say where the true BP should lie or how homogeneous its location should be across observers, and this data point only seems to belong in a different sample of individuals whose true BP is to the right of the physical midpoint. In line with the predictions stated earlier, the bottom row of Fig. 8 shows that MSS-2R renders larger DL estimates than do the other tasks (i.e., the data points in the left and center panels generally fall below the diagonal, and the t tests are significant), whereas DL estimates from MSS-3R and PC-3R are very similar (i.e., the data points in the right panel lie around the diagonal, and the t test is not significant). The stray data point plotted in blue has also been excluded from these computations, but note that its location under the diagonal is consistent with expectations from the model. This data point comes from Observer 3, whose shallow psychometric function in the MSS-2R task (see the leftmost panel in the second row of Figs. 15 or 16) seems to arise from a broad interval of uncertainty and a lack of response bias (see the results to this effect reported in Fig. 11 below).
Fig. 8.
Scatterplots of estimated bisection points (BPs, top row) and estimated difference limens (DLs, bottom row) across variants of the landmark task. Estimates from Observer 11 are excluded (see Appendix C). The inset at the top left of each panel shows the value of the concordance correlation coefficient ρc and either the p value associated with the Bradley–Blackwood (1989) test for equality of means and variances (top row) or the p value associated with a paired-samples t test (bottom row). The sketches near the bottom and left axes in each panel indicate the mean and standard deviation of the data along the corresponding dimension. The stray, colored data point plotted in each panel was excluded from all computations (see the text). Color is available only in the online version
Fig. 15.
Data and psychometric functions fitted separately under each variant of the landmark task for the observers not shown in Fig. 6
Fig. 16.
Data and psychometric functions fitted jointly to all variants of the landmark task for the observers not shown in Fig. 9; Observer 11 is excluded for reasons discussed in the text
Fig. 11.
Widths and locations of the interval of uncertainty (the range from δ1 to δ2) under each variant of the landmark task, as estimated from the joint fit. Numerals at the top are estimated values of ξ (response bias) in the MSS-2R task for each observer. The results for Observer 11 are omitted (see Appendix C). Note that the decision variable is defined differently for MSS and PC variants of the landmark task, and thus the respective widths of the interval of uncertainty are incommensurate. Color is available only in the online version
Figure 9 shows the results of fitting psychometric functions jointly to data from the three tasks under the assumption of common values for parameters α and β in the psychophysical function μ for all tasks but potentially different parameters δ1 and δ2 across tasks, and with the additional parameter ξ in the MSS-2R task. (The results for the remaining observers are displayed in Appendix C.) In this joint fit, the constraint of no decisional bias was no longer imposed on MSS versions of the task, and lapse parameters were also allowed to vary freely across tasks. The most significant aspect in comparison with Fig. 6 (for the separate fits of the model to data from each variant) is that data from all tasks can be nearly identically accounted for on the reasonable surmise that the psychophysical functions are identical in all tasks, and hence that the underlying BP and DL are unique. The resultant joint estimate of the BP was plotted as a red ring for each observer in Fig. 5. Fitting the model separately to data from each task naturally produced different estimates of α and β across tasks (see Fig. 7), partly as a result of sampling error, but also, and more importantly, because MSS versions of the task do not properly allow the estimation of these parameters.
Fig. 9.
Data and psychometric functions fitted jointly to the data from all variants of the landmark task for the observers in Fig. 6 (rows). Graphical conventions are as in Fig. 6. Color is available only in the online version
The good joint fit justifies obtaining estimates of the underlying (or latent; see García-Pérez & Alcalá-Quintana, 2013) BP and DL via the estimated values of α and β from the joint fit. These latent BP and DL are, respectively, estimated as −α/β and 1.349/β, and they may be regarded as the true and uncontaminated quantities that a researcher sets out to estimate. A comparison of these latent BP and DL results with those estimated separately in each task thus indicates the extent to which the tasks are dependable. This is assessed in Fig. 10. In the MSS-2R task (left column), the separate BP estimates (top panel) are much more variable, and the separate DL estimates (bottom panel) are also more variable, and generally larger, than the corresponding latent values, reflecting the contaminating influence of decisional and response biases in this task (see Fig. 1c). In the MSS-3R task (center column in Fig. 10), the separate BP estimates are also affected by larger variability, whereas the separate DL estimates seem essentially accurate, also consistent with expectations based on the absence of influences of response bias in this task (which leaves DL estimates unaffected) but a remaining susceptibility to decisional biases (which affect the BP estimates). Finally, the PC-3R task (right column in Fig. 10) renders separate BP and DL estimates that match the latent values.
Fig. 10.
Scatterplots of estimated bisection points (BPs, top row) and estimated difference limens (DLs, bottom row) from separate (ordinate) versus joint (abscissa) fits of the model to data from each variant of the landmark task. Estimates from Observer 11 are excluded (see Appendix C). The graphical conventions are as in Fig. 8. Reported p values are those associated with the Bradley–Blackwood (1989) test for equality of means and variances. Color is available only in the online version
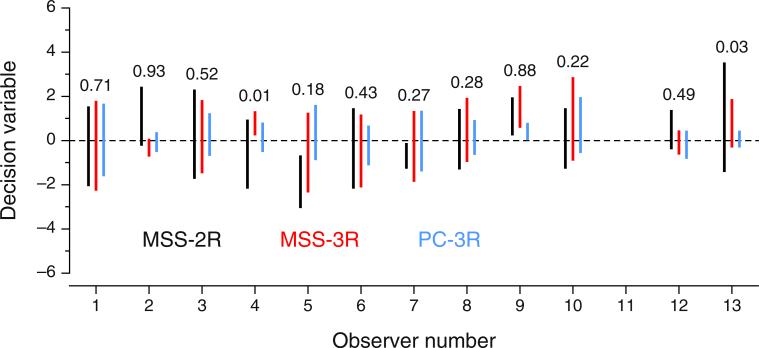
In the joint fit, the data from the PC-3R task constrain parameters α and β so as to make the model for MSS variants identifiable and, thus, permit estimating δ1 and δ2 for the MSS variants. Figure 11 shows estimates of the widths of the interval of uncertainty (the range from δ1 to δ2) in each task that arises from the joint fit. In some cases the interval is roughly centered on zero (indicating little decisional bias), although the interval is generally more centered in the PC-3R task (blue lines) than in the MSS variants. With some exceptions, the widths of the interval of uncertainty appear to be similar in the MSS-2R and MSS-3R tasks for each observer (compare the black and red lines in Fig. 11). Because the dimensions on which the boundaries δ1 and δ2 are defined are the same for both MSS variants (see Fig. 1), we checked out whether the data could also be accounted for in a joint fit under the additional constraint that δ1 and δ2 have the same values in MSS-2R and MSS-3R tasks. The results (not shown) rendered virtually identical outcomes for most observers, revealing that the different interval widths for the MSS-2R and MSS-3R tasks in Fig. 11 might simply reflect sampling error. Nevertheless, the fit turned out to be noticeably worse for some observers (5, 6, 7, 10, and 12), also affecting the estimated α and β and producing psychometric functions that did not always follow the path of the data (even for the PC-3R data) as closely as can be seen in Figs. 9 and 16. This result attests that observers seem to set task-related resolution limits, as has been reported in other studies (see García-Pérez & Alcalá-Quintana, 2012b).
Figure 11 also shows the estimated value of the response bias parameter ξ for each observer in the MSS-2R task. These values cover the entire range, from near zero (i.e., always responding “left” for “center” judgments) to near one (i.e., always responding “right” for “center” judgments). This response bias is essentially an observer characteristic, and there is no a priori reason for it to lean toward one side or the other in the population, or even to remain fixed for a given observer across stimulus conditions or task instructions. To establish the need for ξ as a free parameter, at the request of an anonymous reviewer we tried out an alternative joint fit in which ξ was forced to have a fixed value of .5. The results (not shown) were acceptable only for observers for whom the estimated value of ξ when regarded as a free parameter was within .1 units from .5; for the remaining observers, setting ξ = .5 affected the estimates of α and β and resulted in psychometric functions that showed systematic departures from the path of the data in all variants of the landmark task. This is natural, given the strong effect that the value of parameter ξ has on the shape of the psychometric function for MSS-2R tasks (see Fig. 1c). Forcing this parameter to a fixed value of .5 (or any other value, for that matter) implies a restricted range of shapes that can only accommodate data through substantial changes in the values of α and β, in a way that may not be compatible with the values demanded by data from the other tasks.
Discussion
Summary of results
Our study has investigated the origin of discrepancies in the estimated bisection point across variants of the landmark task. We started off with a model that includes a sensory component and a decisional component. The sensory component is given by the psychophysical function describing how physical space is mapped onto perceptual space, a component that precedes and is unaffected by the task with which observers’ responses are collected. The decisional component consists of a task-dependent rule determining how sensory judgments are made and how responses are given. A theoretical analysis of the model showed that the decisional component determines how and why observed performance should vary across tasks even when the sensory component remains unchanged. These theoretical results have implications on the interpretability of performance measures (BP and DL) obtained with different variants of the landmark task. Specifically, contamination from decisional aspects precludes interpreting the location and slope of the observed psychometric function in MSS-2R tasks as measures of the true BP and DL of the observers; the MSS-3R task suffers from the same problem with respect to the BP although the estimated DL is not contaminated by decisional aspects of the task and, thus, reflects (within sampling error) the true discrimination ability of the observers; finally, only the PC-3R task can separate out sensory and decisional determinants of performance and, thus, render proper estimates (within sampling error) of perceptual midpoint and discrimination ability.
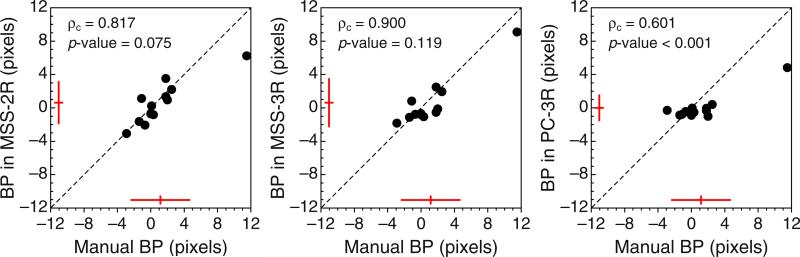
These characteristics were assessed in an empirical within-subjects study that used the three variants of the landmark task and also a manual bisection task. When these data were fitted separately, differences among the BP and DL estimates across variants of the landmark task conformed to the theoretical analysis, but fitting the model jointly to the data from all tasks under a common psychophysical function permitted an equivalent quantitative account that revealed a common BP and DL that gets differently distorted in each task, due to the decisional components. Interestingly, the estimated BP was in this case closer to the physical midpoint than was the observers’ average setting with the method of adjustment in the manual bisection task (see Figs. 5 and 12). This result is somewhat puzzling. Certainly, the different viewing conditions in our landmark and bisection tasks (see the “Method” section) might produce discrepancies, but one would expect them to lie in the opposite direction: In our bisection task (with free viewing and ample time for reconsideration before entering a final location), observers set the transecting bar generally farther from the physical midpoint than they could judge it to be in MSS-3R or PC-3R tasks (with short presentation durations and peripheral viewing). It would seem that observers can judge the midpoint much more accurately than they can place it when the task is entirely in their hands. The reason for this remains unclear, but it is worth noting that other evidence of some form of dissociation has been recently reported by Massen, Rieger, and Sülzenbrück (2014), also in a within-subjects study: Observers were significantly less accurate at bisecting a line when they marked the perceptual midpoint on it with a pencil than when they were asked to use scissors to cut the line in two halves.
Fig. 12.
Scatterplots of estimated bisection points (BPs) in the manual bisection task (abscissa) versus estimated BPs from the separate fits of the model to data from each variant of the landmark task (ordinate). These data were plotted in another form in Fig. 5. Estimates from Observer 11 are excluded (see Appendix C). The graphical conventions are as in Fig. 8, and reported p values are those associated with the Bradley– Blackwood (1989) test for equality of means and variances. Color is available only in the online version
The origin of discrepant results across psychophysical tasks
Discrepancies between bisection and landmark tasks are interpreted as revealing that “very different strategies and underlying neural networks are invoked by the bisection and landmark tasks” (Cavézian et al., 2012, p. 89). Our results show that a substantial part of these discrepancies arise from the widespread use of the MSS-2R variant of the landmark task, in which the lack of a “center” response option invokes response biases when observers are forced to report the result of a “left”/“right” judgment that they cannot make. We have also shown that the PC-3R task is theoretically optimal for eliminating response bias and separating perceptual shifts from decisional biases. However, in clinical settings, the PC-3R task may be difficult to use in the temporal mode and with the short presentations used in this study. A spatial mode with free viewing and unlimited presentation duration might be feasible, but this would significantly lengthen testing time. An alternative approach for use under the constraints and conditions of clinical studies may still be needed, but in the meantime, replacing the conventional two-response format of the MSS-2R landmark task with the three-response format that renders the MSS-3R is advisable, to remove response biases from assessments of space perception in clinical populations.
The results reported here surely apply to studies of time perception, which typically use a temporal bisection task (analogous to our spatial MSS-2R) or a temporal generalization task, which is another version of MSS-2R in which observers are asked to give a same–different response (see Wearden, 1992). Discrepant results across these tasks have also been reported in the estimation of the temporal bisection point (see, e.g., Gil & Droit-Volet, 2011). The indecision model that we have used to explain these discrepancies in measurements of the spatial BP is similar to the model put forth by Wearden and Ferrara (1995; see also Kopec & Brody, 2010) to describe observers’ performance in the temporal bisection task, with the major differences being that their model assumes δ1 = −δ2 and a fixed ξ = .5 (in our notation). These assumptions about decisional and response components cannot be tested with isolated MSS data. The use of three tasks in our study allowed for testing them, and our results show that these assumptions are untenable (see Fig. 11). The temporal bisection task can easily be transformed into temporal MSS-3R (see, e.g., Droit-Volet & Izaute, 2009), from which the DL could be estimated without contamination from decisional aspects. But estimating the temporal BP without influence from decisional determinants would require a temporal analogue of the spatial PC-3R task introduced here.
Discrepant results across variants of MSS have also been reported and analogously explained in other areas of time perception. For instance, in experiments on perception of temporal order, stimuli A and B are presented in each trial with some stimulus onset asynchrony (SOA) and the observer must judge the order of presentation. Because the stimulus variable is SOA and only one SOA is presented in each trial, this paradigm falls into the category of MSS.3 Three variants of MSS are used in this research area. In the temporal-order judgment (TOJ) task, observers are only allowed to respond “A first” or “B first”; in the binary synchrony judgment (SJ2) task, observers are asked to judge the two presentations as being “synchronous” or “asynchronous”; and in the ternary synchrony judgment (SJ3) task, observers are asked to report judgments as being “A first,” “synchronous,” or “B first.” Estimates of the point of subjective simultaneity (PSS) typically differ across tasks even in within-subjects studies (e.g., van Eijk et al., 2008; see also Schneider & Bavelier, 2003), which has led to the notion that each task measures a different process (Spence & Parise, 2010). This is counterintuitive, since the only difference across tasks is the question asked at the end of the trial, once the stimulus has been fully processed: Consider a mixture task in which the observer does not know until the end of each individual trial which of the various questions is going to be asked on this occasion. Schneider and Komlos (2008) reported an experiment carried out with this mixture task in an investigation of the purported effect of attention in visual contrast perception, and they found that the presumed attentional effect that was observed in comparative judgments could be understood as an artifact of a decisionalor response-bias component that is absent in equality judgments. Recent reanalyses have also shown that discrepant results across tasks can be understood as a mere outcome of response bias taking place in the TOJ task, where judgments of “synchrony” cannot be reported and observers are forced instead to give an arbitrary temporal-order response of nonperceptual origin (see García-Pérez & Alcalá-Quintana, 2012b).
Can nonperceptual biases be eliminated in some other way?
We mentioned in the introduction that the landmark task is sometimes administered with instructions to indicate which of the two segments of the transected line is longer (or shorter). Although there is still a single stimulus presentation in this case, the observer is here asked to make a paired comparison for which the model in Fig. 2 does not apply, because the observer compares lengths rather than absolute offsets. This raises the question as to whether a landmark task administered under these length-comparison instructions is free of contamination from response and decisional biases. The answer is negative, as demonstrated next.
First note that the landmark stimulus is conceptualized in this task as two abutting lines demarcated by a vertical divide, and thus the task falls into the category of spatial 2AFC discrimination paradigms. In the typical use of this paradigm, one of the lines (the standard) would have the same length in all trials, whereas the length of the other (the test) would vary across trials. This does not hold under this variant of the landmark task, because changing the position of the transecting bar alters the lengths of the two segments to be compared, so that there is no fixed standard across trials. In addition, the concept of presentation order is alien to this task and does not give rise to two sets of psychometric functions: Although presentation order could be regarded as reversed for stimuli in which the transecting bar was at symmetric locations with respect to the physical midpoint, the data in each case would be plotted on opposite sides of the single psycho-metric function that arises from this task, which has the position of the transecting bar as the stimulus variable. Thus, the negative and positive half-axes on which the psychometric function is defined represent the two possible “presentation orders,” and thus, a single presentation order exists per point on the psychometric function. These two characteristics have consequences for how performance on this task must be modeled, in comparison with conventional 2AFC discrimination tasks with an invariant standard across trials and two possible presentation orders per point on the psychometric function. Figure 13 shows a suitable model for this situation. Here, the psychophysical function (Fig. 13a) reflects the relation of perceived length to physical length, which may differ in the left (L) and right (R) hemifields due to perceptual distortions. For simplicity, and without loss of generality, these psychophysical functions are given by the simple linear function
| (11) |
Fig. 13.
Indecision model and predictions for a length-comparison variant of the landmark task with binary and ternary response formats under four scenarios (columns). a Psychophysical functions μL (light green) and μR (dark green) mapping physical length onto perceived length in each visual hemifield. The two functions are identical in the absence of perceptual distortions (first and second columns), but they differ when perceptual space is distorted in one of the hemifields (third and fourth columns). Vertical–horizontal segments indicate the physical and perceived lengths of the two segments of a sample 60-unit line transected two units to the left of its midpoint (i.e., the length of the left segment is 28 units, whereas that of the right segment is 32 units). b Distribution of the decision variable (difference in perceived lengths of the two segments) for the sample case illustrated in row a. Also shown are the decision boundaries δ1 and δ2, which are symmetrically placed in the absence of decisional bias (first and third columns), but asymmetrically placed when there is decisional bias (second and fourth columns). c Psychometric functions that may be observed under the binary response format, according to the response bias with which the observer guesses when undecided (“I can't tell” judgments). The bisection point and difference limen of the observed psychometric functions are uninterpretable. Graphical conventions are as in Fig. 1. d Psychometric functions for each type of response in the ternary response format (see the legends). The ensemble of psychometric functions is laterally shifted by both perceptual distortions and decisional bias. Color is available only in the online version
In the absence of perceptual distortions affecting perceived length in each hemifield, μL = μR (first and second columns in Fig. 13); otherwise, μL and μR (i.e., βL and βR) will differ (third and fourth columns in Fig. 13). Assume that perceived length is also normally distributed, with unit variance and mean μL(x) or μR(x), according to the hemifield in which the segment is located. If the horizontal line has length l, the two segments to be compared in a given trial have lengths lL and lR according to the position of the transecting bar, with lL + lR = l. Then, the perceived difference in length is normally distributed, with mean μR(lR) − μL(lL) and variance 2 (see Fig. 13b). Assume also that observers cannot give an informed response when the perceived difference in lengths lies in the interval of uncertainty demarcated by boundaries δ1 and δ2, which may be centered (i.e., no decisional bias; first and third panels in Fig. 13b) or displaced (implying decisional bias; second and fourth panels in Fig. 13b). In the binary left/right response format without an “I can't tell” option, observers give an arbitrary response when undecided, with a bias determined by parameter ξ. This renders psychometric functions that may vary in shape and location according to the value of ξ, but also as a consequence of perceptual distortions or decisional bias in a way that cannot be differentiated (cf. the four panels in Fig. 13c). With a ternary response format including an “I can't tell” option, response bias no longer intrudes, and the resultant set of psychometric functions (Fig. 13d) has a bilateral axis of symmetry at the physical midpoint, in the absence of decisional bias and perceptual distortions (first panel in Fig. 13d). Decisional bias without perceptual distortions (second panel in Fig. 13d) shifts the location of the axis of symmetry, but so do actual perceptual distortions without decisional bias (third panel in Fig. 13d) or a combination of perceptual distortions and decisional bias (fourth panel in Fig. 13d). This length-comparison variant of the landmark task is thus unsuitable for separating perceptual effects from decisional and response bias (under the binary left/right format) or from decisional bias (under the ternary response format).
It should be noted that sometimes a measure of response bias has been extracted from data collected under the length-comparison variant by asking observers to indicate in separate blocks which side is shorter or which side is longer (e.g., Bisiach et al., 1998). Alternation of the two questions across trials has also sometimes been used as a means to eliminate (or check for) response bias (e.g., Schmitz, Deliens, Mary, Urbain, & Peigneux, 2011), and this method has also been used in other studies involving paired comparisons (e.g., Gobell & Carrasco, 2005). How this strategy accomplishes its intended goal has never been demonstrated formally, but its use stems from the surmise that informed responses (i.e., those based on solid sensory evidence) will be in the opposite direction when the question is asked in reverse, whereas arbitrary responses, given with response bias when undecided, will remain the same when the question is reversed. The underlying notion is that response bias implies some type of inevitable tendency to give a specific location response when undecided. If this surmise holds true, the observed performance would differ with the polarity of the question only if observers had some response bias. Yet, since the guessing strategy used by observers is unknown, it is not immediately obvious that reversing the question would not also affect this guessing strategy. For one thing, observers cannot be unaware of the polarity of the question and of the use of questions of both polarities, which may induce reversals of their guessing strategy, if only to look consistent to the researcher. Of course, this is not to say that guessing strategies will surely reverse when the question is reversed, but rather that their stability is not guaranteed and also cannot be assessed. A comparison of observed performance across questions of opposite polarity does not speak unequivocally of the presence or absence of response bias. The best way around problems caused by response bias when participants are undecided is certainly to remove the influence of response bias entirely by providing a separate response category to record undecided cases. To additionally remove the effects of decisional bias, a psychophysical task is needed that provides full psychometric functions for each presentation order, such as the PC-3R task used here, or the conventional form of 2AFC discrimination paradigms with a fixed standard and the presentation of test and standard stimuli in both orders or positions (for a formal demonstration and empirical examples of how this alternative strategy attains its goal, see García-Pérez & Alcalá-Quintana, 2013).
It should finally be stressed that the confound of response bias, decisional bias, and perceptual bias in MSS tasks is created by the tasks themselves, and not by the model fitted to data. The conventional practice of fitting an arbitrary (e.g., logistic or Gaussian) two-parameter psychometric function to data from such tasks does not eliminate the problem. In fact, it can easily be seen that any such arbitrary psychometric function implies some form for the psychophysical function μ and, more importantly, the implicit assumptions of no decisional bias and no response bias (i.e., δ1 = δ2 = 0, in terms of our model), so that the location and slope of the fitted psychometric function are forced to masquerade the influences of decisional or response biases as perceptual effects. The use of tasks that can separate out these influences is needed for a proper assessment of true perceptual shifts, whether in studies about the perceptual midpoint in clinical populations or in studies on the role of attention on the perceptual midpoint (e.g., Toba, Cavanagh, & Bartolomeo, 2011). Only the use of tasks that are free of confounds can reveal whether observed effects are caused by true perceptual shifts or by mere decisional or response biases induced by the attentional manipulations.
A retrospective look at experimental findings in the literature
Our results show that BPs and DLs estimated with the conventional MSS-2R variant of the landmark task are affected by the observers’ response and decisional biases. Given that the interval of uncertainty (δ1, δ2) was in our sample generally off-center and that the response bias parameter ξ was generally away from 0.5 (see Fig. 11), MSS-2R estimates of the BP were understandably further away from the physical midpoint than corresponding estimates obtained with the bias-free PC-3R task (compare the relative locations of color circles for each observer in Fig. 5; see also the top row in Fig. 8) and DL estimates were also inflated (see the bottom row in Fig. 8). To what extent should findings obtained with the MSS-2R task be questioned in the light of this evidence? Although it is unlikely that the use of bias-free methods (i.e., the PC-3R task) will overturn major research findings obtained with the non-dependable MSS-2R task or the length-comparison variant discussed in the preceding section, we believe that there is indeed some room for concerns.
Estimates of the DL obtained with MSS-2R or length-comparison tasks are seriously affected and become increasingly larger with increasing width of the interval of uncertainty (i.e., as δ2 − δ1 increases) and decreasing response bias (i.e., as ξ approaches .5). This misestimation is systematic and directional, since estimated DLs will not be smaller than the true DLs except by sampling error (see Figs. 1c and 13c). Given the broad intervals of uncertainty reported by Olk et al. (2004) for hemispatial neglect patients as compared to normal controls and the evidence reported by Bonato, Priftis, Marenzi, and Zorzi (2008), to the effect that the width of the interval of uncertainty correlates positively with neglect severity, comparisons of estimated DLs in patients versus normal controls are affected by this problem.
But large intervals of uncertainty also lend themselves to potentially large effects on estimates of the BP from MSS-2R or length-comparison tasks (see Figs. 1c and 13c again). Although this effect is bidirectional and will arguably average out, provided that the response bias parameter is evenly distributed across observers in a sample, this will certainly produce more variable estimates and less dependable comparisons. This undesirable variability may be responsible for the lack of consistent patterns of results across the various tasks used to diagnose neglect (for a review, see Harvey, 2004).
It should also be noted that accurate estimates of both the BP and the DL are impossible with the MSS-2R variant, even in the absence of decisional bias (see the left panel in Fig. 1c). In these conditions, accurate estimation of the BP is obtained when ξ = .5 (central black curve), but this produces the largest possible overestimate of the DL; on the other hand, accurate estimation of the DL is obtained when ξ = 0 or ξ = 1 (red and blue curves), but then the BP is grossly misestimated in one direction or the other. The same holds under the length-comparison variant of the landmark task (see Fig. 13c). Then, studies in which BPs and DLs have both been estimated with these tasks cannot have obtained accurate estimates of both.
The foregoing discussion should not be misconstrued as indicating that our position is that humans can bisect accurately and that all of the shifts reported in the literature are a spurious consequence of nonperceptual biases, whether in patients or in normal controls. For one thing, even one of our normal observers showed a consistent shift in all tasks, including the bias-free PC-3R task (see Observer 9 in Fig. 5). More importantly, decisional and response biases shift the psychometric function in one direction or the other, which can also completely eliminate or reduce the apparent magnitude of a true perceptual shift (see the center column in Fig. 1 and the third and fourth columns in Fig. 13). Our only points are that (1) under MSS-2R or the alternative length-comparison variant of the landmark task, the resultant estimates are uninterpretable, because they can be shifted in either direction by decisional or response biases, and (2) that only the use of tasks such as our PC-3R can disentangle these influences and provide accurate estimates of true perceptual shifts. Only in these conditions can the perceptual and nonperceptual determinants of observed performance be assessed. In this respect, knowledge of the occasions in which observers are undecided provides valuable information, and thus it is of utmost importance to record them by provision of a separate response category in a ternary response format, instead of letting observers arbitrarily misreport them as “left”/“right” responses on application of their guessing strategies and response bias.
Appendix A
This appendix derives the probability distribution of D = |S2| − |S1|, where S1 and S2 are independent and normally distributed random variables whose densities are given by Eq. 2, with means μ(x1) and μ(x2), respectively. First, Y2 = |S2| and Y1 = |S1| are known to have folded normal distributions (Leone, Nelson, & Nottingham, 1961) with densities
| (A1) |
The probability distribution of a transformation of two random variables is obtained by marginalizing the product of the absolute value of the Jacobian of the transformation and the joint density evaluated at the variables expressed in terms of the transformation (Bain & Engelhardt, 1992, p. 206). When Y1 and Y2 are independent random variables with the folded normal distributions in Eq. A1, their joint distribution is h(y1, y2) = h1(y1) × h2(y2). To obtain the probability distribution of D = Y2 − Y1, let V = Y2, so that Y1 = V − D and Y2 = V. The Jacobian of the transformation is
| (A2) |
The joint density of D and V is then given by h*(d, v) = h(Y1 = v − d, Y2 = v) × |J|. Therefore,
| (A3) |
whose domain is the region of satisfying V ≥ 0 and D ≤ V. The distribution of D = Y2 − Y1 is finally obtained by integrating V out of Eq. A3 within the joint domain—that is,
| (A4) |
yielding
| (A5) |
The distribution function, for which there is no closed-form expression, is given by
| (A6) |
where parameters x1 and x2 have been introduced for later reference and only to make explicit the stimulus levels x1 and x2 presented in the first and second intervals, respectively.
Appendix B
This appendix describes the extension of the model to incorporate the eventuality of response errors upon using response keys to report judgments. The extension is analogous to that described by García-Pérez and Alcalá-Quintana (2012b) for similar psychophysical tasks in research on the perception of temporal order. The reader is referred to García-Pérez and Alcalá-Quintana (2012c) for a thorough discussion of the error parameters and their justification.
The extension requires consideration of the form in which response errors can occur once the judgments have been made. This is illustrated in Fig. 14 for MSS variants of the task. In MSS-2R, in which only “left” or “right” responses are given, let εL be the probability of misreporting a “left” judgment (as a “right” response) and let εR be the probability of misreporting a “right” judgment (as a “left” response). The probabilities of the three possible judgments in a trial in which the line is transected at a given location are given by the areas in the corresponding regions of decision space (see Fig. 1b), and these outcomes are represented by the three starting branches in the tree diagram on the left of Fig. 14. Then, “left” judgments are misreported as “right” responses with probability εL and “right” judgments are misreported as “left” responses with probability εR, whereas “center” judgments are arbitrarily reported as “right” responses with probability ξ. The resultant psychometric function for “right” responses in the MSS-2R task is
| (B1) |
with f being given by Eq. 2, and note that εL = εR = 0 (i.e., no response errors) renders Eq. 3.
Fig. 14.
Tree diagrams describing the sequences of events mapping unobservable judgments onto the observed responses in the MSS-2R (left) and MSS-3R (right) tasks. The starting point at the left of each diagram is the unobservable judgments, which occur with probabilities given by the applicable equations. Once the judgment is made, misreports occur with probabilities given by the ε parameters. In the MSS-2R task (left diagram), misreports result in a response opposite to the “left” or “right” judgment originally made, whereas “center” judgments render an arbitrary “left” or “right” response at random and according to the response bias parameter ξ. In the MSS-3R task (right diagram), misre-ports also render a response different from the judgment that was made, but, since two error responses are possible, which one is given is determined by additional parameters κ
The extension for MSS-3R tasks is analogous, except that the ternary response format implies that each judgment can be misreported in two forms (see the tree diagram at the right of Fig. 14). Thus, let εL, εC, and εR be the probabilities of misreporting “left,” “center,” and “right” judgments, respectively. Also, let κX–Y be the probability of misreporting judgment X as response Y—so that, for instance, κL–C and κL–R are the probabilities of misreporting a “left” judgment as a “center” response or as a “right” response, with κL–C = 1 − κL–R, and analogously for all other possible judgments and misreports. The resultant psychometric functions for “right” and “center” responses in the MSS-3R task are
| (B2a) |
| (B2b) |
with f also given by Eq. 2, and note that εL = εC = εR = 0 (i.e., no response errors) renders Eqs. 4.
In the PC-3R task, the extension proceeds also as illustrated in the tree diagram at the right of Fig. 14, with an inconsequential notational change. Specifically, the judgments and responses are instead “Interval 1,” “I can't tell,” and “Interval 2.” In the PC-3R task, the mapping of judgments onto responses may induce errors with different probabilities when the test configuration is presented first or second (see a discussion to this effect in Appendix C), and hence, independent extensions are used for each presentation order. The resultant psychometric functions are analogously given by
| (B3a) |
| (B3b) |
| (B3c) |
| (B3d) |
with f given by Eq. A5. In the symbols denoting the error parameters, the subscripts 1, C, and 2 refer to the judgments/ responses (“Interval 1,” “I can't tell,” and “Interval 2”), and the parenthetical superscripts refer to the interval in which the test configuration was presented. Note that Eqs. 5 instead obtain when all εs are zero (i.e., no response errors).
The only effect of error parameters is to alter the asymptotes of the psychometric functions (for a detailed explanation, see García-Pérez and Alcalá-Quintana, 2012c). The estimated values of these error parameters were generally null or very small, and their effect on the asymptotes can be seen in Fig. 9, as we describe next for sample cases. For Observer 1 in the MSS-2R task (left panel in the first row of Fig. 9), the estimated εL was 0.04 as a consequence of the (accidental) nonzero proportion of “right” judgments at x = −6, rendering the nonzero lower asymptote of the fitted psychometric function; in contrast, no evidence of response errors is observed at large positive stimulus positions, and hence, the estimated εR was zero. More evidence of response errors can be seen at large negative and large positive stimulus positions in the MSS-2R data of Observer 5 (left panel in the third row of Fig. 9). The estimated error parameters in this case were εL = 0.06 and εR = 0.05, which affect the upper and lower asymptotes of the fitted psychometric functions. A similar effect in the psychometric functions fitted to MSS-3R data can be seen for Observer 12 (second panel in the last row of Fig. 9); for analogous effects in the psychometric functions fitted to PC-3R data, see the results for Observers 1 and 4 (third and fourth panels in the first two rows of Fig. 9).
Appendix C
Figures 15 and 16 show data and fitted psychometric functions for the observers whose results are not shown in Fig. 6 (for the separate fits of data from each variant of the landmark task) or in Fig. 9 (for the joint fits of data from all variants of the landmark task). Note that the data from Observer 11 are very noisy in all variants of the landmark task, and it also looks as if the observer had largely avoided “I can't tell” responses in the PC-3R task and simply guessed at random between “Interval 1” and “Interval 2” responses at all stimulus positions. The observer did not acknowledge this or other wild behavior on debriefing, and also did not report any difficulty carrying out the task. All data from this observer were nevertheless discarded, because they are unlikely to reflect the observer's actual bisection ability.
Large amounts of noise are also apparent for some observers in the PC-3R task, as compared to their own performance in MSS variants of the landmark task. By the observers’ own accounts on debriefing, this seems to have been caused by an unanticipated conflict in the response interface. Specifically, observers gave their responses in the PC-3R task with the “1” (first interval), “2” (second interval), and “3” (“can't tell”) keys on the numeric pad of the computer keyboard. On a nonnegligible number of occasions, presentation of the test configuration in the first interval with the transecting bar clearly on the right induced observers to hit keys “2” or “3” rather than key “1”; analogous errors (but in reverse) occurred when the test stimulus was presented in the second interval and with the transecting bar clearly on the left. These types of response errors are very apparent in the data from Observer 13 in Fig. 1: When the test was presented first (third panel from the left), positive stimulus positions show a noisy mixture of “Interval 1” and “Interval 2” responses (black and red circles); when the test was presented second (fourth panel from the left), an analogous mixture occurs at negative stimulus positions. In retrospect, this conflict would have disappeared, and collected data would arguably have been less noisy, if the observers had instead been requested to indicate which configuration displayed the vertical bar closer to the horizontal midpoint (which is equivalent, as far as the model is concerned). Nevertheless, we do not see any sign in the data to the effect that the extra noise caused by this conflict might invalidate the results obtained with the PC-3R task.
Footnotes
1 The term response bias is often used to denote what will be called decisional bias here, to be described below. And it is also used at other times to refer to a directional bias by which observers preferentially give one of the response options, regardless of the features of the stimulus (Bisiach, Ricci, Lualdi, & Colombo, 1998; Milner, Harvey, Roberts, & Foster, 1993). In this article, response bias will exclusively denote observers’ uneven use of the “left” and “right” response categories when they have to guess in response to a stimulus for which their informed judgment is “at the midpoint.” Note that this type of contingent guessing differs substantially and meaningfully from the wild guessing discussed by Toraldo, McIntosh, Dijkerman, and Milner (2004), which takes place irrespective of stimulus features and without any judgment being made.
2 The unit-variance assumption is inconsequential and only serves to set a common but arbitrary scale in SDT models. As will be clear from Eqs. 3 and 4 below, potential nonunit values of the standard deviation of sensory effects are incorporated into the slope parameter β of the psychophysical function in Eq. 1.
3 For paired-comparison variants involving two SOAs per trial, see Allan and Kristofferson (1974), Fouriezos, Capstick, Monette, Bellemare, Parkinson, and Dumoulin (2007), or Stevenson and Wallace (2013).
Author note This research was supported by Grant Nos. PSI2009-08800, from Ministerio de Ciencia e Innovación, and PSI2012-32903, from Ministerio de Economía y Competitividad, to M.A.G.-P., and by NIH Grant Nos. R01EY05957 and R01EY12890 to E.P. We thank Zachary Reynolds for his help in participant recruitment and data collection.
Contributor Information
Miguel A. García-Pérez, Departamento de Metodología, Facultad de Psicología, Universidad Complutense, Campus de Somosaguas, 28223 Madrid, Spain
Eli Peli, Schepens Eye Research Institute, Massachusetts Eye and Ear Infirmary, Harvard Medical School, Boston, MA 02114, USA.
References
- Alcalá-Quintana R, García-Pérez MA. A model for the time-order error in contrast discrimination. Quarterly Journal of Experimental Psychology. 2011;64:1221–1248. doi: 10.1080/17470218.2010.540018. doi:10.1080/17470218.2010.540018. [DOI] [PubMed] [Google Scholar]
- Allan LG. The location and interpretation of the bisection point. Quarterly Journal of Experimental Psychology. 2002;55B:43–60. doi: 10.1080/02724990143000162. doi:10.1080/02724990143000162. [DOI] [PubMed] [Google Scholar]
- Allan LG, Kristofferson AB. Successiveness discrimination: Two models. Perception & Psychophysics. 1974;15:37–46. doi:10.3758/BF03205825. [Google Scholar]
- Bain LJ, Engelhardt M. Introduction to probability and mathematical statistics. 2nd ed. Duxbury; Pacific Grove, CA: 1992. [Google Scholar]
- Bisiach E, Ricci R, Lualdi M, Colombo MR. Perceptual and response bias in unilateral neglect: Two modified versions of the Milner landmark task. Brain and Cognition. 1998;37:369–386. doi: 10.1006/brcg.1998.1003. doi:10.1006/brcg.1998.1003. [DOI] [PubMed] [Google Scholar]
- Bonato M, Priftis K, Marenzi R, Zorzi M. Modulation of hemispatial neglect by directional and numerical cues in the line bisection task. Neuropsychologia. 2008;46:426–433. doi: 10.1016/j.neuropsychologia.2007.08.019. doi:10.1016/j.neuropsychologia.2007.08.019. [DOI] [PubMed] [Google Scholar]
- Bradley EL, Blackwood LG. Comparing paired data: A simultaneous test for means and variances. American Statistician. 1989;43:234–235. doi:10.1080/00031305.1989.10475665. [Google Scholar]
- Cavézian C, Valadao D, Hurwitz M, Saoud M, Danckert J. Finding centre: Ocular and fMRI investigations of bisection and landmark task performance. Brain Research. 2012;1437:89–103. doi: 10.1016/j.brainres.2011.12.002. doi: 10.1016/j.brainres.2011.12.002. [DOI] [PubMed] [Google Scholar]
- Droit-Volet S, Izaute M. Improving time discrimination in children and adults in a temporal bisection task: The effects of feedback and no forced choice on decision and memory processes. Quarterly Journal of Experimental Psychology. 2009;62:1173–1188. doi: 10.1080/17470210802384180. doi: 10.1080/17470210802384180. [DOI] [PubMed] [Google Scholar]
- Fechner GT. Elements of psychophysics. Holt; New York, NY: 1966. (Original work published 1860) [Google Scholar]
- Fouriezos G, Capstick G, Monette F, Bellemare C, Parkinson M, Dumoulin A. Judgments of synchrony between auditory and moving or still visual stimuli. Canadian Journal of Experimental Psychology. 2007;61:277–292. doi: 10.1037/cjep2007028. doi:10.1037/cjep2007028. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA. Statistical criteria for parallel tests: A comparison of accuracy and power. Behavior Research Methods. 2013;45:999–1010. doi: 10.3758/s13428-013-0328-z. doi:10.3758/s13428-013-0328-z. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA. Adaptive psychophysical methods for nonmonotonic psychometric functions. Attention, Perception, & Psychophysics. 2014;76:621–641. doi: 10.3758/s13414-013-0574-2. doi:10.3758/s13414-013-0574-2. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Sampling plans for fitting the psychometric function. Spanish Journal of Psychology. 2005;8:256–289. doi: 10.1017/s113874160000514x. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. The difference model with guessing explains interval bias in two-alternative forced-choice detection procedures. Journal of Sensory Studies. 2010a;25:876–898. doi:10.1111/j.1745-459X.2010.00310.x. [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Reminder and 2AFC tasks provide similar estimates of the difference limen: A reanalysis of data from Lapid, Ulrich, and Rammsayer (2008) and a discussion of Ulrich and Vorberg (2009). Attention, Perception, & Psychophysics. 2010b;72:1155–1178. doi: 10.3758/APP.72.4.1155. doi:10.3758/APP.72.4.1155. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Improving the estimation of psychometric functions in 2AFC discrimination tasks. Frontiers in Psychology. 2011a;2:96. doi: 10.3389/fpsyg.2011.00096. doi:10.3389/fpsyg.2011.00096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Interval bias in 2AFC detection tasks: Sorting out the artifacts. Attention, Perception, & Psychophysics. 2011b;73:2332–2352. doi: 10.3758/s13414-011-0167-x. doi:10.3758/s13414-011-0167-x. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Correction to “Reminder and 2AFC tasks provide similar estimates of the difference limen: A reanalysis of data from Lapid, Ulrich, and Rammsayer (2008) and a discussion of Ulrich and Vorberg (2009). Attention, Perception, & Psychophysics. 2012a;74:489–492. doi: 10.3758/APP.72.4.1155. doi:10.3758/s13414-012-0274-3. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. On the discrepant results in synchrony judgment and temporal-order judgment tasks: A quantitative model. Psychonomic Bulletin & Review. 2012b;19:820–846. doi: 10.3758/s13423-012-0278-y. doi:10.3758/s13423-012-0278-y. [DOI] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Response errors explain the failure of independent-channels models of perception of temporal order. Frontiers in Psychology. 2012c;3:94. doi: 10.3389/fpsyg.2012.00094. doi:10.3389/fpsyg.2012.00094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Pérez MA, Alcalá-Quintana R. Shifts of the psychometric function: Distinguishing bias from perceptual effects. Quarterly Journal of Experimental Psychology. 2013;66:319–337. doi: 10.1080/17470218.2012.708761. doi: 10.1080/17470218.2012.708761. [DOI] [PubMed] [Google Scholar]
- Gil S, Droit-Volet S. “Time flies in the presence of angry faces”.. depending on the temporal task used. Acta Psychologica. 2011;136:354–362. doi: 10.1016/j.actpsy.2010.12.010. doi:10.1016/j.actpsy.2010.12.010. [DOI] [PubMed] [Google Scholar]
- Gobell J, Carrasco M. Attention alters the appearance of spatial frequency and gap size. Psychological Science. 2005;16:644–651. doi: 10.1111/j.1467-9280.2005.01588.x. doi:10.1111/j.1467-9280.2005.01588.x. [DOI] [PubMed] [Google Scholar]
- Harvey M. Perceptual and premotor neglect: Is there an ideal task to categorise patients? Cortex. 2004;40:323–328. doi: 10.1016/s0010-9452(08)70127-8. doi:10.1016/S0010-9452(08)70127-8. [DOI] [PubMed] [Google Scholar]
- Harvey M, Olk B. Comparison of the Milner and Bisiach landmark tasks: Can neglect patients be classified consistently? Cortex. 2004;40:659–665. doi: 10.1016/s0010-9452(08)70162-x. doi:10.1016/S0010-9452(08)70162-X. [DOI] [PubMed] [Google Scholar]
- Harvey M, Krämer-McCaffery T, Dow L, Murphy PJS, Gilchrist ID. Categorisation of ‘perceptual’ and ‘premotor’ neglect patients across different tasks: Is there strong evidence for a dichotomy? Neuropsychologia. 2002;40:1387–1395. doi: 10.1016/s0028-3932(01)00202-0. doi:10.1016/S0028-3932(01)00202-0. [DOI] [PubMed] [Google Scholar]
- Kopec CD, Brody CD. Human performance on the temporal bisection task. Brain and Cognition. 2010;74:262–272. doi: 10.1016/j.bandc.2010.08.006. doi: 10.1016/j.bandc.2010.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K-H, Bhaker RS, Mysore A, Parks RW, Birkett PBL, Woodruff PWR. Time perception and its neuropsychological correlates in patients with schizophrenia and in healthy volunteers. Psychiatry Research. 2009;166:174–183. doi: 10.1016/j.psychres.2008.03.004. doi:10.1016/j.psychres.2008.03.004. [DOI] [PubMed] [Google Scholar]
- Leone FC, Nelson LS, Nottingham RB. The folded normal distribution. Technometrics. 1961;3:543–550. doi:10.1080/00401706.1961.10489974. [Google Scholar]
- Lin LI-K. A concordance correlation coefficient to evaluate reproducibility. Biometrics. 1989;45:255–268. doi:10.2307/2532051. [PubMed] [Google Scholar]
- Lin L, Hedayat AS, Sinha B, Yang M. Statistical methods for assessing agreement: Models, issues, and tools. Journal of the American Statistical Association. 2002;97:257–270. doi:10.1198/016214502753479392. [Google Scholar]
- Luh KE. Line bisection and perceptual asymmetries in normal individuals: What you see is not what you get. Neuropsychology. 1995;9:435–448. doi:10.1037/0894-4105.9.4.435. [Google Scholar]
- Marshall JC, Halligan PW. When right goes left: An investigation of line bisection in a case of visual neglect. Cortex. 1989;25:503–515. doi: 10.1016/s0010-9452(89)80065-6. doi:10.1016/S0010-9452(89)80065-6. [DOI] [PubMed] [Google Scholar]
- Massen C, Rieger M, Sülzenbrück S. Using scissors to bisect a line: A perception–action dissociation in complex tool use. Attention, Perception, & Psychophysics. 2014;76:172–178. doi: 10.3758/s13414-013-0564-4. doi:10.3758/s13414-013-0564-4. [DOI] [PubMed] [Google Scholar]
- Milner AD, Brechmann N, Pagliarini L. To halve and to halve not: An analysis of line bisection judgements in normal subjects. Neuropsychologia. 1992;30:515–526. doi: 10.1016/0028-3932(92)90055-q. doi:10.1016/0028-3932(92)90055-Q. [DOI] [PubMed] [Google Scholar]
- Milner AD, Harvey M, Roberts RC, Foster SV. Line bisection error in visual neglect: Misguided action or size distortion? Neuropsychologia. 1993;31:39–49. doi: 10.1016/0028-3932(93)90079-f. doi:10.1016/0028-3932(93)90079-F. [DOI] [PubMed] [Google Scholar]
- Morgan M, Dillenburger B, Raphael S, Solomon JA. Observers can voluntarily shift their psychometric functions without losing sensitivity. Attention, Perception, & Psychophysics. 2012;74:185–193. doi: 10.3758/s13414-011-0222-7. doi:10.3758/s13414-011-02222-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Numerical Algorithms Group . NAG Fortran library manual, mark 19. Author; Oxford, UK: 1999. [Google Scholar]
- Olk B, Wee J, Kingstone A. The effect of hemispatial neglect on the perception of centre. Brain and Cognition. 2004;55:365–367. doi: 10.1016/j.bandc.2004.02.048. doi:10.1016/j.bandc.2004.02.048. [DOI] [PubMed] [Google Scholar]
- Raslear TG. Perceptual bias and response bias in temporal bisection. Perception & Psychophysics. 1985;38:261–268. doi: 10.3758/bf03207153. doi:10.3758/BF03207153. [DOI] [PubMed] [Google Scholar]
- Schenkenberg T, Bradford DC, Ajax ET. Line bisection and unilateral visual neglect in patients with neurologic impairment. Neurology. 1980;30:509–517. doi: 10.1212/wnl.30.5.509. doi:10.1212/WNL.30.5.509. [DOI] [PubMed] [Google Scholar]
- Schmitz R, Deliens G, Mary A, Urbain C, Peigneux P. Selective modulations of attentional asymmetries after sleep deprivation. Neuropsychologia. 2011;49:3351–3360. doi: 10.1016/j.neuropsychologia.2011.08.009. doi:10.1016/j.neuropsychologia.2011.08.009. [DOI] [PubMed] [Google Scholar]
- Schneider KA. Attention alters decision criteria but not appearance: A reanalysis of Anton-Erxleben, Abrams, and Carrasco (2010). Journal of Vision. 2011;11(13):7, 1–8. doi: 10.1167/11.13.7. doi:10.1167/11.13.7. [DOI] [PubMed] [Google Scholar]
- Schneider KA, Bavelier D. Components of visual prior entry. Cognitive Psychology. 2003;47:333–366. doi: 10.1016/s0010-0285(03)00035-5. doi:10.1016/S0010-0285(03)00035-5. [DOI] [PubMed] [Google Scholar]
- Schneider KA, Komlos M. Attention biases decisions but does not alter appearance. Journal of Vision. 2008;8(15):3, 1–10. doi: 10.1167/8.15.3. doi:10.1167/8.15.3. [DOI] [PubMed] [Google Scholar]
- Schuett S, Dauner R, Zihl J. Line bisection in unilateral homonymous visual field defects. Cortex. 2011;47:47–52. doi: 10.1016/j.cortex.2010.01.008. doi:10.1016/j.cortex.2010.01.008. [DOI] [PubMed] [Google Scholar]
- Spence C, Parise C. Prior-entry: A review. Consciousness and Cognition. 2010;19:364–379. doi: 10.1016/j.concog.2009.12.001. doi:10.1016/j.concog.2009.12.001. [DOI] [PubMed] [Google Scholar]
- Stevenson RA, Wallace MT. Multisensory temporal integration: Task and stimulus dependencies. Experimental Brain Research. 2013;227:249–261. doi: 10.1007/s00221-013-3507-3. doi:10.1007/s00221-013-3507-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toba M-N, Cavanagh P, Bartolomeo P. Attention biases the perceived midpoint of horizontal lines. Neuropsychologia. 2011;49:238–246. doi: 10.1016/j.neuropsychologia.2010.11.022. doi:10.1016/j.neuropsychologia.2010.11.022. [DOI] [PubMed] [Google Scholar]
- Toraldo A, McIntosh RD, Dijkerman HC, Milner AD. A revised method for analysing neglect using the landmark task. Cortex. 2004;40:415–431. doi: 10.1016/s0010-9452(08)70136-9. doi:10.1016/S0010-9452(08)70136-9. [DOI] [PubMed] [Google Scholar]
- Ulrich R, Vorberg D. Estimating the difference limen in 2AFC tasks: Pitfalls and improved estimators. Attention, Perception, & Psychophysics. 2009;71:1219–1227. doi: 10.3758/APP.71.6.1219. doi:10.3758/APP.71.6.1219. [DOI] [PubMed] [Google Scholar]
- van Eijk RLJ, Kohlrausch A, Juola JF, van de Par S. Audiovisual synchrony and temporal order judgments: Effects of experimental method and stimulus type. Perception & Psychophysics. 2008;70:955–968. doi: 10.3758/pp.70.6.955. doi:10.3758/PP.70.6.955. [DOI] [PubMed] [Google Scholar]
- Wearden JH. Temporal generalization in humans. Journal of Experimental Psychology: Animal Behavior Processes. 1992;18:134–144. doi: 10.1037//0097-7403.23.4.502. doi:10.1037/0097-7403.18.2.134. [DOI] [PubMed] [Google Scholar]
- Wearden JH, Ferrara A. Stimulus spacing effects in temporal bisection by humans. Quarterly Journal of Experimental Psychology. 1995;48B:289–310. doi:10.1080/14640749508401454. [PubMed] [Google Scholar]