Abstract
Saccades are made thousands of times a day, and are the principal means of localizing objects in our environment. However, the saccade system faces a challenge in accurately localizing objects as they are constantly moving relative to the eye and head. Any delays in processing could cause errors in saccadic localization. To compensate for these delays, the saccade system might use one or more sources of information to predict future target locations, including changes in position of the object over time, or its motion. Another possibility is that motion influences the represented position of the object for saccadic targeting, without requiring an actual change in target position. We tested whether the saccade system can use motion-induced position shifts to update the represented spatial location of a saccade target by using a static drifting Gabor patch with either a soft or hard aperture as a saccade target. In both conditions, the aperture always remained at a fixed retinal location. The soft aperture Gabor patch resulted in an illusory position shift, whereas the hard aperture stimulus maintained the motion signals but resulted in a smaller illusory position shift. Thus, motion energy and target location were equated, but a position shift was generated in only one condition. We measured saccadic localization of these targets and found that saccades were indeed shifted, but only with a soft aperture Gabor patch. Our results suggest that motion shifts the programmed locations of saccade targets, and this remapped location guides saccadic localization.
Accurate object localization is absolutely crucial for action. A great deal of work has been done on visuomotor localization of static objects (for reviews, see Desmurget, Pélisson, Rossetti, & Prablanc, 1998; Goodale, 2011; Jeannerod, 1988; Kowler, 2011; Paillard, 1991), but less is known about what kinds of information we use to localize moving objects (Schlag & Schlag-Rey, 2002; Smeets & Brenner, 1995). Object localization presents a challenge for the saccade system in particular, as the targets of saccades are frequently moving across the retina either because they move or because our heads are moving through the world. Neural processing delays might therefore produce differences between the physical and registered location of a target. In particular, visual input cannot influence saccade programming within the last 80–100 ms before saccade onset (Aslin & Shea, 1987; Becker & Jürgens, 1979; Findlay & Harris, 1984) and the saccade system incurs additional delays due to the time required to execute the eye movement (Carpenter, 1988). Therefore, being able to predict where an object will be is of the utmost importance, and previous work has shown that saccades to moving objects reflect a prediction about the future location of an object (Gellman & Carl, 1991; Keller & Johnsen, 1990; Kim, Thaker, Ross, & Medoff, 1997; Robinson, 1973; Ron, Vieville, & Droulez, 1989).
However, it is an open question what source of information, or combination of sources, might be used to perform this prediction. A number of previous studies have shown that physical changes in the position of an object or the motion of an object can be used to guide saccade targeting. For instance, changes in the position of an object over time might be used as an error signal to predict the future location of the saccade target. This is supported by studies demonstrating that the changing location of the target (for example, in a double-step paradigm) can guide saccade targeting (e.g., Becker & Jürgens, 1979; Deubel, Wolf, & Hauske, 1982; Westheimer, 1954). In addition, previous work has shown that velocity information can be used to anticipate the future locations of saccade targets (e.g., Etchells, Benton, Ludwig, & Gilchrist, 2010; Gellman & Carl, 1991; Keller & Johnsen, 1990; Robinson, 1973; Ron et al., 1989). These results are consistent with neurophysiological studies suggesting that neurons the frontal eye fields (FEF) encode information about the velocity of saccade targets (Barborica & Ferrera, 2003; Cassanello, Nihalani, & Ferrera, 2008).
In addition to the changes in the position of the target, or the presence of target motion, another possibility is that position information may be updated in the absence of any changes in the target’s location. For example, previous work has shown that saccades to targets near a moving object are shifted in the direction of the object’s motion, even though the targets themselves do not change their physical location (de’Sperati & Baud-Bovy, 2008; Zimmermann, Morrone, & Burr, 2012). These effects may be similar to the influence of background motion on reaching movements (Gomi, Abekawa, & Nishida, 2006; Saijo, Murakami, Nishida, & Gomi, 2005; Whitney & Goodale, 2005; Whitney, Westwood, & Goodale, 2003). In this case, it is unclear whether the motion shifts the programmed location of the stationary saccade target, or whether the saccade errors are due to the presence of motion in the display.
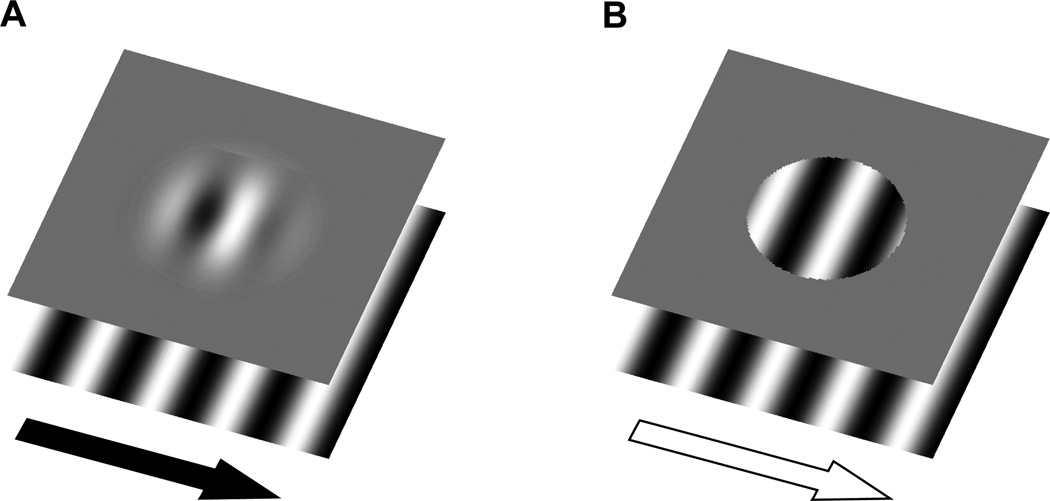
The aim of the present study, then, was to test whether motion can influence the registered location of the stationary object, which in turn could be used to guide saccade targeting. To do so, we took advantage of a perceptual illusion that shows an influence of motion on object location (De Valois & De Valois, 1991; Ramachandran & Anstis, 1990; see Whitney, 2002 for a review) while independently controlling both the target location and the retinal motion that is present. We presented subjects with drifting Gabor patches to examine whether the shift in registered location holds for saccadic targeting as well as perceptual localization. Prior work has shown that the motion of a sinusoidal grating (i.e., the carrier) within a Gaussian contrast envelope (blurred aperture) results in an apparent displacement of the entire stimulus in the direction of motion, while the aperture itself remains stationary (De Valois & De Valois, 1991; Ramachandran & Anstis, 1990). As shown in Figure 1A, the soft aperture condition results in a shift in the perceived location of the Gabor in the direction of the grating’s motion even though the aperture location does not change. However, presenting the same grating within a hard aperture, as illustrated in Figure 1B, greatly reduces the size of the illusion (Whitney et al., 2003; Zhang, Yeh, & De Valois, 1993).
Figure 1.
(A) Soft aperture stimulus, consisting of a sinusoidal carrier within a static Gaussian contrast envelope. The sinusoid moves continuously to the right while the aperture remains stationary. In this condition, the perceived location of the Gabor is shifted to the right. This illusion is greatly reduced in (B) when the Gaussian envelope is replaced with a hard circular aperture. Critically, the same surface motion is present in the hard aperture condition, but no illusion is generated in this condition. The present experiments tested whether this motion-induced shift in position assignment with a Gabor patch can influence saccade targeting.
This simple stimulus is well-suited to examining the effects of motion-induced position shifts on saccade landing location for several reasons. First, unlike many other motion-induced position illusions (Whitney, 2002), the position shift resulting from drifting Gabors is continuously present. As a result, saccade programming can occur while the stimulus is still visible. Second, unlike stimuli used in previous studies (Zimmermann et al., 2012), the illusory position shift of the saccade target is a direct consequence of its own motion, rather than the background. Most importantly, this stimulus allows us to dissociate the target’s motion from the target’s location. We can therefore examine whether previous results showing a shift in either pointing responses (Yamagishi, Anderson, & Ashida, 2001) or in saccade landing location (Kerzel & Gegenfurtner, 2005) to drifting Gabors might be explained by the presence of motion energy or by a shift in the programmed location of the Gabor.
Experiment 1A
Introduction
Our first experiment examined whether motion influences position assignments for the saccade system. Simply put, is the illusory displacement of the Gabor reflected in saccade landing location? We would expect one of two outcomes – either the saccade would land at the physical location of the Gabor patch, regardless of the carrier motion direction, or saccades would be shifted in the direction of the carrier motion, consistent with the perceptual mislocalization of the Gabor reported by subjects in previous studies (De Valois & De Valois, 1991; Ramachandran & Anstis, 1990).
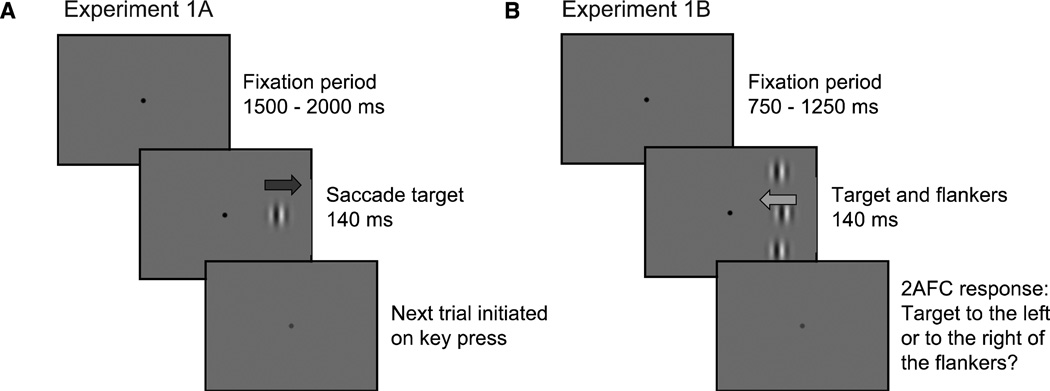
In the first part of this experiment (Figure 2A), we presented subjects with two types of saccade targets—(1) drifting Gabor patches and (2) sinusoidal gratings within hard circular apertures. We measured the landing locations of the initial saccade to each of these stimuli. The inclusion of hard aperture stimuli allowed us to present the same stimulus motion with a reduced shift in perceived position (Arnold, Thompson, & Johnston, 2007; Whitney, Goltz, et al., 2003; Zhang et al., 1993). This allowed us to control for stimulus motion while only generating a shift in perceived location in the soft aperture condition. In Experiment 1B, we measured the perceptual magnitude of the illusory motion-induced position shift and compared those measurements with the illusion's effect on saccade landing position observed n Experiment 1A.
Figure 2.
Trial Sequence for Experiments 1A (left panel) and 1B (right panel). In Experiment 1A, subjects fixated for a random interval and were instructed to saccade to the center of a target (either a Gabor, shown here, or a sinusoidal grating within a hard aperture) in the left or right visual field as quickly as possible. Subjects then initiated the next trial by pressing a key. The trial sequence in Experiment 1B was similar, with the addition of two static flankers, one above and one below the target. Subjects were instructed to maintain fixation and to respond to the offset of the target (left or right) relative to the two flankers. Arrows represent the direction of Gabor drift and were not presented to subjects.
Method
Subjects
Six subjects (4 females), including two of the authors (AK and BW) participated in the experiment (mean age: 24.2, SD = 2.5). All observers reported normal or corrected-to-normal vision and all except the authors were naïve to the purpose of the experiment.
Eye tracking
Eye movements were recorded with an EyeLink 1000 desktop mounted infrared eye tracker (SR Research Ltd., Mississauga, Ontario, Canada) used in conjunction with the Eyelink Toolbox scripts for Matlab (Cornelissen, Peters, & Palmer, 2002). Only the right eye was recorded for each subject. Subjects were calibrated with a standard 9-point calibration procedure before completing each block of trials (average error < 0.5°). The first time point at which the velocity exceeded 30°/s and the acceleration exceeded 8000°/s2 was parsed as the beginning of a saccade. In addition, a motion threshold was used to delay the start of each saccade until the eye had moved at least 0.15°. Time points at which the velocity and acceleration fell below their respective thresholds were used to determine the end of each saccade.
Stimuli and Procedure
Stimuli were presented on gamma-corrected Samsung SyncMaster 997DF monitor controlled by a Mac Mini (Apple, Inc.). The program was written in MATLAB (The MathWorks, Inc.) using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997). Display resolution was set to 1024 × 768 and the refresh rate to 100 Hz. Subjects viewed the stimulus binocularly and head position was stabilized with a chinrest at a viewing distance of 57 cm. At this distance, 30 pixels subtended approximately 1° of visual angle.
Stimuli were presented on a gray background (72.2 cd/m2). Gabors had a spatial frequency of 0.75 cpd and had a peak contrast of 85%. The standard deviation of the contrast envelope was 0.65°. On half the trials, a sinusoidal grating with a circular hard aperture (1.4° radius, uniform contrast envelope) was presented instead of a Gabor. These gratings had a peak contrast and spatial frequency identical to the Gabors (Figures 1A and 1B).
Subjects began each trial by fixating on a dark gray circle (7.4 cd/m2; 0.17° radius) at the center of the screen and initiating the trial by pressing the spacebar (Figure 2A). The fixation point then changed to black, and following a delay interval (selected at random between 1500 and 2000 ms on each trial), subjects were presented with a saccade target in either the left or right visual field. On half the trials, the target was a Gabor, and on the other half of the trials, the target was a sinusoidal grating within a hard circular aperture. The central position of the saccade target was jittered around a point 10° to the left or right of fixation. The range of possible jittered positions spanned 3° horizontally and 3° vertically (maximum deviation of 1.5° in any direction). The position was selected randomly on each trial to avoid stereotyped saccades (see Results section and Figure S3). The bars of the sinusoid inside the aperture drifted either left or right with a temporal frequency of 4 Hz (5.33°/s). The initial phase of the grating was randomly selected on each trial from a set of 25 possible phases.
The saccade target was presented for 140 ms, and subjects were instructed to saccade to the center of the target as soon as it appeared. The fixation dot changed back to gray 240 ms following the offset of the Gabor to signal the end of the trial. Following the completion of the saccade, subjects were instructed to move their eyes back to the fixation point and initiate the next trial manually by pressing the spacebar. Subjects each completed a single block of 400 trials. Subjects did not know in advance on any trial whether the saccade target would be in the left or the right visual field, its motion direction, or whether the target would have a soft aperture (Gabor) or a hard circular aperture. Visual field location (left or right), aperture type (soft or hard), and motion direction (left or right) were counterbalanced across trials.
Data Analysis
The data were drift-corrected offline and the x- and y- coordinates of the eye position at the end of the first large saccade on each trial were used to determine saccade landing location. Trials on which subjects made a saccade too early (in the 1000 ms prior to stimulus onset), blinked immediately prior to the saccade, or failed to make a saccade were excluded from the analysis. In addition, we excluded trials on which saccade landing locations deviated by more than 2.5° horizontally or vertically from the center of the saccade target. Together, this resulted in the removal of an average of 12.1% of trials per subject from the analysis. We repeated our analyses, excluding trials on which landing locations deviated by more than 4.5° from the center of the saccade target. This analysis resulted in the removal of 4.6% of the trials and yielded similar results (for a complete analysis at several window sizes, see Figures S1 and S2).
The data were then normalized individually for each subject to correct for any possible saccadic undershoot (Becker & Fuchs, 1969; Carpenter, 1988). Saccadic undershoot resulted in saccades to the right visual field landing slightly to the left of the saccade target and saccades to the left visual field landing slightly to the right of the target. In order to correct for this commonly reported and systematic bias, we first separately calculated the mean x-coordinates of the landing locations for the left and right motion directions within each aperture and hemifield condition for each subject. Then, the mean landing location within each condition was subtracted from the landing location on each trial for that condition. This was repeated for each possible combination of hemifield and aperture condition. The resulting normalized landing locations were pooled together across the left and right hemifields and then averaged to obtain an estimate of the mean shift in landing location resulting from the carrier motion. This analysis was repeated for each of the six subjects. The distance of each landing location from the mean of the set of normalized landing locations corresponds to the saccade error, in degrees, produced by one direction of motion. Here, positive values represent saccade landing locations consistent with direction of motion and negative values indicate saccade landing locations away from the direction of motion (regardless of whether the motion was leftward or rightward on any given trial).
Results
As expected, the trial-to-trial variations in the central position of the saccade target influenced subjects’ saccade landing positions. Each subject showed a strong positive correlation between the jittered horizontal location of the saccade target and saccade amplitude, indicating that subjects did not simply saccade to the same location on every trial.
The within-subject correlations ranged from 0.57 to 0.77 with a mean correlation of 0.68 (all p values < 0.001). These correlations were similar for both short and long latency saccades (see Figure S3). The mean saccade latency across subjects was 229 ms (SD = 53.5 ms).
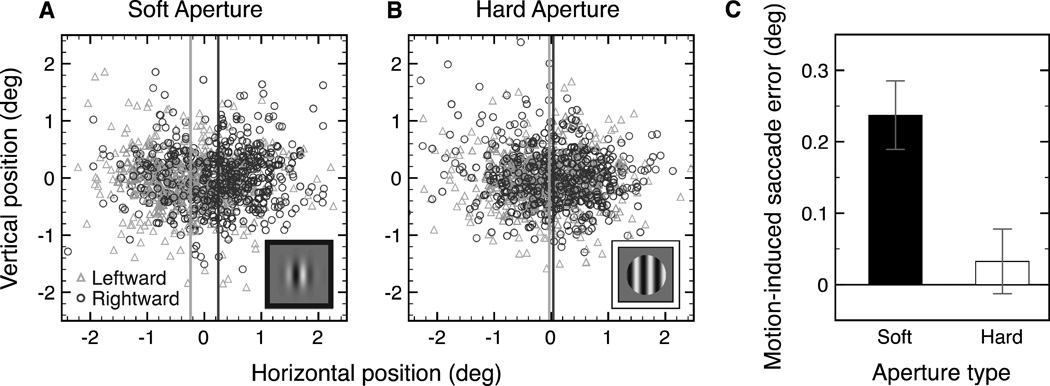
Figures 3A and B show the set of normalized saccade landing positions across all subjects for the soft and the hard aperture conditions. Based on the normalized landing positions, we calculated the saccade error produced by the carrier motion. As shown in Figure 3C, the mean saccade error was 0.24° for the soft aperture condition and 0.03° for the hard aperture condition. Saccade precision, discounting the effect of stimulus motion, was similar between the soft and hard aperture conditions (see Figure S4).
Figure 3.
(A) Normalized horizontal and vertical saccade landing locations for the soft aperture condition for both the leftward (triangle) and rightward (circle) motion conditions for all subjects. The two vertical lines represent the mean saccade landing locations for each motion conditions (B) Normalized saccade landing locations and means for the hard aperture condition. (C) Mean saccade error (resulting from one direction of motion) across subjects within the soft and hard aperture conditions. Error bars represent bootstrapped 95% confidence intervals.
To compare the effect of motion direction for the soft aperture and hard aperture conditions separately, we performed nonparametric bootstrap tests (Efron & Tibshirani, 1993). The mean saccade error was bootstrapped by resampling each subject’s data 1000 times with replacement. The bootstrapped estimates of saccade error were then averaged across the six subjects. The saccade error resulting from the stimulus motion was significantly greater than zero for the soft aperture condition (p < 0.001), but not for the hard aperture condition, p = 0.16 (two-tailed). The difference in the effect of motion between the two aperture conditions was significant, p < .001.
Finally, we tested whether the effect of motion on saccade landing position depended on subjects’ saccade latencies. In the soft aperture condition, mean saccade error was negatively correlated with mean saccade latency across the six subjects (Spearman’s rho: rs = −0.89, p = 0.03). In other words, subjects with shorter-latency saccades had larger saccade errors in the direction of the target’s motion. This correlation was not significant in the hard aperture condition (rs = 0.03, p = 1).
To test the relationship between saccade latency and the effect of motion on landing position on a trial-by-trial basis, we combined the single-trial data from the six subjects. For both the soft aperture and the hard aperture trials, saccade error was negatively correlated with saccade latency across trials (soft aperture: r = −.15, p < .001; hard aperture: r = Saccades are made thousands of times a day, and are the.09, p = .002). Shorter-latency saccades were associated with larger saccade errors in the direction of the target’s motion.
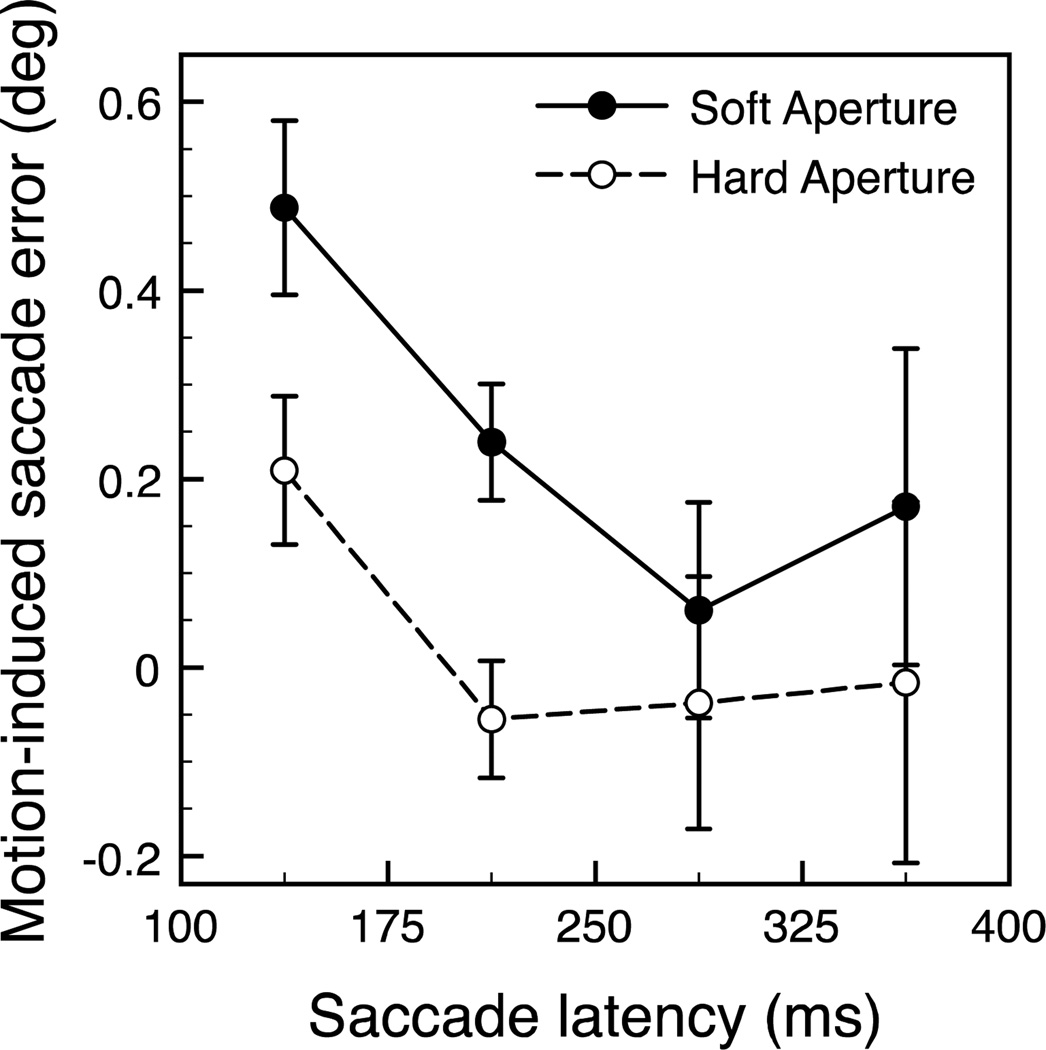
In addition, we binned the data according to saccade latency into four evenly spaced bins between 100 and 400 ms and calculated the average saccade error by averaging the single-trial saccade errors within each bin. Figure 4 shows the saccade errors at each latency bin for the soft and hard aperture conditions separately. Consistent with the correlation analyses, shorter saccade latencies were associated with larger saccade errors. The majority of saccade latencies exceeded the 140 ms duration of the drifting Gabor stimulus, which prevented postsaccadic foveation of the stimulus on most trials.
Figure 4.
Saccade error, represented as the shift in saccade landing location resulting from one direction of motion as a function of saccade latency for both the soft (filled circles) and hard (open circles) aperture conditions. Single-trial data were pooled across subjects, then sorted into one of four latency bins. Numbers with tick marks on the x-axis represent the latency bin edges and values are plotted at the bin centers. Error bars represent bootstrapped 95% confidence intervals.
Discussion
In the soft aperture condition, we found that the direction of the carrier motion biased subjects' saccade landing locations. When the Gabor drifted leftward, subjects’ saccades landed more leftward, on average; when it drifted rightward, subjects’ saccades landed more rightward (Figures 3A and 3C). This is consistent with the direction of the illusory displacement in perceived location reported in previous studies (De Valois & De Valois, 1991; Ramachandran & Anstis, 1990). Notably, we do not find this result in the hard aperture condition; with a hard aperture stimulus, subjects’ saccades were not influenced by the direction of the grating’s motion (Figures 3B and 3C). This is consistent with previous findings describing a reduction in this perceptual mislocalization with a hard aperture (Whitney et al., 2003; Zhang et al., 1993).
The lack of an effect of motion direction on saccade landing location in the hard aperture condition indicates that subjects' saccades were not directed to the individual bars of the sinusoidal grating, since the motion of the bars is identical for the soft and the hard aperture conditions. The presence of motion alone is therefore insufficient to bias saccade landing locations. Moreover, a shift in physical position is not required to bias saccade targeting, as the physical location of the aperture does not change between the leftward and rightward motion conditions. Together, these results suggest that motion can shift the represented target position for saccades.
In addition, we found that this effect depended on saccade latency. Specifically, we observed the largest effect of the motion-induced shift on saccade landing position with saccade latencies in the range of 100–175 ms. Given these saccade latencies, the distance the saccade traveled (10° of visual angle), and the duration of the drifting Gabor stimulus (140 ms), it is highly unlikely that the effect we observed on saccade targeting could be influenced by in flight correction of the saccade or postsaccadic foveation of the stimulus.
Since our results were consistent with the previously reported effects of Gabor motion on perceived position, we wanted to determine how similar the shift in saccade landing location was to the perceptual shift. In Experiment 1B, we presented the same stimuli with the addition of stationary flankers and asked subjects to report the illusory displacement relative to these stationary references.
Experiment 1B
Introduction
In Experiment 1B, we compared the effect of drifting motion on saccade landing position from Experiment 1A to comparable psychophysical measurements of drifting motion on perceived location. As shown in Figure 2B, on each trial, subjects were shown a target: either a drifting Gabor or a sinusoidal grating within a hard aperture along with two stationary reference stimuli, one above and one below the drifting target. Subjects made a two-alternative forced-choice (2AFC) response, indicating whether the target was to the left or to the right of the two reference stimuli.
Method
Subjects
The same subjects from Experiment 1A participated in 1B.
Stimuli and Procedure
The eye tracking set up and procedure in Experiment 1B were identical to those in Experiment 1A and the stimulus was similar to that in Experiment 1A. Figure 2B shows the trial sequence for Experiment 1B. As before, there was a random delay interval (750 – 1250 ms) prior to the onset of the target (either a Gabor or a grating within a hard circular aperture drifting leftward or rightward). The target was presented simultaneously with two flankers—one above and one below the target. The flankers were stationary, but otherwise identical to the target and had a 6.5° vertical center-to-center separation from the target. The positions of the target and flankers were jittered together 1.5 degrees horizontally and vertically around a central location 10° to the left or to the right of the fixation point. The horizontal position of the central Gabor was at one of seven possible linearly spaced offsets relative to the flankers, ranging from 1.75° to the left (represented by negative values) to 1.75° to the right (positive values) of the flankers. Subjects were instructed to judge whether the central target was to the left or to the right of the two flankers by pressing the appropriate key on a keyboard. Subjects were instructed to maintain fixation on the dot at the center of the display for the duration of the trial.
Each subject completed one set of 560 trials. Across trials, motion direction (left or right) was counterbalanced with visual field location (left or right), aperture condition (soft or hard), and with the set of seven possible target positions.
Data Analysis
Trials on which subjects’ eye position deviated by more than 1° horizontally or vertically from the fixation point were excluded from the analysis. This resulted in the removal of an average of 6.2% of trials per subject from the analysis. The remaining trials were fit to a set of logistic functions using a least squares procedure. Trials from the left and right visual field locations were analyzed together, resulting in a pair of logistic functions (one each motion direction) for each type of aperture (soft or hard). The size of the illusory position shift produced by the grating’s motion was calculated as half the difference between the points of subjective equality (PSEs) of the two fitted functions.
Results
Figure 5 shows example pairs of logistic functions (one for each motion direction) for a single observer in the soft aperture condition (4A) and the hard aperture condition (4B). Observers’ responses on each trial for the leftward and rightward conditions were bootstrapped separately by resampling each observer’s responses with 1000 samples and fitting each set of resampled data to a logistic function. The resulting bootstrapped PSEs were then averaged across the six subjects.
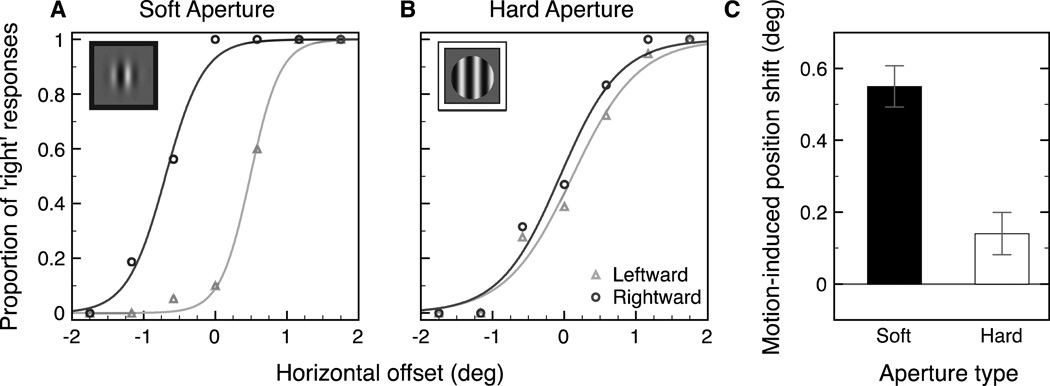
Figure 5.
Example pair of psychometric functions from one subject for the soft aperture condition (A) and the hard aperture condition (B). The x-axis shows the horizontal offset of the central target relative to the two flankers (− left, + right). The y-axis shows the proportion of responses that the target was to the right of the two flankers (triangles: leftward motion, circles: rightward motion). PSEs were calculated individually for each subject and then averaged across all observers for each motion and aperture condition. The motion-induced position shift (C) was calculated as half the difference between the PSEs of the two psychometric functions. Error bars represent bootstrapped 95% confidence intervals.
Figure 5C shows the size of the motion-induced position shift (measured as half the distance between the two PSEs) for each aperture condition. The size of the perceived shift in position was 0.55° in the soft aperture condition and 0.14° in the hard aperture condition. The size of the motion-induced position shift was greater than zero in both the soft aperture condition (p < .001) and the hard aperture condition (p < .001). The interaction between motion condition and aperture condition was significant (p < .001) demonstrating a significantly larger motioninduced shift in perceived position in the soft aperture condition than in the hard aperture condition.
Discussion
Experiment 1B confirmed previously reported results that there is a larger shift in perceived position resulting from stimulus motion when the motion is within a Gaussian aperture compared to a hard circular aperture (Whitney et al., 2003; Zhang et al., 1993). Although our results show that the shift in perceived location is reduced in the hard aperture condition, it is not completely eliminated. It is possible that the large stimulus eccentricity (10 degrees on average) resulted in peripheral blurring of the stimulus edges. Nevertheless, our findings are consistent with the findings in Experiment 1A; we observe a shift in perceived position where there is also a shift in saccade landing location. In other words, shifts in perceived position from motion are associated with corresponding shifts in saccade landing location. If we test subjects with a hard aperture, in which there are motion signals, but a significantly smaller illusory position shift associated with that motion, we also see no difference in saccade landing positions between the leftward and rightward motion conditions. These results support our hypothesis that motion signals, per se, are insufficient to strongly bias saccade landing position. Instead, motion biases the represented location of the target for the saccade system, and that this information is used to guide saccade targeting. In a follow-up experiment, we sought to further examine any potential correlation between the perceptual and saccadic errors by testing whether the pattern of saccade error was similar to the pattern of illusory displacement at different stimulus durations.
Experiment 2A
Given our finding in Experiment 1, that motion can shift the represented locations of saccade targets, we next examined how much motion information is required to shift saccade landing locations in the direction of the Gabor's motion. Previous work has shown that an illusory shift in perceived location is present with durations as brief as 30 ms and reaches its maximum level with a durations of approximately 100 ms or more (Arnold et al., 2007; Chung, Patel, Bedell, & Yilmaz, 2007). Given the results of Experiment 1, we wanted to test whether similarly brief motion durations are sufficient to demonstrate an effect of motion on saccade landing location. To do so, we used the exact same procedure as in Experiment 1, varying only Gabor duration.
Method
Subjects
Three subjects (all female), including one author (AK) participated in Experiment 2A (mean age: 27.3). Two of the participants from Experiments 1A & B participated in Experiments 2A & B.
Stimuli and Procedure
The stimuli and procedure were identical to those in Experiment 1A, with the addition of a duration manipulation. The saccade target was presented randomly for 20, 40, 60, 80, or 100 ms on each trial. Only soft aperture stimuli (Gabors) were presented. Subjects were instructed to fixate the center of the display at the start of each trial and saccade to the target as soon as it appeared. Across trials, stimulus duration was counterbalanced with visual field location (left or right) and with motion direction (left or right). Each subject completed 4 blocks of 260 trials each. Trials on which subjects made a saccade too early, failed to make a saccade, or landed more than 2.5° from the saccade target (11.4% of the trials) were removed from the analysis. The data were then analyzed using the procedure outlined in Experiment 1A.
Results
The average saccade latency across subjects was 213 ms, comparable to that reported in Experiment 1A (229 ms). As before, we calculated the relative saccade error as the distance of each landing location on each trial from the mean of the set of normalized landing locations where positive values represent saccade landing locations consistent with direction of motion and negative values indicate saccade landing locations away from the direction of motion. We then pooled the single-trial data from the three subjects. As in Experiment 1A, there was a negative correlation between the magnitude of the saccade error and saccade latency, r = −0.18, p <0.001. When calculated individually for each of the five duration conditions, there was a negative correlation between saccade error and latency at all but the 20 ms condition; these were significant at a Bonferroni adjusted alpha level (αB) of 0.01 (all r values < −0.15, all p values < 0.001; for the 20 ms condition: r = 0.003, p = 0.94).
Given the observed latency effect, we calculated the effect of the target’s motion on saccade landing position separately for three latency bins: 100–170 ms, 170–240 ms, and 240–380 ms. This resulted in an approximately similar number of trials within each bin. Figure 6A shows the mean saccade landing locations at each duration for all three latency bins. In the shortest latency bin (100–170 ms), there was a significant effect of the Gabor's motion on saccade landing position at all durations of 40 ms or longer (αB = .003; all p values < .001). There was no significant effect at any duration in either the 170–240 ms latency bin or the 240–380 ms bin.
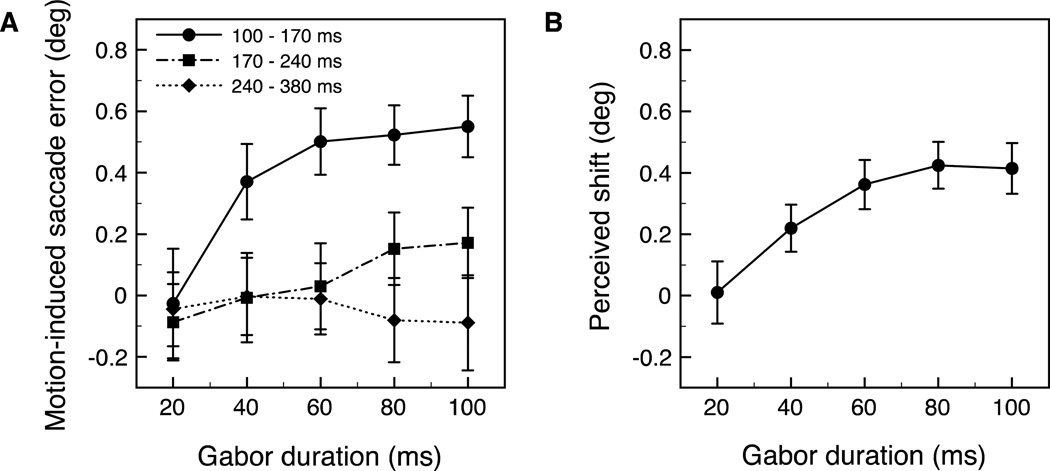
Figure 6.
(A) Saccade error—the shift in saccade landing location resulting from one direction of motion—as a function of Gabor duration (only the soft aperture was used in Experiments 2A and 2B). Single-trial data were pooled across subjects and then sorted into one of three latency bins, represented by the separate lines. (B) Perceived shift resulting from one direction of motion for the same subjects as in (A), calculated as half the difference between PSEs for each pair of psychometric functions (similar to 4A). Error bars represent bootstrapped 95% confidence intervals.
Discussion
We found a significant effect of Gabor motion on saccade landing location, and this effect depended on the duration of the motion. The motion-dependent saccadic mislocalization increased until approximately 60 ms before leveling off (Figure 6A). Consistent with the findings in Experiment 1A, there was a smaller effect of the Gabor's motion on saccade landing position when the saccades were longer in latency.
The pattern of saccade error as a function of stimulus duration is similar to previously reported behavioral measurements of the shift in perceived position with drifting Gabors. Arnold et al (2007) show that the illusory shift has an initial increase, followed by a leveling off around 180 ms. Similarly, Chung et al. (2007) report that the position shift reaches an asymptotic value around 100 ms at high speeds (16°/s). While the shift in saccade landing location as a function of stimulus duration is broadly consistent with previously reported psychophysical results, our stimuli differed in speed, contrast and eccentricity from the previous studies. Therefore, we obtained measurements of the perceived shift within the same set of observers in Experiment 2B to compare the magnitude of saccade error with the perceptual mislocalization at different durations.
Experiment 2B
Introduction
In order to measure the motion-induced position shift at different stimulus durations, we used a paradigm in Experiment 2B similar to that in Experiment 1B. Subjects were asked to report the position (left or right) of a central drifting Gabor relative to two stationary references. In this experiment, we varied stimulus duration using the same set of durations used in Experiment 2A.
Method
Subjects
The same subjects from Experiment 2A participated in Experiment 2B
Stimuli and Procedure
The stimuli and procedure, including eye tracking, were identical to those in Experiment 1B, with the addition of the same duration manipulation from Experiment 2A. Subjects performed the same vernier discrimination task on a central target flanked by two stationary references, one above and one below the target. Only the soft aperture stimuli were presented, and as before, subjects were instructed to maintain fixation at the center of the display. Each subject completed two blocks of 700 trials each, in which stimulus duration, motion direction, visual field location, and the position of the target were counterbalanced across trials. An average of 3.5% of trials were excluded from the analysis due to a failure to maintain fixation.
Results and Discussion
Figure 6B shows the motion-induced perceptual shift in the Gabor’s location as a function of its duration. The motion-induced illusory shift was calculated as half the difference between the PSEs of the pair of psychometric functions (similar to those shown in Figure 5A) for each duration condition. The data were bootstrapped as described in Experiment 1B. There was no significant effect of the Gabor’s motion on position judgments with a 20 ms stimulus presentation (p = .86), but the effect of the Gabor’s motion was significant at all other durations at a Bonferroni adjusted alpha level (αB) of .01 (all p values < .001). Similar to the pattern observed with saccade error, the motion-induced shift in perceived position initially increased with stimulus duration and then reached an asymptotic level with a duration of about 60–80 ms. These findings replicate the pattern of results reported by Arnold et al. (2007) and Chung et al. (2007), demonstrating a shift in perceived location that is present at very brief durations.
General Discussion
The experiments here tested whether the saccade system can use motion-induced position shifts to update the represented locations of objects. In Experiment 1, we show that saccades to a drifting Gabor were shifted in the direction of the carrier motion, exhibiting the same mislocalization effect that has been reported in the psychophysical literature (De Valois & De Valois, 1991; Ramachandran & Anstis, 1990). Importantly, when a hard circular aperture is used, the effect of the carrier motion on perceived location is greatly reduced, and its effect on saccade landing location is eliminated. In Experiments 2A and 2B, we also demonstrated that the pattern of perceptual mislocalization at different durations mirrors that of saccade error at the same set of durations. Specifically, in Experiment 2A we showed that very brief motion (as little as 40 ms) is sufficient to shift the represented position for saccade targeting, consistent with the minimum motion duration required to produce a perceptual shift (Experiment 2B; see also Arnold et al., 2007 and Chung et al., 2007). In addition, the mislocalization effect reaches its maximum with durations of approximately 60–80 ms for both saccades and for perception.
There are several sources of information that the saccade system might use to predict the future locations of moving targets, including changes in the position of a target, or its motion. Although previous work has established that physical changes in object location over time can be used to guide saccade targeting (e.g., Becker & Jürgens, 1979; Deubel, Wolf, & Hauske, 1982; Robinson, 1973; Ron et al., 1989), our results demonstrate that they are not necessary. Experiment 1A showed that object motion alone is insufficient to strongly bias saccade landing locations and that the combination of motion and a soft aperture was required. In the hard aperture condition, where the shift in perceived position was greatly reduced, there was no bias in saccade landing locations even though the same motion was present. Our results are consistent with the idea that motion can bias the represented position of the target, which, in turn, biases saccade targeting. Although previous work using motion-induced position illusions has suggested that position shifts from motion may guide saccade targeting (de’Sperati & Baud-Bovy, 2008; Kerzel & Gegenfurtner, 2005; Zimmermann et al., 2012), it is possible that these effects were simply due to the presence of stimulus motion in the display. In contrast, our study included a control condition with identical stimulus motion, but a shift in perceived position occuring in only one condition. Therefore, we can conclude that it is the position shift produced by the stimulus motion, rather than simply the presence of motion in the display, that accounts for the saccade error observed in these experiments. On the whole, it is likely that the saccade system uses multiple sources of information together to predict the future locations of saccade targets as they move and as observers move in their environment.
Across both sets of our experiments, there are similarities between the pattern of errors in saccade landing location and those in perceived location. However, there are many studies in the dual visual systems literature that suggest object localization for action is dissociated from perceptual localization (for reviews, see Goodale & Westwood, 2004; Goodale & Milner, 1992). Some of the evidence to support this idea comes from work demonstrating that under certain circumstances, saccadic localization may resist illusions of position that the perceptual system is susceptible to. For example, Wong & Mack (1981) induced an illusory displacement in the location of a target dot by shifting the location of a frame that surrounded it. Subjects were instructed to saccade to the target either immediately or following a delay period after its offset. Their results indicated that the target's saccade landing location reflects its perceived location, but only when the saccades were memory-guided. In contrast, saccades directed immediately to the target were not affected by the illusion, suggesting that it is just physical (egocentric) location that determines saccade localization, at least for immediate saccades. This supports a possible dissociation between perception and action.
More recent work has examined the effects of motion-induced position illusions on saccade landing location, and has shown errors in saccade targeting consistent with the perceptual mislocalization of objects. For example, the flash-drag effect (FDE), in which the position of a stationary object is shifted in the direction of motion of a different object (Whitney & Cavanagh, 2000), has been shown to influence saccade targeting (de’Sperati & Baud-Bovy, 2008; Zimmermann et al., 2012). Consistent with the results of Wong and Mack (1981), the effect of the visual motion on saccadic localization increased with longer delays, albeit on a shorter timescale; saccade errors were larger with long-latency saccades, on the order of 250 – 600ms (de’Sperati & Baud-Bovy, 2008; Zimmermann et al., 2012). In addition, memory-guided saccades to a flash-lag stimulus, in which a stationary flash appears to lag behind an adjacent moving object (Nijhawan, 1994) are consistent with the illusion; landing locations are accurate when subjects saccade the flashed object, but are shifted in the direction of the motion when saccades are directed to the location of the moving object (Becker, Ansorge, & Turatto, 2009).
The delay dependence of saccadic mislocalizations leaves open the possibility that immediate saccades are based on physical object position and not the perceived object location. If there is any effect of a perceptual illusion, it might only appear with a delay of a few hundred milliseconds. De'Sperati & Baud-Bovy (2008) suggest that such latency effects are due to the longer time required for processing the position shift. This implies that the veridical location is represented first, which is then updated to reflect additional perceptual processing that produces the illusory shift. This is broadly consistent with studies suggesting that the effects of an illusion on saccade targeting are larger with voluntary saccades (McCarley, Kramer, & DiGirolamo, 2003), which are typically longer in latency (Hallett, 1978). In contrast, our results demonstrate that position updating for the saccade system happens rapidly, as we observe large shifts in saccade targeting consistent with the Gabor's motion when the saccades are reflexive and short in latency.
In summary, we found that the well-established psychophysical effect described by De Valois and De Valois (1991) was also reflected in saccade landing location, and that this effect built rapidly, requiring as little as 40 ms of motion to influence saccade landing position. This supports the idea that the visual system uses motion to change the represented position of an object at early stages of visual processing (Fukiage & Murakami, 2013; Kosovicheva et al., 2012; Whitney et al., 2003), with saccade targeting shifted accordingly. Future work should examine the circumstances under which motion-induced position shifts influence action – and how quickly position information can be updated for perception and action. Our results raise the possibility that the visuomotor system employs motion-induced position shifts to predict the locations of moving objects, thus improving the accuracy of saccadic targeting in dynamic scenes and helping to explain how the visual system allows us to respond to a dynamic world.
Supplementary Material
Acknowledgments
The authors thank Valentina Volk for her assistance with data collection. This research was supported by National Eye Institute grant R01EY018216 (D.W.), NSF CAREER grant 0748689 (D.W.), and NSF graduate research fellowships to A.A.K. and B.W.
References
- Arnold DH, Thompson M, Johnston A. Motion and position coding. Vision Research. 2007;47:2403–2410. doi: 10.1016/j.visres.2007.04.025. [DOI] [PubMed] [Google Scholar]
- Aslin RN, Shea SL. The amplitude and angle of saccades to double-step target displacements. Vision Research. 1987;27:1925–1942. doi: 10.1016/0042-6989(87)90058-7. [DOI] [PubMed] [Google Scholar]
- Barborica A, Ferrera VP. Estimating invisible target speed from neuronal activity in monkey frontal eye field. Nature Neuroscience. 2003;6:66–74. doi: 10.1038/nn990. [DOI] [PubMed] [Google Scholar]
- Becker SI, Ansorge U, Turatto M. Saccades reveal that allocentric coding of the moving object causes mislocalization in the flash-lag effect. Attention, Perception, & Psychophysics. 2009;71:1313–1324. doi: 10.3758/APP.71.6.1313. [DOI] [PubMed] [Google Scholar]
- Becker W, Fuchs AF. Further properties of the human saccadic system: Eye movements and correction saccades with and without visual fixation points. Vision Research. 1969;9:1247–1258. doi: 10.1016/0042-6989(69)90112-6. [DOI] [PubMed] [Google Scholar]
- Becker W, Jürgens R. An analysis of the saccadic system by means of double step stimuli. Vision Research. 1979;19:967–983. doi: 10.1016/0042-6989(79)90222-0. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Carpenter RHS. Movements of the Eyes. 2nd ed. London: Pion; 1988. [Google Scholar]
- Cassanello CR, Nihalani AT, Ferrera VP. Neuronal responses to moving targets in monkey frontal eye fields. Journal of Neurophysiology. 2008;100:1544–1556. doi: 10.1152/jn.01401.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung STL, Patel SS, Bedell HE, Yilmaz O. Spatial and temporal properties of the illusory motion-induced position shift for drifting stimuli. Vision Research. 2007;47:231–243. doi: 10.1016/j.visres.2006.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornelissen FW, Peters EM, Palmer J. The Eyelink Toolbox: Eye tracking with MATLAB and the Psychophysics Toolbox. Behavior Research Methods, Instruments, & Computers. 2002;34:613–617. doi: 10.3758/bf03195489. [DOI] [PubMed] [Google Scholar]
- De Valois RL, De Valois KK. Vernier acuity with stationary moving Gabors. Vision Research. 1991;31:1619–1626. doi: 10.1016/0042-6989(91)90138-u. [DOI] [PubMed] [Google Scholar]
- de’Sperati C, Baud-Bovy G. Blind saccades: An asynchrony between seeing and looking. Journal of Neuroscience. 2008;28:4317–4321. doi: 10.1523/JNEUROSCI.0352-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmurget M, Pélisson D, Rossetti Y, Prablanc C. From eye to hand: Planning goal-directed movements. Neuroscience and Biobehavioral Reviews. 1998;22:761–788. doi: 10.1016/s0149-7634(98)00004-9. [DOI] [PubMed] [Google Scholar]
- Deubel H, Wolf W, Hauske G. Corrective saccades: Effect of shifting the saccade goal. Vision Research. 1982;22:353–364. doi: 10.1016/0042-6989(82)90151-1. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. An Introduction to the Bootstrap. London: Chapman & Hall; 1993. [Google Scholar]
- Etchells PJ, Benton CP, Ludwig CJH, Gilchrist ID. The target velocity integration function for saccades. Journal of Vision. 2010;10:1–14. doi: 10.1167/10.6.7. [DOI] [PubMed] [Google Scholar]
- Findlay JM, Harris LR. Small saccades to double-stepped targets moving in two dimensions. Advances in Psychology. 1984;22:71–78. [Google Scholar]
- Fukiage T, Murakami I. Adaptation to a spatial offset occurs independently of the flash-drag effect. Journal of Vision. 2013;13:1–14. doi: 10.1167/13.2.7. [DOI] [PubMed] [Google Scholar]
- Gellman RS, Carl JR. Motion processing for saccadic eye movements in humans. Experimental Brain Research. 1991:660–667. doi: 10.1007/BF00230979. [DOI] [PubMed] [Google Scholar]
- Gomi H, Abekawa N, Nishida S. Spatiotemporal tuning of rapid interactions between visual-motion analysis and reaching movement. Journal of Neuroscience. 2006;26:5301–5308. doi: 10.1523/JNEUROSCI.0340-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodale MA. Transforming vision into action. Vision Research. 2011;51:1567–1587. doi: 10.1016/j.visres.2010.07.027. [DOI] [PubMed] [Google Scholar]
- Goodale MA, Milner AD. Separate visual pathways for perception and action. Trends in Neurosciences. 1992;15:20–25. doi: 10.1016/0166-2236(92)90344-8. [DOI] [PubMed] [Google Scholar]
- Goodale MA, Westwood DA. An evolving view of duplex vision: Separate but interacting cortical pathways for perception and action. Current Opinion in Neurobiology. 2004;14:203–211. doi: 10.1016/j.conb.2004.03.002. [DOI] [PubMed] [Google Scholar]
- Hallett PE. Primary and secondary saccades to goals defined by instructions. Vision Research. 1978;18:1279–1296. doi: 10.1016/0042-6989(78)90218-3. [DOI] [PubMed] [Google Scholar]
- Jeannerod M. The neural and behavioural organization of goal-directed movements. Oxford: Clarendon Press; 1988. [Google Scholar]
- Keller E, Johnsen SD. Velocity prediction in corrective saccades during smooth-pursuit eye movements in monkey. Experimental Brain Research. 1990;80:525–531. doi: 10.1007/BF00227993. [DOI] [PubMed] [Google Scholar]
- Kerzel D, Gegenfurtner KR. Motion-induced illusory displacement reexamined: Differences between perception and action? Experimental Brain Research. 2005;162:191–201. doi: 10.1007/s00221-004-2139-z. [DOI] [PubMed] [Google Scholar]
- Kim CE, Thaker GK, Ross DE, Medoff D. Accuracies of saccades to moving targets during pursuit initiation and maintenance. Experimental Brain Research. 1997;113:371–377. doi: 10.1007/BF02450336. [DOI] [PubMed] [Google Scholar]
- Kosovicheva AA, Maus GW, Anstis S, Cavanagh P, Tse PU, Whitney D. The motion-induced shift in the perceived location of a grating also shifts its aftereffect. Journal of Vision. 2012;12:1–14. doi: 10.1167/12.8.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowler E. Eye movements: The past 25 years. Vision Research. 2011;51:1457–1483. doi: 10.1016/j.visres.2010.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarley JS, Kramer AF, DiGirolamo GJ. Differential effects of the Müller-Lyer illusion on reflexive and voluntary saccades. Journal of Vision. 2003;3:751–760. doi: 10.1167/3.11.9. [DOI] [PubMed] [Google Scholar]
- Nijhawan R. Motion extrapolation in catching. Nature. 1994;370:256–257. doi: 10.1038/370256b0. [DOI] [PubMed] [Google Scholar]
- Paillard J. Motor and representational framing of space. In: Paillard J, editor. Brain and Space. Oxford: Oxford University Press; 1991. pp. 163–182. [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Ramachandran VS, Anstis SM. Illusory displacement of equiluminous kinetic edges. Perception. 1990;19:611–616. doi: 10.1068/p190611. [DOI] [PubMed] [Google Scholar]
- Robinson DA. Models of the saccadic eye movement control system. Kybernetik. 1973;14:71–83. doi: 10.1007/BF00288906. [DOI] [PubMed] [Google Scholar]
- Ron S, Vieville T, Droulez J. Target velocity based prediction in saccadic vector programming. Vision Research. 1989;29:1103–1114. doi: 10.1016/0042-6989(89)90059-x. [DOI] [PubMed] [Google Scholar]
- Saijo N, Murakami I, Nishida S, Gomi H. Large-field visual motion directly induces an involuntary rapid manual following response. Journal of Neuroscience. 2005;25:4941–4951. doi: 10.1523/JNEUROSCI.4143-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlag J, Schlag-Rey M. Through the eye, slowly: Delays and localization errors in the visual system. Nature Reviews Neuroscience. 2002;3:191–215. doi: 10.1038/nrn750. [DOI] [PubMed] [Google Scholar]
- Smeets JBJ, Brenner E. Perception and action are based on the same visual information: Distinction between position and velocity. Journal of Experimental Psychology: Human Perception and Performance. 1995;21:19–31. doi: 10.1037//0096-1523.21.1.19. [DOI] [PubMed] [Google Scholar]
- Westheimer G. Eye movement responses to a horizontally moving visual stimulus. Archives of Ophthalmology. 1954;52:932–941. doi: 10.1001/archopht.1954.00920050938013. [DOI] [PubMed] [Google Scholar]
- Whitney D. The influence of visual motion on perceived position. Trends in Cognitive Sciences. 2002;6:211–216. doi: 10.1016/s1364-6613(02)01887-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney D, Cavanagh P. Motion distorts visual space: Shifting the perceived position of remote stationary objects. Nature Neuroscience. 2000;3:954–959. doi: 10.1038/78878. [DOI] [PubMed] [Google Scholar]
- Whitney D, Goltz HC, Thomas CG, Gati JS, Menon RS, Goodale MA. Flexible retinotopy: Motion-dependent position coding in the visual cortex. Science. 2003;302:878–881. doi: 10.1126/science.1087839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney D, Goodale MA. Visual motion due to eye movements helps guide the hand. Experimental Brain Research. 2005;162:394–400. doi: 10.1007/s00221-004-2154-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney D, Westwood DA, Goodale MA. The influence of visual motion on fast reaching movements to a stationary object. Nature. 2003;423:869–873. doi: 10.1038/nature01693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong E, Mack A. Saccadic programming and perceived location. Acta Psychologica. 1981;48:123–131. doi: 10.1016/0001-6918(81)90054-8. [DOI] [PubMed] [Google Scholar]
- Yamagishi N, Anderson SJ, Ashida H. Evidence for dissociation between the perceptual and visuomotor systems in humans. Proceedings of the Royal Society of London Series B: Biological Sciences. 2001;268:973–977. doi: 10.1098/rspb.2001.1603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Yeh SL, De Valois KK. Motion contrast and motion integration. Vision Research. 1993;33:2721–2732. doi: 10.1016/0042-6989(93)90231-k. [DOI] [PubMed] [Google Scholar]
- Zimmermann E, Morrone MC, Burr D. Visual motion distorts visual and motor space. Journal of Vision. 2012;12:1–8. doi: 10.1167/12.2.10. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.