Skip to main content
NCBI home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1995 Jul 18;92(15):6689–6696. doi: 10.1073/pnas.92.15.6689

Complexity, contingency, and criticality.

P Bak 1, M Paczuski 1
PMCID: PMC41396  PMID: 11607561

Abstract

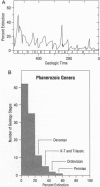
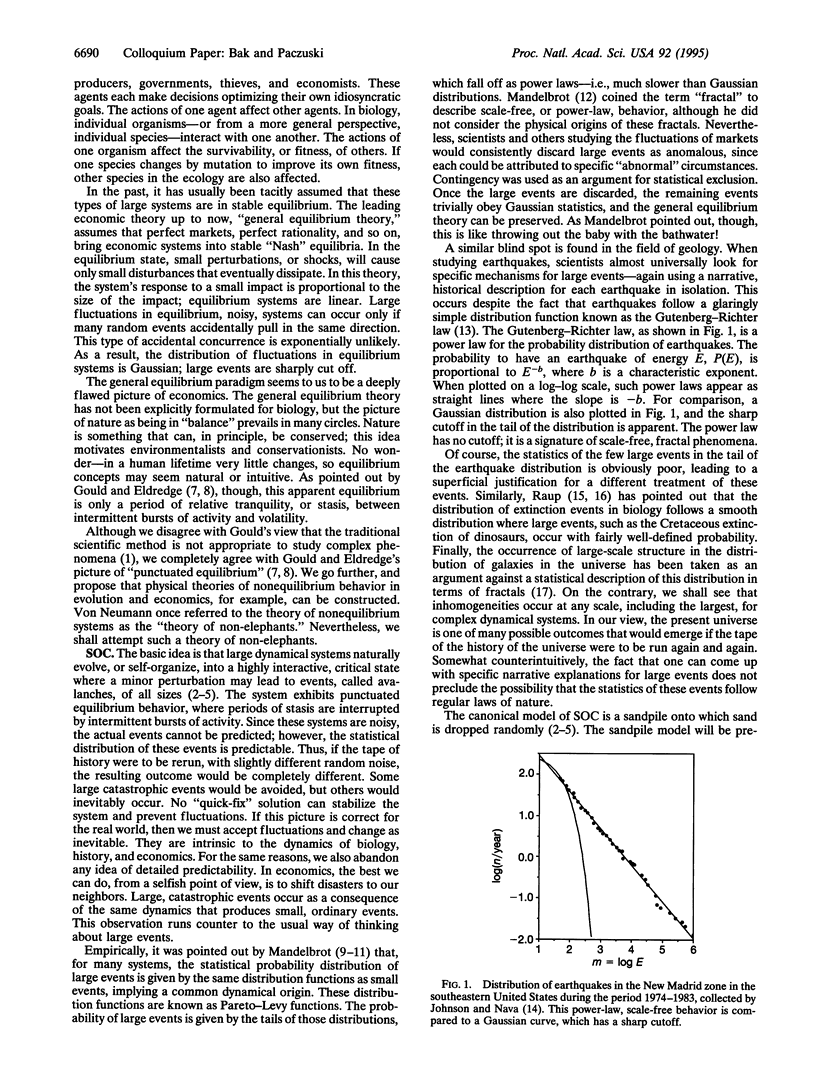
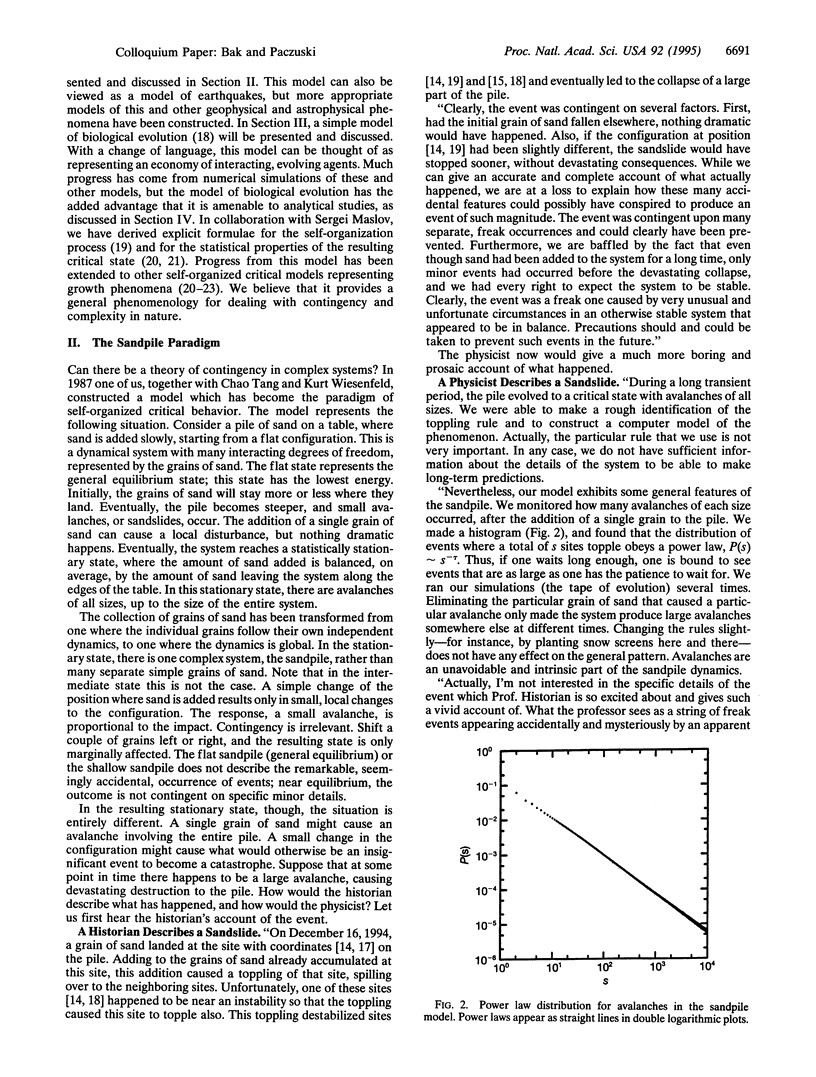
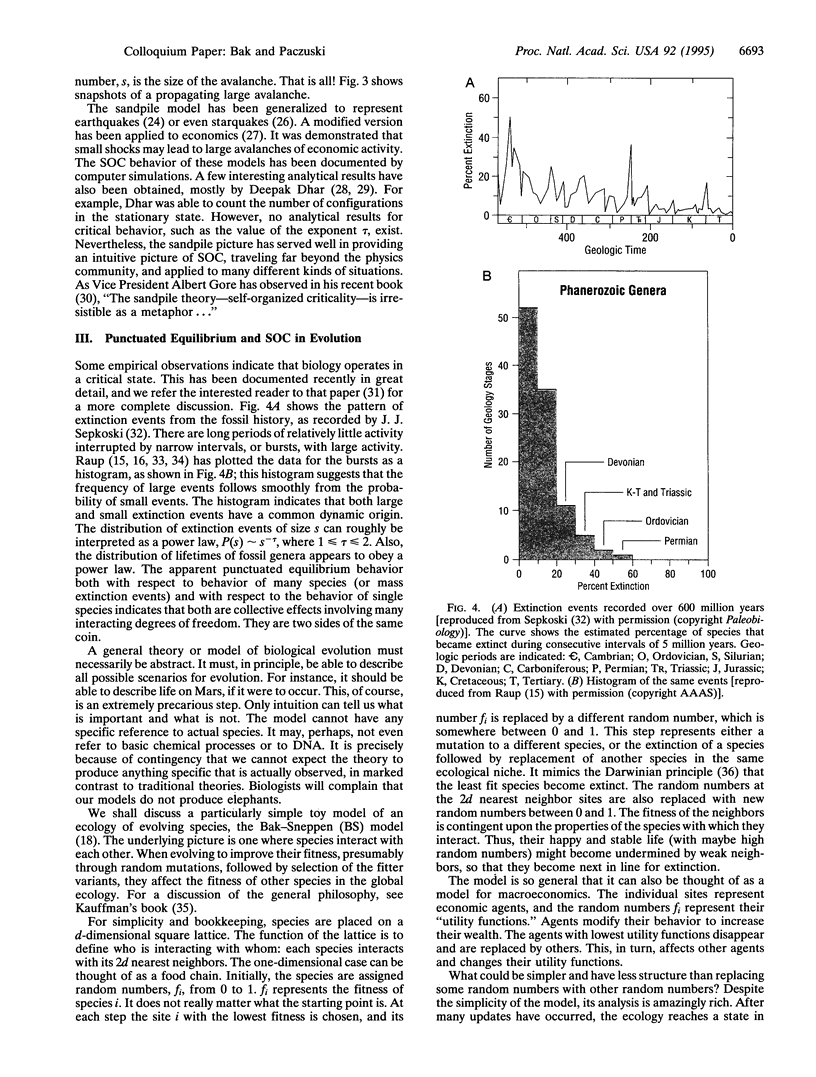
Complexity originates from the tendency of large dynamical systems to organize themselves into a critical state, with avalanches or "punctuations" of all sizes. In the critical state, events which would otherwise be uncoupled become correlated. The apparent, historical contingency in many sciences, including geology, biology, and economics, finds a natural interpretation as a self-organized critical phenomenon. These ideas are discussed in the context of simple mathematical models of sandpiles and biological evolution. Insights are gained not only from numerical simulations but also from rigorous mathematical analysis.

Full text

PDF
6689

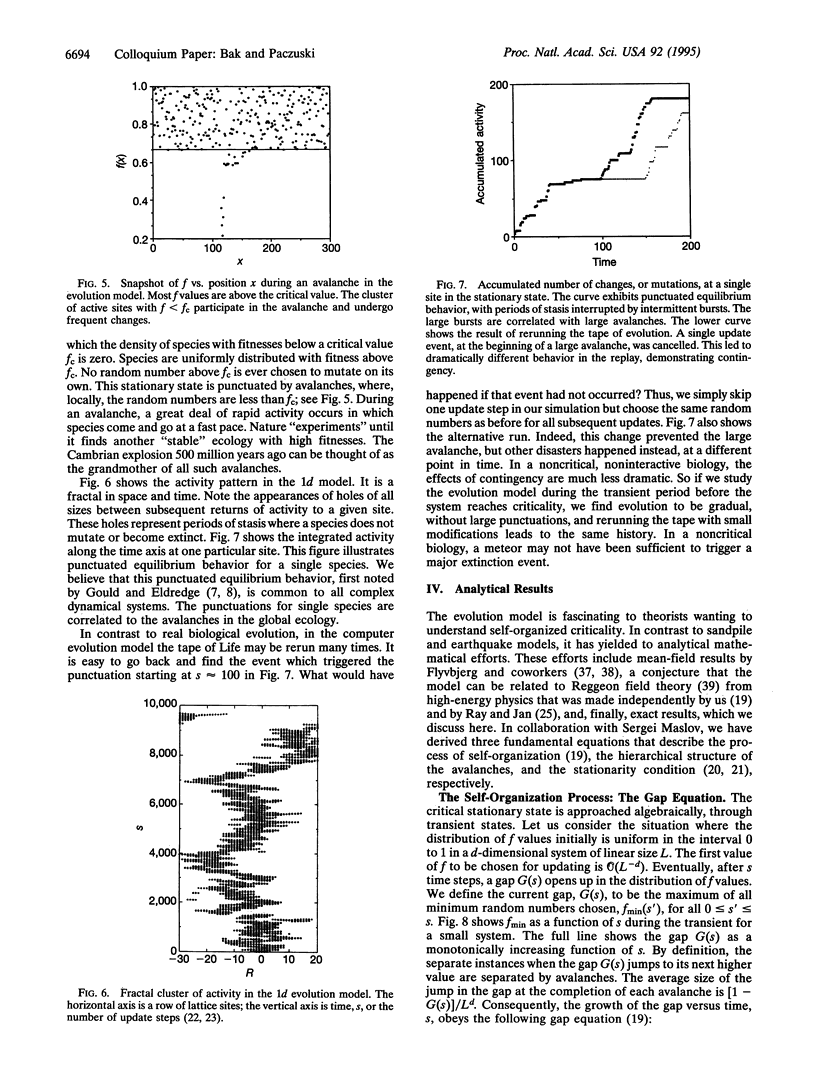
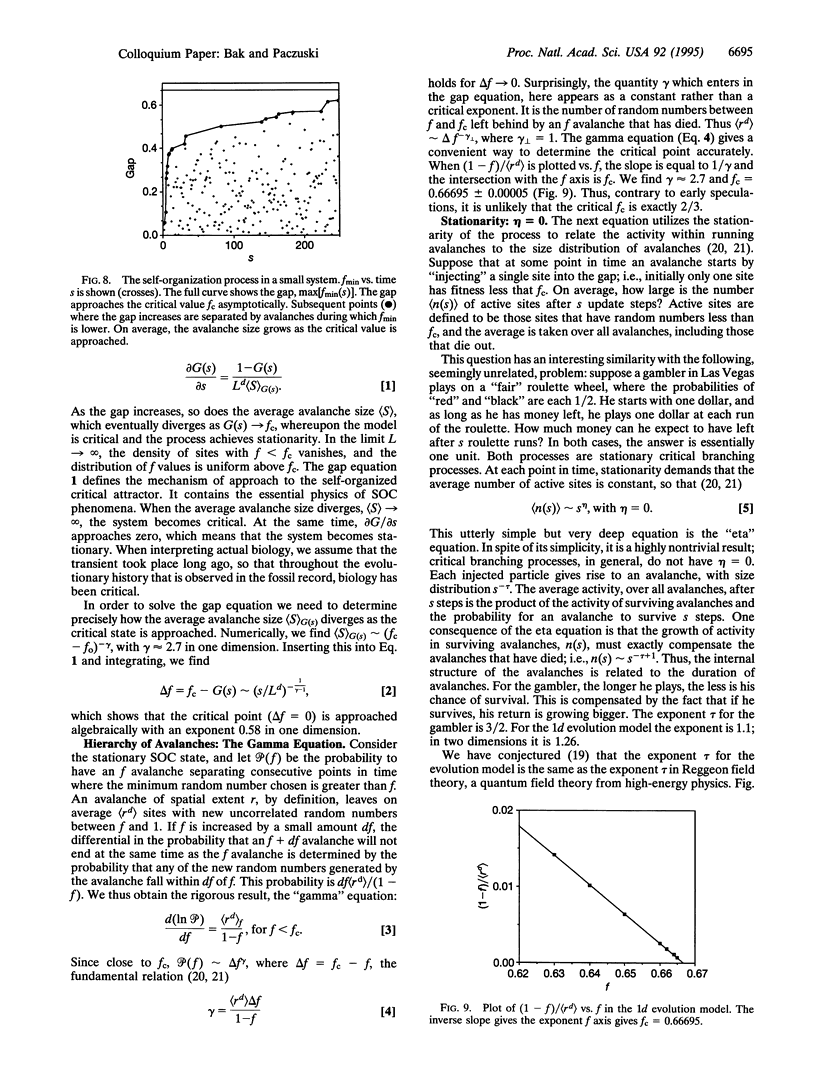
Images in this article

6692Fig. 3
on p.6692
6693Fig. 4
on p.6693

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Bak P, Sneppen K. Punctuated equilibrium and criticality in a simple model of evolution. Phys Rev Lett. 1993 Dec 13;71(24):4083–4086. doi: 10.1103/PhysRevLett.71.4083. [DOI] [PubMed] [Google Scholar]
  2. Bak P, Tang C, Wiesenfeld K. Self-organized criticality. Phys Rev A Gen Phys. 1988 Jul 1;38(1):364–374. doi: 10.1103/physreva.38.364. [DOI] [PubMed] [Google Scholar]
  3. Bak P, Tang C, Wiesenfeld K. Self-organized criticality: An explanation of the 1/f noise. Phys Rev Lett. 1987 Jul 27;59(4):381–384. doi: 10.1103/PhysRevLett.59.381. [DOI] [PubMed] [Google Scholar]
  4. Dhar D. Self-organized critical state of sandpile automaton models. Phys Rev Lett. 1990 Apr 2;64(14):1613–1616. doi: 10.1103/PhysRevLett.64.1613. [DOI] [PubMed] [Google Scholar]
  5. Flyvbjerg H, Sneppen K, Bak P. Mean field theory for a simple model of evolution. Phys Rev Lett. 1993 Dec 13;71(24):4087–4090. doi: 10.1103/PhysRevLett.71.4087. [DOI] [PubMed] [Google Scholar]
  6. Gould S. J., Eldredge N. Punctuated equilibrium comes of age. Nature. 1993 Nov 18;366(6452):223–227. doi: 10.1038/366223a0. [DOI] [PubMed] [Google Scholar]
  7. Maslov S, Paczuski M, Bak P. Avalanches and 1/f noise in evolution and growth models. Phys Rev Lett. 1994 Oct 17;73(16):2162–2165. doi: 10.1103/PhysRevLett.73.2162. [DOI] [PubMed] [Google Scholar]
  8. Olami Z, Feder HJ, Christensen K. Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes. Phys Rev Lett. 1992 Feb 24;68(8):1244–1247. doi: 10.1103/PhysRevLett.68.1244. [DOI] [PubMed] [Google Scholar]
  9. Paczuski M, Bak P, Maslov S. Laws for stationary states in systems with extremal dynamics. Phys Rev Lett. 1995 May 22;74(21):4253–4256. doi: 10.1103/PhysRevLett.74.4253. [DOI] [PubMed] [Google Scholar]
  10. Raup D. M. Biological extinction in earth history. Science. 1986 Mar 28;231:1528–1533. doi: 10.1126/science.11542058. [DOI] [PubMed] [Google Scholar]
  11. Raup D. M., Boyajian G. E. Patterns of generic extinction in the fossil record. Paleobiology. 1988;14(2):109–125. doi: 10.1017/s0094837300011866. [DOI] [PubMed] [Google Scholar]
  12. Raup D. M., Sepkoski J. J., Jr Mass extinctions in the marine fossil record. Science. 1982 Mar 19;215(4539):1501–1503. doi: 10.1126/science.215.4539.1501. [DOI] [PubMed] [Google Scholar]
  13. Ray TS, Jan N. Anomalous approach to the self-organized critical state in a model for "life at the edge of chaos". Phys Rev Lett. 1994 Jun 20;72(25):4045–4048. doi: 10.1103/PhysRevLett.72.4045. [DOI] [PubMed] [Google Scholar]
  14. Sepkoski J. J., Jr Ten years in the library: new data confirm paleontological patterns. Paleobiology. 1993 Winter;19(1):43–51. doi: 10.1017/s0094837300012306. [DOI] [PubMed] [Google Scholar]
  15. Sneppen K., Bak P., Flyvbjerg H., Jensen M. H. Evolution as a self-organized critical phenomenon. Proc Natl Acad Sci U S A. 1995 May 23;92(11):5209–5213. doi: 10.1073/pnas.92.11.5209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. de Boer J, Derrida B, Flyvbjerg H, Jackson AD, Wettig T. Simple model of self-organized biological evolution. Phys Rev Lett. 1994 Aug 8;73(6):906–909. doi: 10.1103/PhysRevLett.73.906. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES