Dissecting the Mechanism of Martensitic Transformation via Atomic-Scale Observations

Abstract

Martensitic transformation plays a pivotal role in the microstructural evolution and plasticity of many engineering materials. However, so far the underlying atomic processes that accomplish the displacive transformation have been obscured by the difficulty in directly observing key microstructural signatures on atomic scale. To resolve this long-standing problem, here we examine an AISI 304 austenitic stainless steel that has a strain/microstructure-gradient induced by surface mechanical attrition, which allowed us to capture in one sample all the key interphase regions generated during the γ(fcc) → ε(hcp) → α′(bcc) transition, a prototypical case of deformation induced martensitic transformation (DIMT). High-resolution transmission electron microscopy (HRTEM) observations confirm the crucial role of partial dislocations, and reveal tell-tale features including the lattice rotation of the α′ martensite inclusion, the transition lattices at the ε/α′ interfaces that cater the shears, and the excess reverse shear-shuffling induced γ necks in the ε martensite plates. These direct observations verify for the first time the 50-year-old Bogers-Burgers-Olson-Cohen (BBOC) model, and enrich our understanding of DIMT mechanisms. Our findings have implications for improved microstructural control in metals and alloys.

The structural transformation involved in fast cooling of iron and steel was first studied by Adolf Martens in the late 19^th century. In honor of his contributions, a category of displacive crystalline structural phase transitions has since been termed “martensitic transformation”¹. Martensitic transformations are diffusionless and characterized by a collective movement of atoms across distances that are typically smaller than one nearest-neighbor spacing. The resulting structural transition is often accompanied by pronounced changes in mechanical (e.g. strength, toughness, and shape memory²,³,⁴,⁵), electromagnetic (e.g. magneto- and mechano- and electro-caloric⁶), and transport (such as conductivity⁷) properties of the materials. In biological systems, some virus species use pressure-induced martensitic transformation to infect bacteria cells⁸,⁹. Martensitic transformations of silicates in the Earth's mantle are thought to play a vital role in plate tectonics and earthquakes¹⁰,¹¹.

The importance of martensitic transformations in nature and engineering has led to tremendous efforts to explore their microscopic mechanisms. Almost enjoying the equal popularity as the classic Kurdjumov & Sachs¹² and Nishiyama¹³ shear models, in 1964, Bogers and Burgers¹⁴ proposed a hard-sphere model for the martensitic transformation in steels from a face-centered cubic fcc-γ austenite phase to a body-centered cubic bcc-α′ martensite phase. Olson and Cohen¹⁵,¹⁶,¹⁷,¹⁸ further developed the Bogers and Burgers model by emphasizing the role of plastic deformation, proposing that the austenite γ phase transits to a hexagonal close-packed hcp-ε martensite phase first and then to the bcc-α′ martensite phase. Hereafter, this model will be referred to as the Bogers-Burgers-Olson-Cohen model (or the BBOC model). (Supplementary Fig. 1) However, half a century later, the shear movements during the γ → ε → α′ transformation hypothesized in the BBOC model have yet to be confirmed by experiments at the atomic level. What has been known so far is that certain crystallographic orientation relationships (ORs) exist between the parent and martensite phases, and the resulting crystals exhibit fine-scale inhomogeneities involving shuffling, slip, twinning, and stacking faults¹⁹,²⁰,²¹,²²,²³. A major obstacle in clarifying experimentally the mechanism of strain-induced martensitic transformation lies in the fact that several processes are expected to occur in parallel in both of the parent and product phases, generating a complex pattern of interface dislocations and diffuse tilt grain boundaries (GBs) that are difficult to correlate and analyze.

Our experiments reported below have captured the early stages of martensite formation. This was accomplished by inducing the γ → ε → α′ DIMT in AISI 304 γ austenitic stainless steel, via surface mechanical attrition treatment (SMAT)²⁴ (See Methods). The SMAT caused a plastic strain field, which was extremely severe at the surface, with a gradient towards to the center of the sample matrix. Therefore, various features of the γ → ε → α′ transformation evolution can be captured at the different locations, along the cross sectional direction in a SMATed sample. The freshly-formed interphase interfaces, including their atomic arrangements with diffuse tilt GBs and dislocations, can then be investigated in detail under HRTEM in correlation with neighboring phases. The high-resolution observations are also compared with atomistic Molecular Dynamics (MD) simulations (See Methods). The unprecedented level of details we have uncovered experimentally provides systematic evidence that verifies the BBOC model for the first time, and enriches our understanding of the DIMT mechanism.

Results and discussion

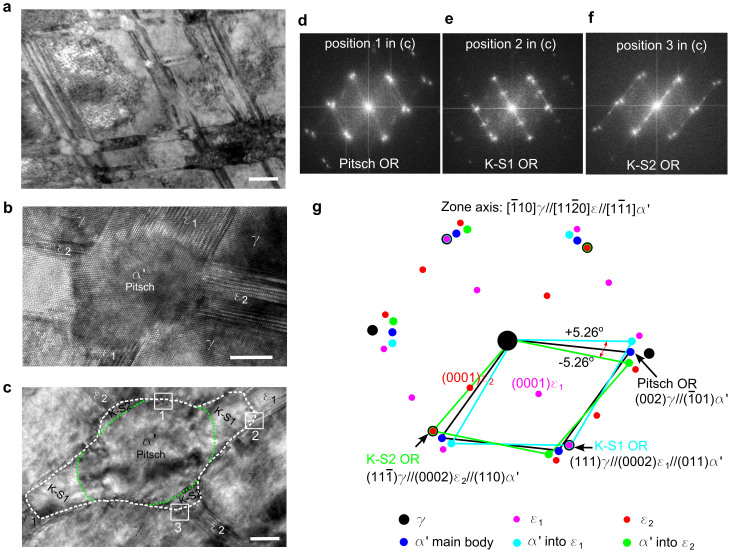
Specifically, in a SMATed sample we observe high densities of dislocation grids in the interior of the sample matrix, the formation of hcp-ε plates in a layer at a depth of ~90 μm from the surface, and finally the bcc-α′ martensite inclusions emerging at the intersection region of two ε plates (Fig. 1a) (Supplementary Fig. 2). Once nucleated, the α′ martensite inclusions grow towards to the neighboring ε plates (Fig. 1b–c). We first analyze the ORs between the γ, ε and α′ phases, which have been determined using the fast Fourier transformation (FFT) spots (Fig. 1d–f) and atomic-resolution images (next section) from adjoining phases in the interfacial transition regions and schematically summarized in Fig. 1g. The α′ inclusion is found to initially exhibit the Pitsch OR with respect to γ, when it nucleates in the intersection region between the two ε. The Pitsch OR in our observations is different from the widely accepted Kurdjumov-Sachs (K-S) ORs, which require the closest packing plane {111}γ unrotated between γ, ε and α′ crystalline structures. However, when α′ inclusion grows along the two ε plates, the orientations are changed from the Pitsch OR to two K-S ORs in the grown parts. The misorientation between the Pitsch OR and either of the two K-S ORs is 5.26°.

Figure 1. Orientation of bcc-α′ martensites.

(a), TEM images taken at the top surface layer of 304 stainless steels after SMAT. High density of bcc-α′ formed at the intersection region of two hcp-ε plates. (b–f), TEM images and the corresponding live FFT spots patterns taken along the zone axis 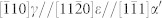. Different from the α′ martensite in (b), that in (c) has grown into two hcp-ε plates. The green and white dash lines in (c) indicate the α′main body with Pitsch orientation relationships (OR), with the parts grown into ε transforming into two Kurdjumov-Sachs (K-S) ORs, with respect to the fcc-γ. (g), Schematic summarizing the diffraction spots taken from adjoining phases in the interfacial transition regions between γ, ε and α′. The black arrows indicate the three ORs with details on parallel planes and the red arrows indicate the 5.26° misorientation angle between the Pitsch OR and either of the two K-S ORs. Scale bars, 200 nm (a), 5 nm (b), 10 nm (c).

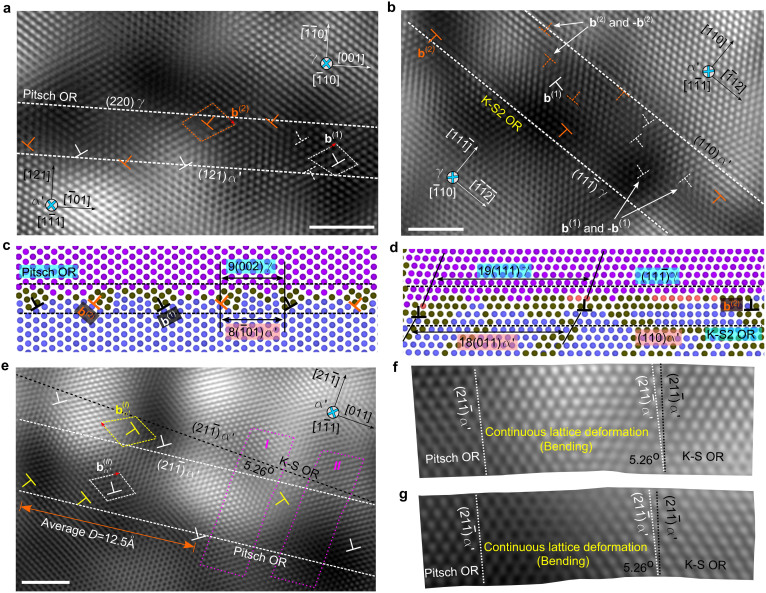
Our atomic-resolution images discern how the above is accomplished at the atomic level for the α′ inclusion. Most of the HRTEM images in this paper are Fourier filtered to enhance the visibility (better contrast), at little expense of the fidelity (see typical unfiltered images in Supplementary Fig. 6). Fig. 2 shows the HRTEM images and MD simulation results on the interfaces between the γ and α′ phases and between the two ORs (all views along 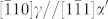direction). We first assume that all dislocation lines are perpendicular to the image planes, i.e., the dislocation lines are parallel to the incident electron beam direction of 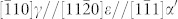. The HRTEM image in Fig. 2a and the MD simulation result in Fig. 2c show that the interface between (220)γ and (121)α′ with the Pitsch OR is semi-coherent and diffuse, in the presence of two sets of misfit dislocations determined as 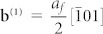on (111)γ planes, and 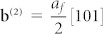on 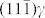planes. These Burgers vectors have the components 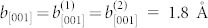along the [001]γ and 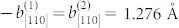along the [110]γ. To completely release the lattice misfit strain of f = 10.94% between (002)γ and 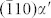, the spacing, l_d, of the misfit dislocation array determined by l_d = b_[001]/f should be 16.5 Å, which is almost equivalent to the sum of the interplanar spacing of either 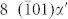or 9 (002)γ planes, as shown in Fig. 2a and c. Furthermore, the observed dislocation number ratio for the two sets is closed to 1:1, which greatly reduces the long-range stress field of dislocations because the b⁽¹⁾ and b⁽²⁾ misfit dislocations have opposite sign for their Burgers vector component along the [110]γ direction.

Figure 2. Interfacial structures for two orientation relationships.

All projections are along 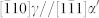. The dislocations are indexed by the “⊥” symbol and its Burgers vector is depicted using Burgers circuit (dash line circuits). (a–d), HRTEM images and MD simulations of the γ/α′ interface with Pitsch OR (a,c) and K-S2 OR (b,d), respectively. (a,c), The Pitsch OR interface with (220)γ//(121)α′. Two sets of dislocations 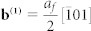on (111)γ planes and 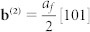on 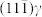planes, distribute with an average distance of 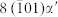and 9 (002)γ planes to release the lattice misfit strain between them. (b,d), The K-S2 OR interface with 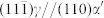, requiring the rotated 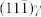to rotate back from the Pitsch OR. To achieve this, another two sets of dislocations, with Burgers vectors of -b⁽¹⁾ and -b⁽²⁾, respectively, are generated to form b⁽¹⁾ and -b⁽¹⁾ and b⁽²⁾ and -b⁽²⁾ dislocation dipoles (dash-lined “⊥” symbol dipoles with opposite sign). The number of -b⁽¹⁾ dislocations is almost the same as the number of b⁽¹⁾ dislocations, with only one un-coupled b⁽¹⁾ dislocation, thereby making the 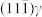unrotated to evolve to the (110)α′. The single b⁽²⁾ on every 19^th 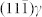plane releases the lattice misfit strain of 5% between (111)γ and (110)α′. (e–g), HRTEM image taken at an α′/α′ interface, showing a 5.26° rotation inside one α′ inclusion, from the Pitsch OR to K-S OR along the 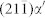interface plane. (e), Two sets of dislocations walls 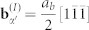on (110)α′ planes and 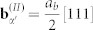on 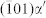planes, form the diffuse small-angle tilt grain boundary. More dislocations are located in the left region of zone I, where the average dislocation spacing D of 12.5 Å meets the requirement in the OR change. (f, g), The enlarged image in two pink-color framed rectangular zones I and II in (e), respectively. No dislocations are found in these regions and the lattice is continuously bending-mode deformed, leading to the diffuse interface region bent obviously and the 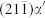plane rotated 5.26°. All scale bars, 2 nm.

Fig. 2b and Fig. 2d show a γ/α′ diffuse and semi-coherent interface with the K-S2 OR of 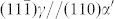When the K-S OR is evolved from the Pitsch OR, the rotated 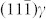must rotate back, which requires no component of Burgers vector along the 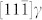and [110]α′directions, as shown in Fig. 2d. To achieve this, another two sets of dislocations are generated, which possess the Burgers vectors of -b⁽¹⁾ and -b⁽²⁾, respectively. The number of -b⁽¹⁾ dislocations is almost the same as the number of b⁽¹⁾ dislocations, as shown in Fig. 2b with only one un-coupled b⁽¹⁾ dislocation, thereby recovering the lattice rotation caused by the b⁽¹⁾ dislocation set. Fig. 2b illustrates that the number of -b⁽²⁾ dislocations is less than the number of b⁽²⁾ dislocations, leaving one b⁽²⁾ dislocation on every 19^th 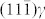plane. The coupled b⁽¹⁾ and -b⁽¹⁾ and b⁽²⁾ and -b⁽²⁾ are dislocation dipoles, which do not cause any lattice rotation, thereby making the 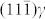unrotated to evolve to the (110)α′. The single b⁽²⁾ dislocation on every 19^th 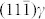plane is to release the misfit strain of 5% between the 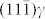and (110)α′ (See more discussions in Supplementary Fig. 3–4).

How can the Pitsch OR and K-S OR co-survive in a α′ particle embedded inside a single γ crystal? The α′ lattice must rotate itself inside the α′ particle to fulfill the OR change. Fig. 2e shows that inside one α′ particle, the 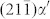planes, or equivalently, the (011)α′ planes, rotate 5.26° about 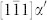, leading to the α′ orientation change from the Pitsch OR region to the K-S OR region. A small-angle tilt GB is formed between the Pitsch and K-S OR regions. Fig. 2e indicates that the tilt GB is diffuse and composed of two sets of dislocation walls, 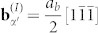on the (110)α′ planes and 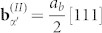on the 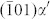planes. The two sets of dislocations have the same edge Burgers vector component of along the 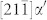direction, with which the dislocation spacing D = 12.8 Å is anticipated from 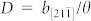. Dislocations are not equi-distantly distributed in the two sets of dislocation walls. There are no dislocations at all in two pink-color framed rectangular zones I and II in the HRTEM image of Fig. 2e. More dislocations are located in the left region of zone I, where the average dislocation spacing D is 12.5 Å, very close to the anticipated value of 12.8 Å, meaning that the crystal lattice in the left region has rotated 5.26° already and meet the requirement in the OR change. Zooming into zones I and II we observe a severe continuous bending-mode deformation of the lattice, as shown in Fig. 2f and 2g, which makes the 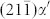plane rotate 5.26°. No dislocations are found in this region and the lattice is continuously deformed, leading to the obviously bent diffuse interface region. The bending-mode deformation is elastic and interacting with the long-range dislocation stress field and other unknown defects under the mechanical constraints of the surroundings of the diffuse tilt boundary²²,²⁵.

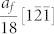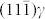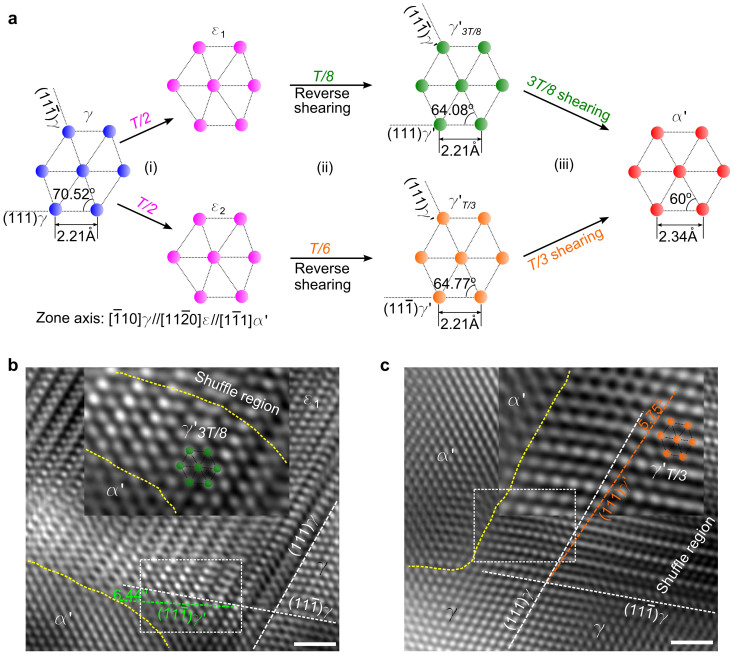
Having worked out the origin of the orientation change of the α′ martensite and the accommodating dislocations, we now move on to discuss shear movements involved in the phase transition. There are two shears in the BBOC model. The first shear is on every plane and the second shear is 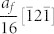on every (111)γ plane, corresponding to the T/3 and 3T/8 transformation dislocations, respectively (T donates a Shockley partial dislocation for fcc twin shear)¹⁶,¹⁷,¹⁸,²³ (Supplementary Fig. 1). We show next the equivalent of 3T/8 and T/3 shearing, in the case of the two intersecting ε plates. The formation of a ε plate can be regarded, on average, as resulting from T/2 transformation dislocations on every {111}γ plane. Excess T/6 and T/8 dislocations are therefore produced. These excess dislocations can spread back to the two intersecting ε plates, in a reverse shear-shuffling process (reverse shear of the dislocations, together with accommodating shuffle displacements on some planes)²¹. In addition to the larger volume of α′, the extremely severe strain/stress field caused by SMAT at the surface layer might be the driving force for the reverse shear-shuffling of the excess dislocations. The austenite-martensite interface might not be atomically flat, where a transition lattice zone could exist to continuously change the lattice structure²²,²⁵,²⁶. Here, the reverse shear-shuffling results in two transition lattices, which will be named γ′_3T/8 and γ′_T/3 transition lattices in the present work, with two sets of uniformly distorted {111}γ′planes¹⁵. Fig. 3a schematically presents the lattice evolution from the original fcc-γ lattice, to hcp-ε lattices, to γ′_3T/8 and γ′_T/3 transition lattices, and finally to bcc-α′ lattice, with the projection zone axis of 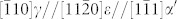The intersecting angle of 70.52° between the original 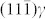and (111)γ, changes to 64.08° in the γ′_3T/8 transition lattice and 64.77° in the γ′_T/3 transition lattice, respectively. The distance between neighboring atomic rows on the {111}γ, 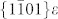and two {111}γ′ are all the same, 2.21Å, which must expand to 2.34Å for the corresponding rows on {011}α′. Fig. 3b–c are, respectively, the HRTEM images taken at the ε₁/α′ and ε₂/α′ interface regions with the Pitsch OR (unfiltered images in Supplementary Fig. 6). There exists a shuffle region between the transition lattice zone and the hcp-ε plates. The shuffle region in the hcp-ε₂ plate is bigger than that in the hcp-ε₁ plate, as the T/6 excess shearing is larger than the T/8 excess shearing. The angle difference of 6.44° and 5.75° (from 70.52°) and the γ′_3T/8 and γ′_T/3 transition lattices (see enlarged insets, rectangle in Fig. 3b and 3c, respectively), are thus indicative of the “3T/8-T/3”, for shearing in the presence of the two ε plates.

Figure 3. BBOC “3T/8-T/3” shearing and evolution routes.

(a), Schematic diagram illustrating the lattice evolution from the original fcc-γ lattice, (i) to hcp-ε lattices, (ii) to γ′_3T/8 and γ′_T/3 transition lattices, and finally (iii) to bcc-α′ lattice. The zone axis is 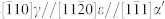. Excess T/8 and T/6 dislocations reversely shear back to two ε lattices, resulting in γ′_3T/8 and γ′_T/3 transition lattices, respectively, satisfying the BBOC “3T/8-T/3” shearing. The intersecting angle of 70.52° between original 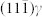and (111)γ, is reduced to 64.08° in the γ′_3T/8 transition lattice and 64.77° in the γ′_T/3 transition lattice. The distance between neighboring atomic rows on the (111)γ and two {111}γ' are 2.21Å, and the corresponding rows on {011}α' are expanded to 2.34 Å. (b–c), HRTEM images taken at the ε₁/α′ (b) and ε₂/α′ (c) interface regions. The reduced angle of 6.44° and 5.75°, and the γ′_3T/8 and γ′_T/3 transition lattices in the enlarge insets (rectangle in (b) and (c), respectively) are indicated, accomplishing the “3T/8-T/3” shearing from the two ε. All scale bars, 1 nm.

We now illustrate further how the T/8 and T/6 excess dislocations function in the shear induced martensitic transformation. Once eight T/8, or six T/6, reversely spread to ε and combine to form a (reverse) Shockley partial dislocation, γ lattices or stacking faults (SFs) would be formed²¹. Normally, SFs or extremely thin γ strips are easily generated to accompany the hcp-ε₁ plate, via the “T/8” action. However, the hcp-ε₂ plate is more easily transformed back to more perfect γ lattices, because T/6 excess dislocations could combine to form more mobile Shockley partial dislocations. The reverse Shockley partial dislocations change the stacking order in the ε₂ plate (Supplementary Fig. 5) at the γ/ε₂ coherent interface, forming a γ neck in the hcp-ε₂ plate, as shown in Fig. 4a–b. There are 8 atomic 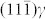planes in the small γ lattice neck zone that penetrates into the ε₂ plate. The number of planes is exactly one-third of the 24 (0002)ε planes or 24 (110)α′ planes. When 24 (0002)ε planes convert into 24 (110)α′ planes, four Shockley partial dislocations must reversely slip back, which form the necks of 8 atomic {111}γ planes. The γ necks in the ε₂ plates are frequently observed at the ε₂/α′ interface regions (Supplementary Fig. 7).

Figure 4. Effect of reverse-shearing dislocations on ε.

(a), HRTEM images taken at the ε₂/α′ interface region, i.e., T/3 shearing part side. Once six T/6 excess shearing dislocations combine to form a reverse Shockley partial dislocation, the ε₂ would be transformed back to γ lattice. White lines outline 8 atomic 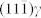planes (4 atomic planes at each side), exactly one-third of the 24 (0002)ε planes, that are reverse-transformed in the neck zones at the γ/ε₂ coherent interface to penetrate into the ε₂ plate. (b), The enlarged images taken at the neck zone in (a). The stacking order of the atomic planes changes in the ε₂ plate, which is caused by the reverse Shockley partial dislocation. Scale bars, 2 nm (a), 1 nm (b).

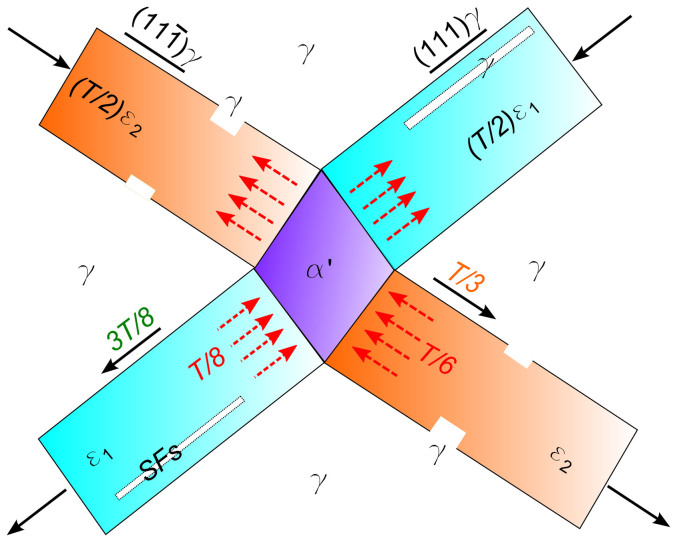
To recapitulate, the atomic-scale observations above demonstrate the γ/α′ Pitsch OR in the intersection region between two ε plates, the γ′_3T/8 and γ′_T/3 transition lattice zones at the ε₁/α′ and ε₂/α′ interfaces, and the excess dislocations involved in reverse shear. Taken together, the high-resolution evidence verifies the BBOC “3T/8-T/3” model of the strain induced γ → ε → α′ transformation. When the yield strength of the γ matrix is lower than the minimum stress required for martensitic transformation, plastic deformation will occur first in the γ matrix¹⁵, mediated by dislocations, especially by partial dislocations in low SF-energy metals. Depending on the loading rate and temperature, the partial dislocation mediated plastic deformation can be accomplished by the γ → ε phase transformation with T/2 dislocation slipping on every {111} plane. The subsequent ε → α′ transformation is depicted in Fig. 5 schematically. Once the ε plates are available in the γ matrix, the formation of the α′ martensite becomes energetically much easier. This is because the hcp-ε plates have already accomplished the T/2 shear displacements in the BBOC “3T/8-T/3” shearing model. With respect to the T/2 ε plates, the “3T/8-T/3” shear displacements are reduced to the “T/8-T/6” reverse shearing, leading to the formation of the γ′_3T/8 and γ′_T/3 transition lattice zones. Furthermore, the excess “T/6” can cause the necks in the hcp-ε plates.

Figure 5. Dislocation behavior in the ε → α′ transformation.

Schematic diagram illustrating that, with respect to the already-finished T/2 ε plates, the BBOC “3T/8-T/3” shearing is reduced to the reverse shearing of excess “T/8-T/6”. Reverse action of excess “T/8-T/6” transformation dislocations results in the SFs and γ strips inside the ε plates and the necks of the ε plates.

In summary, our HRTEM observations clarify the atomic arrangements and crystalline defects associated with deformation induced γ → ε → α′ phase transformation. The findings verify and enrich, for the first time, the half-century-old BBOC “3T/8-T/3” model. Specifically, we showed misfit dislocations at the γ, ε and α′ interfaces to release misfit strains between these phases, and the diffuse tilt GBs that cause the change in crystal orientation of the α′ inclusions. Furthermore, the atomic-scale images reveal the γ′_3T/8 and γ′_T/3 transition lattices within the diffuse ε/α′ interfaces. The plastic deformation induced ε plates reduce the “3T/8-T/3” shear to a “second step”, i.e., the reverse action of excess “T/8-T/6” transformation dislocations, which result in the SFs and γ strips inside the ε plates and the necks of the ε plates. The detailed understanding of the DIMT process elucidated here may stimulate new ideas to judiciously control the various ingredients/stages and the degree of transformation, and hence open new possibilities for the improvement of steels and alloys.

Methods

Sample preparation and TEM observation

The AISI 304 stainless steels used in this study has a composition, in wt%, of 0.04C, 0.49Si, 1.65Mn, 16.8Cr, 0.37Mo and balance Fe. The geometry of 304 stainless steels specimen is 70 mm × 50 mm × 1 mm. Both surfaces of specimens were synchronously SMATed for 15 min at room temperature with a vibrating frequency of 20 kHz and 3 mm diameter bearing balls²⁴. The SMATed 304 stainless steels at different depth was characterized by transmission electron microscopy (TEM, JEOL 2010F), with operating voltage of 200 kV.

Molecular dynamics (MD) simulations

The LAMMPS software²⁷ was employed in all MD simulations. The box size of the simulation system for the Pitsch OR was 100 × 100 × 100 Å, with bcc-α′ and fcc-γ phases occupying the lower, [−50, 0] Å, and upper, [0, 50] Å, halves, respectively, along the z direction. The lattice constants of bcc and fcc crystals are 2.87 Å and 3.602 Å, respectively. When the distance between two atoms in fcc/bcc interface was smaller than 1.2 Å, one of the atoms was removed. The simulation system contained 85,306 atoms. An embedded-atom method (EAM) potential for Fe²⁸ was employed, which favors the bcc structure in the temperature range of 0 to 1820 K. In order to study the interfacial structure, only atoms located between −3 Å and 3 Å of the z direction (total 4,529 atoms) were allowed to relax with all other atoms fixed. Periodic boundary conditions were applied along the x and y directions. With the NVT ensemble at temperature 1 K, energy minimization with conjugate gradient method was performed and followed by 1000 steps relaxation with the time step of 1 fs. For the K-S orientation, the initial configuration was built manually according the BBOC model, with 86,303 atoms in a box of 101 × 101 × 101 Å. The system was relaxed for 500,000 steps (time step of 1 fs) in NVT ensemble at 10 K under the condition that fcc atoms four layers away from the interface were fixed. The software of OVITO²⁹ and the common neighbor analysis method³⁰ were employed to visualize and distinguish the atomic arrangements.

Author Contributions

T.Y.Z. designed and managed the project. X.S.Y. conducted HRTEM observations. S.S. carried out the MD simulations. X.S.Y. and T.Y.Z. performed the data analysis and X.L.W. examined the analysis results. E.M., X.L.W. and T.Y.Z. conceived the storyline of the paper. All contributed to the discussions and wrote the paper.

Supplementary Material

Supplementary Information

Supplementary Information