Temperature Dependent Change in Equilibrium Elastic Modulus After Thermally Induced Stress Relaxation in Porcine Septal Cartilage

Abstract

Background and Objectives

Laser cartilage reshaping (LCR) is a promising method for the in situ treatment of structural deformities in the nasal septum, external ear and trachea. Laser heating leads to changes in cartilage mechanical properties and produces relaxation of internal stress allowing formation of a new stable shape. While some animal and preliminary human studies have demonstrated clinical feasibility of LCR, application of the method outside specialized centers requires a better understanding of the evolution of cartilage mechanical properties with temperature. The purpose of this study was to (1) develop a method for reliable evaluation of mechanical changes in the porcine septal cartilage undergoing stress relaxation during laser heating and (2) model the mechanical changes in cartilage at steady state following laser heating.

Study Design/Materials and Methods

Rectangular cartilage specimens harvested from porcine septum were heated uniformly by a radio-frequency (RF) electric field (500 kHz) for 8 and 12 seconds to maximum temperatures from 50 to 90°C. Cylindrical samples were fashioned from the heated specimens and their equilibrium elastic modulus was measured in a step unconfined compression experiment. Functional dependencies of the elastic modulus and maximum temperature were interpolated from the measurements. Profiles of the elastic modulus produced after 8 and 12 seconds of laser irradiation (Nd:YAG, λ =1.34 μm, spot diameter 4.8 mm, laser power 8 W) were calculated from interpolation functions and surface temperature histories measured with a thermal camera. The calculated elastic modulus profiles were incorporated into a numerical model of uniaxial unconfined compression of laser irradiated cylindrical samples. The reaction force to a 0.1 compressive strain was calculated and compared with the reaction force obtained in analogous mechanical measurements experiment.

Results

RF heating of rectangular cartilage sample produces a spatially uniform temperature field (temperature variations ≤4°C) in a central region of the sample which is also large enough for reliable mechanical testing. Output power adjustment of the RF generator allows production of temperature histories that are very similar to those produced by laser heating at temperatures above 60°C. This allows creation of RF cartilage samples with mechanical properties similar to laser irradiated cartilage, however with a spatially uniform temperature field. Cartilage equilibrium elastic modulus as a function of peak temperature were obtained from the mechanical testing of RF heated samples. In the temperature interval from 60 to 80°C, the equilibrium modulus decreased from 0.08 ± 0.01 MPa to 0.016 ±0.007 MPa, respectively. The results of the numerical simulation of uniaxial compression of laser heated samples demonstrate good correlation with experimentally obtained reaction force.

Conclusions

The thermal history and corresponding thermally induced modification of mechanical properties of laser irradiated septal cartilage can be mimicked by heating tissue samples with RF electric current with the added advantage of a uniform temperature profile. The spatial distribution of the mechanical properties obtained in septal cartilage after laser irradiation could be computed from mechanical testing of RF heated samples and used for numerical simulation of LCR procedure. Generalization of this methodology to incorporate orthogonal mechanical properties may aid in optimizing clinical laser cartilage reshaping procedures.

Introduction

Laser cartilage reshaping (LCR) is a novel technique used to correct septal and auricular deformities [1,2]. LCR is based on thermally induced relaxation of internal stress in mechanically deformed cartilage specimens. After heating, the tissue assumes a new deformed shape [3,4]. A temperature elevation to 65–75°C is required to trigger this transition [3]; however, these temperature regimes may be lethal to chondrocytes and may results in the long term loss of tissue viability, structural integrity and/or calcification [5]. Delivery of laser irradiation to selected distinct target sites simultaneously limits thermal damage to the tissue and facilitates effective reshaping. To optimize spatially selective irradiation, we previously developed a numerical model of stress relaxation for a thermally modified deviated septum [6]. The model approximates a deviated septum as a 24×24×2 mm³ cartilage sample with a bulge running along the central portion of the sample, forming convexity on one side and concavity on the opposite. The model calculates the equilibrium internal stress fields generated in the septum after a mechanical force is applied to straighten it, and calculates reaction force to this straightening deformation both before and after laser irradiation. The effects of laser heating on the deformed cartilage are represented by localized regions with modified values of strain and elastic modulus. The reaction force defined as a surface integral of the stress component normal to the straightened surface is evaluated as a function of the size, number and location of these thermally modified regions and compared with the value of reaction force prior to laser application.

For calculations of internal stress in this numerical model we assumed homogeneous elastic moduli of 6 and 0.07 MPa for native and thermally modified regions, respectively. These values correspond to the average elastic moduli of porcine and lagomorph septal cartilage measured in native cartilage and in cartilage subjected to complete thermally induced stress relaxation [7–9]. However, due to the non-uniform laser beam profile, attenuation of laser light with depth, effects of heat conduction and surface cooling, laser irradiation of tissue produces radially and axially non-uniform temperature distributions [10]. Since the elastic modulus of thermally treated cartilage depends on both temperature and heating rate [9], it should vary across the thermally modified region and also reflect the local thermal history. Hence, consideration of the axial and radial variations in the elastic modulus within the laser heated region is essential for the prediction of stress relaxation effects and ultimately the optimization of LCR.

Accurate determination of changes in cartilage elastic modulus due to heating requires uniform heating of tissue samples that are also large enough for reliable mechanical testing. Irradiation with Nd:YAG laser (λ = 1.32 μm) can create an axially homogeneous temperature field in a sample 2–4 mm thick [10]. However, the limited size and non-uniform radial profile of a typical laser beam ensures that only a relatively small (less than 1 mm in diameter) portion of laser irradiated cartilage can be considered homogenously heated [10]. Alternatively, a large sample can be heated using fast 2D scanning of a powerful laser beam across sample surface. However, a 75–100 W Nd:YAG laser will be required for such a technique, while most of the surgical lasers available for biomedical research produce no more than 10W output. Recently, we reported a method of uniform cartilage heating in a saline bath [11]. However, this method provides heating rate of only 0.1°C/s—much slower than typical rates of 2–5°C/second of laser heating [12]. In the present study, we use RF energy to heat a large portion of cartilage sample uniformly and at rates closely approximating that of laser heating. We measure the equilibrium compressive elastic modulus of cartilage samples RF heated to temperatures equal to maximum achieved during laser heating at various distances from laser spot center. We use this data to generate a parametric function that approximates the elastic modulus distribution within a cartilage specimen after laser irradiation and predict the stress response to uniaxial compression of laser heated sample. The predicted stress response is compared with experimental measurements.

In 2003, we introduced RF heating as an alternative method to laser technology for cartilage thermoforming [13]. Typically, RF surgical generators have output impedance higher than the load and can be considered voltage sources. The RF voltage applied to the tissue creates electro-magnetic field inside it and the field induces electro-magnetic force on tissue ions. The ions move along the field lines and dissipate kinetic energy into heat in molecular collisions. The volumetric heat generation is proportional to the tissue electrical conductivity and the internal electric field [14]. In the present study, we heat a rectangular cartilage sample sandwiched between two flat RF electrodes. In such a configuration the electric field is constant throughout most of the sample but does vary along the air-tissue-electrode interfaces due to electrical edge effect [15]. A constant electric field inside a relatively homogeneous cartilage sample will result in uniform heat generation. Surface evaporation might compromise uniformity of the heating [16]. To minimize non-uniformly heated regions in the specimen we utilized for mechanical testing only central portion of the samples.

Materials and Methods

Laser and RF Heating

Crania from freshly sacrificed domestic pigs were obtained from a local packing house (Farmers John, Vernon, CA). No more than two rectangular samples 15×15×4 mm³ were fashioned from nasal septi extracted from each porcine crania. In the laser heating experiments, cartilage samples were placed on an array of taxidermy needles (0.25 mm diameter) to minimize heat sink effects that would accompany direct placement of tissue on a flat conductive surface and irradiated with an Nd:YAG laser (New Star Lasers, Roseville, CA λ = 1.32 μm) at 8 W for 12 and 8 seconds. Laser energy was delivered through multi-mode silica fiber terminating in a collimating lens (New Star Lasers) (spot diameter on tissue surface 4.8 mm) [11]. Surface temperature was recorded during each irradiation sequence with a thermal camera (Inframetrics 600, FLIR systems, Inc., Boston, MA). Laser fiber and thermal camera were positioned with their axis at 90° and 45° to the sample surface, respectively (Fig. 1a). Averaged surface temperature profiles were determined along the line crossing the center of the heated spot and perpendicular to the thermal camera axis from the temperature recordings. Thermal images were recorded on digital video, transferred to a PC workstation, converted to audio wave interleave (avi) format, and imported into MatLab (Mathworks, Natick, MA) for analysis. The device was calibrated using a blackbody source (BB701, OMEGA Engineering Ltd., Stamford, CT). The device was focused on the surface of the blackbody. Temperatures were recorded for 30 seconds by the thermal camera for each blackbody temperature. The specified blackbody temperatures were plotted versus the temperatures measured by the thermal camera and a calibration curve was constructed. By maintaining the same range and offset settings on the thermal camera for all studies, a look-up table specifying temperature for a given pixel intensity was generated.

Fig. 1.

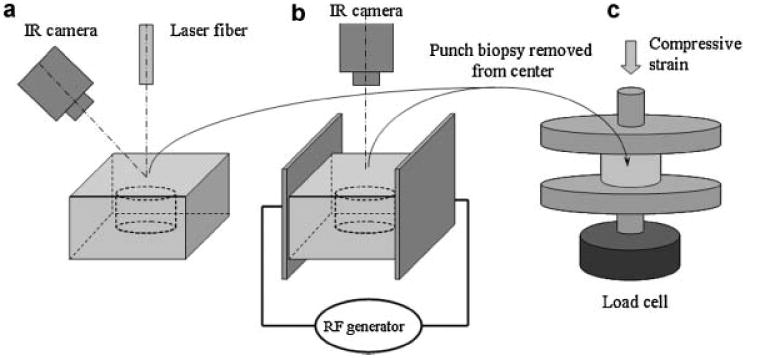
Experimental set up for heating of cartilage samples and mechanical testing: (a) laser heating, (b) RF heating, (c) measurement of elastic modulus in uniaxial compression.

Six samples were irradiated for each irradiation time and irradiation for 8 and 12 seconds were performed on the samples collected from the same animal. Surface temperature as a function of time was obtained at 0, 1, 2, and 3 mm away from the center of the laser spot.

In the RF heating experiments, cartilage samples were sandwiched between two flat copper electrodes separated by 15 mm distance and connected to surgical RF generator (Surgitron, Ellman Int., Hewlett, NY). An electrically insulated thermocouple (5SRTC, Omega Eng., Stamford, CT) was placed inside the cartilage at the sample center. Thermocouple readings were recorded with a signal conditioner (Model, National Instruments, Austin, TX) and PC. Surface temperature was monitored with the thermal camera (Fig. 1b). Output power of the RF generator was adjusted to reach a prescribed peak surface temperature at the end of the heating period. Cartilage samples were heated for 8 and 12 seconds to surface peak temperatures, T_p, of 90 ± 4, 80 ± 4, 75 ± 3, 70 ± 4, 65 ± 4, 60 ± 3, and 50 ± 3°C. In order to compare heating rates produced by laser heating for 12 seconds with RF heating, cartilage samples were heated using the RF system to surface temperatures matching the maximum peak temperatures at 0, 1, 2, and 3 mm away from the center of the laser spot. Three cartilage samples were heated for each time and peak temperature pair. Similar to the laser heating experiments 8 and 12 seconds heating were performed on the samples collected from the same animal.

Mechanical Testing of Laser and RF Heated Cartilage

To obtain cartilage specimens with known temperature distribution and history we removed the cartilage around the laser irradiation site using dermatologic punch biopsy instruments (8, 6, or 4 mm). Diameters of obtained cylinders were 7.7 ± 0.2, 5.8 ± 0.1, and 3.6 ± 0.2 mm, respectively. The central portion of RF heated samples was similarly excised using an 8 mm biopsy punch. Prior to mechanical testing, dissected cartilage cylinders were trimmed to a height of 1.9 ± 0.2 mm by removing top and bottom portions of the cylinder with a custom-made guillotine microtome. Variations in height were less than 0.04 mm across all samples. Cartilage samples were placed between two flat well-polished plexiglass plates attached to mechanical testing apparatus (Electroforce 3200, Bose Corp., Eden Praire, MN) and compressed to 0.10 ± 0.02 strain at displacement rate of 0.05 mm/second. The samples were held in compression for 600 seconds at room temperature following the initial strain application. Force was measured and recorded during both compression and relaxation phases of the experiment. Equilibrium modulus was determined from the value of the force measured at the end of 600 seconds stress relaxation period.

Numerical Simulation of Mechanical Response of Heated Cartilage

Equilibrium elastic modulus data obtained from the mechanical evaluation of the RF heated cartilage samples were used to construct the radial profiles of equilibrium elastic modulus created in cartilage sample after laser irradiation. The profiles were substituted into the numerical model of uniaxial compression of cylindrical cartilage sample and reaction force to 0.1 compressive strain was calculated from the model. The calculated value of the reaction force was compared with experimental measured value.

First, dependences of cartilage equilibrium elastic modulus, E(T_p), from the peak temperature, T_p, reached at the termination of RF heating were interpolated using piecewise rational functions using Stineman's algorithm [17] from the data obtained in mechanical testing of RF heated samples. Then, radial profiles of the peak surface temperature, T_p(r), reached at the end of laser irradiations, were determined from the infrared imaging. Finally, radial profiles of the equilibrium elastic modulus E(r) obtained at the end of laser heating were calculated from the modulus temperature dependences, E(T_p), and peak surface temperature profiles, T_p(r). Accordingly, equilibrium elastic modulus profiles, E₈(r) and E₁₂(r), were obtained for 8 and 12 seconds of laser heating, respectively. These calculated modulus profiles were used in a numerical model simulating the uniaxial compression of a cylindrical cartilage sample using finite element software (FemLab, Comsol, Inc., Stockholm, Sweden). The model describes uniaxial compression of elastic cylinder. Displacement and zero axial motion boundary conditions were applied to the opposite ends of the cylinder and zero force boundary condition was applied to the cylinder side. Mesh resolution was approximately 20 μm. Numerical simulations of the uniaxial compression of native and laser irradiated cylindrical samples of 7.7, 5.8, and 3.6 mm diameter and 1.9 mm height were performed. Reaction force to 0.1 strain was computed and compared with the values obtained in actual mechanical testing experiments.

Results

Comparison of RF and Laser Heating Methods

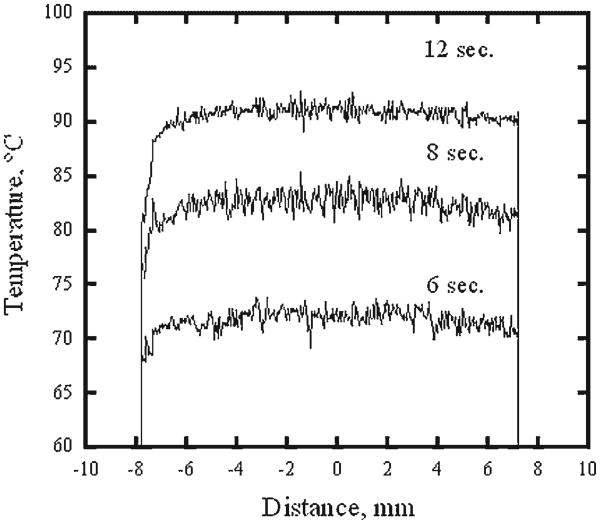
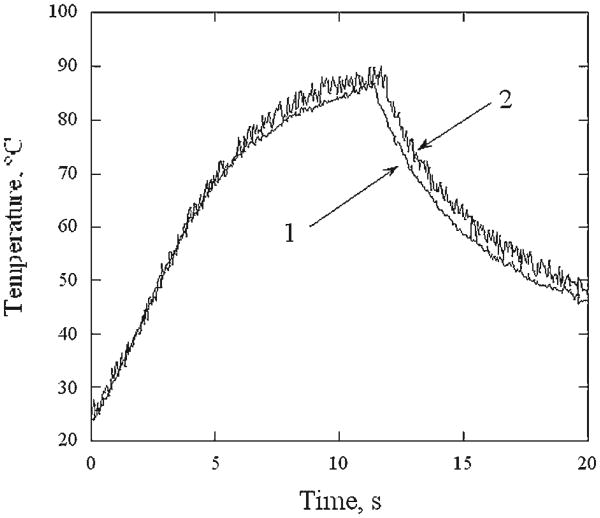
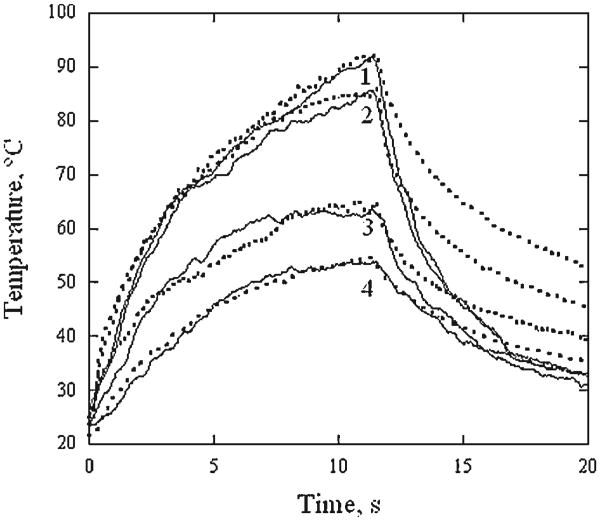
Figure 2 illustrates representative surface temperature profiles across a sample in the direction perpendicular to RF electrodes at 6, 8, and 12 seconds of RF heating. Though temperatures along the periphery of the cartilage sample are significantly lower than in the center, it is relatively uniform in the central region of the 8 mm diameter and equal 72 ± 2, 83 ± 2, and 91 ± 2°C, at 6, 8, and 12 seconds, respectively. Figure 3 shows temperature recorded in the center of the specimen surface (thermal camera) and within the specimen (thermocouple) during 12 seconds of RF heating followed by cooling. From the onset of the heating to approximately 10 seconds after the heating terminates, both curves are within 3°C of each other. Averaged surface temperature histories recorded during 12 seconds of laser and RF heating followed by cooling are plotted against one another on Figure 4. Each temperature curve obtained during the laser heating at 0, 1, 2, and 3 mm distance away from the center of the laser spot is paired with the temperature curves produced using RF at power level selected to produce a similar peak temperature. The temperature curves obtained for the center of the laser spot are approximated by the corresponding RF heating curves to within ± 4°C during the laser and RF heating periods (curve pairs (1) and (2)). The heating curves obtained for the outside of the laser spot do not coincide with corresponding RF heating curves during the first 5 seconds of the heating but closely match each other from that point until the cessation of heating(curve pairs (3) and (4)). The difference between temperatures observed in laser and RF heating experiments widens during cooling. In all cases, the temperature difference is not in excess of ± 4°C unless the temperature is below 60°C.

Fig. 2.

Typical profiles of surface temperature of the RF heated cartilage samples measured at 6, 8, and 12 seconds of the heating.

Fig. 3.

Temperature histories of RF heated cartilage sample: (1) measured in the middle of sample surface with thermal camera, (2) measured within the sample with embedded isolated thermocouple.

Fig. 4.

Typical surface thermal histories of laser irradiated cartilage (solid lines) and corresponding RF heated (dashed lines) cartilage samples. Temperature at the center of the laser spot and 1, 2, and 3 mm away (traces from 1 to 4, respectively) are shown.

Cartilage Steady-State Elastic Modulus After RF Heating

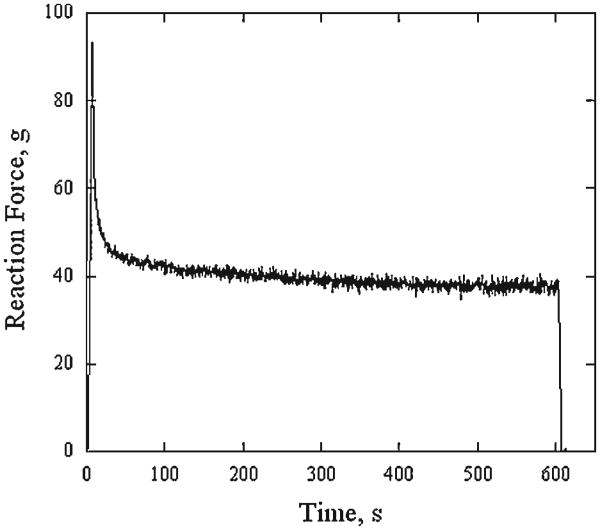
Figure 5 demonstrates typical evolution of reaction force recorded during loading of a control cartilage sample dissected with 8 mm diameter biopsy punch. The peak in reaction force is followed by a rapid decline during first 150 seconds of the steady-state compression. The change in reaction force is much slower during following 300 seconds and almost negligible during remaining 150 seconds. Average reaction force ± standard deviation measured during 10 seconds at 450, 500, and 550 seconds after commencing the steady-state compression were 38.0 ± 0.7, 37.6 ± 0.9, and 37.8 ± 0.9, respectively.

Fig. 5.

Typical history of reaction force recorded during loading of a control cartilage sample dissected with 8 mm diameter biopsy punch.

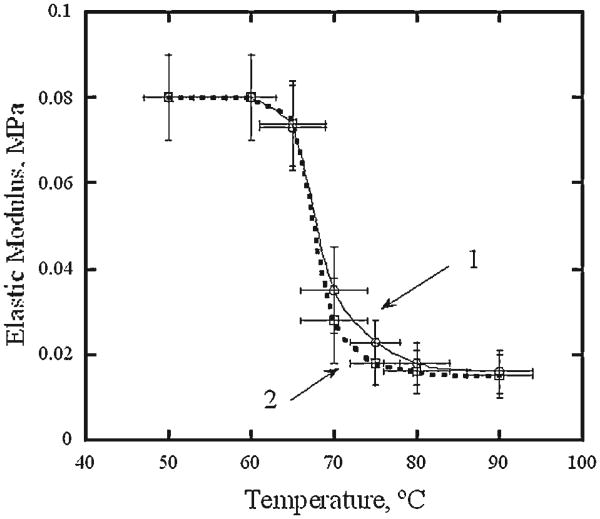
Figure 6 shows average equilibrium elastic modulus of cartilage samples measured after 12 and 8 seconds of RF heating to peak temperatures of 50 ± 3 to 90 ± 4°C, respectively. The equilibrium elastic modulus measured after heating to 50°C is 0.08 ± 0.01 MPa and equals the modulus measured in control experiments without application of RF power. Elastic modulus begins to decrease rapidly with temperature when RF heating produces elevations above approximately 60°C. In the temperature interval from approximately 70–80°C the modulus measured after 12 seconds of heating decreases with temperature faster than that produced after an 8 seconds heating interval. However at temperatures above approximately 80°C, the moduli measured after both heating times are nearly identical (0.016 ± 0.007 MPa).

Fig. 6.

Equilibrium elastic modulus of RF heated cartilage samples as a function of maximum temperature. (1) 8 seconds heating, (2) 12 seconds heating. Error bars represent standard deviation.

A repeated measures ANOVA with elastic modulus as the dependent variable and factors of peak temperature level and heating time was performed across peak temperature interval 60–90°C. Measurements of elastic modulus on the samples collected from the same animal and exposed to 8 and 12 seconds heating were considered repeating. The analysis revealed that the effects of peak temperature and time were significant (P<0.001 and P<0.03 respectively) whereas the effect of the interaction between time and temperature level was not significant (P = 0.83). Tukey post-hoc tests performed for each heating time further revealed that there are significant differences between all peak temperatures from 60 to 80°C but no difference between 80 and 90°C.

Modeling of Elastic Response of Laser Irradiated Cartilage

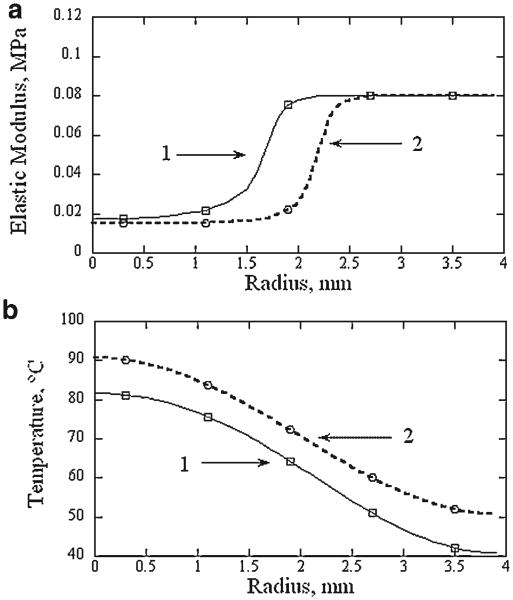
Figure 7 illustrates profiles of the elastic modulus computed by interpolating the data obtained in RF heating experiments and corresponding the average radial surface temperature profiles after 8 and 12 seconds of laser irradiation. The elastic modulus profiles from the value corresponding to native cartilage to cartilage with a maximally reduced elastic modulus over 1 mm distance. After 8 seconds of irradiation the elastic modulus monotonically decreases from the edge of the thermally modified zone to the center of the laser spot, while a homogeneous zone with the minimal modulus (approximately 1 mm radius) is present after 12 seconds of irradiation.

Fig. 7.

Computed profiles of equilibrium elastic moduli in cartilage samples irradiated with 8 W of laser power (λ=1.32 μm, spot diameter 4.8 mm) for (1) 8 seconds and (2) 12 seconds (a). Averaged surface temperature profiles measured at the end of laser irradiation are shown for reference (b).

Figure 8 compares experimentally measured and numerically computed equilibrium reaction force to 0.1 compressive strain applied to cylindrical sections extracted from the cartilage irradiated for 8 and 12 seconds. The force was normalized to cross sectional areas of the sections. Computed equilibrium reaction force to the same strain in cartilage cylinders of native (E = 0.08 MPa) cartilage is shown as control value for reference. Compression of the cartilage sections irradiated for 12 seconds produces lower reaction force than compression of 8 seconds irradiated sections as expected. An increase in the diameter of tested/simulated cartilage sections reduces the relative difference in reaction force between native and laser irradiated cartilage, respectively. The reaction force obtained from numerical simulation underestimates the average experimentally measured value for all irradiation-times–section diameter pairs with the exception of the 12 seconds and 7.7 mm pair. However, the simulated reaction force value falls within standard deviation range of the measured value for all studied irradiation times and diameters. The difference between simulated and measured reaction force decreases as the section diameter becomes larger.

Fig. 8.

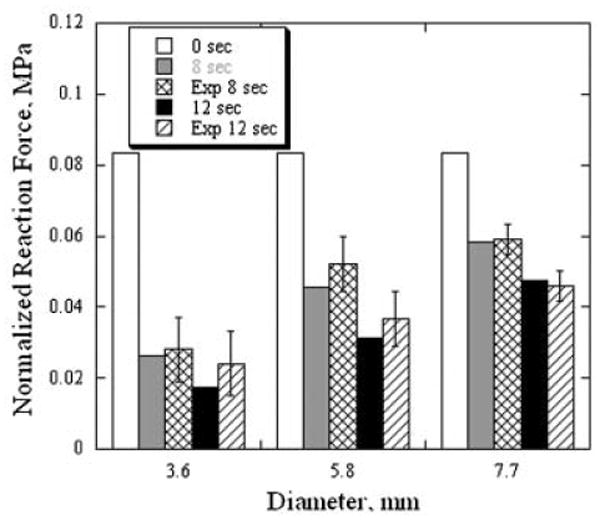
Comparison of numerically calculated and experimentally measured force of reaction to a uniaxial compression of cylindrical cartilage samples of different diameters. Error bars represent standard deviation.

Measured values of normalized reaction force were statistically analyzed using repeated measures ANOVA with irradiation time and section diameter as factors. The analysis demonstrated significance of both factors (P<0.001 and P<0.01, respectively) and insignificance of interaction between them (P = 0.3). Tukey post-hoc tests performed for each irradiation time further demonstrated significant differences between all section diameters.

Discussion

Numerical modeling of the optical and thermal laser-tissue interactions has proven to be a useful tool for the planning and optimization of many clinical procedures involving laser energy [10,18–20]. However, simulation of the relatively new LCR procedures goes well beyond the scope of traditional opto-thermal models and requires consideration of thermally induced changes in the tissue mechanical state. Accurate characterization of these changes using laser light as a heating source is complicated by a non-uniformity in the radial and axial heating of cartilage by fiber-delivered laser light producing a similar non-uniform distribution in cartilage mechanical properties. This spatial variation in mechanical properties makes laser heated samples unsuitable for the typical tension and compression tests used for the characterization of cartilage mechanical properties.

In the present study we use RF heating to obtain a relatively uniform volumetric temperature distribution and accordingly a uniform change in mechanical properties. Electrically conductive cartilage tissue is heated by the action of the electric field created in a rectangular cartilage sample sandwiched between two parallel electrodes. The electric field in such a configuration is relatively homogeneous [14] and creates a uniform volumetric heat source inside the sample. The sample periphery is cooler relative to the center of the specimen due to conductive heat losses through electrodes and by both convective and evaporative cooling of the air-exposed surfaces. However, for the studied sample geometry, heating times, and rates significant temperature gradients are observed only near electrodes (Fig. 2). Temperature variation across 8 mm long central portion of the sample remains within a narrow 4°C interval throughout heating (Fig. 2). The difference between the surface and interior temperatures of the sample is less than 3°C during the heating (Fig. 3). Thus, the temperature variation inside a cylindrical segment of 8 mm diameter and 2 mm height dissected from the center of a RF heated cartilage sample is small. This variation is much less than the variation in actual peak temperature between samples heated to the same target temperature, T_p.

By adjusting RF power we can create a thermal history that matches the temperature history measured inside of the laser spot (Fig. 4) curve pairs (1) and (2). It must be emphasized that RF produces relatively uniform volumetric heating of the specimen, and the task at hand is to heat specimens uniformly using RF to match the temperature-time curve within the center of the laser spot. Uniformly heated specimens were needed to obtain mechanical measurements of specimens with a specific time-temperature history. Notably, both heating methods produce almost constant heating rate during heating from ambient to about 60°C, then, the rate changes sharply at about 65°C, but remains constant during the rest of the heating period (Fig. 4) curve pairs (1) and (2). The constant heating rates suggest that in the central region of the laser spot the tissue is heated in the same manner as with RF heating method: by volumetric heat generation with little effect from heat conduction or convection. Hence, the decrease in the heating rate observed at 65°C is likely a manifestation of the change in cartilage heat capacity as observed previously [9,21]. This temperature threshold corresponds to the changes in cartilage material properties and onset of internal stress relaxation in deformed cartilage specimen [12].

A simple adjustment of the RF power is not sufficient to adequately reproduce the thermal history for regions outside of where laser energy is deposited (Fig. 4) curve pairs (3) and (4). At 2 mm and further away from the laser spot center almost no energy is deposited and tissue is heated by conduction. The rates of conductive heating outside the laser spot and corresponding rates of RF heating are lower than the volumetric heat generation rates observed inside the laser spot. At these lower heating rates convective and evaporative surface cooling contribute significantly and the task of adjusting the RF current to produce a temperature history to match laser heating rates becomes much more challenging. However, by trial and error, we were able to determine the RF generator parameters that produced a match between laser and RF heating curves starting from approximately 6 seconds after the onset of heating. Before this point, the temperature is below 60°C and cartilage is mechanically stable (Fig. 6).

One aspect of RF and laser heating that does differ is in the heat transport mechanisms within the tissue during the cooling period. Observation of the surface temperature demonstrates that the laser irradiated areas are cooled faster than matched cartilage samples heated with RF to the same maximum temperatures (Fig. 4). The RF heated samples have relatively uniform temperature within the tissue bulk and are cooled primarily through surface by convection and evaporation and the heat is transported in the axial direction. The laser heated samples also lose heat in the lateral direction by conduction into non-irradiated regions of the sample. Thus, cartilage heated with RF to the same target temperature as with the laser, is loosing heat slower, exposed to higher temperature for a longer time and might be subjected to a stronger thermal modification.

The equilibrium elastic moduli of native and thermally modified septal cartilage measured in this study were significantly lower than the moduli used in previously described numerical model [6]. The values of elastic moduli used in this model are instantaneous values determined using deformation strains ≤0.1 oscillating with frequencies on the order of 0.1–1 Hz [7–9]. Cartilage is a poro-elastic tissue composed of a solid collagen-proteoglycan matrix permeated with water and its dynamic mechanical properties are largely determined by the liquid flow through deformed matrix [22]. When a step displacement is applied to a cartilage sample, tissue viscosity is responsible for initial high reaction force: high instantaneous elastic modulus. When all flow processes and stress relaxation reach steady state, a new equilibrium distribution of cartilage components is established and the mechanical response is determined by mechanical properties of the solid matrix and can be characterized by equilibrium elastic modulus [23,24]. To predict long-term changes in the shape of cartilage tissue treated with LCR it is important to know stress-strain field established in tissue long after all dynamic processes of stress relaxation caused by initial straightening of deformed shape and laser heating are completed. To determine such a field, the equilibrium elastic modulus as a function of thermal history is required.

Figure 6 demonstrates that for typical laser heating times of 8 and 12 seconds, the equilibrium elastic modulus of porcine septal cartilage does not change at one specific temperature but gradually decreases over the temperature interval from approximately 60 to 80°C. The radial time-dependent temperature gradient produced during laser irradiation creates a central region containing cartilage with a maximally reduced elastic modulus which is in turn surrounded by a ring of partially modified tissue. The present study demonstrates that typical laser heating pattern produces a transition zone of approximately 1.5 mm wide. This width is comparable with 0.5–1.5 mm radius of the zone with a maximal reduction of elastic modulus (Fig. 7a) and transition zone should be considered in numerical modeling of cartilage mechanical response to laser irradiation.

In this study, the purpose of the numerical modeling of deformation of laser irradiated cartilage was to verify that uniform RF heating mimicking local heating rates and temperatures of the laser heating also mimics local changes in cartilage mechanical properties. The numerical simulation of the reaction force to the uniaxial compression of a laser irradiated sample correlates well with actual experimental measurements for all studied sample sizes and laser irradiation times (Fig. 8). Laser heating reduces the cartilage elastic modulus inside a cylindrical volume measuring approximately 3.5–4.5 mm diameter (Fig. 7a). In small diameter sample (e.g., 3.6 mm in diameter) almost all cartilage has undergone significant thermal modification and the average elastic modulus is very small; compression of these samples produces the lowest values for reaction force. Increasing the sample diameter decreases the fraction of thermally modified cartilage, and accordingly leads to a reduction in the relative contribution to reaction force produced irradiated tissue in the sample.

Though the numerical simulation indicates that the reaction force in cylindrical samples of 3.6 mm average diameter irradiated for 8 and 12 seconds should be different, experimentally measured reaction force in these samples is statistically the same (Fig. 8). This may result from variations in diameter of thermally modified zone produced by variations in cartilage elastic modulus and temperature (error bars on Fig. 6) and from slight misalignment of the biopsy punch with laser irradiation axis. In the samples where the diameter of the transition zone is maximal, the 4 mm diameter biopsy punch cuts off most of the non or partially modified tissue and remaining cartilage cylinders contain completely modified tissue and have the same elastic properties for 8 and 12 seconds irradiation. In contrast, all larger cylinders of 5.8 and 7.7 mm diameter contain these types of tissues (completely, partially, and non-modified cartilage), and reaction forces measured in these samples show statistical difference between the two irradiation times. The numerical calculations slightly underestimate the average reaction force for all tested samples except the 7.7 mm diameter specimens, irradiated for 12 seconds. The values of the equilibrium elastic modulus used in the calculations were obtained from mechanical testing of cartilage samples heated to target temperature by RF current. The uniform temperature field produced during RF heating reduces tissue cooling compared to laser heated specimens (discussed above) and may results in some subtle sample overheating. Therefore, elastic modulus of the RF heated sample is understandably slightly lower than of cartilage heated during the same time to the same maximum temperature by the laser.

Correlation between numerical calculations conducted with temperature dependent elastic modulus obtained using mechanical testing of RF heated cartilage and actual measurements of the equilibrium reaction force to the uniaxial compression of laser irradiated cartilage sample demonstrates that RF heating can be used to replicate the mechanical changes produce during the laser heating of cartilage and provide specimens large enough for rigorous biomechanical evaluation. In this study, we characterized the dependence of compressive equilibrium elastic modulus on the maximum temperature and heating time. However, the uniform RF heating can be used to prepare samples for characterization of other mechanical properties of laser irradiated cartilage, such as tensile elastic modulus, stress relaxation constants, instantaneous elastic moduli, etc, that would be required for more comprehensive thermo-mechanical modeling and optimization of the LCR procedure.

Thermally mediated cartilage reshaping involves bending cartilage into a new desirable shape and then heating selected sites where stress is concentrated to above a specified transition temperature. Thus, thermal modification and the subsequent change in mechanical properties occur while cartilage under tensile or compressive deformations. The process might be different when unloaded cartilage undergoing similar heating. Experimental protocol developed in the present study can be modified to heat a specimen during deformation. Compressive force can be applied to the electrodes or electrodes can be modified into grips to produce tensile deformation.

Conclusion

This study demonstrates a method for characterizing thermally induced changes in the elastic modulus of septal cartilage. Creation of a relatively homogeneous RF field in cartilage specimens allows uniform heating of tissue samples sufficiently large for reliable mechanical testing. By adjusting the RF power level it is possible to reproduce the thermal history created during the laser irradiation of cartilage at particular location inside or near the laser spot and obtain a tissue sample with mechanical properties corresponding to that location. By using the RF heating method to heat cartilage samples to target temperatures for prescribed time and then measuring the samples in uniaxial compression, we computed profiles of equilibrium elastic modulus created in cartilage after laser irradiation. Substituting obtained profiles into the numerical model of uniaxial compression of laser irradiated cylindrical samples, the reaction force to the compression was calculated and compared with the value obtained in an analogous mechanical evaluation of laser irradiated samples. Close correlation between calculated and experimentally measured values of reaction force demonstrates the relative accuracy of the present RF-based approach to simulate the laser induced thermo-mechanical modification of cartilage. The RF heating method can be used to comprehensively simulate the mechanical response in cartilage to the laser irradiation and potentially lead the methods needed to optimize clinical laser cartilage reshaping.