A Comparison of Different Dimensionality Reduction and Feature Selection Methods for Single Trial ERP Detection

Abstract

Dimensionality reduction and feature selection is an important aspect of electroencephalography based event related potential detection systems such as brain computer interfaces. In our study, a predefined sequence of letters was presented to subjects in a Rapid Serial Visual Presentation (RSVP) paradigm. EEG data were collected and analyzed offline. A linear discriminant analysis (LDA) classifier was designed as the ERP (Event Related Potential) detector for its simplicity. Different dimensionality reduction and feature selection methods were applied and compared in a greedy wrapper framework. Experimental results showed that PCA with the first 10 principal components for each channel performed best and could be used in both online and offline systems.

I. Introduction

Single trial ERP detection is critical for stimulus-synchronous brain computer interfaces. In most ERP applications, time domain signals within a short window after the onset of the stimuli are used as features to detect ERP. However, the original features are in high dimensional space, and are not feasible for real-time system; hence, effective dimensionality reduction and feature selection must be done. In our previous research, we applied feature selection on original features, as well as channel-wise projected features using LDA [1]. Results were not satisfied with their speed and accuracy. In this study, we are going to investigate and compare more dimensionality reduction and feature selection methods for ERP detection: Principal Component Analysis (PCA), Sparse PCA (SPCA), Empirical Mode Decomposition (EMD), and Local Mean Decomposition (LMD). We will apply these methods on EEG data and rank the EEG channels based on classification performance.

A. Data Acquisition

Three adult subjects were recruited for the study under an approved IRB protocol for RSVP and EEG acquisition. Each subject finished 2 sessions in two days. Each session contained 100, 10-second epochs. An epoch started with an audio presentation of the target letter. At time stamp 0, a one-second fixation screen was presented, followed by 3 sequences of English letters. Each sequence contained 10 images (one letter per image) at 167ms/image in a random order. Within each sequence, there was only one target letter, all others were distracters. There were 0.5 second intervals between two sequences. EEG recordings were made synchronously.

We used two computers to acquire data, one for image display and the other for data collection. The EEG data were collected using a 32-channel Biosemi ActiveTwo system at sampling rate 256Hz. Presentation™ (Neurobehavioral Systems, Albany, CA) software was used to present images with a high degree of temporal precision and to output pulses or triggers to mark the onset of the target and distracter stimuli. The triggers were received by the Biosemi system over a parallel port and recorded concurrently with the EEG signals.

B. Preprocessing

We first filtered EEG signals using a bandpass filter (0-20 Hz, no DC) based on our previous study. Then the filtered data were truncated using a [0 500ms] window following each image stimulus (called a “trial” in what follows) and normalized with the [-100ms, 0] pre-stimulus window. We concatenated data within one trial by channels, and to obtain a data vector with 32×129=4128 dimensions (each channel contains 129 samples).

C. EEG Channel Ranking and Classification

EEG channels were ranked using the wrapper approach (error based approach) with a greedy search strategy. For a given channel subset, all samples from these channels were concatenated to form a new data point for each trial. We used trials from the first 50 epochs as training set, used the remaining data as testing set, applying the LDA classifier on three sequences separately, and fusing results using a majority vote for the final decision. The accuracy of this final decision was used as criterion for ranking the EEG channels.

II. Methods

The EEG data processing and ERP detection scheme is illustrated in Figure 1. In our previous study, we compared feature ranking and classification performance in terms of speed and accuracy using both raw features and channel-wise LDA projected features. Experimental results showed that the classification accuracy using raw features is superior compared to the accuracy of using LDA projected features, however, the former could be too slow to be used in real-time system (Depending on additional computational requests from the system.). In this study, we are going to investigate other dimensionality reduction and feature selection methods, including channel-wise Principal Component Analysis (PCA), Sparse PCA (SPCA), Empirical Mode Decomposition (EMD), and Local Mean Decomposition (LMD), and to compare results with those of our previous study.

Fig. 1.

EEG data processing and ERP detection scheme.

A. Principal Component Analysis (PCA)

Perhaps PCA is one of the most commonly used dimensionality reduction methods. PCA seeks the linear combinations of the multivariate data that capture a maximum amount of variance. However, the projections that PCA seeks are not necessarily related to class labels; hence may not be optimal for classification problems. In this study, we will apply PCA to individual EEG channels, and compare channel ranking performance using the first 1, 5 and 10 components of each channel (in our particular application, typically using 5 components carries 75% variance and using 10 components carries 90% variance).

B. Sparse Principal Component Analysis (SPCA)

PCA has many advantages, such as it captures maximum variance, and the components are uncorrelated. However, the principal components are usually linear combinations of all variables; hence it is not possible to discover a set of low dimensional space that explains most of the variance. For example, we apply PCA on individual EEG channels for a 0.5s window of data (129 points) after the stimuli onset. This projection can not tell that which points (when after the stimuli onset) contain more information for ERP detection. It would be of interest to discover sparse principal components by sacrificing some of the explained variance and the orthogonality. Among many existing SPCA algorithms, we choose DSPCA in our study [2], and compare channel ranking performance using the first 1, 5 and 10 components of each channel.

C. Empirical Mode Decomposition (EMD)

EMD was first proposed by Huang et al. [3] for analyzing signals of nonlinear and nonstationary time series. EMD can be used to decompose any time series into a finite number of functions called intrinsic mode functions (IMFs) without leaving the time domain. The Intrinsic Mode Functions are nearly orthogonal and sufficient to describe the signal. Unlike other time-frequency methods, such as short time Fourier transform and wavelet transform, EMD does not require any assumption of the data; hence it is more flexible in extracting time-frequency information from EEG data.

EMD finds a local mean envelope by creating maximum and minimum envelopes around the signal using cubic spline interpolation through the individual local extrema. The mean envelope, the half sum of the upper and lower envelopes, is then subtracted from the original signal, and the same interpolation scheme is iterated on the remaining signal. This is called the “sifting” process (SP). SP terminates when the mean envelope is approximately zero everywhere, and the resultant signal is designated as an IMF. After the first IMF is removed from the original data, the next IMF is extracted iteratively by applying the same procedure (Appendix A).

By the nature of this decomposition procedure, the data are decomposed into n fundamental components, each with a distinct time scale. More specifically, the first component associates with the smallest time scale, which corresponds to the fastest time variation of data. As the decomposition process proceeds, the time scale increases, and hence, the mean frequency of the mode decreases. By combining different IMFs, EMD can be used as low-pass, high-pass, or band-pass filter.

Although after doing EMD, different feature extraction methods can be further applied, in this study we remove the high frequency component of IMFs (based on the assumption that ERP energy concentrates in lower frequencies). Since IMFs have the same length as original data, we apply PCA on IMFs to reduce the dimension. This procedure is repeated for all EEG channels, and the channel ranking performance is evaluated using an LDA classifier.

D. Local Mean Decomposition (LMD)

The local mean decomposition (LMD) was developed recently by Jonathan [4] to decompose amplitude and frequency modulated signals into a small set of product functions, each of which is the product of an envelope signal and a frequency modulated signal from which a time-varying instantaneous phase and instantaneous frequency can be derived. Like EMD, LMD decomposes data into a series of functions in time domain. It does not require any assumption on the data. Unlike EMD using cubic spline, which may induce information loss, LMD uses smoothed local means (moving average filter) to determine a more credible and reliable instantaneous frequency directly from the oscillations within the signal. The LMD algorithm is shown in Appendix B. In our study, we apply LMD and evaluate the performance using the same way as we mentioned above in EMD section.

III. Experimental Results

A. PCA and SPCA with different number of components

We apply both PCA and SPCA projection to individual EEG channels, and use the first 1, 5 and 10 components of each channel as features, then rank the EEG channels using LDA classifier error. The feature ranking results for different subjects/sessions using different number components are compared (figures not shown here). As we expected, using the first 10 components of each channel for both PCA and SPCA yields the best performances and the computation time using PCA is reasonable low. It is interesting to see that by using only one component, SPCA performs better than PCA. However, the performances of PCA by using the first 5 and 10 components are better than those of SPCA. This indicates that using SPCA does not benefit us considering the computational costs and performances. We will use results from 10 principal components of each channel to compare with other methods in the rest of this study.

B. Compare different methods

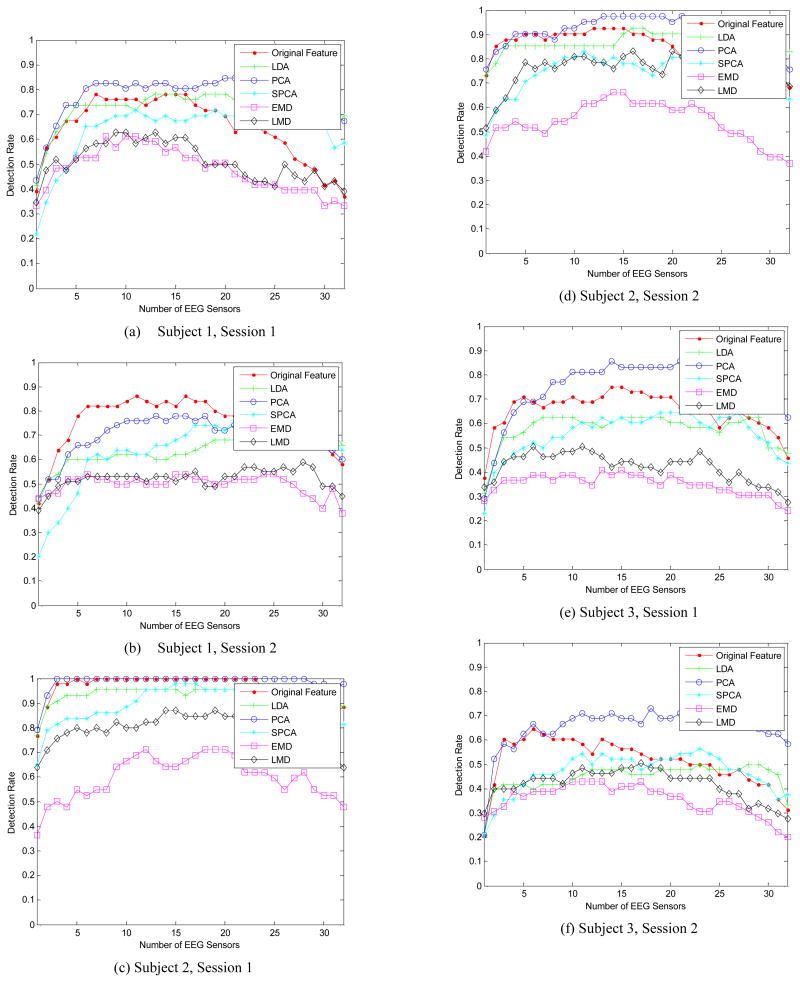
We compare feature ranking results using different dimensionality reduction and feature selection methods: 1) using original features; 2) using channel-wise LDA projection for dimensionality reduction; 3) using channel-wise PCA projection, picking the first 10 components for each channel; 4) using channel-wise SPCA projection, picking the first 10 components for each channel; 5) using channel-wise EMD for feature extraction and the first 10 PCA components of each channel for dimensionality reduction; 6) using channel-wise LMD for feature extraction and the first 10 PCA components of each channel for dimensionality reduction. The results for different subjects/sessions using different methods are shown in Figure 2 (a-f). The performance of using original features and using the first 10 principal component of PCA are comparable. However, using PCA for dimensionality reduction is much faster than using original features. The performance of using channel-wise LDA for dimensionality reduction is acceptable, and it is the fastest method. The performances of using SPCA, EMD and LMD are worst, and they generally cost more computational time.

Fig.2.

Feature ranking results for different subjecs/sessions using different dimensionality reduction and feature selection methods.

IV. Conclusion

Experimental results show that using original features and using PCA with the first 10 principal components for each channel perform best, while the time-consuming SPCA, EMD, and LMD methods perform surprisingly worse, even for an offline system. The performance of LDA projection is acceptable and is the fastest method. Thus, we conclude that:

1. Channel-wise PCA projection with the first 10 principal components of each channel offers the best trade off in terms of accuracy and speed. It can be used in both online and offline systems.

2. Chanel-wise LDA projection is the fastest method with acceptable accuracy. If Channel-wised PCA projection can not satisfied real-time requirement, perhaps LDA is the only method.

3. In theory, the properties of EMD and LMD suggest they should be suitable for EEG data processing. However, neither method benefits our particular application.

Appendix

A. EMD Algorithm

• The EMD will break down a signal into its component IMFs.

• An IMF is a function that:

  1. has only one extreme between zero crossings, and

  2. has a mean value of zero.

• The IMFS is acquired by sifting process:

  1. For a signal X(t), let m₁ be the mean of its upper and lower envelopes as determined from a cubic-spline interpolation of local maxima and minima.

  2. The first component h₁ is computed: h₁=X(t)-m₁

  3. In the second sifting process, h1 is treated as the data, and m₁₁ is the mean of h₁'s upper and lower envelopes: h₁₁=h₁-m₁₁

  4. This sifting procedure is repeated k times, until h_1k is an IMF, that is: h_1(k-1)-m_1k=h_1k

  5. Then it is designated as c₁=h_1k, the first IMF component from the data, which contains the shortest period component of the signal. We separate it from the rest of the data: X(t)-c₁=r₁ The procedure is repeated on r_j: r₁-c₂=r₂,….,r_n-1-c_n=r_n.

B. LMD Algorithm

1. From the original signal x(t), determine the mean value, m_i,k, and local magnitude, a_i,k, with extrema, n_k,c (t: time, i : number of Product Function, k : iteration number in a process of Product Function, c : sequence of the extrema)

   $$\begin{array}{cc}{m}_{i,k,c}=(n_{k,c}+n_{k,c-1})/2,& a_{i,k}=|n_k-n_{k+1}|/2\end{array}$$

2. Interpolate straight lines of mean (local magnitude) values between successive extrema.

3. Smooth the interpolated signal using moving average filter.

4. Subtract the smoothed mean signal from the original signal, x(t).

   $$h_{i,k}(t)=x(t)-m_{i,k}(t)$$

5. Get the frequency modulated signal, s_i,k(t), by dividing h_i,k(t) by a_i,k(t).

   $$s_{i,k}(t)=h_{i,k}(t)/a_{i,k}(t)$$

6. Check whether the a_i,k(t) is equal to 1 or not.

7. If not, multiply a_i,k(t) by a_i,k−1(t) and go to the first step.

8. Envelope, a_i(t), can be derived by multiplying the whole a_i,k(t) until a_i,k(t) equals one.

   $$a_i(t)=a_{i,1}(t)\times a_{i,2}(t)\times a_{i,3}(t)\times \dots \times a_{i,l}(t)$$

   (1 : maximum iteration number)

9. Derive Product Function by multiplying a_i(t) by s_i,l(t)

   $${\mathit{\text{PF}}}_i=a_i(t)\times s_{i,l}(t)$$

10. Subtract PF_i(t) from x(t), and then go to the first step with the remainder.