A Multi-Compartment Mathematical Model of Cancer Stem Cell Driven Tumor Growth Dynamics

Abstract

Tumors are appreciated to be an intrinsically heterogeneous population of cells with varying proliferation capacities and tumorigenic potentials. As a central tenet of the so-called cancer stem cell hypothesis, most cancer cells have only a limited lifespan and thus cannot initiate or re-initiate tumors. Longevity and clonogenicity are properties unique to the subpopulation of cancer stem cells. To understand the implications of the population structure suggested by this hypothesis - a hierarchy consisting of cancer stem cells and progeny non-stem cancer cells which experience a reduction in their remaining proliferation capacity per division - we set out to develop a mathematical model for the development of the aggregate population. We show that overall tumor progression rate during the exponential growth phase is identical to the growth rate of the cancer stem cell compartment. Tumors with identical stem cell proportions, however, can have different growth rates, dependent on the proliferation kinetics of all participating cell populations. Analysis of the model revealed that the proliferation potential of non-stem cancer cells is likely to be small to reproduce biologic observations. Furthermore, a single compartment of non-stem cancer cell population may adequately represent population growth dynamics only when the compartment proliferation rate is scaled with the generational hierarchy depth.

1 Introduction

It is now widely appreciated that tumors contain cells with different tumor-perpetuation capacities and survival fates. So-called cancer stem cells, or tumor initiating cells, make up an often-argued minor subpopulation of cells that are uniquely able to initiate persistent tumor growth, and reinitiate tumors after preferentially surviving immune surveillance or therapeutic interventions. The majority of cancer cells in tumors are cells that lack longevity and have only limited proliferative potential; so-called non-stem cancer cells. Heterogeneous populations of cancer cells composed of subpopulations with and without stemness fate have been identified, for example, in tumors of the breast, brain, prostate and colon (Al-Hajj et al. (2003); Singh et al. (2003); Fioriti et al. (2008); Cammareri et al. (2008)). The proportion of cancer stem cells in a tumor differs among organ systems, and may even span multiple orders of magnitude amongst patients with tumors of the same organ (Visvader and Lindeman (2008)). While the hierarchical structure in a tumor population is conceptually well understood, cancer stem and non-stem cell-cell interactions and their implications for overall tumor growth dynamics are yet to be completely deciphered.

Mathematical, physical, computational and engineering techniques have increasingly been applied to the complex biological system that arises from stem cells and non-stem cell dynamics (Turner et al. (2009); Michor et al. (2005); Sottoriva et al. (2010); Kapitanov (2012); Marciniak-Czochra et al. (2009a); Tomasetti and Levy (2010); Youssefpour et al. (2012); Rodriguez-Brenes and Peskin (2010); Daniel et al. (2002); Beretta and Capasso (2012); Piotrowska et al. (2008); Solé et al. (2008)). Ganguly and Puri (2006) used a compartmental model to study the emergence of abnormal progeny populations after oncogenic hits. The model showed that the growth rate of abnormal cell populations increases with fast consecutive insults that cause sudden cell depletion and subsequent stem and progenitor cell outgrowth.

Focusing on the exponential tumor growth phase, Johnston et al. (2010) and Molina-Peña and Álvarez (2012) developed ordinary differential equation models of stem, transit-amplifying (or progenitor), and fully differentiated cell populations to study constant cancer stem cells fractions in tumors. Depending on the tumor growth and differentiation rates balance, Johnston et al. (2010) showed that stem cells can comprise any proportion of the tumor, and that higher stem cell proportions likely yield more aggressive tumors. Molina-Peña and Álvarez (2012) showed that certain kinetic relationships must be satisfied in order for the calculated tumor growth and stem cell fraction to be consistent with experimental observation. Recently, Hillen et al. (2012) developed an integro-differential equation model of cancer stem and non-stem cell populations, based on an agent-based model by Enderling et al. (2009), and showed that the two populations interact with each other such that higher rates of cell death in the non-stem compartment lead to enrichment of cancer stem cells and thus accelerated overall growth. The Hillen model considered tumor growth beyond the exponential growth phase and introduced a carrying capacity, which could either be spatial limitations due to for example tissue membranes or dense muscle tissues (Enderling et al. (2013)), or vascular diffusion imposed oxygen tension (Hahnfeldt et al. (1999)). Constant cell turnover and competition with the carrying capacity revealed that the cancer stem cell fraction may not be constant, but in fact be continuously increasing, with a pure cancer stem cell state being the only stable steady state in that model (Hillen et al. (2012)).

While differential equation models simulate tumor population dynamics, the interaction of individual cell populations with each other is difficult to analyze. In particular, non-stem cancer cells are either grouped into a single compartment (Hillen et al. (2012)) or divided into transit amplifying cells and fully differentiated cells (Johnston et al. (2010); Molina-Peña and Álvarez (2012)). Agent-based models and cellular automaton approaches, however, have shown that in addition to cancer stem cell self renewal (Sottoriva et al. (2010); Enderling et al. (2013)), the number of amplifications of progenitor cells is one of the most pivotal modulators of overall tumor dynamics (Enderling et al. (2009); Morton et al. (2011))

To model the cellular hierarchy in more detail and quantitatively capture subcompartment interactions, Rodriguez-Brenes et al. (2013) developed a compartment model to investigate cell dynamics within a cell lineage for homeostatic equilibria. Cell division in each compartment occurs at a compartment-specific rate and self-replication probability. The model is aimed to understand how the number of intermediate cell compartments, self-replication probabilities, and division rates affect the distribution of the replication capacities in the non-stem population.

Marciniak-Czochra et al. (2009b) developed a multi-compartment differential equation model for hematopoietic differentiation to study if hematopoiesis is compatible with cell division restrictions. In their model, differentiation and proliferation potential, i.e. number of divisions until senescence, represent independent dimensions with 6 and 50 stages, respectively. The larger number of divisions is obtained by assuming self-renewal throughout the differentiation hierarchy. Simulations of the model showed hematopoiesis with proliferation and self-renewal fractions correlating with differentiation stage. Interestingly, progenitor cell proliferation potential decreases with age, which is compensated for by an increase in cell number (Marciniak-Czochra et al. (2009b)). In a study of different 6-compartment models of the hematopoietic system, Marciniak-Czochra et al. (2009a) showed that the number of cell divisions before terminal maturation is dependent on the rates of stem and progenitor cell proliferation. Taking this analytical approach a step further, in a recent study, Werner et al. developed closed analytical solutions for mutations in a multi compartment model of normal tissue lineages for which they assumed a finite number of cells, a constant number of stem cells and symmetric self-renewal in all compartments (Werner et al. (2011)). The model showed that mutations in non-stem cells die out, whereas an equilibrium of mutated cells can be reached if mutations occur in stem cells or differentiated cells that acquire stem cell properties (Werner et al. (2011)).

Motivated by the analytic inroads made by Marciniak-Czochra et al. (2009b) and Werner et al. (2011), we set out to develop a multi-compartment differential equation model for the development of a heterogeneous cancer cell population where each tumor subpopulation is comprised of cells of comparable remaining proliferation potential. We will analyze the dominant cell population as a function of cancer stem cell kinetics and estimate cell turnover that yield experimentally observed data.

2 Cancer Stem Cells

Reliable experimental isolation of cancer stem cells and their long term in vitro culture maintenance are the subject of extensive ongoing research (Sherley (2002); Lathia et al. (2011); Sottoriva et al. (2013); Driessens et al. (2013)). The cancer stem cell hypothesis, perhaps more aptly termed the cancer non-stem cell hypothesis, postulates that only a stem-like subpopulation can initiate or sustain tumor growth, as well as give rise to the observed phenotypic diversity in a tumor (Al-Hajj et al. (2003)). Conceptually, only cancer stem cells are long-lived and have unlimited replicative potential. Non-stem cancer cells have a limited proliferative potential and will inevitably die when that potential is exhausted. During non-stem cancer cell division, both non-stem daughter cancer cells will inherit a decremented proliferation potential, arguably due to erosion of non-coding DNA end segments, so-called telomeres that serve as the cell’s mitotic clock (Olovnikov (1973); Blackburn and Gall (1978); Harley et al. (1990)). Cancer stem cells can either divide symmetrically to produce two cancer stem cells or asymmetrically to produce a cancer stem cell and a non-stem cancer cell, or undergo symmetric commitment to give rise to two non-stem cancer cells. The fate of cancer stem cell division may also depend on a number of other factors, including modulation by external stimulatory queues (Lathia et al. (2011)) of importance for understanding clinically relevant tumor evolution (Gillies et al. (2012); Orlando et al. (2013)). As a first step toward understanding the entire process, however, we seek here to and elucidate the essential role of intrinsic tumor composition and proliferation kinetics in the process.

3 Linear Multicompartment Model

We focus our analysis on exponential tumor growth, that is physiological regulatory feedback on stem cell division and self-renewal is lost (Rodriguez-Brenes et al. (2011)) and spatial inhibition is neglected (Folkman and Hochberg (1973)). We assume that cancer stem cells have unlimited replicative potential, and perform symmetric division into two cancer stem cells with probability p₁, asymmetric division into one cancer stem cell and one non-stem cancer cell with probability p₂, and symmetric commitment with probability p₃ = 1−p₁ −p₂ resulting in two non-stem cancer cells. We assume that non-stem cancer cells are non-clonogenic and undergo a finite number of divisions before dying. We denote this proliferation capacity by m. We assume that an mth generation non-stem cancer cell suffers replicative cell death as it tries to proliferate. In the model, the proliferation rates (also called the number of cell cycles per unit time) λ and γ of stem and non-stem cancer cells as well as their respective death rates a and b are constant.

Let C(t) denote the number of cancer stem cells at time t and N_k(t) denote the number of kth generation non-stem cancer cells at time t for k = 1, ··· , m. Change in the cancer stem cell population is due to symmetric division, symmetric commitment, and cell death. Cancer stem cells are produced at rate p₁λC, and are removed via cell death at the rate aC and via symmetric differentiation into two first generation non-stem cancer cells at rate p₃λC. In addition to symmetric cancer stem cell differentiation, first generation non-stem cancer cells are created during asymmetric cancer stem cell division at the rate p₂λC. The first generation non-stem cancer cell population gets depleted by division into second generation cells at rate γN₁ and also via cell death at rate bN₁. The kth generation of non-stem cancer cells gain cells with rate 2γN_k−1 cells per unit time and lose cells at the rates γN_k due to further divisions into the next compartments and the rate bN_k due to death. Attempted division in the mth generation results in replicative death. Table 1 summarizes the parameters used in the model and and their typical values. The flow into and out of these generational compartments is illustrated in Figure 1 and is described by the following system of ordinary differential equations:

$$\frac{dC}{dt}=(p_1-p_3)\lambda C-aC,$$ (1)

$$\begin{array}{c}\frac{{dN}_1}{dt}=(p_2+2p_3)\lambda C-\gamma N_1-{bN}_1,\\ ⋮\end{array}$$ (2)

$$\begin{array}{c}\frac{{dN}_k}{dt}=2\gamma N_{k-1}-\gamma N_k-{bN}_k,\\ ⋮\end{array}$$ (3)

$$\frac{{dN}_m}{dt}=2\gamma N_{m-1}-\gamma N_m-{bN}_m.$$ (4)

Table 1.

Model variables and parameters with chosen values and appropriate references

name	meaning	typical values	reference
C(t)	number of cancer stem cells at time t
Nk(t)	number of kth generation non-stem cancer cells at time t
H(t)	total number of non-stem cancer cell population at time t	${\sum }_{k=1}^m{N}_k$
Q(t)	total number of cancer cells at time t	C(t) + H(t)
Γ	total population of cancer cells per cancer stem cell	Q/C
p1	probability of symmetric cancer stem cell division	0.01 − 0.35	Gao et al. (2013)
p2	probability of asymmetric cancer stem cell division	1 − p1 − p3
p3	probability of symmetric cancer stem cell commitment	0
m	proliferation capacity of non-stem cancer cells	3 – 11	Morton et al. (2011)
λ	proliferation rate of cancer stem cells	1	Gao et al. (2013)
γ	proliferation rate of non-stem cancer cells	1	Gao et al. (2013)
a	death rate of cancer stem cells	0 – 0.1
b	death rate of non-stem cancer cells	0 – 0.1
β	net growth rate of cancer stem cells	(p1 − p3)λ − a
θ		2γ/(γ + β + b)

Fig. 1.

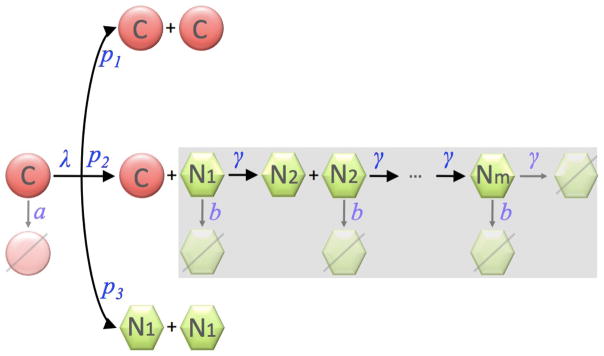
Cell populations in the multicompartment age-structured model. The shaded area highlights the generational hierarchy of non-stem cancer cells. C: cancer stem cells; N_k: the kth generation of non-stem cancer cells.

Let

$$\beta =(p_1-p_3)\lambda -a$$

denote the net growth rate of the cancer stem cell population. To study tumor growth dynamics, we consider β > 0. The exact analytical solution to the linear system (1)–(4) is derived in Appendix 1 and is given as follows:

$$C(t)=C(0)e^{\beta t},$$ (5)

and

$$N_k(t)=\sum _{i=1}^k\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}{N}_{k+1-i}(0)e^{-(\gamma +b)t}+\frac{{\theta }^k(p_2+2p_3)\lambda C_0}{2\gamma }\left(e^{\beta t}-\sum _{i=1}^k\frac{t^{i-1}{(2\gamma )}^{i-1}}{{\theta }^{i-1}(i-1)!}{e}^{-(\gamma +b)t}\right),$$

for k = 1, ··· , m. Here, the parameter θ is

$$\theta =\frac{2\gamma }{\gamma +b+\beta }.$$

Since β, γ, b > 0, θ is positive. Note, if θ = 1, then γ − b = β; essentially, the net growth rate of non-stem cancer cells equals the net growth rate of cancer stem cells. If θ < 1, then γ − b < β expresses that the net growth rate of non-stem cancer cells is less than that of the stem cells.

We denote the total population of non-stem cancer cells by H(t),

$$H(t)=\sum _{k=1}^m{N}_k,$$

and we find that

$$\begin{array}{r}H=\sum _{i=1}^m{P}_{m+1-i}\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}{e}^{-(\gamma +b)t}+(p_2+2p_3)\frac{\lambda }{2\gamma }\frac{\theta (1-{\theta }^m)}{1-\theta }{C}_0{e}^{\beta t}\\ -\frac{\theta (p_2+2p_3)\lambda C_0}{2\gamma }\sum _{i=1}^m\left(\frac{1-{\theta }^{m+1-i}}{1-\theta }\right)\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}{e}^{-(\gamma +b)t},\end{array}$$

where

$$P_i=\sum _{j=1}^i{N}_j(0).$$

The long-term asymptotic behaviors of N_k(t) and H(t) are given by

$$N_{ks}(t)=(p_2+2p_3)\frac{\lambda }{2\gamma }{\theta }^{k}C(t),$$ (6)

and

$$H_s(t)=(p_2+2p_3)\frac{\lambda }{2\gamma }\frac{\theta (1-{\theta }^m)}{1-\theta }C(t).$$ (7)

If we define Γ to be the total tumor population that arises per cancer stem cell, then the total tumor population Q in the long run is

$$Q=H_s+C=\mathit{\Gamma }C$$ (8)

and

$$\mathit{\Gamma }=1+(p_2+2p_3)\frac{\lambda }{2\gamma }\frac{\theta (1-{\theta }^m)}{1-\theta }.$$ (9)

The asymptotic rate of change of the total tumor population is

$$\frac{dQ}{dt}=\mathit{\Gamma }\frac{dC}{dt}=\mathit{\Gamma }\beta C(t)=\beta Q.$$

Therefore, the net change in total tumor population per unit time – a putative measure of tumor aggressiveness – is simply the net growth rate of cancer stem cells β:

$$\frac{dQ}{dt}/Q=\beta .$$

The asymptotic solutions (6) are the direct solutions of the linear system assuming the contributing cancer stem cell population has a net growth behaving like e^βt. This is in agreement with the study of the exponential tumor growth phase as done by Johnston et al. (2010). Beyond the initial transient, we find that if θ > 1, i.e. γ − b > β, the generational contribution to the total population at time t is

$$N_1(t)<N_2(t)<\dots <N_{m-1}(t)<N_m(t),$$

whereas if θ < 1 then the generation sizes are in reverse order

$$N_m(t)<N_{m-1}(t)<\dots <N_2(t)<N_1(t).$$

If θ = 1, all non-stem cancer cell populations contribute equally to the total tumor population with

$$N_1=N_2=\dots =N_{m-1}=N_m=(p_2+2p_3)\frac{\lambda }{2\gamma }C(t)$$

and H_s = mN_1s.

From (8), the long-term proportion of cancer stem cells in the tumor settles to

$$C(t)/Q(t)={\mathit{\Gamma }}^{-1},$$ (10)

and its reciprocal defines the total cancer cell population that arises from a single cancer stem cell, i.e.

$$Q(t)/C(t)=\mathit{\Gamma }$$ (11)

where Γ is defined in (9).

For θ > 1, the ratio of total cells to cancer stem cells grows asymptotically exponentially as the proliferation capacity m of non-stem cancer cells increases, driving the stem cell fraction towards 0. (Figure 2). By contrast, For θ < 1, as m approaches infinity, the cancer stem cell proportion decreases towards a finite value > 0, specifically,

Fig. 2.

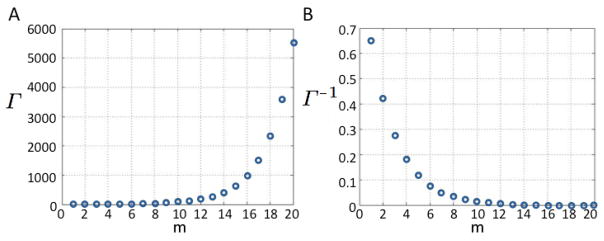
A) Tumor population per cancer stem cell Γ and B) proportion of cancer stem cells Γ⁻¹ for increasing generational hierarchy depths m. Other parameters: β = 0.2, γ = 1, λ = 1, p₁ = 0.3, p₂ = 0.7, a = 0.1, b = 0.1, θ = 1.5385.

$${\mathit{\Gamma }}_{\theta <1,m\to \infty }^{-1}={\left(1+(p_2+2p_3)\frac{\lambda }{2\gamma }\frac{\theta }{1-\theta }\right)}^{-1},$$

and the total population that arises per cancer stem cell increases to Γ_θ<1,m→∞.

For θ = 1,

$${\mathit{\Gamma }}_{\theta =1}^{-1}={\left(1+(p_2+2p_3)\frac{m\lambda }{2\gamma }\right)}^{-1}$$

and as m increases the proportion of cancer stem cells in the tumor decreases towards zero.

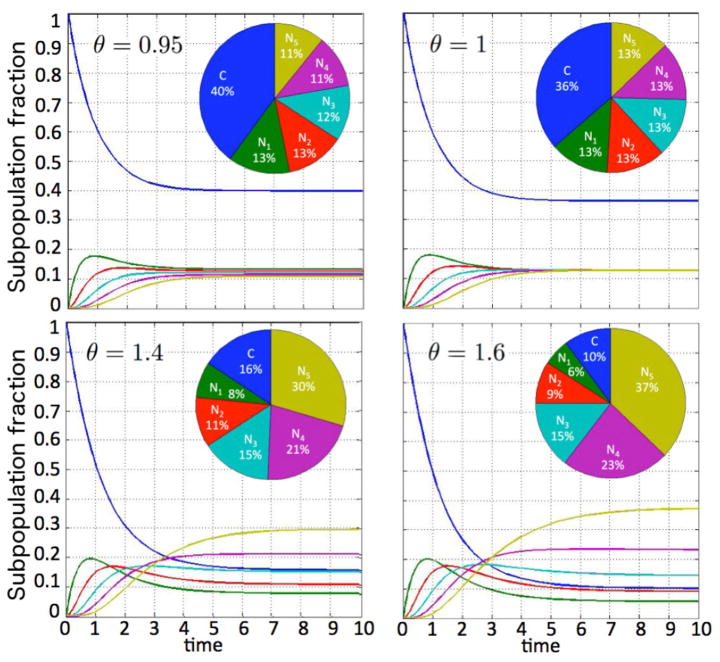
To illustrate the tumor growth dynamics and generational hierarchy within the tumor, let us consider the positive net cancer stem cell growth rate of β = 0.2, and a non-stem cancer cell proliferation capacity of m = 5. Let the proliferation rates of stem and non-stem cancer cells be γ = λ = 1, and assume the cancer stem cell death rate and division fate parameters are a = 0.1 and p₁ = 0.3, p₂ = 0.7, p₃ = 0, respectively. Figure 3 shows how the tumor population per cancer stem cell increases as θ increases. The variation in θ here arises due to changes in the death rate of non-stem cancer cells b (with larger b values yielding smaller θ values). Figure 4 shows how the proportion of the subpopulations in the tumor evolves in time for various θ values, starting from a pure cancer stem cell population (C(0) = 1, N_k(0) = 0). After the initial transience, there is always an eventual strict ordering for the N_k population fractions when θ ≠ 1 as discussed above, but the final proportional contribution of C depends on the chosen parameter set.

Fig. 3.

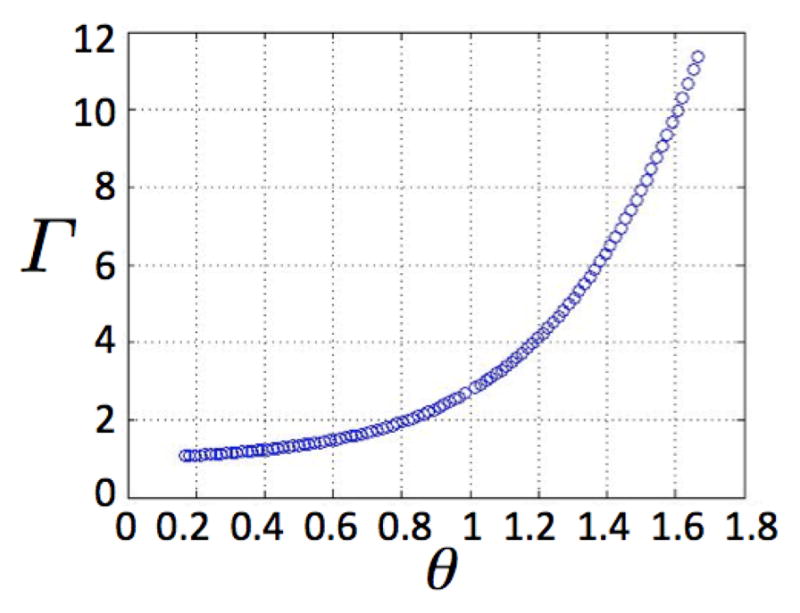
Tumor population per cancer stem cell Γ due to various θ, assuming m = 5. Other parameters: β = 0.2, γ = 1, λ = 1, p₁ = 0.3, p₂ = 0.7, a = 0.1.

Fig. 4.

Temporal evolution of subpopulation fractions dependent on parameter θ.

4 Estimation of non-stem cancer cell proliferation potential

As experimental biomarkers for proliferation potential are yet to be developed, we use the current model to investigate plausible ranges of the non-stem cancer cell proliferation potential. Gao et al. (2013) recently reported that the cell cycle of U87MG human glioblastoma cells varies between 19 and 35 hours in vitro, with an average of 25 hours. These experiments set the limits for the proliferation rates in our model from a low of 24/35 = 0.69 to a high of 24/19 = 1.26. In line with the assumptions and observations in Gao et al. (2013), we set the cancer stem cell division probabilities p₁ = 0.35, p₂ = 0.65, p₃ = 0, and the cell death rates a = 0, b = 0.1. Let C(0)=1, and N_k(0)=0. We calculate the total tumor population Q after t = 50 time steps for varying values of non-stem proliferation rates γ. We fix the cancer stem cell proliferation rate at λ = 1 (Fig. 5A), and λ = 1.26 or λ = 0.69 (Fig. 5B) for a non-stem cancer cell proliferation capacity m = 5. Results show that there exists a non-stem cancer cell proliferation rate γ* such that tumor size is maximized at t = 50. The total tumor population generated per cancer stem cell, i.e. Γ = Q/C, mimics the dynamics of the total population (Fig. 5A). These observed γ* = 1.24, 1.49, and 0.95 for λ = 1, 1.26, and 0.69, respectively, indicate that tumor growth is optimized with cell cycle times between 16 and 26 hours, as observed in experiments (Gao et al. (2013)). For larger m = 10 (with λ = 1), however, the largest populations are achieved with biologically unrealistic γ* = 3.46, 4.18, and 2.65, indicative of cell cycles as short as 5 – 9 hours. In fact, for fixed λ = 1, various proliferation capacities 3 ≤ m ≤ 11 and probabilities of symmetric cancer stem cell division 0 < p₁ ≤ 0.5 reveal that only a subset of the parameter space (4 ≤ m ≤ 9) yields optimal tumor growth within experimentally observed cell cycle times (Figure 6). Interestingly, for increasing progenitor proliferation potential m, the probability of symmetric cancer stem cell division p₁ must decrease for the tumor to grow to the maximum possible size for realistic cell cycle lengths. Reciprocally, for increasing p₁ the progenitor proliferation potential m must decrease to optimize overall tumor growth.

Fig. 5.

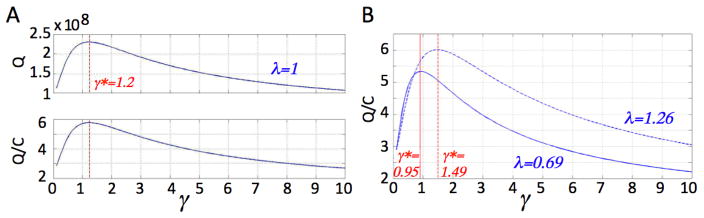
A) Graphs of Q and Q/C versus γ for λ fixed at 1. B) Graph of Q/C versus γ for λ fixed at 24/19 = 1.26 (dashed) and λ fixed at 24/35 = 0.69 (solid). Other parameters: m = 5, p₁ = 0.35, a = 0, b = 0.1

Fig. 6.

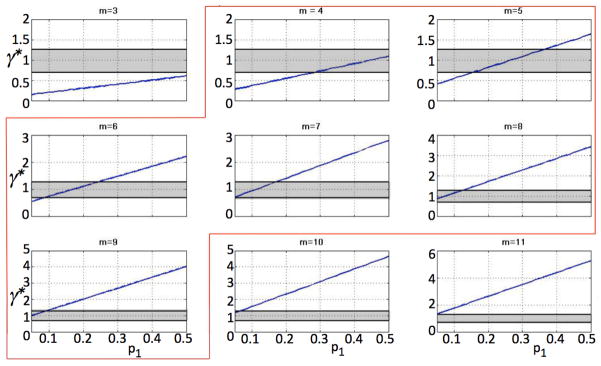
Values of optimal γ* for different p₁ for various m. Shaded areas indicate experimentally observed cell cycle times. Highlighted are parameter sets that yield optimal growth rates γ*(p₁) within biological observations.

5 Two-compartment model

Mathematical models of cancer stem cell driven tumors previously assumed two (cancer stem cells and non-stem cancer cells; Hillen et al. (2012)), three (cancer stem cells, progenitor cells, and terminally differentiated cells; Johnston et al. (2010); Molina-Peña and Álvarez (2012)) or four compartments (cancer stem cells, progenitor cells, differentiated cells and terminally differentiated cells; Michor et al. (2005)). We reduce the introduced multicompartment model (1)–(4)) to a two-compartment model and compare the resulting dynamics to the multicompartment model as well as models from the literature. Summing up the equations for all N_k in system (2)–(4) gives

$$\begin{array}{l}\frac{dH}{dt}=\sum _{k=1}^m\frac{{dN}_k}{dt}\\ =-\gamma \sum _{k=1}^m{N}_k-b\sum _{k=1}^m{N}_k+(p_2+2p_3)\lambda C+2\gamma \sum _{k=1}^{m-1}{N}_k\end{array}$$ (12)

$$\begin{array}{l}=-\gamma H-bH+(p_2+2p_3)\lambda C+2\gamma H-2\gamma N_m\\ \Rightarrow \frac{dH}{dt}=(\gamma -b)H+(p_2+2p_3)\lambda C-2\gamma N_m.\end{array}$$ (13)

This equation, along with (1), would give a two-compartment model to replace (1)–(4) if we could explicitly express N_m in terms of C or H.

Equation (6) for k = m suggests that we use the approximation

$$N_m(t)=(p_2+2p_3)\lambda \frac{{\theta }^m}{2\gamma }C(t),$$

while (6) and (7) lead us to consider the approximation

$$N_m={\theta }^{m-1}\frac{(1-\theta )}{1-{\theta }^m}H(t).$$ (14)

As shown in Appendix 2, approximation of N_m in terms of C is inappropriate. Approximating N_m with H (14) and closing the system yields a two-compartment model:

$$\frac{dC}{dt}=(p_1-p_3)\lambda C-aC$$ (15)

$$\frac{dH}{dt}=\left[(\gamma -b)-2\gamma {\theta }^{m-1}\frac{(1-\theta )}{1-{\theta }^m}\right]H+(p_2+2p_3)\lambda C.$$ (16)

We denote the solution of H in this system as H_2H.

Let m → ∞ and assume that θ < 1, so that $H={\sum }_{k=1}^m{N}_k$ is finite as m → ∞ (hence N_m → 0). Then (12) and (13) give

$$\frac{dH}{dt}=(\gamma -b)H+(p_2+2p_3)\lambda C.$$

This gives exactly the linear version of the two-compartment model for stem and non-stem populations in Hillen et al. (2012) under the assumption of immortal stem cells (a = 0) and no symmetric commitment (p₃ = 0):

$$\frac{dC}{dt}=p_1\lambda C$$ (17)

$$\frac{dH}{dt}=(\gamma -b)H+(1-p_1)\lambda C.$$ (18)

In Hillen et al. (2012), it is assumed that b > 0 reflects exhaustion of proliferation potential as well as spontaneous death. We denote the solution of H in this system as H_∞.

Figure 7 illustrates the agreement of H_2H, the solution of our two-compartment model (15)–(16), with the solution of the multicompartment solution of H in (1)–(4), for various m and θ < 1 fixed. The figures also show that the solution H_∞ of the linear two-compartment model (17)–(18) which does not have an explicit consideration of the proliferation capacity m does not give the correct multicompartment solution for moderate m but matches better as m gets large. Figure 8 illustrates the point that the linear version of the Hillen two-compartment model is quite unsuitable for θ > 1.

Fig. 7.

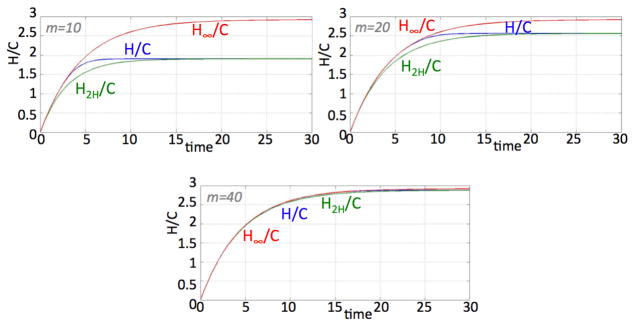
Solutions of H/C in (1)–(4), H_2H/C in (15)–(16), and H_∞/C in (17)–(18) for m = 10, 20, and 40. Other parameters: λ = γ = 1, p₁ = 0.35, p₂ = 0.65, a = 0, b = 0.87222 and θ = 0.9.

Fig. 8.

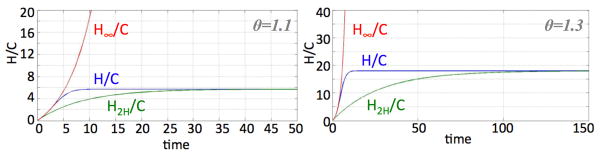
Solutions of H/C in (1)–(4), H_2H/C in (15)–(16), and H_∞/C in (17)–(18) for p₁ = 0.35, p₃ = 0, a = 0, λ = γ = 1 and m = 10 for θ = 1.1 and 1.3.

This suggests that the growth rate value for γ in a two-compartment model (18) would not be equivalent to the value for γ used in a multicompartment model (2)–(4). That is, treating a non-stem cancer cell population with proliferation capacity m as a homogeneously-aged population requires the proliferation rate γ to be replaced for each generation with a net proliferation rate γ_∞ of all generations taken together. For example, (16) and (18) suggests using

$${\gamma }_{\infty }=\gamma \left(1-2{\theta }^{m-1}\frac{(1-\theta )}{1-{\theta }^m}\right).$$

The importance of scaling the net proliferation rate with a generational hierarchy depth dependent proliferation capacity is illustrated in Figure 9. The solution of the two-compartment model (15)–(16) disagrees with that of the full multicompartment solution if an inappropriate m is used.

Fig. 9.

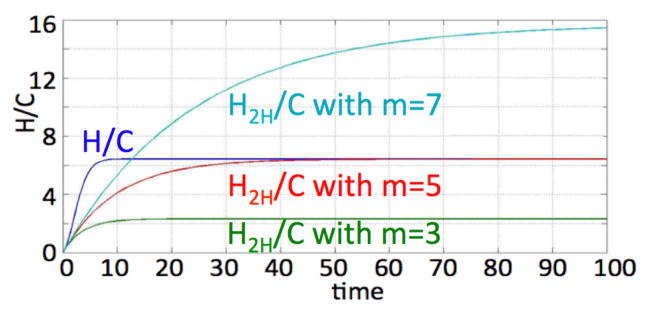
Solution of H/C in (1)–(4) p₁ = 0.35, p₃ = 0, a = 0.1, λ = γ = 1, θ = 1.5 for m = 5 and H_2H/C in (15)–(16) for m = 3, m = 5 and m = 7.

6 Discussion

We have presented a linear multi-compartment mathematical model of tumor growth following the cancer stem cell hypothesis. As an augmentation to the increasing literature on mathematical models of cancer stem cell-driven tumor growth, we introduced different non-stem cancer cell compartments that comprise cells of comparable remaining proliferation potential. This generational hierarchy has been shown to play a prominent role in modulating overall tumor population dynamics in agent-based models (Enderling et al. (2009); Morton et al. (2011)). For simplicity we ignored physiological regulatory feedback (Rodriguez-Brenes et al. (2011)) and focused on the exponential growth phase of the tumor in line with other recent studies (Johnston et al. (2010); Molina-Peña and Álvarez (2012)). Introducing a population carrying capacity or feedback from non-stem cancer cells on cancer stem cells will modulate overall tumor progression rate, but not the generational hierarchy population structure analysis presented here. Analysis of the presented model showed that the net rate of change of the total tumor population, interpretable as tumor aggressiveness, is simply the net growth rate of the cancer stem cell compartment, β. This result is intrinsic to multi-compartment models where a pure non-stem cancer cell population decays. Exploration of the parameter space of the presented model revealed that tumors with identical aggressiveness β can have remarkably different proportions of cancer stem cells. Reciprocally, tumors with identical cancer stem cell fraction, can have different net population growth rates and thus different aggressiveness. This contrasts with observations in Johnston et al. (2010)) that suggested that a higher cancer stem cell fraction correlates with a more aggressive tumor if the total tumor population follows a strict exponential growth regime.

As one focus of our study was on the contribution of the proliferation potential of non-stem cancer cells to overall population dynamics, we investigated the proportion of cancer stem cells in the arising tumor dependent on the generational hierarchy of their non-stem progeny. We found, intuitively, that with increasing non-stem cancer cell proliferation capacity the total tumor population increases as well as the population generated by each cancer stem cell. Inversely proportionally, however, the fraction of cancer stem cells diminishes. At the same time, the contribution of each generational compartment to the total population reverses from predominantly older compartments, that is cells that have proliferated more with consequently decreasing remaining proliferation potential, to preferentially young cells in equally-sized tumors. Despite identical cancer stem cell kinetics, tumor size and overall tumor growth rate, the intrinsic death rate of the non-stem cancer cell compartments may have a pivotal contribution to treatment outcome. Tumors with mostly post-mitotic cells may not benefit from treatment as much as tumors with primarily young cells.

In exploration of the model parameter space we found an unexpected dependence of optimal tumor growth on basic cell kinetics. Analysis of the model revealed that only low non-stem cancer cell proliferation capacities yield optimum tumor growth for cell cycle times that are within biologically observed ranges. That indicates that tumors either grow with sub-optimal cell cycle times, or that non-stem cancer cells must be short-lived. Support to the latter hypothesis comes from the somewhat counterintuitive observation that cancer cell telomere length indicative of proliferative capacity is surprisingly short in most tumors (Shay and Wright (2011)).

The model presented herein is the first attempt to decipher the contribution of the generational hierarchy in the non-stem cancer cell population to overall tumor dynamics. For simplicity, we assumed a rigid cellular phenotype and ignored cell de-differentiation and resulting phenotypic plasticity (Marjanovic et al. (2013)). A mathematical description of stem cell plasticity (Roeder and Loeffler (2002); Leder et al. (2010)) as well as non-linearity from saturations (Johnston et al. (2010)) or population-level carrying capacity limitations (Folkman and Hochberg (1973)) can be incorporated in future model developments to arrive at a more comprehensive understanding of the complex biology underlying cancer stem cell-driven tumor dynamics.

Appendix 1

We introduce the notations

$$\omega =p_2=2p_3,z=\gamma +b.$$

Then, using (5), we rewrite the system of equations (2)–(4) as

$$\begin{array}{c}\frac{{dN}_1}{dt}=\omega \lambda C_0{e}^{\beta t}-{zN}_1\\ \frac{{dN}_2}{dt}=2\gamma N_1-{zN}_2\\ ⋮\\ \frac{{dN}_k}{dt}=2\gamma N_{k-1}-{zN}_k\\ ⋮\\ \frac{{dN}_m}{dt}=2\gamma N_{m-1}-{zN}_m,\end{array}$$

where β = (p₁ − p₃) λ − a. Define

$$n_k(t)=N_t(t)e^{zt}$$

and substitute n_k(t)e^−zt in the system above to arrive at

$$\frac{{dn}_1}{dt}=\omega \lambda C_0{e}^{(\beta +z)t}$$ (19)

$$\begin{array}{c}\frac{{dn}_2}{dt}=2\gamma n_1\\ ⋮\end{array}$$ (20)

$$\begin{array}{c}\frac{{dn}_k}{dt}=2\gamma n_{k-1}\\ ⋮\end{array}$$ (21)

$$\frac{{dn}_m}{dt}=2\gamma n_{m-1}.$$ (22)

The solution to (19)–(22) is

$$n_k=\sum _{i=1}^k{N}_{k+1-i}(0)\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}+\frac{{\theta }^k\omega \lambda C_0}{2\gamma }\left(e^{(\beta +z)t}-\sum _{i=1}^k\frac{t^{i-1}{(2\gamma )}^{i-1}}{{\theta }^{i-1}(i-1)!}\right),$$

so

$$\sum _{i=1}^k{N}_{k+1-i}(0)\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}{e}^{-zt}+\frac{{\theta }^k\omega \lambda C_0}{2\gamma }\left(e^{\beta t}-\sum _{i=1}^k\frac{t^{i-1}{(2\gamma )}^{i-1}}{{\theta }^{i-1}(i-1)!}{e}^{-zt}\right)$$

where

$$\theta =\frac{2\gamma }{\gamma +\beta +b}=\frac{2\gamma }{z+\beta }.$$

The asymptotic behavior of N_k for large t is

$$N_{ks}=\frac{{\theta }^k\omega \lambda C_0}{2\gamma }{e}^{\beta t}.$$

The exact solution for H is found by direct summation over the N_k:

$$H=\sum _{k=1}^m\sum _{i=1}^k{N}_{k+1-i}(0)\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}{e}^{-zt}+\sum _{k=1}^m\frac{{\theta }^k\omega \lambda C_0}{2\gamma }{e}^{\beta t}-\sum _{k=1}^m\left[\frac{{\theta }^k\omega \lambda C_0}{2\gamma }\sum _{i=1}^k\frac{t^{i-1}{(2\gamma )}^{i-1}}{{\theta }^{i-1}(i-1)!}\right]e^{-zt}.$$

Defining

$$P_i=\sum _{j=1}^i{N}_j(0)$$

and using

$$\sum _{k=1}^m\sum _{i=1}^k=\sum _{i=1}^m\sum _{k=i}^m,$$

we get that

$$\begin{array}{l}H=\sum _{i=1}^m\left(\sum _{k=i}^m{N}_{k+1-i}(0)\right)\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}{e}^{-zt}+\frac{\theta \theta \lambda C_0}{2\gamma }\left(\frac{1-{\theta }^m}{1-\theta }\right)e^{\beta t}-\sum _{i=1}^m\left(\sum _{k=i}^m\frac{{\theta }^k\omega \lambda C_0}{2\gamma }\right)\frac{t^{i-1}{(2\gamma )}^{i-1}}{{\theta }^{i-1}(i-1)!}{e}^{-zt}\\ =\sum _{i=1}^m{P}_{m+1-i}\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}{e}^{-zt}+\frac{\theta \omega \lambda C_0}{2\gamma }\left(\frac{1-{\theta }^m}{1-\theta }\right)e^{\beta t}-\frac{\theta \omega \lambda C_0}{2\gamma }\sum _{i=1}^m\left(\frac{1-{\theta }^{m+1-i}}{1-\theta }\right)\frac{t^{i-1}{(2\gamma )}^{i-1}}{(i-1)!}{e}^{-zt}.\end{array}$$

The asymptotic behavior of H for large t is

$$H_s=\frac{\theta \omega \lambda C_0}{2\gamma }\left(\frac{1-{\theta }^m}{1-\theta }\right)e^{\beta t}.$$

Appendix 2

Replacing N_m in (13) with the expression

$$(p_2+2p_3)\lambda \frac{{\theta }^m}{2\gamma }C$$

from (6) gives the two-compartment system:

$$\frac{dC}{dt}=(p_1-p_3)\lambda C-aC$$ (23)

$$\frac{dH}{dt}=(p_2+2p_3)\lambda (1-{\theta }^m)C+(\gamma -b)H.$$ (24)

We denote the solution of H in this system as H_2C.

The exact solution to the two-compartment model with (24) is such that

$$\frac{H_{2C}(t)}{C(t)}=\frac{H_s(t)}{C(t)}+\left[\frac{H(0)}{C(0)}-\frac{H_s(t)}{C(t)}\right]e^{{\kappa }_{1}t}$$

where

$${\kappa }_1=\gamma -b-\beta =2\gamma \frac{(\theta -1)}{\theta },$$

and where H_s is the asymptotic solution of the multicompartment system given in (7),

$$H_s(t)=(p_2+2p_3)\frac{\lambda }{2\gamma }\frac{\theta (1-{\theta }^m)}{1-\theta }C(0)e^{\beta t}.$$

Now θ < 1 ⇒ κ₁ < 0 and, in this case, we see that H_2C/C → H_s/C as time passes but when θ > 1, we have κ₁ > 0 so H_2C/C diverges from H_s/C and this two-compartment model is not reliable.

On the other hand, if we use the equation (16) as the second equation in our two-compartment model:

$$\begin{array}{l}\frac{dC}{dt}=(p_1-p_3)\lambda C-aC\\ \frac{dH}{dt}=\left[(\gamma -b)-2\gamma {\theta }^{m-1}\frac{(1-\theta )}{1-{\theta }^m}\right]H+(p_2+2p_3)\lambda C,\end{array}$$

the solution for H which we have called H_2H is such that

$$\frac{H_{2H}(t)}{C(t)}=\frac{H_s(t)}{C(t)}+\left[\frac{H(0)}{C(0)}-\frac{H_s(t)}{C(t)}\right]e^{{\kappa }_{2}t},$$

where

$$\begin{array}{l}{\kappa }_2=\gamma -b-\beta -2\gamma \frac{{\theta }^{m-1}(1-\theta )}{1-{\theta }^m}\\ =2\gamma \frac{(\theta -1)}{\theta (1-{\theta }^m)}={\kappa }_1/(1-{\theta }^m).\end{array}$$

Here κ₂ < 0 for all θ > 0, so that H_2H → H_s for large time which is what we need.

Figure 10 compares the H/C that comes from the full multicompartment model, the H_2H/C coming from (16), and H_2C/C coming from (24). One can indeed see that when θ < 1, H_2C/C gives a good approximation to H/C, but not when θ > 1. For the parameters used in the latter case, H_2C/C is negative and the solution heads to −∞.

Fig. 10.

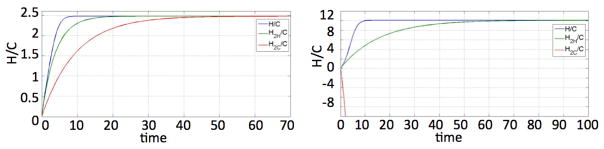
Comparison of H/C, H_2H/C, and H_2C/C for θ = 0.95 and θ = 1.2. Other parameters: m = 10, λ = 1, γ = 1, p₁ = 0.35, p₂ = 0.65, a = 0.1, β = 0.25.