Abstract
Mechanobiological processes are rooted in mechanics and chemistry, and such processes may be modeled in a framework that couples their governing equations starting from fundamental principles. In many biological applications, the reactants and products of chemical reactions may be electrically charged, and these charge effects may produce driving forces and constraints that significantly influence outcomes. In this study, a novel formulation and computational implementation are presented for modeling chemical reactions in biological tissues that involve charged solutes and solid-bound molecules within a deformable porous hydrated solid matrix, coupling mechanics with chemistry while accounting for electric charges. The deposition or removal of solid-bound molecules contributes to the growth and remodeling of the solid matrix; in particular, volumetric growth may be driven by Donnan osmotic swelling, resulting from charged molecular species fixed to the solid matrix. This formulation incorporates the state of strain as a state variable in the production rate of chemical reactions, explicitly tying chemistry with mechanics for the purpose of modeling mechanobiology. To achieve these objectives, this treatment identifies the specific theoretical and computational challenges faced in modeling complex systems of interacting neutral and charged constituents while accommodating any number of simultaneous reactions where reactants and products may be modeled explicitly or implicitly. Several finite element verification problems are shown to agree with closed-form analytical solutions. An illustrative tissue engineering analysis demonstrates tissue growth and swelling resulting from the deposition of chondroitin sulfate, a charged solid-bound molecular species. This implementation is released in the open-source program FEBio (www.febio.org). The availability of this framework may be particularly beneficial to optimizing tissue engineering culture systems by examining the influence of nutrient availability on the evolution of inhomogeneous tissue composition and mechanical properties, the evolution of construct dimensions with growth, the influence of solute and solid matrix electric charge on the transport of cytokines, the influence of binding kinetics on transport, the influence of loading on binding kinetics, and the differential growth response to dynamically loaded versus free-swelling culture conditions.
Keywords: Chemical reactions, Charged reactants and products, Growth and remodeling, Mechanobiology, Finite element modeling
1 Introduction
Most biological processes are driven by chemical reactions, and in many cases, these reactions involve charged molecular species that are either soluble or bound to a solid matrix such as the extracellular matrix of a tissue or the intracellular cytoskeletal network. A framework for modeling such chemical reactions in a system that also accounts for mechanics of matrix deformation and transport in biological tissues and cells provides opportunities to examine important phenomena such as mechanotransduction, growth and remodeling, and tissue engineering. A computational implementation of such a framework has not been previously available in the public domain.
The incorporation of chemical reactions in models of biological tissues has been demonstrated in a number of prior studies, especially in the field of tissue engineering (Martin et al. 1999; Obradovic et al. 2000; DiMicco and Sah 2003; Sengers et al. 2004a,b, 2005; Radisic et al. 2005) and tissue growth (Garikipati et al. 2004), but also in the investigation of the transport and binding of molecular species with the extracellular matrix of biological tissues (Garcia et al. 2003; Albro et al. 2013). These models typically employ classical relations of chemical kinetics that account for diffusion of soluble species, producing standard diffusion–reaction systems. Generally, they do not account for the electrical charges that may be carried by the soluble constituents and solidbound molecular species, preempting the analysis of problems where charge effects play a significant role. Yet, in biological tissues and cells, most proteins and nucleic acids and many polysaccharides are electrically charged such that charge-to-charge attraction or repulsion may significantly influence reactions and transport.
The analysis of non-reactive charged hydrated biological tissues was first presented in the triphasic theory of Lai et al. (1991), who modeled tissues using mixture theory with a charged porous hydrated solid matrix and an interstitial fluid consisting of a solvent (water) and two monovalent counterions. The resulting nonlinear equations have proved challenging to solve with analytical methods, necessitating the formulation of computational frameworks to produce solutions to boundary and initial-value problems for triphasic analyses (Sun et al. 1999; van Loon et al. 2003; Yao and Gu 2007; Ateshian and Weiss 2013). The generalization of the triphasic theory to amultiphasic framework accommodating any number of charged soluble species whose charge number may exceed unity was proposed by Gu et al. (1998), and a computational framework encompassing this multiphasic theory was recently presented by Ateshian et al. (2013). Major challenges in this computational formulation included the necessity to satisfy the electroneutrality condition while simultaneously enforcing the corollary divergence-free current condition, regardless of the number and charge of solutes, and also accommodating finite solid deformation and material and transport properties that may depend on strain and solute concentrations.
Atheoretical framework for modeling reactive mixtures of neutral or charged soluble constituents (Ateshian 2007), formulated based on the classical theory of mixtures (Truesdell and Toupin 1960; Eringen and Ingram 1965; Bowen 1968, 1976), has provided the necessary foundation for the computational approach presented in this study. That theoretical framework has had a number of ramifications in relation to growth mechanics that were investigated in a recent series of reports. It reinforced the existing paradigm (Hsu 1968; Cowin and Hegedus 1976) that growth is primarily modeled by including a source term in the mass balance relation for the solid matrix (Ateshian 2011). By incorporating solutes in a growth framework, it demonstrated that growth may be driven by osmotic effects, as occurs in cell growth or in the deposition of charged solid matrix constituents (Ateshian et al. 2009). By including multiple solid constituents in a constrained solid mixture (Humphrey and Rajagopal 2002), it demonstrated that residual stresses may be described by explicitly associating a different reference configuration for each generation of deposited solid matrix in a multigenerational growth framework (Ateshian and Ricken 2010). By incorporating the referential mass density of solid constituents as state variables in the constitutive relations for solid mass supply and stress functions (Myers and Ateshian 2013), it recapitulated the classical stress or strain-driven remodeling theories developed in the bone mechanics literature (Cowin and Hegedus 1976; Huiskes et al. 1987; Carter et al. 1987, 1989; Weinans et al. 1992; Mullender et al. 1994). However, none of these prior studies explicitly incorporated chemical reactions with charged solutes and solidbound molecular species.
Therefore, the objective of this study was to formulate a novel computational framework for chemical reactions that may involve electrically charged species while maintaining electroneutrality, where reactants and products may consist of solutes and solid-bound molecules such that the deposition or removal of solid-bound molecules contributes to the growth and remodeling of the solid matrix. The resulting finite element code has been incorporated into the open-source FEBio program (www.febio.org, Maas et al. 2012).
2 Governing equations
Section 2.1 reviews governing equations of reactive mixtures, showing how classical treatments of continuum mechanics and chemical kinetics may be unified into a single framework that couples mechanics and chemistry. Though individual aspects of these equations have been reported in the prior literature, the presentation that follows combines all essential elements, using a consistent notation, as needed for a practical computational implementation. Section 2.2 extends the classical treatment of chemical kinetics to incorporate the solid matrix strain as a state variable in the constitutive relation for the molar production rate.
2.1 Mass balance
Chemical kinetics is concerned with modeling the rate at which chemical reactions take place. In continuum frameworks that accommodate mass transport, reaction rates appear in the statement of mass balance. In the theory of mixtures (Bowen 1968), the differential form of the statement of mass balance for any constituent α, in the spatial frame, is given by
| (1) |
where vα is the constituent’s velocity, ρα is its apparent density (mass of α per volume of the mixture in the current configuration), and ρ̂ α is the volume density of mass supply to α, resulting from chemical reactions with all other mixture constituents. Since mass must be conserved over all constituents, mass supply terms are constrained by
| (2) |
In a mixture containing a solid constituent (denoted by α = s), it is convenient to define the mixture domain (and thus the finite element mesh) on the solid and evaluate mass fluxes of constituents relative to the solid,
| (3) |
Substituting (3) into (1), the differential form of the mass balance may be rewritten as
| (4) |
where Ds (·)/Dt represents the material time derivative in the spatial frame, following the solid, J = det F where F is the deformation gradient of the solid matrix; is the apparent density, and is the volume density of mass supply of α normalized to the mixture volume in the reference configuration,
| (5) |
Since is the mass of α in the current configuration per volume of the mixture in the reference configuration (an invariant quantity), this parameter represents a direct measure of the evolving mass content of α in the mixture, which may thus be used as a state variable in a framework that accounts for chemical reactions (Ateshian 2007; Myers and Ateshian 2013). A distinction is now made between solid and solute species in the mixture, since they are often treated differently in an analysis.
2.1.1 Solid matrix and solid-bound molecular constituents
For constituents constrained to move with the solid (Humphrey and Rajagopal 2002), denoted generically by α = σ and satisfying vσ = vs, ∀ σ, the statement of mass balance in (4) reduces to the special form
| (6) |
This representation makes it easy to see that alterations in can occur only as a result of chemical reactions (such as synthesis, degradation, or binding). In contrast, as seen in (4), alterations in for solutes or solvent (α ≠ σ) may also occur as a result of mass transport into or out of the pore space of the solid matrix. Therefore, is the natural choice of state variable for describing the content of solid constituents in a reactive mixture.
When multiple solid species are present, the net solid mass content may be given by , whereas the net mass supply of solid is such that . The referential solid volume fraction, , may be evaluated from
| (7) |
where is the true density of solid constituent σ (mass of σ per volume of σ). According to (5), it follows that the solid volume fraction in the current configuration is given by . Note that 0 ≤ φs ≤ 1 under all circumstances, while , implying that may exceed unity when solid growth occurs (Ateshian et al. 2009). In this study, it is assumed that all mixture constituents are intrinsically incompressible, implying that their true density is invariant.1
The various constituents of the solid matrix may be electrically charged. Let zσ be the charge number (equivalent charge per mole) of solid constituent σ, then the net referential fixed charge density of the solid matrix (equivalent charge per fluid volume in the referential configuration) is given by
| (8) |
where Mσ is the molar mass of σ (an invariant quantity) and represents the referential volume fraction of all fluid constituents (solvent+solutes) in a saturated mixture. Based on the kinematics of the continuum, the fixed charge density in the current configuration is
| (9) |
2.1.2 Solutes
Solutes are denoted generically by α = ι. In chemistry, solute content is often represented in units of molar concentration (moles per fluid volume). It follows that solute molar concentration cι and molar supply ĉι are related to ρι and ρ̂ι via
| (10) |
The molar flux of constituent ι relative to the solid is given by
| (11) |
where it may be noted that mι = Mιjι. Combining these relations with (4)–(5) produces the desired form of the mass balance for the solutes,
| (12) |
This form is suitable for implementation in a finite element analysis where the mesh is defined on the solid matrix (Ateshian et al. 2011, 2013).
In the multiphasic mixture framework adopted here, it is assumed that the electroneutrality condition is satisfied at all times in the continuum, implying that the mixture cannot act as an electrical capacitor. Assuming the solvent is neutral (zw = 0), the electroneutrality condition may be written as
| (13) |
2.1.3 Mixture with negligible solute volume fraction
The volume fraction of each constituent is given by . In a saturated mixture these volume fractions satisfy Σα φα = 1. Substituting into (1), dividing across by (invariant for intrinsically incompressible constituents), and taking the sum of the resulting expression over all constituents produces
| (14) |
This mass balance relation for the mixture expresses the fact that the mixture volume will change as a result of chemical reactions where the true density of products is different from that of reactants.2 We now adopt the assumption that solutes occupy a negligible volume fraction of the mixture (φι ≪ 1), from which it follows that φs + φw ≈ 1 and Σα φαvα ≈ vs + w, where w = φw (vw − vs) is the volumetrix flux of solvent relative to the solid. Thus, the mixture mass balance may be reduced to
| (15) |
2.2 Chemical kinetics
Reaction rates are described by constitutive relations which are functions of the state variables. In a biological mixture under isothermal conditions, the minimum set of state variables needed to describe reactive mixtures that include a solid matrix are: the (uniform) absolute temperature θ, the solid matrix deformation gradient F (or related strain measures), and the molar content cα of the various constituents (Ateshian 2007). This set differs from the classical treatment of chemical kinetics in fluid mixtures by the inclusion of F and the subset of constituents bound to the solid matrix. To maintain a consistent notation in this section, solid-bound molecular species are described by their molar concentrations and molar supplies which may be related to their referential mass density and referential mass supply according to
| (16) |
Consider a general chemical reaction (Prud’homme 2010),
| (17) |
where
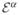 is the chemical species representing constituent α;
and
represent stoichiometric coefficients of the reactants and products, respectively. Since the molar supply of reactants and products is constrained by stoichiometry, it follows that all molar supplies ĉα in a specific chemical reaction may be related to the molar production rate ζ̂ according to
is the chemical species representing constituent α;
and
represent stoichiometric coefficients of the reactants and products, respectively. Since the molar supply of reactants and products is constrained by stoichiometry, it follows that all molar supplies ĉα in a specific chemical reaction may be related to the molar production rate ζ̂ according to
| (18) |
where να represents the net stoichiometric coefficient for
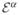 ,
,
| (19) |
Thus, formulating constitutive relations for ĉα’s is equivalent to providing a single relation for ζ̂ (θ, F, cα). When the chemical reaction is reversible,
| (20) |
the relations of (18)–(19) still apply but the form of ζ̂ would be different.
Using the relations of (10), (16) and (18), it follows in general that ρ̂α = (1 − φs ) Mαναζ̂, so that the constraint of (2) is equivalent to enforcing stoichiometry, namely,
| (21) |
Thus, properly balancing a chemical reaction satisfies this constraint.
The mixture mass balance in (15) may now be rewritten as
| (22) |
where
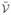 = Σα να
= Σα να
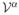 and
is the molar volume of α. Similarly, the solute mass balance in (12) becomes
and
is the molar volume of α. Similarly, the solute mass balance in (12) becomes
| (23) |
These mass balance equations reduce to those of non-reactive mixtures when ζ̂ = 0.
Since the mixture is assumed to satisfy the electroneutrality condition at all times, chemical reactions may not alter this condition. Thus, the net stoichiometric coefficients must satisfy Σα zα να = 0, with the summation taken over all mixture constituents. It can be shown that the combination of this constraint with (13) and the above mass balance relations produces the divergence-free current condition (a specialization of one of Maxwell’s equations), div Ie = 0, where Ie = Fc Σιzιjι is the current density and Fc is Faraday’s constant.
3 Finite element implementation
This section includes the novel implementation of reactive mixtures whose constituents may be electrically charged, building on our recent finite element implementation of nonreactive mixtures.
3.1 Statement of virtual work
The implementation of non-reactive multiphasic mixtures in a finite element framework was presented in a recent study (Ateshian et al. 2013). This implementation may be described by three general principles: (1) The virtualwork integral combines the momentum balance for the mixture, the mass balance for the mixture, and the mass balances for each of the solutes. The momentum balance for the mixture under quasistatic conditions in the absence of external body forces is div σ = 0, where σ = −pI + σs is the mixture stress, p is the interstitial fluid pressure, and σs is the stress produced by the solid matrix strain. (2) The nodal variables, which must be continuous across element boundaries, are the solid displacement, u, the effective fluid pressure, p̃, and the effective solute concentrations c̃ι. The effective fluid pressure represents the mechanical contribution to the mechano-chemical fluid pressure p,
| (24) |
where R is the universal gas constant and Φ is the osmotic coefficient describing the deviation of the fluid chemical potential from the ideal physico-chemical behavior of very dilute solutions. The effective solute concentration is related to cι via
| (25) |
where κ̃ι = κ̂ι exp (−zιFcψ/Rθ) is the partition coefficient of solute ι, κ̂ι is its effective solubility (Mauck et al. 2003; Ateshian et al. 2011, 2013) and ψ is the electric potential in the mixture. Here, Φ and κ̂ι are user-defined functions of J, and cι.3 The electric potential is obtained by solving (13) as explained in Ateshian et al. (2013). (3) The momentum balance relations for the solvent and solutes provide relations for the solvent volumetric flux w and solute molar fluxes jι which are functions of grad p̃ and grad c̃ι (Ateshian and Weiss 2013; Ateshian et al. 2013).
The statement of virtual work is given by
| (26) |
where δv is the virtual solid velocity, δp̃ is the virtual effective fluid pressure, δc̃ι is the virtual molar energy of solute ι, and γ only refers to solutes. This formulation also enforces the divergence-free current condition. Here, δG is the contribution to the virtual work δW resulting from the supply terms from chemical reactions,
| (27) |
where ζ̂ is a function of the solid matrix strain, the solute effective concentrations c̃ι and the solid referential densities . δG and the incorporation of to the list of state variables, together with the incorporation of charged molecular species in chemical reactions, represent the novel additions in this finite element formulation. The objective of a finite element analysis is to solve for the unknown u, p̃ and c̃ι by satisfying δW = 0. Since the resulting equations are nonlinear, the solution is obtained using a Newton scheme whereby δW is linearized according to
| (28) |
where the operator DδW [·] represents the directional derivative of δW at (u, p̃, c̃ι) along an increment in Δu, Δp̃, or Δc̃γ (Bonet and Wood 1997). The time derivatives in (26)
(including vs = Ds u/Dt ) are discretized using the backward Euler method to produce an implicit solution scheme.
Accordingly, for the contribution δG to δW, it follows that
DδG [Δu]
| (29) |
where Δε ≡ (grad Δu + gradT Δu)/2, and
| (30) |
where E is the Lagrange strain tensor. Since ζ̂ is not assumed to depend on the fluid pressure, it follows that,
| (31) |
Finally, for the linearization along increments in effective concentration,
| (32) |
3.2 Implementation details
When modeling multiphasic mixtures, users must provide master tables of all solutes and solid-bound molecules present in a particular finite element model. The values of zα, Mα and
must be provided in these master tables, to be used for example in the evaluation of
in (7),
in (8), cσ and ĉσ in (16), and
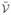 . Each multiphasic material in a model must reference the set (or subset) of solutes and solid-bound molecules present in that mixture; in the case of solutes, additional material functions (such as the diffusivity and solubility) must be defined within the multiphasic mixture definition.
. Each multiphasic material in a model must reference the set (or subset) of solutes and solid-bound molecules present in that mixture; in the case of solutes, additional material functions (such as the diffusivity and solubility) must be defined within the multiphasic mixture definition.
The discretization of δG and DδG needed for the finite element implementation is provided in the “Appendix”. The referential mass concentrations of solid-bound molecules are not treated as nodal variables in FEBio since these may be evaluated from simply integrating (6) with respect to time. Therefore, is stored at the integration points of each finite element. It follows that the incorporation of such solid-bound molecules produces very little computational burden, in contrast to the modeling of solutes which increases the number of nodal degrees of freedom.
An examination of (26) shows that it is necessary to evaluate the time derivatives and Dsκ̃ι/Dt. In the absence of solid growth, the first of these derivatives is normally set to zero; however, in a growth framework, based on (6)–(7), this derivative becomes
| (33) |
The time derivative of the partition coefficient is more involved, since κ̃ι is dependent not only on the solubility κ̂ι, but also the electric potential ψ whose value may evolve with the deposition or removal of neutral or charged solid-bound molecules. Using the chain rule of differentiation as well as (6),
| (34) |
The time derivatives Ds J/Dt and Dsc̃γ/Dt may be evaluated directly from the nodal variables. To evaluate the other derivatives in this expression it is convenient to rewrite κ̃ι = κ̂ιξzι, where ξ ≡ exp (−Fcψ/Rθ). Based on the state variables for κ̂ι, it follows that
| (35) |
The derivatives ∂κ̂ι/∂J, and ∂κ̂ι/∂c̃γ may be evaluated from the constitutive model selected for the solubility. The derivatives of ξ are evaluated by differentiating the electroneutrality condition (13) to produce
| (36) |
If the constitutive relation for the production rate ζ̂ is more conveniently expressed as a function of the variables (θ, F, cσ, cι ), a change of variables to the independent set (θ, F, , c̃ι) is needed to evaluate the derivatives of ζ̂ appearing in (30)–(32). Based on the relations of (16) and (25), it follows that
| (37) |
and
| (38) |
In these expressions, ∂κ̃γ/∂J and ∂κ̃γ/∂c̃ι are evaluated from (35)–(36); ∂cσ/∂J may be derived from (16).
Any number of chemical reactions may be modeled simultaneously in a given mixture. Since FEBio is written in C++, an object-oriented programming environment, a virtual base class is defined, which provides virtual functions for the evaluation of ζ̂,
ζ̂ε and ∂ζ̂/∂c̃ι, respectively. For each chemical reaction, the user specifies the stoichiometric coefficients
and
, as well as a specific constitutive relation for ζ̂ (see examples below). The class for multiphasic mixtures includes a vector of chemical reaction objects to represent all these reactions. At each iteration of the analysis, the rates
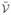 ζ̂ in (22) and νιζ for each solute in (23) are evaluated by summing their respective values over all these reactions.
ζ̂ in (22) and νιζ for each solute in (23) are evaluated by summing their respective values over all these reactions.
If the user chooses not to model all reactants and products of a reaction explicitly, the calculation of
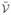 from the partial list supplied may produce unexpected results, in which case the user is provided the option to override the automatic calculation from the supplied list. Recall that
from the partial list supplied may produce unexpected results, in which case the user is provided the option to override the automatic calculation from the supplied list. Recall that
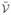 = 0 exactly if all reactants and products have the same true density
, according to (21). Therefore,
= 0 exactly if all reactants and products have the same true density
, according to (21). Therefore,
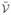 ≈ 0 is an acceptable value as a first approximation when the explicit list of reactants and products is incomplete.
≈ 0 is an acceptable value as a first approximation when the explicit list of reactants and products is incomplete.
Chemical reactions explicitly alter the values of and . Therefore, users must be aware that material behaviors that depend on these parameters will be affected by these changes. Furthermore, users have the option to define solid materials whose properties depend explicitly on , thus allowing the formulation of constitutive relations for solid remodeling.
4 Examples of chemical reactions
4.1 Law of mass action
At this juncture, any number of constitutive relations may be proposed for ζ̂; however, the most common relation used in chemical kinetics is the law of mass action. For the forward reaction in (17), this constitutive relation is given by (Prud’homme 2010)
| (39) |
The constitutive function k (θ, F, ) is known as the specific reaction rate. In classical chemical kinetics, it is only a function of θ; however, due to the presence of a solid matrix in this framework, F and are also included as state variables for this material function. This seemingly innocuous addition represents a significant advance in the unification of classical chemical kinetics with mechanobiology within the continuum mechanics literature, showing that chemical reactions may be formulated to depend explicitly on the state of strain, establishing a direct link between mechanics and chemistry.
For a forward reaction (k ≠ 0), substituting (39) into (37) produces
| (40) |
where
| (41) |
and the dependence of k on E is provided by a user-defined constitutive relation. Similarly, substituting (39) into (38) produces
| (42) |
where δγι is the Kronecker delta. This formula is valid when c̃ι ≠ 0, or else there would be no reaction according to (39) (ζ̂= 0).
For the reversible chemical reaction in (20), the constitutive relation may be given by (Prud’homme 2010)
| (43) |
where Kc = kR/k F is a function that reduces to the equilibrium constant of the reversible reaction at chemical equilibrium (when ζ̂ = 0). For this reaction the formulas of (40)–(42) may be applied similarly to ζ̂F and ζ̂R and the resulting expressions may be subtracted to produce the resultant relations for the derivatives of ζ̂.
Example 1 Reversible Receptor-Ligand Binding
Consider the classical receptor–ligand binding reaction,
| (a) |
where εr may represent a solid-bound receptor (a binding site on the tissue solid matrix), ει is the ligand, and εc is the receptor-ligand complex. Both εr and εc are bound to the solid (σ = r, c), whereas ει is a solute (ι = l). For this reaction the stoichiometric coefficients are and so that
| (b) |
4.2 Solid remodeling
4.2.1 Implicit soluble constituents
In the classic literature on solid remodeling (Cowin and Hegedus 1976; Huiskes et al. 1987; Carter et al. 1989; Weinans et al. 1992), the apparent density of the solid is allowed to evolve in response to the state of strain (and thus stress or strain energy). Solid remodeling theories propose constitutive relations for in the mass balance relation of (6) (Hegedus and Cowin 1976; Weinans et al. 1992).4 Consider the classic bone remodeling framework by Hegedus and Cowin (1976), where the rate of change of the solid density, , was expressed as a quadratic function of the infinitesimal strain tensor of the solid. This framework encompasses the subsequent model proposed by Weinans et al. (1992),
| (44) |
where Ψr is the strain energy density of the solid, ψ0 is the specific strain energy at homeostasis, and B is a material constant. This model predicates that solid mass will increase ( ) when the specific strain energy exceeds ψ0, or decrease ( ) when it drops below ψ0. In these types of models, it is assumed that cells, which mediate the remodeling process, and soluble constituents representing nutrients and waste products are implicitly available.
In their analysis, Weinans et al. assumed that bone behaved as a linear isotropic elastic material, though we may generalize that formulation to finite deformation by using a compressible neo-Hookean material function (Bonet and Wood 1997),
| (45) |
where C = FT ·F is the right Cauchy-Green tensor, ν is Poisson’s ratio, assumed constant, and EY is Young’s modulus, assumed to depend on according to a power law,
| (46) |
where c and γ are material constants (Carter and Hayes 1977).
Two essential concepts emerge from this illustrative application of solid remodeling: (a) a growth process occurs, whereby mass is added or removed in response to a mechanical signal, as given in (44)–(45); and (b) a constitutive relation is needed for the material behavior that relates the material properties to the composition, as in (46). For this constitutive model, ζ̂ is obtained by substituting (44) into (16) and (18) under the assumption that νs = 1, from which it follows that
| (47) |
and
| (48) |
where σ s is the Cauchy stress corresponding to the strain energy density given in (45). Also note that ∂ζ̂/∂c̃ι = 0.
In addition, remodeling processes may involve the reorientation of the material structure in response to mechanical signals, as described for example by Baaijens and co-workers (Driessen et al. 2003, 2005; Baaijens et al. 2010). This latter type of solid remodeling does not involve the mass balance equation of (6), though it may be formulated in a similar rate-type evolutionary relation for a structural tensor or a fiber direction in response to a specific mechanical signal. Reorientation of the material structure is not addressed further in this treatment, since the focus here is on reactions modeled in the mass balance equation.
4.2.2 Explicit soluble constituents
For some tissue systems, solid remodeling may be viewed generically as a pair of reactions whereby cells convert nutrients into solid matrix when the mechanical signal exceeds a certain threshold, or the solid matrix degrades into waste products when the signal falls below that threshold,
| (49) |
Applying the law of mass action in (39) to these two reactions produces the net solid molar supply
| (50) |
where ks for synthesis and kd for degradation depend on the mechanical signal and may alternate their on and off states. No specific constitutive model is proposed here for the dependence of ks and kd on F, since novel formulations would merit a more detailed analysis. Nevertheless, this generic remodeling reaction implies plausibly that both matrix deposition and degradation depend on the concentration of cells, that the rate of matrix formation depends on the concentration of soluble nutrients and that the rate of degradation attenuates with decreasing solid content.
Note that even in this generic form, the relation of (49) is explicitly balanced, with the mass of solutes converted to an equal mass of solid and vice versa. In FEBio, implementing this model thus requires two solutes (ι = nutrients, waste) and two solid-bound molecular species (σ = cells, solid), although the cell concentration may be assumed constant. A more explicit list of solutes may also be provided to represent various nutrients (e.g., glucose and amino acids), growth factors, or degradative enzymes.
This type of system represents one of the several possible options; alternatively, in some tissues such as bone, the cells responsible for matrix synthesis may be different from those responsible for degradation (e.g., osteoblasts and osteoclasts). In other systems, matrix degradation may proceed independently of the activity of cells embedded in that matrix. The reactions for these various systems may be similarly formulated.
5 Verifications
Since the implementation of any number of chemical reactions that can model neutral or charged reactants and products represents a major computational challenge, a number of verification problems are presented below that establish the validity of the code implementation, not just for reactions involving charged species but for other general cases encompassed by this implementation. In each case, an analytical solution is available that allows direct verification of the code; therefore, mesh convergence analyses are straightforward.
5.1 Salt dissociation
Consider the dissociation of a salt, such as NaCl, into two counter-ions dissolved in water,
| (51) |
According to the law of mass action, the reaction rate is ζ̂ = kF cNaCl − kR cNa+ cCl−. Based on the electroneutrality condition, the ion concentrations must be equal, cNa+ = cCl− ≡ c. Furthermore, we may assume that the total concentration of undissociated compound and dissociated ions is constant, cNaCl + c ≡ ct. Combining these relations with the reaction rate, recognizing that ĉ = ζ̂, and assuming homogeneous conditions, produces an ordinary nonlinear differential equation,
| (52) |
Under the initial condition c (0) = 0, the solution to this equation is given by
| (53) |
where Ka ≡ kF/kR is the dissociation constant and . At steady state, the ion concentration becomes c → ηKa/2.
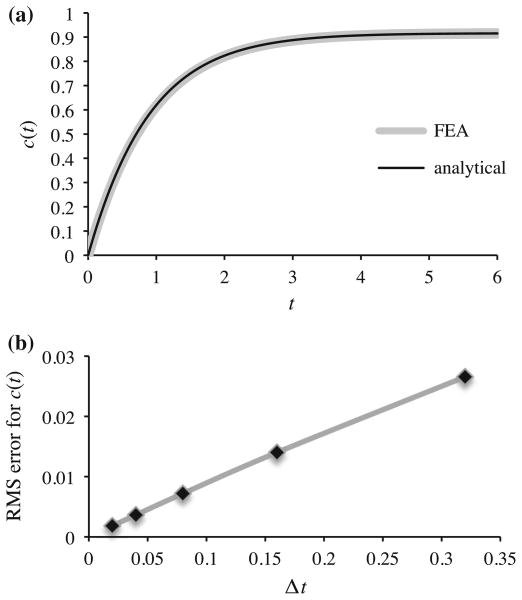
This chemical reaction was modeled in FEBio by including all three solutes appearing in (51); the reaction was explicitly balanced by ensuring that molar masses in the finite element input file satisfied MNaCl = MNa+ + MCl−. Since a homogeneous response was sought, a single brick element sufficed to perform this analysis. However, due to the absence of prescribed boundary conditions for Na+ and Cl−, it was necessary to provide a method for electrically grounding the mixture to prevent numerical ill-conditioning of the finite element analysis, as discussed in our earlier study (Ateshian et al. 2013). Thus, two additional monovalent counter-ions were added to the mixture (e.g., A+ and B−) whose initial concentrations were set to a constant c0, and boundary conditions were prescribed on one of the element faces such that c̃A+ = c̃B− = c0, implying that ψ = 0 according to (25) (when κ̂A+ = κ̂B− = 1). This scheme produced a convergent solution, verifying agreement between the finite element and analytical solutions (Fig. 1a). As expected from the unconditionally stable implicit backward Euler method for time discretization, the root-mean-square (RMS) error between the finite element results and analytical solution, evaluated over all time increments, scaled as
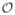 (Δt ) (Fig. 1b).
(Δt ) (Fig. 1b).
Fig. 1.
a Time-dependent dissociation of NaCl into Na+ and Cl−. The ion concentration c(t) was evaluated from a finite element analysis and from the analytical solution of (53), with ct = 1, kF = 1, and Ka = 10. b Time discretization error analysis
This analysis illustrates the modeling of a chemical reaction involving charged constituents.
5.2 Biosynthesis, binding and degradation
In their theoretical study, DiMicco and Sah (2003) examined the one-dimensional spatial distribution of synthesized cartilage matrix products under the following assumptions: (1) Cells synthesize matrix products in soluble form (ι = u), at a constant rate (2) The soluble matrix product binds to the pre-existing solid matrix (σ = b). (3) The bound product may subsequently degrade into a soluble waste product (ι = d). Using the notation of this paper, their analysis may be represented by three chemical reactions,
| (54) |
where cells and nutrients are implicit in their analysis. Applying the law of mass action in (39) to these three reactions produces ζ̂1 = k1ccellscnutrients ≡ kf, ζ̂2 = kbcu ≡ rb, and ζ̂3 = kd cb ≡ rd, where symbols kf, kb, kd, rb and rd are consistent with the notation used by those authors.5 In the first reaction, νu = 1, whereas in the second reaction, νu = −1 so that the net molar supply for the soluble matrix product according to (39) is ĉu = kf − rb. Similarly, it can be shown that ĉb = rb − rd and ĉd = rd.
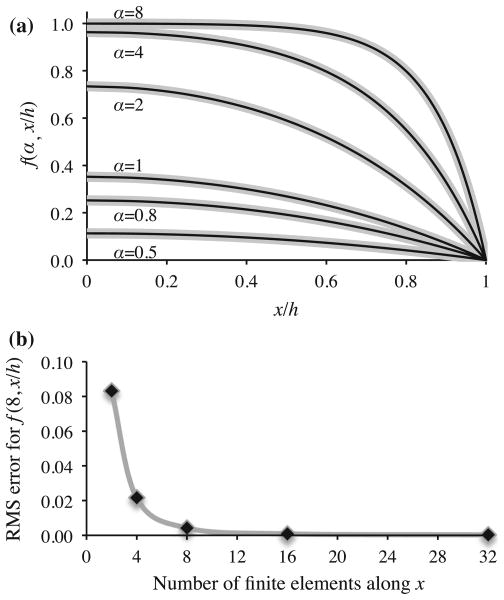
For a one-dimensional analysis in the range 0 ≤ x ≤ h, with symmetry conditions applied at x = 0 and boundary conditions cu = cd = 0 at x = h to represent a well-stirred large bath, these authors provided analytical expressions for the steady-state solution for cu(x), cb(x) and cd (x) in their Eqs. (17)–(25). A FEBio finite element analysis of this problem was reproduced by implementing the three chemical reactions in (54), using the values of h, kf, kb and kd provided in their Table II, and varying the diffusivities Du of the soluble matrix product and Dd of the degraded product in the ranges provided in that same table. Since their approach did not accommodate changes in tissue volume with matrix accumulation or degradation, 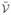 = 0 was assumed for all three reactions. A neo-Hookean model was adopted for the solid matrix, using a value for Young’s modulus that far exceeded the osmotic pressure gradients produced by gradients in solute concentrations, to ensure negligible solid matrix deformation. A comparison of the steady-state FEBio results to the analytical solution of DiMicco and Sah (2003) is presented in Fig. 2a, for different values of the non-dimensional parameter
, verifying that these two approaches agree. The mesh employed for this analysis had 32 elements, with a mesh bias along x such that the width of consecutive elements from 0 to h decreased by a factor of 0.87. Using this biasing scheme, varying the number of elements confirmed mesh convergence for this analysis (Fig. 2b).
= 0 was assumed for all three reactions. A neo-Hookean model was adopted for the solid matrix, using a value for Young’s modulus that far exceeded the osmotic pressure gradients produced by gradients in solute concentrations, to ensure negligible solid matrix deformation. A comparison of the steady-state FEBio results to the analytical solution of DiMicco and Sah (2003) is presented in Fig. 2a, for different values of the non-dimensional parameter
, verifying that these two approaches agree. The mesh employed for this analysis had 32 elements, with a mesh bias along x such that the width of consecutive elements from 0 to h decreased by a factor of 0.87. Using this biasing scheme, varying the number of elements confirmed mesh convergence for this analysis (Fig. 2b).
Fig. 2.
a Comparison of finite element results (thick gray curves) against analytical solution (thin black curves) for the cartilage matrix biosynthesis, binding and degradation study by DiMicco and Sah (2003). The function f (α, x/h) represents the normalized spatial distribution of the soluble matrix product concentration, where cu = kf f/kb, and bound matrix concentration, where cb = kf f/kd, over the range 0 ≤ x ≤ h, for different values of the non-dimensional parameter α (see text). b Mesh convergence results for α = 8
5.3 Solid remodeling
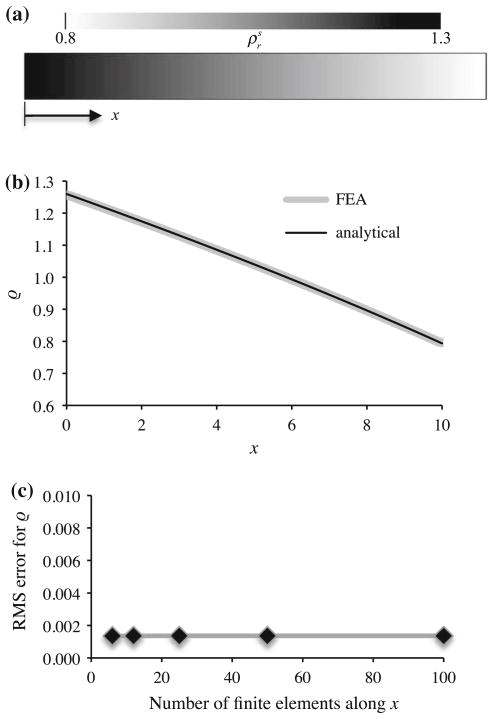
A closed-form solution may be obtained for a solid remodeling analysis based on (44)–(47), for a 1D problem under infinitesimal strains. Consider a prismatic bar whose domain is 0 ≤ x ≤ h, constrained at x = 0, and subjected to a normal traction σ0 at x = h and a uniform body force per volume f0 along its length. The axial stress for this bar is given by σ = σ0 + f0 (h − x). Under infinitesimal strains, the strain energy density is Ψr = σ2/2EY. Substituting (46) into this expression and evaluating (44) in the limit of the steady-state remodeling response ( ) produces the steady-state solid apparent density,
| (55) |
A comparison of this analytical solution with the FEBio steady-state response is presented in Fig. 3, for a representative set of values for h, σ0, f0, c, γ and ψ0, verifying agreement between the finite element and analytical solutions. A mesh convergence analysis demonstrates that the accuracy of the finite element solution is independent of the number of elements in the uniform mesh (Fig. 3c), consistent with the fact that σ is prescribed and varies linearly with position, such that the average force acting on each element is equally accurate for any discretization. The rate of convergence to the steady-state distribution is also unaffected by the mesh size. The solution demonstrates that the density is highest at the fixed end (x = 0), where the stress magnitude is greatest, and decreases monotonically toward the free end (x = h), where |σ| is smallest.
Fig. 3.
Spatial distribution of the solid apparent density at steady state, in a prismatic bar of length h = 10, subjected to an axial traction σ0 = −10 and body force per volume f0 = −1, over the range 0 ≤ x ≤ h, with c = 104, γ = 2, and ψ0 = 0.01. The finite element solution is obtained using B = 1 in (44), with initial condition at t = 0, and with the analysis performed until t = 200. a Prismatic bar geometry and spatial distribution of at steady state. b Comparison of finite element analysis and analytical solution of (55) over the entire range of x. c Mesh convergence results
5.4 Interstitial solid growth
Consider a 1D analysis of interstitial tissue growth modeled by the reaction 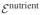 →
→ 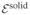 , such that
, such that 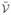 =
= 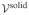 −
− 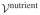 ≠ 0. A closed-form solution may be obtained if the growth process is limited to the range of infinitesimal strains and the nutrient concentration is assumed to change negligibly over the time frame of the analysis so that the only remaining unknown is the solid matrix displacement u (x, t), in the range 0 ≤ x ≤ h.
≠ 0. A closed-form solution may be obtained if the growth process is limited to the range of infinitesimal strains and the nutrient concentration is assumed to change negligibly over the time frame of the analysis so that the only remaining unknown is the solid matrix displacement u (x, t), in the range 0 ≤ x ≤ h.
For a 1D analysis, the axial normal stress is given by σ = −p + HA∂u/∂x, where HA is the aggregate modulus of the solid matrix (assumed to change negligibly with growth) and the relative fluid flux is w = −k∂p/∂x according to Darcy’s law, where k is the hydraulic permeability (also assumed constant). The mixture momentum equation reduces to ∂σ/∂x = 0; the mixture mass balance equation in (22) becomes
| (56) |
where
under infinitesimal strains and ζ̂
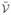 is nearly constant according to the law of mass action, since the nutrient concentration changes negligibly. Given the boundary conditions of zero displacement and fluid flux at x = 0, and zero prescribed stress and fluid pressure at x = h, this analysis reduces to solving the partial differential equation
is nearly constant according to the law of mass action, since the nutrient concentration changes negligibly. Given the boundary conditions of zero displacement and fluid flux at x = 0, and zero prescribed stress and fluid pressure at x = h, this analysis reduces to solving the partial differential equation
| (57) |
subject to
| (58) |
The solution is thus given by
| (59) |
where τ = h2/HAk, from which p = HA∂u/∂x may be evaluated.
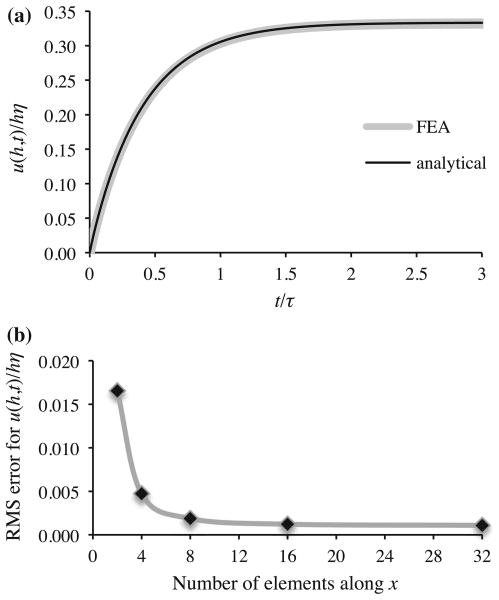
This analysis was implemented in FEBio using a chemical reaction with an implicit nutrient and a prescribed positive constant value for 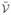 . A comparison of the surface displacement (evaluated from (59) at x = h) between the analytical and finite element solutions shows agreement, verifying code accuracy for the inclusion of the source term in the mass balance relation (22) for the mixture. A physical interpretation of this result is that continuous interstitial solid deposition decreases the solid matrix porosity (φw ≈ 1 − φs) and concomitantly pressurizes the interstitial fluid as it squeezes it out of the decreasing pore volume. The progressive interstitial pressurization causes the tissue to swell initially as shown in Fig. 4a, until the fluid pressure achieves a steady-state value that drives fluid out at the same rate as the pore volume decreases, producing a steady-state swelling response (
). The analytical solution remains valid only as long as φs changes negligibly, though the FEBio solution is able to accommodate finite changes in φs. The mesh employed for this analysis had 32 elements, with a mesh bias along x such that the width of consecutive elements from 0 to h decreased by a factor of 0.87. Using this biasing scheme, varying the number of elements confirmed mesh convergence for this analysis (Fig. 4b).
. A comparison of the surface displacement (evaluated from (59) at x = h) between the analytical and finite element solutions shows agreement, verifying code accuracy for the inclusion of the source term in the mass balance relation (22) for the mixture. A physical interpretation of this result is that continuous interstitial solid deposition decreases the solid matrix porosity (φw ≈ 1 − φs) and concomitantly pressurizes the interstitial fluid as it squeezes it out of the decreasing pore volume. The progressive interstitial pressurization causes the tissue to swell initially as shown in Fig. 4a, until the fluid pressure achieves a steady-state value that drives fluid out at the same rate as the pore volume decreases, producing a steady-state swelling response (
). The analytical solution remains valid only as long as φs changes negligibly, though the FEBio solution is able to accommodate finite changes in φs. The mesh employed for this analysis had 32 elements, with a mesh bias along x such that the width of consecutive elements from 0 to h decreased by a factor of 0.87. Using this biasing scheme, varying the number of elements confirmed mesh convergence for this analysis (Fig. 4b).
Fig. 4.
a Surface displacement u (h, t)/hξ for 1D analysis of interstitial solid growth. The analytical solution is based on (59), with . The finite element solution was obtained using h = 1, HA = 1, k = 1, and . b Mesh convergence results
6 Illustration
In this section, chemical reactions are used to illustrate cartilage tissue engineering when accompanied by significant construct dimensional changes due to synthesis of charged proteoglycans. To model this process, consider a mixture consisting of a porous agarose hydrogel (modeled as a neo-Hookean porous solid with Young’s modulus set to 12 kPa and Poisson’s ratio set to zero), seeded with chondrocytes. The culture bath contains dissociated NaCl at 145mM and MgSO4 at 5mM, as well as glucose at 25mM. These bath conditions are assumed to remain constant and are prescribed as boundary conditions for the dissociated ions.
It is assumed that chondrocytes consume glucose to maintain their normal metabolic functions, 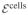 +
+ 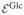 →
→ 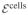 +
+  , a forward reaction modeled by the law of mass action with k = 4 × 10−5 s−1; cells (whose concentration is assumed constant) and waste products are treated as implicit mixture constituents in the finite element model, where as glucose is modeled as a solute. Chondrocytes also consume glucose and sulfate to synthesize the chondroitin sulfate (CS) of proteoglycans according to
, a forward reaction modeled by the law of mass action with k = 1×10−7mM−1 s−1; note that this reaction explicitly satisfies the electroneutrality condition by exchanging the charges of soluble sulfate with CS. It is assumed for simplicity that the synthesized CS is immediately bound to the solid matrix. Also for simplicity, all solute diffusivities are set to 5×10−4 mm2/s within the mixture and 6×10−4 mm2/s in free solution, whereas the hydraulic permeability of the porous hydrogel is set to 10−7 mm4/μN−1 s−1.
, a forward reaction modeled by the law of mass action with k = 4 × 10−5 s−1; cells (whose concentration is assumed constant) and waste products are treated as implicit mixture constituents in the finite element model, where as glucose is modeled as a solute. Chondrocytes also consume glucose and sulfate to synthesize the chondroitin sulfate (CS) of proteoglycans according to
, a forward reaction modeled by the law of mass action with k = 1×10−7mM−1 s−1; note that this reaction explicitly satisfies the electroneutrality condition by exchanging the charges of soluble sulfate with CS. It is assumed for simplicity that the synthesized CS is immediately bound to the solid matrix. Also for simplicity, all solute diffusivities are set to 5×10−4 mm2/s within the mixture and 6×10−4 mm2/s in free solution, whereas the hydraulic permeability of the porous hydrogel is set to 10−7 mm4/μN−1 s−1.
The synthesis of CS increases the tissue fixed charge density magnitude according to (8), which induces changes in the interstitial concentrations of Na+, Cl−, Mg2+ and due to the enforcement of electroneutrality, concomitantly increasing the interstitial osmotic pressure. An axisymmetric analysis of a cylindrical construct (initial radius of 5mm and thickness of 2.2mm) was performed, using a uniform mesh with 10 elements along the radial direction × 4 elements through the thickness. The construct was assumed to rest on the impermeable bottom of a culture dish. The analysis spanned a culture duration of 30 days, using time increments of 10 h.
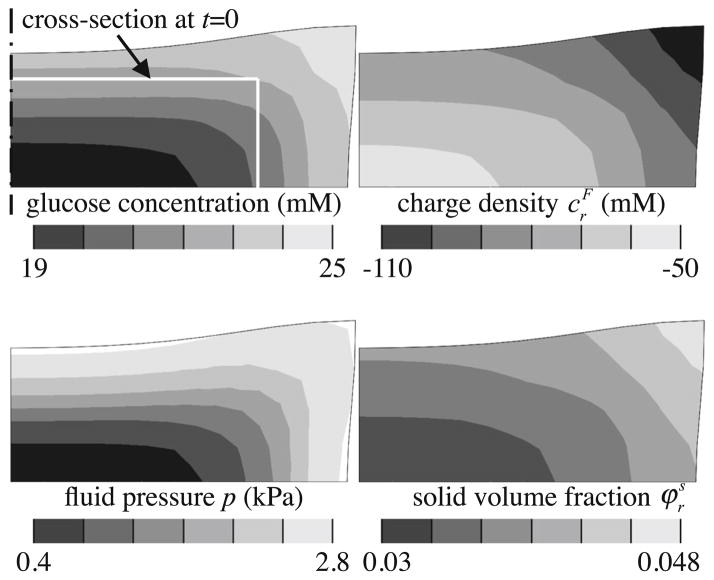
Glucose consumption by cells via both modeled reactions resulted in an inhomogeneous distribution, with decreasing content toward the bottom and center of the construct (Fig. 5). This inhomogeneous glucose availability produced a similarly inhomogeneous CS deposition, with greatest synthesis near the construct periphery as seen in the contour map for . The swelling produced by the inhomogeneous Donnan osmotic pressure p, resulting from the negatively charged CS, altered the construct shape as shown in the figure, with local swelling ratios ranging from 2.8 at the bottom center to 7.8 at the top radial edge, and tissue dimensions increasing to a final radius of 8.4mm and thickness of 4.0mm. The deposition of CS also increased the referential solid volume fraction from a uniform value of 0.02 at day 0 (agarose volume fraction) to values shown in the figure.
Fig. 5.
Axisymmetric analysis of engineered cartilage growth with glucose consumption and synthesis of negatively charged CS. The tissue construct, which is initially cylindrical, rests on the impermeable bottom of the culture dish. This cross-sectional view shows an outline of the construct and contour maps of the glucose concentration, , p and at day 30
7 Discussion
This study has presented the analysis and computational implementation of chemical reactions in a mixture framework involving charged reactants and products that include solutes and solid-bound molecules in a porous hydrated deformable solid matrix. Any number of chemical reactions may be modeled in a mixture, with each reaction described by user-defined constitutive relations. The theory of reactive mixtures naturally lends itself to incorporating the effect of mechanics on chemical reactions by allowing the molar production rate ζ̂ to depend on the state of strain (and thus the state of stress or the strain energy density). This direct link between mechanics and chemistry is shown explicitly in this study for the first time and is further characterized by the need to formulate the tensorial tangent ζ̂ε of this production rate with respect to the strain tensor. The novel computational implementation of this framework demonstrates its applicability in practice; its availability in the public domain addresses a need not met by other commercial or open-source products.
The modeling of charged species in the chemical reactions also represents a novel contribution that exposed challenges not necessarily anticipated in the prior literature. Consistent with the triphasic theory of Lai et al. (1991) and subsequent models in the related literature (Huyghe and Janssen 1997; Gu et al. 1998), this study also assumed that electroneutrality is satisfied at every point in the continuum. The electroneutrality constraint is a modeling assumption akin to the assumption of incompressibility: It is an idealized constraint that approximates the behavior of real materials for the purpose of introducing some level of simplification. In the case of electroneutrality it follows that the mixture cannot allow charge accumulation, as would otherwise occur in a capacitor. The resulting simplification is that the net electric charge is no longer variable so that the electric current density becomes divergence-free. Enforcing electroneutrality in a chemical reaction is achieved by balancing the charges of reactants and products according to their net stoichiometric coefficients. Violating this requirement would otherwise produce spurious electric currents that would fail to satisfy the divergence-free condition.
Another novel feature of this implementation is that it allows modeling of solid-bound molecules that are explicitly involved in chemical reactions, in addition to the standard modeling of solutes as reactants and products. This feature makes it possible to model the growth mechanics of the solid matrix of a tissue or cell by allowing solid mass to be added or removed explicitly in response to chemical reactions. The reactive exchange of mass with the solid matrix leads to the explicit evolution of the referential solid volume fraction and the referential fixed charge density , which must be taken into account in the computational implementation to avoid spurious electric currents. The temporal evolution of makes it possible to model growth mechanics driven by (a) osmotic effects where the change in alters the interstitial osmolarity; (b) osmotic effects where the change in alters the Donnan osmotic pressure; and (c) changes in the molar volume of the constituents of the solid matrix as a result of mass exchanges with soluble species. Furthermore, consistent with prior solid remodeling theories, alterations in can be tied to alterations in solid matrix material properties by providing constitutive relations with explicit dependencies between properties and composition.
In the model of Fig. 5, cells were not modeled explicitly in the mesh; instead, cellular synthesis was assumed to occur throughout the continuum representation of the tissue, with matrix deposition occurring at every point. An alternative approach might be to model cells explicitly as domains within the finite element mesh (using either a single element or a cluster of elements) interspersed in a mesh of elements representing the extracellular matrix, as reported in prior studies (Guilak and Mow 2000; Sengers et al. 2004b; Ateshian et al. 2007). In that case, chemical reactions may be segregated to specific extracellular and intracellular compartments, and even within membrane structures.
Several problems for which analytical solutions are available were used to verify the finite element code. These problems were selected to test various features of the implementation, including the modeling of multiple reactions with explicit or implicit reactants and products, solid remodeling in response to a mechanical signal, interstitial solid growth producing a rate of change of the pore volume, and a reaction involving charged solutes. A cartilage tissue engineering analysis was also presented to illustrate how the synthesis of charged molecular species that bind to the solid matrix may induce finite dimensional changes due to osmotic swelling.
This theoretical framework assumes that each of the mixture constituents is intrinsically incompressible, even though the mixture (whose boundaries are defined on the solid matrix) may gain or lose volume due to fluid exchanges with its environment. Intrinsic incompressibility is an idealization of the behavior of real materials which is adopted primarily to simplify the model formulation. Without this assumption, it becomes necessary to distinguish between the intrinsic compressibility of the constituents and the collapsibility of the pores of the solid matrix, which together combine to produce the compressibility of the mixture. Experimentally, the validity of this modeling assumption may be tested by exposing the mixture to a physiologically relevant hydrostatic pressure and examining its volumetric change. These validations have been reported for articular cartilage by Bachrach et al. (1998) and osteoblast-like cells by Wilkes and Athanasiou (1996). It may be reasonable to assume that most biological tissues and cells, which share similar constituents, can be adequately modeled under this modeling assumption.
Incorporating chemical reactions in a modeling framework for biological tissues facilitates investigations of mechanobiology by providing a modeling environment that can account for a broader range of mechanisms involved in biology and physiology. This framework may be particularly beneficial to optimizing tissue engineering culture systems by examining the influence of nutrient availability on the evolution of inhomogeneous tissue composition and mechanical properties, the evolution of construct dimensions with growth, the influence of solute and solid matrix electric charge on the transport of cytokines, the influence of binding kinetics on transport, the influence of loading on binding kinetics, and the differential growth response to dynamically loaded versus free-swelling culture conditions. Future developments of the code may include modeling chemical reactions that drive molecular motors to produce phenomena such as active solute transport or actin–myosin contraction.
Acknowledgments
Research reported in this publication was supported by the National Institute of General Medical Sciences (Award Number R01GM083925) and the National Institute of Arthritis and Musculoskeletal and Skin Diseases (Award Number R01AR060361) of the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors would also like to acknowledge that Fig. 6 reports experimental results from a study led by Mr. Alexander D. Cigan, with the assistance of Dr. Michael B. Albro and Professor Clark T. Hung.
Fig. 6.
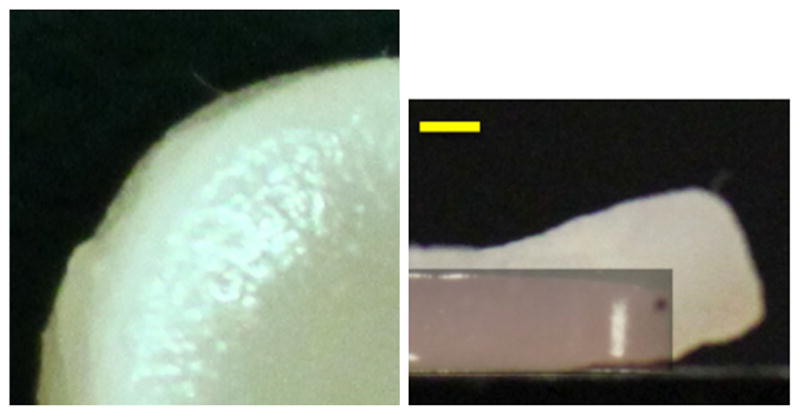
Cartilage construct engineered from chondrocyte-seeded agarose gels. Side view of construct at right shows an overlay of a day 0 construct over the image of the day 53 construct. The increased bulging and construct opacity at the outer periphery is qualitatively consistent with the shape and matrix deposition distribution of the finite element results in Fig. 5 (Scale bar 1mm)
Appendix
Virtual and nodal variables are interpolated as
| (60) |
where Na are the interpolation shape functions. Then, δG in (27) may be discretized as
| (61) |
where
| (62) |
Similarly, the linearization of δG along Δu in (29) may be discretized as
| (63) |
where
| (64) |
and the linearization along Δ c̃ι in (32) becomes
| (65) |
where
| (66) |
Given that δva, δ p̃a and δ c̃a are arbitrary, the contribution from δG to the discretized form of (28) may be summarized in matrix form as
| (67) |
Footnotes
However, the porous solid matrix may experience changes in volume as a result of fluid exchanges with the pore space.
Indeed, assuming that is the same for all α would nullify the right-hand-side of (14) based on (2).
Under ideal physico-chemical conditions it may be assumed that Φ = 1 and κ̂ι = 1.
In this section, it is assumed that there is only a single solid constituent, denoted by s, for consistency with the classical literature.
DiMicco and Sah proposed that , where represents a subpopulation of bound matrix products not allowed to degrade. This relation is a commonly adopted deviation from the law of mass action that may be implemented as an alternative constitutive relation in FEBio. For simplicity, however, is assumed here.
Contributor Information
Gerard A. Ateshian, Email: ateshian@columbia.edu, Departments of Mechanical Engineering and Biomedical Engineering, Columbia University, New York, NY 10027, USA
Robert J. Nims, Departments of Mechanical Engineering and Biomedical Engineering, Columbia University, New York, NY 10027, USA
Steve Maas, Department of Bioengineering, University of Utah, Salt Lake City, UT 84112, USA.
Jeffrey A. Weiss, Department of Bioengineering, University of Utah, Salt Lake City, UT 84112, USA
References
- Albro MB, Nims RJ, Cigan AD, Yeroushalmi KJ, Alliston T, Hung CT, Ateshian GA. Accumulation of exogenous activated tgf-β in the superficial zone of articular cartilage. Biophys J. 2013;104(8):1794–1804. doi: 10.1016/j.bpj.2013.02.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA. On the theory of reactive mixtures for modeling biological growth. Biomech Model Mechanobiol. 2007;6(6):423–445. doi: 10.1007/s10237-006-0070-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA. The role of mass balance equations in growth mechanics illustrated in surface and volume dissolutions. J Biomech Eng. 2011;133(1):011010. doi: 10.1115/1.4003133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Ricken T. Multigenerational interstitial growth of biological tissues. Biomech Model Mechanobiol. 2010;9(6):689–702. doi: 10.1007/s10237-010-0205-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Weiss JA. Finite element modeling of solutes in hydrated deformable biological tissues. Springer; Berlin: 2013. Computer models in biomechanics. [Google Scholar]
- Ateshian GA, Costa KD, Hung CT. A theoretical analysis of water transport through chondrocytes. Biomech Model Mechanobiol. 2007;6(1–2):91–101. doi: 10.1007/s10237-006-0039-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Costa KD, Azeloglu EU, Morrison rB, Hung CT. Continuum modeling of biological tissue growth by cell division, and alteration of intracellular osmolytes and extracellular fixed charge density. J Biomech Eng. 2009;131(10):101001. doi: 10.1115/1.3192138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Albro MB, Maas S, Weiss JA. Finite element implementation of mechanochemical phenomena in neutral deformable porous media under finite deformation. J Biomech Eng. 2011;133(8):081005. doi: 10.1115/1.4004810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Maas S, Weiss JA. Multiphasic finite element framework for modeling hydrated mixtures with multiple neutral and charged solutes. J Biomech Eng. 2013;135(11):111001. doi: 10.1115/1.4024823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baaijens F, Bouten C, Driessen N. Modeling collagen remodeling. J Biomech. 2010;43(1):166–175. doi: 10.1016/j.jbiomech.2009.09.022. [DOI] [PubMed] [Google Scholar]
- Bachrach NM, Mow VC, Guilak F. Incompressibility of the solid matrix of articular cartilage under high hydrostatic pressures. J Biomech. 1998;31(5):445–451. doi: 10.1016/s0021-9290(98)00035-9. [DOI] [PubMed] [Google Scholar]
- Bonet J, Wood RD. Nonlinear continuum mechanics for finite element analysis. Cambridge University Press; Cambridge: 1997. http://www.loc.gov/catdir/toc/cam023/97011366.html. [Google Scholar]
- Bowen R. Theory of mixtures, continuum physics. Vol. 3. Academic Press; New York: 1976. [Google Scholar]
- Bowen RM. Thermochemistry of reacting materials. J Chem Phys. 1968;49(4):1625–1637. [Google Scholar]
- Carter DR, Hayes WC. The compressive behavior of bone as a two-phase porous structure. J Bone Joint Surg Am. 1977;59(7):954–962. [PubMed] [Google Scholar]
- Carter DR, Fyhrie DP, Whalen RT. Trabecular bone density and loading history: regulation of connective tissue biology by mechanical energy. J Biomech. 1987;20(8):785–794. doi: 10.1016/0021-9290(87)90058-3. [DOI] [PubMed] [Google Scholar]
- Carter DR, Orr TE, Fyhrie DP. Relationships between loading history and femoral cancellous bone architecture. J Biomech. 1989;22(3):231–244. doi: 10.1016/0021-9290(89)90091-2. [DOI] [PubMed] [Google Scholar]
- Cowin S, Hegedus D. Bone remodeling I: theory of adaptive elasticity. J Elasticity. 1976;6(3):313–326. [Google Scholar]
- DiMicco M, Sah R. Dependence of cartilage matrix composition on biosynthesis, diffusion, and reaction. Transp Porous Media. 2003;50(1–2):57–73. doi: 10.1023/A:1020677829069. [DOI] [Google Scholar]
- Driessen NJB, Peters GWM, Huyghe JM, Bouten CVC, Baaijens FPT. Remodelling of continuously distributed collagen fibres in soft connective tissues. J Biomech. 2003;36(8):1151–1158. doi: 10.1016/s0021-9290(03)00082-4. [DOI] [PubMed] [Google Scholar]
- Driessen NJB, Bouten CVC, Baaijens FPT. Improved prediction of the collagen fiber architecture in the aortic heart valve. J Biomech Eng. 2005;127(2):329–336. doi: 10.1115/1.1865187. [DOI] [PubMed] [Google Scholar]
- Eringen A, Ingram J. Continuum theory of chemically reacting media-1. Int J Eng Sci. 1965;3:197–212. [Google Scholar]
- Garcia AM, Szasz N, Trippel SB, Morales TI, Grodzinsky AJ, Frank EH. Transport and binding of insulin-like growth factor I through articular cartilage. Arch Biochem Biophys. 2003;415(1):69–79. doi: 10.1016/s0003-9861(03)00215-7. [DOI] [PubMed] [Google Scholar]
- Garikipati K, Arruda E, Grosh K, Narayanan H, Calve S. A continuum treatment of growth in biological tissue: the coupling of mass transport and mechanics. J Mech Phys Solids. 2004;52(7):1595–1625. [Google Scholar]
- Gu WY, Lai WM, Mow VC. A mixture theory for charged-hydrated soft tissues containing multi-electrolytes: passive transport and swelling behaviors. J Biomech Eng. 1998;120(2):169–180. doi: 10.1115/1.2798299. [DOI] [PubMed] [Google Scholar]
- Guilak F, Mow VC. The mechanical environment of the chondrocyte: a biphasic finite element model of cell-matrix interactions in articular cartilage. J Biomech. 2000;33(12):1663–1673. [PubMed] [Google Scholar]
- Hegedus D, Cowin S. Bone remodeling ii: small strain adaptive elasticity. J Elast. 1976;6(4):337–352. [Google Scholar]
- Hsu FH. The influences of mechanical loads on the form of a growing elastic body. J Biomech. 1968;1(4):303–311. doi: 10.1016/0021-9290(68)90024-9. [DOI] [PubMed] [Google Scholar]
- Huiskes R, Weinans H, Grootenboer HJ, Dalstra M, Fudala B, Slooff TJ. Adaptive bone-remodeling theory applied to prosthetic-design analysis. J Biomech. 1987;20(11–12):1135–1150. doi: 10.1016/0021-9290(87)90030-3. [DOI] [PubMed] [Google Scholar]
- Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Math Model Meth Appl Sci. 2002;12:407–430. doi: 10.1002/zamm.201700302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huyghe JM, Janssen JD. Quadriphasic mechanics of swelling incompressible porous media. Int J Eng Sci. 1997;35(8):793–802. doi: 10.1016/S0020-7225(96)00119-X. [DOI] [Google Scholar]
- Lai WM, Hou JS, Mow VC. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng. 1991;113(3):245–258. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]
- Maas SA, Ellis BJ, Ateshian GA, Weiss JA. Febio: finite elements for biomechanics. J Biomech Eng. 2012;134(1):011005. doi: 10.1115/1.4005694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin I, Obradovic B, Freed LE, Vunjak-Novakovic G. Method for quantitative analysis of glycosaminoglycan distribution in cultured natural and engineered cartilage. Ann Biomed Eng. 1999;27(5):656–662. doi: 10.1114/1.205. [DOI] [PubMed] [Google Scholar]
- Mauck RL, Hung CT, Ateshian GA. Modeling of neutral solute transport in a dynamically loaded porous permeable gel: implications for articular cartilage biosynthesis and tissue engineering. J Biomech Eng. 2003;125(5):602–614. doi: 10.1115/1.1611512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mullender MG, Huiskes R, Weinans H. A physiological approach to the simulation of bone remodeling as a self-organizational control process. J Biomech. 1994;27(11):1389–1394. doi: 10.1016/0021-9290(94)90049-3. [DOI] [PubMed] [Google Scholar]
- Myers K, Ateshian GA. Interstitial growth and remodeling of biological tissues: tissue composition as state variables. J Mech Behav Biomed Mater. 2013 doi: 10.1016/j.jmbbm.2013.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obradovic B, Meldon JH, Freed LE, Vunjak-Novakovic G. Glycosaminoglycan deposition in engineered cartilage: experiments and mathematical model. AIChE J. 2000;46(9):1860–1871. doi: 10.1002/aic.690460914. [DOI] [Google Scholar]
- Prud’homme R. Flows of reactive fluids, fluid mechanics and its applications. Vol. 94. Springer; New York: 2010. [Google Scholar]
- Radisic M, Deen W, Langer R, Vunjak-Novakovic G. Mathematical model of oxygen distribution in engineered cardiac tissue with parallel channel array perfused with culture medium containing oxygen carriers. Am J Physiol Heart Circ Physiol. 2005;288(3):H1278–H1289. doi: 10.1152/ajpheart.00787.2004. [DOI] [PubMed] [Google Scholar]
- Sengers BG, Oomens CW, Baaijens FP. An integrated finite-element approach to mechanics, transport and biosynthesis in tissue engineering. J Biomech Eng. 2004a;126(1):82–91. doi: 10.1115/1.1645526. [DOI] [PubMed] [Google Scholar]
- Sengers BG, Van Donkelaar CC, Oomens CWJ, Baaijens FPT. The local matrix distribution and the functional development of tissue engineered cartilage, a finite element study. Ann Biomed Eng. 2004b;32(12):1718–1727. doi: 10.1007/s10439-004-7824-3. [DOI] [PubMed] [Google Scholar]
- Sengers BG, van Donkelaar CC, Oomens CWJ, Baaijens FPT. Computational study of culture conditions and nutrient supply in cartilage tissue engineering. Biotechnol Prog. 2005;21(4):1252–1261. doi: 10.1021/bp0500157. [DOI] [PubMed] [Google Scholar]
- Sun DN, Gu WY, Guo XE, Lai WM, Mow VC. A mixed finite element formulation of triphasic mechano-electrochemical theory for charged, hydrated biological soft tissues. Int J Numer Meth Eng. 1999;45(10):1375–1402. [Google Scholar]
- Truesdell C, Toupin R. The classical field theories, Handbuch der physik. III/1. Springer; Heidelberg: 1960. [Google Scholar]
- van Loon R, Huyghe JM, Wijlaars MW, Baaijens FPT. 3d fe implementation of an incompressible quadriphasic mixture model. Int J Numer Meth Eng. 2003;57(9):1243–1258. [Google Scholar]
- Weinans H, Huiskes R, Grootenboer HJ. The behavior of adaptive bone-remodeling simulation models. J Biomech. 1992;25(12):1425–1441. doi: 10.1016/0021-9290(92)90056-7. [DOI] [PubMed] [Google Scholar]
- Wilkes RP, Athanasiou KA. The intrinsic incompressibility of osteoblast-like cells. Tissue Eng. 1996;2(3):167–181. doi: 10.1089/ten.1996.2.167. [DOI] [PubMed] [Google Scholar]
- Yao H, Gu WY. Three-dimensional inhomogeneous triphasic finite-element analysis of physical signals and solute transport in human intervertebral disc under axial compression. J Biomech. 2007;40(9):2071–2077. doi: 10.1016/j.jbiomech.2006.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]