The cortical angiome: an interconnected vascular network with noncolumnar patterns of blood flow

Abstract

What is the nature of the vascular architecture in the cortex that allows the brain to meet the energy demands of neuronal computations? We used high-throughput histology to reconstruct the complete angioarchitecture and the positions of all neuronal somata of multiple cubic millimeter regions of vibrissa primary sensory cortex in mouse. Vascular networks were derived from the reconstruction. In contrast with the standard model of cortical columns that are tightly linked with the vascular network, graph-theoretical analyses revealed that the subsurface microvasculature formed interconnected loops with a topology that was invariant to the position and boundary of columns. Furthermore, the calculated patterns of blood flow in the networks were unrelated to location of columns. Rather, blood sourced by penetrating arterioles was effectively drained by the penetrating venules to limit lateral perfusion. This analysis provides the underpinning to understand functional imaging and the effect of penetrating vessels strokes on brain viability.

Neuronal computation in the mammalian brain is energetically costly, and the brain has limited reserves of energy^1,2. A solution to this dilemma calls for a vascular system that functions as a reliable, pervasive supply chain. With regard to the cortical mantle, this system begins with the great cerebral arteries that emanate from the circle of Willis and source a planar network of highly interconnected pial arterioles that span the surface of the mantle³. The inherent multitude of paths for flow to any given branch allows the surface network to distribute blood in a manner that is relatively insensitive to blockages in one or a few of the branches of the network^4,5. Furthermore, the distribution can be dynamically shifted toward regions of heightened electrical activity and concurrent metabolic load^6,7. The surface network is connected to an underlying, three-dimensional network of microvessels by radially directed penetrating arterioles. The micro-vascular network is drained by penetrating venules that return blood to the surface of cortex, where it empties into the central sinus to complete the supply chain. Although the microvascular network brokers the bulk of the exchange of metabolites and gases between brain cells and the blood stream, the morphometry of microvessels and the topology of this network remain largely uncharted. Yet this information is fundamental to an understanding of neurovascular coupling in normal and diseased states^8–10 and to the interpretation of functional brain images^11,12.

What ideas guide the discussion of brain microvasculature? The concept of the neurovascular module emerged from functional imaging studies, where sensory input that activates a region of cortex leads to a concomitant increase in the flow of blood in an overlapping volume¹³. In the case of the rodent vibrissa system, neuronal activity in vibrissa primary sensory (vS1) cortex forms an array of clusters, denoted as cortical columns or barrels, in which each column receives afferent input primarily from a specific vibrissa on the face of the animal¹⁴. Thus, cortical columns and neurovascular modules might be expected to be synonymous in vS1 cortex. In fact, it has been suggested that neurovascular modules may be arranged as largely autonomous modules, each sourced by one or more penetrating arterioles and drained by one or more penetrating venules¹⁵. Support for this view comes from experiments in which flow through an individual penetrating arteriole is blocked^5,16,17, leading to the cessation of blood flow in a roughly cylindrical region of surrounding microvessels¹⁸.

We challenged the notion of a neurovascular module. We exploited the overarching columnar features of vS1 cortex and used large-scale automated histology to acquire and vectorize data from tissue in which all vessels and all neuronal and non-neuronal nuclei were labeled^19,20. We asked the following questions. What is the form of the short-range interconnectivity among microvessels? Can the loci of cortical columns be predicted from the topology of the cortical vasculature, the calculated patterns of flow in the vessels or the spatial location of penetrating vessels that source and sink blood? Is the spatial dependence of functional signals, based on changes in blood oxygenation, consistent with the observed vascular anatomy? Are calculated regions of flow predictive of the pathologies observed with microinfarctions to the vascular supply? If so, how do these calculated regions compare with those measured in response to single vessel occlusions^16,17,21,22?

RESULTS

Two forms of data sets were obtained. The first were sets that encompass 12–46 cortical columns, span the full depth of vS1 cortex and extend into the white matter (n = 4 mice, 2–3 mm³ in volume; Fig. 1a–c). All vessels were labeled with a fluorescent gel under conditions that preserved the size of the vessels, all nuclei were labeled with a DNA stain and neuronal nuclei were further labeled with antibody to NeuN, a pan-neuronal marker (Online Methods). The second form of data set encompasses all of vS1 cortex as well as the representation of microvibrissa, typically 60 to 70 columns, and spans from the pia to approximately layer 5a of vS1 cortex (n = 4 mice; Fig. 1d). We used intrinsic optical imaging^23,24 through a transcranial window¹⁸ to map the responses for 20–30 vibrissa before histology (Online Methods). All vessels and all nuclei were labeled as above, and we imaged the full extent of vS1 cortex, albeit over a limited depth. Additional mice (n = 4) provided auxillary data.

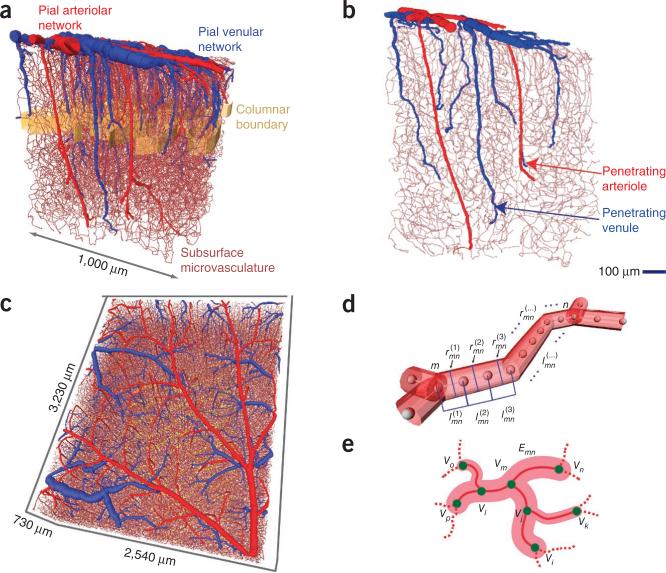
Figure 1.

Examples of the vectorized data sets. (a,b) Example of data obtained throughout the full depth of cortex and extending into the white matter. Surface and penetrating arterioles are colored red, venules blue and the borders of cortical columns are denoted by a golden band. A selected slice from this data set is shown to illustrate the extent of penetrating vessels (b). (c) Example of data obtained through the upper half of cortex from mice used for transcranial imaging of intrinsic optical signals; see Figure 6. (d) Schematic of the make-up of edges in terms of individual centerlines, each with length $l_{mn}^{\left(k\right)}$, where m and n label the vertices and k labels the consecutive centerlines between vertices, and radius $r_{mn}^{\left(k\right)}$, computed as the average between the measured radii at vertices m and n. (e) Schematic of labeling of edges (E_nm) and vertices (V_m) used for topological analyses.

Vessels were automatically identified and vectorized as center points, of degree 2 or 3, that were connected with centerlines that had a length and an associated radius^19,25,26 (Fig. 1d). Two exceptions were that the centerlines of some surface vessels were traced by hand and the labeling of all penetrating vessels was visually confirmed. Consecutive centerlines were joined together to form the vectorized substantiation of individual vessels that preserved the tortuosity of the brain vasculature. The vectorized vessel was abstracted as an edge, whose length is the total length of the vessel and whose radius is the median radius associated with all centerlines (E_mn; Fig. 1e). Different edges predominantly meet as vertices of degree 3; that is, a fraction of 0.93 triads and <0.07 crosses (V_m; Fig. 1e). All vectorized vessels of the data set of one mouse formed a weighted graph²⁷ of edges and vertices, which we refer to as an angiome.

In addition to vessels, we vectorized the location of all cell nuclei¹⁹. The boundaries of cortical columns were based on the increased density of neuronal nuclei at the level of layer 4 (Fig. 1a,c), and, for purposes of analysis, columns are taken to exist only across layer 4 (Online Methods).

The microvasculature forms a highly interconnected network

We focused first on the statistical properties of the microvasculature. These vessels had a broad distribution of lengths between 10 and 200 μm, with a median length of 50 μm, and both median and mean radii near 2 μm (Fig. 2a). We observed no edges that spanned hundreds of micrometers between cortical columns or the nearly 1-mm depth of cortex (101,992 edges across 4 brains). The radii, which have the greatest effect on flow, were essentially constant as a function of depth into cortex (Fig. 2b). Consistent with past data for mice¹⁹, monkeys¹² and humans²⁸, there was a broad variation in the density of the vasculature as a function of depth into cortex (Fig. 2c) that differed from the sharper variation in neuronal density (Fig. 2c).

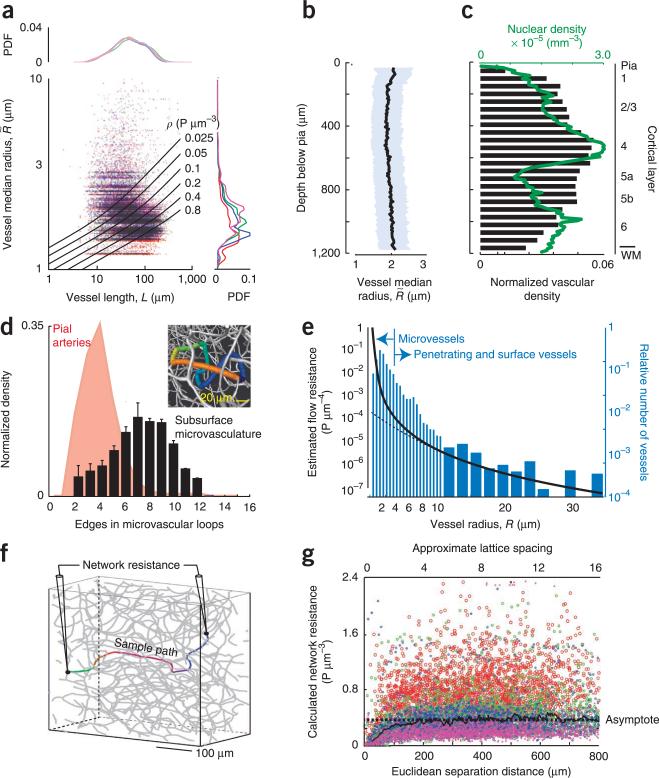
Figure 2.

Analysis of the local geometry and topology of the microvasculature. (a) Scatter plot as a function of the total length of each vessel, defined as $L_{mn}={\sum }_k{l}_{mn}^{\left(k\right)}$, and the median radius, denoted as R_mn. The lines are plots of constant fluid resistance (equation in Edge resistance of Online Methods). Data are from 101,992 edges across four brains. The line plots are probability distribution functions (PDFs) for different brains, found by projecting the data across all lengths (right) or radii (top). (b) Plot of the mean radius across all segments in an axial slice as a function of depth. (c) Plot of the density of the microvasculature and neuronal density as a function of depth. The vascular density in an axial slice was defined as the fractional length of all edges in an axial slice. WM, white matter. (d) PDF of the number of branches in different microvascular loops. Data are from 59,909 loops across four brains. The bars denote 1 s.d. For comparison, the distribution of branches in the surface pial network is reproduced⁵. The inset is a close up of a section of a vectorized network showing only the microvascualture. The colored edges highlight a loop that consists of eight branches, each with a distinct color. (e) Plot of the flow resistance per unit length as a function of vessel radius; the total resistance is found by multiplying by the length, in micrometers. Note the marked increase in resistance for radii below ~5 μm, where the Hagen-Poiseuille law (dashed line) no longer holds. The concurrent histogram shows the distribution of vessel radii for all vessels. (f) Schematic of the numerical probe of total resistance between two vertices in the network. (g) Scatter plot of the resistance between pairs of vertices (1,000 pairs per brain across four brains) as a function of the Euclidian distance between the vertices. The asymptote highlights the constant value averaged across all data sets, indicative of a three dimensional lattice. The slope, (3.0 ± 4.4) × 10⁻⁵ (mean ± 95% confidence interval, found with robust linear regression), was not significant.

We then examined the network properties of the microvasculature. These formed a multitude of loops, with an average of eight edges across the compact loops (Fig. 2d). The prevalence of closed paths was consistent with a rebalancing of flow observed after blockage of a single microvessel²⁹. For comparison, the pial vasculature, which is confined to two dimensions, forms loops with an average of four edges⁵, in which analogous rebalancing of flow occurs after an occlusion of a single surface vessel^4,30.

How does the interconnectivity reveal itself? If we assign a fluid resistance to each edge and view the microvasculature as a three-dimensional resistive network, we would expect that the resistance across pairs of vertices in the network should asymptote to a constant value as we span pairs that are progressively further apart³¹. In contrast, this resistance should increase linearly for one-dimensional networks and logarithmically for two-dimensional networks³¹. We used a previously described empirical model³² (Fig. 2a,e), which corrects the Hagen-Poiseuille law for the granular nature of blood, to assign resistances on the basis of measured radius and length of each vessels (Online Methods). We then calculated the network resistance across pairs of vertices³³ (Fig. 2f) and found that resistance asymptoted as a function of the Euclidean separation distance (Fig. 2g). This implies that the microvasculature forms a highly interconnected irregular lattice in all directions. An asymptotic network resistance of 0.4 P μm⁻³ was reached by ~150 μm (Fig. 2g), which corresponds to thrice the median length of the microvessels (Fig. 2a). Numerically, the asymptotic resistance is consistent with a network that has the same topology and identical resistance values of 1.6 P μm⁻³ at each edge. For comparison, the average resistances from the surface to the depth of layer 4 were 0.1 and 0.2 P μm⁻³ for penetrating arterioles and venules, respectively.

Connectivity does not covary with columnar boundaries

A highly interconnected network may have systematic variations in connectivity. We asked whether such variations clustered in the boundaries of individual cortical columns, and addressed this issue with a previously described graph-theoretic analysis³⁴ (Online Methods). This analysis seeks to form communities of vertices in which the connections in a community are relatively more frequent than chance, but the connections between different communities occur at a level less than chance.

Qualitatively, the communities derived for our angiomes had no clear relation with the location and spatial extent of cortical columns (Fig. 3a–d). They were distributed along the entire depth of cortex with a density that peaked outside of layer 4 (Fig. 3e). What is the strength of these communities? We plotted the number of connections between communities versus connections in the community (Fig. 3f). A network with strong communities would be expected to have interconnections that scale as the surface-to-volume ratio, with a power law exponent of 2/3, down to an exponent of zero for the extreme case of near-isolated communities (Fig. 3f). In contrast, a network with weak communities would have interconnections that scale with a power law exponent between 2/3 and 1, where the latter value corresponds to a fully connected network (Fig. 3f). Our angiomes yielded a power law with an exponent of 0.83 (Fig. 3f), which is statistically greater than 2/3 (P < 10⁻⁵, n = 311 communities). This implies that vertices in a given spatial region make extensive connections with neighboring communities. We conclude that the connectivity of microvessels is sufficiently uniform to negate the existence of strong communities (Fig. 3f).

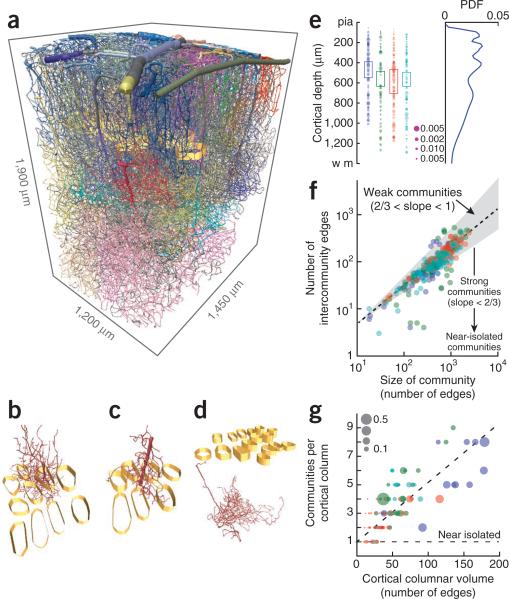
Figure 3.

Community analysis of the global topology of the microvasculature. The analysis makes use of the adjacency matrix for the branches. (a) Views of the complete vectorized vasculature that show different communities, each labeled by an individual color, as well as columnar boundaries (golden bands). (b–d) Representative communities. (e) The distribution of separate communities as a function of depth (362 communities across 4 mice; different colors represent data from different mice). The boxes highlight the extent of layer 4. The area of the dot scales as the size of the community relative to that of each angiome. The PDF on the right was computed by averaging over all examples. (f) Scatter plot of the number of edges between each pair of communities versus the number of branches in the community. The gray region is bounded by power law slopes of 2/3 and 1, and the dashed line is a fit of a power law to the data, with exponent 0.83 ± 0.04 (mean ± 95% confidence interval, found with robust linear regression). (g) Scatter plot of the number of communities that are either encompassed or pass through a cortical column as a function of the size of the column. Size is measured in terms of the number of branches that are either encompassed by or pass through the column. The horizontal line is the expected result when there is one community per column and the dashed line is a linear fit to the data, with slope 0.041 ± 0.004 (mean ± 95% confidence interval). The size of the dot is the fraction of the community that has the largest overlap with a given cortical column.

A network with even weakly defined communities may still form as association between select communities and cortical columns. To test this possibility, we examined the number of communities that passed through each column as a function of the physical volume of the column. We found that the number of communities increased monotonically with volume, with a slope significantly greater than zero (P < 10⁻⁴, n = 98 columns), and that no individual community provided the dominant number of branches (Fig. 3g). Furthermore, we considered the fractional contribution to each column by the community that contributed the largest extent of vasculature to the column. This fraction would be close to 1 if a given vascular community was confined to a single column. In practice, we observed a much smaller contribution, with a median fractional value of 0.06 (98 columns in 4 brains; Fig. 3g). We conclude that vascular topology and geometry do not conform to cortical columnar boundaries.

Flow domains of penetrating vessels do not match columns

A lack of spatial modularity of the microvessels does not, per se, preclude the possibility of domains of flow that result from precise balances of pressures in the penetrating vessels. This led us to calculate the fraction of blood that every subsurface microvessel received from each penetrating vessel. We made use of Kirchhoff's law for current conservation at each vertex, together with the values of the resistance for each edge (Fig. 2e) and the constant pressure difference of 50 torr (ref. 35) between the open ends of the surface arterioles and venules. There were no free parameters. As the first of three checks on self-consistency, the computed median speed of blood through the microvessels in the upper 400 μm of cortex was found to match the observed value of 0.4 mm s⁻¹ (ref. 21) for rat.

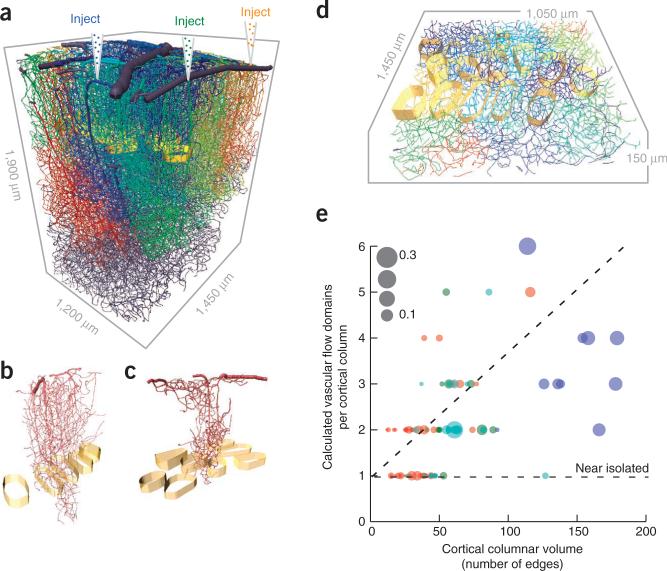
A result of the flow calculation for a given angiome is the domain of vessels that is predominantly sourced by a given penetrating vessel (Fig. 4a–c). These regions may be compared with the cortical columns (Fig. 4d). Qualitatively, there was no relation of perfusion domains with columns. We examined the number of domains that passed through each cortical column as a function of the physical volume of the column. The number of domains increased monotonically with the volume, with a slope significantly greater than zero (P < 10⁻⁴, n = 98 columns), and no individual domain provided the dominant flux (Fig. 4e). Thus, we conclude that there is no modularity in the perfusion of microvessels in relation to cortical columns.

Figure 4.

Calculated fluid flow and domains of common input in complete vectorized networks. (a) Vectorized vasculature in which the blood flow through a given penetrating arteriole is numerically labeled to determine the vessels that receive at least half of their flow from the chosen penetrating arteriole. This exercise is repeated for all penetrating arterioles and each territory is labeled with a different color. (b,c) Examples of different flow domains relative the cortical columns. (d) Overlap of multiple flow domains with cortical columns in layer 4. (e) Scatter plot of the number of flow domains that are either encompassed or pass through a cortical column. The size of the dot is the fraction of the flow domain that has the largest overlap with a given cortical column. The horizontal line is the expected result when there is one domain per column and the dashed line is a linear fit to the data, with slope 0.028 ± 0.003 (mean ± 95% confidence interval).

Penetrating vessels are not aligned to cortical columns

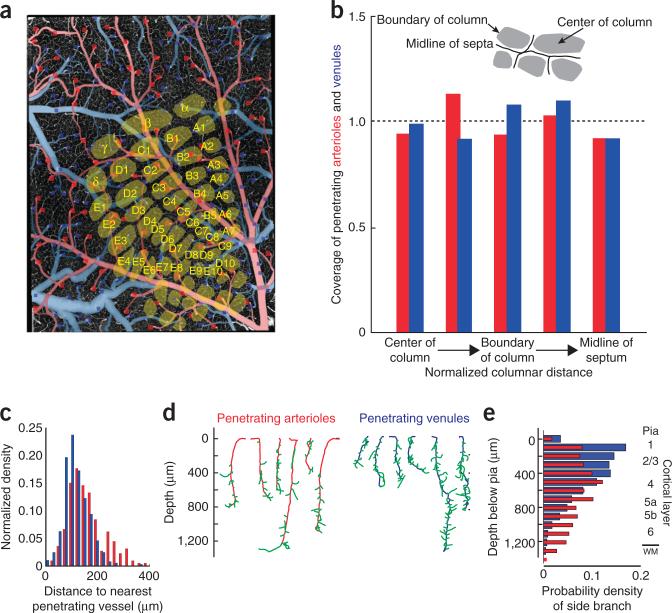
Although microvessels appeared to be distributed at random with respect to the location of cortical columns, the penetrating vessels that source and sink the microvascular network may in principle respect columnar boundaries (Fig. 5a). Thus, we analyzed the areal density of penetrating vessels as a function of distance along lines that started at the centroid of a column, ran through the columnar boundary and ended at the midline contour in the septa (Fig. 5b). We observed large variations in the density on an mouse-to-mouse basis, but as an average over columns and mice (n = 262 columns over 8 mice), we found no significant bias in the distribution of either penetrating arterioles or venules relative to the center of a column (Kolmogorov-Smirnov test, P = 0.94).

Figure 5.

Relation of penetrating vessels to cortical columns. (a) Example data set from a flattened cortex. The location of all penetration arterioles (red squares) and all penetrating venules (blue squares) are superimposed on an axial projection of the upper 150 μm of cortex. The cortical columns are based on imaging data taken with a flattened cortex. (b) Summary statistics on the location of penetrating vessels relative to the centroid of the cortical columns. The numbers of vessels in each bin, beginning at the center of the column and heading toward the midline of the septum (insert), were 15, 55, 47, 31 and 36 for the penetrating arterioles and 30, 84, 102, 63 and 68 for the penetrating venules. The locations of cortical columns boundaries were deduced from the cell density in layer 4. We plotted the fraction of pixels covered by arterioles or venues in each of five bins relative to the fraction expected for uniform coverage. (c) Probability density function for the distance between pairs of nearest penetrating arterioles (red) and between pairs of nearest venules (blue). The two distributions were significantly different (Kolmogorov-Smirnov test, P < 0.0001). (d) Examples of primary branches (green) from penetrating arterioles (red) and venules (blue). (e) Probability density function of the arteriole (red) and venule (blue) primary branches as a function of depth below the pia. The two distributions were significantly different (Kolmogorov-Smirnov test, P < 0.0001); the number of arteriole branches peaked near layer 4, whereas that for venules peaked at the surface.

Penetrating veins were more numerous that penetrating arterioles, by a factor of 3.0 ± 0.1 (mean ± s.e.). This is somewhat larger than past estimates of the ratio for rat, reported as 1.8 (ref. 22) and 2.6 (ref. 21) based on counts in cranial windows. A nearest-neighbor analysis indicates that the relative position of penetrating arterioles and venules are weakly anti-correlated, such that the distance from an arteriole to the nearest venule, and vice versa, is greater than the distance for a random distribution of vessel locations by a factor of 1.1 (P < 0.0001).

Penetrating vessels branch as a function of depth

Penetrating arterioles have a broad range of diameters, with a median value of 11 μm, although some vessels are not much thicker than microvessels. The primary microvessels appeared as fine branches that protruded from these vessels (Fig. 5c–e), whose distribution showed a shallow peak at the level of cortical input layer 4 (Fig. 5e) that is consistent with the shallow peak in the density of microvessels in the same layer (Fig. 2c). Neither the density of branching nor the density of vessels matched the sharp peak in the laminar variation in neuronal density in a cortical column¹⁹ (Fig. 2c).

The penetrating venules also had a broad range of diameters, with a median value of 9 μm. In contrast with the case for arterioles, branching from the penetrating venules peaked near the surface and monotonically decreased with depth (Fig. 5e).

Intrinsic optical signals follow columnar boundaries

It is generally accepted that changes in the strength of the intrinsic optical signal reflect changes in neuronal activity on a column-by-column basis. However, past work has focused on large cortical columns, either in primate vison³⁶, feline vision^13,37 or rat vibrissa somatosensation²⁴, which are sourced by multiple penetrating arterioles. Thus, changes in signal that appeared to match columns could be a result of changes across multiple penetrating vessels, even though there is no relation between the location of cortical columns and penetrating vessels per se (Fig. 5b). To disambiguate these possibilities, we examined the relation of intrinsic optical signals to the boundaries of the relatively small columns, which are associated with less than one penetrating arteriole, as compared with columns associated with multiple penetrating vessels. We worked under conditions for which the diameter of the vessels was insensitive to neuronal activity, as occurs with isoflurane anesthetic²³, a vasodilator³⁸, so that the change in signal strength reflected only a change in oxygenation, and tri-phasic vascular dynamics were eliminated³⁹.

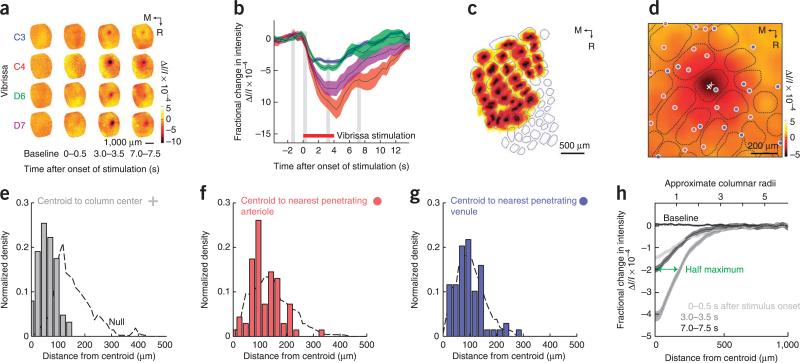
We mapped the intrinsic optical signals for 94 vibrissae for which the areas of the associated cortical columns varied by over an order of magnitude (four mice). Stimulation of a vibrissa led to a decrease in reflectance of red light, which was indicative of a fractional decrease in the oxygenation of blood (Fig. 6a). The magnitude of the signal rose for the period of stimulation and then recovered to baseline without any overshoot (Fig. 6b). A map of the responses revealed that each centroid of the intrinsic signal appeared to be located near the centroid of the column (Fig. 6c); note that errors at the lateral edge of vS1 cortex are a result of the curvature of the brain. The columnar-versus vessel-centric organization was particularly clear for the optical signal from relatively small columns, where the peak of the signal lay centered in the respective column and away from the location of shared vessels (Fig. 6d). As a composite over all data sets, we found that the centroid of the optical signal peaked near the columnar centroid (P < 10⁻⁴, n = 63 columns across four mice; Fig. 6e).

Figure 6.

Relation of images of the intrinsic optical signal (IOS) to the centroids of the cortical columns. A thinned-skull window was prepared above vS1 cortex and individual vibrissae were deflected at 10 Hz for 4 s. The mice were anesthetized with isoflurane so that only a net deoxyhemoglobin signal was observed by reflectance of light with a center wavelength of 625 nm. (a) Selected frames for four different vibrissa from the same mouse. Each frame is 0.5 s in duration and represents an average over ten trials. M, medial; R, rostral. (b) Complete time dependence for the spatial location of maximal change for the data in a. Shaded areas represent s.d. (c) Responses from all columns, normalized in amplitude and thresholded to avoid spatial overlap, are superimposed on a map of cortical columns obtained from flattened tissues optically sectioned with two-photon microscopy. Part of the mismatch at the lateral side results from an incomplete correction for the curvature of the brain. (d) Example of relatively small cortical columns in which the optical signal is centered (×) on the columnar centroid (+) as opposed to nearby penetrating arterioles (red dots) and penetrating venules (blue dots). Smoothed by convolution with a σ = 50 μm Gaussian filter. (e–g) Amplitude of the optical signal as a function of the distance to the columnar centroid (e), to the nearest penetrating arteriole (f) and to the nearest penetrating venule (g). The dashed lines are the null hypotheses, formed from a random distribution of signal centroids. (h) Lateral extent of the column-centered IOS. Maps of 94 individual whiskers from four mice were aligned on the spatial location of maximal change and averaged across time (frames). These column-centered maps were symmetric in all directions. Shaded areas represent s.d.

The predominant determinant of the centroid of the optical signal was that of the cortical column, although there was a slight, yet statistically significant, bias for the centroid to be close to penetrating arterioles (P = 0.025; Fig. 6f), with no orientational bias. There was no relation between the centroid and the penetrating venules (Fig. 6g). These results indicate that the depletion of oxygen from tissue predominantly follows columnar boundaries, as opposed to penetrating vessel location. Lastly, the full-width at half-maximum response was about one column (Fig. 6h). The signal returned to baseline over a distance of about two columns, similar for that observed for the initial ~0.5 s of the response in awake animals⁴⁰.

Perfusion domains predict vascular occlusion volumes

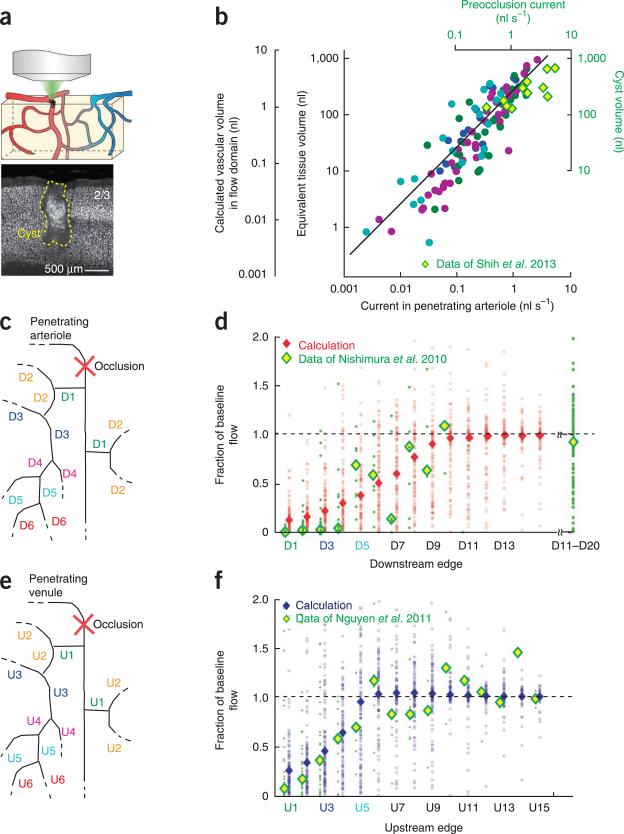
We sought to use the angiome to understand the pathology of micros-trokes. A naive expectation is that the volume of the cyst formed after occlusion of a single penetrating arteriole^18,21 (Fig. 7a) would be on the order of the cortical volume that was predominantly sourced by that vessel (Fig. 4). To test this hypothesis, we calculated the volume of microvasculature that received the majority of perfusion from each penetrating arteriole. We then divided the perfusion volume by the microvascular volume fraction, reported as 0.0074 (ref. 19), to determine the relation of the tissue volume sourced by each penetrating arteriole and the flux through the vessel (Fig. 7b). This relation was consistent with a linear relation for over three orders of magnitude of change (P < 10⁻³, n = 113 domains). Furthermore, the calculated volumes were consistent with previously described experimental data²¹ on the volume of the cyst that is formed after occlusion of vessels with different pre-occlusion values of flux (Fig. 7b).

Figure 7.

Calculated loss of lateral flow under numerically imposed pathological conditions in comparison with experimental observations. (a) Cartoon of local occlusion and representative necrotic cyst formed after occlusion of a rat penetrating arteriole along with thin section stained with the pan-neuronal marker αNeuN. Reproduced from ref. 21. (b) Computed vascular perfusion domains and their estimated parenchymal volume were consistent with measured cyst volumes formed after single artery occlusion. The vascular volume of 115 domains in 4 data sets (colored circles) was computed following numerical dye tracing (Fig. 4) as a function of the perfusion current. The parenchymal volume perfused by each domain was computed as 1/0.0074 of the vascular volume following previous measurements¹⁹. The linear fit to the data holds for a >98.5% confidence limit. We further plotted the cyst volumes (yellow and green diamonds), found from targeted photothrombotic occlusion of rat penetrating arterioles in rat cortex^5,21, as a function of the initial flux in the arteriole. (c) Schematic of the occlusion of an individual penetrating arteriole with scheme for labeling the order of downstream edges. (d) We simulated the occlusion of selected, individual penetrating arterioles and calculated redistribution of flow in microvessels up to 15 edges downstream from the occlusion site. The reduction in vascular flux is plotted as a function of each vessel's topological distance, that is, in terms of vertices, from the occluded plunging arteriole. Shown are the results of 100 simulations per order of the downstream edge (red circles) along with the median reduction in flux (red diamonds). We compared these results with the published in vivo data of downstream flux measurement before and after penetrating arteriole occlusion in rat neocortex (green points are data from 175 vessels with median values shown as yellow and green diamonds)¹⁷. (e) Schematic of the occlusion of an individual penetrating venule with scheme for labeling upstream edges. (f) We simulated the occlusion of selected, individual penetrating venules and calculated redistribution of flow in microvessels up to 15 edges upstream from the occlusion site. The reduction in vascular flux is plotted as a function of each vessel's topological distance from the occluded venule. The distribution of vascular responses is shown for 100 simulations per order of edge (blue circles) along with the median reduction in flux (blue diamonds). The results were compared with the published in vivo data of upstream flux measurement before and after penetrating arteriole occlusion (green points are data from 170 vessels)²².

Lateral connectivity does not guarantee lateral perfusion

Past studies have found that blockage of a single penetrating vessel, either an arteriole (Fig. 7c,d) or venule (Fig. 7e,f), leads to the acute loss of flow in the neighboring subsurface microvasculature^16,17,22 and, chronically, formation of a cyst^18,21 (Fig. 7a). On the one hand, the loss of perfusion appears to be at odds with the potential for collateral flow through the highly interconnected microvascular network (Figs. 2f,g, 3 and 4). On the other hand, drainage through patent penetrating venules may shunt collateral flow (Fig. 5b,c). To distinguish among these possibilities, we calculated the spatial pattern of flow that occurs in response to blockage of a single penetrating arteriole or venule. This calculation was similar to that performed for the flow domains (Online Methods).

For the case of penetrating arterioles, we plotted the calculated decrement in flow through the microvasculature as a function of topological distance, that is, in units of downstream branch order from the penetrating vessel (Fig. 7c). The median values for the decrement yielded a smooth variation (Fig. 7d), with a half-recovery at six downstream edges. Full recovery occurred by ten downstream edges, which corresponds to about half the distance to the next penetrating arteriole. The scatter in the individual calculated values (Fig. 7d) was a consequence of the heterogeneity of the vascular geometry and range of the incident flux of blood through different penetrating vessels. We compared our calculated results with previous experimental data¹⁷ for downstream flow immediately after blockage of an individual penetrating arteriole in rat neocortex (Fig. 7d). Calculation and experiment was in good agreement for the half-recovery distance.

A parallel analysis was performed for penetrating venules (Fig. 7e) and leads to a marked reduction in flow as a function of upstream branches (Fig. 7f). The flow reached the half-recovery level at four downstream edges and full recovery occurred at six edges, or about half the distance to the next penetrating venule. We compared our calculated results with previously experimental data²² for upstream flow following blockage of an individual penetrating venule in rat neocortex (Fig. 7f). Calculation and experiment agreed for the half-and full-recovery distance.

The analysis of the flow in angiomes with occluded penetrating vessels (Fig. 7d,f) provided second and third tests of self-consistency between the calculated flow and the experimental data. The correpondence between the calculated flow and that observed for the case of penetrating arterioles was slightly improved when all microvessels dilated by a small amount, that is, less than 0.5 μm in diameter. In contrast, the correpondence between the calculated flow and that observed for the case penetrating venules was slightly improved when all microvessels constricted. Thus, the angiomes gleamed from this study (Fig. 1a) and published values of vascular parameters^21,32,35, used without alteration, appear to provide a balanced approximation to the calculation of flow patterns.

The experimental data for both penetrating arterioles and venules showed a complete or near complete cessation of flow close to the occlusion, whereas our calculated values were small, but nonzero (Fig. 7d,f). This discrepancy originates from the assumed linear relation of flux and pressure, which ignores the propensity of red blood cells to stall at low pressure differences⁴¹.

DISCUSSION

We obtained geometrically correct angiomes of the cortical vasculature in mouse for volumes that spanned the full thickness of cortex and extended tens of cortical columns across the vibrissa region of primary somatosensory cortex (Fig. 1). We analyzed these data sets in terms of weighted graphs. Segments of vessels were characterized as edges, with a fluid conductance that depends on their length and radius (Fig. 2a,e). Edges joined predominantly as triads. We further obtained the locations of all neuronal and non-neuronal nuclei, from which the location of individual cortical columns was computed and used to further annotate the vascular maps (Fig. 1).

Our results build on the use of eroded casts of brain vasculature that were examined by scanning electron microscopy⁴², as well as dye-filled brains that were physically²⁶ or optically⁴³ sectioned. This past work identified the prevalence of closed loops and determined that microvessels joined only as triads. A recent study^44,45 exploited X-ray tomography to examine relatively large casts and model flow in extended vascular structures⁴⁴. However, as neurons were unlabeled in these studies, the potential relation between microvascular topology and cortical columns remained untested.

Our data and analysis support the notion that the brain cerebral microvascular network is devoid of subnetworks of microvessels that are fully connected among themselves, but only connected to the main network with one or a few edges (Fig. 3). This observation is expected from the fixed number of vessels, or edges, joining at each vertex (Online Methods). Furthermore, variations in the vascular density do not coincide with the location of cortical columns (Fig. 3) and the arrangement of the penetrating vessels that source and drain blood to the microvasculature (Figs. 3 and 5), as well as the resulting calculated patterns of flow, bear no correspondence with cortical columns (Figs. 4 and 7a,b). Thus, we refute the notion of a neurovascular module¹⁵ that is tied to the structure of a cortical column. Rather, we suggest that flow is controlled on the level of microvessels. One possibility is through constriction or stiffening of contractile proteins in pericytes in response to the changing environment of neurotransmitter spillover^46,47.

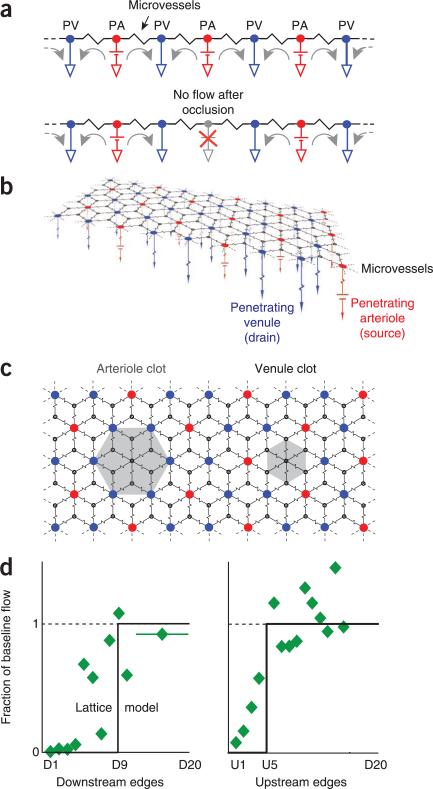
The calculated patterns of blood flow for our angiomes show that microvessels do not provide sufficient collateral flow to perfuse tissue when a penetrating arteriole or venule is blocked. The spatial and topological extent of the reduction in flow (Fig. 7d,f) is consistent with previous experimental results^5,16,17,21 and numerical calculations⁴⁴, and therefore provides a direct link between local ischemia and structural changes in the vascular network^21,48. Physically, the penetrating venules act as sinks that prevent blood in neighboring penetrating vessels from entering the area previously sourced by the occluded vessel. The essence of this explanation is captured by a one-dimensional circuit (Fig. 8a) with alternating penetrating arterioles as ideal sources and penetrating venules as ideal sinks that are linked by a single resistor that represents the asymptotic resistance of the microvasculature (Fig. 2g). Blockage of a source corresponds to occlusion of a penetrating arteriole and isolates a segment of tissue (Fig. 8a).

Figure 8.

Lattice models of the angiome. The sources are penetrating arterioles (red, PAs), sinks are penetrating venules (blue, PVs), network resistors represent the asymptotic value of the microvasculature (Fig. 2e), and the source and sink resistances are about half the value of the network resistances (Fig. 2e). (a) Linear circuit, the directions of current flow indicated for normal conditions (top) and after a block of a penetrating arteriole (bottom). (b) Planar circuit with a rhombic lattice and two penetrating venules for each penetrating arteriole. (c) Blockage of a penetrating arteriole leads to a region of no flow with an effective radius of $\sqrt{3\sqrt{3}∕\left(2\pi \right)}=0.91$ in units of median spacing between penetrating venules, whereas blockage of a penetrating venule leads to a region of no flow with an effective radius of $\sqrt{3}∕\left(2\sqrt{\pi }\right)=0.49$ in the same units. (d) Comparison of the prediction from the lattice model and data for penetrating arterioles¹⁷ and venules²². The number of vertices between a pair of penetrating venules, which sets the distance scale, was estimated from our analysis (Figs. 2e and 5c) as ${(100\mu \mathrm{m}∕(50\mu \mathrm{m}∕\sqrt{2}))}^2=10$ vertices.

A rhombic lattice (Fig. 8b), in which the sources and sinks form super-vertices with a 1:2 ratio, effectively models the consequences of blockages to both penetrating arterioles and venules. Blockage of a source leads to an isolated hexagon of tissue (Fig. 8c,d) whose radius corresponds to about ten vertices and well approximates observations for a blocked penetrating arteriole (Fig. 7d). Blockage of a sink leads to a smaller isolated hexagon of tissue (Fig. 8c,d). Here, the radius corresponds to about five vertices, consistent with observations for a blocked penetrating venule (Fig. 7d). A random arrangement of penetrating vessels (Fig. 5), as well as variability in the resistance of vessels, will smooth the abrupt diminution in flow predicted for the lattice. The essential features of the model are preserved for other source to sink ratios, including a 2:1 ratio that approximates that of the human cortex²⁷. From a cognitive perspective, this model highlights why blockage of any penetrating vessel leads to an infarct and is a catalyst for vascular dementia, consistent with behavioral data for rat²¹ and the reevaluation of data for humans^49,50. From the perspective of functional imaging, this model explains why changes in blood oxygenation can be localized (Fig. 6d,h).

ONLINE METHODS

Tissue preparation

12 C57/BL6 male mice (22–24 g) were used for primary data in this project. Eight of these mice were used to calculate the distribution of penetrating vessels relative to columnar boundaries (Fig. 5b). Although no statistical methods could be used to pre-determine sample sizes, the numbers used established statistical significance of a null hypothesis for all samples, with an average deviation from the null of less than 0.07 and a worst case deviation of 0.12. Our fixation method was designed to minimize the collapse of large surface vessels and preserve the structure of the microvasculature. Briefly, following deep anesthesia under 4% isofluorene (vol/vol) in 95% oxygen and 5% nitrogen, mice were killed by peritoneal injection of Fatal Plus (Vortech Pharmaceuticals) and transcardially perfused with warm heparinized-saline (40–60 ml of 20 units ml⁻¹ of heparin, no. 1181232; Pfizer Injectables) in 0.9% NaCl (wt/vol), using a peristaltic pump whose flow was set to 1 ml min⁻¹ to mimic mouse cardiac output. The mouse was then tilted head down in a custom platform and manually perfused at constant pressure with 20 ml of a 10% fluorescein-conjugated-albumin gel¹⁹ (wt/vol). Curing of the gel was initiated at the end of the perfusion by submerging the carcass of the perfused mouse in ice-cold water for ~30 min; the head was severed and equilibrated with to 4% paraformaldehyde (wt/vol) in phosphate-buffer saline (PBS) for 8–12 h, and the brain was extracted under a fluorescent dissection microscope to avoid damage to pial vessels and rinsed for 8–12 h in PBS. Surface arterioles versus venules were identified in whole brains by tracing them to the middle cerebtal artery versus the superior saggital sinus Rhinal vein. The tissue was then labeled with 4′,6-diamidino-2-phenylindole (DAPI) dilactate to stain all nuclei and NeuN antibody directly conjugated to with Alexa-594 to immunolabel neuronal nuclei, as described¹⁹. All protocols were approved by the Institutional Animal Care and Use Committee at University of California, San Diego.

Tissue from mice that were first imaged by intrinsic optical signal imaging were prepared as described above with the following additional steps to permit imaging of the upper lamina across all of vS1 cortex. After fixation, surface arterioles versus venules were identified as above, the cortices were extracted, flattened between glass slides separated by 1.4 mm, soaked for 8–12 h in 4% paraformaldehyde in PBS, and then removed from the flattening device, washed and rinsed for 8–12 h in PBS, stained as described above, and progressively index-matched in 60% sucrose (wt/vol) and 1% Triton X-100 (wt/vol) in PBS as described^19,22. This procedure was relatively fail-proof and fast compared with the large-scale all-optical histology²⁰ performed on the samples, albeit without the ability to image deep layers.

Intrinsic optical signal imaging

The bone overlying the barrel field of S1 was thinned 1 d before imaging⁸. Throughout imaging sessions, mice were anesthetized with isoflurane at 1.8–2.0% in oxygen, maintained at a constant body temperature of 37 °C using a temperature control system (no. 40-90-8, FHC) and continuously infused with 5% glucose (vol/vol) in 0.9% NaCl subcutaneously at a rate of 10 ml kg⁻¹ h⁻¹ using a syringe pump (no. 780101, Harvard Apparatus).

We followed previously described protocols for imaging^13,24. In brief, a telescope imaged a 4- × 4-mm region on the cortical surface onto a 512 × 512 pixel region of a CCD camera (Pantera TF 1M60, Teledyne Dalsa) at a resolution of 7.87-μm per pixel. Prior to IOS imaging, a single reference vessel image was taken with illumination at 455 nm (no. M455L2, ThorLabs). During imaging, the cortical surface was continuously illuminated at 625 nm (no. M625L2, Thorlabs) and frames were acquired as averages over 0.5-s intervals. For stimulation, an individual vibrissa was trimmed to 20–50% of full length, placed inside a quartz pipette attached to a piezoelectric element, and displaced 0.5 mm in both rostral and caudal directions with a 10-Hz sinewave pattern for 4 s at a distance of 10% of the original length. 6–25 trials per vibrissa were sufficient to reliably detect an evoked signal. A single baseline image (R_base) was created by averaging over eight frames that preceded the stimulus onset. Signal frames (I_f) were generated by subtracting and normalizing individual frames (R_f) by this baseline⁵¹ using the formula ΔI_f = (R_f − R_base) / R_base.

Two-photon automated high-throughput histology

Tissue was imaged throughout its full depth with all-optical histology²⁰, a block-face technique that combines sequential tiled imaging by two-photon laser scanning microscopy⁵² and plasma-assisted ablation mediated by amplified ultra-short laser pulses⁵³ to process fixed tissue. We imaged with a 25 × 0.95 NA Leica dipping objective (no. 11506323, Leica Microsystems) to achieve a 400-μm² field of view and acquired cubic voxels that were 1 μm on edge. On each iteration, the surface of the tissue block was imaged in a tiled fashion, with 50 μm of overlap between tiles, throughout a depth of 150–200 μm. These dimensions were chosen to ensure an adequate signal-to-noise ratio for subsequent processing. We then rastered the sample to ablate the top 50–70 μm of tissue in 10-μm wide and 10-μm deep strips with the use of ~4-μJ per pulse, 200-fs pulses of 800-nm light delivered at 5 kHz (Libra, Coherent). A circulating bath of PBS removed debris. At the end of each ablation round, the objective was raised above the sample and its surface was cleaned from air bubbles with the help of an automated wiper arm. Slabs of index matched tissue were imaged without ablation. The entire process was automated with the MPScope software system⁵⁴.

Stitching

Individual blocks of raw data were stitched to form a single large data. Our process is derived from a previous study⁵⁵ and, in brief, involves three steps. First, we estimated the spatial offset of each pair of neighboring blocks with the use of a mean-normalized three-dimensional cross-correlation that is calculated for the overlap between blocks. Second, we searched for a global solution, found through linear analysis⁵⁵, that positions each block through the simultaneous minimization of all local interactions. Finally, blocks were placed on a common coordinate system. The algorithm was used with data sets of over 2,000 blocks with final volumes of 20 giga-voxels.

Image segmentation and vectorization

These processes converted the stitched data sets into vectors that represent short centerlines in each vessel (Fig. 1d) as well as the location of all neuronal and nonneuronal nuclei¹⁹. Each centerline was associated with a specific radius, points in 1 of 26 directions, and had two neighbors everywhere except at branching points, where three adjacent centerlines overlapped to form a vertex (Fig. 1e). The radii were corrected for the eccentricity induced by differences in axial versus lateral resolution and for the estimated point spread of the focus¹⁹. We automatically corrected for a small fraction of gaps, ~0.05 of all vessels, in the data set²⁵. Identification of surface and penetrating vessels as arterioles versus venules was based on tracing the surface vessels to the middle cerebral artery versus the central sinus or rhinal vein.

Cortical columns in mouse vibrissae cortex were clearly defined in layer IV by their cytoarchitectonic pattern, that is, cell somata organize around the perimeter of the column, whereas cortical and thalamo-cortical projections occupy the center¹⁴. The lateral boundaries and axial extent of cortical columns were delimited by visual examination of the reconstructed volume of α-NeuN image data.

Edge resistance

The vectorized data permitted us to estimate the resistance of each edge, denoted ρ_nm, in terms of L_nm, and R_nm. Conceptually, this is equivalent to expressing the data in terms of a weighted graph where the resistance is the weighting function²⁷. We use a modified Hagen-Poiseuille law to account for the hematocrit of the blood and the interaction of red blood cells with the vessel wall³², for which

$${\rho }_{mn}={\rho }_{nm}=\frac{8{\eta }_{\text{water}}}{\pi }\cdot \frac{L_{mn}}{R_{mn}^4}\cdot 4\cdot \left[1-0.863e^{\frac{-R_{mn}}{14.3\mu \mathrm{m}}}+27.5e^{\frac{-R_{mn}}{0.351\mu \mathrm{m}}}\right]$$

where η_water is the viscosity of water.

The structure of the vascular graph, that is, the connections between vertices, is stored in the form of an adjacency matrix. The adjacency matrix, A, contains exactly three nonzero elements, A_nm = A_mn, per row and column, that correspond to the tri-partite connection.

Network resistance

The resistance between any two vertices in a finite lattice can be calculated from the Laplacian matrix L = A – D, where $D_{mm}={\sum }_{n=1}^N{\mathbf{A}}_{mm}$ forms the diagonal matrix D. Following a previously described proof ³³, the eigenvectors, denoted Ψ_m = (ψ_m;1,..., ψ_m;N), and associated eigenvalues, denoted λ_k, that satisfy LΨ_m = λ_mΨ_m for m = 1,..., N will determine the resistance between any two vertices (a, b), where

$${\rho }_{ab}=\sum _{m=2}^N\frac{1}{{\lambda }_m}{\mid {\psi }_{m;d}-{\psi }_{m;b}\mid }^2$$

and we note that λ₁ = 0. The penetrating vessels were excluded for the calculation of the resistance between two vertices in the microvasculature (Fig. 2f,g).

Community partitioning

We use a previously described method³⁴ and maximize a measure, denoted Q, that reflects the density of edges between vertices inside communities as compared to edges between vertices in different communities. Following previously described notation^56,57, we have

$$Q=\frac{1}{2M}\sum _m^N\sum _n^N\left(A_{mn}-\frac{D_{mm}{D}_{nn}}{2M}\right)\delta (c_m,c_m)$$

where $M={\sum }_{m=1}^N{D}_{mm}$ is the sum of all edge weights and c_m is the community to which vertex m is assigned with δ(c_m, c_n) = 1 if c_m = c_n and δ(c_m, c_n) = 0 otherwise. To analyze large networks (N ~10⁵), we made use of an optimized community detection package modified for weighted edges that is based on previous work⁵⁶ and distributed by the authors. As this heuristic algorithm has a stochastic component, we report a consensus community vertex labeling out of 1,000 runs. This was done with the help of the Cluster Ensemble package (http://strehl.com) based on previous work⁵⁸. This package depends on the METIS graph-partitioning package (http://people.sc.fsu.edu/~jburkardt/c_src/metis/metis.html).

Fluid flow

Flow is calculated from Kirchhoff's law for the conservation of the current of blood at each vertex. Thus each of the N vertex equations is of the form

$$\sum _n^{\text{three entries}}\frac{P_m-P_n}{{\rho }_{mn}}=0$$

where P_m is the pressure at the m^th vertex. An exception occurs for vertices that are directly connected to a truncated surface vessel. These are used to set inflow pressure through surface arterioles, that is,

$$\sum _n^{\text{two entries}}\frac{P_m-P_n}{{\rho }_{mn}}=\frac{P_A}{{\rho }_m}$$

where P_A is the mean surface arteriole pressure and ρ_m is the resistance from the vertex to the open end, and reflect the zero output pressure though surface venules, that is,

$$\sum _n^{\text{two entries}}\frac{P_m-P_n}{{\rho }_{mn}}=0$$

where the mean surface venule pressure is taken as 0. This yields the matrix equation

$$\mathbf{LP}={\mathbf{I}}_{\text{source}}$$

where L is the previously described Laplacian and the surface terms are expressed as currents I_m;_source = P_A/ρ_m. The equation is solved for the P_m values, scaled by the value of P_A. The volume flux in a given edge, with units of volume per unit time, is denoted j_mn, and is found from

$$j_{mn}=\frac{P_m-P_n}{{\rho }_{mn}}$$

The average speed of the blood in the edge is $v_{mn}=\frac{j_{mn}}{\pi R_{mn}^2}$.

Scaling of local connectivity

The microvascular network appears to be devoid of subnetworks of microvessels that are fully connected among themselves, but are only connected to the main network with one or few edges (Fig. 3). Thus, the microvasculature does not form a small world network⁵⁹. Graph theory³⁴ provides an elegant proof that links this observation to the finding that the micro-vessels branch among themselves with a fixed number of vessels, or edges, joining at each vertex. Our analysis for the case of vertices with a fixed coordination number of three shows that the fraction of the network that can be isolated scales as (log₂N)/N, where N is the number of vertices. This fraction is negligible with N ~10⁴ per 1 mm³ volume. The vascular network may be viewed as ‘modestly’ random, that is, it does not support the inclusion of partially isolated subnetworks, yet is not crystalline.

To prove the above statement, we consider the case of a network with vertices of coordination number three only and step through the counting of vertices; for example, see ref. 60. First, we start at some particular vertex and count its three ‘first’ neighbors. Next, we note that each of these three first neighbors has two available edges that will connect to a total of 2 × 3 new vertices, not counting the ones involved in the initial step and not permitting two edges to connect the same two vertices. After this step, we have counted a total number 1 + 3 + 2 × 3 = 10 vertices. Continuing in this way, we see that at the (n + 1)^th step we acquire 2 × S(n) new vertices, where S(n) is the number of vertices acquired at n^th step. If the total number of vertices, denoted N, were almost infinite, we need not correct for the vertices already counted in earlier steps, as they won't appreciably diminish the reservoir of fresh vertices. Then, S(n + 1) = 2S(n), and the total number of vertices counted after the n + 1 steps would be $1+{\sum }_{r=1}^{n+1}{2}^r=1+(2^{n+2}-1)∕(2-1)\approx 2^{n+2}$. Almost all the N vertices will then have been counted in n + 1 steps, so that N ≈ 2ⁿ. Thus, after only log₂N steps, almost all N vertices have been counted, which leaves only a fraction (log₂N)/N for weakly connected inclusions in the networks, such as trees.

When N is not infinite, we must correct for previously counted vertices at each step. Thus, at the m^th step, we must allow for the fact that we have already counted the sum of all vertices, that is, ${\sum }_{r=1}^{m-1}S\left(r\right)$. So the number of vertices counted up to the (n + 1)^th step is given by only ${\sum }_{r=1}^n[S\left(r\right)-{\sum }_{m=1}^{r-1}S\left(m\right)]=2^n$. So even if N is finite, the fraction of the network that can be weakly interconnected is still of order (log₂N)/N.