I_h and HCN Channels in Murine Spiral Ganglion Neurons: Tonotopic Variation, Local Heterogeneity, and Kinetic Model

Abstract

One of the major contributors to the response profile of neurons in the auditory pathways is the I_h current. Its properties such as magnitude, activation, and kinetics not only vary among different types of neurons (Banks et al., J Neurophysiol 70:1420–1432, 1993; Fu et al., J Neurophysiol 78:2235–2245, 1997; Bal and Oertel, J Neurophysiol 84:806–817, 2000; Cao and Oertel, J Neurophysiol 94:821–832, 2005; Rodrigues and Oertel, J Neurophysiol 95:76–87, 2006; Yi et al., J Neurophysiol 103:2532–2543, 2010), but they also display notable diversity in a single population of spiral ganglion neurons (Mo and Davis, J Neurophysiol 78:3019–3027, 1997), the first neural element in the auditory periphery. In this study, we found from somatic recordings that part of the heterogeneity can be attributed to variation along the tonotopic axis because I_h in the apical neurons have more positive half-activation voltage levels than basal neurons. Even within a single cochlear region, however, I_h current properties are not uniform. To account for this heterogeneity, we provide immunocytochemical evidence for variance in the intracellular density of the hyperpolarization-activated cyclic nucleotide-gated channel α-subunit 1 (HCN1), which mediates I_h current. We also observed different combinations of HCN1 and HCN4 α-subunits from cell to cell. Lastly, based on the physiological data, we performed kinetic analysis for the I_h current and generated a mathematical model to better understand varied I_h on spiral ganglion function. Regardless of whether I_h currents are recorded at the nerve terminals (Yi et al., J Neurophysiol 103:2532-2543, 2010) or at the somata of spiral ganglion neurons, they have comparable mean half-activation voltage and induce similar resting membrane potential changes, and thus our model may also provide insights into the impact of I_h on synaptic physiology.

Introduction

Auditory information from sensory receptors in the cochlea is transmitted into the CNS predominantly by a single class of bipolar cells, called spiral ganglion neurons (Kiang et al. 1982). Although they form a single class, spiral ganglion neurons possess a wide array of voltage-gated ion channels that shape their intrinsic firing properties. Thus, these cells provide a unique opportunity to identify the roles of ion channels in action potential initiation and propagation and in sensory processing. One distinctive channel type found in spiral ganglion neurons is the hyperpolarization-activated cyclic nucleotide-gated (HCN) channel, which mediates the I_h current. First found in the sinoatrial node (Noma and Irisawa 1976) and soon confirmed to exist in many systems (Robinson and Siegelbaum 2003), the I_h current impacts both synaptic integration and regulation of neuronal excitability. In the predominant type I neurons of the spiral ganglion, the I_h current reduces the temporal summation of excitatory postsynaptic potentials in dendrites and regulates the resting membrane potential in both dendrites (Yi et al. 2010) and the somata (Liu et al. 2013).

Among the four known α-subunits that can form HCN channels, HCN1, HCN2, and HCN4 are well characterized. These subunits differ in kinetics from fastest (HCN1) to slowest (HCN4), and in activation voltage with HCN1 being most positively activated (Altomare et al. 2003; Chen et al. 2009; Baruscotti et al. 2011; Emery et al. 2011). Some neurons only express one isoform and therefore most likely contain homomeric HCN channels in vivo (Santoro et al. 2000). However, other neurons express multiple isoforms. Neurons in the cerebral, hippocampal, and cerebellar cortices express a combination of HCN2 and HCN1 α-subunits, while thalamic neurons express HCN2 and HCN4 α-subunits (Santoro et al. 2000).

Spiral ganglion neurons express all but the HCN3 α-subunit (Kim and Holt 2013; Yi et al. 2010). HCN1 and HCN4 proteins were found in mouse (Kim and Holt 2013), rat (Yi et al. 2010), and guinea pig spiral ganglion neurons (Bakondi et al. 2009), while HCN2 proteins were either non-detected (Yi et al. 2010) or contributed little postnatally (Kim and Holt 2013). In vitro studies suggest HCN1 and HCN4 can co-assemble to form heterotetramers. For example, the currents produced by concatenated HCN4-HCN1-transfected human embryonic kidney (HEK) cells more closely resemble the native I_h current in sinoatrial node cells, than currents produced by co-transfected channels (Altomare et al. 2003). Thus, it becomes important to characterize the specific intracellular patterns of HCN α-subunit localization within peripheral auditory neurons to reveal whether both the expressed α-subunits are detected uniformly in each cell and reflect the channel composition that potentially affects I_h physiology.

Previous recordings of I_h from spiral ganglion neurons showed an exceptionally wide range of half-activation voltages (Mo and Davis 1997); however, how this diversity is accomplished is unknown. One hypothesis is that part of the diversity arises from a difference in expression of subunits along the tonotopic regions of the cochlea. To test this, recordings of I_h were made from cultured murine spiral ganglion neurons and compared within and between different tonotopic regions. We found the half-activation voltages were more depolarized in the apical spiral ganglion neurons than in the basal ones. To determine whether α-subunit density or differential assembly also contributes to the diverse I_h properties in spiral ganglion neurons, we examined the distribution of HCN1 and HCN4. We observed immunostaining densities that varied widely from cell-to-cell even among neighboring neurons, as well as intercellular variation in the co-localization of the HCN1-HCN4 α-subunits. We further characterized the kinetic analysis of I_h currents and found that activation of I_h in these cells consists of two kinetically distinct components: a fast component activating with second-order kinetics and a slower component with first-order kinetics. We use these data to construct a quantitative model of I_h in spiral ganglion neurons.

Methods

Tissue Culture

All procedures performed on CBA/CaJ mice were approved by the Rutgers University Institutional Review Board for the Use and Care of Animals, protocol 90-073. Cochleae were removed from postnatal days 5 to 8 (P5–8) CBA/CaJ mice that were euthanized by decapitation. The spiral ligament, stria vascularis, and organ of Corti were removed to isolate the spiral ganglion. The ganglion was divided into fifths. The two ends and the center region were plated into separate poly-l-lysine-coated dishes and maintained in growth medium (Dulbecco’s modified Eagle’s medium, supplemented with 10 % fetal bovine serum, 4 mM l-glutamine, and 0.1 % penicillin–streptomycin) for 5–22 days at 37 °C in a humidified incubator with 5 % CO₂.

Electrophysiology

Electrodes were coated with Sylgard® 184 (Dow Corning) and polished (Narishige MF-83). Resistance ranged from 4 to 8 MΩ with standard pipette and bath solutions. The internal solution was (in mM): 112 KCl, 2 MgCl2, 0.1 CaCl₂, 11 EGTA, 10 HEPES, 30 KOH, pH 7.5. The bath solution was (in mM): 137 NaCl, 5 KCl, 1.7 CaCl₂, 1 MgCl₂, 17 glucose, 50 sucrose, 10 HEPES, NaOH, pH 7.5—350 mOsm. Recordings were made at room temperature (19–22 °C). Cs⁺ was dissolved into bath solution for application to neurons with a final concentration of 5 mM to completely block I_h. Rapid solution changes were achieved with a micro-perfusion system (Ogata and Tatebayashi 1991).

The junction potential between pipette and extracellular solution was nulled by the voltage-offset of the amplifier (Axopatch 200A) right before establishing the seal. Voltage clamp recordings were uncorrected for the liquid junction potential of 5.1 mV. Pipette capacitance was compensated after formation of a GΩ seal. Series resistance was compensated in voltage clamp recordings with 95 % prediction, 95 % correction, and 10 μs lag. Signals were filtered at 1 kHz and digitized at 3.3 kHz with a CED Power1401 interface in an IBM-compatible personal computer.

Immunocytochemistry

Tissue was fixed in 100 % methanol (−20 °C for 6 min) and rinsed (3× for 5 min) with 0.01 M phosphate-buffered saline (PBS; pH 7.4). Prior to each primary antibody application, tissue was incubated with 5 % normal goat serum for 1 h to block nonspecific background labeling. The primary antibody (monoclonal anti-β-tubulin, 1:350, Covance; polyclonal anti-β-tubulin, 1:200, Covance; anti-HCNs, see Table 1 for details) was applied and the tissue was incubated for 1 h (for anti-β-tubulin) at room temperature or overnight at 4 °C (for anti-HCNs), then rinsed three times with PBS for 5 min.

TABLE 1.

Summary of anti-HCN antibodies used in this study

Antibody	Immunogen	Source	Species	Concentration
Anti-HCN1, clone N70/28	a.a. 778–910, rat HCN1, GST fusion protein, Intracellular, C-terminus.	NeuroMab (#75–110)	Mouse IgG1, monoclonal	1:100
Anti-HCN1	a.a. 6-24, rat HCN1. Intracellular, N-terminus.	Alomone (APC-056)	Polyclonal	1:150
Anti-HCN4	a.a. 119-155 of rabbit HCN4. Intracellular, N-terminus, GST fusion protein	Alomone (APC-052)	Polyclonal	1:150

For labeling of HCN1 alone, polyclonal anti-HCN1 (1:150, Alomone, APC-056) was used. Polyclonal anti-HCN1 antibody preferentially recognized channels located along the circumference of spiral ganglion neurons and, thus, may reflect distributions of functional HCN channels. For double labeling of HCN1 and HCN4, monoclonal anti-HCN1 (1:100, UC Davis/NIH NeuroMab Facility, N70/28) and polyclonal anti-HCN4 (1:150, Alomone, APC-052) were used (see Table 1) because the monoclonal anti-HCN1 antibody had an additional advantage of having comparable intracellular staining patterns as the polyclonal anti-HCN4 antibody. In contrast to our immunocytochemical data, HCN1 proteins were detected at higher levels in Western blots from the apical third of guinea pig spiral ganglion with an antibody not used in our study (Santa-Cruz Biotechnology Inc., Santa Cruz, CA, USA) (Bakondi et al. 2009). It is unclear whether the antibody, species, dissection and staining procedure, or the age of the animals caused the difference.

The specificity of anti-HCNs (N70/28, APC-056, APC-052) has been confirmed previously with Western blots revealing a single band of expected molecular weight (Stradleigh et al. 2011), along with the expected lack of labeling in HCN1^−/− (Herrmann et al. 2011) and HCN4^−/− knockout mice (Baruscotti et al. 2011), respectively. Moreover, no cross-reactivity has been observed when HCN1 and HCN4 polyclonal antibodies were used in Western blots of lysates from HEK cells overexpressing HCN1-HCN4 (Battefeld et al. 2012). Ideally, identical staining patterns would be observed from antibodies against different epitopes of the same protein. However, conformation changes with fixation or posttranslational protein modifications may lead to variable exposure of the recognized epitopes, and different patterns may be revealed (Anthony and Azmitia 1997). This is evident in our experiments using anti-HCN1 monoclonal and polyclonal antibodies, which both recognize intracellular epitopes yet against opposite terminus of the channel.

Fluorescein-conjugated secondary antibody (anti-mouse Alex-Flour 594/488/350 or anti-rabbit Alex-Flour 594/488, Invitrogen, 1:100) was subsequently applied for 1 h at room temperature and rinsed three times with PBS for 5 min. DABCO (1,4-diazabicyclo[2.2.2]octane) was applied at the end to the preparation for viewing and storage. Most images were acquired with a Hamamatsu ORCA-ER camera on a Zeiss Axiovert 200M inverted microscope controlled by IPLab software (Scanalytics, Inc.). In these experiments, the antibody labeling luminance was measured in IPLab with no digital enhancement by subtracting the mean of 400 pixels at four background areas from the mean of 300 pixels at the three brightest areas inside each neuron. A subset of images was taken on a confocal microscope (Zeiss LSM510 with Axiovert 100M) for co-localization studies of HCN1 and HCN4.

Kinetic Analysis of I_h

Data sets were exported from a custom data acquisition program written by Dr. Mark Plummer (Rutgers University) into an Excel file, and read into a custom program written in Python for further analysis. To isolate the I_h current, traces recorded in tetrodotoxin (0.5 μM) plus 5 mM external Cs⁺ were subtracted from traces in zero Cs⁺. All of the analysis of the voltage and time dependence of current activation, as well as for the analysis of tail currents, was done on the subtracted traces to minimize the influence of K⁺ and leak channels. Cells were excluded from further analysis if the subtraction of currents between the conditions did not yield a smooth, monotonic, steady-state activation or showed fluctuations in the holding current or input resistance during data acquisition. This resulted in the removal of 9 of 39 cells with activation currents measured at multiple voltage levels in Cs⁺, and 6 of 14 cells with tail currents recorded at multiple voltage levels in Cs⁺.

The measurement of activation kinetics was restricted to the voltage range where activation was more than 15 % of maximum as determined from the fit of a Boltzmann function (Eq. 1) to the conductance.

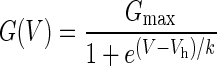1

where V_h is the half-activation voltage and k is the slope factor. In most cells, this analysis included a range from −60 to −140 mV. In the voltage range from −60 to −40 mV, I_h was very small or undetectable, so the I_h kinetics were measured from tail currents (averages of four traces) during 720 ms steps between −100 and −40 mV following activation with a step to −110 mV for 1,440 ms.

The kinetic analysis relied on curve fits for the activation and deactivation time courses. A Chebyshev polynomial approximation to the exponential function to obtain initial values (custom code from P.B. Manis, and also from C. Gohlke (http://www.lfd.uci.edu/~gohlke, University of California, Irvine). The initial estimates were used to seed bounded minimization procedures (“L-BFGS-B” (Zhu et al. 1997), or SLSQP as implemented in Scipy, v0.11, http://www.scipy.org). Additional linear constraints between the parameters were employed to make sure that the two time constants were separated by a factor of at least 2.5. Boltzmann functions were fit using a truncated Newton conjugate gradient algorithm from Scipy, and with a Levenberg–Marquart algorithm that incorporates constraints on the parameters (http://lmfit.github.io/lmfit-py/).

The separated fast and slow time constants for current activation and deactivation as a function of voltage were then each fit against a rate equation of the form:

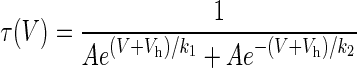2

Where A determines the overall amplitudes of the rate function, V_h determines the voltage midpoint, and k₁ and k₂ determine the steepness of the curve on either side of the midpoint (slowest) rate. This equation has only four free parameters (A, V_h,k₁, k₂), so that the errors in the parameter estimates are relatively small, and there is little trade-off between the parameters. The same equation, but with different coefficients, was used for both the fast and slow components. Fits to Eq. 2 were performed with a constrained version of the Levenberg–Marquardt algorithm.

Modeling

The rate equations, together with the Boltzmann functions describing steady-state activation, were then used to create a Hodgkin–Huxley-like model of the overall conductance. Modeling was carried out in NEURON (version 7.3, www.neuron.yale.edu) controlled by Python scripts.

Statistical Analysis

Data were examined for normality, and either parametric or nonparametric statistical analysis was used as appropriate. Nonparametric analyses used Kruskal–Wallis rank-sum tests, followed by Bonferroni-corrected pairwise comparisons. Additional analysis and statistics was performed in Prism 5.0c (GraphPad Software, San Diego, CA) and in R (Version 2.15, http://www.r-project.org).

Results

Factors Contributing to I_h Heterogeneity

The signature heterogeneity that distinguishes the intrinsic electrical profile of spiral ganglion neurons is exemplified by the I_h current. In some neurons, the magnitude of the hyperpolarizing sag that indicates the presence of this hyperpolarization-activated current is quite large, while a neighboring neuron may show very little of this voltage feature (Mo and Davis 1997). Furthermore, when examining the properties of the underlying current, it was clear that the magnitude of the current as well as the voltage dependence were unusually variable (Mo and Davis 1997). Interestingly, these studies have shown that the distribution of I_h half-activation voltages is much wider in spiral ganglion neurons (Mo and Davis 1997) compared to most cell types (Robinson and Siegelbaum 2003). Therefore, in order to understand better how the heterogeneity of I_h is distributed in the spiral ganglion, we first sought to examine the tonotopic distribution of I_h current and HCN channel α-subunits to test whether the broad range of voltage dependence results from tonotopic variation or whether variation occurs locally within a tonotopic region. Secondly, we examined whether mechanistic factors such as HCN α-subunit density and co-localization contribute to local I_h current heterogeneity.

To address the tonotopic contribution to the wide range of voltage dependence, we first recorded the responses of spiral ganglion neurons isolated from different cochlear regions (apex, middle, and base) to hyperpolarizing voltage steps that resulted in slowly activating, non-inactivating inward currents (Fig. 1A). The currents in spiral ganglion neurons were similar to those reported previously for I_h in murine spiral ganglion neurons (Mo and Davis 1997) and other cell types (Banks et al. 1993; Fu et al. 1997; Bal and Oertel 2000; Cao and Oertel 2005; Rodrigues and Oertel 2006). The I_h current was completely blocked by 5 mM external Cs⁺ (Fig. 1B). Subtraction of the currents in Cs⁺ from the control currents isolated I_h from underlying leak currents and potassium conductances that are active near rest (Fig. 1C). The difference current grew with increasing hyperpolarization, becoming clearly visible near −65 mV, and ranging from −0.5 to −2 nA near −140 mV (Fig. 1D). Although the activation functions varied from cell to cell, normalized conductance–voltage relationships had similar shapes across most cells (Fig. 1E, F).

FIG. 1.

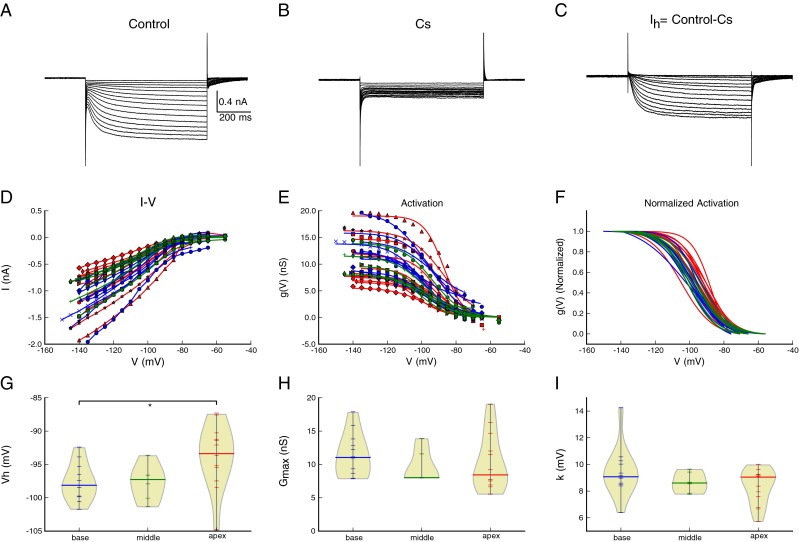
A broad range of I _h activation voltage observed in spiral ganglion neurons results from regional heterogeneity and tonotopic variation. A Whole-cell currents in response to voltage clamp steps from −55 to −140 mV in control conditions. The holding potential was −60 mV. B Whole-cell currents in the presence of 5 mM Cs⁺ from −55 to −140 mV from the same neuron in A, showing block of I _h. C Isolation of I _h currents by subtracting traces in B from those in A. D The steady-state current as a function of voltage (I–V) for basal (blue), middle (green), and apical (red) cells. I _h was isolated by subtracting the currents measured in Cs⁺, as in panel C. E The I–V curves transformed to conductance, assuming a reversal potential of −41.3 mV based on an average value from Mo and Davis (1997). F Overlay of normalized conductance shows similarity of steady-state activation across cells. The conductance G _max, V _h, and slope values were determined from fits of the Boltzmann function to the data in E. G–I The voltage of half-maximal activation (V _h, panel G), maximal conductance (G _max, panel H), and the slope, (k, panel I) of activation plotted against the cochlear origin of each cell. Each point (horizontal line) represents a single recording from a single neuron; the thick black line is the median. The “violin” plots show the density of data points (computed from a kernel density estimate, see (Scott 1992) as a function of the ordinate and demonstrate that the distributions are not normal. There was a significant difference in V _h, between apical and basal neurons (G), but not between apical and middle neurons. There was no tonotopic variation in G _max or the slope, k. *P = 0.034.

We next examined the I_h currents as a function of cochlear position to determine whether the wide variation in V_h (half-activation voltage or half-maximal activation voltage) results from tonotopic changes. The steady-state currents were converted to conductances assuming an E_h of −41.3 mV (Mo and Davis 1997) and fit to a single Boltzmann function (Fig. 1E). Figure 1G shows the distribution of V_h for cells from each region. Although there is heterogeneity in the measured half-activation voltages, as reported previously (Mo and Davis 1997), there was a significant effect of location on the V_h (one-way ANOVA, Kruskal–Wallis, χ² = 7.63, df = 2, P = 0.022). Post hoc comparisons with a Wilcox rank-sum test and a Bonferroni correction for multiple comparisons revealed a significant difference between the apical cells and the basal cells (P = 0.034), and a modest trend between the apical and middle cells (P = 0.14), while there was no difference between the middle and basal cells (P = 1.0). Only V_h showed this location-dependent difference, as there were no significant differences in G_max (Kruskal–Wallis χ² = 1.72, df = 2, P = 0.42) or slope (Kruskal–Wallis χ² = 2.19, df = 2, P = 0.34) between any cochlear regions. We conclude that a tonotopic distribution contributes to the voltage dependence of I_h heterogeneity, but not in maximal conductance or slope, in the mouse cochlea, and that this distribution can partially account for the widely distributed V_h in spiral ganglion neurons (Mo and Davis 1997).

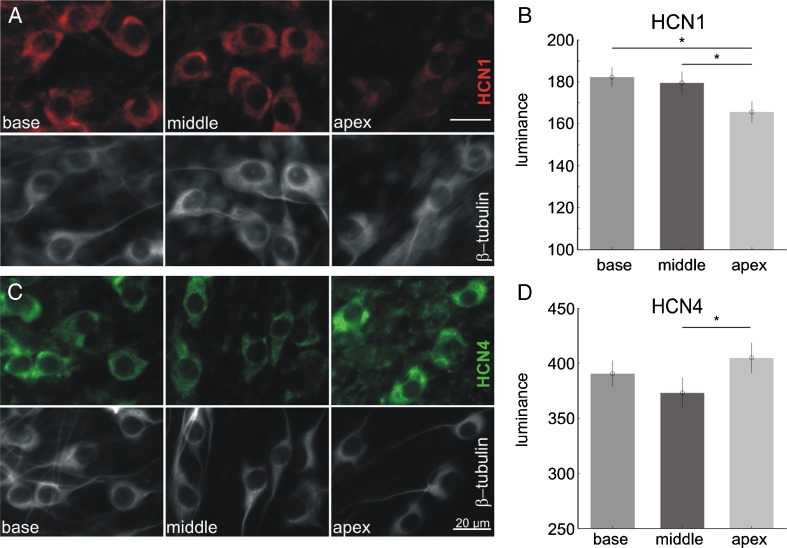
The variation in I_h with tonotopic position could be produced by different levels of HCN α-subunit expression along the tonotopic axis. To investigate this possibility, we evaluated the immunolabeling intensity of anti-HCN1 and anti-HCN4 antibodies in apical, middle, and basal neurons; HCN2 and HCN3 were not evaluated because the protein levels are not detected in early postnatal spiral ganglion neurons (Yi et al. 2010). As shown in Figure 2A, HCN1 (red) was less robustly labeled in the apical neurons compared to the middle or basal cells. In contrast, HCN4 (green, Fig. 2C) showed a different tonotopic distribution with middle neurons showing less staining. These observations were corroborated by measurements made from the brightest area in each neuron while subtracting the surrounding background levels for each cell (Fig. 2B, D). Measurement of the HCN1 to HCN4 ratio was also on average, lowest in the apex (data not shown, P < 0.01).

FIG. 2.

Immunocytochemical labeling of two HCN α-subunits, HCN1 and HCN4, revealed different tonotopic distributions. A Examples showing that monoclonal anti-HCN1 antibody luminance was slightly lower in the apex. B Quantitative measurements of anti-HCN1 antibody luminance (mean ± sem) from three sets of cultures in separate experiments revealed significant differences in between apex and middle, apex, and base (N-way ANOVA, P = 0.0002 with Tukey–Kramer pairwise test). C Examples showing that polyclonal anti-HCN4 antibody luminance was slightly lower in the middle. D Quantitative measurements of anti-HCN4 antibody luminance from four sets of cultures in separate experiments revealed significant difference between apex and middle (N-way ANOVA, P = 0.03 with Tukey–Kramer pairwise test). Error bars show mean and 95 % confidence intervals.

These results suggest that the spiral ganglion cells in the apical region are indeed unique in their expression of significantly lower levels of HCN1 and higher levels of HCN4. However, the relationship between this expression pattern and the depolarizing shift in voltage dependence is not straightforward. Homomeric HCN1 α-subunits have the most positive V_h in many systems (Altomare et al. 2003; Chen et al. 2009; Baruscotti et al. 2011; Emery et al. 2011). However, we observed the lowest levels of this subunit in the apical region with the most depolarized V_h. Additional studies are required to determine whether the voltage dependence of the α-subunits are shifted in the spiral ganglion compared to other systems or whether other factors account for the tonotopic variation in voltage dependence.

In addition to their tonotopic variation, the half-activation, amplitude, total conductance, and activation slope vary from cell to cell within the same cochlear area. This result indicates that other local factors also contribute to the variation in the conductance. Thus, we asked whether this local heterogeneity can be attributed to changes in subcellular patterns of the HCN α-subunit distribution, or to differences in subunit co-localization. To determine whether the α-subunit density itself varies from neuron to neuron within a restricted region of the ganglion, we examined the HCN1 density with a polyclonal anti-HCN1 antibody that preferentially labeled the circumference of spiral ganglion neuronal soma, presumably reflecting channels located in or close to the cell membrane. This immunolabeling suggests that differences in HCN α-subunit density between cells contribute to the variation that we noted in voltage clamp recordings. For example, Figure 3 demonstrates that the amount of anti-HCN1 subunit antibody labeling (green) differed from cell to cell, in contrast to relatively uniform anti-β-tubulin antibody labeling (red) utilized to identify the spiral ganglion neurons in vitro. This can be observed by comparing a neuron lightly labeled with anti-HCN1 antibody (arrowhead) with a neighboring neuron displaying enriched HCN1 immunolabeling (arrow). These results are consistent with the idea that I_h heterogeneity partially results from differential densities of individual α-subunits even for neurons from the same tonotopic region of the spiral ganglion.

FIG. 3.

I _h electrophysiological heterogeneity may result from discrete variations in individual HCN α-subunit densities. The anti-β-tubulin immunolabeled spiral ganglion neurons (red). Polyclonal anti-HCN1 antibody (green) showed heterogeneous peri-somatic staining that appeared to label the channels predominantly at or close to the membrane. Arrows and arrowheads point to neurons with high and low HCN1 labeling, respectively. The staining pattern of HCN1 was different from Figures 2 and 4 because polyclonal anti-HCN1 was used instead of monoclonal anti-HCN1 antibody (see “Methods”).

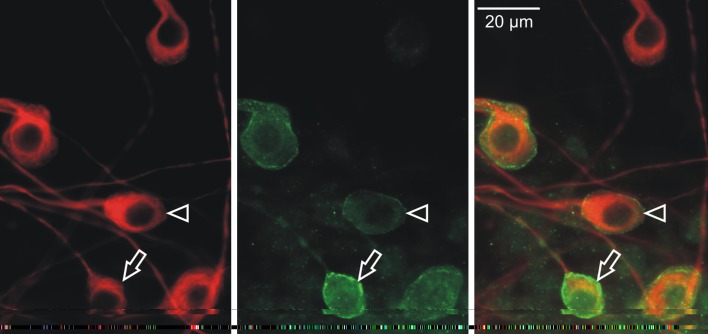
The I_h channel can be assembled from four identical α-subunits to form homomers, or from different α-subunits to form heteromers (Robinson and Siegelbaum 2003). We therefore considered the hypothesis that the intracellular localization of multiple HCN subunits could vary to partially account for the variations in I_h currents. We tested this idea by determining whether individual subunits were co-localized uniformly within a single cell. Cultured neurons were co-labeled with monoclonal anti-HCN1 and polyclonal anti-HCN4 antibodies and examined with immunofluorescence. As shown in Figure 4, all cells possessed both α-subunits. In some neurons, anti-HCN1 and anti-HCN4 antibodies overlapped (Fig. 4A, yellow), whereas in others they were distinct (Fig. 4B, red and green). The observation that both subunits are localized to individual neurons supports the idea that I_h channels in spiral ganglion neurons have the opportunity to form different α-subunit compositions, thus potentially adding an additional dimension to the sources of heterogeneity of the I_h currents in spiral ganglion neurons.

FIG. 4.

I _h electrophysiological heterogeneity may result from differential HCN α-subunit co-localization as HCN1 (green) and HCN4 (red) α-subunits were both identified in individual neurons that are uniformly labeled with anti-β-tubulin antibody (gray). Anti-HCN1 and anti-HCN4 antibodies are overlapping in the cytoplasm of the neurons shown in panel A, appearing yellow (arrow), compared to the group of neurons shown in panel B, that have distinct regions of polyclonal anti-HCN4 (red, red arrowhead) and monoclonal anti-HCN1 antibody labeling (green, green arrowhead).

Mathematical Model of the Spiral Ganglion I_h Current

The physiological and cellular heterogeneity of I_h suggests that I_h may contribute to different aspects of auditory integration in spiral ganglion cells, such as action potential threshold, resting potential, input resistance, and spike afterhyperpolarizations. Understanding the role of I_h variability can in part be addressed by considering hypotheses in the context of a computational model. To begin this process, we developed a model specifically for spiral ganglion cells based on the voltage dependence and kinetics of the I_h currents recorded in culture.

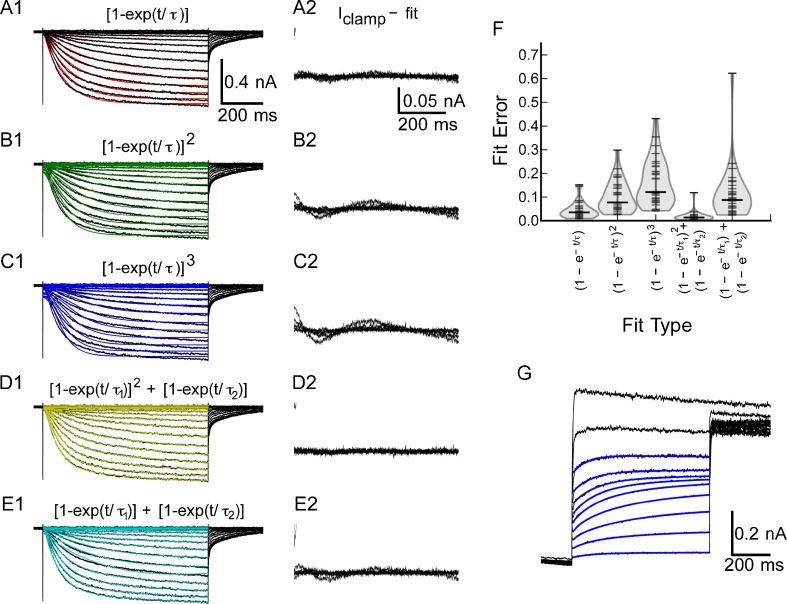
Construction of the model requires identification of kinetic components, followed by measurement of activation and deactivation kinetics and voltage dependence. Activation kinetics of I_h were measured by fitting the rising phase of the current to a family of exponential and mixed exponential functions. As shown in Figure 5(A1), a single-exponential function provided a reasonable fit at all voltages, although there were some deviations both during the rising phase and a slow deviation throughout the trace, as shown by the difference between the fit and the original traces in Figure 5(A2). The best fits to second- and third-order exponentials (Fig. 5(B1, C1)) were worse than those to the first-order function and exhibited large deviations from the data (Fig. 5(B2, C2)). However, a mixed model in which the fast activation was second order and the slow activation was first order (Fig. 5D1) provided an excellent fit (Fig. 5(D2)). A simple sum of two first-order exponentials with different time constants (Fig. 5(E1)) also worked well (Fig. 5(E2)), but was not as consistent as the mixed model. Figure 5(F) summarizes the fit error across all 30 cells for each of the functions. The mixed model that consists of a sum of second- and first-order exponential functions (exp² + exp¹) nearly always produced a better fit to the data than any of the other functions for any given cell. A comparison of the errors was made using a Kruskal–Wallis rank-sum test, which yielded Χ² = 88.7, df = 4, P < 2.2 × 10⁻¹⁶, suggesting that there were large differences in the quality of the fit across the family of functions. Post hoc comparisons using the Wilcox rank-sum tests shows that the mixed model (exp² + exp¹) provides a significantly better fit than any of the other functions (P < 1.6 × 10⁻⁵ versus 1, 2, or 3 exponentials, or the sum of exponentials). The mixed activation function is consistent with an activation process that involves two energetically distinct pathways to open the channels. While mixed activation could reflect the gating in a homogeneous population of heteromeric channels, it is also consistent with the presence of more than one population of heteromeric or homomeric channels.

FIG. 5.

Activation of I _h is best described by a mixed model with a fast second-order exponential and a slow first-order exponential. A1, Example traces with first-order fits superimposed. B1, Example traces with second-order fit. C1, Example traces with a third-order activation function superimposed. D1, Example traces of mixed first plus second-order activation. E1, Example traces of fits to the sum of two first-order exponentials. A2–E2, Expanded views of the difference between the clamp currents and the fit data in A1–E1, respectively. F, Summary of fitting errors across all 30 cells. The mixed second + first-order model resulted in the smallest errors. G, Example subtracted tail currents, with superimposed fits (sum of two exponentials) to measure the time course of I _h deactivation in the voltage range between −85 and −40 mV.

Deactivation of the conductance following hyperpolarization, for example following the afterhyperpolarization of an action potential, is also important in regulating the excitability of neurons in the voltage range from −60 to −40 mV. To study the kinetics in this voltage range, we analyzed the tail currents at various voltage levels following activation of the conductance with a hyperpolarizing step to −110 mV. Again, difference traces between control and Cs⁺ block were used for the kinetic analysis, to minimize contamination of the traces by outward potassium currents. These experiments had a low success rate, since the currents were relatively small which necessitated averaging to reduce noise, requiring long-term recording stability. Only 8 out of 14 cells studied with this protocol had data acceptable for a kinetic analysis. Since the activation consists of two kinetically distinct components, the tail currents are also expected to decay with multiple time constants, and consistent with this, I_h could be separated into two single-exponential components as shown in Figure 5(G). We conclude that the activation of I_h in spiral ganglion cells consists of two kinetically distinct components. A fast component activates with second-order kinetics, while a slower component shows first-order kinetics.

We next compared the voltage dependence of the fast and slow components as a function of cochlear position. Because cells from the middle and basal regions had indistinguishable voltage-dependent properties (Fig. 1), they were combined into a “mid-basal” group and compared against cells from the apex. The results of this comparison are summarized in Figure 6. The extracted voltage-dependent amplitude of the fast component was well fit by a single Boltzmann function (Fig. 6A, E). The Boltzmann parameters were given in Table 2, for all cells (average), and separated by region (apical or mid-basal). Consistent with the voltage dependence of the total current (Fig. 1), the V_h for the isolated fast component was about 5 mV depolarized in the cells from the apex as compared to the rest of the cochlea (unpaired t test, t = 2.264, df = 29, P = 0.031). There was no difference in the slope factor of the currents from the apex as compared to the rest of the cochlea (unpaired t test, t = 0.068, df = 29, P = 0.946).

FIG. 6.

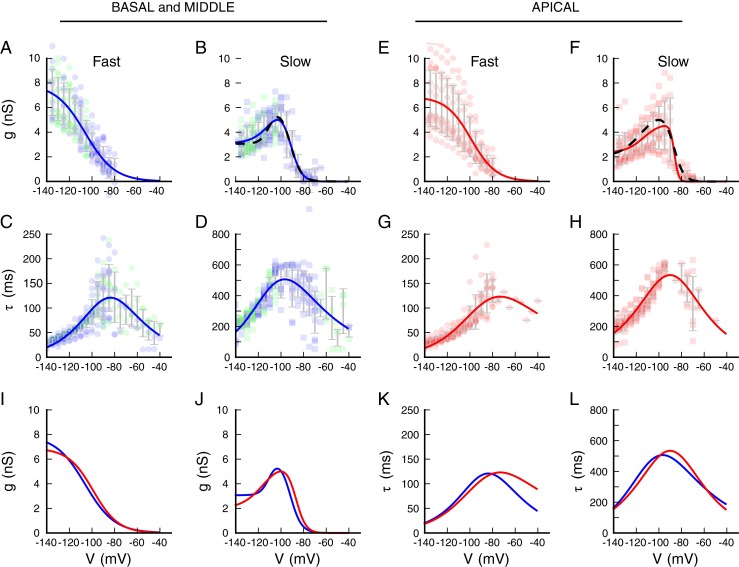
Summary of activation and kinetics for the two components described in the mixed model from Figure 5(D). In each plot, the data points from individual cells are shown in color (blue, base; green, middle; red, apex), and the gray error bars show the mean and standard deviation of the measurements averaged in 5 mV bins. Numerical values of the parameters for all fits are summarized in Tables 2 and 3. A Amplitude of the fast (second-order) component for individual cells (symbols) from the base and apex. B Amplitude of the slow (first-order) component of the current, represented as in A. This component shows rectification for large hyperpolarizations. The red line is the fit of a double-Boltzmann to the average data. The dashed line shows the average best fit to individual cells for which the fits were adequately constrained. C The fast time constant as a function of voltage, determined from both activation and tail current (deactivation) analyses, for basal and middle cells. The red line is a fit of Eq. 2 to the population data. D The slow time constant as a function of voltage, determined from activation and tail current analyses. The red line is a fit of Eq. 2 to the population data. E–H Panels show analyses of data from apical cells, in the same format as A–D. I Comparison of the fast component of the conductance between apical (red) and mid-basal cells (blue), showing the positive shift in activation for the apical cells. Fits are taken from panels A and E. J Comparison of the slow component of the conductance between apical (red) and mid-basal cells (blue), showing that the slow activation component also is shifted positive in the apical cells. Fits are taken from the dashed lines in panels B and F. K Comparison of the fits to the fast activation, from panels C and G. L Comparison of the fits to the slow activation, from panels D and H.

TABLE 2.

Activation functions for I _h in SGNs

	Component	V h (mV)	k (mV)	Fraction	N of cells
Average	Fast	−103.84 ± 4.42	12.39 ± 2.80	0.434	31
	Slow1	−88.86 ± 4.66	4.62 ± 1.24	0.625	17
	Slow2	−113.16 ± 10.90	7.31 ± 4.36	0.375	17
Apical	Fast	−101.83 ± 5.03	12.43 ± 3.37	0.422	13
	Slow1	−86.76 ± 3.62	4.43 ± 1.14	0.599	10
	Slow2	−115.23 ± 11.93	9.67 ± 3.07	0.401	10
Basal + middle	Fast	−105.30 ± 3.20	12.36 ± 2.30	0.447	18
	Slow1	−91.86 ± 4.34	4.88 ± 1.32	0.663	7
	Slow2	−110.21 ± 8.40	3.93 ± 3 .63	0.337	7

Summary statistics for activation fits to Eq. 1 for all cells, apical cells, and combined basal and middle cells. Data are mean and standard deviation of the best fit parameters for the number of cells in the rightmost column. Fraction shows the amount of the fast component, and the relative fractions of the two slow components account for the voltage dependence of the currents. N indicates the number of cells for which acceptable individual fits could be obtained for each component (see “Methods” for details)

Although the amplitude of the slow component showed a clear voltage-dependent increase up until about −100 mV, the current did not increase with further hyperpolarization, as would be expected. Instead, the current amplitude remained approximately constant for voltages negative to −100 mV, indicating that the conductance was decreasing with increasing hyperpolarization (Fig. 6B, F). We found that a double-Boltzmann function, in which the second Boltzmann describes the decreasing conductance at more negative potentials, could adequately describe the voltage dependence of the slow current (population fit, solid red line; best cell fits, dashed black line, Fig. 6B, F). The parameters of the Boltzmann fits for the slow components are also given in Table 2.

The voltage dependence of the slow component differs between cells from the apical and mid-basal regions (red versus blue lines, Fig. 6J). The half-activation of the first (more depolarized) slow component was on average 5.1 mV more positive in the apical cells (unpaired t test, t = 2.471, df = 15, P = 0.026), consistent with the voltage dependence of the fast component. However, the half-activation of the second (more negative) component was not significantly different (unpaired t test, t = 0.901, df = 15, P = 0.38). The slope factor of the more depolarized component was not significantly different between regions (unpaired t test, t = 0.710, df = 15, P = 0.49), whereas the slope factor was more than twice as large in the apical cells (unpaired t test, t = 3.306, df = 15, P = 0.0048). A conductance decrease with hyperpolarization might be associated with an internal block of the channels by cations, or by a structural change in the channel gating that affects the channel conductance or mean open times (Shin et al. 2004). The quantitative differences in voltage dependence suggest a difference in the energetics of the channels between the apical and mid-basal regions. However, lacking more direct experimental insight into a mechanism, the treatment of the second energetic component is hypothetical. The voltage dependence of the time constants for both the fast and slow components of the current was also extracted from the fits (Fig. 6C, D, G, H, K, L). Analysis of the activation kinetics was limited to the voltage range where the conductance is significantly activated (voltages negative to ∼-85 mV). The time constants for voltages positive to this were obtained from the deactivation (tail) analysis. The time constants for the fast component were highly voltage-dependent and peaked at about 120 ms near −90 mV, becoming faster on either side of this voltage. There was a large variance in the time constants at the maximum of the peak because both the activation and deactivation current amplitudes were relatively small in this range. The colored lines are fits to Eq. 2 (see “Methods”), with the kinetic parameters are given in Table 3.

TABLE 3.

Voltage-dependence of rate constants for I _h in SGNs

	τ (V) Eq. 2	A (ms−1) × 103	V h (mV)	k 1 (mV)	k 2 (mV)
Average	Fast	4.268 ± 0.242	86.45 ± 6.73	31.33 ± 7.04	21.65 ± 3.87
	Slow	1.029 ± 0.075	102.29 ± 8.17	38.12 ± 8.76	21.65 ± 5.27
Apical	Fast	4.458 ± 0.703	87.07 ± 12.17	53.03 ± 24.63	21.54 ± 5.51
	Slow	0.937 ± 0.028	89.61 ± 5.69	25.39 ± 5.06	26.42 ± 4.03
Basal + middle	Fast	4.175 ± 0.203	87.08 ± 6.16	28.17 ± 5.77	21.48 ± 3.76
	Slow	1.044 ± 0.091	105.82 ± 8.37	40.03 ± 9.66	20.23 ± 5.42

Fits are to group data sets: 18 cells in the mid-basal group and 13 cells in the apical group. Standard deviations are the errors in the estimate of the fit parameters, as return from the Levenberg–Marquardt fitting algorithm

The time constants of the slow component were also well described by Eq. 2, with the kinetic parameters given in Table 3. Here, the slowest kinetics occurred near −100 mV, with a time constant of about 550 ms. The voltage dependence of the rates was more symmetrical around the peak than for the fast conductance. The parameters for the rate constants for cells from the apex alone, and the average of the cells from the base and middle regions, are also summarized in Table 3. While the fits yielded different parameter values for apex versus middle and basal cells, the curves are very similar to each other, and to the average curve, for all cells. The main difference occurs for voltages positive to −85 mV for the fast component (Fig. 6K), but in this range there was only one cell that could be included in the fit (Fig. 6G), and as a result the curve is not well constrained.

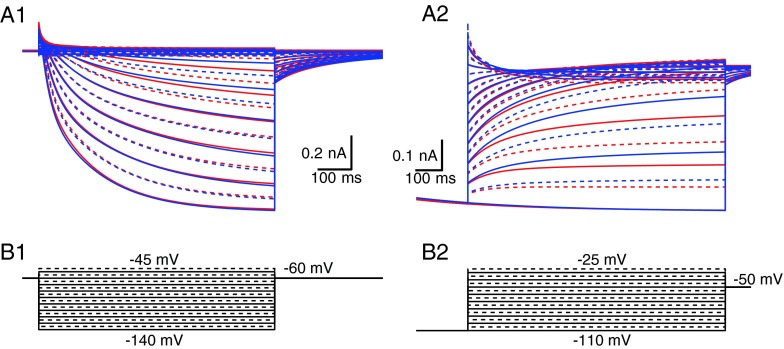
Next, we generated computational descriptions of the I_h conductance for the mid-basal, as well as the apical, spiral ganglion neurons, using a Hodgkin–Huxley formulation, based on the fits to the data in Figure 6 and the parameters in Tables 2 and 3. In this model, the fast and slow components are treated as separate entities (they operate independently and do not interact), but both contribute to the final current. The voltage-clamp currents computed from this model are shown in Figure 7 for the two models, assuming the same maximal conductance. In Figure 7(A1), the difference in the activation of the apical (red) and mid-basal (blue) currents can be seen for −90 and −100 mV steps, reflecting the more positive voltage dependence of I_h activation in the apical cells. Figure 7(A2) shows the tail currents following steps to −110 mV, again revealing that the currents in apical cells decay more slowly and have greater activation for voltages negative to rest. Overall, the currents produced by these models closely resemble the currents measured in the spiral ganglion cells (Figs. 1 and 5).

FIG. 7.

Comparison of kinetic models of I _h in SGNs. A1, Activation. Blue traces are the model for mid-basal cells; red traces are the model for the apical cells. Note the increased current in the middle voltage range for the apical cells. Solid lines are for steps at 10 mV intervals; dashed lines are for intermediate 5 mV intervals. B1, Voltage commands for data in A1. A2, Tail currents (deactivation) following a step to −100 mV, showing the difference in time course and current amplitude between models of mid-basal and apical cells. B2, Voltage commands for the tail currents in A2.

Discussion

I_h Heterogeneity in Spiral Ganglion Neurons May Involve HCN α-Subunit Composition and I_h Modulation

This study extends previous studies by showing that the wide range of I_h activation voltages (Mo and Davis 1997) in spiral ganglion neurons was partially attributable to local heterogeneity of underlying HCN α-subunits as well as tonotopic variation of I_h. Four identical or different subunits (HCN1 to HCN4) compose a single channel that is permeable to both Na⁺ and K⁺ ions and shows inward rectification at voltages below −41.3 mV in our recordings. HCN3 proteins were not detected in the early postnatal spiral ganglion (Kim and Holt 2013; Yi et al. 2010) and HCN2 was found to have minor contribution to I_h total conductance as well as half-activation voltage, while immunolabeling of HCN1 alone or with HCN4 in this study suggests that the properties in I_h could vary according to absolute or relative density in individual subunits, depending on whether HCN subunits form homomeric or heteromeric channels. Although I_h current activation voltage and both HCN1 and HCN4 α-subunits were significantly different in the apex, it is not clear whether the average abundance of the α-subunits serves as an indicator of half-activation voltage. The observation that a lower (rather than higher) abundance of HCN1, an isoform that is often associated with elevated V_h, was found in the apex, the area with more positive V_h, suggest that native HCN1 channels in the spiral ganglion may have more complicated properties than those heterologously expressed channels or that other mechanisms, such as channel phosphorylation or direct cyclic nucleotide binding, also influence the voltage dependence.

Evidence from medial superior olive principal neurons (Khurana et al. 2012) supports the idea that in some neurons V_h variations result from HCN channel modulation rather than HCN subunit composition. Whole-cell recordings of I_h showed a ∼30 mV shift in V_h from P9 to P21 gerbil whereas nucleated patch recordings showed no difference in kinetics and activation voltage range in HCN channels. One potential mechanism for I_h intracellular modulation is through a cyclic nucleotide binding domain, which inhibits HCN channel gating (Wainger et al. 2001; Zagotta et al. 2003). Direct binding by cAMP (or less effectively by cGMP) through a C-linker region has been shown to relieve inhibition and positively shift V_h in both native and heterologous HCN channels (Wainger et al. 2001; Zagotta et al. 2003) including those in spiral ganglion neurons (Mo and Davis 1997). Therefore, it is possible that some of the regulatory elements, such as cAMP levels, are distributed in a way that controls V_h of I_h differentially along the tonotopic axis. It remains to be determined whether the potential differential modulation of I_h across the cochlea reflects the base to apex developmental maturation of spiral ganglion neurons (Rubel and Fritzsch 2002), or instead persists into adulthood similar to the distribution of other voltage-gated ion channels (Adamson et al. 2002).

Kinetic Scheme of I_h in Spiral Ganglion Neurons Includes Fast and Slow Components

Our results show that I_h in spiral ganglion neurons shows both fast and slow voltage-dependent activation and deactivation. Such mixed kinetic behavior has been reported in HCN channels previously and is consistent with reaction schemes in which the open state can be reached from closed states that are energetically close to the open state, leading to a single-exponential rise, or from transitions through multiple other closed states, leading to sigmoidal rises (Altomare et al. 2001). We did not observe sigmoidal closing currents that would be difficult to incorporate into a Hodgkin–Huxley style model, although such deviations from an exponential decay might be small and difficult to detect under our recording conditions.

The differences between the fast and slow components suggest either a complex behavior of a single class of channels (whether homomeric or heteromeric) or the presence of two populations of channels with different kinetics. The different voltage dependence of the fast and slow components does not separate these hypotheses, since a single channel with different gating states could show a similar behavior. One attractive hypothesis is that the different kinetics arises from channel populations that consist of different mixtures of HCN α-subunits, since spiral ganglion neurons indeed express multiple subunits of the HCN family (see Figs. 2 and 4), and each subunit exhibits different kinetics reflected in HCN knockout animals or expressed cell lines (Altomare et al. 2003; Chen et al. 2009; Baruscotti et al. 2011; Emery et al. 2011). Consistent with this idea, both fast and slow components were found in all cells, and this is matched by the presence of multiple HCN α-subunits in every neuron. The most direct approach to distinguish these two hypotheses would be to perform ensemble analyses of single channels in the spiral ganglion neurons.

Functional Significance

What is the importance of the slow component of I_h? Although it looks “small,” for modest hyperpolarizations, the slow component accounts for nearly half the total conductance between −60 and −100 mV. As such, it will impart effects lasting hundreds of milliseconds on neuronal excitability for small perturbations of the membrane potential from rest. Therefore I_h may not only be important for controlling excitability for spike generation but also influence the discharge rate of sustained firing (Shaikh and Finlayson 2005; Thuault et al. 2013).

Spiral ganglion neurons express I_h with a mean maximal conductance of 10.5 nA which is smaller than in most other auditory neurons (Banks et al. 1993; Fu et al. 1997; Bal and Oertel 2000; Cao and Oertel 2005; Rodrigues and Oertel 2006). Compared to V_h ranging from −65 to −90 mV in these neurons, V_h in SGNs is at least 10 mV more negative, and as a result, only 3 % of I_h should be present at rest. When blocked by Cs⁺, this amount of I_h is shown to hyperpolarize the RMP by 4 mV (Liu et al. 2013). These results are consistent with those recordings made ex vivo from the nerve terminals (Yi et al. 2010). The I_h regulation of neuronal excitability such as RMP is particularly interesting, since auditory nerve fibers exist as different populations with different thresholds to sound and spontaneous rates in the absence of sound (Liberman 1982). While a portion of the mechanism contributing to the threshold variation is based on synaptic mechanisms (Liberman et al. 2011; Wong et al. 2013), it is also possible that adjustment of the neuronal excitability post-synaptically could play a role. We recently found that spiral ganglion neuron firing thresholds are largely controlled by K_v1 potassium channels, while a negative V_h of I_h seems to prevent neurons with the lowest voltage threshold from spontaneous firing (Liu et al. 2013). Consistent with this mechanism, modulation of I_h by cAMP produces a positive shift in V_h that enhances neural excitability and spontaneous discharge in superior olivary complex neurons (Shaikh and Finlayson 2005) in vivo. Therefore, multiple modulatory mechanisms such as [Ca²⁺]_i levels (Lüthi and McCormick 1999), neurotransmitters released from efferent fibers (Yamada et al. 2005), and activation of signaling pathways involving cAMP, PIP2, p38 MAP (Khurana et al. 2012), or tyrosine kinases (Thoby-Brisson et al. 2003) make I_h an ideal target to be dynamically adjusted to affect neural rate-level functions.