Experimental Measurement of Utricle System Dynamic Response to Inertial Stimulus

Abstract

The membranous utricle sac of the red-eared turtle was mounted in a piezoelectric actuated platform mounted on the stage of a light microscope. The piezoelectric actuator oscillated the base of the neuroepithelium along a linear axis. Displacements were in the plane of the utricle and consisted of a linear sinusoidal-sweep signal starting at 0 and increasing to 500 Hz over 5 s. This inertial stimulus caused measurable shear displacement of the otoconial layer’s dorsal surface, resulting in shear deformation of the gelatinous and column filament layers. Displacements of the otoconial layer and a reference point on the neuroepithelium were filmed at 2,000 frames/s with a high-speed video camera during oscillations. Image registration was performed on the video to track displacements with a resolution better than 15 nm. The displacement waveforms were then matched to a linear second-order model of the dynamic system. The model match identified two system mechanical parameters—the natural circular frequency ω_n and the damping ratio ζ—that characterized the utricle dynamic response. The median values found for the medial-lateral axis on 20 utricles with 95 % confidence intervals in parenthesis were as follows: ω_n = 374 (353, 396) Hz and ζ = 0.50 (0.47, 0.53). The anterior-posterior axis values were not significantly different: ω_n = 409 (390, 430) Hz and ζ = 0.53 (0.48, 0.57). The results have two relevant and significant dynamic system findings: (1) a higher than expected natural frequency and (2) significant under damping. Previous to this study, utricular systems were treated as overdamped and with natural frequencies much lower that measured here. Both of these system performance findings result in excellent utricle time response to acceleration stimuli and a broad frequency bandwidth up to 100 Hz. This study is the first to establish the upper end of this mechanical system frequency response of the utricle in any animal.

INTRODUCTION

The utricle and saccule are the linear accelerometers of the inner ear. These organs report static head tilt and acceleration of dynamic head motion in their current plane of orientation. It is important to recognize that the nervous system’s use of signals emanating from these sensory organs can have no better frequency response than the capability of their extracellular mechanical system. The lower end of these two organ’s frequency response is obviously static, or zero frequency (DC) used to report static head tilt. To our knowledge, the upper end of the utricle mechanical system frequency response has not been established in any animal. The work reported here is limited to the mechanical aspect of the utricle peripheral end organ and does not explore any aspects of neural transduction or saccule dynamics.

The extracellular structure of the utricle forms a second order mechanical system—of mass, elastic, and damping elements—that responds to inertial motion of the head and gravity. The dynamic behavior of this system is modeled as a linear second order system that is described and quantified using its undamped natural frequency ω_n and the viscous damping factor or damping ratio ζ. The work reported on here measured these two parameters in the utricle of the red-eared turtle by matching the linear model to experimentally measured displacement data. The linearity assumption of the system model in the range of experimental accelerations is verified using tests for nonlinearity. With the two parameters determined, the upper end of the utricle’s frequency response can be predicted.

The first experimental study to report a stiffness and natural frequency of an otolithic organ was conducted on fish with the majority of the measurements made on the saccule of Ruff fish (De Vries 1951). This work on the saccule concluded that the dynamic system was near critically damped and probably slightly overdamped. In the fish studied, the saccule stone is a single crystal and its mass is quite large when compared to the utricle. This large mass also gave the saccular system a low natural frequency of 41 Hz. The small utricle mass in this fish resulted in small displacements that were out of the range of measurement accuracy for the techniques used. This lack of measurement capability prevented any conclusions regarding the utricle’s dynamic behavior.

We completed a previous experimental study of the turtle utricle dynamics (Dunlap et al. 2012). In this study, the relative displacement between the otoconial layer (OL) and neuroepithelial layer (NEL) was measured using high-speed video with an inertial stimulus. The inertial stimulus was administered using a piezoelectric actuator mounted in the microscope stage. In this experiment, the utricle was excited using six independent single frequencies (10, 25, 50, 75, 100, and 125 Hz) all held constant over a time period of seconds. The mean natural frequency was measured as ω_n = 363 Hz, and the damping ratio was ζ = 0.96. The natural frequency result was much higher than expected (De Vries 1951; Wilson and Jones 1979) and the highest stimulus frequency did not exceed natural frequency. These results were surprising and led to the development of the study presented here. Much better experimental results could be achieved using a stimulus frequency spectrum extending above the natural frequency. In the work described here, a continuous increasing stimulus frequency up to 500 Hz was used. In addition to the stimulus frequency past the natural frequency, analysis of the displacement data was much improved by utilizing a model fit to this data that was done in the complex plane. In this model fit to displacement data, both amplitude and phase were matched. Our previous study only matched amplitude ratios. Combining stimulus frequency past the natural frequency and utilizing the complex plane analysis of model fit to the displacement data resulted in a far superior evaluation of the utricle’s dynamic system.

METHODS

Approach and Turtle Utricle Structure

The objective was to stimulate the utricle past its point of resonance as measured from our previous experiment. The turtle was again used for these studies and the utricle was again mounted in a piezoelectric driven microscope stage. High-speed video was used to measure the displacement of the OL and NEL. The stimulus to the piezoelectric driven stage was changed from previous experiments. A linear sine-sweep signal, commonly referred to as a chirp signal, was used that linearly ramped from 0 Hz up to 500 Hz in 5 s. The upper frequency stimulus of 500 Hz was chosen to guarantee passing the previously measured utricles resonance frequency. In the previous experiments, only amplitude was measured and matched to a model. In this new set of experiments reported on in this work, both magnitude and phase data were matched to a model. The combination of chirp stimulus and matching both magnitude and phase data resulted in a superior evaluation of the utricle’s system dynamics. In addition, nonlinearity was evaluated by comparing the results when the stimulus was reversed starting at 500 Hz and decreasing linearly to 0 Hz over the same 5-s time period. Changing stimulus magnitude and comparing the results for proportional linear deflection is also used to check for nonlinearity.

The turtle utricle is comprised of four layers known collectively as the otoconial membrane (OM). The upper three layers starting from above are the following: (1) otoconial layer (OL), (2) compact gel layer (GL), and (3) column filament layer (CFL). The base layer (4) is the neuroepithelium layer (NEL), and this layer contains receptor hair cells (HC). This layer structure is shown in Figure 1A. The OL is composed of carbonate crystals (both calcite and aragonite in the turtle (Carlstrom 1963)) bound together by protein and covered above with endolymph fluid. The middle two layers, GL and CFL, will be referred to here collectively as the shear layer (SL). It is these two layers that are sheared by the relative displacement between the OL and NEL. The shearing displacement between these two layers is induced by acceleration during head motion and gravity during head tilt. Measuring the dynamic mechanical properties of this SL is the major objective of this work. Each HC receptor has an organized structure of mechanosensitive cilia known as a hair bundle (HB) protruding into the SL, adding mechanical stiffness to this layer. The overall SL properties that are measured here include the stiffness contribution of these HBs.

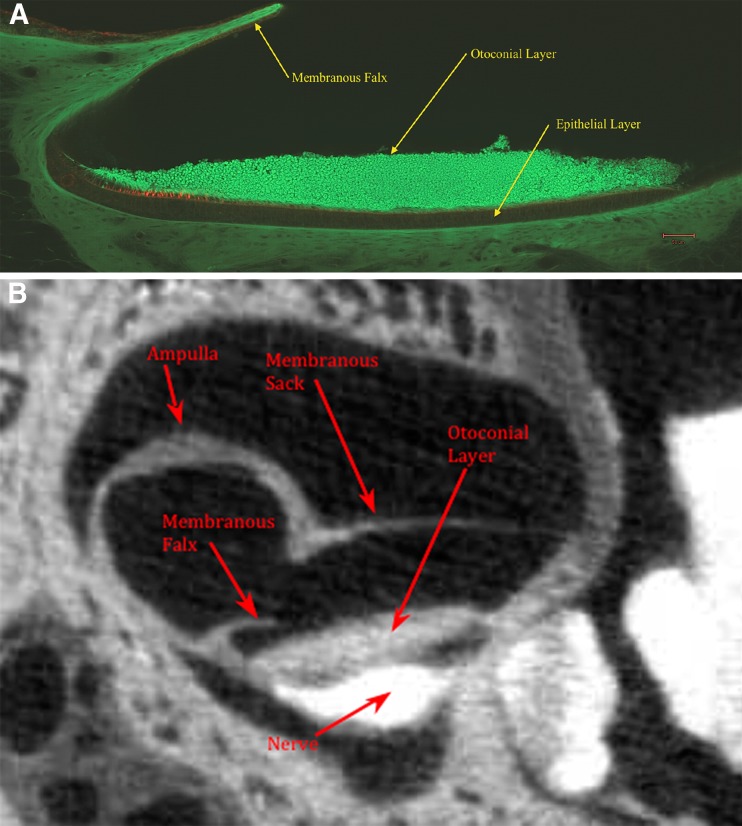
FIG. 1.

A Confocal image of medial-lateral cross section of the turtle utricle. Overlying the lateral surface of the utricle is a falx-shaped rigid structure referred to as the membranous falx (MF). The MF forms a semicircular membrane that is rigidly attached to the membranous utricle-sac walls (see Fig. 2B). The column filament and gelatinous layers are located between otoconial and epithelial layers. Hair cells are tagged red in this layer and can be seen in the striolar regions on left side of this figure. B Single frame of a osmium contrast enhanced micro-CT image of the turtle utricle shown in medial-lateral cross section. This figure shows the general structure of the overall membranous utricle and membranous falx location relative to other structures.

The utricle has a tadpole shape from a top view with the medial end forming the tail as shown in Figure 2A, B. The utricular nerve that innervates the underside of the NEL extends outward from this medial tail and enters the brain cavity through its bony wall. This nerve and the utricular sack anchor the entire structure to the bony wall of the skull as shown in Figure 1B.

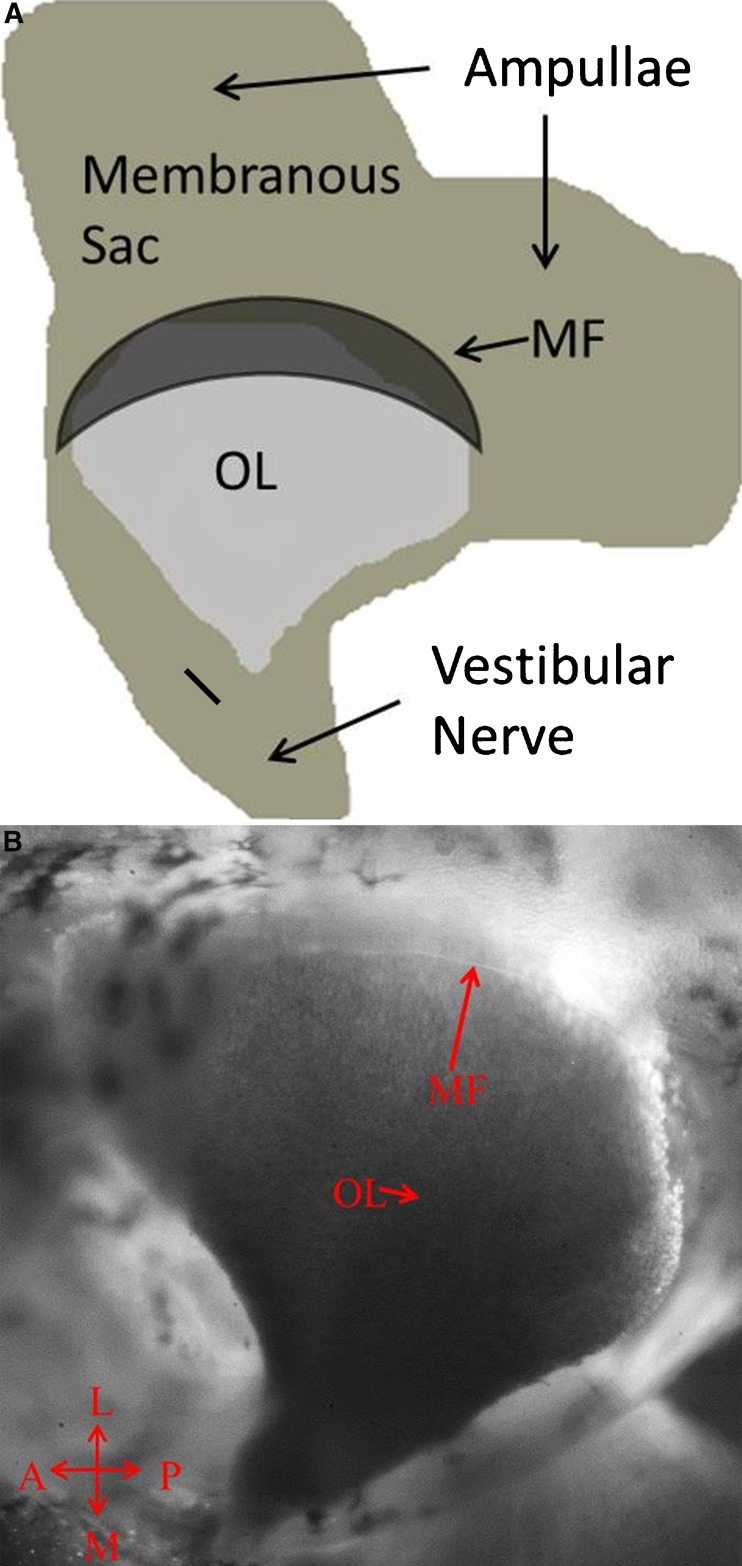
FIG. 2.

A Top view schematic of the utricle after the membranous sack has been opened and the two ampullae layed out for placement on the slide for microscope imaging. The membranous falx (MF) is shown dark to emphasize its location above the otoconial layer (OL). The medial edge of the MF follows the approximate location of the striola. B Light microscope image (×40) of the top view of turtle utricle showing the MF edge, its translucent visability, and ease of location. The MF’s rigid attachment to the membranous utricle wall and its semicircular shape form a solid rigid structure.

Lying just above the lateral surface of the utricle is a rigid membranous structure called the membranous falx (MF) shown in Figure 2A, B. The MF forms a semicircular membrane, a falx, that is rigidly attached to the utricle wall just above the peripheral edge of the NEL. It has origin just below the anterior and horizontal ampulae of the semicircular canals and projects outward over the lateral end of the utricle with its edge terminating over the utricle striolar region. The MF can be seen in both Figures 1 and 2. The MF contains connective tissue, and this combined with its shape and edge support makes it structurally rigid. It is translucent and obscures the lateral end of the utricle from observation through a light microscope. The edge of the MF served as a reference point for the NEL motion as the two perfectly tracked one another’s motion within our displacement measurement capability.

Specimen Preparation and Tissue Preservation

Utricles from red-eared turtles (Trachemys (Pseudemys) scripta elegans), with 4 to 6 in. carapace length, housed in a controlled room temperature environment, were used for all the experiments. An intraperitoneal injection of 0.5 ml Euthasol (390 mg/ml pentobarbital sodium, 50 mg/ml phenytoin sodium; Delmarva Laboratories) was administered to the turtles and followed the guidelines established by the Virginia Tech Institutional Animal Care and Use Committee. The utricle was then removed from the skull and maintained for the duration of the experiment in a buffered Hanks’ balance salt solution (bHBBS) [HBSS: 1.25 mmol L⁻¹ CaCl₂, 0.493 mmol L⁻¹ MgCl₂, 0.407 mmol L⁻¹ MgSO₄, 5.33 mmol L⁻¹ KCl, 0.441 mmol L⁻¹ KH₂PO₄, 4.17 mmol L⁻¹ NaHCO₃, 137.94 mmol L⁻¹ NaCl, 0.338 mmol L⁻¹ Na₂HPO₄, 5.56 mmol L⁻¹ D-glucose; Invitrogen/Gibco; buffering achieved with 10 mmol L⁻¹ Hepes: 4-(2-hydroxyethel)-1-piperazineethanesulfonic acid; Sigma-Aldrich]. The bHBSS solution had a pH = 7.2 and an osmotic concentration of 300 mOsm L⁻¹, and formed a buffered, isotonic, artificial perilymph solution. The pH was confirmed with a pH meter, and the osmotic concentration was confirmed with a vapor osmometer. The utricle membranous saccule was opened exposing the dorsal utricular surface. Opening the utricular saccule in the bHBBS solution results in switching the utricle from endolymph (high in K⁺ concentration) exposure it to the artificial perilymph solution (high in Na⁺ concentration).

Exposure of the utricle surface and its SL to an artificial perilymph solution has been shown to not change the gel mechanical properties of the SL (Benser et al. 1993). In this experiment, using a bullfrog saccule, the shear stiffness of the SL was measured using a dual chambered apparatus that held the saccule and surrounding tissue. After placing the saccule in the dual chamber, the crystal OL was removed, and stiffness was measured using a fine glass fiber pipette. The hair cell body-tissue side was isolated from the bundle side in this two-chambered device. The hair cell body side was in an artificial perilymph solution similar to extracellular fluid composition, and the bundle side was exposed to both artificial endolymph and artificial perilymph solutions. No difference in shear stiffness could be measured with exposure to the two solutions. The artificial perilymph used in this experiment was very similar in composition to the bHBBS used in the current set of experiments.

To further help maintain the SL tissue mechanical properties with this change in surrounding fluid composition, three important aspects of the artificial perilymph solutions were observed. The artificial perilymph solution had (1) divalent ions present in the proper composition to prevent SL swelling, (2) buffered pH to maintain cell and tissue viability, and (3) proper osmotic concentration to prevent tissue swelling (Freeman et al. 2003). Two divalent ions of Ca⁺⁺ and Mg⁺⁺ are present in the bHBSS solution in concentrations that prevent the SL from swelling or shrinking (Shah et al. 1995). The buffered pH helps maintain cell life as these cells are surrounded by natural physiology ion concentrations. The solution’s isotonic osmotic concentration maintains tissue and cell volume preventing any tissue swelling and/or shrinkage, especially the SL gel. It is important that all three of these aspects of the solution be present to aid preservation of tissue and its mechanical properties during the experiment. Microscopic observation of the utricle and its associated tissue during the course of the experiments showed no signs of tissue swelling and time exposure tissue changes or damage. These observations were made throughout the entire range of all experiments.

It is also important for the HC bundles to retain their stiffness as they contribute approximately 50 % to SL stiffness (Benser et al. 1993). This turtle species will retain their HC stiffness for periods of 5 h or more with exposure to this bHBSS artificial perilymph solution (Spoon et al. 2011). This HC bundle stiffness retention time is well beyond any data collection period utilized here, the maximum being 2 h.

Once the utricle was opened, some of the membranous utricular sack was trimmed away, leaving the membranous lateral and anterior ampullae walls and the utricular nerve exposed. The specimen was then fastened to a glass slide using three single strands of dental floss, with two strands passing across each ampullae wall and the final strand passing over the purposefully remaining portion of utricular nerve. This was carefully done so as not to disturb the utricle and its surrounding structure. The glass slide was placed in a custom designed holder and then into the piezoelectric stage. Note that each utricle was examined under magnification (at least ×40), and if obvious defects from the dissection or other apparent artifacts were present, it was not used for experimentation. Discard after examination was not prevalent once the experimental protocol was established; however, some were discarded.

Experimental Procedure

The utricle was transferred to a fixed stage microscope set in a micromanipulator platform that houses a piezoelectric actuated dual-axis displacement stage (PI Inc., P-541.2DD). The microscope and platform were mounted on a vibration isolation table. The utricle was oriented on the piezoelectric stage so that displacements would occur along an approximate medial-lateral (ML) axis and anterior-posterior (AP) axis in later experiments. While the piezoelectric stage was oscillated to induce an inertial stimulus to the OL, a high-speed video camera (Photron APX-RS) connected to the microscope binocular phototube was recording the translation of the OL and MF reference. Video could not be taken of both the OL and MF simultaneously because the microscope field of view was too narrow to see both. Therefore, video was first taken of the OL using the chirp stimulus and then immediately repeated for the MF reference using an identical stimulus. The recorded video was transferred from the cameras internal memory to external storage for further processing after each recording.

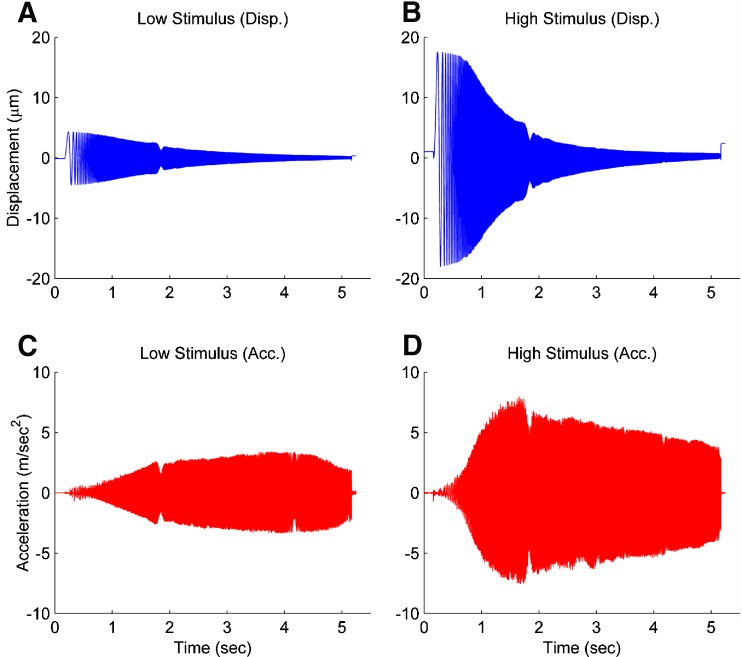
Figure 3 shows the chirp signal displacement and acceleration of the NE for both a low and high amplitude stimuli that were used. These two amplitudes stimuli were used to evaluate the linearity of the utricle dynamics. The displacement amplitude rolls off at the higher frequencies because the upper velocity (slew rate) for the piezoelectric actuator is limited to 6,000 μm/s and that value is reached at the higher frequencies limiting amplitude response. The roll off in the displacement amplitude of the piezoelectric stage at higher frequencies does not impact the use of this as an excitation stimulus because the piezoelectric stage translation does not differ between the OL and MF video recordings. This duplication of stimulus between the two recordings was verified using the same view of a visual contrast area on a control slide.

FIG. 3.

The low and high magnitude stimuli used for the piezoelectric actuated stage. The displacement and acceleration of both low and high magnitude stimulus are shown in the left and right column, respectively. Each stimulus is a linear-sine sweep ranging from 0–500 Hz for approximately 5 s. The displacement of the piezoelectric stage decreases in displacement as the frequency increases because the maximum velocity of the stage is 6,000 μm/s. The low and high stimuli provide different accelerations to verify the linearity of the utricles mechanics.

The high-speed video camera recorded at a rate of 2,000 frames per second (fps). This frame rate was chosen based on the Nyquist-Shannon sampling theory to prevent aliasing of the displacement waveforms (Doebelin 1966). The 2,000 fps also allowed optimal use of the video cameras internal memory for the 5-second duration stimulus.

All video imaging was carried out at ×100 magnification. The OL motion was recorded from a point located in the approximate center of the utricle, defined as half way between the medial-lateral edges and half way from the anterior-posterior edges of the OL. It was a short distance movement of the microscope objective from this center point to the edge of the MF reference. The MF edge proved to be easy to locate in the microscope, and precisely followed the NEL’s movement. The consistent observability due to excellent contrast, ease of location, and precise following of NEL motion, made this the ideal site for reference tracking.

A Zeiss AxioExaminer A1 microscope equipped with an epi-illuminated mercury vapor short arc bulb (X-Cite series 120Q) was used for these experiments. The epi-illumination provides abundant light, creating more image contrast, enhancing feature recognition, and aiding the image registration algorithm.

Data Acquisition and Computations

Data was gathered using a National Instruments sequential NI-6060E data acquisition board with a custom LabView program. A trigger pulse initiated from the data acquisition board started the high-speed video recording and also illuminated a LED that was mounted within the C-mount adapter of the binocular phototube. The LED illumination time stamped the initial image by saturation of the cameras CMOS sensor. The occurrence of each video frame and the piezoelectric stage voltage were recorded in the data acquisition program at 10 kHz. The piezoelectric stage was held motionless for 100 ms before the chirp signal was initiated. This was done so fixed images could be taken for creating a noise reduced reference image. The low noise reference image was later used in the image registration process. The chirp signal was then sent to the piezoelectric stage, while video was taken for the 5-s chirp signal period. The video recordings of the chirp driven displacement formed the motion images that were used to track the OL and MF reference displacements.

All video image analysis, data analysis, calculations, model fitting, and degree of fit of model to data were carried out in Matlab. The operations completed were all standard and utilized standard components in Matlab’s Image Processing, Systems Identification, and Statistics toolboxes.

Image Registration

Image registration is the process of spatially transferring and matching a reference image to a corresponding location on a second translated image (Gonzalez and Eddins 2004). The translated distance is then used as a measure of the relative displacement between images. The frame-by-frame translation of the OL and MF reference was measured using a custom Matlab program. For all high speed video recordings, the signal-to-noise ratio of the reference image was first increased by averaging 50+ motion free images captured during the initial time period the piezoelectric stage was held stationary. A sub-pixel image registration program was implemented to determine each frame’s displacement relative to the reference image (Guizar-Sicairos et al. 2008).

The sub-pixel image registration program was capable of better than a 15 nm translational detection. To validate this registration capability, first the pixel width was determined using known displacements of the piezoelectric stage that was capable of accuracy of 0.1 nm using capacitive displacement sensors. Calibration was achieved by translating a glass slide with adhesively bonded micro-beads that were utilized as visual reference. The pixel width was measured to be 163 nm using known displacements of the glass slide. Sub-pixel image registration was validated again using known displacements of the test image. This validation showed that in its worse case, the sub-pixel displacement could achieve resolving capacity of 0.09 divisions of a pixel width, resulting in an overall image displacement resolution of better than 15 nm. This was validated over the range of displacements used in the experiment.

Earlier trial work with image registration included rotation detection. Observations of rest and maximum displacements did not reveal any detectable rotation. As a consequence, we utilized pixel and sub-pixel registration algorithms that only looked for image translation, not rotation. This considerably reduced computer image registration processing time. As a consequence, the resulting pixel and sub-pixel displacement algorithm used for video image displacement had restrictions of two-dimensional rigid translations that had no rotation, skewing, or scaling.

The translation displacements without rotation information eliminated the possibility of rigid-body analysis of the OL motion. There was transverse axis AP displacement with ML excitation (see “Results”) that would indicate some stiffness difference in the two directions investigated. Without additional rotational information, it is difficult to apply any sort of analysis that would yield preferred specific or eigenvector directions. We have shown that there are preferred directions with FEA models of this very turtle utricle organ (Davis et al. 2007). However, the only hint that these exist was the slight orthogonal displacements to the stimulus direction.

MF Tracking Controls

The MF was used as a reference for filming the NEL motion because it proved to be rigid relative to the NEL, had reliable visibility with optical microscopy, was easily located, and had excellent image tracking quality. The medial tip of the utricle NEL is sparsely speckled with dark pigmented melanin cells and these served as the target images used for control comparison to the easily observable MF. Two control experiments were completed using two different utricles from different turtles. In these control experiments, the MF and the melanin cells in the outer edge of the medial tip of the utricle’s NEL were filmed and tracked using identical sinusoidal oscillations over a range of six frequencies from 25 to 125 Hz. No relative motion between the MF and NEL was detectible. If there was relative motion, it was below the resolution range of the image registration (<15 nm).

Frequency Response Function

The image registration procedure produced displacement data in the time domain. The time domain displacement data is defined as the following: y(t) = OL displacement, and u(t) = MF reference displacement. This time domain data was then converted to frequency domain data using the following process. First, the auto power-spectral density of the system’s output S_yy is computed. Then, the cross power-spectral density of the system’s output to input S_yu is computed (both the auto and cross power-spectral density were computed using Signal Processing Toolbox in Matlab, cpsd was the function used). These were calculated at equal unity frequency increments ω forming a set of data numbered by m increments using the Welch’s averaged, modified periodogram method of spectral estimation (Ifeachor and Jarvis 2002; Williams and Lawrence 2007). These two spectral density data sets were converted to a frequency response function (FRF) using element-by-element complex division, resulting in the output displacement relative to input displacement data set

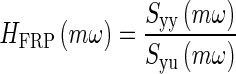1

The frequency response function H_FRF represents the experimentally collected relative displacement data in complex transfer function format in the frequency domain. The coefficients in the model’s transfer function are adjusted to fit this data.

Utricle Model

It has been well established that the utricle behaves as a second order system (De Vries 1951; Wilson and Jones 1979; Grant et al. 1984), and the dynamic equations used to model the utricle originate from Newton’s second law of motion. The utricle’s dynamics come from the intrinsic stiffness and viscous shearing forces of the SL acting upon the OL, as well as the extrinsic forces of fluid shear and buoyancy from the surrounding endolymph. The second order dynamics are characterized by the natural frequency ω_n and damping coefficient ζ.

Applying Newton’s second law of motion to the utricle, summing forces, arranging terms, result in a lumped parameter governing differential equation for the utricle’s OL. Taking the Laplace transform of this differential equation with zero initial conditions, results in a model transfer function (TF) that was used to fit to the H_FRF data. Derivation of this TF and variable definitions are in the “Appendix”. The model TF is termed H_MDL where s is the Laplace transform variable, and the TF is given in Eq. 2 below

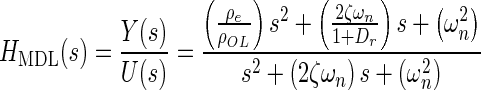2

The TFs characteristic equation is the denominator, which contains the two system dynamic parameters of interest ω_n and ζ. These are also seen in the numerator. The fitting process of the model transfer function H_MDL to H_FRF data was done in the complex plane where the coefficients 2ζω_n and ω_n² were adjusted for the best fit. The parameters ω_n and ζ were then taken from the resulting best-fit characteristic equation of the model to data.

Model Fit to Data and Waveform Time Alignment

In standard digital-signal analysis, the input and output data are collected simultaneously. In these experiments, the input and output had to be collected sequentially due to the restriction of filming in a single location. The OL and reference MF could not be filmed simultaneously because of the limited microscope field-of-view. The OL video was filmed first and the MF reference was filmed immediately afterward using the identical stimulus. This procedure required that the two recordings be time aligned for good data analysis of relative displacement and phase. The initial 100 ms delay to collect reference image data exacerbated this time alignment problem. Small inconsistencies in start time for the stage motion caused by both the hardware and software of the piezoelectric stage controller and driver, and in the data acquisition system, produced small time misalignments between the two video recordings. Start time was initiated and marked electronically by the data acquisition system, and also marked in the video recordings by a flash from an LED in the microscope phototube.

A time alignment procedure was developed where each 500-μs time period between video image displacement points was subdivided into 10 increments of 50 μs each. The new intermediate displacement point values were determined using a cubic-spline fit between the original data points. The OL and MF reference data sets were then aligned to their original time initiation mark, and initially shifted by one single 50-μs time increment. The two data sets were then converted to H_FRF data and fit to the model using the method described previously. The time shifting was continued by incrementing another 50-μs shift. At each time-shifted data set, the degree of accuracy of the model transfer function fit was evaluated using a convergence criteria. The convergence criterion was based on the second order transfer function evaluation of pole convergence in the complex plane (Dunlap et al. 2012). The time shifting increments were continued in both the positive and negative time direction. When the convergence criterion was minimized, the two data sets were deemed best aligned. The coefficients from the characteristic equation in this best time aligned model were used for ω_n and ζ of the utricle from that experiment. In all time shifting analysis, only a few time shifts were made from the original time initiation mark. This time alignment process produced minor changes in the resulting values of ω_n and ζ in a given experiment when compared to values without using time alignment. The time alignment procedure did result in narrowing of the 95 % confidence intervals when all utricle values from each separate experiment were evaluated as a group.

Evaluation of Model Fit to Data

Normalized root mean square error (NRMSE) was used to evaluate the resulting fit of a H_FRF data set to the model H_MDL in each utricle (computed using Systems Identification Toolbox in Matlab, goodnessOfFit was the function used). NRMSE is utilized in frequency response domain (FRD) analysis to compare a model of the system to actual data in the frequency domain. The calculation is made using the complex frequency domain data and the complex transfer function model. Thus, both the magnitude and phase are considered in a combined calculation. This calculation does not utilize a separate fit for magnitude and phase and then combine these two results. Although calculated differently, the output from the NRMSE is equivalent to the correlation coefficient (r), and is expressed as a percent. The NRMSE value is given in the results table for each utricle that was evaluated. The NRMSE value is a measure of how well the model fits the data set and can be evaluated using correlation coefficient criteria.

The NRMSE was not used as the aforementioned convergence criteria for model fit. Instead, the NRMSE was used as a measure of the resulting model fit to the data, and served as a check for the model fitting process to the experimental data.

Linearity Verification

A linear transfer function model was fit to the collected data. The question of appropriateness of this linear model to represent actual utricle dynamic performance was checked and verified using two evaluation techniques. First, the principle of superposition was used where the stimulus frequency chirp signal direction was first applied from 0 to 500 Hz and then from 500 to 0 Hz. Reversing the chirp stimulus frequency starting point verifies the utricle’s linearity for a given stimulus acceleration magnitude if the system’s dynamic response is identical for each direction (Ogata 2002). This was evaluated for each of the signal directions by checking for a statistical difference between ω_n and ζ between the two directions.

The second linearity test utilized acceleration magnitude change. An ideal accelerometer will respond to different applied acceleration magnitude stimuli with proportional proof mass displacement (Beckwith and Marangoni 2007). The stimulus magnitude was administered using amplitudes of both low and high acceleration (see Fig. 3). Since stimulus acceleration magnitudes were not constant over the entire frequency range of the chirp signal, relative high and low descriptions are used here. The high acceleration stimulus was the largest that could be achieved with the piezoelectric displacement stage, and the low stimulus was the minimum acceleration stimulus that could be used and remain in a good data collection range without significant noise. Non-proportional relative displacements to stimulus magnitudes would indicate nonlinearity. Again, significant statistical differences in ω_n and ζ were used for evaluation. These experiments were run in the later half of all experiments (see Table 1).

TABLE 1.

Utricular mechanical parameter measurements and NRMSE fits for all stimuli

	Medial-lateral axis				Anterior-posterior axis
	High acceleration		Low acceleration		High acceleration		Low acceleration
Utricle	0–500 Hz	500–0 Hz	0–500 Hz	500–0 Hz	0–500 Hz	500–0 Hz	0–500 Hz	500–0 Hz
1	341, 0.44 (94.6)	–	–	–	–	–	–	–
2	279, 0.47 (96.5)	–	–	–	–	–	–	–
3	366, 0.49 (97.6)	–	–	–	–	–	–	–
4	326, 0.41 (97.4)	–	–	–	–	–	–	–
5	342, 0.57 (96.9)	–	–	–	–	–	–	–
6	376, 0.60 (89.4)	–	–	–	–	–	–	–
7	340, 0.47 (94.3)	–	–	–	–	–	–	–
8	334, 0.59 (93.5)	–	–	–	–	–	–	–
9	445, 0.55 (95.3)	–	–	–	–	–	–	–
10	445, 0.47 (89.0)	–	–	–	–	–	–	–
11	380, 0.53 (91.5)	–	415, 0.49 (93.9)	–	444, 0.53 (91.5)	–	428, 0.54 (91.0)	–
12	361, 0.49 (89.3)	399, 0.57 (90.2)	–, –	–	407, 0.52 (85.2)	407, 0.47 (77.8)	–	–
13	473, 0.62 (88.0)	–	489, 0.63 (93.2)	–	431, 0.60 (92.1)	–	420, 0.57 (95.0)	–
14	302, 0.42 (75.7)	362, 0.45 (94.2)	–	–	385, 0.49 (81.2)	353, 0.53 (85.8)	–	–
15	382, 0.50 (88.9)	388, 0.51 (80.0)	–	–	331, 0.59 (84.8)	350, 0.59 (94.3)	–	–
16	349, 0.47 (82.3)	399, 0.51 (94.7)	361, 0.40 (79.3)	386, 0.47 (89.2)	460, 0.50 (90.4)	441, 0.51 (92.3)	425, 0.44 (83.7)	444, 0.49 (87.6)
17	408, 0.51 (83.7)	485, 0.54 (93.1)	409, 0.50 (86.9)	386, 0.52 (73.2)	360, 0.51 (91.1)	433, 0.62 (96.0)	386, 0.57 (72.5)	392, 0.61 (92.6)
18	392, 0.49 (90.6)	406, 0.53 (93.0)	–	–	433, 0.59 (95.7)	395, 0.55 (82.1)	430, 0.54 (95.6)	396, 0.50 (92.8)
19	295, 0.40 (87.9)	328, 0.43 (88.4)	315, 0.38 (89.0)	321, 0.34 (73.0)	–	–	394, 0.34 (77.0)	–
20	386, 0.45 (95.0)	383, 0.45 (95.7)	366, 0.42 (89.8)	395, 0.45 (90.8)	425, 0.41 (94.2)	434, 0.42 (96.3)	423, 0.35 (85.0)	439, 0.40 (87.5)

Results reported as: ω _n, ζ (NRMSE)

Average NRMSE = 89.2 % with standard deviation of 6.4 %

Anterior-Posterior Experiments

In the later half of experiments in addition to the medial-lateral direction of stimulation, anterior-posterior stimulations were also investigated. These were done in order to see, within our displacement resolving capability, if any difference in natural frequency and damping could be detected in the two anatomical directions.

RESULTS

The natural frequency, damping coefficient, and NRMSE for all utricles, along with their corresponding high or low acceleration stimuli, are presented in the Table. For the first ten utricles, only medial-lateral data was collected. During the last ten, different stimulus magnitudes, chirp signal frequency direction reversal, and anterior-posterior data were also collected. Even in these last ten utricles, a complete set of data was not gathered for each utricle due to experimental difficulties and limitations.

Each utricle’s reported mechanical parameters were combined to form an overall set of mechanical parameters along corresponding anatomical axis. The median and 95 % confidence interval for ω_n and ζ were developed from this combined data set. The shear modulus G along each anatomical axis was also calculated using the natural frequency and anatomical data (see “Appendix”). The shear modulus was used to compare to other results of similar vestibular structures. The median is presented instead of the average because of the lower sample sizes. Note all medians and 95 % confidence intervals were found using the sample group’s interquartile range and sample size. The M-L anatomical axis parameters were found to be: ω_nML(20) = 374 (353, 396) Hz, ζ_ML(20) = 0.50 (0.47, 0.53), and G_ML(20) = 9.42 (8.36, 10.49) Pa. The A-P anatomical axis parameters were found to be: ω_nAP(10) = 409 (390, 430) Hz, ζ_AP(10) = 0.53 (0.48, 0.57), and G_AP(10) = 11.31 (10.21, 12.41) Pa.

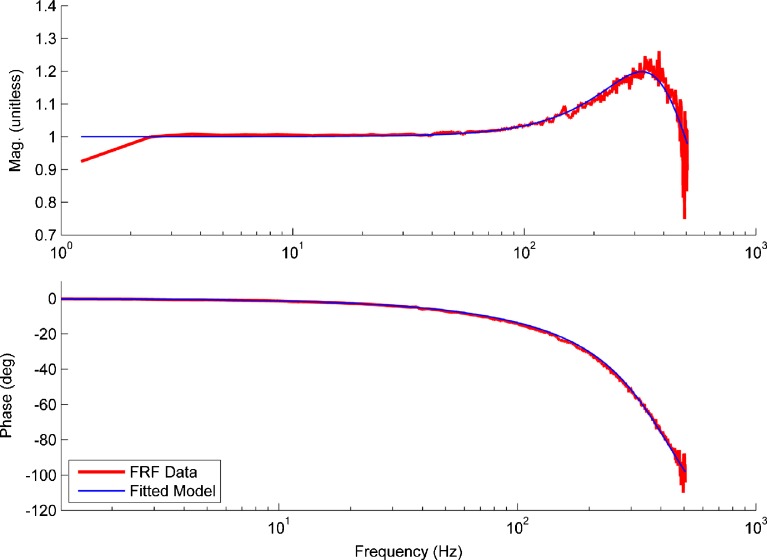
Figure 4 is a graphical representation of FRF data matched to the model for utricle no. 16 (anterior-posterior direction, 0–500 Hz, high acceleration data). The NRMSE for this figure is 90.4 % and is the median value for all experiments. Thus, Figure 4 represents the median fit of the model to data and should be considered exemplary of all cases. Notice that only a single resonance is present in the magnitude response of the utricle, thus indicating the utricle is a second order dynamic system.

FIG. 4.

Plot showing the fit of the model H _MDL (blue line) to the H _FRF data (shown in red). This example is that of the median of all NRMSE values and is thus a median representative of the model fit to data. The image registration waveforms of the MF and OL data are used to form the H _FRF data. Both magnitude and phase were used in the fitting process of model to data. The magnitude data has been normalized to the mean of the flat response region. The magnitude begins to increase from a flat response close to 100 Hz, and the phase begins to lag as well at this point. Only a single resonance is present in the H _FRF data and is indicated by the crest of the magnitude data near 370 Hz. The ω _n and ζ are estimated from the H _MDL model coefficients determined from the data fit.

ML and AP Axis Anisotropy

A comparison of the mechanical parameters of the A-P and M-L anatomical axes were conducted to determine if anisotropic material properties exist for the two directions. The statistical comparisons of the M-L and A-P axes were done using a two-sided nonparametric Wilcoxon rank sum test (U). The anatomical axis comparison of ω_n and ζ provided a U_(10,20) = 56, P = 0.056 and U_(10,20) = 84, P = 0.495, respectively. This statistical comparison indicated that there was no significant difference in mechanical properties between the A-P and M-L axis. Although no significant difference between the directionally mechanical properties could be concluded with a high level of confidence, it did suggest the most influential difference would be in SL stiffness and not damping.

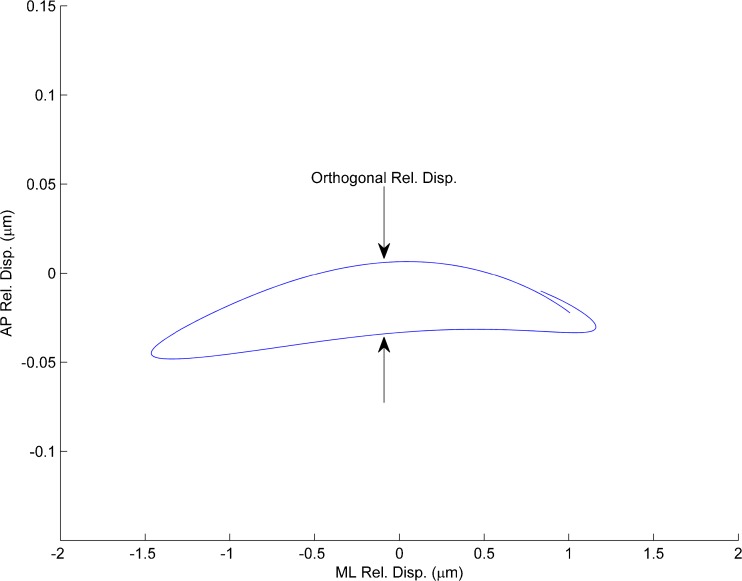
Despite the statistical analysis indication of no significant difference in stiffness in the two stimulus directions, displacement of the OL in the transverse direction to the stimulus did indicate that there was some reason to believe that stiffness difference in the two directions did exist. Such off axis displacement from the stimulus direction would indicate stiffness directional difference or anisotropic behavior in the SL. This off-axis displacement has been show to arise with anisotropic stiffness in Finite Element models of an anatomically correct turtle utricle (Davis et al. 2007) and in simple lumped parameter models with different stiffness values in two orthogonal directions. Eigenvector directions were established with the Finite Element models; however, we were unable to confirm their directions with this study. Figure 5 is a 2-D plot of displacement of OL motion that shows slight transverse displacement from the stimulus direction. Note that the scales on the two directions are different with the transverse scale increased by a factor of 10X for emphasis.

FIG. 5.

Plot of relative displacement (between neuroepithelial layer and the OL) in the plane of the otolith. Displacements in both ML and AP directions shown. The stimulus was in the ML direction and the slight transverse displacement AP direction is shown and emphasized by increasing the transverse scale (AP-axis) by a factor of 10×. Such off axis displacement from the stimulus direction would indicate some slight anisotropic stiffness in the SL.

Linearity of Utricle Sensory Measurement

A two-sided nonparametric statistical group comparison test, the Wilcoxon rank sum, was utilized to check linearity by comparing both: frequency reversal and acceleration magnitude changes. Linearity was examined for both anatomical direction axes individually, by first comparing frequency reversals: (1) high acc. with chirp stimulus from 0 to 500 Hz versus high acc. with stimulus from 500 to 0 Hz, and (2) low acc. stimulus from 0 to 500 Hz versus low acc. stimulus from 500 to 0 Hz. Then linearity was evaluated between the acceleration magnitudes for both anatomical direction axes individually, by comparing the following: (3) high acc. 0–500 Hz versus low acc. 0–500 Hz and (4) high acc. 500–0 Hz versus low acc. 500–0 Hz.

All linearity comparisons of mechanical parameters provided P values much greater than 0.5 indicating that the utricle behaves linearly for the stimuli investigated. This does not mean that the utricle is linear over all acceleration magnitude ranges. In the saccule, larger magnitude accelerations than those used here (0.8 g maximum) have been shown to produce deflections that were not linearly proportional to acceleration (De Vries 1951).

For all experiments, the spectral coherence for the utricle’s dynamic response was greater than 0.9. A coherence of this magnitude is yet another indicator of the utricle’s linearity within the tested acceleration ranges.

It is important to recognize that linearity of acceleration measurement is exactly what is desired in the utricle and in any accelerometer. Linearity here is defined as linearly proportional deflections in response to acceleration magnitudes.

DISCUSSION

Mechanical Parameter Values

The median natural frequency and 95 % confidence values in the M-L direction of ω_n = 374 (353, 396) Hz in this work is similar to our previous experimental work of 363 (328, 397) Hz. However, the damping coefficient ζ was considerably lower at 0.50 (0.47, 0.53) versus the previous 0.96 (0.80, 1.12), again both in the M-L direction (Dunlap et al. 2012). We hypothesize that the increased amount of FRF data, data past the utricles resonance frequency, and Frequency Domain Systems Identification technique used for data curve fitting have improved the measurements of both ω_n and ζ. In the previous experiment, we collected data up to only 125 Hz, not past the utricles resonant frequency, and then fit this data to a TF using only amplitude ratio data without phase data. The work reported here incorporates a much larger data set, over a much broader frequency range, with much better data analysis, and better TF curve fitting routine. We feel that the values of damping coefficients from this work rest on much more solid experimental ground.

The surprising results from this work are the following: (1) the utricle is under damped and by a significant amount, and (2) the natural frequency is much higher than previously thought. Previous experimental and analytical work had always shown and postulated that the otolithic systems were over-critically-damped (De Vries 1951; Kellog 1965; Young and Meiry 1968). Most of the overdamped assumption was based on perceptual data and empirical transfer functions with inherent forms of an overdamped dynamic system (Young et al. 1966). The fact that the canals were over damped lead to some of these conclusions. The natural frequency estimations were based on animals with large mass saccules where De Vries (1951) estimates the natural frequency of the Ruff fish at 40 Hz. Utricles have much lower mass than these large mass saccules leading to much higher frequencies. A good description of this early work can be found in Wilson and Jones (1979).

Shear Modulus

Due to a similar ω_n for this work and our previous experiment, the shear modulus values are in good agreement, of G = 9.52 Pa in this study, versus the previous of 8.86 Pa. These values are in agreement with all previous published data placing this value in the order of 10 Pa (Groen et al. 1952; ten Kate 1969; Kondrachuk 2001; McHenry and VanNetten 2007; Selva et al. 2009). The effective shear modulus from this work is one of the few ways of comparing these results to other measurements and predicted values of similar inner ear structures.

Utricle Mechanical Time Response

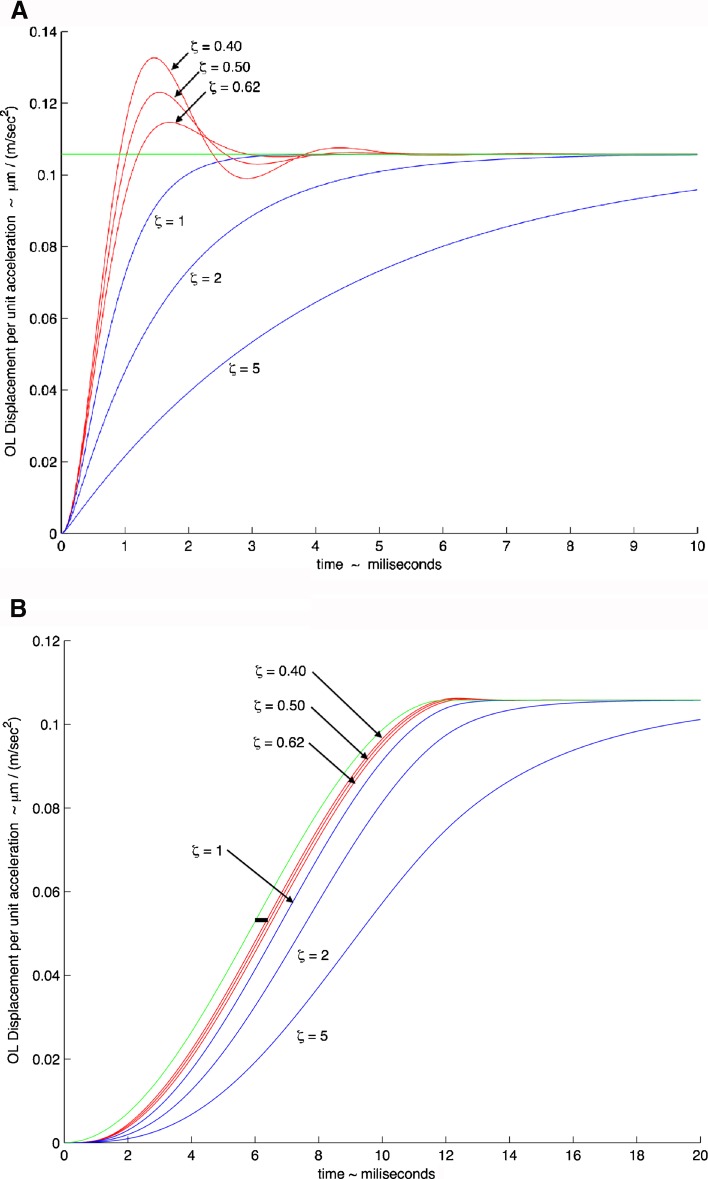
Figure 6A, B shows simulated time response of the utricle system using two different acceleration stimuli. In these two simulations, the median natural frequency value used was ω_n = 374 Hz, the median value found in this study in the M-L direction. Three curves were generated with this natural frequency using the maximum and minimum values of the damping coefficient, ζ = 0.40 and 0.62 as well as the median value of ζ = 0.50, all from the M-L direction with high-acceleration stimulus. The response in both figures is plotted as mechanical gain in terms of displacement per unit acceleration versus time. The green lines represent the ideal instantaneous displacement response of the OL for the two acceleration stimuli shown.

FIG. 6.

Model response to head acceleration showing mechanical gain of OL displacement per unit acceleration (μm (m · s⁻²)⁻¹) versus time (ms). A Response to a step change in head acceleration. A step change is commonly used to observe the response dynamics of a second order system. B Model response to head acceleration using a cycloidal increase in acceleration for a 12-ms time period during a feeding strike. The feeding strike that is used for the model response is taken from an actual behavioral study (Rivera et al. 2012) where the cycloidal shape fits a segment of the acceleration experienced during the strike. In both plots, the natural circular frequency of ω _n = 374 Hz was used; the two extremes of the damping coefficient are shown, ζ = 0.40 and ζ = 0.62, along with the mean value of ζ = 0.50, are all shown in red. Critically damped value of ζ = 1 and overdamped values of ζ = 2 and ζ = 5 are shown in blue to illustrate the effect of increased damping on time response. The green line illustrates a perfect response of the otolith to the acceleration. The thick horizontal black line shown in (B) and located at a gain of approximately 0.055 and time of 5.5 ms, shows a 0.4-ms time period measured from the perfect response (green) line to the mean value response of ζ = 0.5. This short 0.4 ms time illustrates how rapidly the otolith responds to a real head acceleration stimulus.

The rise time and maximum overshoot of any second order dynamic system, like the otolith mechanical system, are generally referred to as its transient-response characteristics, and a step change in the stimulus is generally used to evaluate this response. Figure 6A shows this utricle’s system response to a step change in acceleration. The model response shows significant system oscillations that persist from 3 to 5 ms, depending on the value of the damping coefficient.

In most systems with mass, as in an animal’s head that is moved by muscle activation, it is impossible to achieve a step change stimulus. Most behavior head accelerations are not true step changes; they are more sigmoidal in shape and follow a cycloid dynamic stimulus. Figure 6B shows a second simulation where a segment of a rapid acceleration profile of a turtle’s head as experimentally measured in an actual feeding strike is used (Rivera, et al. 2012). The time period for the actual measured acceleration segment is 12 ms, and the acceleration ranged over a 4.20 g change during this period. The acceleration time profile used for this simulation is in cycloidal form and is modeled as

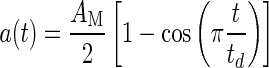3

where a = stimulus acceleration, A_M = acceleration amplitude, t = time, and t_d = stimulus time duration. This profile is an excellent representation of the actual acceleration in a feeding strike. Notice in Figure 6B that over the range of damping coefficients values found in this study there is minimal overshoot. This lack of significant overshoot is a result of natural head motions that are not as abrupt as the step change shown in Figure 6A. This stimulus acceleration can be considered an extremely rapid head movement. Also, note that in Figure 6B, the utricle follows the stimulus acceleration very well. The lag time between stimulus and utricle deflection is only 0.4 ms as shown by the solid black bar whose length represents this short time.

For second order systems, a tradeoff between rise time and maximum overshoot exists; meaning, only one of the two can be reduced simultaneously. Therefore, it is desirable for ζ to be between 0.40 and 0.80 (Ogata 2002). Commercial accelerometers also utilize damping ratio values in this same range, with 0.7 being an optimal desired value (Merovitch 2001). The implications of 0.40 < ζ < 0.62, as shown in Figure 6B, reveal that the compromise between rise time and maximum overshoot is excellent for the turtle utricle. As can be seen in Figure 6B, the otolith relative deflection follows the acceleration stimulus to better than 0.5 ms. Values of ζ > 1.0 will produce delayed transient-responses.

Utricle Mechanical Frequency Response

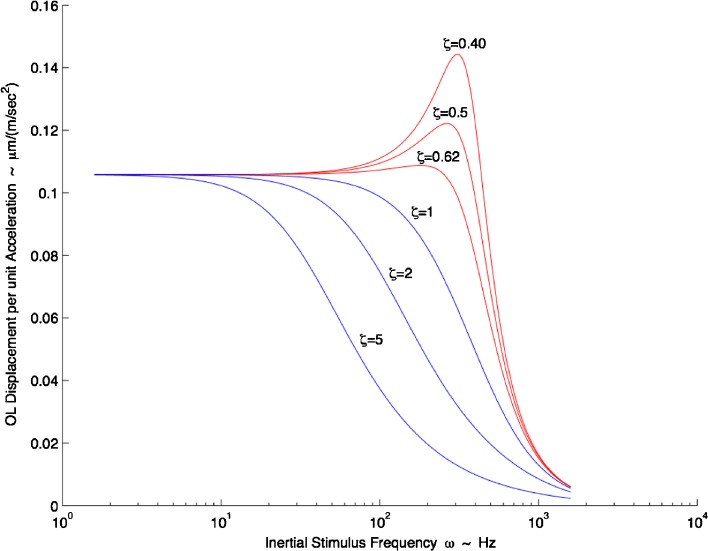
In Figure 7, the OL displacement per unit acceleration is plotted versus frequency. The simulation in this figure used the median natural frequency ω_n = 374 Hz and the same range of damping coefficient values used in the time response simulation (ζ = 0.40, 0.50, 0.62) all from the M-L direction with high-acceleration stimulus.

FIG. 7.

Turtle utricle frequency response. Mechanical gain of displacement per unit acceleration (μm (m · s⁻²)⁻¹) versus frequency (Hz) is shown. Where ω _n = 374 Hz was used; the two extremes of the damping coefficient are shown, ζ = 0.40 and ζ = 0.62, along with the mean value of ζ = 0.50, all shown in red. All values for the frequency response curve are taken from the M-L direction with high-acceleration stimulus. Critically damped value of ζ = 1, and overdamped values of ζ = 2 and ζ = 5 are also shown in blue to illustrate the effect of increased damping on frequency response and bandwidth. There is nearly flat response up to 100 Hz. The upper frequency range for a turtle head accelerations as seen in behavioral studies ranged from 1 up to 70 Hz (Rivera et al. 2012). It is seen in this frequency plot that dynamic bandwidth of the utricle is decreased drastically by having an overdamped system (ζ >1.0) as is shown by the magnitude roll-off at much lower frequencies.

This figure provides insight into the utricle’s dynamics across its frequency and damping coefficient range. The frequency operating range or bandwidth for the mechanical utricle response can be defined as the flat response region from DC up to 100 Hz as seen in Figure 7. There are some small gain increases near the 100 Hz frequency and range from 4.9 % increase with ζ = 0.4 to 1.2 % with ζ = 0.62. Notice that for all ζ > 1.0, the dynamic bandwidth of the utricle is greatly reduced, thus limiting higher frequency mechanical response for neural transduction. It is seen that an overdamped utricle mechanical system is limited not only in its time response (see Fig. 6B) but also in its frequency response.

In a behavioral study performed on the turtle during rapid motion feeding strikes, a power spectral plot indicated that frequency content of this motion in the medial-lateral direction had its maximum power at 40 Hz. For all three strikes shown, this single animal had significant power from 1 up to 70 Hz in both the medial-lateral and anterior-posterior directions (Rivera et al. 2012). These are the result from three feeding strikes from a single turtle and with no specific search looking for maximum frequency content. It is apparent that a 100 Hz upper bound on the utricle frequency response is reasonable for rapid turtle head movements.

Open-Loop Control and Frequency Response

It is important to recognize that in the vestibular open-loop control systems nothing downstream from the otoliths or canals, which are the primary system sensors, can have better frequency response than that of these sensors. This is necessary to ensure effective and accurate control. The utricle is the primary sensor for linear motion in the horizontal head plane of almost all vertebrate animals. The upper frequency response limit of this system is defined by the extracellular structure of the utricle, its mechanical transduction system. It is this mechanical system that sets the upper frequency limit on utilization of head motion information. This principal applies to all the neural elements that come downstream of the mechanical system starting with hair cell transduction. The primary utricle mechanical sensor must have better frequency response than any actuator or other plant system that uses this signal (Grant and Best 1986; Palm 2005; Franklin et al. 2006; Forbes et al. 2013).

In the present study, the high frequency bandwidth shown is generally above the range at which vestibular afferents have been studied (Lyskowski and Goldberg 2004). Neural responses to high frequency vestibular stimuli have been shown in recent published work. Recordings from type I hair cell calyces in the saccule of postnatal rats (P1-P9) have shown that these calyces have frequency responses up in the 100 Hz range (Songer and Eatock 2013). The stimulus for this study was direct displacement of striolar bundles, and all calyces studied contained two to four hair cells. Rowe and Neiman (2012) have shown that posterior canal afferents in turtles show strong response at 100 Hz.

Human subjects exposed to electrical vestibular stimuli over a bandwidth of 0–70 Hz showed sternocleidomastoid muscle response over this entire frequency range (Forbes et al. 2013). These results indicate a wide bandwidth of head-neck mechanical response utilizing frequency capability of the vestibular system.

The turtle species used in this experiment are generally considered to have lateral-eyed vision. Recently, these red-eared slider turtles have been shown to have the ability to shift from lateral-eyed vision to frontal-eyed vision, similar to mammals with this capability. These turtles utilize this frontal vision in a vestibulo-ocular reflex (VOR) for inertial eye stabilization during rapid head motion. Part of this, VOR has a linear component driven by the utricle. This study used electrical nerve stimulation to move the turtle’s eyes with stimuli up to 100 Hz (Dearworth et al. 2013). In both this and the human study cited above, the stimulus was electrical, with one directed to the inner ear and the other to the nerves innervating the eye muscles. Using electrical stimulation is one of the few ways that high frequency stimuli can be delivered to the inner ear and nerves innervating muscles. In both cases, it was shown that the bandwidth of these reflexes range up to 100 Hz.

Armand and Minor (2001) reported head movement transients as high as 80 Hz in lightly restrained squirrel monkeys and noted that even higher frequencies may be present in unrestrained animals. This recent evidence suggests that head movements may contain higher frequency transients requiring higher motion bandwidth detection than previously thought.

It is clear that utricular higher frequency measurement capability shown in this study is also being utilized in many animals as shown by the recent studies cited above.

Bandwidth and Behavior Significance

Based on the measurements in this work, the turtle utricle mechanical system is an under critically damped system. This is different from all the assumptions about the utricle mechanical system dynamics to date, where all previous measurement and analysis has assumed a near critically damped or overdamped system. The shear layer properties that make the system underdamped result in increased bandwidth which accommodates the rapid head motion as seen in natural behavioral studies. In addition, the higher than expected natural frequency of the system of 374 Hz contributes to this increased bandwidth. The trade off on these two parameters—system damping and natural frequency—would appear to be optimized in this species for bandwidth and rapid response time. It is the combination of high natural frequency and significant under damping in the utricle that is responsible for its high bandwidth and rapid response time to an acceleration stimulus.

The fast response time and bandwidth of the utricle is functionally significant because it sets the upper frequency limit for later stages of signal processing by hair cells, primary afferents, and central vestibular neurons. These later processing stages can be no faster, nor contain frequency content higher than the primary signal generated by the mechanical system of the utricle. The behavioral significance of the fast response time and wide frequency bandwidth of utricular mechanics appears to match their head behavioral motion. Turtles have traditionally been considered slow moving animals; but they have small heads on long, flexible necks. Thus, their head movements may contain high frequency components (e.g., during feeding strikes, escape maneuvers, fast head transients during prey tracking or responses to perturbations) even if locomotion frequencies are low. Clearly, there is a need for additional data on natural head movements in all vertebrates, especially regarding upper frequency content.

List of Acronyms

CE

Characteristic equation

CFL

Column filament layer

FRF

Frequency response function

HB

Hair bundles

HC

Hair cells

GL

Gelatinous layer

MF

Membranous falx

NEL

Neuroepithelium layer

OL

Otoconial layer

SL

Shear layer (combined GL + CFL)

TF

Transfer function

List of Variables

a_x

Acceleration of the OL with respect to the absolute inertial reference frame

A

Ventral area of the OL where shear stress is applied

A_M

Acceleration amplitude for the cycloidal stimulus

B_f

Buoyant force acting on the OL

C_f

Coefficient relating viscous force acting on dorsal surface of OL to the velocity of the OL measured with respect to an inertial reference frame

C_g

Coefficient relating viscous force acting on ventral surface of OL to the relative velocity between OL and NEL

D_r

Ratio of endolymph to gelatinous viscous damping coefficients

E_g

Shear layer elastic force acting on the ventral surface of the OL

G

Shear modulus

h_SL

Height or thickness of SL

H_FRF

Transfer function—experimental frequency response data

H_MDL

Transfer function—model frequency response

j

Imaginary number,

k

Image quality constant

K_g

Coefficient relating elastic force acting on ventral surface of OL to relative displacement between OL and NEL

m_OL

Otoconial layer (OL) mass

m_DF

Mass of fluid displaced by the volume of the OL

t

Time for the experiment stimulus and for the cycloidal stimulus

t_d

Time duration for the cycloidal stimulus

u(t)

Displacement of sensory base (NEL) measured with respect to a fixed inertial reference frame—in the time domain

U(s)

Laplace transform of u(t) = displacement of the NEL in the frequency domain

V_CR

Viscous damping coefficient for critical damping

V_f

Viscous force acting on dorsal surface of the OL

V_g

Viscous force action on the ventral surface of the OL

V_OL

Volume of the OL

y(t)

Displacement of otoconial layer measured with respect to a fixed or inertial reference frame—in the time domain

Y(s)

Laplace transform of y(t) = displacement of the OL in the frequency domain

ρ_e

Density of the endolymph

ρ_OL

Density of the OL

ω

Excitation frequency

ω_n

Undamped natural circular frequency

ζ

Viscous damping factor or damping ratio

γ

Effective shear strain of the SL

τ

Shear stress of the SL acting on the ventral surface of the OL

δ

Deflection of otoconial membrane caused by shear force

Appendix—Model Development

Forces Acting on Otoconial Layer

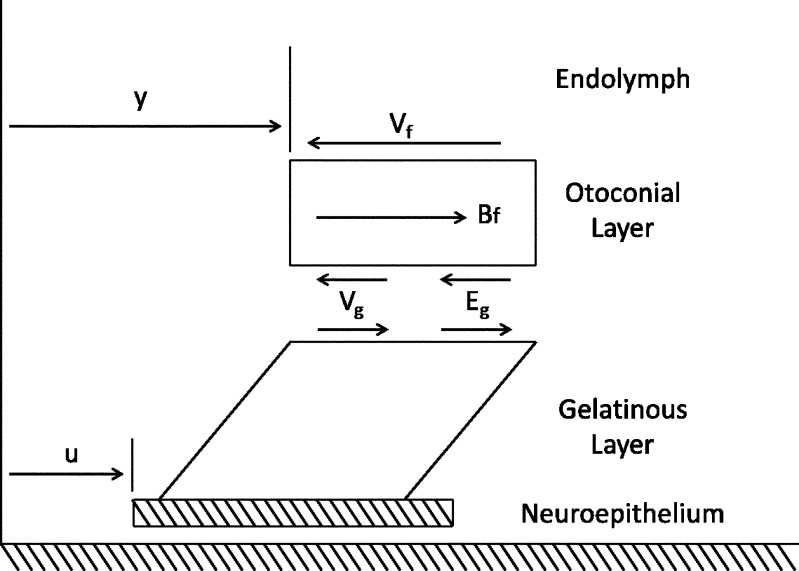
Forces acting on the OL are shown in the free body diagram in Figure 8 and are listed with explanation below.

FIG. 8.

Free body diagram of the forces acting upon the OL during linear acceleration. The displacement of the neuroepithelium (u) and OL (y) are both measured with respect to a fixed frame inertial reference.

The displacement of the OL and NEL are represented by the variables y and u, respectively. The y and u measurements are made relative to an absolute inertial reference frame that is the supporting stage of the microscope. The relative displacement between OL and NEL (y−u) is responsible for HC bundle displacement and is the variable usually used to describe utricle dynamic behavior. The measured variables y and u are those directly measured in the experiment and are used in this transfer function for direct application to the displacement data.

Forces in the free body diagram:

1. The viscous force V_f from contact between the dorsal otoconial layer surface and endolymph. This force is linearly proportional to 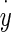= velocity of the OL relative to an inertial reference frame. The over dot notation is used for time derivatives, and the constant coefficient relating velocity to force is C_f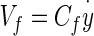

   
2. A viscous force generated from the shear layer V_g is linearly proportional to the rate of relative velocity 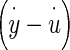where 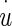= velocity of the NEL relative to an inertial reference frame, and the constant coefficient relating force to relative velocity is C_g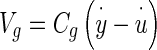

   
3. An elastic force E_g generated from the shear layer is linearly proportional to the relative displacement (y − u), and the constant coefficient relating force to the relative displacement is K_g

   
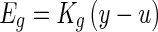
4. Buoyant force B_f = m_DFu, where m_DF = mass of displaced fluid (endolymph) and 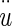= acceleration of the NEL. The m_DF  =  ρ_eV_OL, and m_OL = ρ_OLV_OL, are combined and the buoyant force becomes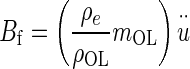

   

   Density values used for all model calculations: ρ_e  = 1,003 kg m⁻³, ρ_OL  = 2,412 kg m⁻³

Equation of Motion for the Otoconial Layer

Incorporating the above forces in Newton’s second law of motion applied to the OL results in the governing equation for the OL dynamics

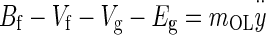A-1

Substituting the force expressions, dividing by m_OL, expanding, and rearranging, Eq. A-1 becomes

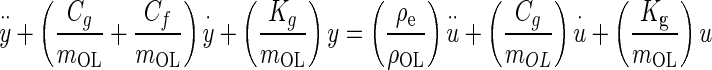A-2

Introducing standard mechanical system parameters for second order dynamic: 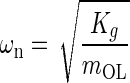the undamped natural circular frequency and 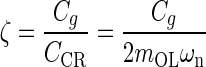the viscous damping factor or damping ratio, where C_CR is the critical damping coefficient. C_CR is defined as the damping value that just prevents displacement overshoot in oscillatory motion with zero initial conditions. The natural frequency ω_n represents the undamped natural frequency of vibration. The damping coefficient ζ is a measure of the severity of the damping in a second order mechanical system, where ζ < 1 is the underdamped range with oscillations, ζ = 1 is critical damping where the system responds as fast as possible to a stimulus without overshoot, and ζ >1 is the overdamped range where system oscillations are completely damped out. Converting Eq. A-2 using these standard parameters it becomes

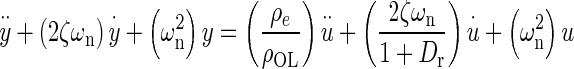A-3

where 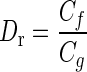is the ratio of the viscous coefficients of endolymph to SL. The utricle experimental dynamic response is measured in terms of ζ and ω_n; these are evaluated for a given utricle by applying Eq. A-3 to the experimentally measured displacements. The numerical value of D_r is relatively low with D_r < 0.01, implying the gelatinous SL dominates the viscous damping forces. A value of 0.01 was used for D_r.

Applying Laplace transforms to Eq. A-3, where s is the Laplace transform variable, and solving for the displacement gain transfer function results in

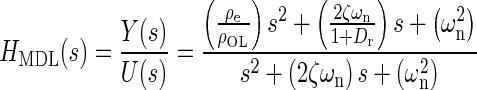A-4

This transfer function was used for the frequency curve fitting to the displacement data. The denominator in this expression is the characteristic equation of utricle dynamics and represents its fundamental behavior in responding to an acceleration stimulus.

Shear Modulus

The shear deformation was modeled using the shear stress-shear strain relationship τ = Gγ, where G is the effective shear modulus of the shear layer, τ = shear stress (τ = F/A_SL, where F is an applied shear force to the otoconial layer, A_SL is the sheared area), and γ = effective shear strain (γ; sin γ = δ/h_SL, where the approximation for small γ is used; δ is the linear deflection of the OL relative to the NE (δ = y−u), and h_SL is the height or thickness of SL). Using the system natural frequency ω_n²  = K_g/m_o and stiffness K_g = F/δ, and combining with the shear stress-shear strain relationship, yields an expression for the effective shear modulus of the utricle SL

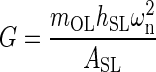A-5

The effective shear modulus was calculated using Eq. A-5 with the measured experimental value of ω²_n, and parameter values of the following: m_OL = 0.097 mg, h_SL = 14.16 μm, and A_SL = 0.805 mm², from previous work (Davis et al. 2007).