Response inhibition during perceptual decision making in humans and macaques

Abstract

Response inhibition in stop signal tasks has been explained as the outcome of a race between GO and STOP processes (e.g., Logan, 1981). Response choice in two-alternative perceptual categorization tasks has been explained as the outcome of an accumulation of evidence for the alternative responses. To begin unifying these two powerful investigation frameworks, we obtained data from humans and macaque monkeys performing a stop signal task with responses guided by perceptual categorization and variable degrees of difficulty, ranging from low to high accuracy. Comparable results across species reinforced the validity of this animal model. Response times and errors increased with categorization difficulty. The probability of failing to inhibit responses on stop signal trials increased with stop signal delay, and the response times for failed stop signal trials were shorter than those for trials with no stop signal. Thus, the Logan race model could be applied to estimate the duration of the stopping process. We found that the duration of the STOP process did not vary across a wide range of discrimination accuracies. This is consistent with the functional, and possibly mechanistic, independence of choice and inhibition mechanisms.

The goal of this study was to investigate whether the mechanisms responsible for choosing responses share resources with or are independent from the mechanisms responsible for inhibiting responses. To do so, we designed a paradigm that unifies two major approaches employed in the cognitive sciences to study how we choose among alternative responses and how we inhibit responses. The findings provide evidence that perceptual choice and response inhibition are independent processes, and they establish a foundation to develop cognitive models and neurophysiological recordings within the well-understood visual saccadic system.

Perceptual categorization is usually studied using two-alternative forced choice tasks and is described by sequential-sampling models like the drift diffusion and competing-accumulator models (reviewed by Bogacz, 2007; Gold & Shadlen, 2007; Smith & Ratcliff, 2009). The premise of sequential-sampling models is that evidence about the stimulus category accumulates through repeated sampling. A categorical choice is committed when the accumulated evidence reaches a criterion. Versions of these models account well for accuracy and response times (RTs) in choice tasks.

Response inhibition is often studied using stop signal (countermanding) tasks, and the race model of response inhibition describes how we initiate or withhold a prepared response (reviewed by Schall & Godlove, 2012; Verbruggen & Logan, 2009). During a stop signal task, a subject is cued to respond to a primary stimulus on each trial, but on some trials a subsequent stimulus—the stop signal—is presented, instructing the subject to withhold the response to the primary stimulus. The premise of the race model is that the outcome of stop signal trials is the result of a race between stochastically independent GO and STOP processes. If the STOP process finishes first, the response is withheld (a canceled, or signal-inhibit, trial), whereas if the GO process finishes first, the response is initiated (a noncanceled, or signal-respond, trial). The race model accounts for inhibition probabilities and RTs and allows for estimation of the stop signal reaction time (SSRT), which is the time needed to react to the stop signal by canceling the response.

Most stop signal tasks use a primary stimulus that requires a choice response. However, few studies have manipulated the perceptual discriminability of the choice stimulus, and none have done so parametrically. One human study used a primary buttonpress task that required deciding whether a visual stimulus appeared on the left or the right side of a display screen (Logan, 1981), and choice difficulty was varied by presenting the stimulus near or far from the center of the screen. SSRTs were not compared between the choice difficulty conditions. A similar study incorporated both buttonpress and saccadic response versions of a primary task that required discriminating a left- or right-pointing arrow (Logan & Irwin, 2000), and choice difficulty was varied by presenting the arrow in the center or at the periphery of the screen. SSRTs did not vary when choice stimuli were presented centrally or in the periphery, for either hand responses or saccadic responses. Finally, in one study, researchers used alphabetic letters as the choice stimuli and manipulated discriminability by using letters that were easy (“G” and “X”) or difficult (“I” and “i”) to distinguish (Osman et al., 1986). SSRTs were not calculated, but the authors concluded that discriminability did not affect stopping, on the basis of comparison of the inhibition functions and RT distributions between the two conditions. Each of the previous studies had varied choice difficulty in a blocked design, and Logan (1981) and Logan and Irwin (2000) used stimulus locations that varied from trial to trial. In the present design, the trial conditions were randomly interleaved instead of blocked, to ensure that each trial would require the same level of engagement and effort from the outset. In addition, the choice stimulus appeared at the same location across trials to ensure that choice difficulty would vary with the perceptual evidence, and not with other potential factors. This experimental design would provide the data necessary to elucidate the relationship between choosing and stopping in a way that would empirically link the rich research histories of these two fields.

Presently, it is unknown whether sequential-sampling models and the race model describe elements of one decision-making process, or whether categorical choice and response inhibition are functionally independent mechanisms. Sequential-sampling models do not explicitly account for the process of initiating a response. Instead, response initiation is included in a “nondecision time” parameter that is assigned some variability from trial to trial that does not depend on task-related variables (e.g., Hanks, Ditterich, & Shadlen, 2006; Palmer, Huk, & Shadlen, 2005; Ratcliff & Tuerlinckx, 2002; Smith & Ratcliff, 2009). The countermanding race model does not explicitly account for the choice process. Although most stop signal tasks are based on measuring choice RTs, the alternative choices are modeled as one GO process racing the STOP process (but see Camalier et al., 2007). Previous implementations of the race model have successfully accounted for response inhibition without accounting for the errors in the choice process, usually because the choice errors were so rare (e.g., Hanes & Schall, 1995; Logan, 1981; Logan, Cowan, & Davis, 1984). Under those circumstances, the stimuli require relatively little perceptual processing, and the choice process may have negligible effects on the STOP process. In addition, most stop signal studies have included choice stimuli that did not vary in difficulty from trial to trial (but see Logan, 1981; Logan & Irwin, 2000). Under blocked conditions, the stimuli require consistent processing from trial to trial, which may minimize dynamic interactions between the choosing and stopping processes.

We designed a behavioral experiment to unify these two task domains, with the ultimate goal of unifying the modeling domains. Two monkeys and eight humans performed a choice-countermanding task with saccadic responses. The difficulty of categorical choice and the difficulty of response inhibition were manipulated independently. We used established methods to analyze choice performance and stopping performance and to test how the processes are related. We studied both monkeys and humans, so as to provide a comparative link between the behavioral performance in both species and future neurophysiological studies in monkeys. Our prediction was that monkey and human performance would be qualitatively indistinguishable, even if they were quantitatively different.

In the stop signal task literature, three types of relations between the GO process and the STOP process are distinguished (reviewed by Verbruggen & Logan, 2009). Stochastic independence refers to the assumption that GO RTs and SSRTs vary independently from trial to trial. Context independence refers to the assumption that the GO RTs are equivalent on no-stop and stop trials. The stochastic and context independence assumptions underlie the race model and are required for estimating SSRTs, predicting signal-respond RTs, and aligning the inhibition functions. Finally, functional independence refers to the assumption that the factors affecting RT_GO do not affect the SSRT, and vice versa. It is important to note that functional dependence does not imply stochastic context dependence. Indeed, we obtained evidence consistent with stochastic and context dependence in these task conditions. We tested the functional independence of the choice and stopping processes by evaluating these alternative hypotheses: On the one hand, choice and response inhibition mechanisms may overlap entirely, or at least share a common resource (Kahneman, 1973; Navon & Gopher, 1979). If so, we should observe interactions between choice difficulty and stopping efficiency, assuming that these two processes share resources in a common stage of processing, creating a capacity limitation. Difficult choice trials should impair response inhibition, as indexed by longer SSRTs. On the other hand, choice and response inhibition mechanisms may be functionally independent. If so, we should observe no interaction between choice and stopping difficulty. We obtained results consistent with the functional independence hypothesis.

Method

Choice-countermanding task

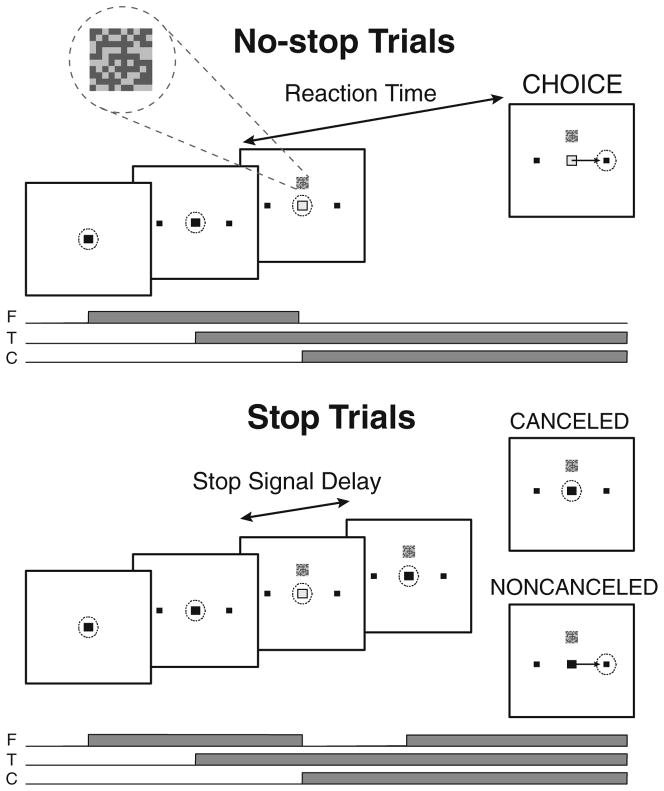
The goal of the choice-countermanding task was to choose whether a discriminatory stimulus contained more cyan or magenta and to respond appropriately, though some trials would require canceling the response when a stop signal was presented. Each trial began when the subject fixated a spot in the center of the display (Fig. 1; dashed circles indicate gaze position). After a variable duration (400–800 ms), two targets (1° squares) appeared in the periphery, one in each hemifield, 10° in amplitude from the central fixation spot and 180° from each other. The subjects maintained fixation for another variable duration (400–800 ms); then the fixation spot was extinguished, and simultaneously a choice stimulus appeared on the vertical meridian 3° above the central fixation spot. The choice stimulus was a 10 × 10 square checkerboard (magnified in the inset in Fig. 1) with a randomized pattern of isoluminant (30 cd/m² on a 13-cd/m² gray background for monkeys, 45 cd/m² on a 5-cd/m² gray background for humans) cyan and magenta checker squares; the stimulus subtended 1° for both monkeys and humans. The appearance of the choice stimulus and the coincident disappearance of the fixation spot cued subjects to choose a saccade target by discriminating whether the checkerboard contained more cyan or magenta checkers. The color–target side associations were counterbalanced between the two monkeys; four humans were tested with magenta–right and cyan–left associations, and four humans with the opposite mapping. Stimulus discriminability was manipulated trial to trial by randomly varying the percentage of cyan and magenta checkers from among a set of seven possible percentages. The sets of percentages were separately determined for each monkey to ensure a broad range of choice accuracy (B: [41, 45, 48, 50, 52, 55, 59], X: [35, 42, 47, 50, 53, 58, 65]), and all humans were presented with the same set ([35, 42 46 50 54 58 65]). During trials with 50% cyan–magenta, one target was assigned randomly as being correct. After the choice stimulus appeared, on no-stop trials (Fig. 1, top), monkeys earned a juice reward for a saccade to the correct target within 1,000 ms, whereas humans received positive feedback via a message display for a saccade to the correct target within 1,700 ms. RTs were defined as the duration between the onset of the checkerboard stimulus and when the eye movement velocity exceeded 30°/s away from fixation in the direction of one of the targets. Stop trials (Fig. 1, bottom) for monkeys occurred on 40% of trials in most sessions, but they could vary between sessions (30%–45% of trials) as we adjusted the task parameters, and stop trials for humans occurred on 40% of trials in all sessions. During a stop trial, the fixation spot reappeared after a variable stop signal delay (SSD). Monkeys earned a juice reward for canceling the saccade and maintaining gaze on the fixation spot, whereas humans received visual feedback via a message indicating that their response was successfully inhibited. The SSD was adjusted trial to trial by using a staircase procedure within each signal strength level, to elicit equal proportions of canceled and noncanceled stop trials. The SSD was increased randomly by one to three steps (for monkeys, the step size was constant within each session but could vary between sessions: 14, 29, 43, 57, 72, 86, or 100 ms/step, or from three to seven 70-Hz screen refreshes, using constant step increments within each session; for humans, the step size was always 70 ms/step, or six 85-Hz screen refreshes) after a canceled stop trial, and it was decreased randomly by one to three steps after a noncanceled stop trial. The randomness of the stepping procedure was used to prevent SSD tracking by the subjects. A saccade to the incorrect target on no-stop trials or a saccade to either target on stop trials resulted in a brief time out for both monkeys and humans, and a negative feedback message for the humans. A saccade to the checkerboard stimulus at any time aborted the trial and resulted in a brief time out. Humans made zero checkerboard aborts (after a 20-trial warm-up session), and the aborts were rare for the macaques (for macaque B, 1.8%; for macaque X, 0.8% of all trials). After receiving a reward, feedback, or time out, monkeys experienced a 1-s intertrial interval. Humans controlled the initiation of each trial (the eyetracking software was calibrated on each trial), so the humans’ intertrial interval varied (M = 2,083 ms, SD = 1,141). Macaque B performed 15 training sessions, for a total of 18,873 trials (M = 1,258 trials per session). Macaque X performed 15 training sessions, for a total of 18,404 trials (M = 1,227 trials per session). The humans performed one to two sessions each, totaling 7,290 trials (M = 911 trials per subject).

Fig. 1.

Choice-countermanding task. No-stop trials (top panel) began by fixating a central spot (“F” line below the task panels). After a variable delay, two targets appeared in the periphery (“T” line). After another variable delay, a 10 × 10 cyan–magenta checkerboard choice stimulus (magnified inset) appeared 3° directly above the fixation spot (“C” line), and the fixation spot simultaneously disappeared. This cued subjects to discriminate whether the checkerboard contained more cyan or magenta and to make a saccade to either the left or the right target. On a minority of trials (stop trials, bottom panel), the fixation spot reappeared after a variable stop signal delay, cuing subjects to cancel their response. During no-stop trials, a reward (monkeys) or positive feedback (humans) was earned for a saccade to the correct target, and a time out (monkeys) or negative feedback (humans) occurred for an incorrect choice. During stop trials, canceling the response (canceled) earned a reward or positive feedback, and failing to cancel the response (noncanceled) resulted in a time out or negative feedback

Experimental design

Monkeys

Data were collected from two macaques (one female M. mulatta, 5.4 kg, and one male M. radiata, 7.4 kg, both over 15 sessions). All surgical and experimental procedures were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and were approved by the Vanderbilt Institutional Animal Care and Use Committee. The monkey data were collected using the EyeLink 1000 infrared eyetracking system (SR Research Kanata, Ontario, Canada) and streamed to a Plexon data acquisition system (Dallas, TX). Monkeys sat in a primate chair with a head-post restraint and faced a CRT monitor display. The stimulus presentation, reward delivery, and task contingences were controlled by TEMPO/VIDEOSYNC software (Reflective Computing, Olympia, WA).

Humans

Data were collected from eight humans (seven males, one female, all right-handed; average age = 29 years old). Informed consent was obtained prior to the experimental sessions. The Vanderbilt University Institutional Review Board approved the experiment procedures. Subjects sat in a chair and immobilized their head using a chinrest. Eye position data were collected using the EyeLink II infrared eyetracking system (SR Research Kanata, Ontario, Canada). The stimulus presentation, feedback, and task contingences were controlled using Psychophysics Toolbox running on MATLAB software (The MathWorks Inc., Natick, MA).

Behavioral analyses

Each monkey provided multiple data collection sessions, so behavioral analyses throughout the study were performed within subjects (across sessions). Each human provided one or two data collection sessions, so analyses were performed across subjects. A few training sessions included unusually long noncanceled RTs during the earliest SSD trials. We considered these trials to be outliers, because they could have been due to subjects not noticing the stop signal (because it appeared so rapidly after fixation offset) or making an inadvertent saccade to a target without holding central fixation long enough to complete a stop trial. Therefore, throughout our analyses we excluded trials that contained RTs greater or less than three standard deviations of the mean of the no-stop RT distribution in a given session. No results differed when the outlier trials were included.

Choice performance

Choice performance was analyzed with respect to accuracy and RTs. Accuracy was quantified in psychometric functions, which plot the probability of making a saccade to the rightward target as a function of the percentage of rightward target color (signal strength) in the checkerboard. Psychometric functions were fit with a Weibull curve using maximum likelihood methods. The variation of RTs was quantified as a function of signal strength in chronometric functions.

Stopping performance

To compare stopping performance across categorical choice difficulty levels, we estimated SSRTs within each signal strength level. Given the large number of experimental conditions, each signal strength level was based on relatively few trials for calculating SSRTs (~50–60 stop trials in each signal strength per session). Recent work has indicated that the SSRT is estimated most accurately using the “integration” method, as opposed to the “mean” method (Verbruggen, Chambers, & Logan, 2013). For each discrimination signal level, the no-stop RT distribution was rank ordered. Then, for each SSD, we determined the no-stop RT value at the point in the distribution corresponding to the proportion of noncanceled trials produced at that SSD (e.g., if a subject failed to cancel on 40% of the trials, the no-stop RT of the 40th percentile in the distribution was determined). SSRT was calculated by subtracting the given SSD from the no-stop RT at that nth proportion; these values were averaged across SSDs in order to obtain an overall SSRT for each signal strength level. The results were not different if the “mean” method was used to estimate SSRTs.

Results

Choice and stopping performance were analyzed independently, in order to link behavior in our choice-countermanding task with behavior in previous choice RT and stop signal tasks. To determine whether categorical choice and response inhibition are functionally independent processes, we tested for a possible relationship between choice and stopping performance.

Choice performance

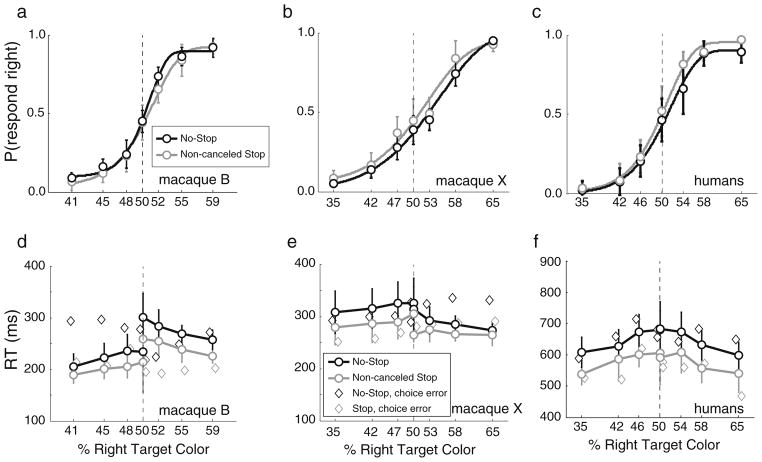
To assess choice performance, we measured accuracy and RT as a function of signal strength (i.e., percentages of magenta and cyan in the checkerboard). For each monkey, averaged across sessions, the probability of making a saccade to the right target increased monotonically with right-color signal strength (see Fig. 2a and b) during both no-stop (black circles and fitted curves) and noncanceled (gray circles and fitted curves) trials. The same pattern of choice accuracy was observed for humans (Fig. 2c), averaged across subjects (each subject completed one or two sessions). These data indicate that both the monkeys and humans were most accurate when the checkerboard stimulus was dominated by one color (easier discrimination), and were least accurate (closer to chance level, 50%) when the checker color proportions were similar (more difficult discrimination).

Fig. 2.

Choice performance. (a–c) Probabilities of making a saccade to the rightward target as a function of the right-target color percentage for no-stop (black) and noncanceled stop (gray) trials for (a) macaque B, (b) macaque X, and (c) humans. The mean (open circles) and SD (bars) across monkey sessions and human subjects were fit with Weibull functions. (d–f) RTs as a function of right-target color percentage. The means and SDs across monkey sessions and human subjects are shown for correct choices during no-stop (black circles and lines) and noncanceled stop (gray circles and lines) trials, and diamonds are incorrect choices. Note that the y-axes for the monkeys differ from that for humans in panels d–f

Likewise, for each monkey and across human subjects, RTs varied as a function of trial difficulty (Fig. 2d–f). During both no-stop trials (black) and noncanceled stop trials (gray), the mean RT increased as the checkerboard color mixture increased in difficulty toward 50%. A 2 (no-stop vs. stop trial) × 8 (signal strength, with two 50% conditions: one for each randomly assigned “correct” side) × 2 (correct choice vs. choice error) analysis of variance (ANOVA) revealed a main effect of signal strength on RTs [macaque B, F(7, 427) = 11.30, η_p² = .16, p < .001; macaque X, F(7, 444) = 3.50, η_p² = .05, p = .001; human, F(7, 199) = 3.42, η_p² = .11, p = .002]. Human choice performance was qualitatively similar to that of monkeys, although humans displayed longer RTs. The monkeys exhibited different RTs in the two choice directions, but such asymmetries are common in choice tasks with monkeys (e.g., Ding & Gold, 2012; Hanks et al., 2006). We observed no main effect of choice accuracy on RTs for either the monkeys or the humans [macaque B, F(1, 427) = 0.03, η_p² < .01, p = .855; macaque X, F(1, 444) = 0.29, η_p² < .01; p = .590; human, F(1, 199) = 0.48, η_p² < .01, p = .488]. An interaction between choice accuracy and trial type (no-stop vs. noncanceled stop trials) emerged for each monkey [macaque B, F(1, 427) = 8.02, η_p² = .02, p = .005; macaque X, F(1, 444) = 4.04, η_p² = .01, p = .045], but not for humans [F(1, 199) = 3.20, η_p² = .01, p = .075]. During no-stop trials, choice error RTs tended to be slower than correct choices (Table 1), as is typically observed in choice RT tasks (e.g., Ratcliff, Cherian, & Segraves, 2003; Ratcliff & McKoon, 2008; Roitman & Shadlen, 2002). During noncanceled stop trials, choice error RTs tended to be faster than correct choices. This was unusual, for one would expect the same pattern to occur for stop and no-stop trial correct relative to incorrect choices. We are unaware of previous research reporting noncanceled choice errors, probably because choice errors are infrequent in most stop signal tasks. One explanation for the differing patterns is that the noncanceled stop trial choice errors, which are already fast due to their status as noncanceled RTs, largely consist of fast-guess trials that are purported to occur when subjects’ responses are guesses, without previous processing of the choice stimuli (Ollman, 1966; Yellott, 1967). Presumably fast guesses are a subpopulation of the no-stop choice error distribution, as well, but are infrequent relative to other errors. Future research could explore this issue further. Overall, choice accuracy and RTs varied across choice difficulty levels as had been observed in previous studies.

Table 1.

Mean (with SD) response times (in milliseconds) across sessions (monkeys) and subjects (humans), collapsed across signal strength levels

	No-Stop Trials		Stop Trials
	Correct Choice	Incorrect Choice	Correct Choice	Incorrect Choice
Macaque B	251 (42)	264 (58)	224 (46)	214 (62)
Macaque X	302 (37)	309 (46)	277 (25)	274 (38)
Humans	648 (64)	665 (111)	579 (63)	561 (98)

Stopping performance

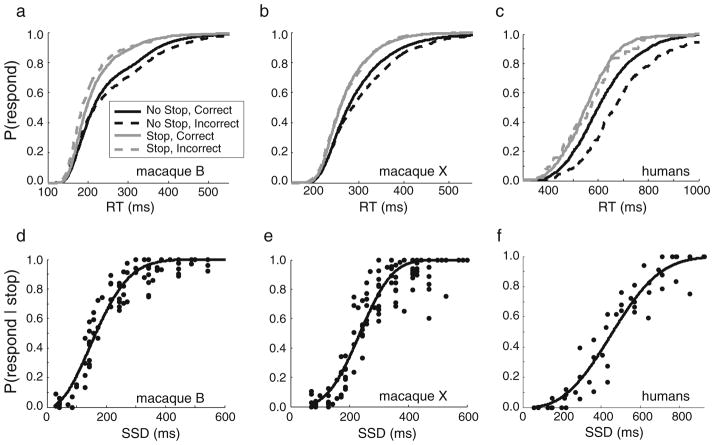
The well-established predictions of the race model were borne out in the behavioral data (Logan & Cowan, 1984). First, noncanceled RTs were faster than no-stop RTs. This occurs because noncanceled RTs are based on winning the race against the STOP process. Noncanceled RTs (gray lines in Fig. 3a–c, and Table 1) were faster than no-stop RTs (black lines in Fig. 3a–c) for both correct (solid lines) and incorrect (dashed lines) choice responses [paired t tests with unequal variances: macaque B, correct, t(25.0) = 4.3, r = .65, p < .001; incorrect, t(25.4) = 4.9, r = .69, p < .001; macaque X, correct, t(23.3) = 2.9, r = .52 p = .007; incorrect, t(22.7) = 3.7, r = .61, p < .001], for each monkey, collapsed across sessions. The same pattern was observed for humans [Fig. 3c and Table 1; paired t tests with unequal variances: correct, t(14.0) = 2.9, r = .61, p = .011; incorrect, t(13.8) = 2.9, r = .62, p = .011]. The results were the same when the 50%-signal-strength conditions were excluded from the analyses.

Fig. 3.

Response inhibition performance. (a–c) Grand normalized cumulative distribution functions for response times (RTs) during no-stop (black) and noncanceled stop (gray) trials, for correct (solid lines) and incorrect (dashed lines) choices for (a) macaque B, (b) macaque X, and (c) humans. (d–f) Grand inhibition functions, plotted as the probability of responding during stop trials as a function of stop signal delay (SSD). Each data point is the p(respond) at a given SSD from one session. The data were collapsed across signal strength levels and sessions and were fit with Weibull functions

Second, the proportion of noncanceled stop trials increased with SSD. This relationship, known as the inhibition function, occurs because the later a stop signal occurs with respect to a go signal, the greater the likelihood that noncanceled responses will win the race against the STOP process. The probability of responding on stop trials increased with SSD from near zero, at the earliest SSDs, to near one, at the later SSDs, for each monkey (Figs. 3d–e) and for humans (Fig. 3f), collapsed across sessions and signal strengths.

Third, noncanceled RTs increased with SSD. This relation occurred because initiation of the STOP process is delayed for late SSDs, allowing more noncanceled responses to win the race against the STOP process. Collapsed across sessions and signal strengths, noncanceled RTs increased with SSD for both monkeys and humans [for macaque B, slope = 3.0, r² = .49, p < .001; for macaque X, slope = 1.1, r² = .22, p < .001; for humans, slope = 1.5, r² = .65, p < .001]. In addition, according to the race model, noncanceled RTs can be predicted at each SSD by calculating the mean of the distribution of no-stop RTs up to the point that matches the proportion of noncanceled stop trials for that SSD. We calculated the predicted noncanceled RTs at each SSD and each signal strength level and compared the values with the observed noncanceled RTs, listed for each SSD/signal strength condition in Table 2. The observed and predicted values were similar, though on average the predicted values were less than the observed values [mean (and SD) of observed minus predicted: for macaque B, 14 (47) ms; for macaque X, 14 (44) ms; for humans, 7 (56) ms], as has been shown in previous studies in both monkeys and humans (e.g., de Jong, Coles, Logan, & Gratton, 1990; Hanes & Schall, 1995).

Table 2.

Noncanceled response times as a function of signal strength percentage (rows) and stop signal delay (SSD; columns)

Macaque B
Signal Strength (%)		SSD (ms)
		43	86	129	143	158	172	215	244	258	272	301	344	444	487	544	644
	41	175 (136)	x	167 (163)	171 (171)	178 (168)	180 (174)	190 (185)	200 (191)	184 (195)	184 (187)	260 (211)	202 (202)	242 (194)	x	221 (204)	x
	45	x	x	188 (157)	167 (172)	171 (182)	175 (183)	187 (197)	199 (210)	222 (203)	228 (204)	233 (214)	220 (223)	241 (240)	x	279 (252)	275 (273)
	48	270 (143)	x	165 (172)	179 (168)	183 (178)	197 (199)	200 (198)	213 (211)	185 (204)	211 (202)	207 (235)	232 (222)	245 (264)	x	239 (252)	377 (286)
	50	512 (143)	x	167 (163)	172 (171)	186 (195)	174 (171)	215 (216)	210 (205)	208 (207)	205 (219)	225 (240)	236 (231)	246 (258)	x	326 (267)	201 (274)
	52	x	207 (151)	186 (158)	192 (170)	204 (175)	204 (207)	213 (216)	212 (216)	239 (224)	214 (220)	240 (262)	256 (254)	285 (278)	x	292 (272)	358 (277)
	55	186 (148)	x	192 (167)	191 (179)	207 (196)	204 (199)	207 (222)	223 (219)	222 (237)	249 (228)	270 (266)	261 (244)	253 (252)	x	337 (266)	397 (265)
	59	184 (154)	x	198 (172)	201 (182)	204 (189)	201 (206)	210 (220)	225 (218)	229 (210)	220 (245)	238 (242)	245 (249)	245 (254)	259 (256)	266 (257)	217 (265)
Macaque X
Signal Strength (%)		SSD (ms)
		72	129	172	186	215	244	258	301	344	358	387	415	429	472	515	530
	35	x	x	215 (212)	214 (226)	231 (238)	252 (254)	250 (256)	274 (270)	282 (284)	309 (297)	311 (282)	336 (307)	296 (290)	359 (318)	x	476 (327)
	42	x	x	221 (218)	218 (221)	235 (243)	253 (243)	257 (252)	274 (276)	297 (284)	302 (298)	x	340 (317)	285 (298)	325 (333)	264 (291)	x
	47	x	422 (204)	226 (214)	228 (225)	238 (237)	244 (265)	257 (249)	272 (274)	293 (279)	324 (300)	299 (270)	305 (313)	282 (292)	333 (310)	293 (297)	x
	50	372 (210)	x	232 (208)	232 (227)	241 (233)	256 (258)	262 (261)	275 (277)	290 (285)	289 (291)	306 (284)	319 (311)	291 (312)	x	276 (305)	x
	53	x	x	217 (216)	229 (226)	236 (242)	258 (254)	268 (255)	272 (275)	299 (286)	293 (303)	320 (264)	316 (307)	308 (299)	334 (323)	x	x
	58	x	x	244 (220)	227 (224)	253 (238)	252 (253)	260 (256)	267 (270)	281 (273)	285 (287)	272 (277)	297 (300)	291 (300)	x	277 (297)	x
	65	x	435 (208)	369 (224)	241 (224)	242 (238)	245 (248)	260 (260)	256 (255)	271 (281)	256 (261)	x	282 (272)	265 (280)	x	280 (289)	x
Human
Signal Strength (%)		SSD (ms)
		291	361	432	502	572	643	713	784	854
	35	460 (449)	451 (492)	518 (496)	557 (553)	581 (557)	618 (581)	537 (572)	627 (647)	x
	42	425 (468)	479 (492)	496 (496)	561 (557)	618 (581)	631 (589)	713 (641)	724 (604)	x
	47	454 (484)	589 (522)	487 (542)	540 (539)	575 (576)	638 (590)	632 (643)	716 (662)	730 (658)
	50	442 (475)	480 (508)	521 (516)	558 (577)	605 (606)	632 (597)	656 (650)	684 (686)	869 (670)
	53	475 (517)	464 (508)	556 (540)	571 (557)	660 (578)	640 (645)	680 (643)	746 (703)	682 (728)
	58	527 (466)	437 (464)	518 (511)	561 (562)	582 (561)	621 (597)	629 (637)	725 (650)	x
	65	470 (450)	486 (461)	519 (506)	555 (521)	551 (552)	550 (601)	x	x	x

Observed (vs. predicted) values are listed in milliseconds; an “x” indicates too few or no data points for that condition

SSRT is the key metric provided by the race model, because it estimates the covert RT to the stop signal. The grand average SSRTs across signal strengths and sessions for the monkeys (M ± SD: for macaque B, 70 ± 8 ms; for macaque X, 55 ± 11 ms) were somewhat shorter than those previously observed (e.g., Emeric et al., 2007; Hanes & Schall, 1995). The grand average SSRT across signal strengths and sessions for the humans (166 ± 43 ms) was comparable to values previously observed (e.g., Akerfelt, Colonius, & Diederich, 2006; Colonius, Ozyurt, & Arndt, 2001; Hanes & Carpenter, 1999; Logan & Irwin, 2000; Ozyurt, Colonius, & Arndt, 2003; Reinhart, Carlisle, Kang, & Woodman, 2012). In sum, the performance of monkeys and humans in the choice stopping task was consistent with the race model account of response inhibition.

Effects of choosing on stopping

Our main goal was to test whether categorical choice formation and the control of response initiation are functionally independent processes. The choice-countermanding task was designed to independently manipulate the difficulty of perceptual choice (via signal strength) and the difficulty of stopping (via SSD). This design afforded an opportunity to test the relation between categorical choice and response inhibition.

SSRTas a function of signal strength

We compared SSRTs for each level of perceptual choice difficulty (signal strength). We considered two hypotheses, with alternative predictions regarding the relation between choice stimulus signal strength and SSRT. If the choice process and the control of responses are components of the same process, then some interaction would be evident. One hypothesis is that the decision-making process is capacity-limited, similar to other capacity-limited information processes such as visual detection and working memory (for a review, see Marois & Ivanoff, 2005). Under this hypothesis, a difficult choice stimulus would consume more resources, leaving less for response inhibition. Consequently, SSRT would increase as choice difficulty increased. A second hypothesis is that the choice process does not share resources with the stop process, so that discrimination is functionally independent from control of the response. If so, SSRTs would be invariant across signal strengths.

For each monkey, SSRTs were calculated within each signal strength level in each session and then averaged across sessions. SSRTs were invariant across signal strength levels for both monkeys [Fig. 4a and b; one-way ANOVAs: macaque B, F(6, 84) = 1.24, η² = .08, p = .303; macaque X, F(6, 84) = 1.08, η² = .07, p = .375]. Humans SSRTs were calculated within each signal strength level for each subject, and the signal strength SSRTs were averaged across subjects. Human SSRTs were also invariant across signal strengths [Fig. 4c; one-way ANOVA: F(6, 49) = 0.59, η² = .32, p = .736]. These results are inconsistent with functional dependence and support the hypothesis that the choice and stopping processes are functionally independent.

Fig. 4.

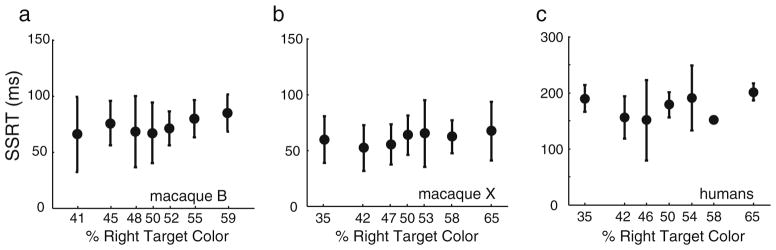
Stop signal reaction times (SSRTs) as a function of perceptual choice difficulty. Mean and SD SSRTs are plotted within each signal strength level for (a) macaque B, (b) macaque X, and (c) humans. Note the y-axes for the monkeys differ from that for humans

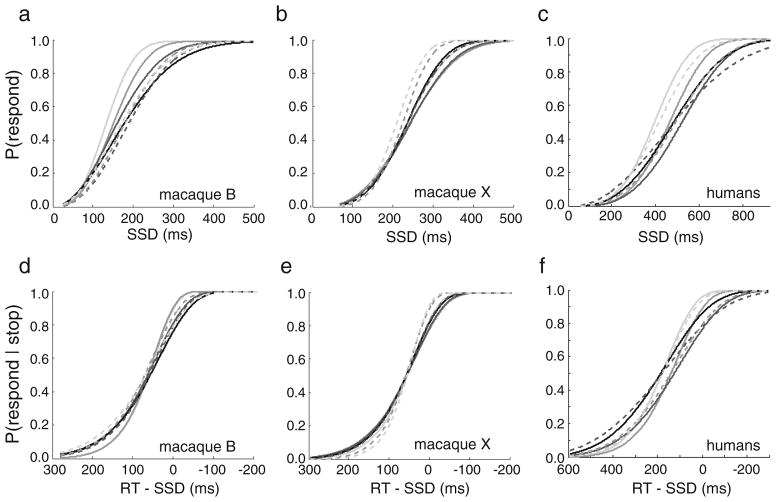
Inhibition functions as a function of signal strength

An alternative assessment of response inhibition is to compare inhibition functions between conditions (Fig. 5a–c). Variation in inhibition functions has been observed between stop signal experiments in which the task parameters varied (e.g., Logan et al., 1984; Logan & Irwin, 2000; Schachar & Logan, 1990). To test whether differences in RTs can account for differences in the inhibition functions, inhibition functions were transformed by calculating the probability of responding on stop trials as a function of noncanceled RT minus SSD (Fig. 5d–f). As we mentioned, we used an SSD staircase procedure at each signal strength level and obtained separate inhibition functions for each signal strength. Variation between the inhibition functions was expected, because RTs increased with choice difficulty (Fig. 2d–f). ANOVAs on the probability of responding, with Signal Strength and SSD as factors, confirmed that inhibition functions differed between signal strengths [macaque B, F(6, 635) = 8.04, η_p² = .07, p < .001; macaque X, F(6, 712) = 6.26, η_p² = .05, p < .001; human, F(6, 279) = 4.20, η_p² = .08, p < .001]. We repeated the ANOVAs on transformed inhibition functions, using a mixed-effect design with Signal Strength as a fixed factor and RT – SSD as a random factor. The transformation removed the significant variation between inhibition functions [macaque B, F(6, 662) = 0.37, η_p² < .01, p = .899; macaque X, F(6, 741) = 0.88, η_p² < .01, p = .510; human, F(6, 302) = 1.05, η_p² = .02, p = .395]. Thus, variation in RTs did account for the variation in inhibition functions between signal strength levels.

Fig. 5.

Response inhibition performance within each signal strength level for (a, d) macaque B, (b, e) macaque X, and (c, f) humans. (a–c) Probabilities of responding during stop trials as a function of stop signal delay (SSD). (d–f) Transformed inhibition functions, plotted as the probability of responding during stop trials as a function of the mean no-stop response time (RT) minus SSD. Fitted Weibull functions are shown. Solid gray lines depict right-target color percentages under 50%, and dashed gray lines depict percentages over 50%, with darker colors denoting percentages closer to 50%. The solid black lines depict the 50% right-target color percentage

Effects of choice error

Although SSRT was invariant with categorization difficulty, it was possible that the choice process could exert an indirect influence on stopping performance. If a choice error on one trial led to RT slowing on the subsequent trial (e.g., Laming, 1979; Rabbitt, 1966; Rabbitt & Phillips, 1967), it could increase the probability of successful inhibition if the subsequent trial was a stop trial (Bissett & Logan, 2011; Nelson, Boucher, Logan, Palmeri, & Schall, 2010). This can be understood simply in terms of the race model, because a slower GO process after a choice error would increase the likelihood that the STOP process would finish first. We determined whether subjects slowed their RTs after choice errors by calculating the difference between no-stop-trial RTs after a no-stop-trial choice error and before a no-stop-trial choice error. Using trial triplets accounted for gradual RT fluctuations that have been overlooked in previous analyses of posterror slowing (e.g., Dutilh et al., 2012). We found no evidence of postchoice error slowing [no-stop RT after choice error minus no-stop RT before choice error, given as mean (SD): macaque B, 8 (23) ms; macaque X, −6 (15) ms; human, 13 (28) ms; t tests: macaque B, t(14) = 1.32, r = .33, p = .207; macaque X, t(14) = −1.49, r = .37, p = .158; human, t(3) = 0.95, r = .48, p = .412], indicating that choice performance did not have incidental effects on response inhibition under these conditions. Curiously, when we applied a conventional trial-pair analysis, we found a weak trend of postchoice error speeding [mean (and SD) RT reduction: macaque B, 10 (21) ms; macaque X, 22 (13) ms; human, 49 (80) ms], that was significant for macaque X [t(15) = −6.8, p < .001]. This weak trend may be related to previous work that has shown RT speeding over successive no-stop trials (Cabel, Armstrong, Reingold, & Munoz, 2000; Emeric et al., 2007; Kornylo, Dill, Saenz, & Krauzlis, 2003).

Effects of stopping on choosing

We considered it unlikely that variation in stopping performance would affect choosing performance, because response initiation occurs after perceptual categorization, and because countermanding occurs late in processing, around the “point of no return” (de Jong et al., 1990; Logan, 1981; Osman, Kornblum, & Meyer, 1986), requiring late and potent interruption of the GO process (Boucher, Palmeri, Logan, & Schall, 2007). Nevertheless, we performed analyses to evaluate possible covariation in the stopping and choice performance.

No-stop versus stop trials

First, we tested whether choice performance varied between no-stop and stop trials (Fig. 2a–c). To determine whether choice sensitivity varied between no-stop and stop trials, we compared the slopes of fitted psychometric functions. The psychometric function slopes did not differ between no-stop and noncanceled stop trials [t tests: macaque B, t(28) = 0.96, p = .343; macaque X, t(30) = −0.66, p = .130; human, t(6) = −1.19, p = .277]. Although the slopes did not differ, the psychometric function for stop trials was shifted relative to that of the no-stop trials for macaque X. To compare choice performance more rigorously, we performed ANOVAs comparing the probability of a rightward response, with Signal Strength and Stop Versus No Stop as factors. Both monkeys’ choice performance varied as a function of stop versus no-stop trials [macaque B, F(1, 14) = 5.59, η_p² = .29, p = .033; macaque X, F(1, 14) = 36.25, η_p² = .72, p < .001]; however, humans’ choice performance did not vary [F(1, 48) = 0.49, η_p² < .01, p = .489]. Countermanding tasks inherently produce noncanceled RTs that are faster than no-stop RTs (Figs. 2d–f and 3a–c), so it was possible that the difference in choice performance between stop and no-stop trials could be explained by differences in RTs between those conditions. We repeated the ANOVA analyses, therefore, using a subset of no-stop trials that was latency-matched with the stop trials. Controlling for RT accounted for the effect of trial type on choice performance in one monkey [macaque B: F(1, 14) = 0.15, η_p² = .10, p = .241] and reduced the effect in the second [macaque X: F (1, 14) = 12.50, η_p² = .47, p = .003]. We concluded that the presence of the stop signal by itself had little to no effect on choice performance.

Low versus high stop-trial proportion

Next, we compared choice performance as a function of the proportions of stop trials occurring in the recent trial history within sessions (e.g., Bissett & Logan, 2011; Emeric et al., 2007; Logan, 1981; Logan & Burkell, 1986; Nelson et al., 2010; Verbruggen & Logan, 2009). For each session, we determined the mean stop-trial proportion and calculated an exponentially weighted moving average of the recent-stop-trial percentage, with a time constant of five preceding trials and no influence after 20 trials. The trials were then binned into low or high proportions, according to whether the trial occurred in a region of the stop-trial proportion moving average that was less than or greater than the overall average. A 2 (no-stop vs. stop trial) × 7 (signal strength) × 2 (low vs. high stop-trial proportion) ANOVA showed no significant main effect of stop-trial proportions on choice accuracy for either monkey [macaque B, F(1, 14) = 1.14, η_p² = .08, p = .303; macaque X, F(1, 14) = 0.20, η_p² = .01, p = .665], but humans showed a small effect [F(1, 84) = 3.57, η_p² < .01, p = .012]. To determine whether differences in RTs between low and high stop-trial proportions could account for the effect on choice accuracy in humans, we repeated the ANOVA using a subset of the high-proportion stop and no-stop conditions, latency-matched to their low-proportion counterparts. Controlling for RTs, we found no effect of stop-trial proportion on choice performance [F(1, 84) = 0.40, η_p² < .01, p = .530]. To account for possible interspecies differences in trial history effects, we repeated these analyses, using windows of 10 and 40 trials and time constants of 20 and 40 trials, and the results were not different. In sum, under these testing conditions, as expected we found no evidence that variation in stop trial patterns affected choice performance.

Discussion

An elaborated choice-countermanding task was developed to test whether categorical choice and response inhibition are functionally independent processes. Behavior from two monkeys and four humans indicated that both the categorical choice component and the response inhibition component of the task were performed as expected. Stopping performance, indexed by SSRT, was invariant with respect to levels of perceptual choice difficulty. In addition, variation in the inhibition functions between levels of choice difficulty was removed by transforming the inhibition functions to account for noncanceled stop-trial RTs, confirming that the variation was due to differences in RTs rather than SSRTs. Choice performance, indexed by psychometric functions, was invariant with respect to stop-trial proportions within sessions.

Species comparison

We obtained data in the same task from humans and macaque monkeys. This information was necessary for the interpretation of eventual neurophysiological and neuroimaging studies. Although quantitative differences were found, with RTs and SSRTs being substantially faster for macaques than for humans, qualitatively, performance was similar in all respects for humans and macaques, as has been reported previously (e.g., Camalier et al., 2007; Emeric et al., 2007; Hanes & Carpenter, 1999). The common patterns of results further validate this animal model for investigations of neural mechanisms in this task.

Independence of choosing and stopping

Although the inclusion of stop signals in a task tends to increase RTs, our results show that RT varied with choice difficulty independently from interleaved stop signal presentation. Critical for our purposes was the nature of the influence of choice difficulty on stopping. In the literature on the stop signal task, three types of relations between the GO process and the STOP process have been distinguished (reviewed by Verbruggen & Logan 2009). Stochastic independence refers to the assumption that GO RTs and SSRTs vary independently from trial to trial. Stochastic independence means that on a given trial, the value of the SSRT does not depend on the value of the GO RT (RT_GO). Specifically, P (RT_GO < t ∩ SSRT < t) = P(RT_GO < t ) × P(SSRT < t), where t is time. This assumption underlies the race model and is required for estimating SSRT, predicting signal-respond RTs, and aligning inhibition functions. Context independence refers to the assumption that the GO RTs are equivalent on no-stop and stop trials. Specifically, f(RT_GO | no stop signal) = f(RT_GO | stop signal). Stochastic and context independence were demonstrated by showing that noncanceled RTs were shorter than no-stop RTs, that noncanceled RTs increased with SSD, and that the observed and predicted noncanceled mean RTs were comparable. These results validate the measurement of SSRT.

Finally, functional independence refers to the assumption that the factors affecting RT_GO do not affect SSRT, and vice versa. The results here indicate that categorical choice and response inhibition are indeed functionally independent processes, although this was not guaranteed. Functional independence between GO and STOP processes has been found in some stop signal tasks based on task switching (Verbruggen et al. 2005a, b) and incompatible responses (Logan, 1981; van den Wildenberg & van der Molen, 2004). Functional dependence has been found in some other studies, including a stop signal task in which choice and simple RTs were compared (Logan et al., 1984), and in Stroop, Eriksen flanker, and Simon tasks in which congruent and incongruent trials were compared (Chambers et al., 2007; Ridderinkhof, Band, & Logan, 1999; Verbruggen et al. 2005a, b; Verbruggen, Liefooghe, & Vandierendonck, 2004; Verbruggen, Liefooghe, & Vandierendonck, 2006). The results also provide the first evidence for functional independence in nonhuman primates.

It is possible that the functional independence between choosing and stopping that we observed would not generalize to other sensory and/or motor modalities, such as auditory stop signals and/or keypress responses, since different modalities rely on different sensorimotor neural pathways. SSRT estimates can be longer or shorter for visual than for auditory stop signals (e.g., Boucher et al., 2007; Colonius et al., 2001; van der Schoot, Licht, Horsley, & Sergeant, 2005), and SSRT S are consistently shorter for saccadic responses than for hand motor responses (Boucher et al., 2007; Logan & Irwin 2000). Future studies will need to test whether the independence of choosing and stopping generalizes across stimulus and response modalities.

How could the functional independence that we report be accomplished? Mechanistically, categorization and response production with inhibition could be implemented by different neurons instantiating different stages of processing. Evidence for distinct stages of categorization and response preparation has been reported in a wide range of studies, including electroencephalographic recordings in humans (e.g., O’Connell, Dockree, & Kelly, 2012; Smulders, Kok, Kenemans, & Bashore, 1995), fMRI studies in humans (e.g., Filimon et al. 2013; Hebart, Donner, & Haynes, 2012), and single-neuron recordings in monkeys (e.g., Bennur & Gold 2011; Murthy, Ray, Shorter, Schall, & Thompson, 2009; Murthy, Thompson, & Schall, 2001; Sato & Schall, 2003; Thompson, Hanes, Bichot, & Schall, 1996). Likewise, stochastic-accumulator models account for visual search behavior and neurophysiology using an early selection process followed by a response preparation process (Purcell et al., 2010; Purcell, Schall, Logan, & Palmeri, 2012).

Relation to previous work

To our knowledge, this is the first stop signal study to compare SSRTs across parametrically varied choice difficulties. In turn, it is also the first parametrically varied choice RT study to implement a stop signal. Choice difficulty has been varied in previous stop signal tasks. One human study was based on a primary buttonpress task that required deciding whether a visual stimulus appeared on the left or the right side of a display screen (Logan, 1981), and choice difficulty was varied by presenting the stimulus near or far from the center of the screen. A similar study was based on both buttonpress and saccadic response versions of a primary task that required discriminating a left- or right-pointing arrow (Logan & Irwin, 2000), and choice difficulty was varied by presenting the arrow in the center or at the periphery of the screen. Neither of these studies showed that stopping was affected by choosing. As we mentioned, some advantages of our task were that the choice stimulus appeared at the same location on each trial (to prevent interactions with attention) and that the trial conditions were randomly interleaved instead of blocked (to maintain consistent engagement in the task). In addition, parametrically manipulating choice difficulty elicited the full range of performance (accuracy ranged from nearly perfect to chance), whereas previous stop signal tasks had produced few errors. These features of this choice-countermanding task provide an empirical link with the rich literature on perceptual decision making (reviewed by Gold & Shadlen, 2007; Smith & Ratcliff, 2009).

In other studies, researchers have manipulated choice difficulty by varying primary task factors unrelated to perceptual difficulty. For example, Logan and Irwin (2000) manipulated response difficulty by comparing pro- versus antisaccades and hand movements. Osman et al. (1986) manipulated task difficulty by comparing stimulus repetition trials with nonrepeated trials, and they manipulated language-based processing by presenting words versus nonwords. Finally, the primary task itself has been manipulated by requiring subjects to make a judgment on word pairs’ categories or on whether the words rhymed (Logan, 1983, 1985). None of these studies directly compared estimates of SSRTs across conditions, but by using additive-factor methods (Sternberg, 1969), they concluded that stopping was not affected by these choice difficulty manipulations.

A future goal of implementing the choice-countermanding task will be to unify stochastic accumulator models of choice with the race model of response inhibition. Although stop signal tasks are based on measuring choice RTs, the race model features a single GO process racing the STOP process. Previous work has shown that the race model can accommodate alternative GO processes (Camalier et al., 2007; Verbruggen, Schneider, & Logan, 2008). For example, Camalier et al. designed a stop-change task with visual search; on change trials, a singleton target swapped locations with a distractor, so that a saccade to the initial target location was to be replaced by a saccade to the final target location. The success of updating the saccade plan varied with target-step delay, just as here the variation of stopping varied with SSDs, and change-trial errors occurred with the shortest RTs. Thus, similar to SSRTs in stop signal tasks, the target step reaction time (TSRT) quantity could be determined. The performance of humans and macaques in this search-change task could be modeled with one stochastic GO process for the initial location and a STOP process proceeding in parallel with a second GO process toward the final location.

Camalier et al. (2007) manipulated the discriminability of the target relative to distractors in a search array. The TSRT was longer when the target step was less discriminable. This can be understood as simply reflecting longer perceptual processing of the target-step signal before the interruption of the first GO process. In the present choice-countermanding task, the stop signal was easily detectible on each trial, and the difficulty of categorization of the choice stimulus was manipulated. Perceptual processing did take longer when the checkerboard stimulus was less discriminable, but SSRTs did not vary.

In conclusion, these data provide a foundation for an integrated formal model of choosing and stopping that can be informed and constrained by the neurophysiology and anatomy of the primate visual system (Ding & Gold, 2012; Hanes, Patterson, & Schall, 1998; Murthy et al., 2009; Paré & Hanes, 2003; Ratcliff et al., 2003; Roitman & Shadlen 2002).