Abstract
All images are highly ambiguous, and to perceive 3-D scenes, the human visual system relies on assumptions about what lighting conditions are most probable. Here we show that human observers' assumptions about lighting diffuseness are well matched to the diffuseness of lighting in real-world scenes. We use a novel multidirectional photometer to measure lighting in hundreds of environments, and we find that the diffuseness of natural lighting falls in the same range as previous psychophysical estimates of the visual system's assumptions about diffuseness. We also find that natural lighting is typically directional enough to override human observers' assumption that light comes from above. Furthermore, we find that, although human performance on some tasks is worse in diffuse light, this can be largely accounted for by intrinsic task difficulty. These findings suggest that human vision is attuned to the diffuseness levels of natural lighting conditions.
Keywords: lightness, prior, lighting statistics, diffuseness, ideal observer
Introduction
The image of an object can vary enormously depending on the direction, diffuseness, and complexity of its illumination. As a result, when the human visual system attempts to recover the 3-D shape and surface properties of an object from retinal images, whether it succeeds often depends on whether it has accurate information about the scene's lighting. The visual system estimates lighting conditions from cues in individual scenes (Brainard & Maloney, 2011; Pont & Koenderink, 2007), but it also relies on general assumptions about what lighting conditions are most likely to occur (Metzger, 1936/2006, pp. 148–150). Two central problems for understanding human visual perception are determining what the true statistical distributions of lighting conditions, shapes, and materials are in the real world and what prior assumptions the visual system relies on to perceive 3-D scenes (Kersten, Mamassian, & Yuille, 2004; Knill & Richards, 1996). Here we study these problems as they relate to lighting.
Previous research on lighting statistics
Previous studies have developed mathematical tools for describing the spatial and directional distribution of light (Adelson & Bergen, 1991; Debevec, 1998; Gershun, 1936; Moon & Spencer, 1981). The main concepts we borrow from this work are the light field, a function F(x⃗,v⃗) giving the luminance in each direction v⃗ at each point x⃗ throughout a region of space, and the light probe, a sample E(v⃗) = F(x⃗0,v⃗) from the light field at a single location.
Dror, Willsky, and Adelson (2004) used omnidirectional photographs of real-world scenes to examine the directional properties of natural lighting. They found that although natural lighting is highly variable, it also has strong regularities. They showed that the luminance histograms of light probes peak at low luminances with a few very high luminance values due to small, bright sources, such as the sun. They also found similarities between the spatial frequency spectra of light probes and conventional photographs of natural scenes, including a pink-noise-like amplitude distribution; kurtotic wavelet coefficient distributions; and statistical dependencies between wavelet coefficients at adjacent scales, orientations, and positions. Fleming, Dror, and Adelson (2003) reported psychophysical experiments supporting the idea that human vision relies on these regularities in order to perceive surface reflectance and material properties.
Mury, Pont, and Koenderink (2007; Muryy, 2008) used a similar approach but paid special attention to the low-pass components of natural lighting that are relevant to shading of convex Lambertian objects (Basri & Jacobs, 2003; Ramamoorthi & Hanrahan, 2001). They found that, although high-spatial-frequency components of light probes vary rapidly as one moves through a scene, the low-frequency components are much more stable. They examined a few different types of scenes, such as open-sky locations and forests, and showed that the pattern of changes in the low-spatial-frequency lighting structure throughout a scene is determined largely by the scene's coarse geometry.
Dror et al. (2004) and Mury et al. (2007) examined high-dynamic-range light probes that were produced by combining conventional photographs or photographs of mirrored balls taken in several directions and at several exposures. Light probes created this way capture lighting patterns precisely, and faithfully represent sharp features, such as edges and specularities, but they are time-consuming to produce. For some purposes, such as understanding the shading of convex Lambertian objects, much coarser measurements are adequate.
With this in mind, Mury, Pont, and Koenderink (2009a, 2009b; Muryy, 2008) built a multidirectional photometer, which they call the plenopter, to measure low-pass light probes. They used the plenopter to investigate the low-pass structure of lighting in natural scenes. Mury et al. (2009b) measured light probes in several environments, and consistent with their previous work (Mury et al., 2007), they found that a lighting model with a coarse description of the scene layout accounted for the structure of the measured light probes.
The human visual system's assumptions about the directional distribution of natural lighting
Most work on the human visual system's assumptions about lighting has examined the light-from-above prior, the assumption that light comes from overhead1 (Metzger, 1936/2006; Morgenstern, Murray, & Harris, 2011; Ramachandran, 1988). An equally important property of lighting, though, is its diffuseness, the extent to which light comes mostly from a single direction as on a sunny day or from all directions as on a cloudy day (Langer & Bülthoff, 2000; Tyler, 1998). Lighting diffuseness has a large effect on object appearance, and the assumptions that observers make about diffuseness can have a correspondingly strong influence on their perception of 3-D scenes. Five recent psychophysical studies have investigated the assumptions that observers make about lighting diffuseness when estimating shape and reflectance, and they found that observers tend to assume high levels of diffuseness—often higher than the actual diffuseness of the light in the scene being viewed (Bloj et al., 2004; Boyaci, Doerschner, & Maloney, 2004, 2006; Boyaci, Maloney, & Hersh, 2003; Schofield, Rock, & Georgeson, 2011). This suggests that observers may have a prior for highly diffuse lighting.
A prior is adaptive when it matches the observer's environment, but almost nothing is known about the diffuseness of natural lighting. In Experiment 1, we measure the diffuseness of natural lighting in a wide range of real-world scenes, and we compare these measurements to previous psychophysical estimates of the assumptions that observers make about lighting diffuseness. In Experiment 2, we examine human and ideal performance in a lighting direction discrimination task to see whether human vision works more efficiently in some levels of lighting diffuseness than in others.
Experiment 1
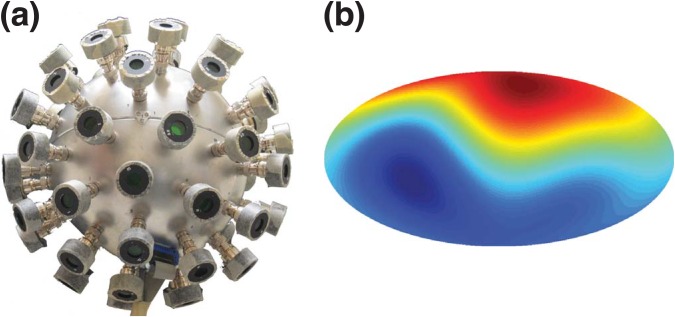
We used a custom-built multidirectional photometer (Figure 1) to record natural lighting in several hundred diverse scenes. The photometer recorded low-resolution, omnidirectional light probes: snapshots of the pattern of illumination incident from all directions at a point in space at a given time (Dror et al., 2004; Mury et al., 2007, 2009a, 2009b). We measured lighting conditions in rural and urban environments, under sunny and cloudy conditions, and in indoor environments.
Figure 1.
(a) The multidirectional photometer. (b) A Mollweide equal-area projection of a typical low-resolution light probe captured with the multidirectional photometer, illustrating the level of detail that is captured. Red regions indicate high luminance, and blue regions indicate low luminance.
We define a new measure of diffuseness, illuminance contrast energy (ICE), which allows us to describe our lighting measurements and the results of previous psychophysical studies in a common language. Let E(θ,φ) be the illuminance pattern over the surface of a unit sphere illuminated by a light probe, described in spherical coordinates where θ is the declination from the north pole (i.e., 0° at the north pole, 90° at the equator, 180° at the south pole) and φ is the azimuth. We define the ICE of the light probe to be the coefficient of variation of the illuminance over the sphere, i.e., its standard deviation divided by its mean:
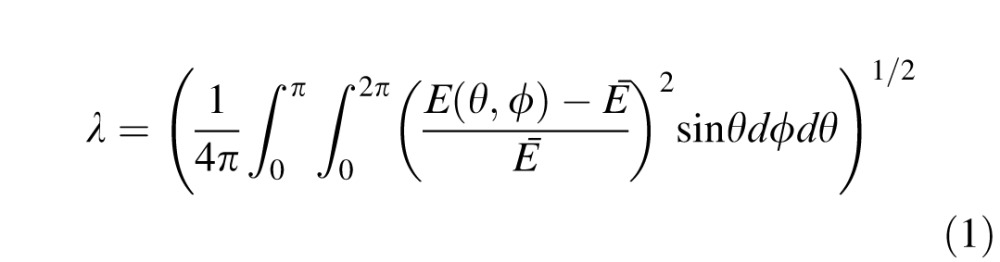 |
Here Ē is the mean illuminance over the sphere. Under diffuse light, illuminance is largely constant across surface orientations whereas under directional light the illuminance depends on the orientation of a surface relative to the dominant light sources. ICE is a measure of the variation of illuminance across orientations, and hence of diffuseness. ICE ranges from 0 for a completely uniform, ambient light source to 1.29 for a distant point light source (Morgenstern, 2011). Santa Clara (2009) independently developed an equivalent measure of lighting diffuseness.
ICE is not the coefficient of variation of the light probe. It is the coefficient of variation of the illuminance pattern that the light probe generates on the surface of a sphere, and illuminance is the lighting property that is most relevant to the shading of Lambertian surfaces.2 The light probe L(θ,φ) is a function that reports the luminance in direction (θ,φ). The illuminance pattern E(θ,φ) generated by the light probe on a sphere is the cosine-weighted integral of the light probe over a full hemisphere of directions:
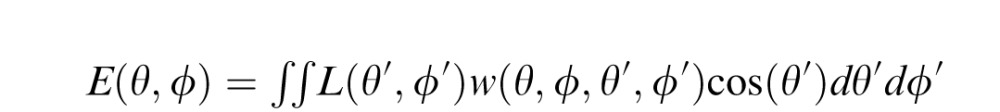 |
Here w(θ,φ,θ′,φ′) is the cosine of the angle between directions (θ,φ,) and (θ′,φ′), half-wave rectified so that negative values of the cosine are clipped to zero. As a result, the illuminance pattern E(θ,φ) is much more low pass than the light probe itself. Even a rich and detailed lighting environment creates a simple, smoothly varying illuminance pattern (Figure 2). Ramamoorthi and Hanrahan (2001) and Basri and Jacobs (2003) describe a simple method of using spherical harmonics to convert the luminance of a light probe to the illuminance it generates on a sphere.
Figure 2.
A light probe and the illuminance pattern it generates. The light probe at the position of this sphere has many detailed features because lighting in the surrounding environment varies strongly from one direction to another. The illuminance pattern generated over the surface of the matte sphere is much smoother, mostly just declining from high illuminance on the left to low luminance on the right. This image was rendered in RADIANCE (Ward, 1994) using a light probe captured by Debevec (1998).
We compared the ICE of natural lighting measurements with the ICE of the diffuseness levels assumed by human observers as measured in five previous psychophysical studies.
Method
Measurements of natural illumination
We used a custom-built multidirectional photometer that recovers light probes up to their second-order spherical harmonics, which is the component of lighting that is relevant to illumination of convex Lambertian objects (Basri & Jacobs, 2003; Ramamoorthi & Hanrahan, 2001). The device is a 20-cm-diameter aluminum sphere equipped with 64 evenly spaced photodiodes (UDT Sensors, Inc., model PIN-10AP) that are filtered to have the same spectral sensitivity as human observers under photopic viewing conditions. A laptop computer records the activation of each photodiode. We developed the multidirectional photometer independently of Muryy (2008). For further information on the device, see Morgenstern (2011).
All light probe measurements were made at York University. We report two types of measurements. The first type were measurements made between 12:00 p.m. and 1:30 p.m. from August to October 2010. Each measurement site was chosen so that previous sites could not be seen from the new site. The photometer sat on a microphone stand, 122 cm above the ground. We kept it 30 cm away from objects except in forested areas where this was not always possible. We made 570 measurements in several environments, listed in the legend to Figure 3. The second type were measurements taken on the roof of the Lassonde building at York University over the course of 1 day on November 20, 2010. The photometer was always in the same location, and the light probe measurements were made approximately every 20 min from sunrise to sunset. There were 53 measurements in total, in which the sky conditions varied from sunny to slightly overcast to completely overcast. For these measurements, the center of the photometer was at a lower position (104 cm above the ground) to make the device more stable. All measurements are available online as supporting information.
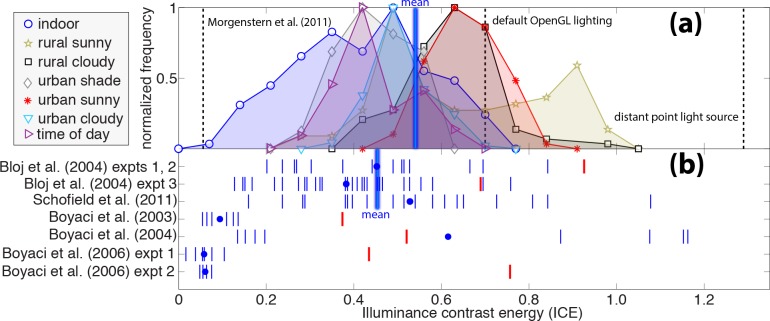
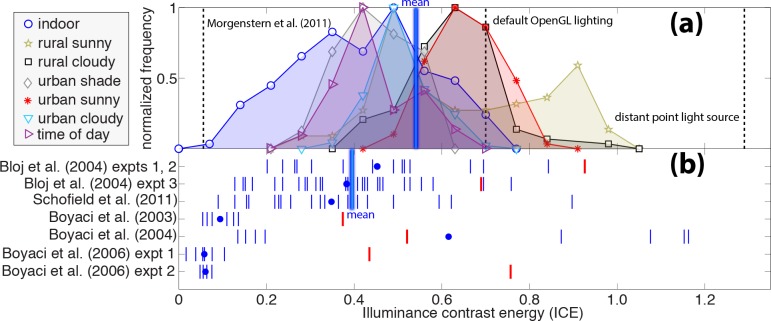
Figure 3.
Comparison of lighting diffuseness from natural lighting and psychophysical performance. (a) Histograms of the ICE of natural lighting in several environments, each scaled to peak at one. The “time of day” histogram shows the measurements made over the course of a single day. The dashed vertical lines show the ICE of a light source matched to Morgenstern et al.'s (2011) “weak cue” condition (the line labeled “Morgenstern et al., 2011”), default OpenGL lighting, and a distant point light source. The thick vertical blue line shows the mean ICE over all environments. (b) Psychophysical estimates of observers' assumptions about diffuseness. Small vertical blue lines show the ICE assumptions of individual observers. Blue dots show averages across observers. The thick vertical blue line shows the mean ICE over Bloj et al.'s (2004) and Schofield et al.'s (2011) experiments, which, as we explain in the main text, are the studies we think most relevant for a comparison with natural lighting. Red lines show the ICE of the actual illuminants in the experiments. Schofield et al. ran their experiments in the dark and with a highly ambiguous sine wave stimulus, so we do not show a red line indicating an ICE value for their lighting.
Data from psychophysical studies
We compared the diffuseness of our lighting measurements to the results of five previous psychophysical studies that quantified observers' assumptions about lighting diffuseness (Bloj et al., 2004; Boyaci et al., 2004, 2006; Boyaci et al., 2003; Schofield et al., 2011). To describe actual lighting conditions and the lighting conditions assumed by human observers, these studies used the notion of a point-plus-ambient (PA) illuminant (Phong, 1975). A PA illuminant consists of a distant point source and an ambient source, and under such lighting, the illuminance on a surface patch is
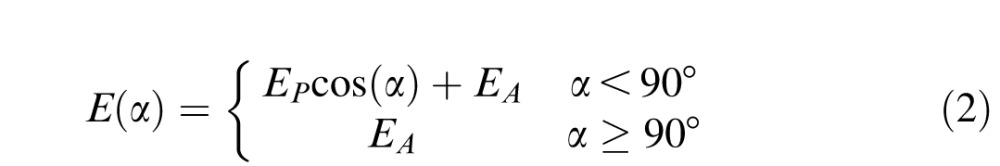 |
Here α is the angle of the surface normal relative to the point source direction, EP is the maximum illuminance from the point source, and EA is the illuminance from the ambient source.
Morgenstern (2011, pp. 141–143) shows that the ICE of a PA light source is
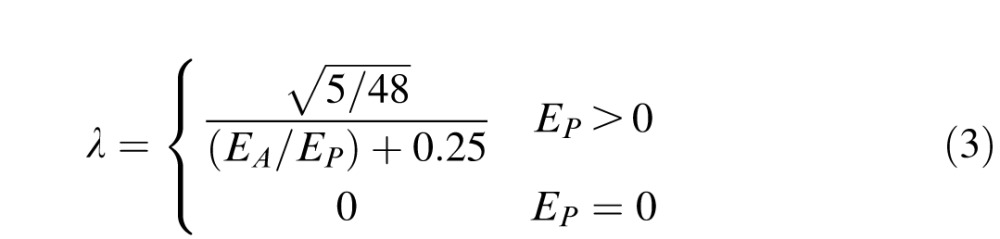 |
In Appendix A, we explain how we recovered the ratios EA/EP from the previous psychophysical studies. We used Equation 3 to convert these ratios to ICE.
Here we briefly describe the previous psychophysical studies and explain how we used their data.
Bloj et al. (2004)
Ripamonti et al. (2004) examined how lightness constancy varies with surface orientation. Their observers looked into a chamber that contained a spotlight, several objects, some gray frontoparallel paint chips, and a gray test patch that the experimenter could rotate. Observers judged which paint chip had the same reflectance as the test patch at various orientations. Ripamonti et al. found that lightness constancy was reasonably good but that observers consistently underestimated the reflectance of the test patch at orientations at which it was illuminated obliquely by the spotlight.
Bloj et al. (2004) showed that a simple normative model, an equivalent illumination model (Brainard & Maloney, 2011), could account for Ripamonti et al.'s (2004) findings. According to this model, the observer assumes that the scene is illuminated by a PA light source described by Equation 2, and the observer estimates the point illuminance EP and ambient illuminance EA. The model assumes that the observer perceives the orientation and luminance of the test patch accurately. Using this information, the observer uses a Lambertian shading model to calculate the reflectance of the test patch in a physically realistic way. Bloj et al. showed that the pattern of observers' lightness matches across test patch orientations is just what one would expect if observers followed this model but overestimated the amount of ambient light EA in the scene.
This diffuseness-based explanation accounts for Ripamonti et al.'s (2004) findings as follows: When the test patch is oblique relative to the light source, it has a low luminance. If the observer knows the true lighting conditions in the scene, he or she can (according to the model) infer that the low luminance is due to the orientation of the test patch and can infer the reflectance correctly from the test patch's luminance and orientation. However, if the observer overestimates the diffuseness of the illumination, he or she expects the luminance of the test patch to be largely independent of its orientation. When the patch is oblique relative to the light source, it has a low luminance, and the observer incorrectly attributes this to a low reflectance.
Using this model, Bloj et al. (2004) calculated the level of diffuseness that would explain each observer's lightness matches. Below we compare their results to the ICE values we measured for natural lighting. In Appendix A, we show how to convert the diffuseness estimates from Bloj et al.'s study as well as from Boyaci et al.'s (2003, 2004, 2006) and Schofield et al.'s (2011) studies, to ICE.
Boyaci et al. (2004, 2006) and Boyaci et al. (2003)
Boyaci et al. (2003) ran an experiment that was broadly similar to Bloj et al.'s (2004), and they examined lightness constancy as a function of test patch orientation. They used computer-generated scenes instead of real objects. Boyaci et al. (2006) ran a similar study in which they manipulated lighting cues to see which ones would affect observers' estimates of the illuminant; here we use data from their “all cues” condition, in which scenes contained shadows, shading, and specular highlights. Boyaci et al. (2004) ran a study in which the point light source was yellow and the ambient light was blue, and observers adjusted a test patch at various orientations so that it appeared achromatic. In all these studies, the experimenters calculated the PA illuminant that best accounted for observers' performance under an equivalent illuminant model.
Schofield et al. (2011)
Schofield et al. (2011) found that the 3-D shape percept generated by a sinusoidal luminance grating depends on the grating's orientation. They showed that this is what one would expect from an observer who assumes a PA illuminant when recovering shape from shading, and they estimated the level of diffuseness that would account for each observer's shape judgments.
Results and discussion
Figure 3a shows the ICE of our lighting measurements. Each environment's histogram is scaled to peak at one to reduce the overlap between the distributions. Figure 3a also shows two reference values: the dashed vertical line at the right shows the ICE of a distant-point light source, and the dashed vertical line near the middle shows the ICE of the default lighting in OpenGL (a PA source with the point source five times as strong as the ambient), an example of an illumination condition in simple computer-generated scenes. (We explain the vertical line at the far left, labeled “Morgenstern et al. [2011], ” in the Discussion.) The histograms show that natural light is more diffuse than one might have expected. The light probes mostly fall in the bottom half of the range of physically possible ICE values, and only the most directly illuminated environments are as direct as default OpenGL lighting. (We use “direct” to mean the opposite of “diffuse.”) The lowest ICEs come from indoor environments, and the highest come from rural environments, probably the forested environments on sunny days that we included in our light probes, in which the sun is sometimes visible through openings in the canopy. The vertical blue line in Figure 3a shows the mean ICE over all measurements, but this is only a rough measure of central tendency because it depends on the number of measurements in each environment. Table 1 gives the means and standard deviations of the ICE in individual environments.
Table 1.
Summary statistics of ICE lighting diffuseness measurements. Notes: The ICE values describe the data shown in Figure 3 except for “Schofield et al. (2011), revised,” which describes data shown in Appendix B, Figure B1.
| Mean ICE |
Standard deviation |
Standard error of mean |
|
| Indoor | 0.4132 | 0.1498 | 0.0122 |
| Rural sunny | 0.6514 | 0.1909 | 0.0208 |
| Rural cloudy | 0.6197 | 0.0984 | 0.0100 |
| Urban shade | 0.4478 | 0.0790 | 0.0109 |
| Urban sunny | 0.6598 | 0.0752 | 0.0079 |
| Urban cloudy | 0.5071 | 0.0659 | 0.0068 |
| Time of day | 0.4424 | 0.0830 | 0.0115 |
| Bloj et al. (2004), expts 1, 2 | 0.4526 | 0.1922 | 0.0533 |
| Bloj et al. (2004), expt 3 | 0.3828 | 0.1580 | 0.0304 |
| Schofield et al. (2011) | 0.5281 | 0.2314 | 0.0546 |
| Schofield et al. (2011), revised | 0.3481 | 0.1989 | 0.0469 |
| Boyaci et al. (2003) | 0.0942 | 0.0369 | 0.0165 |
| Boyaci et al. (2004) | 0.6139 | 0.4886 | 0.1847 |
| Boyaci et al. (2006), expt 1 | 0.0581 | 0.0302 | 0.0135 |
| Boyaci et al. (2006), expt 2 | 0.0632 | 0.0034 | 0.0019 |
Figure 3b shows the assumptions about diffuseness that guided observers' behavior in the five psychophysical studies. Each blue line represents the ICE assumption of a single observer, and each blue dot represents a mean across observers. ICE covers a limited range within most studies but varies substantially across studies. Red lines show the ICE of the actual illuminants. Bloj et al. (2004) measured the illumination conditions in their apparatus (including primary lighting and interreflections), and Boyaci et al. (2003, 2004, 2006) reported the parameters of the PA illuminant that lit their computer-generated scenes. (Thus, the true lighting conditions in some of Boyaci et al.'s scenes, including interreflections, may have had lower ICEs than the values reported. In particular, Boyaci et al. [2003] had a large surface immediately adjacent to the test patch, possibly adding substantial interreflections that would have made the lighting more diffuse.) Schofield et al.'s (2011) experiments were run in the dark, so we do not show an ICE value for their lighting conditions. Table 1 gives the means and standard deviations of the ICE values in each study.
Bloj et al. (2004)
Figure 3b shows that the ICEs of the actual illuminants in Bloj et al.'s (2004) scenes were at the upper end of natural lighting ICE values, but their observers behaved as if the scenes had ICE in the middle of the range of natural illumination. That is, observers overestimated the diffuseness of the spotlight illumination in the experiment (as Bloj et al. pointed out) and assumed levels of diffuseness that were typical of natural scenes, just as would occur if they were guided by a diffuseness prior that matched natural illumination.
These results also suggest that if the visual system does have a prior on lighting diffuseness, it is not easily overridden. Morgenstern et al. (2011) showed that the light-from-above prior is easily overridden by lighting-direction cues, such as shadows and shading. The scenes in Bloj et al.'s (2004) experiments contained cues, such as shadow contrast, that observers could have used to estimate lighting diffuseness, and yet observers' diffuseness estimates did not match the actual diffuseness of the scene's lighting. Lighting cues apparently do not override the diffuseness prior as easily as they override the light-from-above prior. These suggestions are speculative, of course, because Bloj et al. did not measure or manipulate diffuseness cues in their scenes. Furthermore, there is room for doubt about how strong the diffuseness cues really were because all the surfaces in Bloj et al.'s scene were flat and only a few of them had clearly visible cast shadows and penumbrae.
Schofield et al. (2011)
Schofield et al.'s (2011) observers also assumed diffuseness levels that were consistent with the levels we found in natural lighting. Schofield et al.'s method of inferring diffuseness priors was different from Bloj et al.'s (2004)—based on shape judgments instead of lightness judgments—so their data provide an independent test of observers' assumptions about lighting. Furthermore, Schofield et al.'s measurements are the most direct indicators of the visual system's prior on diffuseness as their experiments were run in the dark and their stimulus was simply a sine wave grating, which is highly ambiguous with regard to lighting conditions; Bloj et al.'s and Boyaci et al.'s (2003, 2004, 2006) scenes were more complex and contained cues to lighting diffuseness that may have affected observers' estimates of the lighting conditions. Appendix B shows ICE values based on a refinement of Schofield et al.'s lighting model. The revised ICE values are slightly lower but still well within the range of natural lighting.
Boyaci et al. (2004, 2006) and Boyaci et al. (2003)
Boyaci et al. (2003, 2004, 2006) obtained rather different results. The lighting in Boyaci et al.'s scenes had ICE values that were more typical of natural environments (except Boyaci et al.'s [2006] experiment 2), but their observers seem to have assumed that lighting was highly diffuse and, in fact, much more diffuse than almost any realistic lighting condition.3 However, there are good reasons to think that their results are biased toward high estimates of diffuseness (i.e., low ICE). Boyaci et al.'s observers' lightness constancy was poor: Their lightness matches were partway between matching the luminance of image patches on the computer screen and matching the reflectance of the surface patches they depicted, with a strong bias toward matching luminance (e.g., Boyaci et al. [2003] figure 8). The “equivalent illuminant” model that Boyaci et al. used to infer observers' diffuseness assumptions attributes such failures of lightness constancy to assumptions of high diffuseness. However, there are many reasons why lightness constancy can fail besides observers assuming unrealistically high levels of diffuseness. Unlike Bloj et al.'s (2004) scenes, Boyaci et al.'s scenes were computer-generated, and if observers did not see them as completely realistic, then they may have been biased toward matching screen luminance instead of matching the depicted surface reflectance. Supporting this view, Lee and Brainard (2014) found that a computer-generated replication of Gilchrist's (1977) paper-based lightness perception experiments led to much weaker constancy. Furthermore, failures of lightness constancy occur when observers judge lightness in scenes that have dark backgrounds, small frameworks, and low articulation (Gilchrist, 2006, p. 276), which are all factors consistent with weak lightness constancy in Boyaci et al.'s experiments. Thus, Boyaci et al.'s estimates of observers' assumptions about diffuseness were probably biased, and we do not see them as persuasive evidence against a diffuseness prior that matches natural lighting. (Furthermore, it was not Boyaci et al.'s goal to estimate observers' diffuseness priors. Their main goal was to test the equivalent illuminant model of lightness perception.)
To summarize, all five psychophysical studies suggest that human observers have a prior on lighting diffuseness, and Bloj et al.'s (2004) and Schofield et al.'s (2011) results indicate that observers' priors fall in the same range as our measurements of the diffuseness of real-world lighting. Observers showed a wide range of assumptions about lighting diffuseness, but this is consistent with studies of the light-from-above prior, which have also found large individual differences in assumed lighting directions (Adams, 2007).
Lighting engineers and designers use a diffuseness measure called the vector/scalar ratio, which we describe further in the General discussion. Interestingly, human factors experiments have found that people prefer vector/scalar ratios of 1.2 to 1.8 for lighting of human faces (Cuttle, 2003, p. 88). This corresponds to an ICE range of 0.39 to 0.58 and brackets both the average ICE across all our natural light probes (blue vertical line in Figure 3a) and the average ICE level that the equivalent illuminant model attributes to Bloj et al.'s (2004) and Schofield et al.'s (2011) observers (blue vertical line in Figure 3b).
Our measurements show that the average of observers' diffuseness assumptions is in line with the average diffuseness of natural lighting. This leaves open the question of how strong observers' diffuseness priors are, i.e., how narrow the priors are as statistical distributions, and whether they usually override diffuseness cues in individual scenes. On the one hand, the large individual differences in observers' diffuseness assumptions as well as the wide range of diffuseness in natural lighting, suggest that the priors may be weak. On the other hand, the fact that Bloj et al.'s (2004) stimuli provided observers with cues to diffuseness and yet observers' diffuseness estimates consistently had lower ICE than the actual lighting suggests that the prior may be strong. Further work is needed to decide this question.
Experiment 2
If human vision is tuned to the relatively high diffuseness levels of natural lighting, then why do human observers perform some tasks poorly under diffuse lighting? For example, Pont and Koenderink (2007) found that observers are much worse at estimating the dominant lighting direction under diffuse lighting than under direct lighting. Furthermore, it is well known that the image of a Lambertian sphere rendered under completely diffuse lighting is simply a uniform disk and does not appear spherical at all. One possibility suggested by the latter example is that diffuse lighting makes some tasks intrinsically harder in the sense that diffusely lit scenes simply provide less task-relevant information to the observer. If so, then poor performance under diffuse lighting might be explained by the reduction in task-relevant information and could be logically consistent with the idea that human vision is optimized for relatively diffuse lighting. To test this possibility, we designed a lighting direction–discrimination task in which we measured the performance of both human observers and an ideal observer that makes optimal use of the stimulus information, achieving the best possible performance (Geisler, 1989). We measured lighting direction–discrimination thresholds Δα for human and ideal observers under five levels of lighting diffuseness. We calculated human observers' efficiency, the squared ratio of ideal and human thresholds (Tanner & Birdsall, 1958):
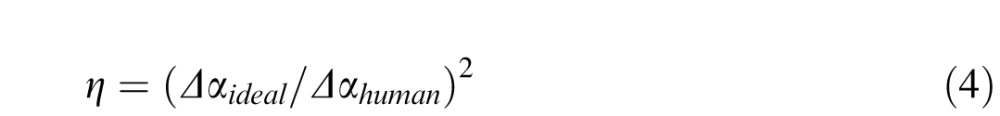 |
Efficiency is 1.0 for a human observer who has the same threshold as the ideal observer and less for an observer who has a higher threshold. Efficiency corrects for intrinsic task difficulty, so it gives an effective way of comparing performance across diffuseness conditions.
Method
Participants
Five observers from York University participated. Four naive observers participated for payment ($15/hr), and the third author (RFM) was also an observer. All observers reported normal or corrected-to-normal vision.
Stimuli
The stimuli were OpenGL renderings of a hemispherical polyhedron composed of 152 Lambertian triangles (Figure 4). The polyhedron subtended 9° of visual angle. The simulated lighting consisted of a distant point source with direction p⃗ and maximum illuminance EP and an ambient source with illuminance EA. The luminance of each triangular patch with reflectance ρ and surface normal n⃗ was calculated using the Lambertian shading model:
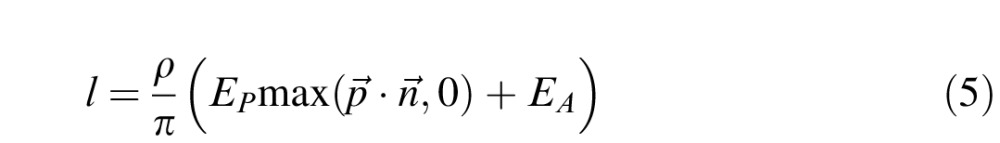 |
Here · is the vector dot product. We report the values of the lighting parameters p⃗, EP, and EA below under “Procedure.”
Figure 4.
Typical stimuli in the lighting direction–discrimination experiment illuminated from slant 60° and tilt 20° (i.e., lighting above and to the right). The stimuli show the five diffuseness levels used in the experiment, namely ICE values of (a) 0.2, (b) 0.4, (c) 0.6, (d) 0.8, and (e) 1.0.
The reflectance of each triangle making up the polyhedron was drawn independently for each new stimulus from a truncated normal distribution gtr(x,μ,σ) with mean 0.6 and standard deviation 0.2. The distribution was truncated at two standard deviations from the mean, so reflectance ranged from 0.2 to 1.0.
Stimuli were shown on a CRT monitor (Sony Trinitron G520, 19-in., resolution 1600 × 1200, pixel size 0.240 mm, frame rate 75 Hz) in a dark room at a viewing distance of 57 cm. The color lookup table of the computer's video card linearized the relationship between RGB values in video memory and luminance on the monitor. A simulated surface patch with the mean reflectance value (0.60) had luminance 58 cd/m2 when directly facing the virtual point light source, and the stimuli were shown on a low-luminance background (0.3 cd/m2).
Procedure
We describe lighting directions in terms of slant and tilt. Slant is the angle of the lighting direction relative to a line perpendicular to the computer monitor, so a slant of 0° is directly toward the viewer and 90° is in the plane of the monitor. Tilt is the angle of the lighting direction projected into the plane of the monitor, defined so that 0° is upward and positive angles are clockwise.
All five observers participated in 25 blocks of a slant-discrimination task and 25 blocks of a tilt-discrimination task. The blocks were interleaved in random order and spread over a few weeks.
In the slant-discrimination task, observers discriminated between two lighting directions with different slants. We used simulated lighting with ICE values 0.2, 0.4, 0.6, 0.8, and 1.0. We held the maximum simulated illuminance EP + EA constant at 304 lux for all ICE values. (This constraint, along with the ICE value and Equation 3, determines EP and EA.) Each ICE condition was shown in five blocks for a total of 25 blocks. Each block contained 150 trials and took approximately 8 min.
Each trial began with a blank screen for 500 ms, followed by the first stimulus for 500 ms, another blank screen for 500 ms, the second stimulus for 500 ms, and, finally, a blank screen until the observer responded. One stimulus interval showed a hemisphere illuminated from slant 60° + Δθ and tilt 0°, and the other showed a hemisphere illuminated from slant 60° − Δθ and tilt 0°. The two slant directions were randomly assigned to the two stimulus intervals. The observer pressed a key to indicate which interval had a lighting direction closer to the line of sight. Auditory feedback indicated whether the response was correct. The next trial began immediately. The task was not trivial because reflectances were assigned randomly in each new stimulus, so the luminance variations that provided information about lighting direction were partly masked by luminance variations caused by the random assignments of reflectance. The perturbation angle Δθ varied over trials according to two interleaved staircases converging on 71% and 79% correct performance (Wetherill & Levitt, 1965). The blank screens and the stimulus background were shown at the monitor's lowest luminance (0.3 cd/m2). For each block, we made a maximum-likelihood fit of a Weibull psychometric function to proportion correct as a function of the angle between the two lighting directions, and we took the angle corresponding to 75% correct performance as the observer's threshold. This gave five thresholds for each observer in each ICE condition.
The tilt-discrimination task was the same as the slant task except that the two stimulus intervals showed polyhedral hemispheres illuminated from tilts ±Δφ and slant 60°, and observers pressed a key to indicate which stimulus had lighting from a more clockwise direction.4
Ideal observer analysis
We measured the performance of an ideal observer on the slant- and tilt-discrimination tasks at the same five diffuseness levels seen by human observers, and we found the ideal observer's 75% thresholds. In Appendix C, we describe the ideal observer, and we provide MATLAB code for our ideal observer calculations as online supporting information.
Ideal observer analysis is a classical signal-detection tool used in spatial vision to measure human efficiency for pattern detection and discrimination. In recent years, it has been extended and used to understand how human observers interpret 2-D images that arise from 3-D scenes (e.g., Burge & Geisler, 2011; Ernst & Banks, 2002). In terms of the human perception of lighting, shape, and reflectance from shading, such ideal observers have helped researchers understand perceptual strategies for detecting lighting-direction changes on a surface (Gerhard & Maloney, 2010) and shown how observers combine scene lighting cues with prior assumptions when estimating 3-D shape (Morgenstern et al., 2011). Recent work has also used ideal observers to measure how well human observers distinguish between different illuminants within a scene (Lee & Brainard, 2011). Here we apply the ideal observer paradigm in a novel way by incorporating a Lambertian shading model, illustrating how ideal observers can be used to understand perception of lighting and potentially also shape and reflectance from shading.
Results and discussion
Figure 5a and b show thresholds as a function of lighting diffuseness. Thresholds were much higher under diffuse light in both tasks. In the slant task, the average threshold (averaged across observers) was 5.8 times higher at ICE 0.2 (diffuse light) than at ICE 1.0 (direct light). In the tilt task, the average threshold was 4.1 times higher at ICE 0.2 than at ICE 1.0. These findings are consistent with Pont and Koenderink's (2007) finding that observers are less accurate at estimating the direction of diffuse lighting than of direct lighting.
Figure 5.
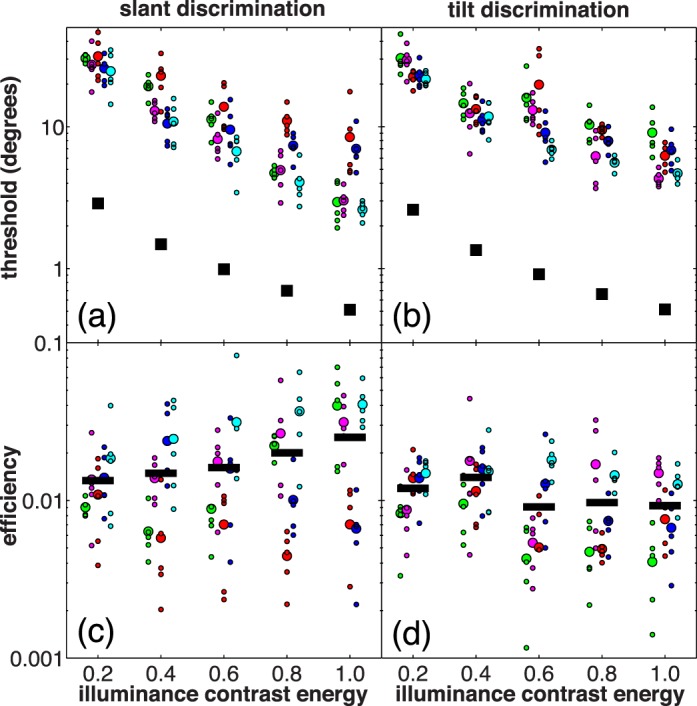
Thresholds and efficiency in the lighting direction discrimination experiment. Each color corresponds to a different observer. Each small colored data point shows a threshold or efficiency from one 150-trial block, and each large colored data point represents the average threshold or efficiency for a single observer over five blocks. The black squares in the top two panels show the ideal observer's thresholds. The black lines in the bottom two panels show efficiency averaged over all observers at a single ICE level. All observers viewed lighting conditions with the same five ICE values, but we have jittered the data points horizontally so that they do not overlap. (a) Thresholds in the slant task. (b) Thresholds in the tilt task. (c) Efficiency in the slant task. (d) Efficiency in the tilt task.
The black squares in the same panels show the ideal observer's thresholds, which follow a similar pattern to human thresholds even though they are an order of magnitude lower. This suggests that much of the variation in human performance across diffuseness levels is due to the intrinsic difficulty of the tasks. Figure 5c and d show human efficiency as a function of lighting diffuseness and support this interpretation. Efficiency varied much less across ICE levels than thresholds did. In the slant task, the average efficiency was 1.9 times lower at ICE 0.2 (diffuse light) than at ICE 1.0 (direct light), but there were large individual differences with some observers more efficient with diffuse light and some more efficient with direct light. In the tilt task, the average efficiency was 1.3 times higher at ICE 0.2 than at ICE 1.0. These differences between ICE 0.2 and 1.0 are smaller than the corresponding differences for thresholds. Thus much of the difference in thresholds across diffuseness conditions can be accounted for by intrinsic task difficulty, and the fact that human performance is better with directly illuminated scenes does not mean that vision is optimized for direct illumination. To a large extent, observers' performance patterns simply reflect the fact that directly illuminated scenes provide more task-relevant information.
In the experiments with human observers, we drew reflectances from a truncated normal distribution instead of the full normal distribution for the pragmatic reason that reflectances can only span the range [0,1] whereas the normal distribution has tails that go to infinity. In ideal observer simulations with the truncated normal distribution, we found that almost all the ideal observer's responses were determined by the truncated tails: On most trials, a few of the stimulus luminances were so high or low that they could have only been generated by one of the two possible lighting directions because to be generated by the other lighting direction would require reflectances outside the range [0.2,1.0] that was spanned by the truncated normal distribution. This seemed problematic to us as a benchmark for human performance because it relies almost entirely on knowledge of how quickly the outer 5% of the reflectance distribution goes to zero. For this reason, we reran the ideal observer simulations using the full normal distribution for reflectances even though this meant that reflectances could take values outside [0,1]. This change had little effect on the overall pattern of efficiency. Efficiencies were about three times higher. In the slant task, efficiency did not rise quite as quickly as a function of ICE, and in the tilt task, efficiency fell slightly faster as a function of ICE. These findings give support to our conclusion that people perform better in direct light (high ICE) largely because direct lighting provides more task-relevant information.
We did not find observers to be consistently more efficient under diffuseness levels typical of natural lighting as we might have expected if they had a prior for natural levels of diffuseness. However, our stimuli showed many polygon faces covering a hemisphere of orientations, and this provided a great deal of information about the lighting direction and diffuseness in the scene. We confirmed this using ideal observer simulations: Ideal thresholds for lighting-direction discrimination are on the order of just a few degrees, and ideal thresholds for lighting-diffuseness discrimination are on the order of 0.01 ICE units. Thus any prior assumptions about diffuseness may have been overridden by the very precise lighting information conveyed by these stimuli. Similar experiments with less informative stimuli, such as polyhedra with fewer faces, may force observers to rely more heavily on their lighting priors and so may reveal larger differences in efficiency across diffuseness conditions. Another possibility, though, is that a direction discrimination task may be a poor choice for probing observers' assumptions about diffuseness, i.e., it may be that observers use a direction-discrimination strategy that makes no strong assumptions about lighting diffuseness. This possibility remains to be explored. In any case, the main point of Experiment 2 is to address a possible objection to the idea that human observers have a prior for high diffuseness, namely that observers often perform worse under diffuse light. Experiment 2 shows that (in at least one case), when observers perform substantially worse under diffuse light, this is almost entirely due to intrinsic task difficulty rather than to observers using a strategy unsuited to diffuse lighting.
General discussion
Previous studies have also measured light probes in order to examine the statistical structure of natural lighting (Dror et al., 2004; Mury et al., 2007, 2009a, 2009b). The contribution of our measurements with the multidirectional photometer has been to collect a large number of low-resolution light probes in diverse environments, to characterize the diffuseness of the lighting in these scenes, and to relate the diffuseness of natural lighting to psychophysical findings. Mury et al. (2009a, 2009b) used a multidirectional photometer similar to our own, but they examined a smaller number of low-resolution light probes in a limited range of environments and did not examine diffuseness. Although these low-resolution light probes provide a characterization of lighting useful for Lambertian surfaces, a higher resolution is necessary to understand the lighting relevant to more specular surfaces (such as a mirror or apple peel). Natural light probes certainly contain features at high spatial frequencies that are not captured by our or Mury et al.'s (2009a, 2009b) devices. With this in mind, Dror et al. used Debevec's (1998) and Teller et al.'s (2003) high-resolution light probes to examine the statistics of natural lighting. Debevec measured a small number of high-resolution light probes, and Dror et al. used just nine light probes of this type, so high-resolution light probes have not yet been characterized as thoroughly as low-pass light probes.
ICE and spherical harmonics
Just as planar images can be represented as sums of sinusoids, light probes can be represented as sums of spherical harmonics (e.g., Ramamoorthi & Hanrahan, 2001). ICE has a particularly simple relationship to the spherical harmonic representation. Suppose we represent a light probe L(θ,φ) as a sum of orthonormal spherical harmonics Ylm:
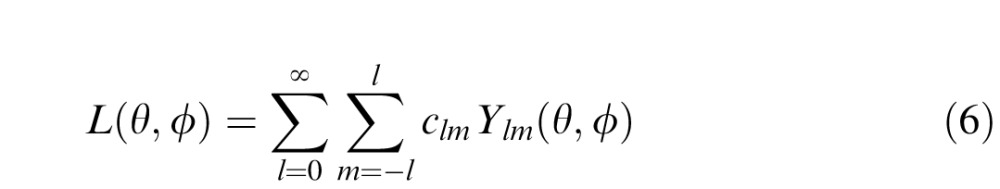 |
Basri and Jacobs (2003) and Ramamoorthi and Hanrahan (2001) show that the illuminance pattern E(θ,φ) generated over a sphere by the light probe is
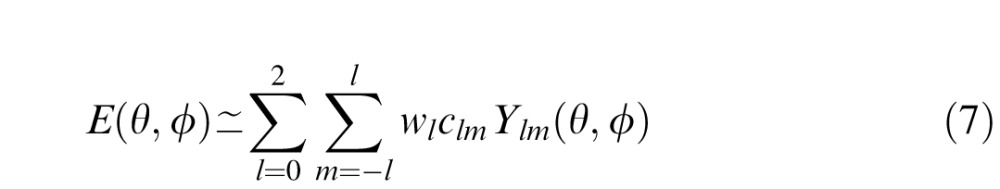 |
Here clm are the spherical harmonic coefficients, and wl are fixed weights assigned to each order of spherical harmonics. The magnitudes of the weights wl represent how important each order is in the mapping from luminance to illuminance. For an exact result, the expansion can be continued beyond order l = 2, but the higher-order weights wl are small, so the higher-order terms can usually be omitted. In Appendix E, we show that substituting this expansion into Equation 1 gives an expression for ICE in terms of spherical harmonic coefficients:
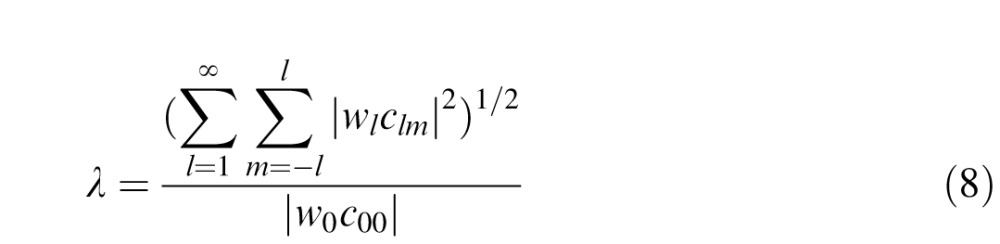 |
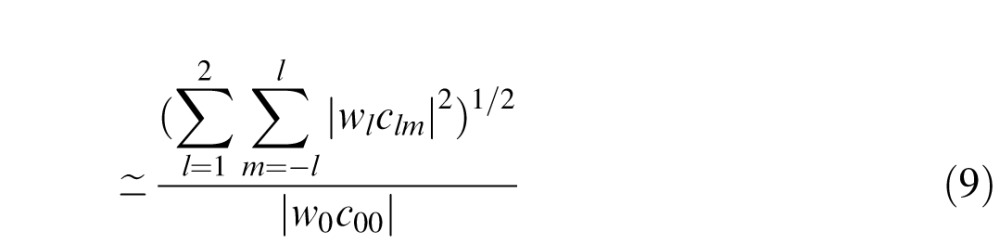 |
Equation 9 shows that ICE is simply the rms energy in the higher-order (l ≥ 1) harmonics of the illuminance, divided by rms energy in the zero-order component of the illuminance (which is equivalent to the absolute value of the DC coefficient because there is just one term).
ICE and diffuseness perception
ICE gives us a measure of diffuseness, but other measures are possible too. Lighting engineers sometimes use the vector/scalar ratio as a measure of diffuseness (Cuttle, 2003, p. 302). To find the “vector” in this ratio, we orient a disk in space so as to create the greatest difference between the illuminance on the two sides of the disk; the direction of the vector is then the surface normal to the side with the greater illuminance, and the magnitude of the vector is the illuminance difference. The “scalar” in this ratio is the mean illuminance over the surface of a sphere. The vector/scalar ratio is defined to be the ratio of the vector magnitude to the scalar. In Appendix F, we show that for the special case of a PA light source, the vector/scalar ratio is simply ICE multiplied by
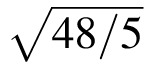 .
.
We developed ICE because the vector/scalar ratio assigns implausible diffuseness ratings in some cases. For example, at a point halfway between two equally bright point sources in an otherwise dark room, the vector/scalar ratio is zero, just as it would be in an environment with completely uniform diffuse lighting.
Nevertheless, any diffuseness measure that maps the high-dimensional space of all possible illuminants onto a one-dimensional scale will predict diffuseness metamers. In the previous section, we showed that ICE can be calculated from the squared amplitudes of the spherical harmonic coefficients of a light probe, and this means that varying the phase of the spherical harmonics or shifting energy between harmonics within a single order will have no effect on the ICE value. It is an open question what diffuseness measure corresponds best with human judgments of diffuseness.
Equation 8 suggests a possible modification to the definition of ICE. The weights wl represent the importance of the spherical harmonic orders l in the mapping from luminance to illuminance, and they fall off rapidly with l. Higher-order spherical harmonic components of light probes are important in rendering specular surfaces, though, so a modification of ICE in which the weights wl fall off less rapidly may be useful in predicting diffuseness judgments in scenes containing non-matte surfaces.
ICE and the light-from-above prior
Morgenstern et al. (2011) showed that the light-from-above prior is weak in the sense that it is easily overridden by lighting direction cues, such as shading and shadows. Does this mean that natural lighting usually overrides the light-from-above prior so that this well-known prior is actually unimportant in everyday perception? Our diffuseness measurements provide an answer to this question.
Morgenstern et al. (2011) created a lighting condition (their “weak cue” condition) that is matched to the light-from-above prior: Lighting conditions that provide stronger lighting direction cues than this matched condition override the prior, and lighting conditions that provide weaker cues do not. The dashed vertical line at the left of Figure 3a, labeled “Morgenstern et al. (2011),” shows the ICE of a lighting condition that provides lighting-direction cues as strong as those in Morgenstern et al.'s matched lighting. (See Appendix D for details of this calculation.) Almost all our natural lighting measurements had much higher ICEs than this, so they almost certainly provided stronger lighting-direction cues. The strength of lighting-direction cues also depends on whether there are 3-D shapes in the scene that generate shading and shadow cues, of course, but few scenes are completely devoid of such shapes, and Morgenstern et al.'s equivalent illuminant is so far below the natural ICE distribution that observers will rarely encounter light that approaches this level of diffuseness. These observations suggest that the light-from-above prior is unimportant in everyday perception. Nevertheless, lighting direction cues are stronger in some parts of a scene than in others, and little is known about how the visual system propagates lighting direction information across a scene, so this conclusion must be tentative (although see Ostrovsky, Cavanagh, & Sinha, 2005, and Morgenstern et al.'s figure 3c).
Final remarks
The Bayesian view of vision has been influential, but it has often been difficult to compare the psychophysically determined assumptions that guide perception with independently measured statistical distributions that characterize the real world. Fortunately, there has been much work recently on characterizing perceptually important properties of real-world scenes (Attewell & Baddeley, 2007; Dror et al., 2004; Geisler, 2008; Mury et al., 2007, 2009a, 2009b; Potetz & Lee, 2003). The case of natural lighting illustrates how we can advance our understanding of the human visual system by comparing its performance to properties of the world whose ambiguous signals it must use to create accurate and reliable percepts.
Acknowledgments
We thank James Elder, Laurence Harris, Denise Henriques, Kari Hoffman, Laurence Maloney, and the reviewers for helpful comments. This work was funded by Ontario Graduate Studentship in Science and Technology scholarships to Yaniv Morgenstern, Canada Foundation for Innovation and Natural Sciences and Engineering Research Council of Canada grants to Richard Murray, and NIH grant EY11747 to Wilson Geisler.
Commercial relationships: none.
Corresponding author: Yaniv Morgenstern.
Email: yaniv.morgenstern@gmail.com.
Address: Department of Psychology, University of Minnesota, Minneapolis, MN, USA.
Appendix A: Calculating ICE from previous studies
Bloj et al. (2004) show plots where diffuseness is given by data points' radial positions (their figures 5 to 10). The radial position is v = 1/(FA + 1) (their equation 7). FA is the ratio of the illuminance EA from ambient light to the illuminance ID sin(φD)/d2 from a point source of luminous intensity ID at distance d and elevation φD: FA = d2EA/ID sin(φD) (unnumbered equation below their equation 6). The illuminance that a surface would receive directly facing the illuminant is EP = ID/d2, so EA/EP = FA sin(φD). In Bloj et al., φD = 30°. We read ν from their plots using data capture software and calculated EA/EP = FA sin(30°) = ((1/ν) − 1) sin(30°). Equation 3 converts EA/EP to ICE.
Boyaci et al. (2003) report the ratio π̂ = EP/(EP + EA) that explains each observer's behavior (their table 1). EA/EP = (1/π̂) − 1, and Equation 3 converts EA/EP to ICE.
Boyaci et al. (2004) report ratios Δ = EA/EP, and Equation 3 converts this to ICE.
Boyaci et al. (2006) show plots on which the radial coordinate is π̂ = EP/(EP + EA), which can be converted to ICE the same way as Boyaci et al.'s (2003) π̂.
Schofield et al. (2011) fit their equation 5 to observers' shape judgments and reported diffuseness parameters γ in their table 1. The first term in their equation 5, in parentheses following (1 − γ), approximates the luminance pattern of a sinusoidal surface under a point source that would create a luminance of 1 − γ on a surface facing it directly. The second term, following γ, approximates the luminance pattern of a sinusoidal surface under an ambient source that creates a maximum luminance of 0.5γ. Thus EA/EP = 0.5γ/(1 − γ), and Equation 3 converts EA/EP to ICE.
Note that all these psychophysical studies described observers' assumptions about lighting in terms of the PA model. Observers' representations of scene lighting are almost certainly more sophisticated than this, e.g., Doerschner, Boyaci, and Maloney (2007) show that observers can discount at least two point light sources when judging lightness. If the psychophysical studies described in this appendix were reanalyzed to characterize observers' lighting assumptions using a more sophisticated lighting model, then, presumably, the ICE values of the assumptions would be somewhat different. We doubt that this would change the ICE values substantially, but, of course, this is an open question.
Appendix B: Revised ICE values for Schofield et al. (2011)
Andrew Schofield (personal communication, April 4, 2012) suggested that Equation B1 approximates the luminance profile of a sinusoidal surface better than Schofield et al.'s equation 5.
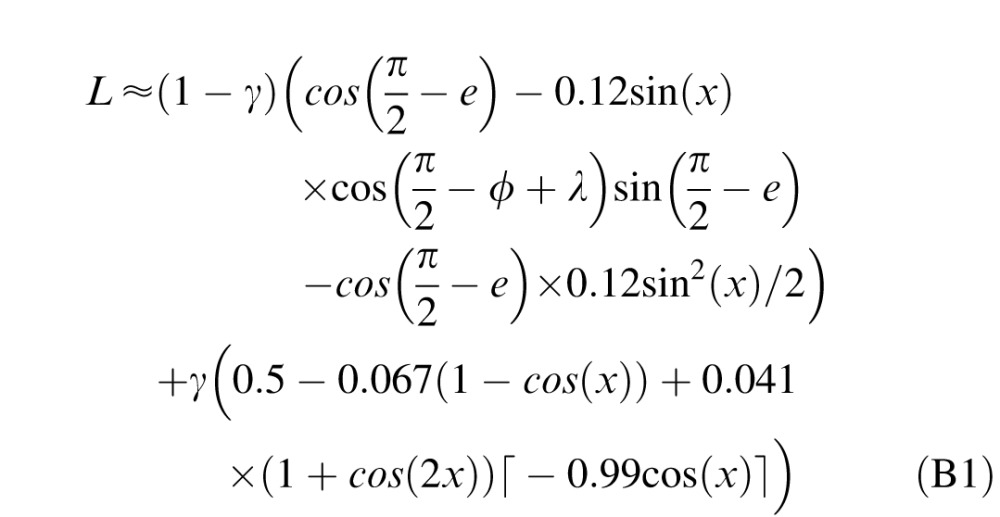 |
Here the variables are the same as in Schofield et al.'s equation 5, and ⌈x⌉ is x rounded to the next higher integer. Andrew Schofield provided us with the values in Table B1 as an improvement on Schofield et al.'s table 1. The values in Table B1 were obtained by fitting Equation B1 (instead of Schofield et al.'s equation 5) to Schofield et al.'s data. The ICE values that we calculated from these revised data are shown in Figure B1 and described with summary statistics in Table B1.
Figure B1.
Same as Figure 3 except for the data for Schofield et al. (2011). The revised ICE values from Schofield et al. are slightly lower than the corresponding values in Figure 3 but still within the range of natural lighting.
Table B1.
Refined Schofield et al. (2011) ICE values.
|
γ |
γ |
||
| Observer 1 | 0.62 | Observer 8 | 0.50 |
| Observer 2 | 0.34 | Observer 9 | 0.87 |
| Observer 3 | 0.59 | Observer 10 | 0.82 |
| Observer 4 | 0.52 | Observer 11 | 0.56 |
| Observer 5 | 0.37 | Observer 12 | 0.67 |
| Observer 6 | 0.78 | Observer 13 | 0.60 |
| Observer 7 | 0.70 | Observer 14 | 0.54 |
Appendix C: Ideal observer for lighting-direction discrimination
The ideal observer knows the polyhedron's 152 normal vectors, the probability distribution of reflectances, and the two lighting directions on each trial, p⃗1 and p⃗2. The stimulus is two sets of 152 luminances, Li =
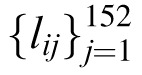 , i = 1,2, corresponding to the two stimulus intervals. The posterior probabilities that the lighting directions are shown in order (p⃗1,p⃗2) or (p⃗2,p⃗1) are
, i = 1,2, corresponding to the two stimulus intervals. The posterior probabilities that the lighting directions are shown in order (p⃗1,p⃗2) or (p⃗2,p⃗1) are
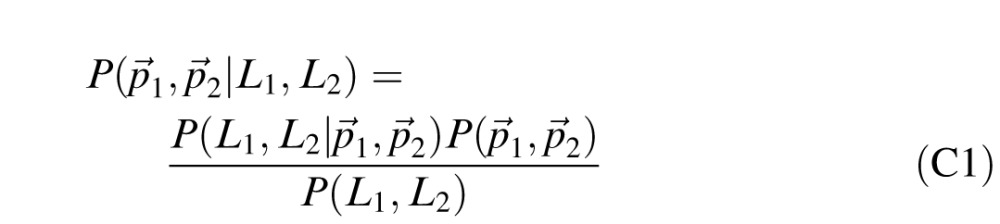 |
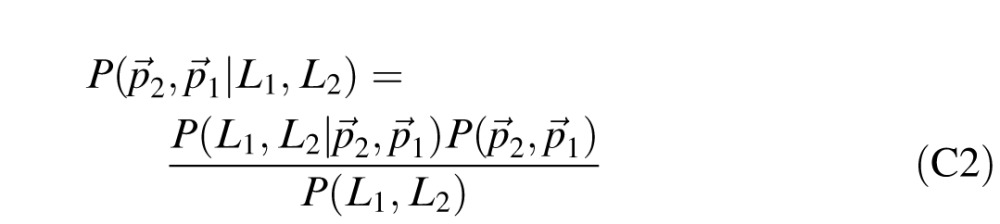 |
The ideal observer finds the probability ratio
 |
The two lighting orders are equally probable, so Equation C3 is equivalent to the likelihood ratio
 |
The luminances lij of different patches are independent, so the numerator in Equation C4 is
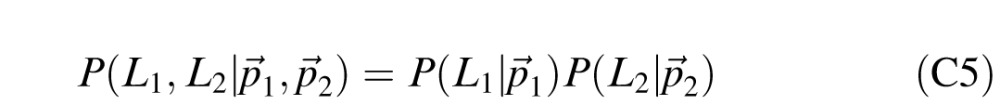 |
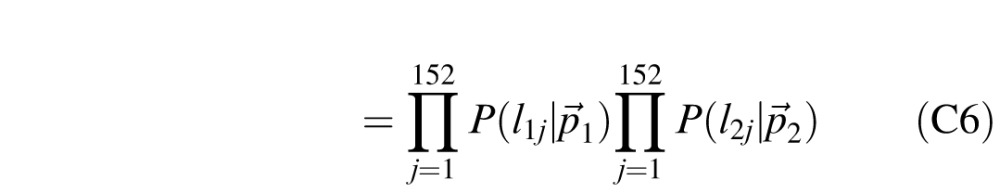 |
Equation 5 shows that the distribution of each luminance lij is a rescaling of the reflectance distribution with constant of proportionality ckj = (EP max(p⃗k·n⃗j, 0) + EA)/π. If stimulus interval i has lighting direction p⃗k, the probability density of lij is
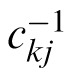 gtr(
gtr(
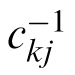 lij,μ,σ), where gtr(x,μ,σ) is the truncated normal distribution of reflectances. Equation C6 becomes
lij,μ,σ), where gtr(x,μ,σ) is the truncated normal distribution of reflectances. Equation C6 becomes
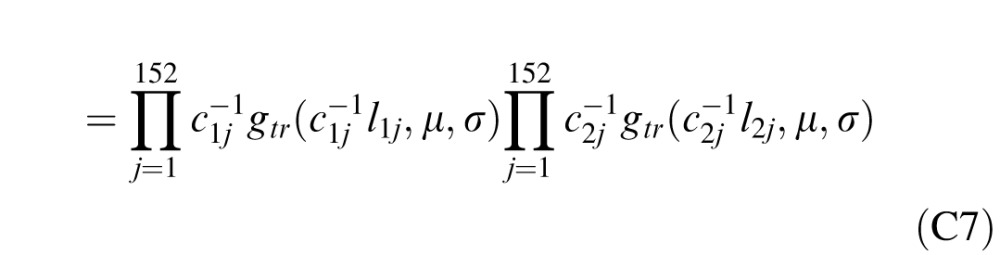 |
The likelihood of the observed luminances under the opposite lighting order is
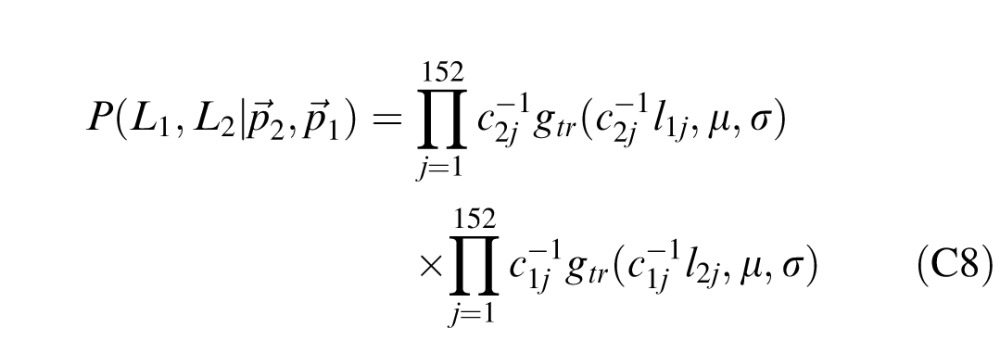 |
The ideal observer calculates the likelihoods of the luminances under the two lighting orders using Equations C7 and C8 and chooses the order that generates the higher likelihood. Using simulations, we found the ideal observer's 75% thresholds in the slant- and tilt-discrimination tasks under the five diffuseness levels viewed by human observers.
Appendix D: ICE of the light-from-above prior
Morgenstern et al.'s (2011) “weak cue” lighting condition was about as strong as the light-from-above prior in terms of its influence on observers' lighting direction estimates. We cannot simply calculate the ICE of this illuminant and compare it to natural lighting, though. In their strong cue condition, the light was a point source in the direction of the viewer and a stronger source slightly forward of the frontoparallel plane. In their weak cue condition, they switched the two sources so that most light came from the viewing direction. Thus, lighting in the two conditions had the same ICE, and the weak condition provided weak cues only because the stronger source was accidentally aligned with the viewing direction.
We circumvented this problem by finding the PA illuminant that provides lighting cues that are equally informative to an ideal observer as the weak cue condition. First, we measured ideal performance at discriminating between lighting directions 10° apart in Morgenstern et al.'s (2011) weak cue scenes covered in pixelwise white Gaussian noise. (This ideal observer is simply a template matcher.) We averaged ideal performance across 36 such tasks with lighting directions 0° versus 10°, 10° versus 20°, etc. Second, we measured ideal performance at the same task but with a PA illuminant. The point source varied across the same directions as in the first simulation. A point-to-ambient ratio EA/EP = 5.54 gave the same ideal performance as in the first task. Equation 3 converts this to an ICE of 0.056, shown by the dashed line in Figure 3.
Appendix E: ICE and spherical harmonics
Equation 1 gives the definition of ICE:
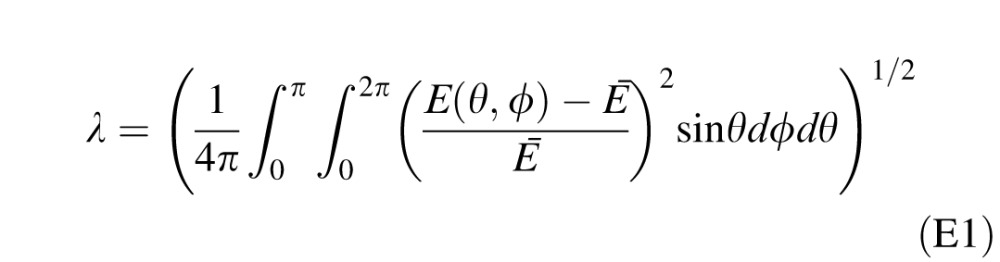 |
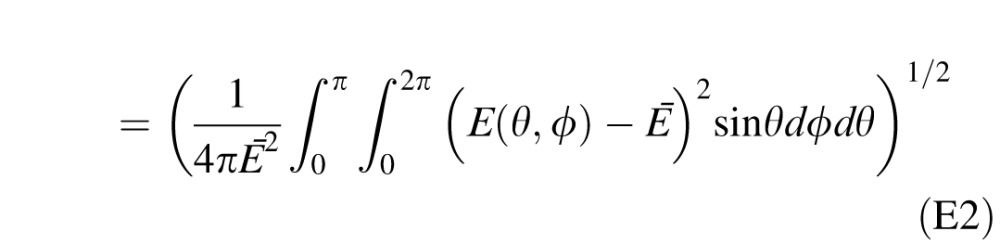 |
E(θ,φ) − Ē is the illuminance pattern E(θ,φ) minus its DC component. The spherical harmonics Ylm are orthonormal, so the integral of this factor squared is the sum of the squared amplitudes of its spherical harmonic coefficients. The DC component of E(θ,φ) − Ē is zero, so c00 = 0. Thus,
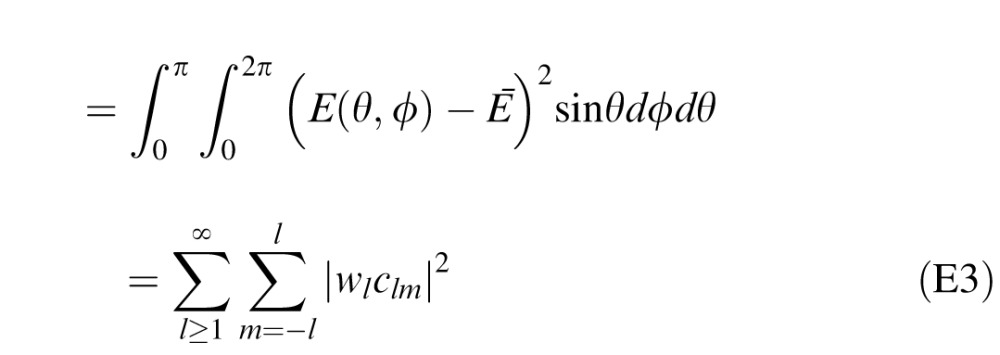 |
Here we use wl and clm as defined in Equations 6 and 7.
The zero-order harmonic Y00 has a constant value of (4π)−1/2, so the mean illuminance is
 |
Substituting Equations E3 and E4 into Equation E2 gives an expression for ICE in terms of the spherical harmonic coefficients of the light probe:
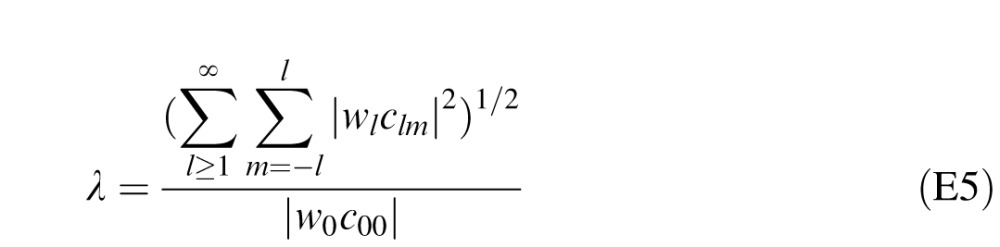 |
Appendix F: ICE and the vector/scalar ratio for a PA light source
For the PA light source described by Equation 2, the largest difference between the illuminance on two sides of a disk is obtained when one side of the disk directly faces the point light source, and then the difference is (EP + EA) − EA = EP. The mean illuminance over the surface of a sphere is EA from the ambient source and EP/4 from the point source for a total of EA + EP/4. Thus the vector/scalar ratio is ((EA/EP) + 0.25)−1. Comparing this to Equation 3, we see that, for a PA light source, the vector/scalar ratio is ICE times
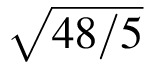 .
.
Footnotes
Brewster (1826) is often credited with discovering the light-from-above prior. In fact, he mostly elaborated Rittenhouse's (1786) observation that we perceive ambiguous shaded patterns as having a 3-D shape that is consistent with whatever we believe about the lighting direction in the scene being viewed. Neither Rittenhouse nor Brewster suggested that we have a default assumption that light comes from overhead.
In Morgenstern (2011), we used the term Lambertian contrast energy instead of ICE. The two terms are synonymous.
We believe that the four unusually high ICE values from Boyaci et al. (2004) are artifacts. The wide range of ICE values for Boyaci et al. (2004) in our Figure 3 reflects their table 2, where Δ = EA/EP was highly variable. Large differences in Δ do not always reflect clear differences in behavior. Consider their observer BH, who had Δ = 1.39 for light from the left and Δ = 0.12 for light from the right (their table 2). These correspond to ICE values of 0.20 and 0.87, respectively. Their Figure 11 shows observers' chromaticity settings, and BH's settings were not drastically different for lighting from the left and right. Similar comments apply to RG. Furthermore, their figure 10 suggests that MM's chromaticity settings varied less with patch orientation than MD's, and yet their table 2 attributes more direct illumination assumptions to MM. Thus, their estimates of Δ may have had a large variance.
In order to make the slant and tilt thresholds comparable, we used the actual angle between the two lighting directions when calculating the psychometric function, not the nominal angles 2Δθ and 2Δφ. For example, at a slant of 10°, the angle between tilt directions +90° and −90° is just 20°, not 180°.
Contributor Information
Yaniv Morgenstern, Email: yaniv.morgenstern@gmail.com.
Wilson S. Geisler, Email: geisler@psy.utexas.edu.
Richard F. Murray, Email: rfm@yorku.ca.
References
- Adams W. J. (2007). A common light-prior for visual search, shape, and reflectance judgments. Journal of Vision, 7 (11): 15 1–7, http://www.journalofvision.org/content/7/11/11, doi:10.1167/7.11.11. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Adelson E. H., Bergen J. R. (1991). The plenoptic function and the elements of early vision. In Landy M., Movshon J. A. (Eds.), Computational models of visula processing (pp 3–20) Cambridge, MA: MIT Press; [Google Scholar]
- Attewell D., Baddeley R. J. (2007). The distribution of reflectances within the visual environment. Vision Research , 47, 548–554 [DOI] [PubMed] [Google Scholar]
- Basri R., Jacobs D. (2003). Lambertian reflectance and linear subspaces. IEEE Transactions on Pattern Analysis and Machine Intelligence , 25, 218–233 [Google Scholar]
- Bloj M., Ripamonti C., Mitha K., Hauck R., Greenwald S., Brainard D. H. (2004). An equivalent illuminant model for the effect of surface slant on perceived lightness. Journal of Vision , 4 (9): 15 735–746, http://www.journalofvision.org/content/4/9/6, doi:10.1167/4.9.6. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Boyaci H., Doerschner K., Maloney L. T. (2004). Perceived surface color in binocularly-viewed scenes with two light sources differing in chromaticity. Journal of Vision , 4 (9): 15 664–679, http://www.journalofvision.org/content/4/9/1, doi:10.1167/4.9.1. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Boyaci H., Doerschner K., Maloney L. T. (2006). Cues to an equivalent lighting model. Journal of Vision , 6 (2): 15 106–118, http://www.journalofvision.org/content/6/2/2, doi:10.1167/6.2.2. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Boyaci H., Maloney L. T., Hersh S. (2003). The effect of perceived surface orientation on perceived surface albedo in binocularly-viewed scenes. Journal of Vision , 3 (8): 15 541–553, http://www.journalofvision.org/content/3/8/2, doi:10.1167/3.8.2. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Brainard D. H., Maloney L. T. (2011). Surface color perception and equivalent illuminant models. Journal of Vision, 11 (5): 15, 1–18, http://www.journalofvision.org/content/11/5/1, doi:10.1167/11.5.1 [PubMed] [Article] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brewster D. (1826). On the optical illusion of the conversion of cameos into intaglios, and of intaglios into cameos, with an account of other analogous phenomena. The Edinburgh Journal of Science , 4, 99–108 [Google Scholar]
- Burge J., Geisler W. S. (2011). Optimal defocus estimation in individual natural images. Proceedings of the National Academy of Sciences, USA , 108 (40), 16849–16854 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuttle C. (2003). Lighting by design. New York: Architectural Press; [Google Scholar]
- Debevec P. (1998). Rendering synthetic objects into real scenes: Bridging traditional and image-based graphics with global illumination and high dynamic range photography. In Cohen M. (Ed.), Computer graphics (proceedings of SIGGRAPH 1998) (pp 189–198) New York: ACM Press; [Google Scholar]
- Doerschner K., Boyaci H., Maloney L. T. (2007). Testing limits on matte surface color perception in three-dimensional scenes with complex light fields. Vision Research , 47, 3409–3423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dror R. O., Willsky A. S., Adelson E. H. (2004). Statistical characterization of real-world illumination. Journal of Vision, 4 (9): 15 821–837, http://www.journalofvision.org/content/4/9/11, doi:10.1167/4.9.11. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Ernst M. O., Banks M. S. (2002). Humans integrate visual and haptic information in a statistically optimal fashion. Nature, 415 (6870), 429–433 [DOI] [PubMed] [Google Scholar]
- Fleming R. W., Dror R. O., Adelson E. H. (2003). Real-world illumination and the perception of surface reflectance properties. Journal of Vision, 3 (5): 15 347–368, http://www.journalofvision.org/content/3/5/3, doi:10.1167/3.5.3. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Geisler W. S. (1989). Sequential ideal-observer analysis of visual discrimination. Psychological Review , 96, 267–314 [DOI] [PubMed] [Google Scholar]
- Geisler W. S. (2008). Visual perception and the statistical properties of natural scenes. Annual Review in Psychology , 59, 167–192 [DOI] [PubMed] [Google Scholar]
- Gerhard H. E., Maloney L. T. (2010). Estimating changes in lighting direction in binocularly viewed three-dimensional scenes. Journal of Vision , 10 (9): 15 1–22, http://www.journalofvision.org/content/10/9/14, doi:10.1167/10.9.14. [PubMed] [Article] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershun A. (1939). The light field ( Moon P., Timoshenko G. Trans.) Journal of Mathematics and Physics, 18, 51–151 (Original work published in 1936) [Google Scholar]
- Gilchrist A. L. (1977). Perceived lightness depends on perceived spatial arrangement. Science, 195 (4274), 185–187 [DOI] [PubMed] [Google Scholar]
- Gilchrist A. L. (2006). Seeing black and white. New York: Oxford University Press; [Google Scholar]
- Kersten D., Mamassian P., Yuille A. (2004). Object perception as Bayesian inference. Annual Review of Psychology , 55, 271–304 [DOI] [PubMed] [Google Scholar]
- Knill D. C., Richards W. (1996). Perception as Bayesian inference. New York: Cambridge University Press; [Google Scholar]
- Langer M. S., Bülthoff H. H. (2000). Depth discrimination from shading under diffuse lighting. Perception , 29, 649–660 [DOI] [PubMed] [Google Scholar]
- Lee T. Y., Brainard D. H. (2011). Detection of changes in luminance distributions. Journal of Vision , 11 (13): 15 1–16, http://www.journalofvision.org/content/11/13/14, doi:10.1167/11.13.14. [PubMed] [Article] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T. Y., Brainard D. H. (2014). The effect of photometric and geometric context on photometric and geometric lightness effects. Journal of Vision, 14 (1): 15 1–17, http://www.journalofvision.org/content/14/1/24, doi:10.1167/14.1.24. [PubMed] [Article] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzger W. (2006). Laws of seeing. Cambridge, MA: MIT; Press. (Original work published 1936) [Google Scholar]
- Moon P., Spencer D. E. (1981). The photic field. Cambridge, MA: MIT Press; [Google Scholar]
- Morgenstern Y. (2011). The role of low-pass natural lighting regularities in human visual perception. (Doctoral dissertation, York University, Toronto) [Google Scholar]
- Morgenstern Y., Murray R. F., Harris L. T. (2011). The human visual system's assumption that light comes from above is weak. Proceedings of the National Academy of Sciences, USA , 108, 12551–12553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mury A. A., Pont S. C., Koenderink J. J. (2007). Light field constancy within natural scenes. Applied Optics , 46, 7308–7316 [DOI] [PubMed] [Google Scholar]
- Mury A. A., Pont S. C., Koenderink J. J. (2009. a). Representing the light field in finite three-dimensional spaces from sparse discrete samples. Applied Optics , 48, 450–457 [DOI] [PubMed] [Google Scholar]
- Mury A. A., Pont S. C., Koenderink J. J. (2009b). Structure of light fields in natural scenes. Applied Optics , 48, 5386–5395 [DOI] [PubMed] [Google Scholar]
- Muryy A. A. (2008). The light field in natural scenes. (Doctoral dissertation, Technische Universiteit Delft, Netherlands) [Google Scholar]
- Ostrovsky Y., Cavanagh P., Sinha P. (2005). Perceiving illumination inconsistencies in scenes. Perception , 34, 1301–1314 [DOI] [PubMed] [Google Scholar]
- Phong B. T. P. (1975). Illumination for computer generated pictures. Communications of the ACM , 18, 311–317 [Google Scholar]
- Pont S. C., Koenderink J. J. (2007). Matching illumination of solid objects. Perception & Psychophysics , 69, 459–468 [DOI] [PubMed] [Google Scholar]
- Potetz B., Lee T. S. (2003). Statistical correlations between 2D images and 3D structures in natural scenes. Journal of the Optical Society of America A , 20, 1292–1303 [DOI] [PubMed] [Google Scholar]
- Ramachandran V. S. (1988). Perception of shape from shading. Nature , 331, 163–166 [DOI] [PubMed] [Google Scholar]
- Ramamoorthi R., Hanrahan P. (2001). On the relationship between radiance and irradiance: Determining the illumination from images of a convex Lambertian object. Journal of the Optical Society of America A , 18, 2448–2459 [DOI] [PubMed] [Google Scholar]
- Ripamonti C., Bloj M., Hauck R., Mitha K., Greenwald S., Maloney S. I., Brainard D. H. (2004). Measurements of the effect of surface slant on perceived lightness. Journal of Vision , 4 (9): 15 747–763, http://www.journalofvision.org/content/4/9/6, doi:10.1167/4.9.6. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Rittenhouse D. (1786). Explanation of an optical deception. Transactions of the American Philosophical Society , 2, 37–42 [Google Scholar]
- Santa Clara M. (2009). Digital photography, a tool for lighting research: High resolution sampling of spherical luminance maps with digital photographic technologies applied to diffuseness descriptors. In Demers C. M. H., Potvin A. (Eds.), Proceedings of the 26th International Conference on Passive and Low Energy Architecture (pp 391–395) June 22–24, Quebec City, Canada: [Google Scholar]
- Schofield A. J., Rock P. B., Georgeson M. A. (2011). Sun and sky: Does human vision assume a mixture of point and diffuse illumination when interpreting shape from shading? Vision Research , 51, 2317–2330 [DOI] [PubMed] [Google Scholar]
- Tanner W. P., Birdsall T. G. (1958). Definitions of d' and η as psychophysical measures. Journal of the Acoustical Society of America , 30, 922–928 [Google Scholar]
- Teller S., Antone M., Bodnar Z., Bosse M., Coorg S., Jethwa M., Master N. (2003). Calibrated, registered images of an extended urban area. International Journal of Computer Vision , 53, 93–107 [Google Scholar]
- Tyler C. W. (1998). Diffuse illumination as a default assumption for shape-from-shading in graded images. Journal of Imaging Science and Technology , 42, 319–325 [Google Scholar]
- Ward G. J. (1994). The RADIANCE lighting simulation and rendering system. Computer Graphics, 28 (2), 459–472 [Google Scholar]
- Wetherill G. B., Levitt H. (1965). Sequential estimation of points on a psychometric function. The British Journal of Mathematical and Statistical Psychology , 18, 1–10 [DOI] [PubMed] [Google Scholar]