Nucleic Acid Nanostructures: Bottom-Up Control of Geometry on the Nanoscale

Abstract

DNA may seem an unlikely molecule from which to build nanostructures, but this is not correct. The specificity of interaction that enables DNA to function so successfully as genetic material also enables its use as a smart molecule for construction on the nanoscale. The key to using DNA for this purpose is the design of stable branched molecules, which expand its ability to interact specifically with other nucleic acid molecules. The same interactions used by genetic engineers can be used to make cohesive interactions with other DNA molecules that lead to a variety of new species. Branched DNA molecules are easy to design, and the can assume a variety of structural motifs. These can be used for purposes both of specific construction, such as polyhedra, and for the assembly of topological targets. A variety of two-dimensional periodic arrays with specific patterns have been made. DNA nanomechanical devices have been built with a series of different triggers, small molecules, nucleic acid molecules and proteins. Recently, progress has been made in self-replication of DNA nano-constructs, and in the scaffolding of other species into DNA arrangements.

1. BUILDING WITH DNA

The Watson-Crick proposal for the structure of DNA is now over 50 years old. This proposal provided the chemical basis for understanding genetics; indeed, the last half-century of biology has been devoted to the exploitation of the implications of this model. The impact of DNA on society is just beginning to be felt, with the culmination of the Human Genome Project, and in the forensic and medical applications of DNA analysis. Regardless of its central importance in biology, the applications of DNA are not limited to the biological sciences. DNA is a molecule, and it functions successfully as genetic material because of its chemical properties. These properties include the affinity of complementary sequences, a well-stacked antiparallel double helical backbone that is largely regular regardless of sequence and a persistence length (a measure of stiffness) around 50 nm under standard conditions. It is logical to examine whether these properties can be exploited outside of biology. Structural DNA nanotechnology aims to use the properties of DNA to produce highly structured and well-ordered materials from DNA. This effort that has been underway since the early 1980’s [1].

The structure of the DNA double helix is illustrated in Figure 1. This classical DNA structure is known as B-DNA. On the left is the right-handed double helical molecule; it consists of a pair of backbones whose units are alternating sugars and phosphates that are connected by hydrogen bonding between flat molecular units, called bases. The base-sugar-phosphate unit is called a 'nucleotide'. Note that the two backbones have a directionality, and that they are rotated upside down from each other; hence, there is a dyad axis of symmetry relating the backbones that is perpendicular to the helix axis. There is such a dyad going through every base pair and also half-way in between them. The phosphates are ionized at physiological pH, so the backbones are polyanions requiring neutralization by cations. The right side of Figure 1 shows the Watson-Crick base pairs between adenine (A) and thymine (T), and between guanine (G) and cytosine (C). Although other forms of base pairing are possible [ns-natco], these pairs are most favored within the double helical context. The double helical DNA molecule is inherently a nanoscale species: Its diameter is about 2 nm, and its helical repeat is about 3.5 nm, consisting of 10–10.5 nucleotide pairs separated by 3.4 Å (Figure 1).

Figure 1. B-DNA.

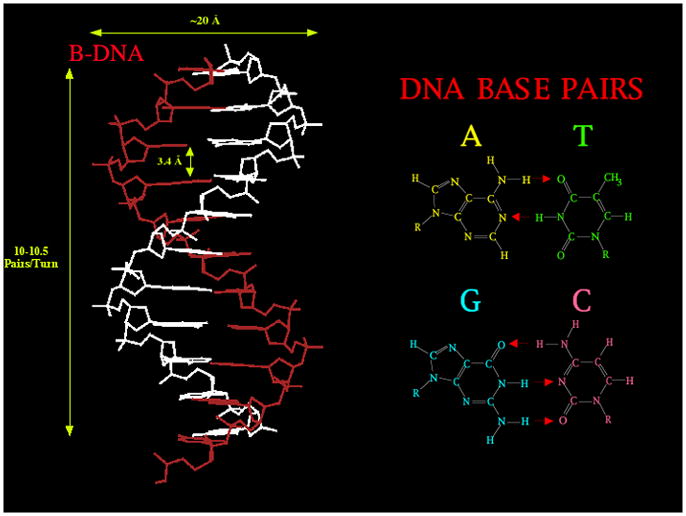
The molecular structure and dimensions of key freatures of the molecule is shown on the left. The base pairs are shown on the right, where red arrows represent hydrogen bonded interactions.

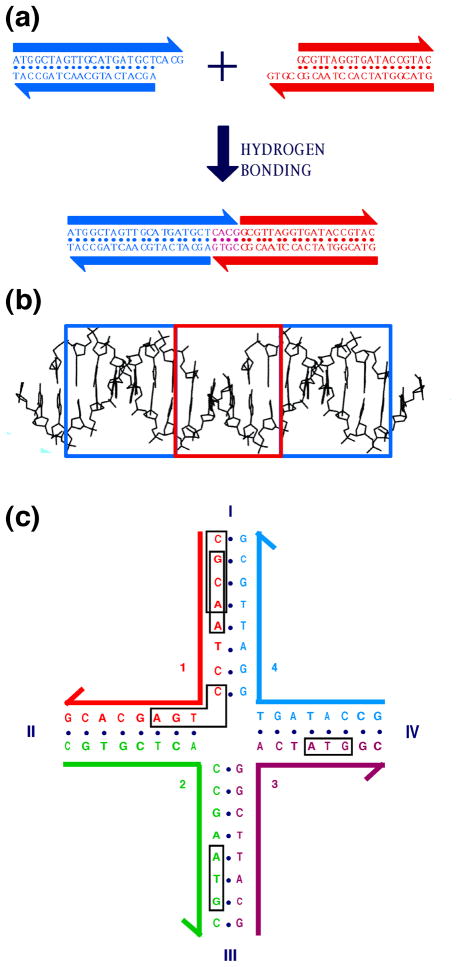
The early 1970's saw molecular biologists begin to exploit enzymes that modify the DNA molecule to produce new arrangements of DNA sequences. Using restriction enzymes that cleave at specific sites and ligases that fuse nicks in backbones, they were able to cut and splice DNA molecules, in much the same way that a film editor uses his tools to re-order sequences of film, creating a new overall effect [2]. The upshot of this activity was genetic engineering, which has led to the worldwide biotechnology industry. For our purposes, the key feature of their efforts was the use of single stranded overhangs (called 'sticky ends') to specify the order in which molecules were to be assembled. Sticky-ended cohesion between DNA molecules is illustrated in Figure 2a. An important feature of sticky-ended cohesion is that when two sticky ends cohere, they form classical B-DNA [3], the structure established by Watson and Crick and refined by their successors. This principle is illustrated in Figure 2b Thus, if one knows the positions of the atoms of one component of a cohesive pair, one knows the positions of the other component. Hence, sticky-ends provide the most readily programmable and predictable intermolecular interactions known, from the perspectives of both affinity and structure [4].

Figure 2. Sticky Ended Cohesion and Branched DNA.

(a) Affinity in Sticky Ended Cohesion. Two double helical strands with complementary overhangs are shown. Under appropriate conditions, they will cohere in a sequence-specific fashion, and can be ligated, if desired. (b) Structure in Sticky-Ends. A portion of the crystal structure of an infinite DNA double helix formed by sticky-ended cohesion is shown. The part cohering by sticky ends is in the red box, whereas the blue boxes surround continuous DNA segments. The DNA in all three sections is B-DNA. (c) A Stable Branched Junction. There is no dyad symmetry flanking the branch point; tetramers, such as the boxed sequences CGCA and GCAA are unique, and there is no TCAG to complement the CTGA flanking the corner.

Of course, naturally-occurring DNA is a linear molecule. From a topological standpoint, the DNA double helix is just a line. The line may be curved, and closed ones can be knotted or catenated; nevertheless, concatenating a bunch of lines together end-to-end just results in longer lines. Specific arrangements of DNA are of significant value to genetic engineers, because this establishes the presence and regulation of gene products, but linear DNA helical structures are not great structural components for nanoscale structural engineering. The notion that rescues DNA from its linearity is to make synthetic branched molecules [1].

DNA is found to be branched at the level of secondary structure in biological systems; this means that conventional DNA strands associate to produce junction points. Thus, if we think of the strands of DNA as the lanes of a two-lane highway, a junction point would correspond to the lanes going through an intersection. Traffic could flow through four different lanes in a traditional intersection; in the US, northbound traffic would turn east, westbound traffic would turn north, southbound traffic would turn west and eastbound traffic would turn south. A branched DNA molecule would be the same.

Typically, branched DNA is an ephemeral intermediate in DNA metabolism; for example, the four-arm Holliday junction is an intermediate in genetic recombination [5]. Although branched DNA of biological origin usually displays symmetry that allows its branch point to migrate, it is a simple matter to design [1] and assemble synthetic DNA sequences that are stable because they lack this symmetry. An example of a stable asymmetric Holliday junction analog lacking this symmetry is shown in Figure 2c. Branched junctions containing three, five or six arms have also been assembled and characterized [6,7]; in recent work our laboratory has made junctions with eight and twelve arms [X. Wang and NCS, in preparation]. This is important, because the connectivity of the graph produced by cohesion or ligation of junctions is limited by the number of arms that flank its junctions. Space-filling lattices built from the classical Platonic or Archimedean polyhedra have connectivities up to twelve [8]. The ability to generate stable branched DNA molecules opens new opportunities for the bottom-up construction of nanoscale objects.

As the reader has surely imagined by now, the basic notion behind structural DNA nanotechnology is to combine the concepts of stable branched DNA molecules with sticky ended cohesion. This idea is illustrated in Figure 3, which shows a branched junction with sticky ends assembling as a group of four units to produce a square-like object. The outside of this object contains further sticky ends, so this arrangement could be extended to produce a lattice in two dimensions [1]. As in Figure 3, DNA is often drawn as a ladder-like molecule, with parallel backbones, rather than as a double helix. While often convenient, this representation obscures a key property of branched DNA constructs: The relative orientations of two junctions joined by an edge of double helical DNA is a function of their separation [9]; consequently, the system described here is not a two-dimensional system, but rather a three-dimensional system. Once one recognizes that branched DNA molecules can be fused in three dimensions, molecular graphs and connected networks whose edges are DNA helix axes can be constructed in an almost limitless variety.

Figure 3. Sticky-Ended Assembly of Branched Molecules.

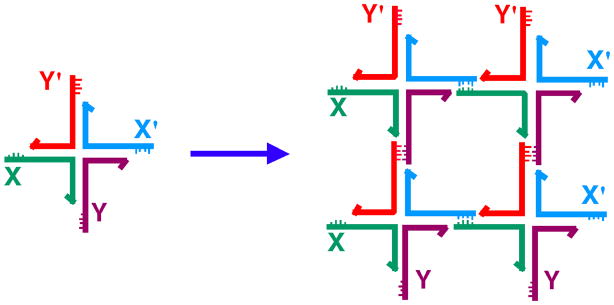
A branched molecule is shown on the left with four sticky ends, X, complementary to X', and Y, complementary to Y'. Four of them are shown to assemble to form a quadrilateral, with further sticky ends on the outside, so that an infinite lattice could be formed by the addition of further components.

It should be clear that DNA nanotechnology is a bottom-up approach to nanotechnology. The components are a few nm in size, so the exquisite placement of individual atoms or molecules that characterizes some of the top-down work done with scanning probe microscopes [e.g. 10, 11] is beyond the scope of this methodology. However, it is important to recognize that bottom-up approaches are able to take advantage of the vast parallelism of chemical reactions. Thus, in the worst of constructions, a billion or a trillion product molecules typically will be produced. The parallelism of DNA nanotechnology is related to the parallelism exploited in DNA-based computation [12], so that the two fields have convergent features, as will be described below.

2. THE GOALS OF STRUCTURAL DNA NANOTECHNOLOGY

Ideally, the systems we have described above should be able to be used like molecular Lego: It should be possible to throw together a variety of branched-DNA components and exploit their well-defined combining properties to get them to self-assemble into a variety of shapes and arrangements. We will discuss below some of the limitations on this ideal system, but here is a good point for us to think about what we would like to be able to make, if this system behaved in an ideal fashion.

The key motivating goal in this system has been the desire to conquer the macromolecular crystallization experiment. Although quite a lore now exists, every macromolecule presents different crystallization problems. The problem of crystallizing a macromolecule of unknown structure is that one does not know how to promote the organization of the molecules into a periodic lattice in a rational fashion, because the structure is unknown. Furthermore, in contrast to experiments that are easily debugged, every relevant parameter must be within the correct window for the crystallization to be successful; consequently, the independent factors cannot easily be optimized individually, although incomplete factorial methods have been developed [13].

The approach we suggest is to use DNA to form periodic arrays that organize the macromolecule of interest [1]. The notion is illustrated in Figure 4a. A 'box' of nucleic acid [drawn in magenta] is designed to act as the repeating unit of a 3D periodic lattice. A series of boxes are to be held together by sticky ends. These boxes act as the host lattice for a series of macromolecular guests that are positioned and oriented within the host lattice. If all are ordered adequately, then the x-ray diffraction experiment can be performed on the entire contents of the crystal. In addition to the ability perhaps to organize otherwise molecules that are otherwise intransigent to crystallization, this system offers the advantage that guest molecules that change their structures while binding to ligands would not destroy the lattice, because only DNA would be involved in maintaining lattice contacts.

Figure 4. Scaffolding Applications of Structural DNA Nanotechnology.

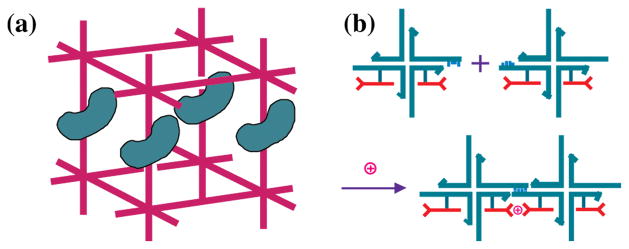
(a) Scaffolding of Biological Macromolecules for Crystallographic Purposes. A DNA box (magenta) is shown with sticky ends protruding from it. Macromolecules are organized parallel to each other within the box, rendering them amenable to crystallographic structure determination. (b) Scaffolding Nanoelectronics. Blue branched DNA junctions direct the assembly of attached nanoelectronic components (red) to form a molecular synapse stabilized by the presence of an ion.

If one can imagine organizing macromolecules, it is also possible to imagine organizing other species that do not readily self-organize. Prominent amongst them would be nanoelectronic components. The idea of using DNA to organize nanoelectronic components is not very new [14], but only recently has it started to gain favor. The concept, illustrated for a simple component in Figure 4b, is that the outstanding architectural properties of DNA be used to act as scaffolding for species that are intractable to simple bottom-up organization with nanometer precision.

A further goal of DNA nanotechnology is the use of DNA's structural and informational properties to build nanomechanical devices. The earliest DNA devices were predicated on structural transitions of the molecule. There are two kinds of DNA-based devices, those based on structural transitions triggered by the addition of small molecules to the solution, and those that are sequence dependent, although these can be further subdivided. As we will see below, the latter are more useful, because a variety of them can co-exist in solution at the same time, yet they can be individually activated. This is closer to the notion of acting as a successful basis for nanorobotics, and this is the route that current investigators largely are taking at this time.

It is may be useful to distinguish structural DNA nanotechnology from a less precise form of DNA nanotechnology, termed compositional DNA nanotechnology. Structural DNA nanotechnology uses well-structured components, combined by using both affinity and structure to control geometry, or at least, strand topology; the goal of this approach is structural predictability with a precision (or resolution) of 1 nm or less in the products. By contrast, in compositional DNA nanotechnology, these conditions are not completely met: The components may be flexible or the cohesive interactions by which they are combined are uncharacterized; as a consequence, the composition of the product may be known, but its 3D structure cannot be predicted. Incompletely characterized forms of cohesion such as paranemic cohesion [15] or the osculating interactions of tecto-RNA [16] may eventually be used in structural nucleic acid nanotechnology when they have been as characterized as well as sticky ends have been characterized in a periodic context.

A detailed description of the work produced by compositional DNA nanotechnology, in which DNA is used largely as 'smart-glue', rather than a precise structural component, is beyond the scope of this article. Thus, high-resolution structural DNA nanotechnology works on the scale where DNA is both the bricks and the mortar in nano-scale assemblies; by contrast, compositional or low-resolution nanotechnology uses the DNA only as the mortar, as cartooned in Figure 5. As shown on the bottom of the low-resolution side, DNA mortar can make well-defined structures on a large-enough scale, but the highest levels of control require DNA acting in rigid motifs with rigid connections to other species. It is important to recognize that numerous laboratories have made useful and valuable materials by this approach. For example, this approach has been used in diagnostics [17], to organize DNA nanoparticles on small [18] and on large [19] scales, in combination with non-DNA organic components [20,21], and in the production of DNA-protein aggregates [22]. Although they do not provide the high resolution structural features sought in structural DNA nanotechnology, using smart-glue approaches to organize nanoparticles can lead to organized products, but with lower precision, 10's to 100's of nanometers. In a complementary vein, G-wires [23,24] are examples of well-structured nucleic acid systems that lack the sequence diversity central to structural DNA nanotechnology.

Figure 5. Types of DNA Nanotechnology.

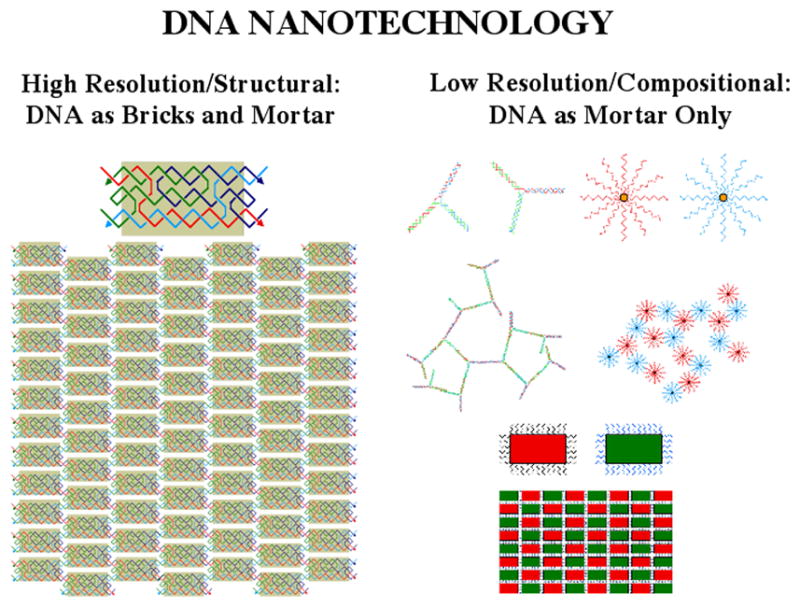
High resolution/structural DNA nanotechnology is shown on the left, where DNA is both the bricks and mortar of an assembly. A TX molecule is shown assembled into a 2D array. Low resolution/compositional DNA nanotechnology is shown on the right with floppy components or applications using DNA as 'smart glue' (top). This type of DNA nanotechnology can also be used to build structures, as shown at bottom, but the resolution is not as high.

3. FEATURES OF DNA THAT MAKE IF USEFUL FOR NANOTECHNOLOGY

The primary advantage of DNA for these goals lies in its outstanding molecular recognition properties, enabling precise structural alignment of diverse DNA molecules that can scaffold various molecular species. DNA and its congeners appear to be unique among biopolymers in this regard. Antibodies, for example, may lead to specific binding, but the detailed geometry of antibody-antigen interactions must be worked out experimentally in every case. It is only with nucleic acids (and currently only with sticky-ended cohesion) that the detailed 3D geometries known in advance, because sticky ends form B-DNA when they bind to link two molecules together [3]. It is a very good approximation to assume that all sticky ends, regardless of length have the same overall B-DNA structure when they cohere with their complements.

The convenience of chemical synthesis [25] is another advantage of DNA; "vanilla" DNA is available from a number of vendors, and DNA synthesizers are readily capable of generating a number of varied molecules based on commercially available phosphoramidites. It is routine to synthesize DNA molecules whose lengths are 120 nucleotides or shorter. A variety of enzymes are commercially available to manipulate DNA and to trouble-shoot errors: DNA ligases catalyze the covalent joining of complexes held together by sticky-ended cohesion; exonucleases (which require an end to digest DNA) are useful in purifying cyclic target molecules from linear failure products [26]; restriction endonucleases are employed both to trouble-shoot syntheses and to create cohesive ends from topologically-closed species [27]; topoisomerases, which catalyze strand-passage reactions, can be used to correct folding errors [28].

We noted above several features of DNA that help it to perform its genetic functions. One of these was the persistence length, about 500 Å [29], leading to a predictable overall structure for the short (70–100 Å) lengths typically used. In fact, it is possible to design branched species with longer persistence lengths [30]. Thus, the self-assembled structure of DNA constructs and of some of its interactions can be taken for granted, just as one can take for granted the shape of a Lego tile. The external code on DNA can be read, even when the double helix is intact [31]; thus, if DNA is used for scaffolding, absolute positions can be addressed within a pre-designed cavity. The ability to pack nanoelectronics or other scaffolded materials very tightly is likely to be aided by the high density of functional groups (every 3.4 Å or so) on DNA; Consequently, DNA tile motifs with dimensions of 10–20 nm do not place an inherent limit in the close-packing of components that can be scaffolded by DNA.

Most of the work done to date utilizes DNA molecules like the molecules evolved in nature for use as genetic material. However, nanotechnology is not limited to the natural DNA molecule. A vast number of DNA analogs have been produced and analyzed for therapeutic purposes [e.g., 32]. This means that systems prototyped by conventional DNA may ultimately be converted to other backbones and bases, as required by specific applications. For example, it is unlikely that nanoelectronic components will be scaffolded successfully by conventional poly-anionic DNA molecules. However, there are numerous neutral analogs, most prominently PNA (a molecule with a peptide backbone to which bases are attached) [33], that may be much better suited to act as scaffolds for this purpose.

MOTIF GENERATION AND SEQUENCE DESIGN

Numerous motifs have been used in DNA nanotechnology. The simplest motifs are those described above, DNA junctions that resemble intersections, from which between three and six [or more] double helical arms emanate. These junctions are easy to design, but, with the exception of the four-arm junction, they do not appear to have well-defined structures [6,7]. The four-arm junction has a fairly well-defined structure, but it certainly is not the simple cruciform indicated in Figure 2c or in Figure 3. The structure is a right-handed cross involving two stacking domains [34,35], but even for this molecule, the connection between the domains is somewhat flexible [36].

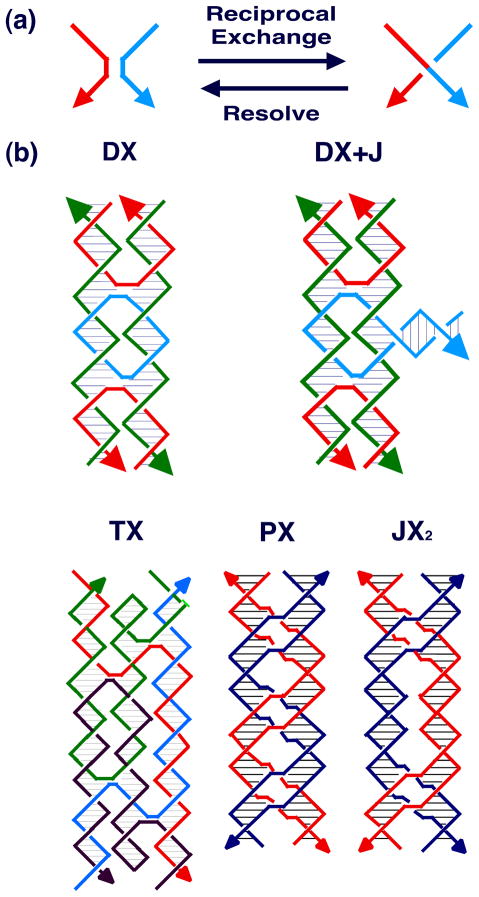
Consequently, other motifs have been sought whose structural integrity is greater. This search has proved less difficult than one might imagine, because one of the mechanisms that biology uses to produce the Holliday junction provides a general mechanism to derive stiff motifs. This mechanism is known as reciprocal exchange [37], and is illustrated in Figure 6a. It can be performed multiple times between strands of the same polarity or of opposite polarity, leading to different products. Although the process of reciprocal exchange is often complicated in living systems, nanotechnological systems do not actually have to undergo reciprocal exchange to produce new motifs; once the structural design process is complete, new motifs are generated directly by using a sequence assignment procedure to design strands that will self-assemble into the motif. Figure 6b illustrates the DX molecule (opposite polarity) [38], the DX+J molecule [39], the TX molecule (opposite polarity) [40] and the PX and JX₂ molecules (same polarity) [41]. There are five different isomers of the DX molecule, depending on the polarities of the exchanging strands and on their separations [38]; the complete set of DX molecules is illustrated in Figure 7. The DX molecule is known to be about twice as stiff as conventional linear duplex DNA [30]; the DX, DX+J and TX motifs have been used to produce patterned 2D DNA arrays [40, 42] and the DX, PX and JX₂ motifs have been used as components of DNA nanomechanical devices [43,44]. The rigidity of these motifs is key to their utility in these applications.

Figure 6. Motif Generation.

(a) The Process of Reciprocal Exchange. A red strand and a blue strand exchange to form a red-blue strand and a blue-red strand. (b) Motifs used in Structural DNA Nanotechnology. Two reciprocal exchanges between strands of opposite polarity yield the DX molecule shown. The 'D' means that there are two double helices. The DX+J (a DX combined with a junction) motif, usually made with the extra helix roughly perpendicular to the plane of the other two, is made by combining a DNA hairpin and a DX molecule. The TX (indicating three fused double helices) motif results from combining the DX molecule with another double helix. The PX (standing for paranemic crossover DNA) motif is derived by performing reciprocal exchange between two helices at all possible positions where strands of the same polarity come together. The JX₂ (indicating a PX with two juxtaposed backbone groups) motif is similar to the PX motif, except that reciprocal exchange is omitted at two adjacent juxtapositions.

Figure 7. DX Conformational Isomers.

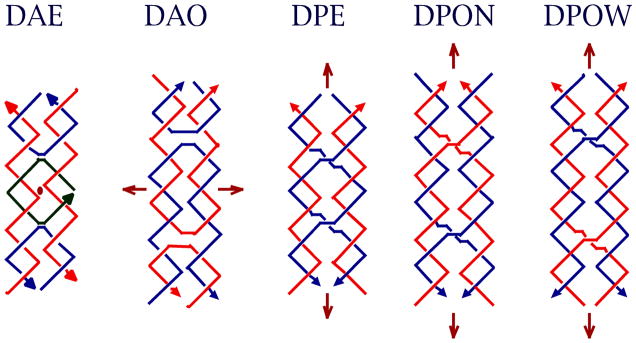
Brown arrows indicate dyad axes, and arrowheads on strands indicate 3' ends. The second character of the name indicates antiparallel (DAE and DAO), with dyad axes perpendicular to the plane of the helix axes, or parallel (DPE, DPON, DPOW), with the dyad axis coplanar with the helix axes. The third character indicates whether there is an even (DAE or DPE) number of half-turns between crossovers, or an odd number (DAO, DPON, DPOW). Odd parallel molecules are further differentiated by a fourth character, N or W, indicating whether the extra half turn is a minor (N -- narrow) groove separation or a major (W -- wide) groove separation.

Stable branched junctions are derived from synthetic molecules, so there must be a method to assign sequences to them. The method of sequence symmetry minimization [1,45] has proved to be up to the task of designing sequences. The basic idea is that DNA strands will maximize the double helical structures that they form. Although an early approach [46] involved calculating a likelihood of formation from nearest-neighbor equilibrium thermodynamic parameters, no constructs built to date appear to require a calculation this extensive. The method used can be understood readily by reference to Figure 2c. This molecule contains four 16-mers, labeled 1, 2, 3 and 4. We break up each of these single strands into a series of thirteen overlapping tetramers, such as the CGCA or GCAA that have been boxed; we insist that each of these be unique. In addition, we insist that each tetramer that spans a branch point, such as the boxed CTGA, not have its linear complement (TCAG) present; this restriction results in these tetramers being unable to form linear double helices. Consequently, competition with the four octamer double helical targets can occur only from trimers, such as the boxed ATG sequences. The reason to go through the exercise of sequence-symmetry minimization is that the molecules that are designed correspond to conformations of DNA that are of higher free energy than the 'ground state', i.e., the simple Watson-Crick double helix. The aim of sequence design is to ensure that the 'excited state' that they system chooses is also the target state sought by the investigator.

The assumption used in all of the sequence design is that molecular geometry and structure formation are sequence-independent. In those cases where it is known that sequences result in structural features, e.g., the bends associated with tracts of several A;s [47], the issue is handled in an ad hoc fashion by forbidding those sequence within a molecule. Likewise, runs of G's that often form their own secondary structure [48], are avoided. This approach has largely worked to date. A second issue, of course, is folding. It is difficult to model the folding of and pairing of a large number of DNA strands. Nevertheless, it is often a good idea to examine the associations that one wishes to promulgate in the construction of a given motif. If, for example, it seems that the ends of a strand are likely to pair earlier than the middle of the strand, perhaps because of higher G-C content, then re-design may be indicated, because the middle may not be able to wrap around its complementary strand if its ends are already tied down.

MOTIF CHARACTERIZATION

Just because a given motif appears as though it will self-assemble successfully does not mean that it will. It is key that one have a battery of techniques available to characterize it. Of all of the motifs discussed here, to date only the structure of the Holliday junction has been established crystallographically [49]. Consequently, it has been necessary to use somewhat less direct forms of structure analysis to establish the proper self-assembly of branched DNA motifs. The first question one must ask is whether each strand participates in the designed complex with the expected stoichiometry. This may be readily determined through the used of non-denaturing polyacrylamide gel electrophoresis [50]. The material is loaded onto one end of a slab of polyacrylamide and driven by an electric field acting on the negatively charged backbone to the other end. Mobility on such a gel is a function of molecular weight and surface properties. The target complex, the individual strands and various incomplete complexes can be loaded onto the same gel in the presence of various markers. A single band near [but rarely exactly at] the predicted molecular weight is a good indication of successful formation. Bands with lower mobility corresponding to dimers, trimers or higher complexes are sometimes seen, indicating a motif whose structure has internal stresses likely resulting from electrostatic repulsion [38]. Likewise, products migrating with the mobilities of various partial products indicate that the complex is dissociating from its target composition for some reason. Sometimes incomplete stoichiometry is the cause of a gel that does not conform to expectations. Cutting out the target band and re-hybridizing it will yield a product with correct stoichiometry, and will indicate if the single band has re-equilibrated to a multiple product.

The qualitative shape of a DNA motif can be compared usefully and conveniently with standards by means of a Ferguson plot [51]. This is a plot of log(mobility) vs. acrylamide concentration, and its slope is proportional to the friction constant of the molecule. Ferguson analysis has been used to characterize the stacked character of 4-arm junctions, in comparison to 3-, 5-, and 6-arm junctions [7] and to demonstrate that the addition of helices to linear duplex and to DX molecules results in similar changes in friction constant [40]. Likewise, the qualitative structure of PX-DNA has been compared usefully to that of double crossover molecules to establish their similar shapes. Both denaturing and non-denaturing Ferguson analysis have been applied to a DNA cube-like molecule and its sub-catenanes [52].

The highest resolution technique that is used conveniently to characterize the structures of unusual DNA motifs is hydroxyl radical autofootprinting. Hydroxyl radical autofootprinting [34] is a variation on the technique of hydroxyl radical footprinting, used to establish the binding sites of proteins on DNA. Branched junctions [7,34], DX [38], TX [40] and PX [41] molecules have all been analyzed by this method. The analysis is performed by labeling a component strand of the complex and exposing it to hydroxyl radicals. The products are driven through a denaturing gel (sensitive only to size for a given topology), and the intensities of the bands corresponding to each individual nucleotide are quantitated. The key feature noted at crossover sites in these analyses is decreased susceptibility to attack when comparing the pattern of the strand as part of the complex, relative to the pattern of the strand derived from linear duplex DNA. Decreased susceptibility is interpreted to suggest that access of the hydroxyl radical may be limited by steric factors at the sites where it is detected. Likewise, similarity to the duplex pattern at points of potential flexure is assumed to indicate that the strand has adopted a conventional helical structure in the complex, whether or not it is required by the secondary structure. The technique is particularly powerful as a method to establish whether crossovers occur where they are expected to occur.

COHESIVE INTERACTIONS

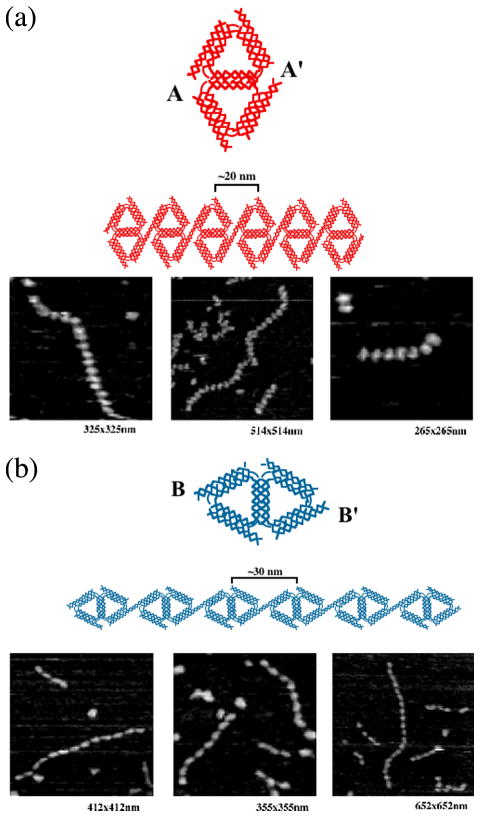
We have introduced sticky-ended cohesion in the introductory section above. However, this is not the only means available to bring molecules together in a sequence-specific fashion. Sticky-ended cohesion can be thought of as analogous to the familiar corner-sharing motifs of inorganic chemistry. However, that discipline has provided us with other models for the cohesion of its polyhedra. One of these is edge-sharing, and another is face-sharing. Face-sharing has yet to be developed in DNA nanotechnology, but it is possible to join triangular motifs in an edge-sharing mode that is mediated by DX molecules [53]. A schematic diagram of one-dimensional arrangements of edge-sharing triangles is shown in Figure 8. Hairpin loops with complementary sequences have been known to molecular biologists since the 1970's. Recently, Jaeger et al. [16] have used non-Watson-Crick interactions to employ a motif that they have dubbed 'Tecto-RNA'. A generalization of that type of pairing is found in paranemic cohesion [15], illustrated in Figure 9; neither type of interaction requires the opening of closed DNA molecules. Two double helices appear to wind around each other to produce a cohesive interaction. In contrast to sticky-ends generated by restriction enzymes, topologically-closed molecules can be made to cohere with interactions of any strength desired. The importance of this is that only topologically-closed molecules are readily purified by the best method currently available, denaturing gels electrophoresis.

Figure 8. Edge-Sharing Cohesion.

(a) A 1D array of Edge-Sharing Diamonds Joined in their Short Direction. A schematic of the molecule is shown at top in red, as is a schematic of the 1D array. Three AFM views of arrays are shown beneath the schematics. (b) A 1D array of Edge-Sharing Diamonds Joined in their Long Direction. The same conventions apply as in (a), except that the schematics are in blue. Note the difference in the 1D arrays.

Figure 9. Paranemic Cohesion.

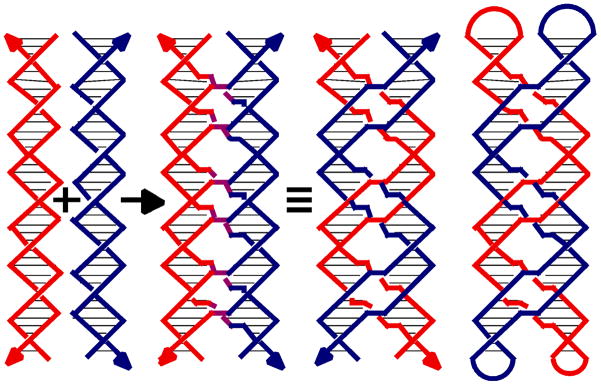
The origin of the motif is shown at the left, where a red and a blue double helix exchange strands at every point, that they come in contact, to produce purple crossovers. The covalent strand structure is shown to the right of the identity sign, where a red and a blue double helix are seen to inter-wrap. The paranemic relationship of the inter-wrapped helices is emphasized on the right where the blue and red helices are capped in hairpin loops.

TOPOLOGICAL ASPECTS OF DNA NANOTECHNOLOGY

We often represent the double helical DNA backbone as a pair of antiparallel lines [e.g., Figure 3]. This is often a useful approximation, but the true structural flavor of the DNA molecule is lost if the wrapping of the double helical strands around each other is ignored. For example, Figure 10 illustrates an extended version of the lattice shown in Figure 3, but now with topology taken into account. The left panel shows a junction ligated to form a quadrilateral containing two turns per edge, and the right panel shows the formation of a quadrilateral with 1.5 turns per edge. The lattice with two turns per edge contains a cyclic molecule and four others paired with it directly; an infinite lattice of such squares would be a network of linked circles. By contrast, the lattice with 1.5 turns per edge contains no cycles, but rather is a woven meshwork of long strands [9, 54].

Figure 10. Impact of Topology in Branched Networks.

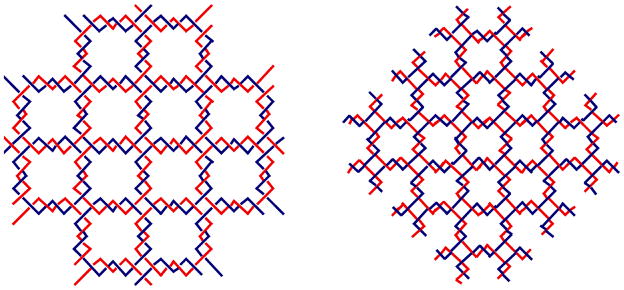
Both arrays are extended versions of the array illustrated in Figure 3, but the twisting of the helices is indicated. The array on the left contains an even number of half-turns between vertices, leading to an array that consists of molecular chain main, red circles linked to blue circles. The array on the right contains an odd number of half-turns between vertices, leading to an interwoven structure, blue chains going lower right to upper left, and red chains going lower left to upper right.

The double helical nature of DNA also places constraints on the lengths of edges in DNA figures. Two branched junctions at either end of a double helical DNA edge are related to each other like wing nuts on a screw: Their relative orientation is a function of the length of the intervening DNA. Although it appears possible to design objects with edges of any length, the simplest architectures derive from the use of an integral number of double helical half-turns. Most (but not all [55]) geometrical objects built from DNA to date have been designed with this constraint in mind [e.g., 26,42,56, 57].

The difficulties of designing molecules from double helical components are more than compensated by the properties of the products and by new windows of synthetic control that are opened by this feature [58]. Closed geometrical objects constructed from DNA are not weakly associated hydrogen bonded complexes. Rather, they are robust catenanes, whose components are topologically bonded to each other. If each edge of a DNA polyhedron contains an integral number of double helical turns, each face corresponds to a cyclic single strand of DNA, linked to each of its neighboring faces once for each turn in the edge that they share. The catenation between strands permits rigorous topological analysis of products under denaturing conditions [26,52,57]. As a logical extension, it is possible to design periodic arrays from DNA whose topology is that of molecular chain mail [54,58].

POLYHEDRAL CATENANES AND OTHER GRAPHS PRODUCED FROM DNA

The earliest interesting DNA constructions involved polyhedral stick figures whose edges consist of double helical DNA, and whose vertices correspond to the branch points of branched junctions. The formation of the edges was implicit in these constructions, just the result of joining junctions together. Figure 10 illustrates a molecule whose edges have the connectivity of a cube or rhombohedron. Although the DNA in the arms of DNA branched junctions is stuff, the angles between the arms are apparently floppy [6,36]. Consequently, DNA polyhedra are characterized topologically, rather than structurally. The cube in Figure 11a is a hexacatenane, with two turns of DNA per edge. There are two turns per edge, so each strand corresponds to one of the faces of the cube, and each strand is linked twice to the four strands that flank it. The molecule was constructed in solution, by methods that had little control over the products of the synthesis [26]. Proof of synthesis was by breaking down the final product to sub-catenanes that could be constructed and characterized independently.

Figure 11. Polyhedral Catenanes.

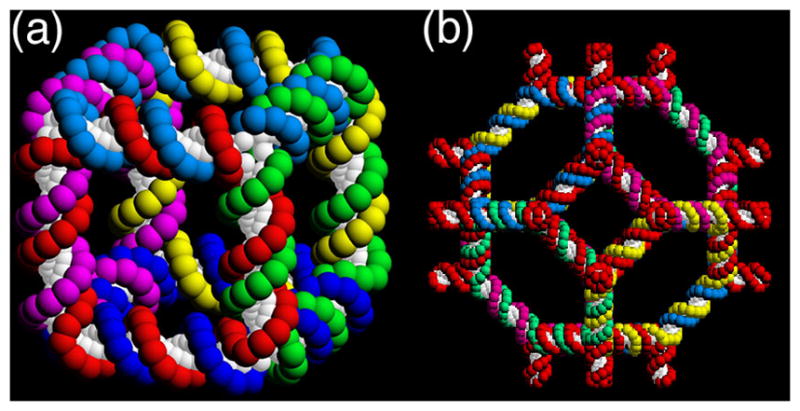
(a) A Stick Cube and (b) a Stick Truncated Octahedron. The drawings show that each edge of the two figures contains two turns of double helical DNA. There are two turns of DNA between the vertices of each polyhedron, making them, respectively, a hexacatenane and a 14-catenane.

Many of the problems of the synthesis of the cube were eliminated by the development of a solid-support-based methodology [27], which allowed the use of the full logical control implicit in sticky-ended construction. As a test case, this approach was used to build a truncated octahedron (Figure 11b), again with two turns per edge [57]. Thus, the DNA representation of this Archimedean polyhedron is a 14-catenane. Six of its faces correspond to squares and eight of its faces correspond to hexagons. The faces corresponding to squares contain an extra arm at each junction, so that this 3-connected polyhedron was built with 4-arm junctions. Consequently, it might have been able to make a 4-connected lattice, such as the zeolite A lattice, but not enough material was produced to use it as starting material for a lattice construction.

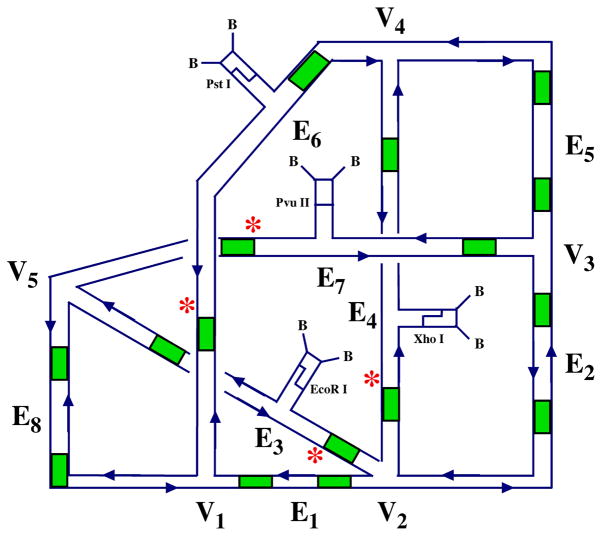
Both of these polyhedra correspond to regular graphs. In an exercise related to DNA-based computation, we have also constructed an irregular graph [59]. The construction prototyped a monochromatic version of a solution to a graph 3-colorability problem. Whereas the two previous polyhedral constructions entailed step-wise syntheses, the nature of DNA-based computation entails doing as many steps as possible at once. Similarly, the requirements of the calculation entail mixing edges of different properties, so that molecules corresponding to edges were added explicitly to the solution containing the junctions. This single-pot reaction resulted in the construction of the irregular graph illustrated in Figure 12. Unlike the cube and the truncated octahedron, this graph is a single-stranded knot, rather than a catenane. Proof of synthesis in this case requires the breakdown of the final strand to predictable restriction fragments.

Figure 12. An Irregular Graph.

The graph shown has explicit edges (E1–E8) as well as junctions (V1-V5). The sites of the sticky ends are indicated by patches of green. Restriction sites are indicated by the names of the restriction enzymes, biotin groups are labeled as 'B' and radioactive labeling sites are shown by asterisks. Note that this is a knot, not a catenane.

TOPOLOGICAL DNA CONSTRUCTS

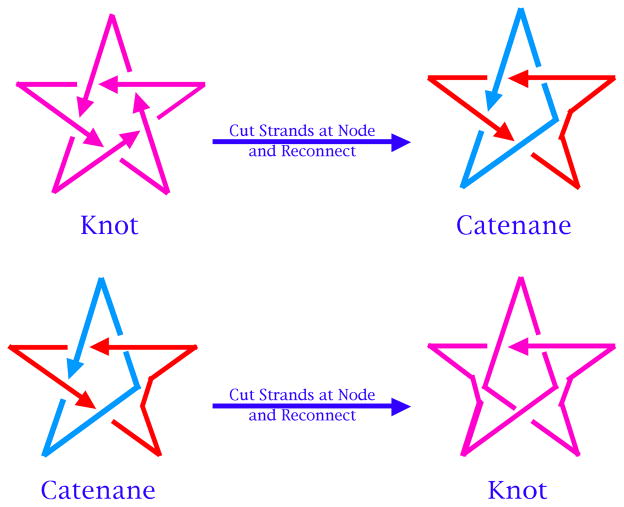
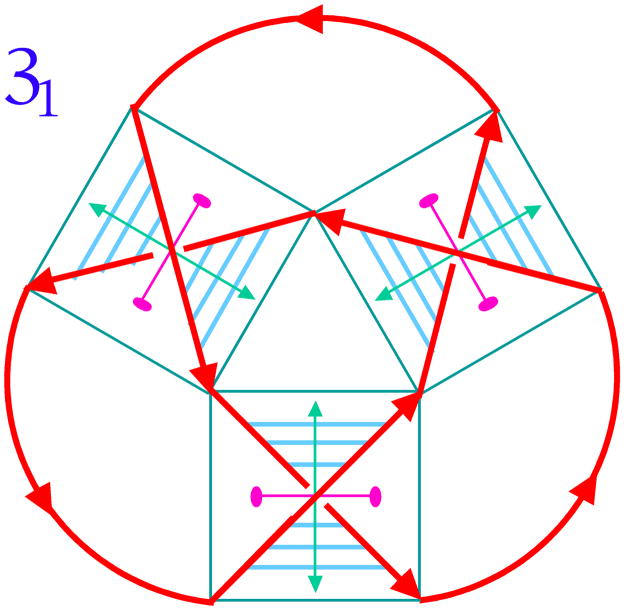
Figure 13 illustrates a simple relationship between catenanes and knots [e.g., 60]. A 5-noded knot is shown in the upper left of the drawing, with arrowheads indicating an arbitrary polarity to the strand. If one imagines a node to be made up of four strands, one before and one after the node on the top and the bottom, one can destroy the node by disconnecting the intact strands, and reconnecting them while maintaining local polarity. This converts the knot to a catenane. The catenane can then converted to a knot using the same operation. Thus, it appears that a system that is successful at making catenanes can also be successful at making knots and other topological targets. Figure 14 shows the relationship between DNA and a node in a knot. The trefoil knot, is shown as a red strand. A box is drawn around each of its three nodes, and the strands of the knot act as diagonals of the box, dividing it into four zones, two between parallel strands and two between antiparallel strands. Whereas the DNA backbone is antiparallel, one can make the transition from topology to nucleic acid structure by placing about a half-turn (six base pairs) of double helix between the antiparallel backbones [61].

Figure 13. The Relationship Between Knots and Catenanes.

At the upper left is a 5₁ knot with an arbitrary polarity. In the transition to the upper right, a node is destroyed by cutting both strands and rejoining them, while maintaining local polarity; a catenane results. The catenane is repeated on the lower left. Performing the same operation on a different node converts the catenane to a knot.

Figure 14. The Relationship of Nodes to DNA Half-Turns.

The simplest knot, 3₁ is drawn with red strands and arbitrary polarity. Blue boxes are drawn about its nodes, and the strands that make the nodes serve as the diagonals of the boxes; they divide the boxes into four regions, two between parallel strands and two between antiparallel strands. Drawing a half-turn of DNA (about 6 nucleotide pairs) between the antiparallel strands effects the transition from strand topology to nucleic acid structure.

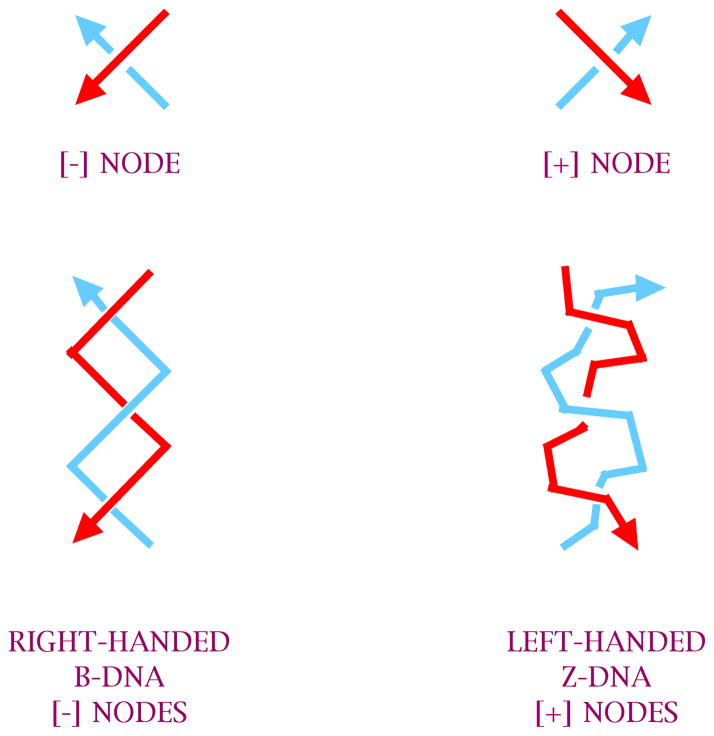
The nodes shown in Figure 14 are all of the same sign, corresponding to the negative nodes produced by right-handed B-DNA. However, knots and other topological constructs are not limited to negative nodes. Fortunately, a left-handed form of DNA exists, known as Z-DNA [62], which can supply positive nodes; the differences between B-DNA and Z-DNA are cartooned in Figure 15. This molecule requires particular sequences (typically CG_n) to form, and it also requires conditions that promote the formation of Z-DNA, usually high salt or effector molecules, such as Co(NH₃)₆³⁼. By using appropriate sequences and conditions, it is possible to produce a variety of topological targets containing positive nodes, negative nodes, or both.

Figure 15. B-DNA and Z-DNA.

The two forms of DNA are cartooned here. B-DNA has a simple helical structure and is right-handed, leading to negative nodes. Z-DNA is a helix with a zigzag backbone resulting from a dimer being the helical repeat unit. It is left-handed, leading to positive nodes.

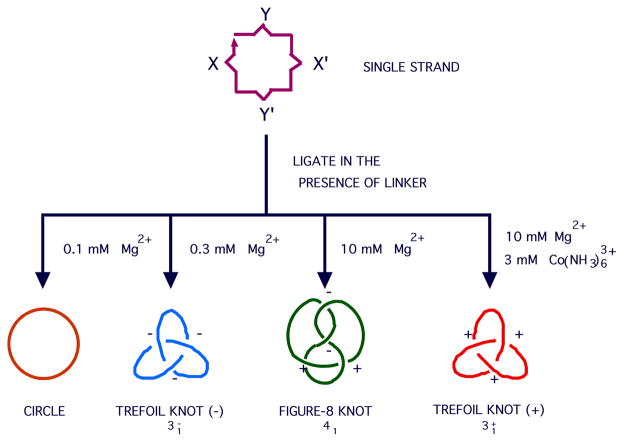
An example of a collection of topological targets is illustrated in Figure 16. By changing conditions, it is possible to use sequences of different Z-forming propensity to make a circle, a trefoil knot with negative nodes, a figure-8 knot and a trefoil knot with positive nodes, all from the same strand of DNA [63]. Topoisomerases are molecules that transform DNA molecular topologies by catalyzing strand-passage events. It is possible to make one of the knots shown in Figure 16 and then change the solution conditions, and then observe the knot identity change if a topoisomerase is present to catalyze the transition [64]. This approach has been used to discover an RNA topoisomerase activity by using observing strand-passage transitions occur in knotted RNA molecules [65].

Figure 16. Synthesis of Four Topologies from a Single Strand of DNA.

X and X' represent a turn of DNA and its complement, as do Y and Y'. Both have a Z-forming propensity, but that of Y-Y' is higher. As the Z-forming nature of the solution increase, the main ligation product changes from a circle (very low ionic strength), to a trefoil knot with negative nodes (both turns B-DNA), to a figure-8 knot (the Y turn is Z-DNA), to a trefoil knot with positive nodes (both turns are Z-DNA).

Borromean rings are a complex topological target that has been obtained relatively simply from DNA [66]. Figure 17a shows that they consist of three interlocking rings, no two of which are themselves linked. The signs of the three inner nodes are opposite from the signs of the three outer nodes. If one of the rings is cut, the other two will fall apart. To produce this property in DNA, it was easiest to change the individual nodes to triple nodes, i.e., to replace the half-turn of DNA with three half-turns of DNA. If one thinks of the structure in Figure 17a as a polar projection, so that the central point corresponds to the north pole and every point on the outside is the south pole, then one can put a B-DNA junction flanking the north pole. If every point on the outside corresponds to the south pole, one can put a Z-DNA junction there. Hairpin loops that do not change the topology are added to the equator for synthetic and analytical purposes. Their assembly is illustrated in Figure 17b.

Figure 17. Borromean Rings.

(a) The Topology of Borromean Rings. Note that cleaving any ring leaves the other two rings unlinked; the key is that the nodes on the inside are of a different sign from those on the outside. (b) Forming Borromean Rings from DNA. A 3-arm DNA branched junction made of B-DNA (top) is linked to a 3-arm junction made of Z-DNA (bottom) through hairpins at the equator of the product molecule.

2D PERIODIC ARRAYS

Individual objects like polyhedra, knots and Borromean rings may demonstrate the versatility and convenience of DNA branched junctions as a system for the construction of difficult targets. Nevertheless, the goals of structural DNA nanotechnology go beyond the construction of individual objects to periodic arrays, and even to aperiodic arrays (see below in DNA-Based Computation). The ability to make specifically-patterned 2D and 3D structures is central to the success of this enterprise. The floppiness of individual branched junctions usually makes them unsuitable as components for such constructions. However, as noted above, DX molecules (Figure 6b) are branched species that are roughly twice as stiff as linear DNA [30,39], and therefore substantially stiffer than simple branched junctions. They, and TX molecules (Figure 2b) are therefore well-suited to serve as components for periodic arrangements.

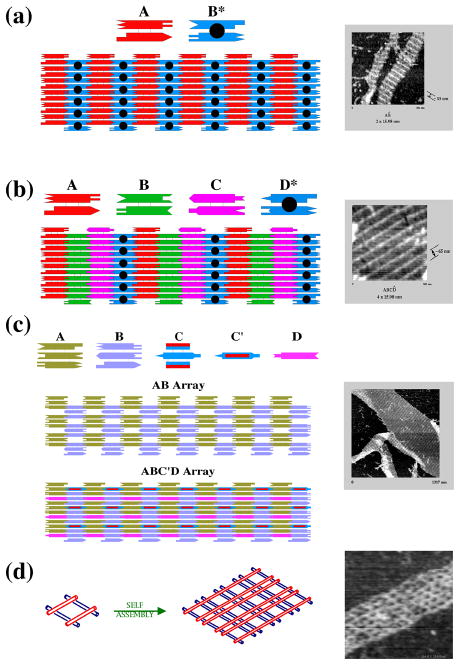
The first examples of two dimensional periodic arrays were DX arrays that contained the capability to produce patterns [42]. Figure 18a illustrates an array produced from a DX molecule and a DX+J molecule. The dimensions of these 2 nm-thick tiling components are about 4 nm x 16 nm. The DX+J molecule has its extra domains rotated out of the plane of the array, so that they can act as topographic markers for the atomic force microscope. Thus, a series of striped features should appear on the pattern, separated by about 32 nm, as seen on the right of the drawing. To demonstrate the level of control over the pattern, a second DX array is shown in Figure 18b. Here, three DX tiles are combined with a DX+J tile, to produce a pattern where the stripes are separated by 64 nm.

Figure 18. DNA Arrays.

(a) Two DX Molecules Tile the Plane. A conventional DX molecule, A, and a DX+J molecule, B*, are seen to tile the plane. The extra domain on B* leads to stripes. The molecules are 4 x 16 nm in this projection, so the stripes are ~32 nm apart, as seen in the AFM image at the right. (b) Four DX Molecules Tile the Plane. This arrangement is similar to (a), but there is only one DX+J molecule, D*, so the stripes are separated by ~64 nm, as seen on the right. (c) A TX Array. Two TX tiles, A and B are connected by complementarity between their first and third double helical domains, resulting in spaces between the tiles. D is a linear duplex that fits in the yellow rows, and C is a TX re-phased by three nucleotide pairs; it fits into the gray rows and extends helices beyond the AB plane in both directions, as shown in the micrograph at the right. (d) A DNA Parallelogram Array. Four Holliday junction analogs form a parallelogram that is extended to produce a periodic array. The sizes of the cavities in the array may be tuned. Those in the array the right are ~13 nm x ~20 nm.

TX molecules also can be used to produce 2D arrays. One can take the same approach to making patterns used with the DX arrays, using a TX+J tile [40]. However, the TX tile offers a convenient way to insert specimens within the array: It is possible to produce a gap in a continuous lattice by connecting individual tiles 1–3, i.e., by designating sticky ends that connect the first domain to the third domain, as illustrated in the AB array of Figure 18c. One way to demonstrate a robust insertion into this array is to re-phase a third TX tile (C in Figure 18c) by three nucleotide pairs (~102 ), so that it is roughly perpendicular to the AB array (designated C' in Figure 4c). This tile fits into the blue-gray column in the AB array by cohesion of its central domain. A fourth component, a piece of linear duplex DNA (D in Figure 18c) is also shown inserted into the gold row.

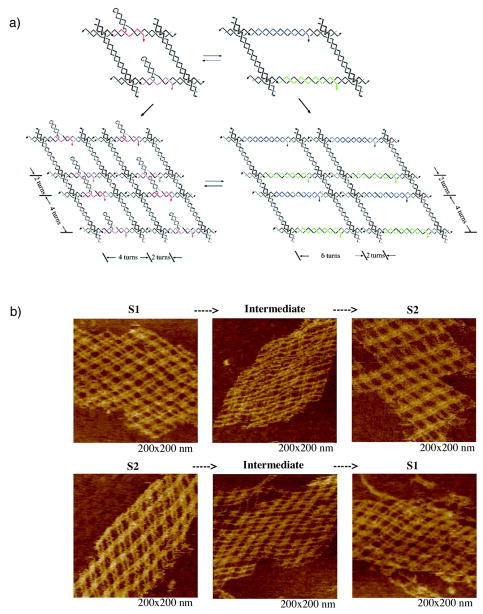
An unlikely, but effective system results from combining four 4-arm branched junctions into a parallelogram [56], as illustrated in Figure 18d. The 4-arm branched junctions assorts its four arms into two double helical domains [34], which are twisted with respect to each other [24]. The twist can be 40–60 from antiparallel [35,49,56] or (with 3',3' and 5',5' linkages in the crossover strands) 70 from parallel [67], so that a variety of parallelograms can be produced. The parallelograms can be connected through sticky-ended cohesion to produce an array containing cavities, such as the one shown in Figure 18d. It is straightforward to alter the sizes of the cavities, so that the porosity of this system is readily tunable.

In addition, Yan, Reif and their colleagues [68] have developed a motif that they call the 4 x 4. it consists of four DX molecules that flank a central cavity. The molecules fail to stack within the cavity because of loops that proceed from one domain to another. The system is nearly, but not exactly tetragonal. This is a substantially new motif that appears to be robust, and is likely to have a number of applications in DNA nanotechnology.

All of the periodic motifs described so far are basically low-symmetry motifs, corresponding to translations or twofold rotations normal to the plane. Recently, we have developed a trigonal motif that produces a pseudo-hexagonal array [69]. There have been a number of significant failures to make hexagonal structures, the 'stick' version of hexagonal close packing within the plane [e.g., 28]. We have adapted the unsuccessful bulged junction triangle motif by doubling its height, so that it is made of DX molecules, rather than double helices. This molecule forms an excellent honeycomb structure. Analysis of the system reveals that the key to the formation of the 2D array is the DX cohesion: Blunting one of the sticky ends leads to failure in honeycomb array generation. This approach to DX cohesion has now been applied to a large number of motifs that were intractable or at least recalcitrant to 2D periodic array formation. An approach from Adleman and his colleagues [70] uses DX cohesion in structures confined to a single plane, and is largely successful, but inspection of their results demonstrates that the stiffness of the DX sides to the triangles is apparently partially responsible for the uniquely stiff nature of the DX triangle motif and the other DX cohesive systems being investigated.

DNA-BASED NANOMECHANICAL DEVICES --THE PATH TO NANOROBOTICS

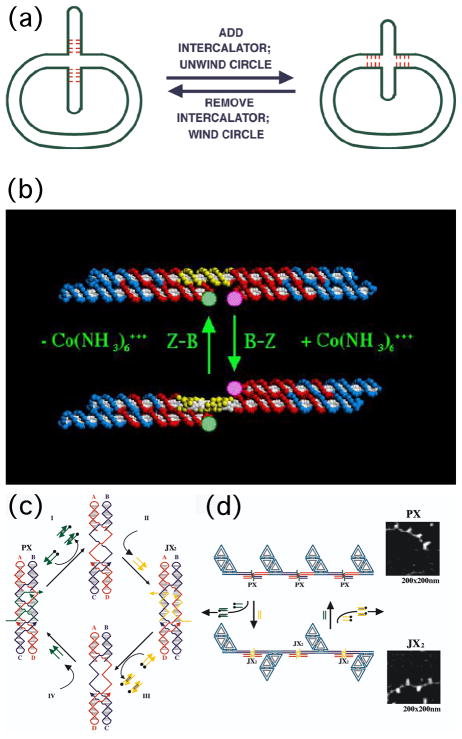
There are at least three different routes to obtaining nanomechanical devices from DNA-based systems. The first of these is the use of DNA structural transitions. Such transitions are well-known, and they can be used to change the structure of DNA in a reliable fashion. The very first of these devices entailed a DNA cruciform with several nucleotides at the middle that could undergo branch migration [71]. As illustrated in Figure 19a, the addition or removal of ethidium, an intercalating drug (which binds between the bases and in doing so unwinds the helix), changes the position of the branch point. The change in twist in the body of the circle as a consequence of the presence or absence of the drug results in the extrusion or intrusion of the cruciform branch. This device is indeed under the control of an external agent, but it is not a convenient system from which to obtain work.

Figure 19. DNA Devices.

(a) A Mobile Control Device. The cruciform structure on the left contains four mobile base pairs at its base. Addition of an intercalator (ethidium) unwinds the circle, moving them into it. Removal of the ethidium reverses the action of the device. (b) A DNA Nanomechanical Device Based on the B-Z Transition. The device consists of two DX molecules connected by a shaft containing 20 nucleotide pairs (yellow) capable of undergoing the B-Z transition. Under B conditions the short domains are on the same side of the shaft, but under Z-conditions (added Co(NH₃)₆³⁼) they are on opposite sides of the shaft. The pink and green FRET pair are used to monitor this change. (c) The Machine Cycle of a PX-JX₂ Device. Starting with the PX device on the left, the green strands are removed by their complements (Process I) to leave an unstructured frame. The addition of the yellow strands (process II) converts the frame to the JX₂ structure, in which the top and bottom domains are rotated a half turn relative to their arrangement in the PX conformation. Processes III and IV reverse this process to return to the PX structure. (d) AFM Demonstration of the Operation of the Device. A series of DNA trapezoids are connected by devices. In the PX state, the trapezoids are in a parallel arrangement, but when the system is converted to the JX₂ state, they are in a zigzag arrangement.

A second system that is better designed is based on the B-Z transition of DNA [43]. As noted above, Z-DNA has two requirements for formation: An appropriate sequence (called 'proto-Z-DNA') and Z-promoting conditions; lack of either of these keeps the structure in the B-form. The need for a special sequence allows us to control the transition in space (i.e., where, and over how much DNA it will occur), and the necessity of Z-promoting conditions allows us to control the transition in time (i.e., when it happens). A device that takes advantage of the B-Z transition is illustrated in Figure 19b. It consists of two DX molecules connected by a shaft (yellow backbone) that can undergo the B-Z transition. In the absence of Z-promoting conditions, the shaft is in the B-conformation, and both domains unconnected to the shaft are on the same side of it. However, addition of the effector, Co(NH₃)₆³⁼, switches it to the Z-conformation. This in turn rotates an unconnected domain of a DX molecule to the other side of the shaft. The transition is demonstrated by a pair of dyes using fluorescent resonance energy transfer (FRET).

The problem with devices based on DNA structural transitions is that they are triggered by a single molecular species, and are not individually addressable. A couple of devices have been developed that utilize a transition between B-DNA and G₄ tetrad structures [72–74], or based on pH [75] but these devices suffer from the same problem. The breakthrough in this area was made by Yurke and his colleagues [76], who developed a sequence-dependent device. This was molecular tweezers that contracted when a particular strand was added to the solution, and then relaxed to an expanded state when the strand was removed. The removal of the strand was achieved by adding a short, unpaired segment (called a toehold) to its end. Addition of the complete complement to this strand resulted in its binding first to the toehold and then ultimately the complement branch migrates its way through the structure until the entire strand is in duplex form; this is a largely irreversible state, because there is much more base pairing with the complement than with the device structure. Numerous devices have been built using this approach [e.g., 44], including a bipedal walker [77] and a transcriptionally-controlled device [78].

A robust two-state device was developed that is based on this principle [44]. That device is illustrated in Figure 19c. It shows a molecule in the PX structure (left), with two green 'set' strands that put it into that state. The addition of the complements to the set strands ('unset' strands) results in their removal, leaving a naked frame. The addition of two yellow set strands puts the system in a different state, called JX₂, because there are two juxtapositions between the helices. The feature of the JX₂ structure that is central to its role here is that its is rotated a half- turn from the bottom of the PX structure. Note that the sequence complementary to the set strands can be varied, so that there are a lot of different frames that can be developed, and which can be addressed independently. Figure 19d shows that this system can do work, by rotating a marker visible in the AFM. In the PX state, the markers should all be on the same side of a 1D array, but in the JX₂ state, they should alternate.

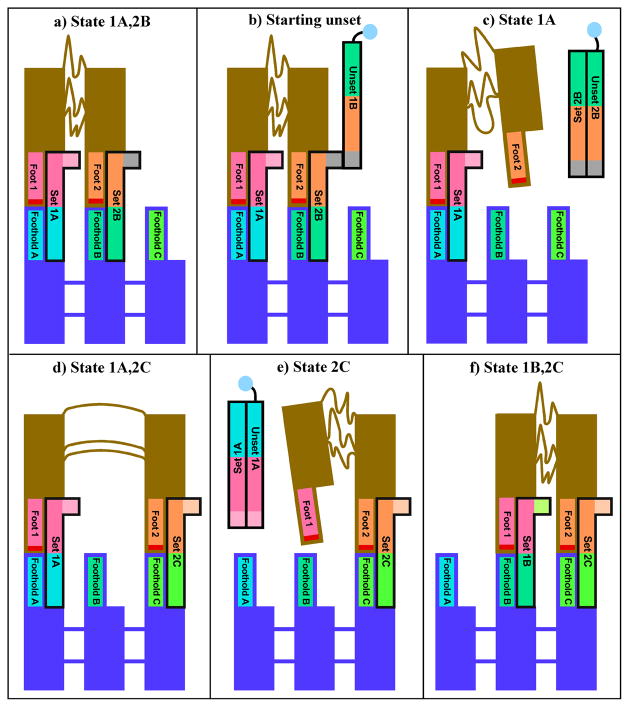
This same notion has been used to build a device that walks on a sidewalk. Figure 20 shows that this device consists of two double helical legs that are connected to each other by a flexible linker. It is connected to the sidewalk by set strands that hydrogen bond it in position. As can be seen in Figure 20, removal of one set strand by its unset strand releases one foot that can then be bound to a different position by a different set strand. The same position can be used to release the other foot, and then it, too, can be set down on the sidewalk in a new position. It is possible to move this device in both directions. Proof of movement consists in crosslinking the feet in aliquots of the solution at every point along the walk, and then examining them in a denaturing gel, which will reveal bands corresponding to the crosslinked species [77].

Figure 20. A DNA-Based Walker Walking on a Sidewalk.

The states through which the system passes sequentially are shown in the panels of the drawing. Matching colors indicate complementary sequences between strands. The red section at the end of each foot indicates psoralen, which is crosslinked for analysis. (a) Initial State of the Walker Feet 1 and 2 are attached to the sidewalk by hydrogen-bonded strands. (b) and (c) Removal of the Connection of Foot 2. The Unset complex is removed from solution via a biotin group (depicted as a blue circle) attached to the unset strand. (d) Re-Attachment of Foot 2 at a New Position. (e) Release of Foot 1. (f) Re-Attachment of Foot 1 at a New Position. At this point the device has moved a complete step.

An exciting hybrid of a device and a 2D lattice has been pursued by Yan, Reif and their colleagues [79]. As shown in Figure 21a, a parallelogram-like lattice has been built that contains a hairpin. A strand can be removed from the base of the hairpin, and a complement to the entire hairpin and base can be added. This expands the lattice dimensions of the parallelogram in one direction from four turns to six turns. The dramatic AFM evidence in Figure 21b suggests that ultimately this approach can be used to change the dimensions of crystalline samples.

Figure 21. A Two-Dimensional Array Capable of Changing Cavity Dimensions.

(a) Strand Diagram of the Tiles and Their Incorporation into Arrays. The red and purple set strands correspond to a contracted state, while the blue and green strands correspond to the expanded state. (b) AFM Images Illustrating the Transition. The 'before' (left), 'transition' (center) and 'after' (right) states of the array are illustrated in both directions. Reproduced with permission.

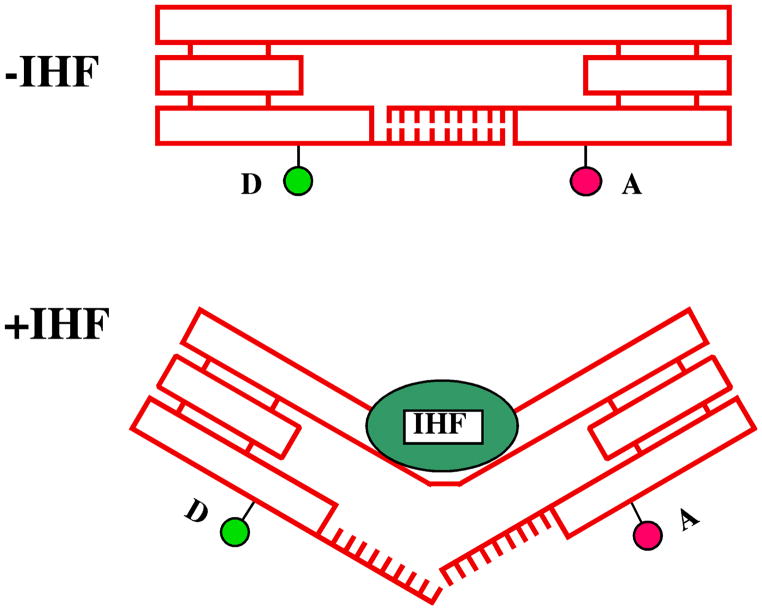
A third form of device is the activation of a DNA transition by a protein. This is the closest to a phenomenon that actually occurs within a living cell. This type of device is sequence-specific, but a new protein much be found for each different transition, thereby decreasing the convenience and generality of the approach. This type of device was prototyped recently in a context similar to that of the B-Z device; the proto-Z segment of the device was replaced with the binding site for a DNA-bending protein [80] known as integration host factor (IHF). The binding of IHF to the DNA was monitored by FRET, just as it was in the B-Z device. The interesting feature of this device is that it was used to measure the amount of work that the protein could do upon binding. As schematized in Figure 22, the protein was required to break a number of hydrogen bonds so as to bind. By titrating the number and type of interactions, it was possible to estimate that the protein is capable of doing 7–8 kcal/mol of work when it binds to DNA.

Figure 22. The Action of a Nanomechanical Device Working Against a Load.

Double-helical DNA is shown as rectangular boxes. Triple crossover motifs (TX) are shown as three fused rectangular boxes. The upper domain connects the two TX motifs with the binding site for IHF. IHF is shown as a green ellipse, and in the lower panel its binding distorts the connecting shaft. In the upper panel the lower TX domains are held together by a sticky end. In the lower panel, these are disrupted by the binding. By changing the strength of the sticky end, the amount of work the protein can do upon binding is estimated.

The devices described above are all clocked devices: They respond to a particular stimulus in a way that is designed. However, there is a great deal of interest in autonomously operating devices. One has been developed recently by Mao and his colleagues [81]. He has employed a DNAzyme, a DNA molecule that binds to a given short sequence of RNA, and then catalyzes its cleavage. When the RNA molecule binds, it brings together a tweezer-like molecule. Following cleavage, however, the two RNA molecules no longer hold the tweezers together, so it expands. In addition, the RNA is so short following cleavage that it is no longer bound to the DNA; it dissociates when a new substrate molecule is present, and the cycle repeats. Numerous other autonomous devices are being developed currently.

SELF-REPLICATING SYSTEMS

The use of DNA as a building material immediately suggests the notion that a self-replicating system could be developed. One of the key features of DNA in cells, however, is its linearity. The replication of branched DNA by the cellular enzyme, DNA polymerase, will only result in further linear molecules, even if the ends are joined by hairpin loops. A number of schemes have been advanced [82,83], but only two have been realized experimentally. The first is a scheme devices by von Kiedrowski et al., which entails branching at the primary structure level [84]. He has three strands of DNA attached to a small organic molecule at one of their ends. He then adds the complements to the three strands, which bind to the first three strands. They are then bonded to a second organic molecule. Dissociation leads to the ability to continue the replication.

Another suggestion by von Kiedrowski was that one could make polyhedra whose were not covalently bonded to all of their vertices, but only to one vertex. This idea was adopted elegantly by Shih et al. [85] to form a self-replicating octahedron. Seven of the edges of the octahedron are held together by PX cohesion, as drawn schematically in Figure 23a. To make all twelve edges structurally equivalent, five helper strands were also added, so that the other five edges could be DAE-DX molecules. The design of the octahedron is illustrated in Figure 23b. Electron micrographs of the final molecule are shown in Figure 23c, and symmetrized structures are shown in Figure 23d. This is a remarkable achievement, which may ultimately remove much of the drudgery from DNA nanotechnology.

Figure 23. An Octahedron Consisting of One Long and Five Short DNA Strands.

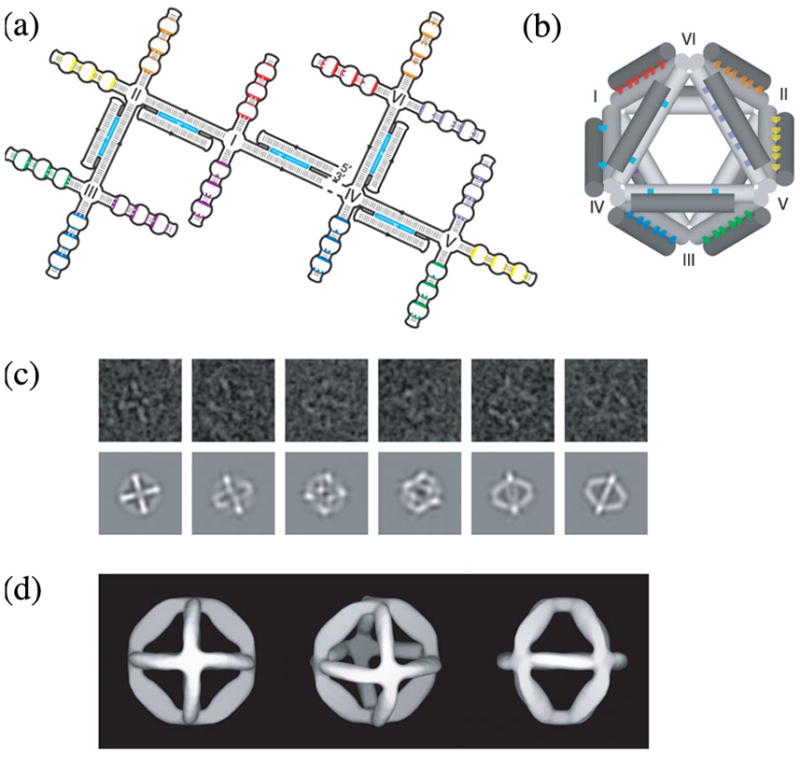
(a) Strand Diagram of the ‘Branched Tree’ Structure. The structure consists of DX struts (double helical regions with light blue central strands), four-arm junction joints (labeled I-VI) and half-PX domains (complementary domains labeled with the same colors) destined to fold into struts. (b) 3-Dimensional Representation of the Folded Octahedron. The drawing shows the crossovers in the DX molecules as two light blue dots between cylinders and the PX associations as a series of colored dots between cylinders. (c) Electron Microscopic Images. Raw EM data are shown at top and maps onto projected octahedral symmetry of the folded octahedron are shown at the bottom. (d) Views of the 3-Dimensional Electron Density Model Based on EM Data. Reproduced with permission.

STRUCTURAL DNA NANOTECHNOLOGY AND DNA-BASED COMPUTATION

DNA-based computation was originated as a laboratory science by Adleman [12], who solved a Hamiltonian path problem using DNA. The field has grown large, and space does not allow for a description of all branches of the discipline. Its central approach is to use the parallelism of the vast number of molecules in a solution to solve solutions in parallel. Two approaches bring it within the sphere of DNA nanotechnology, and those are described here. We have already noted that it is possible to make irregular graphs from DNA. A goal is to solve 3-colorability problems using branched DNA molecules. The problem is to color a given graph so that no two nodes joined by an edge have the same color. Jonoska [86] has pointed out that if one mixes junctions of all possible colors and joins them specifically with edges that only permit differently colored nodes at then ends, a successful solution will be characterized by a molecule that is cyclic. This is easily detected either as an off-diagonal spot on 2D polyacrylamide gels (gels where the material is driven through two different concentrations of polyacrylamide), or by exonuclease resistance. Although the rigidity of components normally is valued highly in structural DNA nanotechnology, this is an instance in which flexibility must be maximized, because one does not want rigidity to get in the way of structure formation.

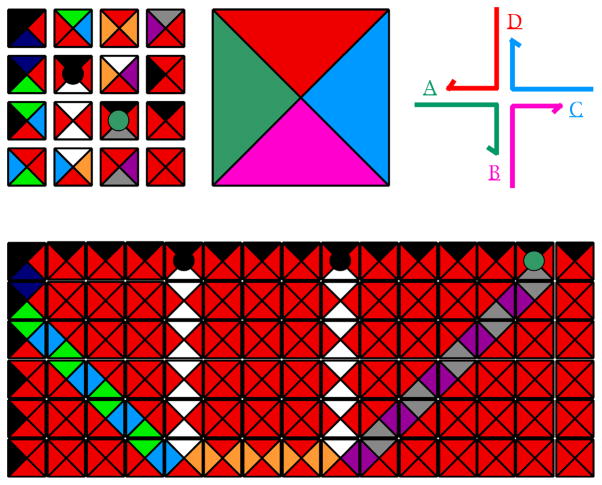
The other way in which DNA-based computation is convergent with structural DNA nanotechnology is due to Winfree, who approached DNA-based computation from the perspective of Wang tiles [87]. Figure 24 illustrates a group of Wang tiles in the upper left corner; they have a variety of differently-colored edges. In theory, Wang tiles assemble into a mosaic, such as the one shown at the bottom of Figure 24, according to the local rule that every edge in the mosaic is flanked by the same color. This form of assembly emulates the operation of a Turing machine; indeed, the mosaic shown illustrates a simple calculation, the addition of 5 to 9 to yield 14 [88]. Winfree noted that branched junctions with sticky ends are logically equivalent to Wang tiles, and that branched DNA molecules could be a way to reduce Wang tiles to practice in computation. Recently, Rothemund et al. have demonstrated the successful assembly of a Sierpinski triangle, using DNA self-assembly [89]. This is the first successful 2D algorithmic DNA assembly, although a 1D assembly of a cumulative XOR was demonstrated in 2000 [90].

Figure 24. Wang Tiles and their Relationship to Branched Junctions.

The upper left corner illustrates 16 Wang tiles of various types. The bottom shows a mosaic formed from them using the rule that all edges in the mosaic are flanked by the same color; this mosaic assembly that performs the calculation of adding 5 to 9 to get 14. The upper right is a color coded branched junction that, when compared to the enlarged tile at the center shows the relationship between Wang tiles and branched junctions with particular sticky ends.

SCAFFOLDING OTHER SYSTEMS

The goals of structural DNA nanotechnology noted above entail the scaffolding of heterologous species of molecules, for example proteins or nanoelectronic components. Some progress has been made in this direction. Kiehl and his colleagues have been successful in organizing small goal nanoparticles on a 2D DNA periodic lattice similar to those illustrated in Figure 18a [91]. This work lends credence to the notion that DNA can organize species that are not necessarily similar chemically. A different goal has prototyped the use of DNA to direct the topology of industrial polymers. Derivatives of uridine (the variant of thymine found in RNA) have been synthesized that have a branched side-chain on the outside of the helix. One variant contains a di-amino group, and the other contains a di-carboxyl group. These are the constituents of nylon. A knotted DNA chain containing alternating di-amino and di-carboxyl groups would impart this topology to a nylon molecule that was formed from these side-chains. A prototyped system was successful in the condensation of these groups [92].

CONCLUDING REMARKS

We have described a new architectural system on the nanometer scale that is derived from the central biological molecule, DNA. There well may be biological applications to structural DNA nanotechnology, but biology is not the goal of the effort. Some of the practical aims of the field have been noted earlier, particularly in terms of biological crystallography, nanoelectronics, nanorobotics and new materials. However, the key intellectual goal is to establish the connection between the molecular scale and the macroscopic scale. Being able to design materials by choosing DNA sequences, and then to examine their properties on the macroscopic scale will be a major milestone in our understanding of matter. To this end, there are several efforts currently underway to extend the 2D results noted above to 3D. Crystals of some motifs have been developed that are over a millimeter in length, although they only diffract to about 10 Å resolution at this time. Clearly, a concomitant effort is needed to incorporate nanomechanical devices within such crystals, so that their properties of can be altered in a specific fashion, as a consequence of particular triggers.

It is natural for one to look at a system based on DNA or its derivatives and ask, "Where's the biology?" DNA derives from biology, but it does not need to be biological. We continue to learn from biology, but often we are not asking the types of analytical questions that rely on a biological context. In current work we and the other practitioners of structural DNA nanotechnology have used only Watson-Crick base pairing. However, many new tertiary interactions for RNA [e.g., 93] and DNA motifs [94] are being discovered. As we learn about the thermodynamics and structural requirements of these interactions, they ultimately will lead to a whole new generation of capabilities for structural nucleic acid nanotechnology. Likewise, as we learn more about the metabolism of DNA, we may discover new motifs that are currently exploited by living systems that can be used in this effort. Structural DNA nanotechnology is a field whose growth is increasing rapidly. The prospects are extraordinarily exciting!