Dynamics and instabilities of lipid bilayer membrane shapes

Abstract

Biological membranes undergo constant shape remodeling involving the formation of highly curved structures. The lipid bilayer represents the fundamental architecture of the cellular membrane with its shapes determined by the Helfrich curvature bending energy. However, the dynamics of bilayer shape transitions, especially their modulation by membrane proteins, and the resulting shape instabilities, are still not well understood. Here, we review in a unifying manner several theories that describe the fluctuations (i.e. undulations) of bilayer shapes as well as their local coupling with lipid or protein density variation. The coupling between local membrane curvature and lipid density gives rise to a ‘slipping mode’ in addition to the conventional ‘bending mode’ for damping the membrane fluctuation. This leads to a number of interesting experimental phenomena regarding bilayer shape dynamics. More importantly, curvature-inducing proteins can couple with membrane shape and eventually render the membrane unstable. A criterion for membrane shape instability is derived from a linear stability analysis. The instability criterion reemphasizes the importance of membrane tension in regulating the stability and dynamics of membrane geometry. Recent progresses in understanding the role of membrane tension in regulating dynamical cellular processes are also reviewed. Protein density is emphasized as a key factor in regulating membrane shape transitions: a threshold density of curvature coupling proteins is required for inducing membrane morphology transitions.

1. Introduction

Cellular membranes are highly dynamic and are a feature of the structural complexity of biological cells [1–3]. Membrane shape transitions are often coupled with specific functions of cellular compartments [4–6]. For example, remodeling of membranes, such as during vesicle budding [1,3,7] and membrane tubulation [8–11], is required for cellular signaling and cargo transportation. Thus, the diversity and dynamics of membrane shapes are vital for cell physiology [5].

The lipid bilayer is the most fundamental structural component of biological membranes [12]. The physical properties of the bilayer have been extensively studied since the early 1970s [12–15], as a first step toward understanding complicated cellular membrane behaviors. The membrane’s curvature elastic energy was found by Wolfgang Helfrich to play the major role in determining the shape of vesicles [14]. A large variety of experimentally observed shapes of red blood cells (RBC) can be nicely explained simply by minimizing the curvature elastic energy F_elastic:

$$F_{\mathit{elastic}}=\int \frac{1}{2}\kappa {(C-C_s)}^{2}dA,$$ (1)

with appropriate constraints[16,17], where κ is the bending rigidity, C is the local mean curvature, C_s is the spontaneous curvature of the bilayer and A is the membrane surface area.

In Helfrich’s spontaneous curvature model, the membrane is treated as a two-dimensional flexible film. While the model captures the essence of membrane geometries, the understanding of detailed, experimentally observed mechanical behaviors requires accounting for details of the membrane’s bilayer architecture [18,19].

Equilibrium studies of membrane geometries revealed the underlying physics that contribute to cellular shapes. On the other hand, the mobility and shape transitions of cellular membranes are influenced by membrane dynamics. One of the most fundamental dynamic behaviors of a lipid bilayer is its fluctuations under thermal agitation. Analyzing the fluctuation spectrum can yield basic physical properties of the membrane and its interaction with the surrounding environment [20,21]. Another aspect of cellular dynamics involves the membrane deformation under external forces, which can be exerted either by solution flow [22,23] or through the interaction with the cytoskeleton [24,25]. Studies of membrane dynamics are able to disclose the spatiotemporal aspects of biological activities. For example, the motility of cells is usually driven by a cyclic generation and healing of membrane blebs or protrusions, with velocities ranging from 0.1 μm/min to over 10 μm/s [26–28].

There are many diseases in which membrane instability is believed to play a role. During fever, high body temperature induces RBC hemolysis and membrane fragmentation [29,30]. In Alzheimer’s disease, altered membrane lipid composition is believed to cause an inherent tendency toward destabilization of cellular membranes [31,32]. More recently, the irreversible collapse of nuclear membrane envelopes was found to be responsible for massive DNA damage and tumor formation [33].

Leibler proposed in a theoretical study that membranes can become intrinsically unstable in a scenario where local membrane curvature and membrane composition couple [34]. However, these theoretical predictions have not been fully tested by experiments, due to the difficulties in quantifying membrane properties in or near unstable regimes.

Endocytosis is one of the best understood biological processes which potentially involve membrane curvature instabilities [35–37]. The formation of highly curved membrane structures is believed to be a result of the interplay between lipids and various peripheral proteins [3,38,39]. The mechanism by which proteins generate and stabilize/destabilize membrane shapes, however, is still under debate. Understanding protein binding and assembling behaviors on membranes will serve as a starting point for explaining these processes.

The purpose of this contribution is to provide an overview of membrane shape dynamics and their coupling with protein–membrane interactions with an emphasis on the origin of curvature instabilities. We will begin with reviewing the basic concepts of thermal membrane fluctuations. Both conventional bending mode [20] and a more recently discovered slipping mode [21] are considered. Membrane tension as a result of constraining membrane fluctuations will also be reviewed. Curvature instability will be defined as the situation where fluctuation amplitudes grow divergently with time [34] and an instability criterion will be derived for a near-planar membrane. We will next discuss protein–membrane interactions and situations where proteins may induce curvature instabilities. Finally, we will suggest, from our perspective, several interesting directions and open questions in these areas.

2. Dynamics of membrane shape

2.1. Basic aspects of membrane shape fluctuations

Thermal out-of-plane fluctuations of membranes, also known as the “flicker phenomenon” [20], can be experimentally quantified through a variety of methods such as phase contrast microscopy [20], reflection interference contrast microscopy [40] or a recently developed optical tweezers method [41]. Recent reviews on this topic are available, see Refs. [42–44].

The free energy of a near-planar bilayer as determined by its curvature elastic energy can be written in the Monge representation [19,34,44],

$$F=\int \frac{1}{2}\kappa {({\nabla }^{2}h)}^2\mathit{dxdy}$$ (2)

where h denotes the height profile of the bilayer relative to the x, y plane (spontaneous curvature of the membrane is here neglected for simplicity).

The thermal average of the fluctuation amplitudes is connected with membrane properties through the equipartition theorem.

$$\langle {\mid h(q)\mid }^2\rangle =\frac{k_{B}T}{A\kappa q^4}$$ (3)

A is the observed membrane surface area, and h(q) and h(r) are related through Fourier transform,

$$h(q)=\frac{1}{A}{\int }_{A}h(r)e^{i\overrightarrow{q}·\overrightarrow{r}}d\overrightarrow{r}h(r)=\sum _{q}h(q)e^{-i\overrightarrow{q}·\overrightarrow{r}}.$$ (4)

Thus, by measuring the spatial frequency spectrum at q > π/L (when fluctuation wavelength is comparable to the size of the cell or vesicle L, this analysis is no longer accurate [20,45]), the membrane’s bending rigidity κ can be determined.

The dynamics of membrane fluctuations is governed by the hydrodynamics of the surrounding solution through the Navier–Stokes equation for incompressible liquids:

$$\begin{array}{l}\rho \frac{\partial \overrightarrow{v}}{\partial t}+\rho \left(\overrightarrow{v}·\nabla \right)\overrightarrow{v}=\eta {\nabla }^2\overrightarrow{v}-\nabla p\\ \nabla ·\overrightarrow{v}=0.\end{array}$$ (5)

ρ is the density, v⃗ is the velocity, η and p are the viscosity, and the pressure of the enclosed fluid, respectively. For small amplitude motions discussed here, the nonlinear convective term (v⃗ · ∇) v⃗ can be neglected [20,46,47].

If we consider a planar wave in the x-direction with wavenumber q₀, then the velocity and pressure of the liquid can be written as v⃗ = v⃗ (z)e^iq₀x+iwt, p = p(z)e^iq₀x+iwt and the height of the membrane as h = h₀e^iq₀x+iwt. For simplicity, we will only consider the liquid below the membrane as illustrated in Fig. 1. However, it can be easily shown that a membrane with liquid on both sides will exhibit the same general behavior [46,48].

Fig. 1.

Sketch of a fluctuating membrane (black curve) in liquid environment (gray).

The solution of the equation of motion, assuming the liquid to be stationary at z = −∞ is,

$$\begin{array}{l}{v}_x=\left({iC}_1{e}^{q_{0}z}+\frac{il}{q_0}{C}_2{e}^{lz}\right)e^{{iq}_{0}x+\mathit{iwt}}\\ v_z=\left(C_1{e}^{q_{0}z}+C_2{e}^{lz}\right)e^{{iq}_{0}x+\mathit{iwt}}\\ p=\frac{-iw\rho }{q_0}{C}_1{e}^{q_{0}z}{e}^{{iq}_{0}x+\mathit{iwt}}\end{array}$$ (6)

with $l^2=q_0^2+\frac{iw\rho }{\eta }$. C₁ and C₂ are constants and can be determined from the following boundary conditions at the bilayer–liquid interface:

$$\begin{array}{l}{T}_{xz}{\mid }_{z=0}={\eta \left(\frac{\partial v_x}{\partial z}+\frac{\partial v_z}{\partial x}\right)|}_{z=0}=0\\ T_{zz}{\mid }_{z=0}=P_z=-\frac{\delta F}{\delta h}\iff {\left(2\eta \frac{\partial v_z}{\partial z}-p\right)|}_{z=0}=\kappa q_0^{4}h.\end{array}$$ (7)

T_ij = −pδ_ij + η(∂_jv_i + ∂_iv_i) is the viscous stress tensor and P_z is the elastic restoring force due to membrane deformation. The first equation indicates there is no external force in the x-direction. The second equation describes the balance of forces in the z-direction, between liquid stress and the restoring force caused by membrane bending.

Continuity of the velocity at the membrane–liquid interface requires,

$$\frac{\partial h}{\partial t}=v_z{\mid }_{z=0}=(C_1+C_2)e^{{iq}_{0}x+\mathit{iwt}}$$ (8)

which is a first order approximation of the kinematic boundary condition $\frac{\partial h}{\partial t}=v_z{\mid }_{z=0}-\frac{\partial h}{\partial x}{v}_x{\mid }_{z=0}$ [49].

With h = h₀e^iq₀x+iwt and the expressions for C₁ and C₂ obtained from Eq. (7), Eq. (8) leads to the dispersion relation:

$$w^2{\rho }^2-\kappa \rho q_0^5-4iw\rho q_0^2\eta +4q_0^4\eta \left(\frac{l}{q_0}-1\right)=0.$$ (9)

If we define unitless quantities: $S_0=\frac{-iw\rho }{2\eta q_0^2}$ and $y=\frac{\kappa q_0\rho }{4{\eta }^2}$, the dispersion relation becomes:

$${(S_0-1)}^2+y-\sqrt{1-2S_0}=0.$$ (9′)

The roots of the dispersion relation give the eigen frequencies of fluctuation modes. Since y ≪ 1 (as will be discussed later), Eq. (9′) has two roots for a certain wave vector q₀, with the smaller one close to S₀ = 0 and the larger root close to S₀ = 1 / 2.

For S₀ ~ 0, one obtains the slow mode,

$$S_0=y\Rightarrow w_1=i\frac{\kappa q_0^3}{2\eta }.$$ (10)

In this case, the inertial term $\rho \frac{\partial \overrightarrow{v}}{2\eta }$ can be neglected while solving the Navier–Stokes equation (Stokes approximation). Eq. (8) then becomes $\frac{\partial h}{\partial t}=-\frac{\kappa q_0^3}{2\eta }h$ (this can be shown either by calculating a new general solution to replace Eq. (6) or by setting ρ = 0 in the expressions for C₁ and C₂). Assuming h = h₀e^iq₀x+iwt leads directly to the slow dissipation mode $w=i\frac{\kappa q_0^3}{2\eta }$.

For S₀ ~ 1 / 2, we get the fast mode

$$S_0\approx \frac{1}{2}\Rightarrow w_2\approx i\frac{\eta q_0^2}{\rho }.$$ (11)

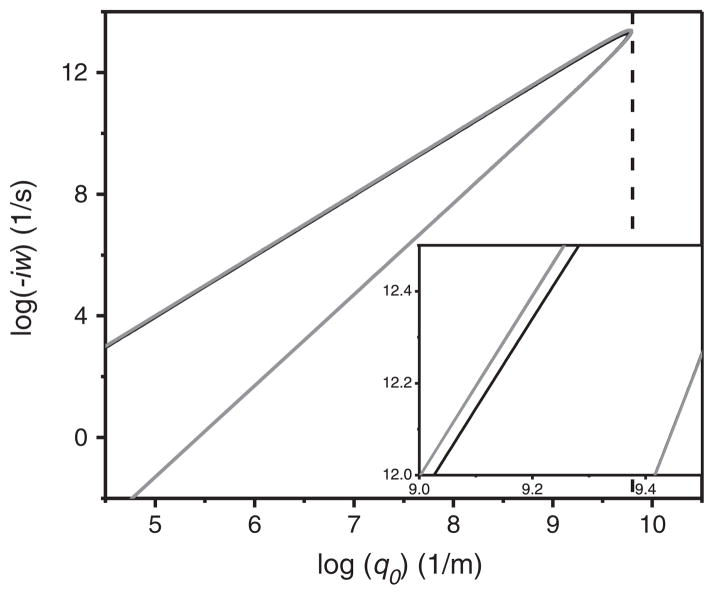
Numerical solutions for the slow and fast modes are shown in Fig. 2. It is worth noting that both modes are non-propagating since exp(iwt) decays exponentially with time, indicating that the membrane is stable against perturbation [20]. Actually it is easy to see that when y < y^* ~ 0.145, there are always two real roots lying between S₀ = 0 and S₀ = 0.5 for Eq. (9′). This also means that for any wavenumber smaller than q₀ ^* = 4η²y^*/κρ, there are two pure imaginary values for the eigenfrequencies w, as shown in Fig. 2. Therefore, the membrane fluctuations will always exhibit two stable dissipating modes when q₀ < q₀^*.

Fig. 2.

A comparison of the two dispersion relations resulting from Eqs. (9′) (black) and (9″) (gray) respectively. As can be seen in the figure, the slow modes (lower part) of two dispersion relations are indistinguishable (overlapped). However, the fast mode (upper part) shows a difference (as becomes clear in the zoomed-in figure of the inset) between two dispersion relations. κ = 10⁻¹⁹ J, ρ = 10³ kg/m³, η = 10⁻³ J s/m³ were used for the plot and the dashed line represents the corresponding value for log(q₀^*).

Taking typical values for the bending rigidity, liquid viscosity and density: κ ≈ 10⁻¹⁹ J, η ≈ 10⁻³ Pa · s, ρ ≈ 10³ kg · m⁻³, we have y ≈ 2.5 × 10⁻¹¹ × q₀. Since the upper cutoff for q₀ is defined by the spacing of lipids a₀ (about 1 nm) as q₀ < π/a₀ ~ 10⁹ m⁻¹ [20,50], this leads to y < 0.025. Thus, physically meaningful membrane fluctuations are always stable.

For the boundary condition Eq. (7), Brochard et al. [20] used v_x|_{z = 0} = 0 instead of T_xz|_{z = 0} = 0. If we assume the former boundary condition, the dispersion relation will be

$$w^2\rho -\kappa q_0^5\left(1-\frac{q_0}{l}\right)=0\text{or}{S}_0^2\sqrt{1-2S_0}+y\left(\sqrt{1-2S_0}-1\right)=0.$$ (9″)

For a certain y < y^** ~ 0.155 (or q₀ < q₀^**), Eq. (9″) also gives two dissipation modes between S₀ = 0 and S₀ = 0.5. As shown in Fig. 2, the dissipation modes resulting from two different boundary conditions behave very similarly. In fact, the two slow modes are indistinguishable; only the fast modes differ slightly without affecting the $q_0^2$ dependency. We note that both boundary conditions have been successfully applied to explain experimental data [20,21,34,51]. Only techniques with an extremely high tempo-spatial resolution would have the potential to identify the ‘correct’ boundary condition.

The foregoing discussion describes the dissipation of membrane fluctuations into the bulk liquid beneath the membrane. If both sides of the membrane are immersed in bulk liquid, the slow dissipation mode should be modified to $w=i\kappa q_0^3/4\eta$.

For a membrane in the vicinity of a substrate, the fluctuation spectrum of the membrane will be modified due to the presence of steric repulsion and van der Waals attraction between the membrane and substrate [46,47,51]. In biological systems, this substrate effect could be a result of membrane adhesion to the cell cortex, cytoskeleton, or to other surfaces [19,52–54].

In this case, the free energy of the membrane can be modified as follows,

$$F=\int \left\{\frac{1}{2}\kappa {\left({\nabla }^{2}h\right)}^2+V(z)\right\}\mathit{dxdy}$$ (2′)

with V(z) representing an effective interaction potential. In a harmonic approximation, the interaction potential can be approximated as V(z) ≈ Ωh²/2, with Ω = d²V/dz² evaluated at the average position of membrane.

The velocity field of the liquid between the membrane and the substrate should be vanishing at the position of the substrate instead of at z = −∞ as was used for deriving Eq. (6). Consequently, the dispersion relation of a fluctuating (monolayer) membrane at a distance l₀ from the substrate becomes (only the slow mode is considered) [51],

$$\begin{array}{l}w=i\frac{\kappa q_0^4+\mathrm{\Omega }}{\eta q_0}\frac{{sinh}^2(q_0{l}_0)-{(q_0{l}_0)}^2}{{sinh}^2(q_0{l}_0)-{(q_0{l}_0)}^2+sinh(q_0{l}_0)cosh(q_0{l}_0)+(q_0{l}_0)}\\ \to w=\{\begin{array}{c}{{il}_0}^3\frac{\kappa q_0^6+\mathit{\Omega }{q}_0^2}{\eta },(q_0{l}_0\ll 1)\\ i\frac{\kappa q_0^4+\mathit{\Omega }}{2\eta q_0},(q_0{l}_0\gg 1).\end{array}\end{array}$$ (10′)

Once the dispersion relation is obtained, the power spectrum of membrane undulations can be calculated from the fluctuation dissipation theorem. It can be shown that the power spectrum is entirely dominated by the slow mode [20,34]. Thus, for the following discussion, we will focus on the slow mode only.

2.2. An additional dissipation mode as the result of inter-leaflet friction

2.2.1. General theory

As discussed above, membrane shape fluctuations are influenced by the membrane’s bending rigidity and therefore Eq. (10) is also called the ‘bending mode’ of dissipation [2,21,55]. A second way of damping membrane fluctuations takes into account the double-leaflet structure of the lipid bilayer [19,21,56]. Local membrane bending generates a lipid density difference between the two monolayers, a process which can be damped by the friction in the tail region of the hydrocarbon chain while two monolayers are sliding over each other [19]. As will be shown below, the presence of inter-leaflet friction will change the fluctuation spectrum and give rise to an additional dissipation mode. This effect is more pronounced when two leaflets are intrinsically asymmetric [8], which is biologically significant since peripheral proteins as well as lipids are known to distribute asymmetrically across the plasma membrane [57].

Consideration of the lateral redistribution of lipids leads to the following modified free energy expression,

$$F=\int \left\{\frac{1}{2}\kappa {\left({\nabla }^{2}h\right)}^2+\frac{1}{2}k\left[{\left({\rho }^{+}+d{\nabla }^{2}h\right)}^2+{\left({\rho }^{-}-d{\nabla }^{2}h\right)}^2\right]\right\}\mathit{dxdy}.$$ (12)

k is an elastic area compressibility modulus, d is the distance between the mid-surface of the bilayer and the neutral surface of a monolayer, ρ^± is the scaled deviation of lipid density from its equilibrium value, and ‘+’ and ‘−’ represent the outer and inner leaflet respectively. In the presence of the interaction potential V(z), additional modifications of the membrane fluctuation spectra are thoroughly discussed in Ref. [47].

Dynamics of the liquid on both sides of the membrane are still determined by the Navier–Stokes equation but the balancing of forces at the boundary (Eq. (7)) is altered by the lateral redistribution of lipids. The modified boundary conditions are [21],

$$\begin{array}{l}\pm T_{xz}^{\pm }{\mid }_{z=0}=\nabla \left(\frac{\delta F}{\delta {\rho }^{\pm }}\right)-{\mu {\nabla }^2{v}_x^{\pm }|}_{z=0}\pm {b_f\left(v_x^{+}-v_x^{-}\right)|}_{z=0}\\ -T_{zz}^{\pm }{\mid }_{z=0}+T_{zz}^{-}{\mid }_{z=0}=P_z=-\frac{\delta F}{\delta h}=-\stackrel{\sim }{\kappa }{q}_0^{4}h+2{kq}_0^2\rho d.\end{array}$$ (13)

The first equation displays the balancing of forces in the x-direction, between the viscous stress of 3D liquid motion and the 2D forces on membrane: surface pressure gradient, viscous stress in the membrane and inter-leaflet friction, where μ is the membrane viscosity and b_f is the inter-leaflet friction coefficient. The second equation describes the balancing of forces in the z-direction. Here, κ̃ = κ + 2d²k describes the renormalization of bending rigidity by the effect of elastic stretching and compression, ρ is defined as ρ ≡ (ρ⁺ − ρ⁻)/2, representing the density difference between two monolayers.

The equation of motion is determined by the continuity of velocity ∂h/∂t = v_z|_{z = 0}, and lipid density $\partial {\rho }^{\pm }/\partial t=-\partial v_x^{\pm }/\partial x{\mid }_{z=0}$. Solving Eq. (5) with the new boundary conditions and applying the Stokes approximation to get the expressions for v_x and v_z, yields the following equation of motion for the membrane:

$$\frac{\partial }{\partial t}\left(\begin{array}{c}h\\ \rho \end{array}\right)=-M\left(\begin{array}{c}h\\ \rho \end{array}\right)=-\left(-\frac{\begin{array}{r}\stackrel{\sim }{\kappa }{q}_0^3/4\eta \\ {\mathit{kdq}}_0^4\end{array}}{2b_f+2\eta q_0+2\mu q_0^2}\frac{\begin{array}{c}-q_{0}kd/2\eta \\ {kq}_0^2\end{array}}{2b_f+2\eta q_0+2\mu q_0^2}\right)·\left(\begin{array}{c}h\\ \rho \end{array}\right).$$ (14)

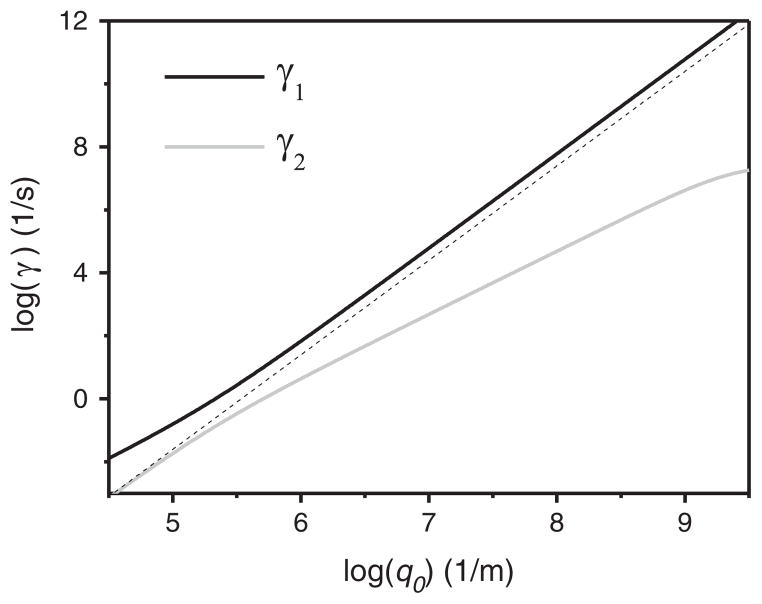
The two eigenvalues of the dynamical matrix M, γ₁ and γ_2, represent two dissipation modes of the membrane fluctuation (γ = −iw); these are shown in Fig. 3 for a typical set of membrane parameters. In order for the membrane to be stable, γ_1,2 should be larger than zero so that exp(−γt) will decay with time. This leads to κ̃ ≥2d²k, which is always true considering κ̃ = κ + 2d²k and κ is positive. Thus, lateral redistribution of lipids only provides an alternative way to damp membrane fluctuations; the linear stability of the bilayer with respect to perturbation is not altered. Since the system has three degrees of freedom (h, ρ, ρ̄), where ρ̄ ≡ (ρ⁺ + ρ⁻)/2 is the average lipid density, there is a third dynamic mode corresponding to ρ̄. However, it is easy to see that fluctuation of ρ̄ is decoupled from the other two degrees of freedom and therefore won’t influence the shape of the membrane [21,58].

Fig. 3.

Dispersion relation for a single bilayer membrane with interleaflet damping. The black and gray solid lines are the fast and slow viscous modes respectively. The dotted line represents the conventional bending mode: $\gamma =\kappa q_0^3/4\eta$ (adapted from Fig. 2 of [21], κ = 10⁻¹⁹ J, k = 0.07 J/m², d = 10⁻⁹ m, η = 10⁻³ J s/m³, μ = 10⁻⁹ J s/m², b_f = 3 × 10⁹ J s/m⁴ are used for the plot).

At small q₀, expanding about q₀ = 0 the expressions for γ that result from Eq. (14) gives ${\gamma }_1=\frac{{{kq}_0}^2}{2b_f}$ and ${\gamma }_2=\frac{\kappa {q_0}^3}{4\eta }·{\gamma }_2$. γ₂ corresponds to the damping of the conventional bending mode via the surrounding liquid. It differs from Eq. (10) by a factor of two, which is due to the fact that we only considered the liquid on one side of the membrane in deriving Eq. (10). γ₁ is a new ‘slipping mode’ which describes the damping of inhomogeneous lipid density by inter-leaflet friction. At large q₀, ${\gamma }_1=\frac{\stackrel{\sim }{\kappa }{q_0}^3}{4\eta }$ and ${\gamma }_2=\frac{k\kappa }{\mu \kappa }$; here, γ₁ becomes the rate for dissipation in the surrounding liquid, with an effective bending rigidity κ̃. The increase of the effective bending rigidity is due to the inability of lipid density to respond as fast as the decay rate of height fluctuations [21]. In this regime, the dissipative mechanism for γ₂ is related to the properties of the 2D membrane, which changes from inter-leaflet friction to the membrane viscosity.

A number of studies have contributed to the measurement of the inter-leaflet friction coefficient b_f [8,21,56,59–61]. The results vary largely for different systems, from 2.7 × 10⁷ up to 3 × 10⁹ J · s · m⁻⁴, making it hard to estimate the contribution of interleaflet friction. Here, we take the result from the most recently developed experimental technique [60], where b_f was measured as 3 × 10⁹ J · s · m⁻⁴ for an unsupported bilayer and found to be independent of lipid chain length. Taking typical values for the physical constants: κ ≈ 10⁻¹⁹ J, k ≈ 7 × 10⁻² J · m⁻², η ≈ 10⁻³ Pa · s, we find that γ₂ is comparable to γ₁ at around q₀ = 0.5 μm⁻¹. For smaller wavelengths (λ < 1 μm), the dominating pathway for dissipation begins to be controlled by membrane properties instead of the bulk liquid viscosity. For the membrane viscosity μ, recent measurements have obtained μ ≈ 10⁻⁹ J · s · m⁻² for a liquid disordered phase and μ ≈ 10⁻⁸ J · s · m⁻² for a liquid ordered phase [62], consistent with earlier measurements [59,63]. Thus, the contribution from membrane viscosity can usually be neglected compared to interleaflet friction considering $\mu q_0^2<b_f$ for q₀ < 10⁹ m⁻¹.

The additional dissipation mode discussed above has been confirmed both by molecular dynamics simulations of a coarse-grained (CG) bilayer model [55], and by flicker spectroscopy studies of the fluctuation spectrum of giant vesicles [61]. The simulation observed a double-exponential decay of the fluctuation, with decay rates nicely agreeing with the predicted values for γ₁ and γ₂ [55]. The experimental fluctuation spectra were found to systematically deviate from the pure-bending behavior at large wavenumber and the relaxation rates of the fluctuation clearly obeyed $~q_0^2$ [61]. These findings directly support the existence of the slipping mode and the crossover of the dominating dissipation mode from bending to slipping as q₀ increases.

It should be noted that, in the above discussions, a number of simplifying assumptions were made. For example, the overall (average) geometry of the membrane was not considered beyond a planar geometry, the magnitude of fluctuations was assumed to be small, and membrane shear dissipation was neglected. These simplifications, while valid in most cases, do not capture certain phenomena that occur in special situations. For example, membrane shear viscosity becomes essential in highly curved membrane tethers [58]. It is also likely that the presence of peripheral proteins on the bilayer can greatly enhance the shear viscosity of the membrane. A model regarding the complex dynamic behaviors of biological membrane without making most of these simplifications is discussed numerically in a recent paper [58], illustrating new and nontrivial dynamics of lipid membranes.

2.2.2. Chemically triggered membrane undulations experimentally confirm the presence of the ‘slipping mode’

Besides the above-mentioned flicker spectroscopy study [61], the slipping mode of bilayer was revealed in experiments that involved local delivery of a basic pH solution to giant vesicles. In these experiments, upon the arrival of chemicals at the vesicle surface, Fournier et al. observed a large-amplitude undulation of the membrane followed by ejection of membrane tubules [5,8,64,65]. In interpreting these observations, the basic solution was assumed to increase the repulsion between lipid head groups, thus locally decreasing the lipid density of the outer monolayer. By measuring membrane undulations under chemical modification, one can test the coupling between lipid density and bilayer shape which is controlled by inter-leaflet friction as discussed in the preceding section.

Consider that, at time zero, the basic chemical reduces the equilibrium lipid density of the outer leaflet by ε. The free energy of the bilayer as in Eq. (12) then becomes

$$F=\int \left\{\frac{1}{2}\kappa {\left({\nabla }^{2}h\right)}^2+\frac{1}{2}k\left[{\left({\rho }^{+}+d{\nabla }^{2}h+\epsilon \right)}^2+{\left({\rho }^{-}-d{\nabla }^{2}h\right)}^2\right]\right\}\mathit{dxdy}.$$ (15)

Carrying out a derivation equivalent to Eq. (14) and considering the fact that ηq₀ ≪ b_f and $\mu q_0^2\ll b_f$ for the lipid bilayer, the relaxation dynamics for the chemically modified bilayer can be written as

$$\frac{\partial }{\partial t}\left(\begin{array}{c}h\\ \rho +\epsilon \end{array}\right)=-\left(\begin{array}{cc}\stackrel{\sim }{\kappa }{q_0}^3/4\eta & -q_{0}kd/2\eta \\ -{{\mathit{kdq}}_0}^4/2b_f& {{kq}_0}^2/2b_f\end{array}\right)·\left(\begin{array}{c}h\\ \rho +\epsilon \end{array}\right).$$ (16)

The eigenvalues of this modified dynamical matrix are

$${\gamma }_{1,2}=\frac{1}{2}\left[\frac{\stackrel{\sim }{\kappa }{q_0}^3}{4\eta }+\frac{{{kq}_0}^2}{2b_f}\pm \sqrt{{\left(\frac{\stackrel{\sim }{\kappa }{q_0}^3}{4\eta }-\frac{{{kq}_0}^2}{2b_f}\right)}^2+\frac{k^2{d}^2{q_0}^5}{\eta b_f}}\right].$$ (17)

We have h(t) = Pe^−γ₁t + Qe^−γ₂t, with P and Q determined by the initial conditions: h(t = 0) = 0 and ρ(t = 0) = −ε/2. This leads to:

$$h(0)=P+Q=0$$

$$h^{\prime }(0)=-{\gamma }_{1}P-{\gamma }_{2}Q=\frac{q_{0}kd\epsilon }{4\eta },$$

giving

$$P=-Q=\frac{q_{0}kd\epsilon }{4\eta ({\gamma }_2-{\gamma }_1)}.$$

Finally,

$$h(t)=\frac{q_{0}kd\epsilon }{4\eta ({\gamma }_2-{\gamma }_1)}\left(e^{-{\gamma }_{1}t}-e^{-{\gamma }_{2}t}\right).$$ (18)

From Eq. (18) we see that the membrane undulation converges to zero at infinite time, thus indicating stability of the bilayer. At t = ln(γ₁/γ₂)/(γ₁ − γ₂), h(t) achieves its maximum:

$$h_{max}=\frac{q_{0}kd\epsilon }{4\eta {\gamma }_1}{\left(\frac{{\gamma }_2}{{\gamma }_1}\right)}^{{\gamma }_2/({\gamma }_1-{\gamma }_2)}.$$ (19)

For a few percent variation of the effective headgroup area (ε ~ 0.01), h_max can easily achieve a macroscopic value (~1 μm). By measuring the shape undulation of the chemically modified vesicle, the inter-leaflet friction coefficient was fitted as 2 × 10⁹ J ·s ·m⁻⁴ [8], in good agreement with the most recently measured value mentioned above. More realistic and complicated models were also discussed by Bitbol and Fournier: spontaneous curvature of the membrane was accounted for and was allowed to be modified by chemicals [5,64]; both the membrane binding kinetics and the effect of inhomogeneous concentration of chemicals were examined [65].

3. Membrane tension

3.1. Entropic tension as result of geometrically constraining membrane fluctuations

As we discussed above, membranes undergo thermally excited shape fluctuations to increase their configurational entropy [2]. In reality, instead of being a free-floating bilayer, biological membranes are usually constrained by the shape of the cell and the dynamic coupling with the cytoskeleton [19,24,54,66,67]. The geometrical constraints imposed by the membrane shape, or any external restrictions, will reduce the configurational entropy and create a lateral tension in the membrane [50,68]. Taking these contributions into account, the free energy as in Eq. (2) should then be written as,

$$F=\int \frac{1}{2}\left\{\kappa {\left({\nabla }^{2}h\right)}^2+\sigma {\mid \nabla h\mid }^2+\mathit{\Omega }{h}^2\right\}\mathit{dxdy}$$ (20)

where σ is membrane tension and Ω = d²V/dz²|_{z = 0} again, represents the contribution from the harmonic interaction potential. Accordingly, the fluctuation spectrum as determined from the equipartition theorem is modified to yield [20,69],

$$\langle {\mid h(q)\mid }^2\rangle =\frac{k_{B}T}{A(\kappa q^4+\sigma q^2+\mathit{\Omega })}.$$ (21)

Macroscopic observation of projected surface area as a function of membrane tension allows determining the compressibility of membranes. The decrease of effective or projected membrane area relative to the real membrane surface area (ΔA) due to the undulations can be calculated from the fluctuation amplitude [50],

$$\mathrm{\Delta }A=-\frac{1}{2}\underset{A}{\int }{\mid \nabla h\mid }^{2}dA$$ (22)

or more conveniently, in Fourier space

$$\mathrm{\Delta }A(q)=-\frac{A}{2}{q}^2{\mid h(q)\mid }^2.$$ (22′)

Eqs. (21) and (22′) lead to,

$$\mathrm{\Delta }A=\sum _q\mathrm{\Delta }A(q)=\sum _q\frac{-k_B{Tq}^2}{2(\kappa q^4+\sigma q^2+\mathit{\Omega })}.$$ (23)

Replacing the sum by an integral,

$$\sum _q\to \frac{A}{{(2\mathrm{\pi })}^2}\int 2\mathrm{\pi }\mathit{qtq}$$ (24)

and considering the lower and upper limit for the integration as defined by π/A^0.5 (A ~ L²) and π/a₀, the total decrease of projected area can be calculated from Eqs. (23) and (24),

$$\begin{array}{l}\frac{\mathrm{\Delta }A}{A}=\frac{-k_{B}T}{8\mathrm{\pi }\kappa }\underset{\mathrm{\pi }/A^{0.5}}{\overset{\mathrm{\pi }/a_0}{\int }}\frac{q^{2}d{q}^2}{q^4+(\sigma /\kappa )q^2+\mathit{\Omega }/\kappa }\\ =\frac{k_{B}T}{8\mathrm{\pi }\kappa \sqrt{{(\sigma /\kappa )}^2-4(\mathit{\Omega }/\kappa )}}\left[x_{1}ln\frac{{\mathrm{\pi }}^2/A-x_1}{{\mathrm{\pi }}^2{a_0}^2-x_1}-x_{2}ln\frac{{\mathrm{\pi }}^2/A-x_2}{{\mathrm{\pi }}^2/{a_0}^2-x_2}\right]\end{array}$$ (25)

with, $x_{1,2}=\frac{-\sigma /\kappa \pm \sqrt{{(\sigma /\kappa )}^2-4(\mathit{\Omega }/\kappa )}}{2}$.

In the limit of σ ≫ κΩ, x₁ = 0 and x₂ = −σ/κ. Eq. (25) then simplifies to,

$$\frac{\mathrm{\Delta }A}{A}=\frac{k_{B}T}{8\mathrm{\pi }\kappa }ln\frac{{\mathrm{\pi }}^2/A+\sigma /\kappa }{{\mathrm{\pi }}^2/{a_0}^2+\sigma /\kappa }.$$ (25′)

Thus, a certain amount of area is hidden in the roughness of membrane undulations. At zero tension, the amount of hidden area is |ΔA/A| = k_BT/8πκ × ln (A/a₀²); increasing membrane tension will serve to flatten out undulations and increase projected area. If we define ΔA_exp as the change of membrane area relative to the initial membrane state with tension σ₀, then Eq. (25′) changes into the more commonly used format [70],

$$\frac{\mathrm{\Delta }{A}_{exp}}{A}=\frac{k_{B}T}{8\mathrm{\pi }\kappa }ln\frac{1/A\sigma /{\mathrm{\pi }}^2\kappa }{1/A{\sigma }_0/{\mathrm{\pi }}^2\kappa }.$$ (25″)

When a stretching force is applied to the bilayer (experimentally this is usually done by aspirating a vesicle with hydrostatic pressure [68,71] or by expanding the substrate of a supported lipid bilayer [67,72]), entropic tension adds to the normal elastic stretch response of a fluid membrane [50]. Thus, the total area change (ΔA_t) as one increases membrane tension (compared to the initial σ = σ₀ membrane) can be written as

$$\frac{\mathrm{\Delta }{A}_t}{A}=\frac{k_{B}T}{8\mathrm{\pi }\kappa }ln\frac{1+A\sigma /{\mathrm{\pi }}^2\kappa }{1+A{\sigma }_0/{\mathrm{\pi }}^2\kappa }+\frac{\sigma -{\sigma }_0}{K}$$ (26)

where K is the elastic modulus of membrane stretching.

Accordingly, two different regimes of membrane tension response to stretching of the projected area can be observed: In the low-tension regime, Eq. (26) is dominated by the entropic term and membrane area will increase logarithmically with tension. In the high-tension regime, the enthalpic or elastic stretching term becomes important, leading to a linear relation between area and tension. By fitting experimental data in the two regimes, bending and elastic stretching moduli can be extracted respectively, and the crossover tension for the two regimes is found to be around 0.5 mN/m [68]. This two-regime behavior is also verified by CG simulations [73], from which one can obtain a more detailed description of the structural rearrangements of bilayers under tension.

For simplicity, we used a plane-wave approximation in treating fluctuation modes. For vesicles, it is more appropriate to expand the membrane with respect to a spherical shape [74]. However, the resulting physical relations are very similar. Regarding Eq. (26), for example, in the quasi-spherical approach, we only need to change the pre-factor for membrane tension from π² to 24π [68]. For a discussion of the entropic tension of non-spherical shapes, and more precise evaluation of the tension induced by constraining membrane fluctuations, see Ref. [75].

In deriving Eq. (25), the conservation of total membrane area sets a constraint that relates entropic tension to the hidden membrane area. During membrane fusion, however, lipids will be added into the bilayer and total membrane area will increase. Studies have shown both theoretically [76], and by experiments [77], that during fusion of oppositely charged vesicles, membrane tension will become negative and local instabilities of the vesicle can occur. Conversely, increasing membrane tension was found by mesoscopic simulations to facilitate the fusion of vesicles into membrane bilayers [78]. Another example of tension regulation of the membrane area was demonstrated by reversibly straining a lipid bilayer that was coupled to an elastic PDMS sheet [67,72]. By stretching the elastic support, the bilayer expands laterally by fusing adhered lipid vesicles which compensates for the membrane tension induced by the lateral strain. Upon compression, spherical or tubular protrusions are found to nucleate and subsequently grow out of the membrane [72]. The formation of tubules under compression indicates the existence of a critical (negative) membrane tension, beyond which the planar bilayer is destabilized and expels lipid tubes to relax its area in the plane [67]. The membrane tubes, stabilized by a negative pressure imbalance between two sides of the bilayer, transform its shape dynamically when the liquid volume enclosed between the bilayer and PDMS sheet is changed. Interestingly, the tubules will thin out, collapse, and detach after a rapid decrease in liquid volume [72].

3.2. Biological significance of membrane tension

The role of membrane tension in regulating dynamic cellular behaviors is gaining attention in recent years, with studies ranging from cell shape and motility, exo- and endocytosis, to intracellular signaling and gene expression [53,79–88]. Cells are known to maintain their unique membrane tensions which usually arise from two sources: hydrostatic pressure across the lipid bilayer and cytoskeleton-membrane adhesion [53]. The latter contribution is postulated to play the primary role, considering the large surface area-to-volume ratio of most mammalian cells [52]. However, separating the relative magnitude of each source is difficult since they are not independent from each other [83]. In order for the cells to maintain a relatively stable membrane tension, sudden tension changes need to be buffered by depleting/restoring membrane reservoirs [81,83]. Membrane reservoirs can store 20%–40% of the plasma membrane area and usually exist in the form of membrane folds, caveolae and blebs [80,83].

The dynamic membrane shape transition required for cell migration is determined by the elastic free energy of the membrane, in which tension plays a major role. Membrane tension is also closely involved in the regulation of membrane trafficking processes since the addition or removal of lipids during vesicle fusion or fission directly alters the magnitude of stress in the membrane. Generally speaking, increasing membrane tension will slow down the rate of cell motility [88,89], activate exocytosis [82], and inhibit endocytosis [90]. Particularly, during the membrane invagination stage of clathrin-mediated endocytosis (CME), vesicles can easily form when membrane tension is low, however, extra force from actin polymerization is required if the cellular plasma membrane is under high tension [91].

4. Membrane shape instability

4.1. Spontaneous tubulation and membrane curvature instability

As discussed above, negative membrane tension accomplished by physically compressing or adding lipids into the membrane could cause a planar membrane to become unstable, leading to the formation of non-planar shapes, including membrane tubules [67,77]. Spontaneous tubule formation can also be triggered chemically by the binding of polymers [92,93] or even the addition of a simple basic pH solution to giant vesicles, as mentioned above [8]. More importantly, membrane tubules play important biological roles and can be induced by membrane curvature sensing and generating proteins [38]. Some peptides are also known to induce protrusions from supported lipid bilayers [94]. Real-time tubulation of giant vesicles has recently been observed for F-BAR domain proteins [95]. However, unlike the dynamics of membrane fluctuations, the rate and mechanism of membrane tube formation have not been well described.

There are numerous phenomena involving membrane shape instabilities. Apart from the above-mentioned spontaneous membrane tubulation, externally applied perturbations such as by means of optical tweezers or the anchoring of polymers/nanoparticles can induce a pearling instability [96–99]. Vesicles can also undergo shape transitions induced by temperature change or by the coupling between local membrane composition and curvature [19,100–103]. Among these phenomena, the ones induced by macromolecule- (in particular protein-) binding to membranes are especially interesting due to their biological significance.

Several models have been proposed to explain membrane shape instabilities [15,34,93,104,105]. The model directly applicable to curvature-inducing proteins considers the coupling between membrane curvature and protein density [34,99]. When a planar membrane becomes unstable, the effective bending rigidity of the membrane will become zero and shape fluctuations of the membrane will increase with time until reaching macroscopic levels [34]. Here, we will once again mainly focus on membranes with a near-planar geometry, so that membrane fluctuations can be easily represented by planar waves. For membrane shape transitions between nontrivial configurations, extensive discussions can be found in the following contributions [19,100,106,107].

Proteins with a normalized local density ϕ (equivalent to fractional protein coverage, ranging from 0 to 1) can diffuse in the membrane with a diffusion coefficient D. The interaction between proteins can be described by the Ginsburg–Landau free energy [34,48,108],

$$F_{\mathit{protein}}=\int \left\{\frac{1}{2}a{\varphi }^2+\frac{1}{2}b{\mid \nabla \varphi \mid }^2\right\}\mathit{dxdy}$$ (27)

where ‘a’ is the inverse osmotic compressibility which is dependent on protein density [109], ‘b’ is normally a constant and can be expressed (in a simple lattice model) as, ‘λ/β · k_BT’ where β is the excluded area of the protein and λ represents an effective ‘interaction area’ for molecular interactions a protein density gradient [110]. The first term describes the free energy density for a homogeneous system while the second term represents the energy cost of inhomogeneous protein distribution.

If the protein has an intrinsic curvature, as most curvature sensing and generating proteins do [38], the elastic energy of the bilayer with the contribution from membrane tension will be written as:

$$F_{\mathit{elastic}}=\int \left\{\frac{1}{2}\kappa {\left[\left({\nabla }^{2}h\right)-C_0\varphi \right]}^2+\frac{1}{2}\sigma {\mid \nabla h\mid }^2\right\}\mathit{dxdy}$$ (28)

where C₀ describes the spontaneous curvature of the membrane induced by protein binding.

For simplicity, the coupling between protein and membrane is assumed to be isotropic and the contributions from membrane inter-leaflet friction and the interaction potential V(z) are not considered in the following dynamic analysis. We will briefly discuss the modification of membrane instability criteria in the presence of a harmonic interaction potential at the end of this section. For inclusions anisotropically coupled to membrane curvature, the Gaussian curvature of the membrane will be affected in addition to the mean curvature [111,112].

It can be easily seen from Eq. (28) that the presence of spontaneous curvature leads to an effective coupling between protein density and local membrane shape, with the coupling strength described by κC₀.

$$F_{\mathit{couple}}=-\int \kappa C_0\varphi {\nabla }^{2}h\mathit{dxdy}.$$ (29)

Thus the total energy of the membrane and protein can be written as,

$$F=\int \left\{\frac{1}{2}\kappa {\left({\nabla }^{2}h\right)}^2+\frac{1}{2}\sigma {\mid \nabla h\mid }^2-\kappa C_0\varphi {\nabla }^{2}h+\frac{1}{2}{a}_{\mathit{eff}}{\varphi }^2+\frac{1}{2}b{\mid \nabla \varphi \mid }^2\right\}\mathit{dxdy}$$ (30)

here, $a_{\mathit{eff}}=a+\kappa C_0^2$ is the effective inverse osmotic compressibility after accounting for the spontaneous curvature of a membrane patch covered by a protein molecule. Both a_eff and b are assumed to be positive to exclude the situations of spontaneous demixing of proteins [34].

The dynamics of the bulk liquid is still determined by the Navier–Stokes equation (Eqs. (5) and (6)) and the corresponding force balance equations at the membrane–bulk liquid interface (Eq. (7)). The restoring force of the membrane includes the contributions from membrane tension and protein distribution:

$$\begin{array}{l}{T}_{xz}{\mid }_{z=0}={\eta \left(\frac{\partial v_x}{\partial z}+\frac{\partial v_z}{\partial x}\right)|}_{z=0}=0\\ T_{zz}{\mid }_{z=0}=P_z=-\frac{\delta F}{\delta h}\iff {\left(2\eta \frac{\partial v_z}{\partial z}-p\right)|}_{z=0}=-\kappa {q_0}^{4}h-\sigma {q_0}^{2}h-\kappa C_0{q_0}^{2}c.\end{array}$$ (7′)

Here, c(x,y) ≡ ϕ(x,y) − ϕ_avg is the deviation of local protein density from its average value ϕ_avg, and it is assumed to follow c = c₀e^iq₀x+iwt.

Motions of the membrane and of the proteins on the membrane are described by

$$\begin{array}{l}\frac{\partial h}{\partial t}=v_z{\mid }_{z=0}=(C_3+C_4)e^{{iq}_{0}x+\mathit{iwt}}\\ \frac{\partial c}{\partial t}=\nabla ·\overrightarrow{j}=\frac{D}{a_{\mathit{eff}}}{\nabla }^2\left(\frac{\delta F}{\delta c}\right)=-{{Dq}_0}^{2}c-\frac{b}{a_{\mathit{eff}}}{{Dq}_0}^{4}c-\frac{\kappa C_{0}D}{a_{\mathit{eff}}}{q_0}^{4}h.\end{array}$$ (31)

The first equation is identical to Eq. (8) with C₃ and C₄ representing the constants determined by the new set of boundary conditions in Eq. (7′). The second equation describes the diffusion of proteins on the membrane. Here, protein binding from the bulk liquid is ignored since protein/membrane binding is usually diffusion-controlled and the diffusion of protein in the bulk solution is typically much faster than on the lipid membrane. If protein molecules binding to and unbinding from the membrane are considered, the time dependence of the local protein density will be modified to [48],

$$\frac{\partial c}{\partial t}=-\left({{Dq}_0}^2+\frac{L\xi }{\tau (1+L\xi )}\right)\left[\left(1+\frac{b}{a_{\mathit{eff}}}{q_0}^2\right)c+\frac{\kappa C_0{q_0}^2}{a_{\mathit{eff}}}h\right]$$ (31′)

where $L=\sqrt{{q_0}^2+iw/D_b}$, D_b and ξ are the protein’s diffusion coefficient and characteristic diffusion length in the bulk, respectively, and t is the residence time of the protein on the membrane. The presence of bulk diffusion will affect the fluctuation spectrum. For example, an oscillatory damping mode emerges at large q₀, but the curvature instability criteria will not be changed as discussed in Ref. [48].

In Eq. (31), C₃ and C₄ can be determined from Eq. (7′) and the resulting equation of motion for the membrane is:

$$\frac{\partial }{\partial t}\left(\begin{array}{c}h\\ c\end{array}\right)=-\left(\begin{array}{cc}\kappa {q_0}^{4}m+\sigma {q_0}^{2}m& \kappa C_0{q_0}^{2}m\\ \frac{\kappa C_0{{Dq}_0}^4}{a_{\mathit{eff}}}& \left({{Dq}_0}^2+\frac{{{\mathit{bDq}}_0}^4}{a_{\mathit{eff}}}\right)\end{array}\right)·\left(\begin{array}{c}h\\ c\end{array}\right).$$ (32)

Here, m is independent of h and c

$$m=\frac{iw\rho q_0}{4{q_0}^3{\eta }^2(q_0-l)+4iw\rho {q_0}^2\eta -w^2{\rho }^2}.$$ (33)

Using h = h₀e^{iq₀x+iwt and c = c₀eiq₀x+iwt}, Eq. (32) gives the dispersion relation of the system:

$${(S_0-1)}^2-\sqrt{1-2S_0}+y_t+\frac{\chi }{S_0\zeta -b{q_0}^2/a_{\mathit{eff}}-1}=0$$ (34)

with unitless variables defined as

$$S_0=\frac{-iw\rho }{2\eta {q_0}^2},y_t=\frac{\left(\kappa q^2+\sigma \right)\rho }{4{\eta }^2{q}_0},\chi =\frac{\rho {\kappa }^2{C_0}^2{q}_0}{4{\eta }^2{a}_{\mathit{eff}}},\zeta =\frac{2\eta }{\rho D}.$$

When there is no coupling between protein density and membrane curvature (C₀ = 0), Eq. (34) reduces to Eq. (9′).

In the slow mode limit (S₀ ≪ 1), since 1/ζ ~ 10⁻⁸ ≪ 1, and if we can also assume $b{q}_0^2/a_{\mathit{eff}}\zeta \ll 1$ as in [34], the dispersion relation approximates to:

$${S_0}^2-S_0\left(y_t+\frac{b{q_0}^2}{a_{\mathit{eff}}\zeta }+\frac{1}{\zeta }\right)+y_t\left(\frac{b{q_0}^2}{a_{\mathit{eff}}\zeta }+\frac{1}{\zeta }\right)-\frac{\chi }{\zeta }=0.$$ (35)

The fluctuation modes as the roots of the dispersion relation are:

$${iw}_{\pm }=-\left[\frac{\kappa {q_0}^3+\sigma q_0}{4\eta }+\frac{{{Dq}_0}^2}{2}+\frac{{{\mathit{bDq}}_0}^4}{2a_{\mathit{eff}}}\pm \sqrt{{\left(\frac{\kappa {q_0}^3+\sigma q_0}{4\eta }-\frac{{{Dq}_0}^2}{2}-\frac{{{\mathit{bDq}}_0}^4}{2a_{\mathit{eff}}}\right)}^2+\frac{{\kappa }^2{C_0}^2{{Dq}_0}^5}{2a_{\mathit{eff}}\eta }}\right].$$ (36)

Here, iw is always real, indicating that the mode remains non-propagating [34]. Fig. 4 shows iw as a function of q₀ for both zero and non-zero tension situations.

Fig. 4.

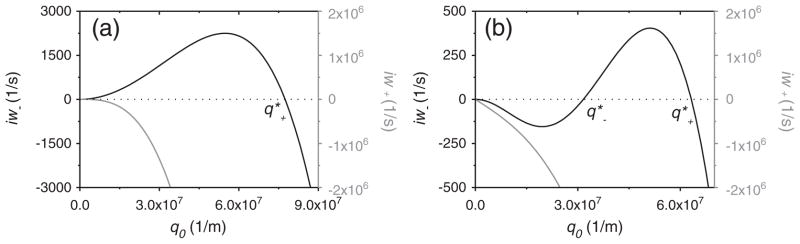
iw as a function of q₀, the planar membrane is stable when iw < 0. Membrane tension σ = 0 in Figure (a) and σ = 10⁻⁴ N/m in Figure (b). The black lines represent the ‘iw₋’ branch, the gray lines represent the ‘iw₊’ branch, the dotted lines are iw = 0. As shown, ‘iw₊’ is always negative while ‘iw₋’ is positive for 0 < q₀ < q^*₊ in (a) and for q^*₋ < q₀ < q^*₊ in (b). It can be seen that the presence of membrane tension lowers the range and amplitude of the unstable (iw>0) regime. (κ = 10⁻¹⁹ J, η = 10⁻³ J s/m³, D = 10⁻¹² m²/s, a_eff = 4 × 10⁻⁴ N/m, b = 10⁻¹⁹ J, C₀ = 10⁸ m⁻¹ were used for the plots).

While the iw₊ branch is negative for all values of q₀, iw₋ can become positive in certain situations for q^*₋ < q₀ < q^*₊ (in the case of zero tension, q^*₋ = 0), indicating the possibility of unstable modes. q^* can be easily determined by equating iw₋ to zero:

$$q{\ast }_{\pm }=\sqrt{\frac{-\left(\kappa a_{\mathit{eff}}+b\sigma -{\kappa }^2{C_0}^2\right)\pm \sqrt{{\left(\kappa a_{\mathit{eff}}+b\sigma -{\kappa }^2{C_0}^2\right)}^2-4a_{\mathit{eff}}b\sigma \kappa }}{2b\kappa }}.$$ (37)

Thus, the criterion for the existence of unstable fluctuation modes is equivalent to the existence of real values for q^* satisfying Eq. (37), which is:

$${\kappa }^2{C_0}^2-a_{\mathit{eff}}\kappa -b\sigma \ge \sqrt{4a_{\mathit{eff}}b\sigma \kappa }$$ (38)

or

$$\sqrt{a_{\mathit{eff}}\kappa }+\sqrt{b\sigma }\le \kappa \mid C_0\mid .$$ (38′)

If $b{q}_0^2/a_{\mathit{eff}}\zeta \ll 1$ does not hold, Eq. (35) becomes,

$$\left(1+\frac{3b{q_0}^2}{2a_{\mathit{eff}}\zeta }\right){S_0}^2-S_0\left(y+\frac{b{q_0}^2}{a_{\mathit{eff}}\zeta }+\frac{1}{\zeta }\right)+y\left(\frac{b{q_0}^2}{a_{\mathit{eff}}\zeta }+\frac{1}{\zeta }\right)-\frac{\chi }{\zeta }=0.$$ (35′)

However, the expression for q^* is not altered, because q^* was determined by equating the constant term (0th order term in S₀) in Eq. (35) to zero. Thus, the curvature instability criterion shown in Eq. (38) is the same irrespective of the magnitude of $b{q}_0^2/a_{\mathit{eff}}\zeta$.

The instability criterion does not contain any information about the dynamics of the system (that is, η or ρ for the hydrodynamics of the bulk liquid and D for the diffusion of proteins on membrane), meaning that we should be able to obtain Eq. (38) directly from the free energy of the membrane and protein. This will be shown in the following.

From Eq. (30), the free energy density can be written as,

$$\begin{array}{l}f~=\frac{1}{2}\kappa {\left({\nabla }^{2}h\right)}^2+\frac{1}{2}\sigma {\mid \nabla h\mid }^2-\kappa C_0\varphi {\nabla }^{2}h+\frac{1}{2}{a}_{\text{eff}}{\varphi }^2+\frac{1}{2}b{\mid \nabla \varphi \mid }^2\\ =\frac{1}{2}\kappa {q_0}^4{h}^2+\frac{1}{2}\sigma {q_0}^2{\mid h\mid }^2+\kappa C_0{q_0}^2\varphi \mathrm{h}+\frac{1}{2}{a}_{\text{eff}}{\varphi }^2+\frac{1}{2}b{q_0}^2{\mid \varphi -{\varphi }_{\text{avg}}\mid }^2.\end{array}$$ (39)

The breakdown of local thermodynamic stability is described by the spinodal equation [113],

$$\frac{{\partial }^2\stackrel{\sim }{f}}{\partial h^2}\frac{{\partial }^2\stackrel{\sim }{f}}{\partial {\varphi }^2}-{\left(\frac{{\partial }^2\stackrel{\sim }{f}}{\partial h\partial \varphi }\right)}^2=\left(\kappa {q_0}^4+\sigma {q_0}^2\right)\left(a_{\mathit{eff}}+b{q_0}^2\right)-{\kappa }^2{C_0}^2{q_0}^4=0$$ (40)

which is equivalent to Eq. (37) and the resulting instability criterion is the same as Eq. (38) [48].

In the presence of the interaction potential V(z), an additional term Ωh²/2 should be added to Eq. (39), modifying the spinodal equation to,

$$\left(\kappa {q_0}^4+\sigma {q_0}^2+\mathit{\Omega }\right)\left(a_{\mathit{eff}}+b{q_0}^2\right)-{\kappa }^2{C_0}^2{q_0}^4=0.$$ (40′)

Therefore, the instability criterion becomes equivalent to the existence of a real and positive q₀, which satisfies Eq. (40′). Analyzing this third order (in $q_0^2$) equation gives the instability criterion in the presence of the harmonic interaction potential,

$${\kappa }^2{C_0}^2-a_{\mathit{eff}}\kappa -b\sigma >\sqrt{3b\kappa \left(a_{\mathit{eff}}\sigma +b\mathit{\Omega }\right)}$$ (38″.1)

and

$$\begin{array}{l}\left[2\sqrt{{\left({\kappa }^2{C_0}^2-a_{\mathit{eff}}\kappa -b\sigma \right)}^2-3\left(a_{\mathit{eff}}\kappa b\sigma +b^2\kappa \mathit{\Omega }\right)}-\left({\kappa }^2{C_0}^2-a_{\mathit{eff}}\kappa -b\sigma \right)\right]·\\ {\left[\sqrt{{\left({\kappa }^2{C_0}^2-a_{\mathit{eff}}\kappa -b\sigma \right)}^2-3\left(a_{\mathit{eff}}\kappa b\sigma +b^2\kappa \mathit{\Omega }\right)}+\left({\kappa }^2{C_0}^2-a_{\mathit{eff}}\kappa -b\sigma \right)\right]}^2\ge 27a{b}^2{\kappa }^2\mathit{\Omega }.\end{array}$$ (38″.2)

If Ω = 0, these two equations reduce to Eq. (38). It can be seen from the instability criteria that (positive) σ and Ω serve to stabilize the membrane.

From equilibrium analysis, the height fluctuation can also be easily determined from the equipartition theorem,

$$<{\mid h(q)\mid }^2>=\frac{k_{B}T\left(a_{\mathit{eff}}+b{q}^2\right)}{A\left[\left(\kappa q^4+\sigma q^2+\mathit{\Omega }\right)\left(a_{\mathit{eff}}+b{q}^2\right)-{\kappa }^2{C_0}^2{q}^4\right]}.$$ (41)

Thus, the stability of a planar membrane is only determined by the system’s free energy. However, dynamic analysis is required to understand the detailed behaviors of the membrane while crossing into the unstable regime. For example, the fluctuation modes in Eq. (36) which correspond to the rate of macroscopic membrane shape change can only be given by solving the dynamic equations. The dynamic analyses of membrane shape instability in the presence of cytoskeleton–membrane interactions are discussed in Refs [87,114].

4.2. Membrane shapes after planar geometry becomes unstable

A remaining question is what kinds of shapes the membrane will transform into after the planar geometry becomes unstable, for example due to proteins binding to and coupling with curvature of the membrane. Experiments indicate the formation of membrane tubules [8,92,95,115] or microvesicles [116,117] when a flat membrane experiences a curvature instability. Phenomena such as the formation of membrane protrusions during RBC crenation [34,48] and the curling of ruptured RBC membranes [118] could also be the results of curvature instabilities. Once the instability threshold is reached, nonlinear effects become important (such as, membrane shape can no longer be accurately described by the small slope approximation as in Eq. (2)) and accurate shape transitions of the membrane can only be evaluated numerically. A simplified simulation of a one-dimensional membrane indicated the development of membrane fingers and buds (depending on the strength of the curvature coupling) with a tendency toward vesicle emission [48].

Another way to understand the phase diagrams of new membrane shapes is through a mean-field treatment of the Ginsburg–Landau free energy. In this approach, mean field energies of different undulated phases (represented by trial functions with undulation wavelengths determined by the coupling strength) are compared with the planar homogeneous phase to figure out the lowest energy configuration [119]. In-plane meso-structures such as stripe phase and hexagonal phase will form when the coupling strength is strong. In the case of anisotropic coupling, membrane phases of both positive and negative curvature can be induced [120]. Similar methods can also be applied to study buckling phenomena of lipid monolayers [121,122] or polymer thin films which, unlike fluid lipid layers, have a non-zero in-plane shear elasticity [123].

5. Peripheral proteins on membranes

5.1. Membrane-mediated protein interactions

Apart from the lipid bilayer structure, proteins are major components of biological membranes. Thus, it is important to understand variations of membrane shapes and fluctuation spectra in the presence of protein inclusions. Membrane inclusions can perturb the bilayer structure and impose restrictions on thermal fluctuations; both effects will lead to membrane-mediated modifications of the interaction between inclusions [120,124–127]. The disturbance-induced attraction is short-ranged, fading away exponentially with a characteristic length l₀ ≡ (κ/σ)^1/2 [124,126]. The fluctuation-mediated interaction falls off as 1/R⁴ for a distance R ≪ l₀ [126,127]. For R ≫ l₀, the distance dependence becomes 1/R⁸ [126]. The latter force, which exists as long as there is a difference between membrane and inclusion rigidity, will dominate at a length scale large comparable to the dimension of the inclusion. More comprehensive descriptions of the fluctuation-induced force between inclusions of arbitrary shapes embedded in membranes under tension can be found in Refs. [126,128].

Energetically speaking, the perturbation of the fluctuation spectrum will contribute to the free energy associated with protein or peptide insertion into the membrane. Thus, the larger fluctuations of low-tension membranes will make it harder for inclusions to incorporate into the lipid bilayer compared with the corresponding high-tension situation [120]. The diffusion of these fluctuation-suppressing particles on membranes is also expected to be slowed when membrane tension is increased [129].

The influence of proteins on fluctuation spectra and thus membrane tension has been relatively well studied for active membranes [130,131]. The presence of active protein pumps adds a non-equilibrium noise source to the dynamic equations. This will lead to an amplification of membrane fluctuations, equivalent to an increase of effective temperature or decrease in effective bending rigidity in Eq. (26) [130]. Additionally, membranes will become thinner under tension, which affects the hydrophobic mismatch interaction between membrane inclusions [73]. Thus, by properly controlling membrane tension, one may control the amount, and the distribution, of proteins on the membrane.

Coarse-grained simulations revealed that proteins adsorbed on lipid bilayers can experience attractive interactions purely as a result of induced-membrane curvature [6], similar to what was observed for the much larger membrane-bound colloidal particles [132]. For proteins with an intrinsic curvature or anisotropic shape, this curvature-mediated attraction can lead to spontaneous aggregation and formation of highly ordered protein structure on the membrane [6,133–135]. Additionally, the interactions between membrane inclusions depend on factors such as charge and hydrophobicity of the inclusions, and their hydrophobic mismatch or orientation relative to the membrane [6,124,136,137].

5.2. Protein assemblies on membranes and protein-induced membrane shape transitions

As discussed above, there are many different types of forces leading to protein aggregation on membranes. Formation of aggregates may significantly change the physical properties and membrane interaction behaviors of protein [136]. Thus, the aim to understand membrane binding and subsequent two-dimensional assembly of peripheral proteins has become an active area of research. Biologically, this is important for understanding protein-mediated cellular membrane phenomena such as exo- and endocytosis, protein sorting, and biogenesis of organelles such as the endoplasmic reticulum and the Golgi apparatus [6,137]. Clathrin-mediated endocytosis as one of such processes has become better understood in recent years [7,138]. During CME, the engulfing of cargo through membrane invagination and subsequent vesicle formation requires coordinated action of more than 30 proteins, ranging from clathrin, adaptor proteins, and epsin, to BAR domain proteins and dynamin [39,139–142]. Thus, topics such as membrane binding kinetics, assembly and cooperativity between these proteins on membranes are of essential biological importance.

The structure of many membrane binding interfaces of most endocytic proteins have been well characterized by crystallography studies [7]. For proteins with a high intrinsic curvature such as BAR domain proteins, ordered protein lattices were directly observed on highly curved membrane tubules through cryo-electron microscopy [143,144]. However, little attention has been paid to these proteins’ dynamic behaviors on membranes with low curvature, which is critical for revealing the curvature initiation process during endocytosis. Thus, there exists a clear gap between our understandings of these proteins’ intrinsic molecular properties and their final configurations on highly curved endocytic structures. Studies of protein–membrane interaction dynamics will serve to link this gap.

Kinetic membrane binding studies of endocytic proteins have been initiated a few years ago [145,146]. More recently, endophilin, which is an N-BAR domain protein, was found to be able to oligomerize on relatively flat membranes both experimentally [147] and through CG simulations[148,149]. The presence of an oligomerization step in the protein–membrane interaction mechanism highlights the role of protein density in this dynamic process. For example, in the study of membrane interaction kinetics of endophilin, the protein density dependence of the observed dissociation rate turns out to be the key evidence to confirm the presence of protein oligomers on flat membranes [147]. In experiments probing membrane curvature sorting of amphiphysin, another N-BAR domain protein, protein density was argued to determine the mechanism by which amphiphysin can sense membrane curvature [150]. CG simulations have also shown a critical particle number required for driving the formation of small vesicle buds [151], further supporting the idea that protein density is a regulator of two-dimensional protein assembly on the membrane.

From simulation studies, it was concluded that the aggregation of particles precedes membrane vesiculation and tubulation [6,134,152], and a sufficiently high density of particles is needed to influence membrane topography [151,153]. Experimentally, protein concentrations leading to near saturation of proteins on the membrane surface were used when studying the formation of protein lattices on membrane tubules [143,144]. Taking these together, it is tempting to speculate that, at least for BAR domain proteins, the oligomerization of proteins on the membrane acts as a precursor for the generation of highly curved membrane structures and the overall dynamic process is controlled by protein density on the membrane. This has been suggested to explain experimental observations using simpler peptides, where membrane-bound peptides were found to undergo an in-plane segregation before inducing membrane tubules at higher peptide density [94].

6. Conclusion and perspectives

The purpose of this review is to reemphasize the dynamic nature of cellular membranes. There are numerous fascinating phenomena associated with the thermal fluctuations of the lipid bilayer. Some of them, e.g. dissipation modes of small fluctuations, fluctuation-induced membrane tension, and membrane-mediated force between membrane inclusions, were reviewed in the foregoing discussions. On the way to understanding the dynamic behavior of cellular membranes, currently the most intriguing challenge is to understand the influence of membrane proteins on the dynamics of lipid bilayers. As a first step toward resolving the open questions, we reviewed the linear theory regarding the modification of membrane fluctuation spectra in the presence of diffusive proteins. There, instability of planar membranes arises as a result of the coupling between protein density and membrane shape. The recent progress in understanding the assembly of curvature inducing proteins on membranes was also discussed. Protein density on the membrane is proposed as a key factor in regulating the behavior of proteins on the membrane as well as the effect of proteins on membrane geometry.

We suggest the following topics for further attention in future research:

1. Fully characterizing the dynamics of protein-induced membrane shape instabilities will be a key to our understanding of the behaviors of biological membranes. Experimentally, we need to identify and characterize the factors that control the instability process.

2. It is also important to understand the physical properties of protein-decorated membranes in more detail, such as the fluctuation spectra and bending rigidities of protein-covered membranes. The possibility of tubular/planar membrane shape coexistence will make this task nontrivial. Simulation studies can provide additional guidance for designing experiments in this part. Towards accomplishing this goal, the flexibility of a protein-coated membrane tube was recently calculated [134].

3. Considering the various types of proteins involved in biological processes, another important issue is to understand the cooperativity between different types of proteins as well as proteins of the same species. Cooperativity of membrane binding between BAR domain proteins and dynamin has been examined recently [154]. However, a theoretical description of the cooperative kinetics is still missing. For example, studies regarding the cooperativity between the same kind of proteins during membrane binding are still mostly at a theoretical level [155]. Interestingly, it has been suggested by theoretical studies that different protein species may segregate on the membrane according to their intrinsic curvature [134,135], similar to what has been observed in in vivo experiments [156].

4. It is well known that the charge [147,157] and packing defects [158,159] of lipid bilayers can greatly influence protein/membrane binding kinetics and affinity. It is likely that these factors can also regulate the protein behaviors on the membrane such as their lateral diffusion and aggregation ability as well as their coupling strength with membrane curvature.

5. For simulation studies of membrane shape transitions and protein–membrane interactions, we suggest that membrane tension should be considered with a high priority. This is because, as discussed above, membrane tension may significantly influence the binding and assembly of proteins on the membrane. Additionally, membrane tension factors into the instability criterion of the planar membrane geometry and determines the dynamics of membrane shape transitions.