Costs and benefits of mutational robustness in RNA viruses

Summary

The accumulation of mutations in RNA viruses is thought to facilitate rapid adaptation to changes in the environment. However, most mutations have deleterious effects on fitness, especially so for viruses. Thus, tolerance to mutations should determine the nature and extent of genetic diversity that can be maintained in the population. Here, we combine population genetics theory, computer simulation and experimental evolution to examine the advantages and disadvantages of tolerance to mutations, also known as mutational robustness. We find that mutational robustness increases neutral diversity and, and as expected, can facilitate adaptation to a new environment. Surprisingly, under certain conditions robustness may also be an impediment for viral adaptation, if a highly diverse population contains a large proportion of previously neutral mutations that are deleterious in the new environment. These findings may inform therapeutic strategies that cause extinction of otherwise robust viral populations.

Introduction

Mutational robustness provides a population with the ability to maintain a given phenotype despite mutational perturbation (de Visser et al., 2003; Wagner, 2005). Previous theoretical studies have suggested that mutational robustness can enhance adaptation (Draghi et al., 2010; Masel and Trotter, 2010; Wagner, 2008). These studies proposed that in asexual organisms, robustness might allow higher connectivity of the neutral network of genotypes in a population, allowing better exploration of the sequence space and future access to potentially beneficial genotypes. In sexual organisms, it is expected that robustness will directly increase the amount of hidden (“cryptic”) genetic variation within a population(Gibson and Dworkin, 2004). Thus, robust populations should harbor substantial neutral genetic variation that may provide as “stepping stones” to future adaptation(Masel, 2006; Waddington, 1957).

The concept of mutational robustness has gained much interest in the context of RNA viruses (Elena, 2012; Lauring et al., 2013; O'Dea et al., 2010; Sanjuan et al., 2007), which display exceptionally high mutation rates, roughly on the order of 10^-4 to 10^-6 errors per base per replication round (Sanjuan et al., 2010). Given the compact genome size of viruses, this level of replication fidelity results in 0.01-1 errors per genome per replication. Furthermore, since viruses typically generate enormous population sizes in the infected host (e.g., Haase et al., 1996), it has been estimated that all possible single mutations are created each day in a host (Coffin, 1995). Several recent studies have shown that a large proportion of these mutants will be either lethal or deleterious (reviewed in Sanjuan, 2010), suggesting that viruses suffer from an exceptionally high mutation load. Indeed, it has been shown that viral populations can be pushed to near extinction both through mutational meltdown (e.g., Crotty et al., 2001)and as deleterious mutations accumulate irreversibly in the genome(Chao, 1990; Duarte et al., 1992; Jaramillo et al., 2013)following the “Muller's ratchet” effect(Smith, 1978).

Given this extreme selection regime, it is puzzling how viruses preserve functionality. Accordingly, it has been proposed that RNA viruses maintain different mechanisms of robustness that allow them to buffer the negative effects of mutations (Lauring et al., 2013). Large population size is an efficient strategy employed by viruses to purge and tolerate high mutation load(Elena, 2012). Cellular mechanisms like mutation “buffering” by molecular chaperones may play an important role in mitigating the negative effects of mutant viral proteins (Geller et al., 2011; Geller et al., 2007). Another, highly prevalent, mechanism of robustness in viruses involves co-infection, when two or more viruses co-infect the same cell, and low fitness genotypes may be rescued by complementation with high-fitness genotypes (Froissart et al., 2004; Montville et al., 2005).

Viral populations constantly experience new environmental challenges: they may experience different temperatures, infect different tissues, different hosts of the same species and different host of different species. However, the central question whether mutational robustness is beneficial for evolvability in new environments (Draghi et al., 2010; Wagner, 2008) has remained experimentally unanswered and challenged. Some studies have shown that robust viruses were better prepared to evolve than their brittle counterparts in response to heat adaptation (McBride et al., 2008). Further, cryptic neutral networks have also been implied in the adaptability of Influenza virus (van Nimwegen, 2006). In contrast, a recent report showed that a more brittle viral strain adapted better to a host switch as compared to a robust strain (Cuevas et al., 2009).

Here, we examined the importance of mutational robustness (hereby termed robustness) as virusesestablish an infection in a novel environment. We began by developing a theoretical framework that defines robustness through the distribution of mutational fitness effects (DMFE) of a viral population. While the model we use is general, in this study we focused on robustness as manifested during viral co-infection. We first experimentally demonstrated that co-infection indeed buffers detrimental mutations, and then used this data to guide our theoretical modeling.

Most evolutionary studies have focused on mutations that are beneficial in a novel environment(Draghi et al., 2010; Gagneux et al., 2006; Hermisson and Pennings, 2005; Otto and Whitlock, 1997; Pennings and Hermisson, 2006). However, there has been little attention on the impact of novel deleterious changes. One exception is the study by Masel (2006), which examined how fixation of beneficial mutations (arising from cryptic genetic variation) is affected by a background of deleterious variants. Cryptic genetic variation was found to most likely allow more rapid adaptation.

Here, we set about to explore the effects of cryptic genetic variation in the unique settings affecting viruses: (a) rapid rate of mutation, (b) relatively frequent and often drastic environmental changes, and (c) large population size coupled with frequent bottlenecks. Importantly, in contrast to the assumptions in the Masel (2006) study, we consider environmental changes where alleles may completely change their fitness effects. This type of scenario has been described for drug-resistance and immune-evasion mutations(Agranovich et al., 2011; Andersson, 2006), and modeling these changes are important for understanding viral adaptation. Our model considers that following an environmental change, alleles might become either beneficial or deleterious in the new environment. We note that due to the high rate of viral mutation, these changes will encompass both variants previously segregating in the population, as well as emerging mutations that occur after the environmental shift. We evaluated two types of environmental change in viruses: transmission to a susceptible host, and encountering a host response (e.g., drug) during infection. By computationally varying the MOI of different populations, we were able to modulate levels of robustness of a population in realistic scenarios of viral infection and environmental change. We then were able to estimate the conditions under which viral populations have a higher probability of establishing a successful infection. Our results suggest that populations evolving at low MOI, and hence lower robustness, may be more likely to successfully adapt to new environments.

Results

Defining mutational robustness

During their life cycle, RNA viruses encounter a number of different environments and challenges. It is generally accepted that the genetic diversity of RNA virus populations affords them greater capacity for adaptation to novel environments. To test this hypothesis and gain further insight in the role of robustness in virus adaptation, we began by formulating a precise evolutionary definition of mutational robustness (r). We considered the distribution of mutational fitness (w) effects at each site of a genome (Fig. 1A-B). We propose that mean fitness across all non-beneficial mutants in the genome, r = w̄, defines the mutational robustness of a population. Robustness can then be estimated as r ≈ q + p_del · w̄_del where q is the fraction of neutral mutations, p_del is the fraction of deleterious mutations, and w̄_del is the mean fitness effect of a deleterious mutation. Essentially, r measures the mean fitness of new mutations. Hence, higher values of r correspond to more robust populations. We note that robustness is here defined as a property of the environment in which the population is replicating.

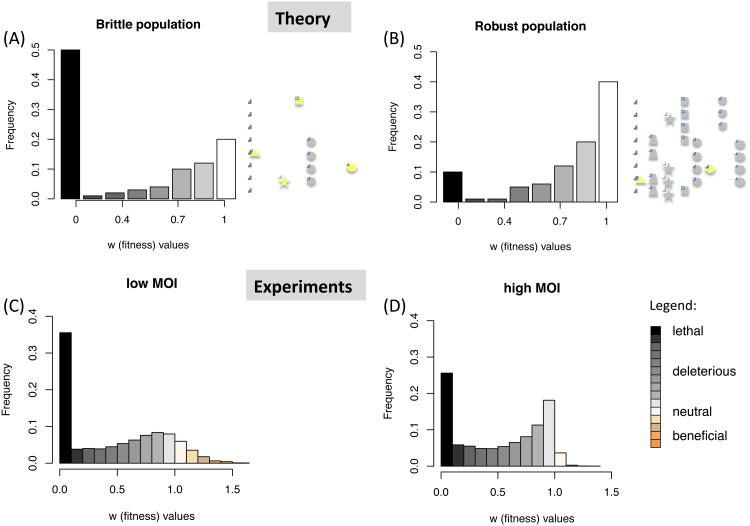
Figure 1. Mutational fitness effect distributions in brittle and robust populations.

Theoretical mutational fitness effectdistributionsin (A) brittle populations, and (B) robust populations, evolving at equilibrium. Brittle populations are defined by their lower mean fitness effect, and hence have a lower proportion of neutral mutations (grey shapes), and a higher proportion of deleterious mutations (yellow shapes). Robust populations have a relatively higher proportion of neutral mutations. Neutral mutations tend to segregate at a higher frequency than deleterious mutations, and thus robust populations hold a larger reservoir of hidden diversity. Mutational fitness effect distributions determined experimentally in RNA virus populations grown at low (C) and high (D) MOI at non-equilibrium conditions. Note that the distribution of mutational effects shifts towards neutrality at high MOI.

Mutational robustness is mediated by viral multiplicity of infection

To provide an experimental context in which robustness can be modulated, we focused on the condition under which viral populations are produced with respect to the virus-to-cell ratio. During higher multiplicities of infection, a given cell supports replication of two ore more different genomes. In this scenario, genetic complementation can increase the robustness of the viral population. While a mutated viral protein can limit or even halt viral replication at a low multiplicity of infection, this defect will be masked by “wild type” versions of the same gene product in cells infected with more than one genome.

To determine whether indeed higher levels of co-infection correspond to higher robustness, we passed oral polio vaccine (OPV)type 2 strain under low multiplicity of infection (MOI=0.1) or high multiplicity (MOI>10)(Methods). We then used a novel and highly accurate sequencing method to determine the genetic landscape of the population(Acevedo et al., 2014). This new approach enables us to detect rare mutational events with unprecedented accuracy at the single-nucleotide level. Our approach allowed estimation of the DMFE of the virus populations growing at low MOI and high MOI. OPV2 grown at high MOI showed a DMFE consistent with higher mutational robustness (r=0.49) as compared to low MOI (r=0.37) (p<1e-15, t-test; p<1e-15, Kolmogorov-Smirnov test). Indeed, we observed that populations that replicated at high MOI bear a larger proportion of neutral alleles and a lower proportion of lethal alleles than those populations replicating at low MOI (Fig. 1C-D). These results are consistent with previous observations suggesting that co-infection buffers the effects of deleterious alleles via complementation (Froissart et al., 2004). Thus, buffering allows alleles to be present at higher frequencies in the population, and to present as less deleterious (more neutral) than under low co-infection conditions. Notably, we evolved the OPV2 strain in an environment where it is not at equilibrium. This strain was originally produced in non-human cells, while our experiment was carried out in HeLa cells (Methods). Under these conditions we detected beneficial alleles, which we have not included in our approximate estimation of robustness (r). The role of robustness on beneficial mutations and adaptation is discussed in supplementary section 5.

Modeling a transmission to a susceptible host

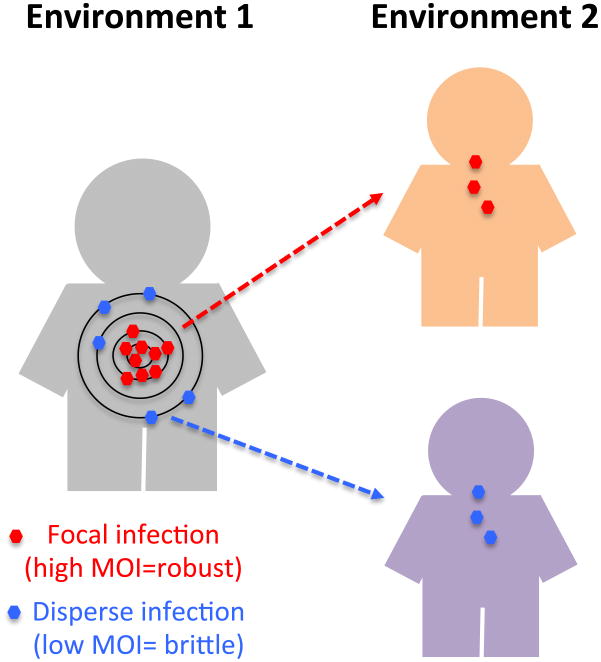
We next carried out numerical simulations to determine how robust and brittle virus populations adapt following transmission between hosts. Our model compares two different situations: one in which the transmitting virus population derives from the focal point of infection, where MOI is presumable high, and a second scenario in which virus derives from a more disperse infection, where MOI is assumed to be lower (Fig. 3). Upon transmission to a novel host, viral populations experience a population bottleneck (e.g., Betancourt et al., 2008), i.e. reduction in population size, and thus the initial replication cycles will likely occur at low MOI(Abrahams et al., 2009). Our aim was to compare the effect on population fitness upon infection of a new host of viruses produced at low MOI infection (brittle) to those produced high MOI infection (robust)

Figure 3. A model of viral evolution following among-host transmission.

In the first environment, a viral population evolves to high viral titers typical of viremia. In some organs, including presumably the focal point of infection, viral density and MOI is higher (red particles; inner circles) than in more distal organs (blue particles; outer circles). During transmission (right), a bottleneck in the viral population occurs, and the viral founder population (derived either from low or high co-infection sites) will initially evolve at low MOI.

To model transmission between hosts, we computationally imposed an environmental change on populations of viruses evolving at equilibrium (Methods). Such a change was introduced through reassigning selection coefficients to a random number of sites in the genome: some sites were reassigned with a negative (deleterious) selection coefficient whereas some sites were assigned with a positive (adaptive) selection coefficient (Fig. 2A). In order to consider a realistic case of transmission, we further modeled a strong reduction in population size during the environmental change, followed by logistic growth (see also Supplementary text Section 1 and Fig. S1). Notably, since we reassign selection coefficients randomly, robustness in our study is related directly to revelation of cryptic genetic variation(see also Richardson et al. (2013) on the complex relationship between robustness and revelation of cryptic genetic variation).

Fig. 2.

(A) Illustration of the simulation process: following an environmental change (viral transmission) one allele becomes beneficial or deleterious. (B) Given an initial frequency, this allows tracking the frequency of the changed allele across time till it reaches a certain threshold, and calculating the waiting time in generations accordingly. Mean waiting times in generations are shown for (C) adaptation of a novel beneficial allele, and (D) purging of a deleterious allele, following an environmental change. The red circles show a constant N = 10⁶, green diamonds show a constant N = 100. Triangles show a population with a bottleneck of N = 100 at the environmental change, followed by logistic growth with parameter r that defines the rate of growth (Methods). Robustness is shown to both reduce the time for adaptation and increase the time to purging of deleterious mutations.

We used simulation and theory to estimate mean waiting times as a function of robustness till (a) a novel beneficial allele takes over a population (adaptation), and (b) a novel deleterious allele is purged from the population (clearance) following transmission (Methods).Our results show that mean waiting time for adaptation decreases as robustness increases (Fig. 2). This occurs since robustness shifts the DMFE to include more sites where mutations have neutral fitness effects, and thus robust populations harbor a larger number of neutral genetic variants segregating at appreciable frequencies as compared to brittle populations. When such higher frequency “hidden” alleles become beneficial, the rate of adaptation will be faster (Hermisson and Pennings, 2005). However, the higher frequency of neutral alleles has an additional consequence. When measuring the rate at which deleterious mutations are removed, we observed that robust populations purge the novel deleterious mutations more slowly (Fig. 2; Supplementary text Section 1), and they appearto be at a disadvantage as compared to more brittle populations.

We next examined which of these two opposite effects dominate during an environmental change. While the effect of purging appears to be less significant than the effect of adaptation (Fig. 2), the first few generations of viral replication are critical for establishing a novel infection. To this end we determined the mean fitness of the population as it adapted to the new environment, which affects multiple sites and their fitness, over time. This allowed us to compare a robust (r=0.97, q=0.8) with a non-robust (r=0.9, q=0.2) population and determine which population has a higher probability to establish a productive infection. We first derived a simple analytic expression to estimate the difference in log mean fitness over time of robust and brittle populations, given the effect of an environmental change on numerous alleles in the previous environment (Supplementary text Section 2). Under these conditions, the difference in log mean fitness of a robust versus brittle population is approximated by $\mathrm{\Delta }w=\mathrm{\Delta }q\cdot \sum _{i}log(({(1+s_i^{\mathit{\text{new}}})}^T-1)\cdot {\overline{x}}_0+1)$, where Δw is the difference in log mean fitness between a robust and brittle population over T generations, $s_i^{\mathit{\text{new}}}$ is the selection co-efficient at site i in the new environment, and x̄₀ is the mean frequency of a neutral allele in the first environment. This term can be positive or negative depending on the number of positive and negative selection coefficients in the new environment.

The analytic term above relies on the assumption of deterministic selection. Yet fluctuating viral population sizes may allow a powerful role for genetic drift. We thus used stochastic simulations to explore the adaptation of viral populations to a new environment (Methods) (Fig 3). Notably, it has been shown that exponential microbial growth leads to a loss of beneficial mutations due to stochastic effects (Wahl and Gerrish, 2001; Wahl et al., 2002) and this might cause deviations from the analytic approach described above.

Initially, we explored two extreme cases. In one scenario, the environmental change results in a larger proportion of beneficial alleles in the new environment ( $\sum _i{s}_{i+}^{\mathit{\text{new}}}=100,\sum _i{s}_{i-}^{\mathit{\text{new}}}=5$, Fig 3A). In the other case, only a few alleles became beneficial while the majority of them become deleterious ( $\sum _i{s}_{i+}^{\mathit{\text{new}}}=5,\sum _i{s}_{i-}^{\mathit{\text{new}}}=100$, Fig. 4B). In order to test which population would outperform its counterpart, we calculated the log mean fitness of the robust and brittle population during the first generations following the environmental change. The difference in fitness between the two populations hence corresponds to the shaded differences between the robust (grey) and brittle (black) curves(Fig. 4A and 4B). We observed that while the originally robust populations adapt more rapidly when many alleles become beneficial in the new environment, they are also significantly less fit during the initial rounds of replication in the new environment if a large proportion of neutral alleles becomes detrimental. Indeed, under this scenario, the originally robust population suffers from a severe drop in fitness following the environmental change, due to the sudden influx of deleterious variants in the population segregating at a higher frequency (Fig. 4B).

Figure 4.

Comparison between robust (r=0.97) and brittle (r=0.9) populations as measured by difference in log population mean fitness after an environmental change (denoted by Δw). Two extreme environmental changes are illustrated: a large magnitude of beneficial (A) or deleterious (B) changes, as measured by $\sum _i{s}_i^{\mathit{\text{new}}}$, occurs following the change. (C) A map of fitness differences between robust and brittle populations over 400 different “transmission” environmental changes. Each box represents an environmental change defined by the sum of changes in adaptive (y-axis) and deleterious (x-axis) selection coefficients, where fitness differences are measured over 10 generations. Red and blue shades indicate an advantage for the robust and brittle populations, respectively, with darker shades corresponding to a larger advantage. The circle points out extrapolations of eight experimentally determined environmental changes, which all coincide on the map, in the form of different host shifts for an RNA virus (Lalic et al., 2011) and a DNA virus (Vale et al., 2012) (see text).

To examine the larger spectrum of possible scenarios we next simulated a series of 400 environmental changes, which encompassed relatively widespread changes of selection coefficients in the genome defined by randomly drawing N₊ and N_- sites, whose selection coefficient was reassigned after the environmental switch to s=0.1 and s=-0.1, respectively (Fig. 4C). Both N₊ and N_- varied between 50 and 1000 (encompassing 0.05% to 1% of the sites in the genome), and all combinations of N₊ × N_- were simulated. Calculating the differences in log mean fitness across the first 10 generations allowed us to create a heatmap that defines condition under which robust or brittle populations would be more fit and less likely to establish a productive infection following the environmental changes (Fig.(Fig. 3C).

These results show that under many of the simulated conditions, robust populations are more fit than their brittle counterparts, illustrated by the large red portion of the heatmap (Fig. 4C). We also identify a range of conditions where the brittle population outperforms the robust population, namely when the magnitude of adaptive sites is much smaller than the magnitude of deleterious sites (blue region in Fig. 4C). Under the latter scenario, there is an increase in the genetic load, which is more pronounced in robust populations during the initial generations in the new environment. Notably, this pronounced disability of the robust population disappears after a few rounds of replication in the new environment, as novel deleterious alleles are purged and as the population adapts (Fig. 4B)

To date, few studies have documented the changes on the distribution of mutational fitness following an environmental change. Recently, this distribution was examined in phage ΦX174 distribution during host change from Escherichia coli (the native host) to Salmonella typhimurium (a novel host) (Vale et al., 2012) and in Tobacco etch potyvirus (TEV) across eight different hosts(Lalic et al., 2011). Strikingly, the majority of mutations conferred lower fitness as compared to the wildtype fitness in the native host (caption in Fig. 4C and Methods). This set of results suggests that a switch to a new environment may result in a predominantly higher load of deleterious alleles in the new environment. Under this scenario, we can roughly extrapolate that the brittle virus populations would outperform their more robust counterparts (Fig. 4C dashed circle; Supplementary section 3 and Table S1).

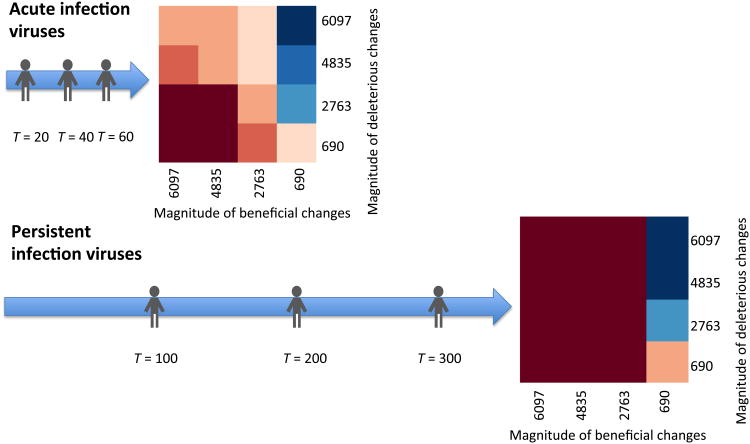
Acute versus persistent modes of viral infection

Our analytic results coupled with the simulations showed that mean fitness of a virus population depends on the level of neutral diversity in the population prior to the environmental change. Theoretical models often assume that allele frequencies are at mutation-selection balance. However, for acute virus infections, this balance is unlikely to be attained given that the environment and other features of infection frequently fluctuate. Of note, the current and previous studies showed that that some acute viral infections accumulate limited diversity during infection of a host (Acevedo et al., 2014; Thai et al., 2012). In contrast, during persistent infections, population diversity should increase with time as the virus replicates within the infected individual, akin to a population accumulating genetic charge, see (Le Rouzic and Carlborg, 2008). Accordingly, we hypothesized that the effect of robustness will be more pronounced in persistent infections.

To test this hypothesis, we examined whether or not acute versus persistent viruses are equally affected by the level of robustness during transmission events. We simulated two possible scenarios: (1) for acute viruses, we allowed shorter waiting times between environmental changes (corresponding to transmission events) (T = 20) and larger maximal population size (N_max=10⁶), (2) for persistent viruses we allowed longer waiting times between transmission events (T = 100) yet smaller maximal population sizes (N_max=10³) (Methods). These parameters were selected based on evidence suggesting that acute infections produce large population sizes in a short period of time, while persistent infections often are characterized by smaller size populations(Grenfell et al., 2004). As a consequence of the increased time for replication, under persistent infection conditions we observed a significant increase in genetic diversity (not shown). Importantly, our simulations showed that robust populations have an advantage for adaptation to some new environmental conditions, but in the majority of new environments brittle populations have a larger advantage as compared to the acute infection viruses. This effect is also observed in acute infectionsbut the effect isless pronounced (Fig. 5). We conclude that robustness determines diversity, diversity is increased in robust populations that replicate for a longer period of time in the same environment (persistent infections), and diversity can be either beneficial or detrimental in a new environment.

Figure 5.

A comparison between brittle and robust viruses under two types of transmission scenarios: following acute or following persistent infection. Three consecutive environmental changes, in the form of transmission events (marked as people) are simulated. For each type of infection the timing of the environmental change is different, as well as the population size at the time of the change. The heat map, with notations and colors as in Fig. 4, displays the magnitude of adaptive versus deleterious changes summed across all three environmental changes. Fitness differences are measure for the first 10 generations after the last environmental change.

Discussion

The role of mutational robustness in evolution has remained controversial. In this study, we begin with a simple quantitative definition of mutational robustness(see also Elena et al., 2007; Krakauer and Plotkin, 2002). This definition is highly amenable to direct measurement in populations of evolved RNA viruses, and we show that viral co-infection is a relevant model for studying the effects of mutational robustness. We then construct a theoretical model that is guided by our experimental results (Fig. 1). This process allows us to predict how viral populations, modulated by different levels of MOI, would adapt to new different conditions.

Mutational robustness has been shown to be prevalent in many organisms. In several cellular organisms it is present in the form of gene redundancy, modularity, and alternative regulatory pathways. In fact, for many organisms most gene knockouts are viable(Costanzo et al., 2011). In principle, it would be reasonable to expect selection to maximize mutational robustness, since this serves to decrease mutational load and increase diversity. However, experimental evidence suggests that virus populations are mostly composed of lethal or deleterious mutations (Acevedo et al., 2014; Rihn et al., 2013; Sanjuan, 2010). This has been explained largely by the small genome sizes of viruses, which limit redundancy. However, an alternative explanation is that brittle populations may also have an advantage under certain conditions. This advantage of brittle populations manifests as lowered sensitivity to novel deleterious mutations, and subsequently higher fitness in a new environment. Thus, brittle populations suffer less from the transient decrease in fitness in a novel environment (Fig. 4B).

One limitation of our study is in the decoupling of the mechanisms that generate robustness in the first environment, and the proportion of beneficial to deleterious mutations in the new environment. Supplementary section 4 and Table S2 discuss different mechanisms of robustness and their potential effects on fitness. In the study herein, we find that high MOI buffers deleterious mutations and masks the effects of beneficial mutations, as evident from the changed distributions in Fig 1C versus Fig. 1D (see also supplementary text 5 and Fig. S2). However, other mechanisms of robustness may well directly affect the distribution of fitness effects in the new environment, and an explicit model, which ties the effects of robustness with the effects of the new environment, is warranted.

Our current model, for simplicity, does not take into account linkage among sites, entailing infinite recombination. Background selection, genetic hitch-hiking, and genetic interference are all manifestations of the Hill-Robertson (HR) effect (Felsenstein, 1974; Hill and Robertson, 1966), which occur when selection and linkage combine. Someof the important derivations of the HRcomplex effectare that the effective population size is reduced, genetic variance is reduced, and selection is less effective(e.g., McVean and Charlesworth, 2000; Roze and Barton, 2006). Multi-locus HR interference has been shown to be prevalent in simulations, and in fact may lead to a selective advantage for recombination (Barton and Otto, 2005; Keightley and Otto, 2006).Interestingly, negative disequilibrium (associations between deleterious and beneficial alleles) is expected to prevail over positive disequilibrium (Barton and Otto, 2005). Even more complex effects may take place when rates of recombination are low, such as clonal expansion of a beneficial genotype. Furthermore, viral colonization may involve structured populations replicating autonomously, different degrees of co-infection and genetic complementation, effects of migration, and strong competition for resources (Turner and Chao, 1999). It remains to be studied how these different phenomena affect the relationship between robustness and adaptation. This will be facilitated by developing explicit models of viral evolution, which take into the account the complex processes occurring during viral establishment of an infection.

The framework proposed in this study may help resolve conflicting evidence on the role of mutational robustness in promoting evolvability: while McBride et al. (2008) showed that robust Φ6 phage clones adapted more successfully to a new thermal niche, Cuevas et al. (2009) showed that brittle vesicular stomatitis virus populations were more adaptable to a new host cell type than their robust counterparts. The results of our study support the notion that, depending on the conditions, either robust or brittle populations can successfully establish an infection following host changes. We conclude that the change in the distribution of fitness effects in the novel environment as compared to the previous environment will determine the outcome of an infection.

Previous studies by Masel (2006) concluded that robustness should promote evolvability even in the presence of cryptic alleles that are deleterious in a new environment. Our results on the other hand identify a range of conditions where a brittle population would prevail, namely when many neutral (or near neutral) mutations drastically change their selection coefficient into a deleterious one. These conditions will largely depend whether mutation effect distributions are correlated or not across environments. While Masel (2006) assumed that mutational fitness values are correlated between environments, we relaxed this assumption and considered that fitness values of mutations do not necessarily correlate between two given environments. Another difference between these studies is that the Masel (2006) study takes into account conditionally lethal mutations, whereas we focus only on conditionally deleterious mutations. However, we argue that considering conditionally lethal mutations would not change the conclusions of our study, given that they increase the negative effects on fitness of a population in the new environment.

We, thus propose that different modes of virus replication and different types of environment conditions will most likely dictate whether fitness effects are indeed correlated. For instance some viruses that infect multiple hosts (such as vector-borne viruses) are expected to regularly alternate between very different environments, whereas other viruses may experience relatively similar environments and hence the mutation effect distributions might not change dramatically. Interestingly, it has been shown that vector-borne RNA viruses experience more purifying selection than non vector-borne viruses (Woelk and Holmes, 2002). As evolutionary rates and mutation rates are highly correlated in viruses (Sanjuan, 2012), increased purifying selection implies more deleterious and lethal mutations. Since vector-borne viruses experience frequent dramatic environment changes, and hence a higher proportion of deleterious mutations in the new host (i.e., the blue region in Fig. 4), this suggests that selection may have favored such brittle populations over the course of evolution of vector-borne viruses.

Finally, our results suggest an interesting relationship between the rate of environmental change, the accumulated diversity, and mutational robustness. The time to accumulate neutral mutations in a relatively constant environment is significantly longer during persistent infection of robust populations. As a result, robust populations, replicating under persistent infection, should accumulate a considerably larger diversity than brittle viruses. Indeed, we show that persistent infection exacerbates the effects of robustness (Fig. 5) and, depending on the conditions of the new environment, the degree of robustness in the population would be a critical factor in the establishment of infection in the new environment. Considering thousands of years of evolution, brittle populations of persistent viruses would have an increased probability of establishing infection if a large proportion of neutral mutations become detrimental in the new environment. We thus speculate that under these conditions, brittle viruses that use a persistent mode of infection are more likely than robust viruses to successfully infect in diverse environments. On the other hand acute infection viruses, which undergo rapid transmission, and generate less genetic diversity, will be less affected by robustness. This conclusion seems counterintuitive in the light of theory and experiments, which show an increased rate of extinction as the rate of environmental change increases (e.g., Lindsey et al., 2013). However, this may be explained given that our framework assumes a random process of environmental change, and hence lack of correlation between selection coefficients before and after an environment changes. While this requires further empirical study, it is likely that successive viral transmission events do not adhere to a gradual process of unidirectional change (e.g., climate change). Under the latter scenario, populations would gradually climb to a new fitness peak, and we would not expect an abundance of novel deleterious mutations as the unidirectional change proceeded. The ability to precisely measure the DMFE of viral populations as they adapt to different environmental changes will be central to establishing the constraints affecting viral evolution, and will allow a better understanding of the link between standing genetic variation, mutational robustness, and capacity to evolve.

Methods

Experimental evolution of viruses and fitness measurements

To understand population diversity and robustness dynamics under different pressures, we passaged oral polio vaccine (OPV) type 2 in HeLa S3 (ATCC, CCL2.2) cells at low and high MOI. For lowMOI passages, 10⁷ HeLa S3 cells seeded the day before the experiment were infected with OPV2 at MOI of 0.1 at 33°C for 1 hour to allow virus adsorption, and then replaced with virus culture medium. The infected cells were maintained at 33°C for 10 hours and then harvested by freezing at -80°C. After three freeze-thaw cycles, virus suspension was clarified by centrifugation at 3,500 ×g for 10 minutes at 4°C, and stored at -80°C for future passages. Plaque assays were performed to determine virus titer of each passage for a subsequent seven passages.

For high MOI passages, all passages were obtained by infecting HeLa S3 cells at MOI of 0.1 as described above, but harvested at 24 hours post infection. Thus, viruses experienced one replication cycle at low MOI of 0.1, and an additional cycle at a higher MOI (>10; inferred assuming a burst size of >100 infectious particles per infected cell, based on low MOI titres). Plaque assay was also performed to determine virus titer of each passage for subsequent passages. All viral populations were amplified once in HeLa S3 to increase the percentage of viral RNA for sequencing. Library preparation, base-calling and mutational fitness were calculated based on time-series allele frequency measurements as described in ref. (Acevedo et al., 2014) for CirSeq. Briefly, we assume deterministic selection, which is approximated by

$$P(t+1)=wP(t)(1-\mu )+(1-P(t))\mu$$ (1)

where P(t) is the frequency at generation t. Assuming linear behavior at small time intervals, we obtain the following ordinary differential equation:

$$\frac{\partial P}{\partial t}=\frac{P(t+\mathrm{\Delta }t)-P\left(t\right)}{\mathrm{\Delta }t}=P\left(t\right)\alpha +\mu$$ (2)

where α = (w(1 − μ) − μ − 1). Solving this equation yields

$$P(t)=c{e}^{\alpha t}-\frac{\mu }{\alpha }$$ (3)

The mutation rate μ is estimated based on the median frequencies of lethal mutations as described in (Acevedo et al., 2014). Thus, eq. 3 allows us to infer the constant c and fitness w for any allele, given a pair of frequency estimates P(t₁) and P(t₂) at any two passages. For multiple passages we use linear regression to estimate a unique w value. We note that this approach will attribute all changes in allele frequencies to the combined effect of mutation and selection, while ignoring the effect of genetic drift and sampling. For rare alleles, with small allele counts the effect will be to overestimate the effect of selection. There are a number of approaches for incorporating genetic drift and sampling variance into the estimation of selection coefficients(Bollback et al., 2008; Mathieson and McVean, 2013; Song and Steinrucken, 2012). However, these methods are highly computationally demanding and are not developed for analyses of thousands of sites. Furthermore, our results rely on comparing distributions rather than comparing estimates for single sites. For that reason we use the deterministic approximation and interpret the results accordingly.

Virus evolution model

We assume a haploid population of N individuals, with a genome of length L = 10,000 bp. Mutations were modeled assuming two allelic states in each site with an equal rate of mutation between the two states of 10^-4 mutations/replication/base. Each population is assigned a distribution of mutation fitness effects (DMFE), from which a selection coefficient is drawn for one of the alleles at each position (labeled the alternative allele), whereas the fitness of the other allele (labeled the wild-type, WT, allele) is set at 1. The total fitness was calculated assuming multiplicative effects across sites (see below). We assume that the DMFE follows a mixture of a log-normal distribution of non-lethal deleterious selection coefficients (s< 0) with probability 1 − q, and a point mass at s = 0 with probability q. Robustness of a population of viruses is defined as r = ω̄. A survey across several DMFEs of various RNA and DNA viruses has shown a highly similar distribution for non-lethal deleterious selection coefficients (Sanjuan, 2010). Here we use scale parameter m = 0.092 and a shape parameter σ = 1.2 for the log-normal distribution as found by (Sanjuan et al., 2004). Hence, here q effectively defines the robustness of the population, and values of 0.2, and 0.8 are explored, corresponding to r = 0.896 and 0.974, respectively. We note that q will also capture any near-neutral mutations that “behave” neutrally when s < 1/N_e (where N_e is the effective population size).

To simplify our calculations we made several assumptions: (i) we assume absence of linkage disequilibrium, and (ii) we considered only non-lethal mutations across both environments modeled. The latter assumption allows us to focus on the “effective” portion of the genome where genetic variability exists. The former assumption on lack of linkage entails infinite recombination. While this is not a realistic assumption, for many RNA viruses, the rate of recombination is exceptionally high (e.g., Kirkegaard and Baltimore, 1986; Runckel et al., 2013; Tromas et al., 2014). Thishigh rate is especially true for Poliovirus studied herein. We have addressed this important limitation of our model in the discussion and in Supplementary Information section 6, where we show that our results may likely hold when alleviating the assumption of lack of linkage.

Simulations

We perform Wright-Fisher simulations with selection, where binomial sampling probabilities are weighted by the fitness of the allele:

$$\text{Pr}(X_t=x_t|X_{t-1}=x_{t-1},s,\mu ,N)=(\begin{array}{c}N\\ N{x}_t\end{array})P_t^{N{x}_t}{(1-P_t)}^{N-N{x}_t}$$ (4)

where X_t is the frequency of the minor allele at time t, s is its selection coefficient, μ is the mutation rate, and N is the population size. P_t is the probability of sampling an allele in the next generation and is determined by it relative fitness as compared to the WT: P_t = (1 + s)· x_t−1 · (1 − μ)+μ· (1 − x_t−1)·1 (as in Eq. 1)

Each site in the population of genomes is simulated independently. To initialize the first environment, each site is first simulated with the WT allele frequency set to 1, and evolved for 150,000 generations with a population size N = 10⁶. Then, an environmental change is imposed, which changes the selection coefficients at a varying number of random sites in the genome. Since selection coefficients are always relative to the WT allele (which is assigned a value of 1), changes are only made to the alternative allele. We note that this implicitly captures all types of changes in selection, both to the WT and mutant alleles, since we allow a change in the magnitude and sign of the novel selection coefficient. Thus, for example, a situation where the WT allele becomes deleterious in the new environment would be captured in our simulations as the alternative allele becoming beneficial. The population is then simulated for several generations in the new environment. For the “transmission scenario”, a severe bottleneck is assumed and the population size is reduced to N₀ = 100 as the environmental change take place. This is followed by population growth modeled as a logistic density-dependent growth of the population (Acevedo et al., 2014; Sanjuan et al., 2004): $N_t=K\frac{N_0}{N_0+e^{-rt}(K-N_0)}$ where K (maximal carrying capacity) was set to 10⁴ for the “transmission scenario”, and r (intrinsic growth rate) was set to 2. This allowed explosive growth, as observed during the acute infection phase of several viruses (Otto and Whitlock, 1997). Different values of r (0.5, 1 and 2) yield essentially the same results (data not shown). For the “within-host scenario”, population size remained large (N=10⁶) before and after the environmental change. When a buffering effect is modeled, the beneficial fitness effect is reduced from 1.1 to 1.04 (∼6% decrease) and the deleterious fitness effect is increased (selection co-efficient is decreased) from 0.9 to 0.93 (∼4% increase), in line with the experimental results determined on the effects of high MOI.

Mean fitness of the digital viral populations

Assuming sites are independent, log mean population fitness at a given generation of simulated populations was calculated as $log(\overline{w})={\sum }_{i=1}^{L}log[(1+s_i)f_{A_i}+1\cdot (1-f_{A_i})]$ where s_i and f_Ai are the selection coefficient and frequency of the alternative allele at position i of the genome, respectively. The supplementary information elaborates on calculating mean fitness over time analytically.

Mapping experimental DMFE measurements

For the TEV measurements (Lalic et al., 2011), values of w (fitness) were measured across eight hosts: the native host and seven additional hosts of varying phylogenetic relatedness to the native host. Selection coefficients in the novel hosts (corresponding to the novel environment) were calculated as $w_{\mathit{\text{mut}}}^{\mathit{\text{host}}}/w_{\mathit{\text{WT}}}^{\mathit{\text{native}}}-1$, where each w was obtained by averaging across the 6 replicas performed in the study. The ΦX174 study (Vale et al., 2012)directly reported selection coefficients in the single novel host tested. For each host shift, we calculated the extrapolated difference in log fitness $\sum _{i}log(({(1+s_i^{\mathit{\text{new}}})}^T-1)\cdot {\overline{x}}_0+1)$ for those selection coefficients that had changed from neutral in the natural host to either positive or deleterious, with T=10 and x̄₀ = 0.5. As per the ΦX174 study, mutations were classified as non-neutral based on a t-test when mean s values significantly deviated from zero. Since both studies only measured selection coefficients for a sample of n sites in a genome of length L, we corrected for this by multiplying the result by L/n. Accordingly, for all but one of the novel hosts, the results showed a higher extrapolated fitness for a brittle host had it been competed against a robust one during a host shift (see supplementary text part 3 for more details).