Evaluation of an in silico cardiac safety assay: Using ion channel screening data to predict QT interval changes in the rabbit ventricular wedge

Abstract

Introduction

Drugs that prolong the QT interval on the electrocardiogram present a major safety concern for pharmaceutical companies and regulatory agencies. Despite a range of assays performed to assess compound effects on the QT interval, QT prolongation remains a major cause of attrition during compound development. In silico assays could alleviate such problems. In this study we evaluated an in silico method of predicting the results of a rabbit left-ventricular wedge assay.

Methods

Concentration–effect data were acquired from either: the high-throughput IonWorks/FLIPR; the medium-throughput PatchXpress ion channel assays; or QSAR, a statistical IC₅₀ value prediction model, for hERG, fast sodium, L-type calcium and KCNQ1/minK channels. Drug block of channels was incorporated into a mathematical differential equation model of rabbit ventricular myocyte electrophysiology through modification of the maximal conductance of each channel by a factor dependent on the IC₅₀ value, Hill coefficient and concentration of each compound tested. Simulations were performed and agreement with experimental results, based upon input data from the different assays, was evaluated.

Results

The assay was found to be 78% accurate, 72% sensitive and 81% specific when predicting QT prolongation (>10%) using PatchXpress assay data (77 compounds). Similar levels of predictivity were demonstrated using IonWorks/FLIPR data (121 compounds) with 78% accuracy, 73% sensitivity and 80% specificity. QT shortening (<−10%) was predicted with 77% accuracy, 33% sensitivity and 90% specificity using PatchXpress data and 71% accuracy, 42% sensitivity and 81% specificity using IonWorks/FLIPR data. Strong quantitative agreement between simulation and experimental results was also evident.

Discussion

The in silico action potential assay demonstrates good predictive ability, and is suitable for very high-throughput use in early drug development. Adoption of such an assay into cardiovascular safety assessment, integrating ion channel data from routine screens to infer results of animal-based tests, could provide a cost- and time-effective cardiac safety screen.

1. Introduction

Drug interactions with cardiac ion channels can lead to lengthening of the QT interval on the electrocardiogram (ECG) (Grant, 2009; Yap & Camm, 2003). This phenomenon has been linked with the potentially lethal ventricular arrhythmia Torsades de Pointes (TdP) (Dessertenne et al., 1966; Pollard et al., 2010). Cardiovascular toxicity remains the main safety reason for the discontinuation of development and market withdrawal of compounds (Valentin, 2010). 21.4% of the withdrawn compounds from major international markets between 1990 and early 2012 were as a consequence of QT prolongation liability and/or association with TdP (Shah, 2012). Compound withdrawal not only implies that a risk to patient safety has been posed, but also results in a substantial loss of invested time, money and resources. It is thus important for pharmaceutical companies to identify compounds that prolong QT as early as possible during drug development (Laverty et al., 2011).

Often, compounds which prolong the QT interval inhibit the rapid component of the delayed rectifier potassium current I_Kr (encoded by human Ether-a-go-go Related Gene (hERG), whose protein forms the pore alpha-subunit of the I_Kr channel) (Sanguinetti, Jiang, Curran, & Keating, 1995). Due to its fundamental role in controlling repolarisation of the ventricular action potential, hERG channel block leads to a lengthening of the Action Potential Duration (APD) of a single cell, manifested as QT prolongation on the ECG. Thus, hERG channel block and QT prolongation are considered important factors in the detection of pro-arrhythmic liability (Pollard, Valentin, & Hammond, 2009). However, consideration of drug interactions with multiple ion channels is important for improved pro-arrhythmic risk prediction (Davies et al., 2012; Mirams et al., 2011; Obiol-Pardo, Gomis-Tena, Sanz, Saiz, & Pastor, 2011). Some pharmaceutical companies now routinely screen a selection of ion channels in addition to hERG, including sodium and L-type calcium channels to facilitate such investigations.

The International Conference for Harmonization (ICH) proposed the ICH S7B (Anon, 2005b) and E14 (Anon, 2005a) guidelines, which provide advice for preclinical and clinical assessment of drug-induced QT prolongation liability (Darpo, Nebout, & Sager, 2006). ICH S7B suggests that in vitro I_Kr and in vivo QT measurements are performed as standard during drug development. These tests typically comprise patch clamp experiments using a hERG expression system and a conscious animal QT study (typically in dog), but can non-exclusively include: rabbit and dog ventricular wedge studies, Langendorff heart preparations and in vivo studies in other animals (Pugsley, Authier, & Curtis, 2009). The ICH E14 suggests that a human thorough-QT trial is conducted during clinical development (Pollard et al., 2010; Recanatini, Poluzzi, Masetti, Cavalli, & De Ponti, 2004).

The ICH guidelines were intentionally written in an unrestrictive manner, enabling pharmaceutical companies to explore new in vivo, in vitro and in silico methodologies for acquiring QT measurements (Darpo, 2009; Picard et al., 2011). In silico assays have great potential, particularly in early drug development, to provide integrative, high-throughput, cost-effective and efficient solutions. Pharmaceutical companies are currently exploring such approaches (Mirams, Davies, Cui, Kohl, & Noble, 2012). Through integrated risk assessment, these approaches could complement existing safety tests and reduce the current use of animal-based experiments. An in silico approach, frequently enlisted within pharmaceutical companies, is Quantitative Structure Activity Relationship (QSAR) modelling which uses information regarding the chemical structure of compounds to infer properties of their biological activity (Inanobe et al., 2008).

Additional in silico approaches, developed in collaboration with, and having applicability to inform decisions within, pharmaceutical companies, include the work of Bottino et al. (2006), Mirams et al. (2011) and Davies et al. (2012). These approaches all use ion channel data acquired from routine high-throughput screens performed early in preclinical development, to infer results which would be of interest during later compound development. Davies et al. (2012) evaluate the ability of an in silico assay in predicting the results, and the associated inter-individual variability, of drug effects on canine APD in isolated myocytes. The assay demonstrates high levels of sensitivity and specificity.

The approach adopted in this study is similar. We evaluate the ability of an in silico action potential simulation assay, which uses concentration–effect data from high-throughput ion channel screens, to predict the results of the rabbit left-ventricular wedge assay. The rabbit wedge assay is performed during compound development at GlaxoSmithKline (GSK) and the preclinical data obtained has been found to correlate well with clinical outcomes (Joshi, Dimino, Vohra, Cui, & Yan, 2004; Liu et al., 2006). The number of compounds we include for evaluation in this study is much increased to that of Davies et al. (2012), strengthening the confidence in conclusions drawn. Compounds included belong to a wide variety of chemical and therapeutic categories. Additionally, we examine the use of ion channel data from three different stages of assay; (QSAR, IonWorks/FLIPR and PatchXpress). Simulated action potentials generated from single cell simulations, and pseudo-ECGs from one-dimensional tissue simulations, are compared to ECGs recorded in the rabbit ventricular wedge assay. The predictivity of the model is assessed when using the available ion channel data in a number of different ways. In addition to evaluating the assay’s predictive capacity, the evaluation has allowed us to infer the most advantageous use of available ion channel data, and where in the drug development process such an in silico approach would be most beneficial.

2. Methods

2.1. Statement on use and care of animals

All animal studies were ethically reviewed and carried out in accordance with Animals (Scientific Procedures) Act 1986 and the GlaxoSmithKline Policy on the Care, Welfare and Treatment of Animals.

2.2. Electrophysiology

2.2.1. Ion channel screens

Ion channel screens are performed on cell lines, based on Human Embryonic Kidney-293 (HEK-293) and Chinese Hamster Ovary (CHO) cells. The Molecular Devices PatchXpress 7000A assay was used to screen hERG, NaV1.5 and CaV1.2 channels. The Molecular Devices IonWorks Quattro assay was used to screen hERG, NaV1.5 and KCNQ1 channels. The Molecular Devices FLuorescence Imaging Plate Reader (FLIPR) assay was used to screen the CaV1.2 channel. CaV1.2 data from FLIPR was gathered alongside data from the IonWorks assay for the hERG, NaV1.5 and KCNQ1 channels.

Details of the cell culture and preparation process, the solutions prepared for ion channel screening and the controls used are described in Supplementary material S.3. Voltage protocols applied to obtain IC₅₀ value estimates from the IonWorks and PatchXpress assays and the method of fluorescence measurement used in the FLIPR assay are also outlined. Details of the methodologies used for PatchXpress assay screening of the hERG and NaV1.5 channels can be found in Donovan et al. (2011). A curve of the form shown in Eq. (1) was fitted to the concentration-response data derived from the normalised data produced by each of the assays in order to determine IC₅₀ values (and in some cases Hill coefficients).

2.2.2. QSAR models

QSAR models for hERG, NaV1.5 and CaV1.2 were created from available measured data from ion channel assays described in Section 2.2.1. The structures and measured responses were presented to an automated modelling software application (QSAR Workbench (Accelrys Inc.)). Models based upon Support Vector Machines (SVM) (Burbidge, Trotter, Buxton, Holden, et al., 2001) were developed for the hERG and NaV1.5 channels, whilst a random forest classifier (Svetnik et al., 2003) was selected for the CaV1.2 channel. The output from the SVM was a predicted pIC₅₀ value for each compound. The output for the CaV1.2 channel was a predicted class which was then equated with a pIC₅₀ value.

2.3. Rabbit ventricular wedge assay

Details of the preparation of rabbit left-ventricular wedge have been described previously in Liu et al. (2006). Briefly, female rabbits were sedated with 6 mg/kg xylazine (i.m.), anticoagulated with 800 U/kg heparin (i.v.) and anaesthetised with ketamine (30–35 mg/kg, i.v.), or with pentobarbital (50 mg/kg, i.v.). The left circumflex or anterior descending branch of the coronary artery of the excised rabbit heart was cannulated and perfused in cardioplegic solution. A transmural left-ventricular wedge was dissected and placed in a tissue bath and arterially perfused with Tyrode’s solution. After approximately 1 h of equilibration in the bath at a stimulation frequency of 1 Hz, the stimulation frequency was reduced to 0.5 Hz for 5 min of stabilisation where the baseline ECG was measured. The preparations were then returned to a stimulation frequency of 1 Hz and perfused with Tyrode’s solution containing a test compound. For each test compound concentration, the preparation was perfused for approximately 30 min at a frequency of 1 Hz followed by 5 min at a frequency of 0.5 Hz, where again the ECG was recorded.

2.4. Simulations

2.4.1. Concentration–effect curve fitting

Where more than a 50% block of an ion channel was observed at the compound concentrations tested in the PatchXpress and IonWorks/FLIPR assays, the concentration–effect data were fitted with the procedure outlined in Section 2.2.1, and the IC₅₀ value (and Hill coefficient in some cases) recorded was used directly. Where a 50% block was not achieved, concentration–effect data acquired from the assays were fitted with a sigmoidal curve, of the form described in Eq. (1), using an implementation of the Nelder and Mead (1965) optimisation algorithm.

$$b=\frac{1}{\left(1+{\left(\frac{{\left[{\mathit{IC}}_{50}\right]}_j}{\left[C\right]}\right)}^n\right)}$$ (1)

Here, b is the proportion of blocking effect, [C] is the compound concentration, [IC₅₀]_j is the IC₅₀ value for channel j and n is the corresponding Hill coefficient. Fitting of the Hill coefficient was constrained so that a value in the experimentally expected range (between 0.5 and 5) was obtained. Data from the QSAR model took the form of an IC₅₀ value and so did not require any fitting.

All IC₅₀ and Hill coefficients considered in this study are available to download, see Supplementary material S.1 for details.

2.4.2. Mathematical model

A biophysical model of the rabbit ventricular myocyte (Shannon, Wang, Puglisi, Weber, & Bers, 2004) was modified to incorporate drug interactions with the hERG, NaV1.5, CaV1.2 and KCNQ1 channels. Drug interaction is modelled with a simple pore-block mechanism (Brennan, Fink, & Rodriguez, 2009), scaling the maximal conductance of each channel by the factor in Eq. (1).

The mathematical model is comprised of a system of Ordinary Differential Equations (ODEs) describing the action of individual ionic currents. Ionic currents are of the form shown in Eq. (2).

$${\mathit{I}}_j=g_j(1-b)O(V-E_{\mathrm{ion}})$$ (2)

where g_j is the maximal conductance of channel j, O is the probability of the channel being in the open state, V is the membrane potential and E_ion is the reversal potential of the channel. The parameter b is a scale factor from Eq. (1) used to incorporate the effects of drug block. For example, a value of b = 0.2 corresponds to a 20% reduction of the maximal conductance.

2.4.3. Single cell simulations

Pacing was initiated by applying a stimulus current of magnitude 9.5 μA/μF and duration of 5 ms. Pacing was continued at 0.5 Hz, corresponding to the pacing frequency performed in the rabbit ventricular wedge experiments. The stimulus was applied at 0.5 Hz until a steady state was reached. Steady state is defined to be when the square root of the sum of the squared differences of the state variables at the start of successive paces is less than 10⁻⁶. Eq. (3) was solved to determine the action potential following administration of a given compound concentration.

$$\frac{\mathit{dV}}{\mathit{dt}}=-\frac{1}{{\mathit{C}}_m}\left(\sum _{\text{channels}}{\mathit{I}}_j+{\mathit{I}}_{\text{stim}}\right)$$ (3)

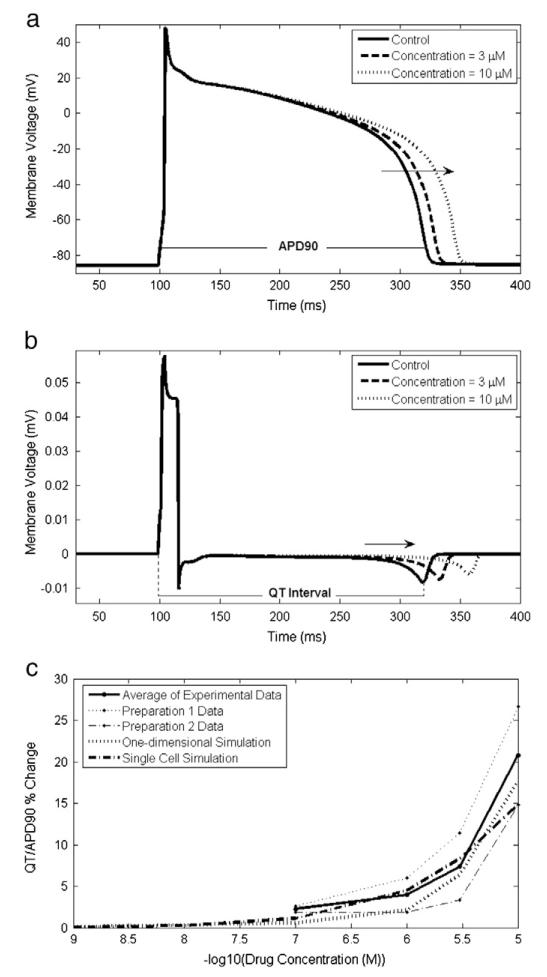
Here, V is the membrane voltage, C_m is the membrane capacitance, I_j represents the current from channel j and I_stim is the stimulus current applied to pace the cell. The APD90 value, that is the duration between times at which the membrane potential is at 90% of its repolarisation potential, was calculated and the percent change in APD90 at each concentration, as compared to the control, was recorded (see Fig. 1).

Fig. 1.

a) An action potential generated from a single cell simulation and b) a pseudo-ECG from a one-dimensional tissue simulation at a range of concentrations for compound 2659 (see Supplementary data). Simulations were performed using PatchXpress data, parameterising the drug block model with the IC₅₀ value and Hill coefficient in the single cell simulation and with just the IC₅₀ value (and assuming the Hill coefficient is 1) in the one-dimensional simulation. The intervals used for calculation of the APD90 value and QT interval from the simulated control result are indicated in a) and b). Arrows indicate the effect observed in the APD90 value/QT interval with increasing compound concentration. In c) the percent change in APD90/QT interval determined from the simulation results and experimental results (both individual preparation results and the average of these) in the rabbit ventricular wedge assay is plotted for comparison.

2.4.4. One-dimensional tissue simulations

The one-dimensional simulation setup is analogous to a line of coupled cells, forming a 1 cm long homogenous fibre. Simulation nodes were spaced 0.1 mm apart. The monodomain Partial Differential Equation (PDE), as shown in Eq. (4), was solved, using a time step of 0.01 ms and an adaptive ODE time step for Eq. (3), to determine the voltage across the tissue over time,

$${\mathit{C}}_m\frac{\partial V}{\partial t}=-({\mathit{I}}_{\mathrm{ion}}+{\mathit{I}}_{\text{stim}})+\nabla \cdot (\sigma \nabla V)$$ (4)

Here, V is the membrane potential over space and time, σ is the conductivity tensor, I_stim is the stimulus current applied to pace the tissue and I_ion is the flow through the cell membrane per unit area, as dictated by the action potential model. A stimulus of 250,000 μA/cm² was applied at one end of the fibre for 5 ms in order to initiate propagation. The fibre was paced at 0.5 Hz until steady state was reached. Here, steady state was defined to be when the difference in the APD90 at the central node on successive time steps was less than 0.1 ms. The intracellular conductivity was set to 0.174 S/m (Bishop et al., 2010). A pseudo-ECG, as defined in Gima and Rudy (2002) was generated from the solution by measuring the membrane potential through a virtual electrode situated at the central node of the chain, from which the QT interval was estimated. We define the QT interval to be the time between the application of the initial stimulus and the peak of the T-wave on the ECG (or minimum where the T-wave is inverted on the pseudo-ECG), corresponding to the measurement taken in the rabbit wedge assay. The definition of the QT interval (as well as the APD90 value), as measured from the simulation results, is indicated in Fig. 1. The QT interval was calculated at the drug concentrations tested in the rabbit wedge assay, as well as lower concentrations of 0.001 μM, 0.01 μM, 0.1 μM and 1 μM where these were not included. The percentage change in the QT interval at each concentration as compared to the control was recorded.

In Fig. 1, a simulated action potential and pseudo-ECG from a single cell and one-dimensional tissue simulation respectively, are plotted for one example compound (compound 2659 in the Supplementary data). The simulated percent change in the APD90 value and QT interval is plotted together with the rabbit wedge assay results at a range of compound concentrations.

2.4.5. Implementation

An XML representation of the Shannon et al. (2004) rabbit action potential model was taken from the CellML repository (Lloyd, Lawson, Hunter, & Nielsen, 2008) and PyCML (Garny et al., 2008) was used to translate the CellML format into C++ code. Simulations were performed using the Chaste library (Mirams et al., 2013), with PETSc PDE solvers (Balay et al., 2012) and the CVODE package for ODEs (Hindmarsh et al., 2005), based upon adaptive time stepping with numerical differentiation formulae, using relative and absolute tolerances of 10⁻⁶ and 10⁻⁸ respectively. The full code used, together with input data, is available to download from www.cs.ox.ac.uk/chaste as detailed in Supplementary material S.1.

2.5. Statistical evaluation

The simulated percentage change in APD90/QT interval from single cell/one-dimensional tissue simulations respectively was compared to the percent change in QT interval recorded in the rabbit wedge assay. Where multiple assay repeats were performed, the average of the experimental results was used for comparison. Here we discuss how the ability of the assay to predict both QT prolongation and shortening in the rabbit ventricular wedge experiments was assessed.

Experimental and simulation results for each compound were independently classified into one of two categories. When focusing on predicting QT prolongation, if at any concentration tested, the experimental/simulation result showed more than a 10% change in the recorded QT interval/APD90 value, the compound was classified as a “prolonger” of the QT interval in the experimental/simulation result as appropriate. Otherwise, the compound was classified as a “non-prolonger”. When focusing on predicting QT shortening, if at any concentration tested the percentage change in APD90 value/QT interval was less than −10%, the compound was classed as a “shortener”. Otherwise the compound was classified as a “non-shortener”. 10% was chosen as the threshold for defining prolongation and shortening based upon the authors’ experience in recognising that a compound causing such a change in QT interval may be a cause for concern and warrant further investigation. This threshold also coincided with the value at which greatest correspondence between simulation and experimental results was seen in a preliminary threshold analysis.

The classification matrix in Table 1 presents the classification results obtained when considering the assay’s ability to predict QT prolongation when using PatchXpress data, assuming drugs interact with multiple ion channels (hERG, NaV1.5 and CaV1.2), and parameterising the drug block model with both the IC₅₀ value and the Hill coefficient.

Table 1.

Classification matrix presenting categorical classification of simulation and experimental results when considering the assay’s ability to predict QT prolongation. The results were obtained when using PatchXpress assay data, assuming compounds can interact with multiple channels and parameterising the drug block model with both the IC₅₀ value and the Hill coefficient for a set of 77 compounds. The accuracy, sensitivity, specificity, and positive and negative predictive values are calculated as indicated.

	Simulation prolonger	Simulation non-prolonger
Experimental prolonger	18	7	Sensitivity = 18/(18 + 7)
Experimental non-prolonger	10	42	Sensitivity = 42/(42 + 10)
	Positive predictive value = 18/(18 + 10) = 64.3%	Negative predictive value = 42/(42 + 7) = 85.7%	Accuracy = (18 + 42)/(18 + 7 + 10 + 42) = 77.9%

The classification matrix is used to calculate performance-related metrics to assess the agreement between experimental and simulation results. The overall accuracy is the proportion of compounds for which the experimental and simulation classification categories coincide. The sensitivity and specificity indicate the proportion of true positive and true negative results correctly identified. The positive and negative predictive values represent how likely a positive or negative simulation result is to be true. The method for calculating these metrics is included in Table 1, as calculated in Valentin et al. (2009). These metrics are calculated when focusing on predicting QT prolongation and shortening in the rabbit wedge experiments separately.

The Kappa value (Cohen, 1968) is also calculated, which measures agreement between simulation and experimental results whilst compensating for chance agreement, as determined by the distribution of experimental results across each category. The Kappa value is calculated according to

$$\text{Kappa}=\frac{p_a-p_e}{1-p_e}$$ (5)

where p_a is the proportion of compounds where simulation and experimental classification categories coincide and p_e is the proportion of compounds where agreement is expected by chance. p_e is calculated by multiplying the proportion of compounds with simulation results in a given category by the proportion of compounds whose experimental results are in that category and summing these results for all categories. A value between 0 and 0.2 represents poor agreement, 0.21–0.4 represents fair agreement, 0.41–0.6 moderate agreement, 0.61–0.8 good agreement and 0.81–1 very good agreement (Cohen, 1968).

95% confidence intervals are included for each metric. For the Kappa value it is assumed that the Kappa value is normally distributed when the data set being considered is sufficiently large. Intervals of size 1.96 times the standard error above and below the calculated value can then be taken. The standard error is calculated as described by Cohen (1968). Confidence intervals on the accuracy, sensitivity, specificity, positive and negative predictive values are obtained using Wilson’s score for binomial proportions, as described in Wilson (1927).

3. Results

3.1. Qualitative evaluation of assay predictivity

Table 2 presents the performance of the in silico assay when predicting QT prolongation in the rabbit wedge assay when considering different uses of the available ion channel screening data. Table 3 presents the performance of the assay when predicting QT shortening. Predictive capacity of the assay is compared when:

1. assuming drugs interact with just the hERG channel or with multiple channels (hERG, NaV1.5, CaV1.2, KCNQ1),

2. parameterising the drug block model with just the IC₅₀ value (and assuming the Hill coefficient is 1) or both the IC₅₀ value and Hill coefficient,

3. using IC₅₀ values obtained from data from the IonWorks/FLIPR and PatchXpress ion channel assays and the QSAR statistical model, and

4. performing single cell and one-dimensional tissue simulations.

Table 2.

Prolongation metric values calculated (with 95% confidence intervals indicated) for evaluation of the assay’s predictivity of QT prolongation in the rabbit ventricular wedge experiments when considering the different uses of the available ion channel data described. Entries are ordered alphabetically by the data type used in the simulations.

Case number	Ion channel data use combination	Accuracy (%)	Kappa value	Sensitivity (%)	Specificity (%)	Positive predictive value (%)	Negative predictive value (%)
1	IonWorks/FLIPR data, multiple channel block, fitting for IC50 value (121 compounds)	77.7 (69.5–84.2)	0.50 (0.33–0.67)	73.0 (57.0–84.6)	79.8 (70.0–87.0)	61.4 (46.6–74.3)	87.0 (77.7–92.8)
2	IonWorks/FLIPR data, multiple channel block, fitting for IC50 value & Hill coefficient (121 compounds)	75.2 (66.8–82.0)	0.45 (0.28–0.62)	70.3 (54.2–82.5)	77.4 (67.4–85.0)	57.8 (43.3–71.0)	85.5 (75.9–91.7)
3	IonWorks/FLIPR data, multiple channel block including KCNQ1 interactions, fitting for IC50 value (121 compounds)	77.7 (69.5–84.2)	0.51 (0.34–0.67)	75.7 (59.9–86.6)	78.6 (68.7–86.0)	60.9 (46.5–73.6)	88.0 (78.7–93.6)
4	PatchXpress data, hERG block only, fitting for IC50 value (77 compounds)	72.7 (61.9–81.4)	0.48 (0.29–0.67)	96.0 (80.5–99.3)	61.5 (48.0–73.5)	54.5 (40.1–68.3)	97.0 (84.7–99.5)
5	PatchXpress data, multiple channel block, fitting for IC50 value (77 compounds)	74.0 (63.3–82.5)	0.41 (0.18–0.63)	60.0 (40.7–76.6)	80.8 (68.1–89.2)	60.0 (40.7–76.6)	80.8 (68.1–89.2)
6	PatchXpress data, multiple channel block, fitting for IC50 value & Hill coefficient (77 compounds)	77.9 (67.5–85.7)	0.51 (0.31–0.72)	72.0 (52.4–85.7)	80.8 (68.1–89.2)	64.3 (45.8–79.3)	85.7 (73.3–92.9)
7	PatchXpress data, multiple channel block, fitting for IC50 value, one-dimensional simulation (77 compounds)	71.4 (60.5–80.3)	0.41 (0.20–0.62)	76.0 (56.6–88.5)	69.2 (55.7–80.1)	54.3 (38.2–69.5)	85.7 (72.2–93.3)
8	QSAR data, multiple channel block (372 compounds)	55.4 (50.3–60.3)	0.17 (0.08–0.27)	91.4 (86.0–94.8)	27.6 (22.0–34.0)	49.3 (43.7–55.0)	80.6 (70.0–88.0)

Table 3.

Shortening metric values calculated (with 95% confidence intervals indicated) for evaluation of the assay’s predictivity of QT shortening in the rabbit ventricular wedge experiments when considering the different uses of the available ion channel data described. Entries are ordered alphabetically by the data type used in the simulations. The missing entry is due to the inability to calculate the metric due to there being no compounds in the relevant categories for its computation.

Case number	Ion channel data use combination	Accuracy (%)	Kappa value	Sensitivity (%)	Specificity (%)	Positive predictive value (%)	Negative predictive value (%)
1	IonWorks/FLIPR data, multiple channel block, fitting for IC50 value (121 compounds)	69.4 (60.7–76.9)	0.13 (−0.10–0.37)	29.0 (16.1–46.6)	83.3 (74.3–89.6)	37.5 (24.7–52.3)	77.3 (68.0–84.5)
2	IonWorks/FLIPR data, multiple channel block, fitting for IC50 value & Hill coefficient (121 compounds)	71.1 (62.4–78.4)	0.23 (0.02–0.45)	41.9 (26.4–59.2)	81.1 (71.8–87.9)	43.3 (30.0–57.8)	80.2 (70.9–87.1)
3	IonWorks/FLIPR data, multiple channel block including KCNQ1 interactions, fitting for IC50 value (121 compounds)	69.4 (60.7–76.9)	0.13 (−0.10–0.37)	29.0 (16.1–46.6)	83.3 (74.3–89.6)	37.5 (25.0–51.9)	77.3 (68.0–84.5)
4	PatchXpress data, hERG block only, fitting for IC50 value (77 compounds)	76.6 (66.0–84.7)	0.00 (−0.40–0.40)	0.00 (0.00–17.6)	100 (93.9–100)	–	76.6 (66.0–84.7)
5	PatchXpress data, multiple channel block, fitting for IC50 value (77 compounds)	76.6 (66.0–84.7)	0.26 (−0.04–0.56)	33.3 (16.3–56.3)	89.8 (79.5–95.3)	50.0 (31.8–68.2)	81.5 (70.4–89.1)
6	PatchXpress data, multiple channel block, fitting for IC50 value & Hill coefficient (77 compounds)	75.3 (64.6–83.6)	0.24 (−0.06–0.54)	33.3 (16.3–56.3)	88.1 (77.5–94.1)	46.2 (29.3–63.9)	81.3 (70.0–88.9)
7	PatchXpress data, multiple channel block, fitting for IC50 value, one-dimensional simulation (77 compounds)	72.7 (61.9–81.4)	0.22 (−0.06–0.51)	38.9 (20.3–61.4)	83.1 (71.5–90.5)	41.2 (26.5–57.6)	81.7 (70.1–89.4)
8	QSAR data, multiple channel block (372 compounds)	79.8 (75.5–83.6)	0.10 (−0.09–0.28)	14.1 (7.58–24.6)	93.5 (90.2–95.8)	31.0 (26.1–36.5)	84.0 (79.7–87.5)

In Tables 2 and 3 we present our main evaluation of the predictions for QT prolongation and shortening respectively when using all the available compound data for each assay. The performance upon considering further variations of use of the available ion channel data can be found in the Supplementary material (Tables S1 and S2). The performance metrics calculated when predicting QT prolongation and shortening when including a subset of 44 compounds for evaluation for which data were available from all three ion channel assays and the rabbit wedge assay can be found in Tables S3 and S4 in the Supplementary material.

The highest valued performance metrics, when predicting both QT prolongation and shortening, were obtained when using PatchXpress assay data, and assuming that drugs interact with multiple channels (case 6 in Table 2 and case 5 in Table 3). The assay has an improved ability to predict QT prolongation when parameterising the drug block model with both the IC₅₀ value and the Hill coefficient (case 6) as opposed to just the IC₅₀ value (assuming the Hill coefficient is 1) (case 5). An accuracy of 77.9% for predicting QT prolongation and 76.6% for predicting QT shortening was found; according to the European Centre for the Validation of Alternative Methods (ECVAM) (Genschow et al., 2002) this corresponds to a good level of predictivity. A Kappa value of 0.51 for the prediction of prolongation and 0.26 for predicting shortening was calculated, corresponding to moderate and fair agreement respectively (Cohen, 1968).

3.2. Multiple ion channel interactions

The metric values presented in Tables 2 and 3 can aid in identifying the most advantageous uses of the available ion channel data. Across all three assays, improved predictivity was demonstrated when assuming drugs interact with multiple channels (hERG, NaV1.5, CaV1.2 (and KCNQ1 for the IonWorks assay)) as opposed to just the hERG channel. Increased accuracy is demonstrated, as well as an improved balance between sensitivity and specificity values. Improved predictivity is most apparent in the prediction of QT shortening. When assuming compounds interact only with the hERG channel (case 4), a Kappa value of 0 is obtained. This indicates the same level of agreement as expected if classification had been performed by chance. A sensitivity for shortening of 0% is also observed. This is because, by assuming that drugs interact solely with the hERG channel, the model is unable to predict shortening, as hERG channel block always leads to APD90/QT prolongation, with no additional channel interactions to counterbalance this effect.

The inclusion of IonWorks/FLIPR data on block of the KCNQ1/minK channel (carrying I_Ks current), in addition to the hERG, fast sodium and L-type calcium channels, leads to only a small improvement in the assay’s predictive ability. Comparing cases 1 and 3, for the prediction of QT prolongation, the inclusion of interactions with the KCNQ1/minK channel yields no increase in accuracy, and a 2.7% improvement in the sensitivity (75.7% as compared to 73.0%). Whilst only a slight improvement, this is concordant with the increased importance of interactions with the KCNQ1 channel that may be manifested when drugs block the hERG channel (consequently leading to increased APD prolongation).

3.3. Including Hill coefficients in drug block parameterisation

Differences in predictivity exhibited when parameterising the drug block model with both the IC₅₀ value and Hill coefficient, or just the IC₅₀ value (and assuming the Hill coefficient is equal to 1) are also subtle. When using PatchXpress assay data and assuming drugs interact with multiple ion channels (cases 5 and 6), an improved ability to predict QT prolongation is seen when parameterising the drug block model with both the IC₅₀ value and Hill coefficient (case 6 as compared to case 5 in Table 2). However, a decreased ability to predict shortening is seen (cases 5 and 6 in Table 3). When using IonWorks/FLIPR data to parameterise the drug block model, the opposite behaviour is seen. In all cases, the majority of the performance metric values being compared fall within each others’ 95% confidence intervals, indicating that, where differences are seen, these are not large.

3.4. PatchXpress versus IonWorks & FLIPR

The highest level of predictivity for both QT prolongation and shortening is demonstrated when using PatchXpress assay data. When predicting QT prolongation, a Kappa value indicating moderate agreement is obtained and an accuracy of 70–80% is demonstrated when using PatchXpress data (cases 4–7 in Table 2). A Kappa value indicating fair agreement is obtained when predicting QT shortening and assuming drugs can interact with multiple channels (cases 5–7 in Table 3), which is superior to when using IonWorks/FLIPR assay data (cases 1 and 3) or QSAR model data (case 8). When using IonWorks/FLIPR data and parameterising the drug block model with both the IC₅₀ value and Hill coefficient (case 2), fair agreement when predicting QT shortening is also demonstrated. Focusing on predicting QT prolongation, when assuming compounds interact with multiple channels, a similar level of predictivity is seen when using IonWorks/FLIPR data (case 1), as when using PatchXpress data (case 6). An accuracy of 77.7% as compared to 77.9% and a sensitivity and specificity of 73.0% and 79.8% as compared to 72.0% and 80.8%, respectively, are observed. This suggests it is possible to use IonWorks/FLIPR assay data in the in silico assay without a marked loss in accuracy. At GSK this data is available earlier in the drug development process than PatchXpress.

3.5. QSAR data

Using the QSAR model as the source of ion channel data, the Kappa values calculated when predicting both QT prolongation and shortening indicate a small improvement over chance (case 8 in Tables 2 and 3). However, when predicting QT shortening, the predictivity demonstrated is not vastly lower than when using IonWorks/FLIPR assay data (case 8 compared to cases 1 and 3 in Table 3). For all cases in Table 3, where IonWorks/FLIPR and PatchXpress assay data were used, the Kappa values calculated all fall within the 95% confidence interval calculated on the Kappa value when QSAR model data is used. However, when predicting QT prolongation, the performance of the model when using QSAR data is markedly worse than when using data from the other assays. It can be seen that the Kappa values obtained in cases 1–7 do not fall within the 95% confidence interval on the Kappa value from evaluation of the QSAR model, illustrating this vast difference. With further development and improvements to the QSAR model, it could potentially be used as a source of ion channel data for the in silico assay, in the very earliest stages of drug development. This would enable chemists to identify QT prolongation liability, and modify and optimise the design of compounds appropriately, before beginning to synthesise compounds.

3.6. Single cell versus one-dimensional tissue simulations

We evaluate the predictivity of the model when performing single cell simulations (case 5) as compared to one-dimensional tissue simulations (case 7), when using PatchXpress data, parameterising the drug block model with just the IC₅₀ value (assuming the Hill coefficient is 1), and assuming drugs interact with multiple ion channels. Reduced predictive ability was demonstrated for predicting both QT prolongation and shortening when performing one-dimensional simulations as compared to single cell simulations (an accuracy of 71.4% as compared to 74.0% for QT prolongation and an accuracy of 72.7% as compared to 76.6% and Kappa value of 0.22 as compared to 0.26 for QT shortening). However, the same Kappa value of 0.41, corresponding to moderate agreement, is yielded in both cases when predicting QT prolongation, and a higher sensitivity (and consequently lower specificity) is associated with the use of one-dimensional simulations in the prediction of both QT prolongation and shortening. The metric values calculated when performing one-dimensional simulations fall within the 95% confidence intervals of the metrics calculated when performing single cell simulations, illustrating that the difference in the predictivity demonstrated between the two methods is not large.

3.7. Quantitative evaluation of assay predictivity

Whilst the performance metrics in Tables 2 and 3 allow an evaluation of the ability of the assay to predict QT “prolongation” or “shortening”, an appreciation of the quantitative accuracy of these predictions can be gained through consideration of a plot of the form presented in Fig. 2. In this figure, the results of case 6, when using PatchXpress data, are presented.

Fig. 2.

Plot of concentrations (EC10 values) at which a 10% change in APD90 value/QT interval is expected, as interpolated from simulation and experimental results, for each compound. The results from case 6, using PatchXpress data, are presented. Compounds exhibiting more than 10% change in their experimental or simulation results after drug administration, as compared to the control measurement, at at least one test concentration were included. This enabled interpolation of the EC10 values. Points plotted with an asterisk (*) are compounds for which more than a 10% change in the QT interval length (as compared to the control measurement) is exhibited in both simulation and experimental results. These points are plotted in one of four quadrants according to the classification of the simulation and experimental results: both experimental and simulation results show prolongation (quadrant 1), both show shortening (quadrant 3), experimental results show shortening and simulation results show prolongation (quadrant 2), simulation results show shortening and experimental results show prolongation (quadrant 4). Points plotted with a circle (○) are compounds for which only one of the experimental and simulation results show more than a 10% change in the QT interval as compared to the control. Interpolation is used to determine the EC10 value from this result. For the remaining experimental or simulation result, the percent change in QT interval is between −10% and 10% (showing “no effect”) at all concentrations tested. This result is assumed to have an EC10 value corresponding to the maximum concentration tested in the rabbit wedge assay amongst all the compounds which show “no effect” (with the percent change in APD90 or QT interval between −10% and 10%), which has a value of 500 μM. Half log unit lines which correspond to the error commonly associated with the ion channel assays are included as an indication of the range of accepted error.

Fig. 2 includes compounds for which at least one of the simulation or experimental APD90 value/QT interval measurements demonstrates more than a 10% change at one of the drug concentrations tested as compared to the control. For these compounds, the percentage change in APD90/QT interval and corresponding concentrations tested are interpolated to determine the concentration at which a 10% (for results classified as demonstrating prolongation) or −10% (for results classified as demonstrating shortening) change in APD90 value/QT interval is expected (EC10). The EC10 values from the experimental and simulation results for each compound are plotted against one another in one of the quadrants 1 to 4 marked in Fig. 2. The half log unit lines included in Fig. 2 indicate the margin of error commonly associated with the ion channel assays used and so can be thought to provide an indication of the boundaries of acceptable error. Where less than 10% change was observed in either the experimental or simulation results, but over 10% was observed in the other result, the EC10 values for compounds are plotted on the relevant axis.

Most compounds are plotted in quadrants 1 and 3, indicating qualitative agreement between simulation and experimental results. Most of these points are also plotted within, or close to, half log unit boundaries, further indicating the quantitative accuracy of the predictions. Few compounds are plotted in quadrants 2 and 4, which would indicate that simulation and experimental predictions were opposite (one being shortening and the other prolongation). Points plotted along the inner axes of Fig. 2 are located mostly along the central and inner portions of the axes (closest to the origin). This indicates that where a disagreement between the classification of experimental and simulation results occurs (with one predicting that the drug will induce more than a 10% change in the QT interval and the other not), it is often the case that the EC10 value is low, corresponding to a relatively weak action. Thus, whilst a qualitative agreement is not evident using the binary classification system, there is still a degree of quantitative agreement between the simulation and experimental results.

4. Discussion

We have evaluated an in silico assay which uses ion channel data from high-throughput ion channel screens to predict the results of the rabbit left-ventricular wedge assay. Simulations yielded good qualitative and quantitative predictions. The in silico assay demonstrates high levels of sensitivity and specificity for the detection of QT prolongation, as required for an assay suitable for use in preclinical safety assessment. This indicates that a high proportion of true positive results are recognised by the assay and there is a high level of confidence that a simulation result predicting QT prolongation will translate into a rabbit wedge assay result showing QT prolongation. The assay also performs well in the prediction of QT shortening, although a lower sensitivity is demonstrated. 77 compounds were included for evaluation when using ion channel data from the PatchXpress assay, 121 compounds when using data from the IonWorks/FLIPR assay, and 372 compounds when using predicted IC₅₀ values from the QSAR model. This constitutes an unprecedented number of compounds for the evaluation of such an in silico assay.

We identified the most advantageous ways of using the available ion channel screening data. The best predictions occurred using the PatchXpress assay as the source of concentration–effect data for parameterisation of the drug block model, when assuming drugs interact with multiple ion channels (hERG, NaV1.5 and CaV1.2), and fitting the drug block model with both the IC₅₀ value and Hill coefficient (case 6).

Performing one-dimensional tissue simulations in place of single-cell simulations did not appear to greatly enhance the predictivity of the model. Using ion channel data for the KCNQ1 channel from the IonWorks/FLIPR assay, the predictivity of the model was compared when assuming drugs interact with the KCNQ1 channel in addition to the hERG, NaV1.5 and CaV1.2 channels (case 3 as compared to case 1). A slight improvement in predictivity was observed; however, in the compound set considered, there were few compounds exhibiting very strong block of the KCNQ1 channel (with the highest pIC₅₀ value observed being 5.6). Inclusion of interactions with the KCNQ1 channel would likely have more of an influence on the level of predictivity demonstrated by the assay if the compound set had included more compounds with a strong affinity for this channel. On the basis that evaluation results are no worse with the inclusion of interactions with the KCNQ1/minK channel, if available, it would probably be advantageous to include these interactions.

The observation of improved predictivity when assuming drugs interact with multiple ion channels is concordant with the findings of Mirams et al. (2011) and Obiol-Pardo et al. (2011). Improved predictivity when using PatchXpress assay data is as expected, due to this being the best quality data available for the study. However, it is encouraging to see similar predictive ability when using IonWorks/FLIPR data, which is acquired earlier in the drug development process, at a lower cost and a higher throughput. This indicates the potential for the use of this in silico assay early in the drug development process.

The level of predictivity demonstrated when performing one-dimensional tissue simulations as compared to single cell simulations showing little improvement suggests that the use of single cell simulations, which have lower computational cost, may be sufficient for the intended purpose.

Low predictive ability is demonstrated when using IC₅₀ values from the QSAR model. This indicates the value of using direct measurement of ionic current inhibition from the PatchXpress and IonWorks screens. However, some predictive capacity is demonstrated by the QSAR method, with metrics indicating levels of predictive power above those achieved by chance alone, and this is improved when including interactions with multiple ion channels. Thus, with further improvements to the QSAR model, there may be future potential for its use with this assay. Such improvements could include replacing the class prediction for the CaV1.2 channel with an actual IC₅₀ value as is the case with the hERG and NaV1.5 channels. Using only data from one test system could also decrease the subsequent data variability.

The effect on simulation predictions when parameterising the drug block model with just the IC₅₀ value (and assuming a Hill coefficient of one), as has often previously been the method adopted (Bottino et al., 2006; Mirams et al., 2011) and both the IC₅₀ value and Hill coefficient has also been explored. The effects of including Hill coefficients in the drug block parameterisation are not conclusive. Improvements in predictivity were seen in some cases but reductions in others: in all cases the differences were only slight. Further investigation, comparing the impact of the inclusion of Hill coefficients in the drug block model, dependent on the quantity and quality of concentration–effect data available for fitting would clarify this further.

4.1. Limitations of the in silico assay

The evaluation presented demonstrates the ability of this in silico assay to predict the results of the rabbit left-ventricular wedge assay using integrated concentration–effect data for four cardiac ion channels (hERG, NaV1.5, CaV1.2 and KCNQ1). However, elevated levels of predictivity would be desired before this approach would be considered as a replacement for this experiment. A number of limitations of the present approach could be addressed in order to improve the predictive capacity. The conductance block drug block model we assumed, representing drug interactions with the individual ion channels, is commonly adopted (Bottino et al., 2006; Davies et al., 2012; Mirams et al., 2011), and easily parameterised with readily available high-throughput ion channel screen data. However, it is a simple representation, lacking in its ability to describe complex drug-ion channel interactions. It includes no consideration of the rate of binding and unbinding of the drug, and assumes that the drug block is immediately in steady state. The incorporation of a Markov model drug block formulation, which could capture and represent kinetic effects of the ion channels would thus be desirable, as has recently been investigated in Di Veroli, Davies, Zhang, Abi-Gerges, and Boyett (2013).

The comparison of model predictions when using single-cell and one-dimensional tissue simulations was performed to acknowledge that differences inherent in tissue may not be fully captured by single cell models. Initial comparison has shown that the model demonstrates marginally increased sensitivity when one-dimensional simulations are performed. It would be desirable to explore simulation setups more akin to those used in the rabbit wedge assay and compare the predictivity demonstrated. This would include considering higher dimensional simulations, including variation in cellular properties across the ventricular wall, and the addition of a perfusing bath. Increasing the number of compounds used for evaluation, as well as investigating the inclusion of interactions with additional ion channels, would add further weight to findings and conclusions drawn from this evaluation. Such investigations would aid in finding the most suitable in silico assay for use in pharmacological practice for the prediction of the results of animal-based tests.

The assay does not perform as well when predicting QT shortening as when predicting QT prolongation. As the QSAR model is unable to identify hERG activators, which can be the cause of QT shortening, this could offer an explanation for the reduced predictive ability in this case. Whilst the IonWorks and PatchXpress assays have the capability to detect such compounds, no such compounds were included for evaluation of these two assays. It would be of interest to compare the performance of the in silico assay when including a selection of hERG activators in the compound set used for evaluation.

There are many other ionic currents in cardiac tissue, travelling through additional ion channels, pumps and exchangers, that are not screened, and hence blockade of these cannot be accounted for by this in silico assay. Similarly, pharmaceutical compounds have also been known to interfere with trafficking of ion channel proteins to the cell membrane, and whilst some in vitro screens can detect such effects (Wible et al., 2005), high-throughput screens typically used in safety assessment are unlikely to detect these. Such effects can be detected using an in vivo animal-based screen. So whilst the in silico assay could be used to reduce animal-based testing, complete replacement of all animal-based pro-arrhythmic screening is not yet practical.

The variability associated with high-throughput screens can be considerable. In related work, we have quantified this uncertainty, and proposed a method for estimating the subsequent confidence in simulation outputs (Elkins et al., 2013, in this issue). This technique will be applied to rabbit wedge QT predictions in future work. Variability is also seen across the screening platforms depending upon the cell type used and the voltage protocol adopted. As can be seen from the ion channel screening methods detailed in the Supplementary material (S.3), some such variations exist between the methods adopted which may contribute to differences in predictive ability seen when using data acquired from different assays. In addition, the ion channel screens are performed at room temperature. If experiments were instead to be performed at physiological temperatures, any temperature-dependent effects would be eliminated and hopefully an improved agreement between simulation and experimental results would be seen.

We have demonstrated the ability of an in silico assay which integrates concentration–effect data from high-throughput ion channel assays to predict the results of the rabbit left-ventricular wedge assay. The evaluation of this approach has been undertaken on a substantial number of compounds. The predictive ability of the model is found to be good, particularly for detecting QT prolongation, which is a large focus of safety assessment. It also performs well in the prediction of QT shortening, albeit with lower levels of sensitivity demonstrated. Furthermore, the assay demonstrates good quantitative agreement with experiment.

Simulations are suitable for very high-throughput use in the early stages of the drug development process and have the potential to complement, reduce, and possibly, in the future, replace some existing animal-based assays and reduce the associated levels of attrition later in drug development. It is entirely possible that the use of human mathematical electrophysiology models, based on the human ion channel screens, will yield more relevant predictions for human clinical QT prolongation, than the current assay does for rabbit tissue. This is an avenue of future work.

Incorporation of an in silico action potential assay into safety pharmacological practice will provide a time- and cost-effective method for assessment of pro-arrhythmic liability, capable of much higher throughput, and more complex mechanistic investigation, than is possible with the existing methods.

Abbreviations

AP (D)

Action Potential (Duration)

ECG

electrocardiogram

ECVAM

European Centre for the Validation of Alternative Methods

FLIPR

FLuorescence Imaging Plate Reader

GSK

GlaxoSmithKline

hERG

human-Ether-a-go-go Related Gene

IC₅₀

Concentration for 50% Inhibition

ICH

International Conference for Harmonization

I_Kr

rapid delayed rectifier potassium current

I_Ks

slow delayed rectifier potassium current

QSAR

Quantitative Structure Activity Relationship

pIC₅₀

minus log₁₀ of IC₅₀

TdP

Torsades de Pointes