Radiobiological Optimization of Combination Radiopharmaceutical Therapy Applied to Myeloablative Treatment of Non-Hodgkin’s Lymphoma

Abstract

Combination treatment is a hallmark of cancer therapy. Although the rationale for combination radiopharmaceutical therapy was described in the mid ‘90s, such treatment strategies have only been implemented clinically recently, and without a rigorous methodology for treatment optimization. Radiobiological and quantitative imaging-based dosimetry tools are now available that enable rational implementation of combined targeted radiopharmaceutical therapy. Optimal implementation should simultaneously account for radiobiological normal organ tolerance while optimizing the ratio of two different radiopharmaceuticals required to maximize tumor control. We have developed such a methodology and applied it to hypothetical myeloablative treatment of non-hodgkin’s lymphoma (NHL) patients using ¹³¹I-tositumomab and ⁹⁰Y-ibritumomab tiuxetan.

Methods

The range of potential administered activities (AA) is limited by the normal organ maximum tolerated biologic effective doses (MTBEDs) arising from the combined radiopharmaceuticals. Dose limiting normal organs are expected to be the lungs for ¹³¹I-tositumomab and the liver for ⁹⁰Y-ibritumomab tiuxetan in myeloablative NHL treatment regimens. By plotting the limiting normal organ constraints as a function of the AAs and calculating tumor biological effective dose (BED) along the normal organ MTBED limits, the optimal combination of activities is obtained. The model was tested using previously acquired patient normal organ and tumor kinetic data and MTBED values taken from the literature.

Results

The average AA values based solely on normal organ constraints was (19.0 ± 8.2) GBq with a range of 3.9 – 36.9 GBq for ¹³¹I-tositumomab, and (2.77 ± 1.64) GBq with a range of 0.42 – 7.54 GBq for ⁹⁰Y-ibritumomab tiuxetan. Tumor BED optimization results were calculated and plotted as a function of AA for 5 different cases, established using patient normal organ kinetics for the two radiopharmaceuticals. Results included AA ranges which would deliver 95 % of the maximum tumor BED, which allows for informed inclusion of clinical considerations, such as a maximum allowable ¹³¹I administration.

Conclusions

A rational approach for combination radiopharmaceutical treatment has been developed within the framework of a proven 3-dimensional personalized dosimetry software, 3D-RD, and applied to the myeloablative treatment of NHL. We anticipate combined radioisotope therapy will ultimately supplant single radioisotope therapy, much as combination chemotherapy has substantially replaced single agent chemotherapy.

INTRODUCTION

Combination chemotherapy is the mainstay of lymphoma treatment. In contrast, despite more than 25 years of clinical study and a number of theoretical studies (1–3), radiopharmaceutical therapies have only recently been combined in a clinical trial (4–8), principally due to the technical difficulties and concerns over toxicity (9), such treatment strategies have only been implemented clinically recently, and without a rigorous methodology for treatment optimization.

Anti CD-20 targeted monoclonal antibodies, both unlabeled and radiolabeled, are active agents in the treatment of B-cell lymphomas (10). The unlabeled monoclonal antibody rituximab mediates its therapeutic effects through several mechanisms including antibody-dependent cellular cytotoxicity, complement fixation and the direct induction of apoptosis (11). The addition of radioactivity to the anti CD20 antibody has been shown to increase response rates and therapeutic efficacy over the unlabeled antibody alone in several trials (12). The two FDA-approved radioimmuonotherapies for lymphoma, ¹³¹I tositumomab plus unlabeled tositumomab (Bexxar therapeutic regimen) and rituximab plus ⁹⁰Y-ibritumomab tiuxetan (Zevalin) are effective therapies for follicular lymphomas; however their administered radioactivity doses, and quite likely their efficacy, are limited by hematopoietic toxicity.

High dose single agent radioimmunotherapy with ¹³¹I-tositumomab with autologous stem cell support was introduced by Press and colleagues over two decades ago (13): they were able to achieve high response rates and manageable non-hematopoietic toxicity. More recently, ⁹⁰Y-ibrutumomab tiuxetan has also been used in clinical trials in conjunction with blood or marrow transplantation without excess toxicity (14). Individualized patient dosimetry to determine the administered activity required to deliver tolerable normal organ absorbed doses was essential to the safe conduct of these trials (15).

The combination of ¹³¹I-tositumomab and ⁹⁰Y-ibritumomab tiuxetan in a myeolablative regime has the potential to substantially increase efficacy for two reasons: (a) the combination may target a wider range of tumor diameters, given the different mean path lengths of β-particles for the respective isotopes (~1 mm with ¹³¹I, ~3–5 mm with ⁹⁰Y) (2); (b) the radiopharmaceuticals have orthogonal toxicity (predominantly lungs and kidneys from¹³¹I-tositumomab, and liver from⁹⁰Y-ibritumomab tiuxetan) (16, 17) which may permit a greater total absorbed dose to the targets (tumors). However, there are several limitations in the currently available combination models, which the methodology presented here seeks to address. First, the current combination methodologies are based on criteria that limit the maximum tolerated absorbed dose (MTD) for the organs at risk (9). However, it has been shown that the relevant dosimetric quantity related to toxicity in normal organs (18) is the biological effective dose (BED). This is especially important for therapies combining two radionuclides since the dose rates are different. Therefore a model based on maximum tolerated BED (MTBED) constraints would be preferable. Second, the end point of the proposed model, that is the quantity which is maximized, is the tumor BED, or, for a patient with multiple tumors which is often the case for this disease, the equivalent uniform biological effective dose (EUBED), which has also shown promise as a relevant quantity for tumor response. Finally, the present methodology has been developed in the context of a personalized 3-dimensional dosimetry package, 3D-RD, with the objective and the proven ability to be implemented clinically in real time (19).

MATERIALS AND METHODS

Overview

The method presented here optimizes the administration of ¹³¹I-tositumomab and ⁹⁰Y- ibritumomab tiuxetan for treatment of lymphoma at myeloablative doses. It may be generalized to any combination of therapeutics whose toxicities are orthogonal. It is dosimetrically-driven and, more specifically, founded on radiobiological modeling and the linear-quadratic formalism. The methodological steps are as follows: first, establish the equations for limiting toxicities based on limiting normal organ BED. Note that this is an extension of previous work (9) using absorbed dose and treatment to both MTDs. Next, instead of focusing solely on toxicity, seek to optimize response by maximizing the tumor BED while respecting the established normal organ constraints. Finally, extend the optimization to multiple tumors by calculating the disease EUBED.

Normal Organ Absorbed Dose Constraints

Mathematical modeling for the constraints imposed by normal organ toxicity for combined radioimmnotherapy has been previously developed (9) in the context of non-myeloablative neuroendocrine tumor therapy. For NHL, the typical constraints for myeloablative ¹³¹I-tositumomab, or Bexxar (B) and ⁹⁰Y-ibritumomab tiuxetan, or Zevalin (Z) are the lungs (lu) and liver (li), respectively, with kidneys (ki) as a possible concern for Bexxar. Using this formalism and given the MTD constraint values and the dose per unit of administered activity of agent A (A=Z or B for Zevalin or Bexxar, respectively), d_A,O, to the dose limiting organ O (O=lu or li, for lung or liver, respectively), a system of two equations and two unknowns can be set up and solved for the amount of injected activities of ¹³¹I-tositumomab, A_B, and ⁹⁰Y-ibritumomab tiuxetan, A_Z:

$$\{\begin{array}{c}{\mathit{MTD}}_{lu}=A_Z{d}_{Z,lu}+A_B{d}_{B,lu}\\ {\mathit{MTD}}_{li}=A_Z{d}_{Z,li}+A_B{d}_{B,li}\end{array}.$$ (1)

While equations (1) allow for any mathematical solution, additional physical constraints are imposed, namely, the administered activities must be positive and the total absorbed dose to kidneys must not exceed the threshold for renal toxicity. Strictly speaking, both equations should be written as inequalities. However, it is clear that from an optimization standpoint, the limiting values are the ones of interest. Note that since the MTD and d values are positive, it is not possible for both A_Z and A_B to be negative solutions to (2), and an optimal solution will exist. An example of this formalism is illustrated graphically in Figure 1a using d values taken from previously published patient data for ¹³¹I-tosituimomab (20) and ⁹⁰Y-ibritumomab tiuxetan (21), as are all the examples in this manuscript. An MTD value of 27 Gy was chosen for both the liver and the lungs (19).

Figure 1.

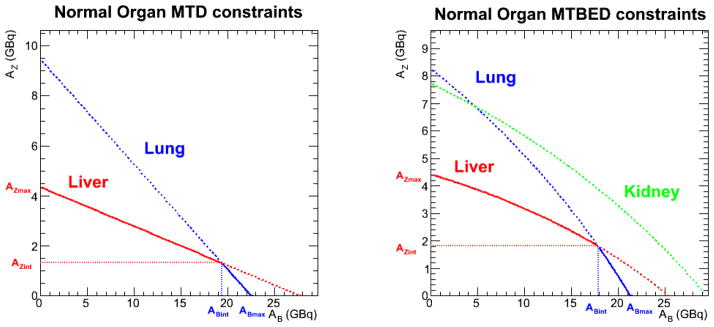
Optimization based on normal organ MTD (Figure 1a from equation 1) and MTBED (Figure 1b from equations 6 or 8) constraints in A_B versus A_Z plots. The blue line shows the lungs constraint; the red line shows the liver constraint; the green line is for the kidneys. The lines are solid when they represent the activity limiting constraint, dotted line constraints are automatically satisfied by the solid line criteria

BED Constraints

The BED (22) relates absorbed dose and absorbed dose rate to the biological effect it would have if the total absorbed dose were delivered at an infinitesimally low dose-rate. As validation of its biological importance, the BED has been shown be predictive of toxicity thresholds in normal organs (18). Consequently, a model which incorporates radiobiology and more specifically the BED into its constraints is more likely to be successful in limiting toxicity. The formula for the BED is:

$$\mathit{BED}=D\left(1+\frac{G(\infty )}{\alpha /\beta }·D\right)$$ (2)

where α and β are the organ specific radiobiological parameters from the linear quadratic model of cell survival (23), D is the absorbed dose, and G(∞) is the Lea-Catcheside G-factor:

$$G(\infty )=\frac{2}{D^2}·{\int }_0^{\infty }\stackrel{.}{D}(t)dt{\int }_0^t\stackrel{.}{D}(W)·e^{-\mu (t-w)}dw.$$ (3)

Here μ is the DNA repair constant, assuming exponential repair, and t and w are integration variables. For a simple exponential fit of the dose rate, Ḋ, as a function of time

$$\stackrel{.}{D}(t)={\stackrel{.}{D}}_0{e}^{-\lambda t},$$ (4)

which is typical for normal organ kinetics for both ¹³¹I-tosituimomab and ⁹⁰Y-ibritumomab tiuxetan individually, the G-factor reduces to:

$$\frac{\lambda }{\lambda +\mu },$$ (5)

where λ is the exponential dose rate decay rate from equation (4). The normal organ MTBED values constrain the two administered activities, A_Z and A_B, according to the following formulae:

$${\mathit{MTBED}}_i=(A_Z{d}_{Z,i}+A_B{d}_{B,i})\left(1+G{(\infty )}_i·\frac{A_Z{d}_{Z,i}+A_B{d}_{B,i}}{{\alpha }_i/{\beta }_i}\right)$$ (6)

where the index i can stand for any dose-limiting organ and the d_A,i values still represent the absorbed dose per unit activity for Bexxar (A=B) or Zevalin (A=Z) for the respective organ i. The dose rate is now a sum of the two (B and Z) exponential dose rate functions and no longer a simple exponential. The G-factor thus becomes:

$$G{(\infty )}_i=\frac{1}{{(A_Z{d}_{Z,i}+A_B{d}_{B,i})}^2}\left(\frac{A_Z^2{d}_{Z,i}^2{\lambda }_{Z,i}}{{\lambda }_{Z,i}+{\mu }_i}+\frac{A_B^2{d}_{B,i}^2{\lambda }_{B,i}}{{\lambda }_{B,i}+{\mu }_i}\right)$$ (7)

The values used for the α/β and μ parameters are given in Table 1 and are taken from the literature.

Table 1.

Radiobiological Parameters Used.

Parameter	NHL	Lungs	Liver	Kidneys
α/β (Gy)	8.6 (28)	3.3 (29)	2.5 (30)	2.6 (18)
λB(h−1)	N/A	0.0106 (31)	0.0124 (31)	0.0115 (31)
λZ(h−1)	N/A	0.0182 (32)	0.00728 (32)	0.00957 (32)
μ(h−1)	1.3 (33)	0.46 (34)	0.28 (35)	0.25 (18)

Numbers in parentheses indicate the reference from which the value was taken.

Equation (6) is quadratic in A_Z (and A_B). By solving for A_Z and plotting as a function of A_B (or vice versa) a graphical representation of equation (6) is obtained; these are shown in Figure 1b using the same measured patient parameters as for Figure 1a but with MTBED constraints of 30 Gy for the lungs and 35 Gy for the liver. Note that we have included the kidneys as a possible limiting organ although in this illustrative example the kidney constraints will always be met if the lung and liver constraints are met. The equations derived from equation (6) that are graphed in Figure 1b are:

$$A_Z=\frac{({\lambda }_{Z,i}+{\mu }_i){\alpha }_i/{\beta }_i}{2{\lambda }_{Z,i}{d}_{Z,i}^2}\left(-d_{Z,i}+\sqrt{d_{Z,i}^2-4\frac{{\lambda }_{Z,i}{d}_{Z,i}^2}{({\lambda }_{Z,i}+{\mu }_i){\alpha }_i/{\beta }_i}\left(A_B{d}_{B,i}+\frac{{\lambda }_{B,i}{A}_B^2{d}_{B,i}^2}{({\lambda }_{B,i}+{\mu }_i){\alpha }_i/{\beta }_i}-{\mathit{MTBED}}_i\right)}\right)$$ (8)

where the index i can stand for any dose-limiting organ (lungs, liver and kidneys in Figure 1b).

The limiting constraints are shown in solid color in Figure 1: any combination of A_B and A_Z whose corresponding point on the graph is located within the bounds of the 2 axes and the solid colored lines will deliver a dose (or BED) less than or an equal amount to the maximum tolerated dose (or MTBED) to both organs. Concretely, in the case where a combination of two BED-based constraints (lungs and liver, as illustrated in Fig. 1b) are used, the intersection of the two curves (A_Bint, A_Zint) may be found be setting equation (8) for liver (li) equal to equation (8) for lungs (lu), solving for A_B and then substituting this value of A_B into the version of equation (8) for either organ to find A_Z. These activity values (A_Bint, A_Zint) from the intersection point will deliver the MTBED to both organs, lungs and liver. In theory, an algebraic formulation of A_Bint (and A_Zint) may be derived; however, the formula is a 4^th order polynomial and it is much simpler to arrive at the solution numerically.

The intersection values for A_B and A_Z maximize the BED to the constraining organs, but it does not necessarily follow that those are the desired or optimal activities to administer, since normal organs are not the target of the radiopharmaceutical therapy. Ultimately, a dosimetric quantity that translates the effect of the administered activities upon the target, i.e., the tumor(s), is the quantity that should be maximized. Intuitively, the intersection point represents a probable good first order estimate of this optimization point. However, for a more rigorous optimization, the target quantity to be maximized needs to be determined and then calculated and plotted as a function of A_B and A_Z taken along the solid path plotted in Figure 1b. The application of this concept is demonstrated using (a) the tumor BED and (b) the disease EUD for multiple tumors.

Tumor BED Optimization

The tumor is a more complex object than a normal organ from a radiobiological standpoint and a single dosimetric value such as the mean BED is not expected to be predictive of response in tumors that have a non-uniform absorbed dose distribution and, depending upon tumor size, a spatially variable radiosensitivity. However, BED remains a reasonable first order predictor of response for smaller tumors. Moreover, more predictive radiobiological quantities applicable to larger heterogeneous tumors, such as surviving fraction, EUD and tumor control probability, are all derived from BED values, typically taken at the voxel level. Thus, any methodology based on BED optimization may easily be extended to those other, more comprehensive radiobiological parameters. As a first order single value response or activity escalation criterion, the BED is superior to administrated activity or even absorbed dose.

The expression for the tumor BED is a variation of equation (6) where the subscript tum denotes tumor:

$${\mathit{BED}}_{\mathit{tum}}=(A_Z{d}_{Z,\mathit{tum}}+A_B{d}_{B,\mathit{tum}})\left(1+G{(\infty )}_{\mathit{tum}}·\frac{A_Z{d}_{Z,\mathit{tum}}+A_B{d}_{B,\mathit{tum}}}{{\alpha }_{\mathit{tum}}/{\beta }_{\mathit{tum}}}\right)$$ (9)

The values of BED_tum as a function of A_B are obtained by substituting the expression for A_Z from the organ-appropriate version of equation 8 into equation (9). That is, in the example illustrated in Figure 1b, by using the liver constraint (eq. 8) for A_B<A_Bint and the lung constraint (eq. 8) for A_B≥A_Bint, the dependence of the tumor BED as a function of A_B may be obtained and thus the optimal value for A_B (and consequently A_Z). The calculation of G(∞)_tum is no longer trivial, however, as it depends on the sum of the contributions from both the ¹³¹I-tositumomab (B) and ⁹⁰Y-ibritumomab tiuxetan (Z) whose uptake in tumor are typically best described as a two-component exponential fit:

$$\stackrel{.}{D}(t)={\stackrel{.}{D}}_{0,B}(1-e^{-{\kappa }_{B}t})e^{-{\lambda }_{B}t}+{\stackrel{.}{D}}_{0,Z}(1-e^{-{\kappa }_{Z}t})e^{-{\lambda }_{Z}t}$$ (10)

where the κ parameters are the uptake constants, typically on the order of 24–48 hours. Although the biological uptake and clearance rates may be assumed to be the same, since ¹³¹I and ⁹⁰Y have different physical half-lives, the κ and λ values will be different for each isotope. For purposes of illustration, we will assume a biological half-life, T_λbio of 4 days and a biological uptake, T_κbio of 48 hours, values typically seen in clinical dosimetry, and the ¹³¹I and ⁹⁰Y dose rate constants may be calculated using:

$$\left\{\begin{array}{c}{\lambda }_i=\frac{ln2}{T_{{\phi }_i}}+\frac{ln2}{T_{\lambda \mathit{bio}}}\\ {\kappa }_i=\frac{ln2}{T_{{\phi }_i}}+\frac{ln2}{T_{\kappa \mathit{bio}}}\end{array}\right\},$$ (11)

where the index i is valid for both B and Z and T_φi is the physical half-life of the isotope, 64.0 hours for Z (⁹⁰Y) and 8.02 days for B (¹³¹I). By integrating the two terms in equation (10) separately, the parameters Ḋ_0,i may be solved for, giving:

$${\stackrel{.}{D}}_{0,i}=D_i\frac{{\lambda }_i({\lambda }_i+{\kappa }_i)}{{\kappa }_i}$$ (12)

where D_i is the absorbed dose for the isotope i. The values for D_i are taken from the literature (24, 25) and are listed in Table 3 as d_tum, the absorbed dose per unit activity. By substituting expression (10) into equation (3) the G-factor may be obtained, and then the value calculated numerically (26).

Table 3.

Parameters for disease EUBED-based optimization.

	Tumor 1	Tumor 2	Tumor 3	Tumor 4
dBtum (Gy/GBq)	2.5	2.0	3.0	1.6
dZtum (Gy/GBq)	10.0	12.0	14.0	10.0
mtum (g)	10	12	5	25

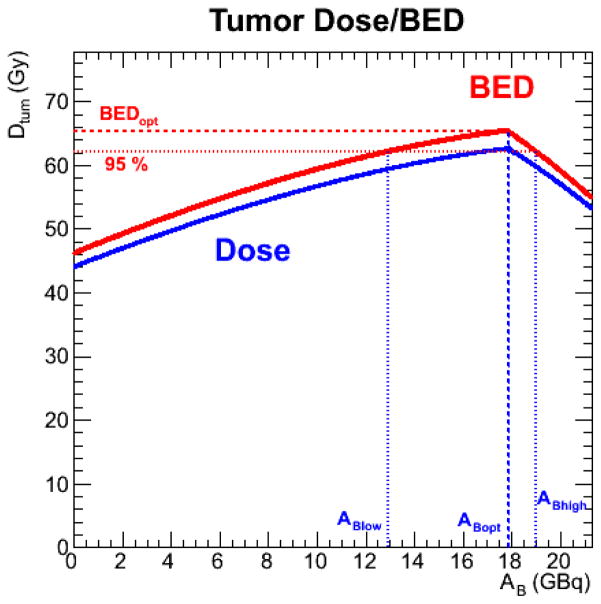
The tumor BED as a function of A_B is illustrated in Figure 2 for the same case as shown in Figure 1b (case 1) and using the same normal organ parameters; further examples are given in the results section in Table 4 and Figure 3 for a range of input values obtained from the same patient data sets whose normal organ parameters are given in Table 2. The MTBED values are the same as previously for the lungs and liver; the kidney MTBED is taken to be 28 Gy. The illustrations include A_Blow and A_Bhigh values which are the Bexxar administered activities which bracket the range for which the tumor will receive 95 % of the maximum BED.

Figure 2.

Illustration of tumor BED-based optimization (case 1). The tumor dose and BED are plotted as a function of A_B. Here the optimal A_B (and A_Z) values (A_Bopt, A_Zopt) are the same as the intersection values (A_Bint, A_Zint).

Table 4.

Results for tumor BED-based optimization.

	Case 1	Case 2	Case 3	Case 4	Case 5
ABmax (GBq)	21.3	19.4	26.3	19.4	21.3
ABint (GBq)	17.9	18.0	11.3	-	17.0, 20.4
ABopt (GBq)	17.9	17.9	2.40	3.93	17.1
95 % range	12.9–19.0	15.8–18.5	0.0–12.1	0.0–12.0	15.7–21.0
AZmax (GBq)	4.41	2.62	7.14	7.14	3.11
AZint (GBq)	1.82	0.98	5.15	-	0.50, 1.62
AZopt (GBq)	1.82	0.98	6.77	5.97	1.64
95 % range	1.24–2.71	0.59–1.24	4.90–7.14	3.30–7.14	0.15–1.82
BEDli (Gy)	35.0	35.0	35.0	31.9	35.0
BEDlu (Gy)	30.0	30.0	27.7	30.0	28.0
BEDki (Gy)	20.9	24.9	24.0	21.8	28.0
ADtum (Gy)	62.7	54.6	86.1	71.5	67.6
BEDtum (Gy)	65.4	56.6	93.7	76.4	70.6

Figure 3.

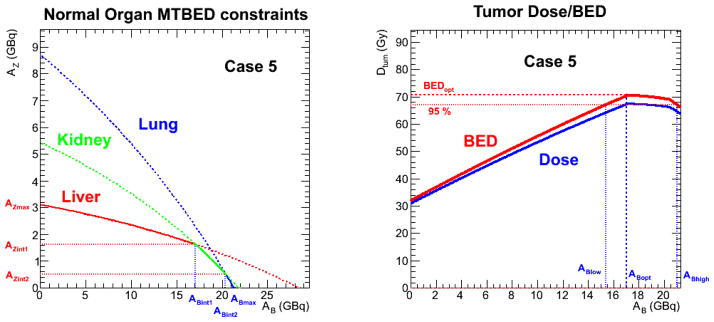
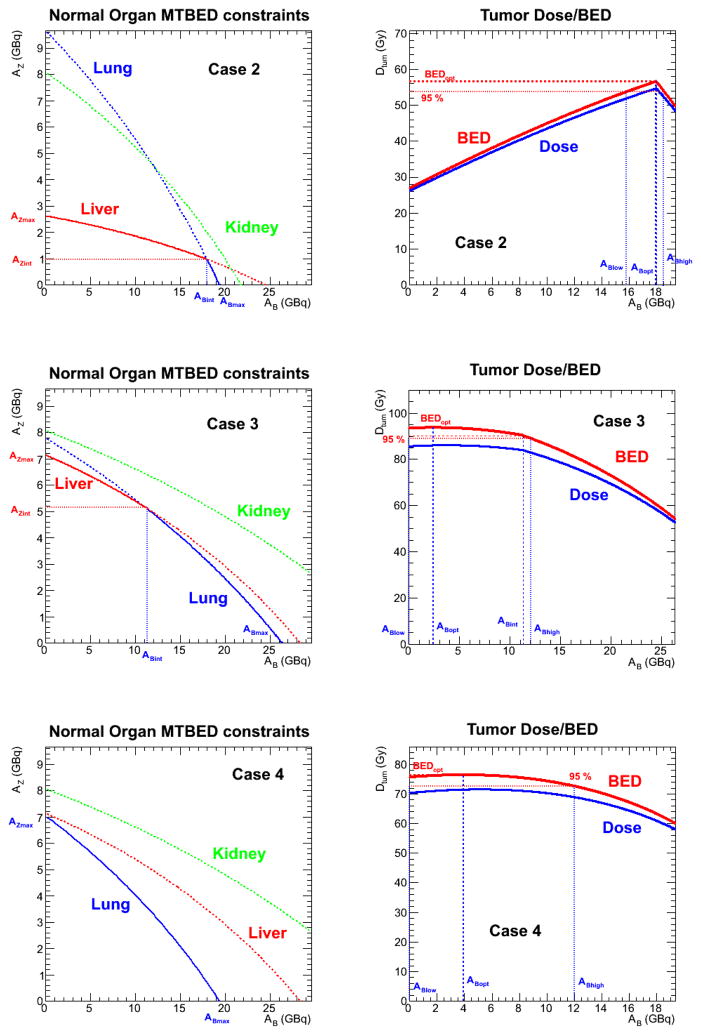
Illustration of the different cases. Case 2 shows constraints and tumor BED for the case where the optimal dosing is not equal to the intersection of the MTD constraints. The 3^rd row (Case shows a case for a single limiting organ. 4^th row illustrates a case where all three organ constraints must be considered.

Table 2.

Parameters for tumor BED-based optimization.

	Case 1	Case 2	Case 3	Case 4	Case 5
dBLi (Gy/GBq)	0.97	1.01	0.87	0.87	0.87
dZLi (Gy/GBq)	6.21	10.46	3.84	3.84	8.81
dBLu (Gy/GBq)	1.20	1.32	0.97	1.32	1.20
dZLu (Gy/GBq)	2.85	2.44	3.03	3.35	2.70
dBKi (Gy/GBq)	0.72	0.98	0.55	0.55	0.98
dZKi (Gy/GBq)	2.85	2.73	2.73	2.73	4.05
dBtum (Gy/GBq)	2.50	2.50	2.00	3.0	3.0
dZtum (Gy/GBq)	10.0	10.0	12.0	10.0	10.0

Multiple Tumor Optimization

Since the optimization point depends on tumor kinetics, it is quite possible for a patient with more than one tumor to have different optimal combinations for the different tumors. In these instances, the EUBED (27) may be used to optimize the activities relative to multiple tumors. The EUBED is given by:

$$\mathit{EUBED}=-\frac{1}{\alpha }ln\left(\frac{{\sum }_{i=1}^N{e}^{-\alpha {\mathit{BED}}_i}}{N}\right)$$ (11)

for N equally-contributing components (voxels, e.g.) of a single tumor. This expression may easily be extended to several tumors:

$$\mathit{EUBED}=-\frac{1}{\alpha }ln\left(\frac{{\sum }_{i=1}^N{w}_i{e}^{-\alpha {\mathit{BED}}_i}}{{\sum }_{i=1}^N{w}_i}\right)$$ (12)

Where the weighting factor, w_i, is proportionate to the preponderance (mass) of the tumor and i now iterates over the number of tumors, N. This approach is illustrated by considering 4 tumors using the case 1 normal organ kinetics:

The normal organ parameters are the same for all tumors, since they are from the same patient (Table 2, Case 3). The tumor parameters are given in Table 3 and are chosen from within the ranges given in the literature. The masses were arbitrarily attributed for illustrative purposes. The optimization process is essentially the same as for a single tumor: as A_B varies from 0 to A_Bmax, the appropriate organ-specific version of equation (8) for A_Z is substituted into equation (9) for each tumor. Once the different tumor BEDs are calculated, the disease EUBED is obtained using equation (11) and the results are plotted, from which the optimal A_Bopt (and then A_Zopt) value is determined.

RESULTS

MTD Intersection Points and Optimal Activities

By considering sets of patient data from twelve ⁹⁰Y-ibritumomab tiuxetan (from myeolablative NHL therapy (21)) and five ¹³¹I-tositumomab (from non-myeloablative NHL (20)) for whom lung and liver kinetics were available, we calculated the intersection points (A_Bint, A_Zint) for all sixty possible patient data combinations as well as the optimal tumor BED points (A_Bopt, A_Zopt) using the average tumor d values reported in the literature (14.9 mGy/MBq for ⁹⁰Y-ibritumomab tiuxetan and 3 mGy/MBq for ¹³¹I-tositumomab) (24, 25).

The average A_Bint value was (19.0 ± 8.2) GBq with a range of 3.9 – 36.9 GBq and the average tumor dose contribution from ¹³¹I-tositumomab was (57.0 ± 24.4) Gy; the average A_Zint value was (2.77 ± 1.64) GBq with a range of 0.42 – 7.54 GBq and the average tumor dose contribution from ⁹⁰Y-ibritumamoab tiuxetan was (41.3 ± 24.5) Gy, for MTBEDs of 30 Gy and 35 Gy for the lung and liver, respectively. Eleven of the sixty scenarios showed a ⁹⁰Y contribution of less than the maximum allowed non-myeloablative activity of 1.18 GBq using the MTBED constraints alone. When optimizing to the tumor BED, the average A_Bopt value was (18.0 ± 9.2) GBq with a range of 0.1 – 36.8 GBq; the average A_Zopt value was (2.75 ± 1.63) GBq with a range of 0.43 – 10.2 GBq and ten of the sixty scenarios required administering less than maximum allowed non-myeloablative ⁹⁰Y-ibritumomab tiuxetan activity. However, the point of such a methodology is not to obtain average values, but to personalize the therapy to the individual patient. Thus, it is important to notice that while, on average, the contribution from ¹³¹I-tositimomab may have been higher, the amount of optimal activity of ⁹⁰Y-ibritumomab tiuxetan was greater than the maximum allowed activity for non-myeloablative single therapeutic therapy in fifty of sixty cases with a maximum nearly twelve times that of the standard activity and in twenty-four cases the ⁹⁰Y contributed more AD (and BED) to the tumor than the ¹³¹I.

Tumor-BED Optimization

Several different scenarios have been chosen to illustrate the different possible cases that may arise and to show the greater detail available through this methodology which may inform a clinical decision regarding the quantities of activity to administer beyond the simple calculation of a single (A_Bopt, A_Zopt) optimization point. The results are shown in Table 4 and are graphed in Figure 3, in addition to those already shown in Figures 1 and 2. Case 1 represents the average values from the patient data and is the methodological example illustrated in Figures 1 and 2. Case 2 is a typical example with results similar to the mean values (Case 1), but using data from individual ¹³¹I-tositumomab and ⁹⁰Y-ibritumomab tiuxetan data. Case 3, illustrated in Figures 3c and 3d shows a case in which the tumor BED optimization point differs from the MTBED intersection point. Case 4 shows an example of no intersection point: here the lungs are the constraining organ for all activity combinations (Figure 3e and 3f). Case 5 shows an example of three organs constraining the activity, lungs, liver and kidneys; there are two intersection points, one of which is also the optimization point. The last two cases are somewhat contrived and did not occur naturally using the patient data set at the MTBED values (30 Gy for lungs, 35 Gy for liver, 28 Gy for kidneys); the kinetics values used for the normal organs have been taken from different patients to create the desired scenarios. However, given a sufficiently large number of patients, it is indeed possible that these scenarios would occur, thus their inclusion.

Multiple Tumor Optimization

The tumor dose per AA for the different tumors were judiciously chosen in order to illustrate a case where no two tumors individually had the same optimization point. The optimization was implemented for each tumor separately (see Table 5) and at each (A_B,A_Z) point the EUBED was calculated. The results are also graphed in Figure 4. Figure 4b is an enlargement of the EUBED results and shows the range using the 95 % of maximum EUBED threshold.

Table 5.

Results for tumor BED-based optimization.

Optimization:	Tumor 1	Tumor 2	Tumor 3	Tumor 4	Combined
ABopt (GBq)	17.9	12.2	17.9	11.3	15.3
AZopt (GBq)	1.81	2.84	1.81	2.99	2.30
BEDtum1 (Gy)	54.6	49.3	54.6	48.3	52.4
BEDtum2 (Gy)	59.8	61.2	59.8	61.1	60.8
BEDtum3 (Gy)	83.3	80.9	83.3	80.2	82.6
BEDtum4 (Gy)	48.2	49.7	48.2	49.8	49.2
EUBED (Gy)	54.7	54.6	54.7	54.3	55.0

The numbers in bold represent the maximum BED values obtained for the optimization of the respective tumor, e.g.: the maximum BED for tumor 1 is obtained when the optimization is run for tumor 1 itself, etc.

Figure 4.

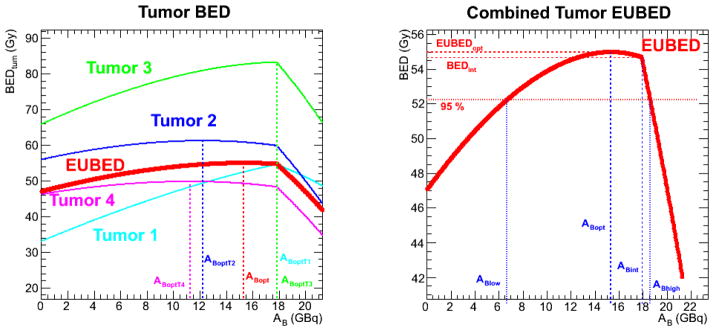
Multiple tumor optimization. Figure 4a shows the optimization for the tumors separately in different colors as well as for the EUBED (in red). Figure 4b shows a blow-up of the EUBED curve.

DISCUSSION

The significance of the proposed methodology is threefold: (a) the inclusion of radiobiological quantities for normal organ constraints (BED) and the tumor target (EUBED), widely regarded as more relevant to biological endpoints; (b) the graphical representation of the results which allows for easy understanding of quantitative effects of deviations from the optimal solutions; i.e.: the knowledge of how much tumor BED is lost by choosing different AAs is available, and (c) the development of the model within the context of a functional 3-dimensional dosimetry software package, 3D-RD, with the ability to implement sophisticated methodologies within clinical time frames (19). Concerning the graphical representation, we have chosen to show the administrative activity limits, AB_low and AB_high which correspond to a threshold where the tumor BED (or the EUBED) is at 95 % of the maximum. Clearly this is an arbitrary threshold which can be varied; however, it serves to illustrate the point that a graphical representation allows for a better understanding of the effect of varying the ratio of A_B to A_Z. In order to accomplish the objective of clinical implementation, several other technical difficulties must be overcome, some of which are discussed.

A clinical consideration for this dual isotope myeloablative methodology is the choice of procedure for the myeloablation. Cyclophosphamide combined with 300 cGy total body irradiation (TBI) is a widely used myeloablative conditioning regimen for autologous and allogeneic stem cell transplant. However, for this particular combination, cold antibody tositumomab in conjunction with the cyclophosphamide would be preferable to TBI. The cold antibody would be given before cyclophosphamide in order to minimize the window between administration of radioactive drugs and infusion of the autograft (the timing of which is based on the estimated radiation dose rate in the blood and bone marrow (21)).

The accurate calculation of the dosimetric quantities needed for the model depends critically upon the ability to measure the quantities of the pre-therapeutic activities, ¹¹¹In-ibritumomab tiuxetan, used as a surrogate for ⁹⁰Y-ibritumomab tiuxetan, and ¹³¹I-tositumomab, present simultaneously in the patient through quantitative (SPECT) imaging. This requires using multiple energy window imaging with correction for crosstalk from the higher energy ¹³¹I gamma rays into the mid energy ¹¹¹In energy range (see ref 6 in attached). Simulation and phantom studies are currently underway to optimize the reconstruction method and determine the optimal timing and activity ratios of the ¹¹¹In and ¹³¹I agent planning injections to achieve accurate organ dose estimates. From these studies, the requisite sequence of delivery of ¹³¹I and ¹¹¹In radio-antibodies will be determined.

This method is designed to serve as a guide to administered activities of the agents; during implementation it is clear that clinical or practical considerations may override the suggested AAs. Such considerations may include (a) availability of large amounts of one of the radiopharmaceuticals, (b) concerns over radiation safety issues from large quantities of ¹³¹I, and (c) the desire for a minimum AA for one or both radiopharmaceuticals. An advantage of this method is the ability to visually quantify how such clinical or practical considerations might affect the dosimetric end point and better enable the treating physician to balance the different considerations when choosing the therapeutic AA. A further caveat is that although the optimization is radiobiologically-driven and personalized, many clinical personal factors are not taken into consideration and the clinical outcomes may be different.

One of the motivations for combining these two radiopharmaceuticals is the different average range of the emitted ionizing radiation (~1 mm with ¹³¹I, ~3–5 mm with ⁹⁰Y) indicating that the two isotopes are optimally suited for treating different tumor sizes (2.6 – 5.0 mm for ¹³¹I and 2.8 – 4.2 cm for ⁹⁰Y) (2). This facet has not been explicitly factored into the current method, as the relative advantages of the two isotopes for tumors are limited to direct dosimetric measurements of whole tumors from the patient images. However, it must be noted that this only considers visible tumor sites, while in lymphoma one may expect a distribution of tumor sizes spanning clinically observable, > 2 cm-diameter lesions, to occult disease that is below the resolution of current imaging modalities. While the optimal tumor size distribution for ⁹⁰Y is at the limit of detectability and may or may not appear in SPECT/CT images, it is clear that the optimal tumor size distribution for ¹³¹I is well below the conventional imaging threshold of detectability. In addition, the ¹³¹I provides a non-negligible dose to the whole body, including all tumors, from the photon emissions. For these reasons, it may indeed be preferable to include a minimum ¹³¹I-tositumomab constraint in the optimization. A possible extension of the model would include quantification of the number and size distribution of invisible disease and the use of GEANT4 Monte Carlo to integrate the treatment optimization of the microscopic tumor distribution with the macroscopic measurable tumors.

CONCLUSIONS

A rational approach for combination radiopharmaceutical treatment has been developed and applied to the myeloablative treatment of NHL. The methodology outlined provides a rigorous, dosimetry-driven and radiobiologically-based path towards combination radiopharmaceutical therapy.