An Active Oscillator Model Describes the Statistics of Spontaneous Otoacoustic Emissions

Abstract

Even in the absence of external stimulation, the cochleas of most humans emit very faint sounds below the threshold of hearing, sounds that are known as spontaneous otoacoustic emissions. They are a signature of the active amplification mechanism in the cochlea. Emissions occur at frequencies that are unique for an individual and change little over time. The statistics of a population of ears exhibit characteristic features such as a preferred relative frequency distance between emissions (interemission intervals). We propose a simplified cochlea model comprising an array of active nonlinear oscillators coupled both hydrodynamically and viscoelastically. The oscillators are subject to a weak spatial disorder that lends individuality to the simulated cochlea. Our model captures basic statistical features of the emissions: distributions of 1), emission frequencies; 2), number of emissions per ear; and 3), interemission intervals. In addition, the model reproduces systematic changes of the interemission intervals with frequency. We show that the mechanism for the preferred interemission interval in our model is the occurrence of synchronized clusters of oscillators.

Introduction

The sense of hearing exhibits several striking features. Our ears are sensitive to faint sounds, but can also process stimuli differing in power by 12 orders of magnitude, and distinguish nearby frequencies well. These attributes, namely a high sensitivity, a wide dynamic range, and a sharp frequency selectivity, are associated with an active nonlinear amplification process (1,2), which is physiologically vulnerable and relies on the integrity of the inner ear. This cochlear amplifier is acting on the level of mechanical vibrations before neural processing takes place. The general attributes of the cochlear amplifier are those of a dynamical system close to an oscillating instability or Hopf bifurcation. It has therefore been suggested that the cochlea contains many oscillatory elements tuned to the proximity of a Hopf bifurcation (2–4).

A remarkable consequence of the amplification mechanism is that the ear can actively emit sounds without external stimulation. These so-called spontaneous otoacoustic emissions (SOAEs), which can be detected as pressure variations in the ear canal, were predicted theoretically by Gold in 1948 (5) and found experimentally for the first time by Kemp in 1979 (6). SOAEs have been reported in many vertebrate species including lizards (7–9), birds (10), and mammals (11,12). SOAEs are prevalent among humans with healthy ears and have been studied both experimentally and theoretically (13–16). An extensive experimental study of human SOAEs (152 ears) (14) revealed a large variability of emission spectra of individual ears, while the statistics of emissions exhibited a number of remarkable features. Fig. 1 A and B show two examples of typical spectra found in experiments. Emission frequencies ranged from 500 Hz to 8 kHz and the distribution of the number of emissions per ear is a monotonically decreasing function. Interestingly, neighboring emissions exhibit a most probable frequency difference of about 1 semitone. The existence of such a characteristic interemission interval was already pointed out earlier (16,17). In addition, SOAEs with characteristic interemission intervals have also been observed in other vertebrates such as lizards, although their inner ear anatomy is strikingly different from mammals (18). In particular, the basilar membranes of lizards lack traveling waves (19).

Figure 1.

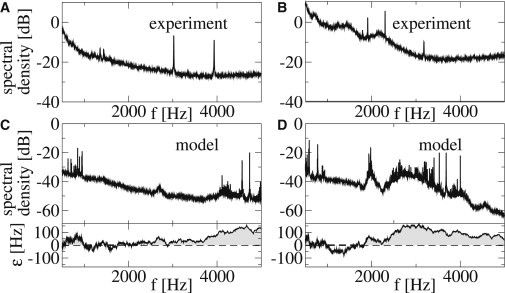
Spontaneous otoacoustic emissions. (A and B) Two examples of experimental power spectra S(f) of the ear canal pressure variations p_e(t) of two individuals as a function of frequency f, by courtesy of Talmadge et al. (14). (C and D) Power spectra S(f) of ear canal pressure variations p_e(t) obtained for two realizations of the disorder ε(x) in our model. The corresponding irregularities ε(x) are shown below as a function of the local characteristic frequency f(x) = ω(x)/(2π). (Shaded areas) Regions where oscillators are active in the sense that an isolated element would oscillate spontaneously, i.e., ε > 0.

The origin of SOAEs is still unclear and different mechanisms for their generation have been suggested. Shera (13) and Shera and Zweig (20) proposed that SOAEs are collective wavelike excitations of the basilar membrane which are selected by repeated reflections at the middle ear and inhomogeneities along the cochlea. According to this view, the corresponding modes extract particular frequencies from the broadband fluctuations of the system and generate peaks at those frequencies in the emission spectrum. The mode structure of the cochlea then gives rise to characteristic interemission intervals.

An alternative idea is that individual oscillatory elements become unstable and generate emissions at a particular frequency (5,21,22). This idea is more natural for vertebrates without a cochlea such as lizards. At the first glance, in such a picture it is unclear how characteristic frequency distances between emissions could arise. Motivated by the lizard ear, Vilfan and Duke (21), however, have shown theoretically that many coupled oscillating elements can give rise to characteristic interemission intervals (see Wit and van Dijk (23) for a similar approach in the human cochlea). In their model, dissipative and elastic coupling of active Hopf oscillators leads to frequency clustering, resulting in distinct emissions with characteristic interemission intervals. The biological equivalent to the individual spontaneously oscillating element comprises a group of hair cells and may involve, in particular, active hair bundle motility (24) and in the mammalian cochlea also the interplay between hair bundle motility and electromotility (25).

Several models of cochlear mechanics have discussed the generation of SOAEs. These works have considered irregularities of the frequency profile (15) or of the active gain (26–28) within active models of cochlear waves. Despite these efforts, there is yet no model that can reproduce all the main features of the SOAE frequency statistics observed in humans, e.g., the probability distribution of emissions with respect to frequency. In this article, we introduce a one-dimensional cochlear model based on dynamical oscillators that are coupled both hydrodynamically and via elastic and dissipative elements such as the tectorial membrane. The individuality of a cochlea is represented by a random disorder of the bifurcation parameter of the Hopf oscillators. This time-independent disorder leads to a specific spectrum with identifiable SOAEs. Two examples of calculated spectra of the pressure variations, p_e, in the ear canal for individual realizations of the disorder are shown in Fig. 1 C and D.

We obtain statistics of numerically determined SOAEs by simulating a comparable number of realizations as cochleas studied in the experiments. Our model can reproduce the statistics of SOAEs observed in humans, such as the distributions of emission number and frequency and of the interemission interval. We show how specific parameters control interesting statistical features of these distributions. For example, the characteristic interemission interval is set by the coupling strength between oscillators, whereas the amplitude and correlation length of the irregularities of the bifurcation parameter shape the distribution of emission numbers.

Theoretical Approaches: Models and Methods

Physical description of the noisy cochlea with small irregularities

We extend a previously proposed model of coupled nonlinear oscillators (29). We describe cochlear dynamics in a simplified one-dimensional model, based on the geometry sketched in Fig. 2. Two fluid-filled chambers are separated by the cochlear partition, which includes the basilar membrane (BM). The vertical displacement of this partition is denoted by h(x,t). Force balance in the fluid and conservation of fluid volume imply (29–31)

$$\frac{2\rho }{\ell }{\partial }_t^{2}h={\partial }_x^{2}p,$$ (1)

where ρ is the mass density of the fluid, $\ell$ is the chamber height, and p is the fluid pressure difference between the two chambers. We consider a set of noisy dynamic Hopf oscillators, which are distributed along the BM. The amplitude and phase of an oscillator at distance x from the base is given by the complex function z(x,t) = h(x,t) + iu(x,t), where the imaginary part u of z is a hidden state variable. Note that in our model we choose the real part of z to correspond to the vertical BM deflection h. This is motivated by the relation of our model to a mechanical oscillator (21). Oscillators are coupled both hydrodynamically and via longitudinal coupling mediated, for example, by the tectorial membrane. The oscillators obey a generalized complex Ginzburg-Landau equation

$${\partial }_{t}z=\left[ϵ\left(x\right)+i\omega \left(x\right)\right]z-\beta {\left|z\right|}^{2}z+\left(\kappa +i{\kappa }^{\prime }\right){\partial }_x^{2}z-\frac{i}{\alpha }p+\xi \left(x,t\right).$$ (2)

The characteristic frequency of oscillators ω(x) = ω₀e^−x/d is position-dependent, approximating the tonotopic map of the cochlea (32) (dashed line in Fig. 2 B). Here, ω₀ denotes the maximal frequency, d is the characteristic length, and β is the strength of the oscillator’s nonlinearity. Coupling of oscillators is described by an elastic and a dissipative coupling κ′ and κ, respectively. In addition, hydrodynamics (Eq. 1) leads to an effective coupling of oscillators because the pressure difference p acts on the BM. This effect is characterized by the coefficient α, where the imaginary unit i implies an elastic response and αω(x) is the local static BM stiffness. The dynamic noise ξ(x,t) accounts for intrinsic fluctuations of the oscillatory elements. We choose zero-mean Gaussian noise with intensity D that is uncorrelated in space and time:

$$\langle \xi \left(x,t\right)\xi \left(x^{\prime },t^{\prime }\right)\rangle =2D\delta \left(x-x^{\prime }\right)\delta \left(t-t^{\prime }\right).$$

Figure 2.

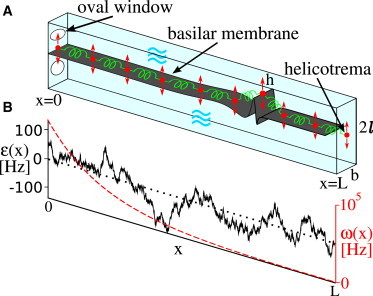
(A) Schematic representation of the one-dimensional cochlear model of length L, breadth b, and height 2 $\ell$. The cochlea is separated by the BM (dark shaded) in two fluid-filled chambers. The oval window is at position x = 0, the helicotrema at x = L. Vertical displacements of the BM are denoted by h(x). The BM is represented by a chain of oscillators (indicated by dots), which are coupled via hydrodynamic interactions (waves) and elastic and dissipative coupling (springs). (B) Profile of the characteristic frequency ω(x) (dashed line) together with a typical profile of irregularities ε(x) along the cochlea (solid line). To see this figure in color, go online.

The spatially extended dynamics (Eq. 2) uses a generic Hopf oscillator that describes any dynamical system in the vicinity of a Hopf bifurcation (2,3). The state of the oscillators is governed by a bifurcation parameter ε, which for ε = 0 poises the isolated oscillators at a Hopf bifurcation. We describe cochlear imperfections by static spatial variations ε(x) of the bifurcation parameter. We thus assume that each oscillator may be slightly offset from criticality, either in the oscillating (henceforth referred to as active) or nonoscillating regime. In our model, this irregularity is described by a set of stochastic variables with a Gaussian distribution and a simple exponential correlation in space. This disorder lends individual time-independent characteristics to a cochlea and is generated by a spatial version of an Ornstein-Uhlenbeck process via the stochastic differential equation

$$\lambda \frac{d}{dx}ϵ\left(x\right)=-ϵ\left(x\right)+\eta \left(x\right).$$ (3)

Here, η(x) is a Gaussian stochastic variable with zero mean and correlations 〈η(x)η(x′)〉 = 2σ²λδ(x − x′), where σ and λ are the standard deviation and the correlation length of ε(x), respectively. Each realization of a stochastic process ε(x) corresponds in our model to one realization of an individual ear. Note that our model also includes the important case of uncorrelated Gaussian perturbations (λ = 0, σ > 0). Correlations over a finite correlation length emerge in many simple physical systems. In this context, correlations of the irregularities could also be a result of irregularities in the developmental process that builds the cochlea. The continuum description of Eqs. 1–3 was introduced for conceptual clarity and the ease of notation. In our numerical study, we solve a discrete version of these equations for variables h_n, u_n, p_n, and ε_n at N + 1 discrete sites with positions x_n = Δx⋅n, n = 0,…, N, and Δx = L/N = 10⁻⁵ m. The human cochlea is endowed with four parallel rows of 3500 hair cells that run along the longitudinal axis of the organ (33). Accordingly, we choose N = 3500, i.e., each oscillator corresponds to one element of the organ of Corti containing one inner hair cell and 3–5 outer hair cells (34). Boundary conditions for p_n and z_n at the base and at the apex complement the model. For simplicity we do not constrain z₀(t) and z_N(t), corresponding to open boundary conditions for z(x,t) at both ends. Furthermore, the helicotrema connecting the fluid-filled chambers at the apex for x = L implies p_N(t) = 0. The boundary condition for the pressure difference p_n(t) at the base stems from the force balance at the base inside in the cochlea,

$$-b\ell \frac{p_1\left(t\right)-p_0\left(t\right)}{\Delta x}=\rho \frac{d}{dt}{j}_0\left(t\right),$$ (4)

where b is the breadth of the basilar membrane and j₀ is the difference in fluid volume flow in the upper and lower chamber at the base (29), which is related to deflections q(t) of the oval window $j_0\approx 2S_{\text{ow}}\dot{q}$. Here, the dots denote the time derivative, S_ow is the oval window area, and we have neglected contributions from movements of h₀(t). The boundary condition for the pressure at the base therefore reads

$$p_1\left(t\right)-p_0\left(t\right)=-2\frac{\rho S_{ow}\Delta x}{b\ell }\ddot{q}.$$ (5)

The acceleration $\ddot{q}$ of the oval window is determined by the mechanics of the middle ear, which we describe by a passive oscillator with an effective mass m, damping constant γ, and eigenfrequency ω_ow, following Talmadge et al. (15):

$$m\ddot{q}+\gamma \dot{q}+m{\omega }_{ow}^{2}q=\text{Γ}{S}_{ty}{p}_{in}\left(t\right)-S_{ow}{p}_0\left(t\right).$$ (6)

The oval window is subject to the force S_owp₀ originating in the cochlea and the force ΓS_typ_in due to incoming sound pressure p_in. Here, S_ty is the area of the tympanum and Γ is a dimensionless lever factor describing middle ear transmission (15). If air pressure changes are adiabatic, the pressure variation in the ear canal is given by (15)

$$p_e\left(t\right)=p_{\text{in}}\left(t\right)-\frac{{\gamma }_{\text{air}}P{S}_{\text{ty}}\text{Γ}}{V}q\left(t\right),$$ (7)

where γ_air is the specific heat ratio of air, and P and V are the ambient pressure in and the volume of the ear canal, respectively. To study spontaneous otoacoustic emissions, we set the incoming sound pressure to zero, p_in = 0. Spontaneous emissions, as measured in experiments, correspond to peaks in the power spectrum of p_e(t).

Parameter values

Our model contains 24 parameters, 19 of which we adopted from previous studies including experimental observation and detailed models. Note that some of the parameters in a more detailed description would depend on frequency or position along the cochlea, but that the values stated in Table 1 must be regarded as effective values. Unknown parameters are, in particular, the strength D of dynamic noise, and the parameters characterizing the static imperfection of the cochlea, described by an Ornstein-Uhlenbeck process ε(x) with standard deviation σ and correlation length λ. Two parameters, the viscous and elastic coupling coefficients κ and κ′, can have an important influence on the statistics of spontaneous emissions.

Table 1.

List of parameters

Parameter	Definition	Value	Ref.
Experimentally measured parameters
α	BM stiffness proportionality factor	5⋅103 Pa s m−1	(29)
b	Average breadth of BM	1.1 mm	(15)
d	Decay constant	7 mm	(29)
Δx	Distance between oscillators	10 μm	(33)
γair	Specific heat ratio of air	1.4	(15)
l	Height of upper/lower chamber	1 mm	(29)
L	Length of cochlea	35 mm	(29)
Pe0	Ambient pressure in ear canal	105 Pa	(15)
ρ	Density of fluid in cochlea	103 kg m−3	(29)
ω0	Characteristic frequency at x = 0	105 Hz	(29)
ω(x)	Characteristic frequency	ω0e−x/d Hz	(29)
Ve	Volume of ear canal	160 mm3	(15)
Parameters from previous models
β	Nonlinearity	8⋅1019 Hz m−2	(29)
Γ	Lever factor	1.3	(15)
γ	Middle ear damping coefficient	0.0295 N s m−1	(15)
m	Mass of middle ear	5.9⋅10−5 kg	(15)
Sow	Area of oval window	3.2 mm2	(15)
Sty	Area of tympanum	49 mm2	(15)
ωow	Eigenfrequency of middle ear	2π⋅1500 Hz	(15)
Free parameters
D	Noise strength	10−26 m3 s−1
κ	Dissipative coupling	3.9⋅10−9 m2 s−1
κ′	Elastic coupling	−3⋅10−8 m2 s−1
λ	Correlation length of ε(x)	5 mm
σ	Standard deviation of ε(x)	58.5 Hz

Simulation procedures

The discretized versions of Eqs. 1 and 2 can be written in the form

$$\begin{array}{c}\frac{d\overrightarrow{h}}{dt}=\overrightarrow{f_h}\left(\overrightarrow{h},\overrightarrow{u}\right),\\ \frac{d\overrightarrow{u}}{dt}=\overrightarrow{f_u}\left(\overrightarrow{h},\overrightarrow{u},\overrightarrow{p}\right),\end{array}$$ (8)

$$\frac{d{\overrightarrow{f}}_h}{dt}=\overline{\Delta }\overrightarrow{p}.$$ (9)

Here, $\overrightarrow{p}=\left(p_0,\dots ,p_N\right)$ is the set of values on the discrete sites, and similarly for $\overrightarrow{h},\overrightarrow{u}$. The symbol $\overline{\Delta }$ denotes the matrix that discretizes the operator [ $\ell$ /(2ρ)]${\partial }_x^2$. The functions ${\overrightarrow{f}}_h,{\overrightarrow{f}}_u$ correspond to the real and imaginary parts of the right-hand sides of Eq. 2. Equation 9 can be rewritten as

$$\frac{d\overrightarrow{f_h}}{d\overrightarrow{h}}{f}_h+\frac{d\overrightarrow{f_u}}{d\overrightarrow{u}}{f}_u=\overline{\Delta }\overrightarrow{p}$$ (10)

and contains no time derivative. We discretize the dynamics equation, Eq. 8, in time using finite time steps Δt = 10⁻⁵ s. At each time step, the pressure is determined from Eq. 10 together with the boundary condition p_N = 0 and Eq. 5 by solving a set of linear equations. Equation 6 is also discretized in time, and provides the value of $\ddot{q}$ in Eq. 5 at each time step. The set of oscillator parameters ε_n is determined from sampling one realization of Eq. 3 at discrete values x_n.

Detection of spontaneous emissions

From our simulations, we obtain, via Eq. 7, the time traces of the ear canal pressure variation p_e(t) over 300 s. From these time traces, we compute the spectral density S(f) by averaging the squares of the Fourier coefficients obtained for 1 s intervals. Here, we define spontaneous otoacoustic emissions as peaks in the spectrum S(f) that rise above the background level by more than a threshold level, which we choose at 20 dB (see dark shaded line in Fig. 3). The background is defined as the running average of the spectrum over a 1000-Hz interval (dashed line in Fig. 3). We compare the statistics of the so-defined spontaneous otoacoustic emissions, completely characterized by their frequencies, to those determined in experiments by Talmadge et al. (14). For the peak detection in experimental spectra, slightly different criteria were used because of considerable amounts of noise affecting both the background as well as introducing additional AC peaks (14). Because such artifacts are absent in our simulations, we can detect peaks by the simpler criterion stated above. We stress that a detailed description of spectral peaks at emission frequencies as well as of the background spectrum is beyond the scope of our study.

Figure 3.

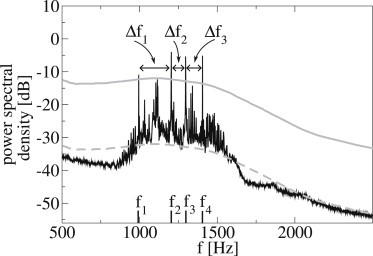
Detection of spontaneous emissions. Example of a power spectrum obtained in our model (black solid line) in a small frequency interval exhibiting four emissions at frequencies f₁–f₄. Emission frequency intervals are denoted Δf. The running average over 1000 Hz (dashed line) of the spectral density and the threshold line 20 dB above the average (dark shaded line) are used to identify emissions (for details see text).

The uniqueness of steady-state emission spectra is caused in our model by the irregularities of the bifurcation parameter ε_n in a given realization. From the procedure specified above, we obtain for a given realization of ε_n a discrete sequence of peak frequencies f_m with m = 1,…,M, where M is the number of emissions in the spectrum. To compare the statistics of SOAEs in our simulations with human cochleas, we use 152 different realizations of ε_n, which corresponds to the number of individual cochleas studied in the experiment (14).

Results

Two examples of emission spectra of our model are presented in Fig. 1, C and D. Shown below are the corresponding irregularities ε as a function of characteristic frequency ω(x)/(2π). The spectra typically contain emissions in frequency regions where oscillators are active (i.e., ε(x) > 0), whereas the converse is not necessarily true, i.e., positive excursions of ε do not necessarily lead to emissions in the spectra. This is so because emissions result from the synchronization of groups of active oscillators (see below), which also depends on global features of the system. Emissions are not caused by individual oscillators. Model spectra can be compared to those observed in experiments (Fig. 1, A and B). Although spectra differ in number and frequencies of the emissions for different ears (experimental data) or realizations of disorder (simulation data), numbers and frequencies fall into comparable ranges. Furthermore, peak power in experiments and of calculated spectra are similar. Note that the backgrounds of simulated spectra differ from those of experimental spectra, because in our model we neither include microphone noise nor all of the possible biological noise sources. In the following, we focus exclusively on the statistics of SOAE frequencies, but do not intend to describe the shape of SOAE peaks and background spectra.

In the experimental data (14), the number of emissions per cochlea M varied broadly; 67 of the 152 cochleas studied did not show any SOAEs, and emission numbers beyond 20 were observed occasionally. A histogram of emission numbers in the experiments and the frequency histogram are shown in Fig. 4 A (circles) and Fig. 4 B (solid line), respectively.

Figure 4.

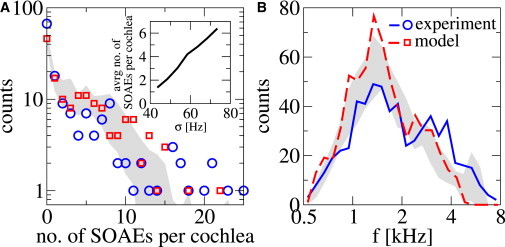
(A) Histogram of SOAE number per cochlea detected in experiments on 152 individual ears (circles), together with the histogram of SOAE number per cochlea obtained in our model from 152 realizations of the irregularities (squares). (Inset) Average number of SOAEs per cochlea as a function of the standard deviation σ of the irregularities. (B) Histograms of emission frequency in the experiments (solid line) and the model (dashed line). (Shaded regions, A and B) Standard deviation around the average determined from 10 repetitions of 152 realizations in the model. To see this figure in color, go online.

We can quantitatively account for the key features of these observations by our model. Using the known parameters given in Table 1, we find that the dissipative coupling κ as well as the standard deviation σ and the correlation length λ of the irregularities ε_n have a strong influence on the average and the distribution of the total count M. In addition, σ and λ also affect the frequency distribution of emissions. For the choice of κ, σ, and λ given in Table 1, the histograms obtained in simulations and in experiments correspond closely (Fig. 4). In particular, the shoulder in the experimental histogram at about M = 5 in Fig. 4 A, the maximum at 1.5 kHz, and the range of emissions (0.5–8 kHz) in Fig. 4 B are reproduced by the model. Of particular interest is the statistics of intervals Δf = f_n – f_n−1 between adjacent emissions. We consider the inverse relative interval $\overline{f}/\Delta f$, where $\overline{f}={\left(f_{n-1}{f}_n\right)}^{1/2}$, and alternatively, the interval in Cent units, defined as

$$I\left(f_n,f_{n-1}\right)=1200\cdot {\text{log}}_2\left(f_n/f_{n-1}\right).$$

Both interval measures have been used before to characterize SOAEs (13,17,35). Fig. 5 A shows experimental data for the inverse relative intervals as a function of mean frequency $\overline{f}$, scattering around $\overline{f}/\Delta f\approx 15$. In addition, there is a trend toward larger $\overline{f}/\Delta f$ for increasing frequency: The probability to find an interval with $\overline{f}/\Delta f$ attains a maximum close to a straight line corresponding to a power law (13),

$$\frac{\overline{f}}{\Delta f}\sim {\overline{f}}^{\nu }.$$ (11)

A value of $\nu \approx 0.3\pm 0.1$ was estimated in Shera (13). Using the data shown in Fig. 5 A, we estimate $\nu \approx 0.4\pm 0.2$ and indicate the respective power law by a dashed line in Fig. 5 A. (Note: For both experiment and model, we determined ν as follows: The data were divided in 12 logarithmically binned frequency intervals. For each interval, the value of $\overline{f}/\Delta f$ where the histogram count is maximal was determined. The exponent ν was determined by a fit of a power law to the 12 data points. Each point was weighted by the number of points lying in each interval. If an interval contained <20 counts in the experimental data, the weight was set to zero both in the evaluation of experimental and model data.)

Figure 5.

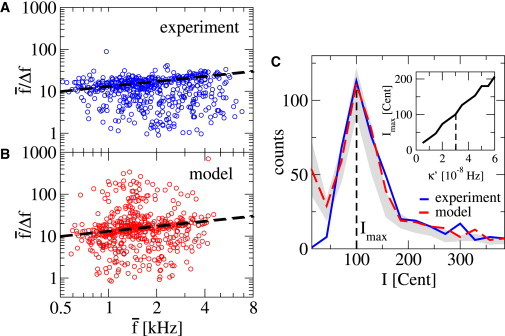
Statistics of emission frequency intervals. (A) Scatterplot of the inverse relative frequency intervals $\overline{f}/\Delta f$, where $\overline{f}={\left(f_1{f}_2\right)}^{1/2}$ and Δf = f₂ – f₁ for adjacent emissions in 152 individual cochleas in the experiment as a function of $\overline{f}$. (B) Same as in panel A, but for model data. (Dashed line in panels A and B) Power-law growth $\overline{f}/\Delta f\sim {\overline{f}}^{\nu }$ with ν = 0.4. (C) Histogram of relative frequency intervals I = 1200 log₂(f₂/f₁) in Cent units for the same data as in panel A (experiment, solid line; model, dashed line). (Shaded region) Standard deviation around the average determined from 10 repetitions of 152 realizations in the model. (Inset) Position I_max of the distribution’s maximum as a function of elastic coupling strength κ′. To see this figure in color, go online.

We can compare these statistics to the interemission interval statistics obtained in our model, shown in Fig. 5 B. In the model, there are more of the shorter frequency intervals $\overline{f}/\Delta f>100$ than in experiments, presumably caused by different peak detection schemes in experiments and simulations. However, the general features of the scatterplots in Fig. 5, A and B, such as the trend of inverse relative intervals described by the exponent ν, are similar. From the simulations, we estimate ν ≈ 0.3 ± 0.2. This is consistent with the experimental values mentioned above.

Distributions of intervals in Cent units both of experiments (solid line) and model (dashed line) are shown in Fig. 5 C. In the experimental data the most probable interval occurs at about 100 Cent, corresponding to one semitone (17,35). We find a similar histogram in the model (dashed line) that captures not only the maximum at 100 Cent but also the asymptotic behavior for large Cent values. In particular, this histogram does not display peaks at multiples of 100 Cent, even if we use a subset of cochleas with many emissions (not shown), which is in agreement with experimental data (36). The most probable interval I_max depends on the value of the elastic coupling coefficient κ′ (see inset, Fig. 5 C). To gain some insight into the variability of the histograms, we have generated 10 realizations of 152 cochleas and indicate the mean value plus/minus one standard deviation as shaded areas in Figs. 4 and 5. These figures demonstrate that our model can account for all statistical features that characterize experimentally observed emissions and emission intervals. In addition, we note that our model also produces BM vibrations in response to a sinusoidal external pressure stimulus p_in(t), which exhibits the main features found in the frequency domain description of an active cochlea based on critical oscillators (29).

Some of the key features of emission statistics in our model can be understood as follows: Each realization of ε_n defines regions in which ε > 0 and the oscillators are active (see Fig. 6 A). The length of these regions is of the order of λ. Within an active region, oscillators tend to oscillate spontaneously, albeit at a gradually varying characteristic frequency ω(x_n). Because of elastic and dissipative coupling between neighboring elements, clusters of synchronized oscillators appear. These clusters correspond to plateaus in the local frequency, defined as the average number of oscillation periods per unit time determined for oscillator n in our simulations (Fig. 6 B, solid line). This local frequency has to be distinguished from the characteristic oscillator frequency ω(x_n)/(2π) (Fig. 6 B, dotted line). The corresponding spectrum of emissions p_e(t) is shown in Fig. 6 C, revealing spectral peaks at frequencies that correspond to the plateaus, indicated by dashed lines. Thus, the number of oscillators, N_syn, that participate in a synchronized cluster, determines the distance between two emissions. In the realization of the model shown in Fig. 6, N_syn ≈ 40, corresponding to $\overline{f}/\Delta f\approx 15$. Note that N_syn < λ/Δx, implying that the synchronized cluster is smaller than the number of correlated oscillators. Put differently, the active regions typically break up in several synchronized clusters.

Figure 6.

Oscillation frequencies of a small active cochlear region. (A) Bifurcation parameter ε_n for a range of oscillator index n. The shaded area indicates active oscillators (ε_n > 0). (B) Local oscillation frequency determined from the inverse average oscillation period in the simulation (solid line) together with characteristic frequency (dotted line). (C) Spectral density of ear canal pressure variations in the simulation (solid black line). Emissions are identified by a threshold (shaded line) and correspond to frequency plateaus (dashed lines).

The typical intervals

$$2\pi \Delta f=\omega \left(x_{n-N_{\text{syn}}\text{/}2}\right)-\omega \left(x_{n+N_{\text{syn}}\text{/}2}\right)$$

between emissions are related to the size N_syn of synchronized clusters. Using

$$2\pi \Delta f\approx N_{\text{syn}}\left(\omega \left(x_{n-1}\right)-\omega \left(x_n\right)\right)$$

and

$$\omega \left(x_{n-1}\right)-\omega \left(x_n\right)\approx -\frac{d}{dx}\omega \left(x_n\right)\Delta x=\omega \left(x_n\right)\Delta x\text{/}d,$$

we find

$$\frac{\overline{f}}{\Delta f}\approx \frac{d}{N_{\text{syn}}\Delta x}.$$ (12)

To discuss the typical intervals between emissions, we need to understand the size N_syn of synchronized clusters (29,37). There exists no general theory for the cluster size of coupled nonlinear oscillators. For purely dissipative coupling of strength κ, the maximal cluster size N_syn obeys (37)

$$\left|\frac{\left(\omega \left(x_n\right)-\omega \left(x_{n-1}\right)\right)N_{\text{syn}}^2}{8\kappa }\right|\approx 1\text{.}$$ (13)

Using this relation as an approximation even in the presence of elastic coupling, by means of Eq. 12 we obtain Eq. 11 with ν = 1/2. This value is slightly larger than the values from the experimental data (ν ≈ 0.3,0.4) and from the model simulation (ν ≈ 0.3). Our consideration, however, illustrates why the differences between emission frequencies drop systematically with increasing frequency: For an exponential frequency map, the difference between characteristic frequencies of adjacent oscillators appearing in Eq. 13 grows with the frequency $\overline{f}$ and, according to Eq. 13, N_syn has to decrease as $N_{\text{syn}}\sim {\overline{f}}^{-\nu }$. A smaller size of the cluster in turn implies a smaller relative distance (or, equivalently, a higher inverse relative distance) between SOAE frequencies.

Discussion

In this article, we developed a theory of otoacoustic emissions of the mammalian cochlea that can reproduce key statistical properties of emission spectra observed in humans. Our model differs from previous ones (see, e.g., Talmadge et al. (15), Wit and van Dijk (23), Elliot et al. (26), and Ku et al. (27,28)) by combining viscoelastic and hydrodynamic interactions between oscillatory modules with a static disorder of the modules’ activity parameter. In our model, SOAEs are elicited by a synchronization of local oscillators, which is in agreement with the SOAE generation mechanisms found in other vertebrates (21,22) and also suggested to be at work in the cochlea (23). This is in contrast to the notion of SOAEs arising as a global phenomenon from wavelike excitations (13,20).

We extended a one-dimensional description of cochlear mechanics based on nonlinear oscillators coupled by hydrodynamical and viscoelastic interactions. We took into account irregularities that capture cochlear imperfections. To this end, we introduced small perturbations of the bifurcation parameter away from criticality. Regions in the cochlea where the bifurcation parameter is positive are active and can power spontaneous emissions. The size and location of these emissions depend on the realization of irregularities that characterize an individual cochlea. In our model, spontaneous emissions correspond to peaks in the power spectrum of calculated ear canal pressure p_e(t) that rise above a threshold beyond background level.

By varying only four key parameters, we could achieve strong similarity of basic statistical features of the emission frequencies and interemission intervals between model and experiments. This includes the following:

• 1.The range of frequencies in which SOAEs are observed,
• 2.The total number of SOAEs in a population of subjects,
• 3.The monotonic decay of the number of emissions per cochlea, and
• 4.The most likely relative distance between adjacent emission frequencies.

Note that the statistical distributions in experiment and model are very similar, but not identical.

In our model, certain statistical features correspond to specific parameters. The standard deviation σ and correlation length λ of the irregularities control the number and distribution of spontaneous emissions and attain nonvanishing values when we fit the model to the experimental data. In particular, we were not able to obtain statistics similar to the experimental ones when using uncorrelated Gaussian disorder (corresponding to λ = 0). The longitudinal coupling of oscillators, characterized by elastic and dissipative coefficients κ′ and κ, govern the synchronization of neighboring oscillators and the size of synchronized clusters. Hence, longitudinal coupling is essential to determine the most probable interemission interval by influencing cluster size. In the cochlea, this longitudinal coupling could be mediated by the overlying tectorial membrane (38), but also by the basilar membrane (39) and other connecting tissues (40). We emphasize that in our model, correlations of irregularities and longitudinal coupling have distinct roles: while the correlation length λ determines the size of the active regions in which SOAEs might originate, the longitudinal coupling causes the breakup of the active region into synchronized clusters.

The model can be extended in several ways to capture additional features of emission spectra. Here, we have used an Ornstein-Uhlenbeck process for which the average of the bifurcation parameter ε is zero. For zero average, we find a slightly higher prevalence of emissions (i.e., the fraction of cochleas that show at least one emission) than found in human ears (see the count for zero emissions in Fig. 4 A). The prevalence can be matched more closely by allowing for a small negative mean value of the bifurcation parameter. Another extension is to take into account additional noise sources. Indeed, although the power of spectral peaks between model and experiments is similar, the peak width in our model is smaller than the typical peak width of about 0.4–40 Hz reported in experiments (14,41,42). Taking into account external noise that varies slowly and affects the phase of oscillators globally leads to an increase of the peak widths in our model, while keeping emission frequency and power constant. Such noise could stem for example from blood flow, breathing, or other physiological processes (43).

Parameters chosen in our model largely stem from experimental measurements (see Table 1). The four free parameters of our model characterize the irregularities of the bifurcation parameter ε (its standard deviation and correlation length) and the longitudinal coupling of oscillators. These parameters are constrained in several respects.

The feature that gives individuality to the cochlea in our model is the irregular variation of the bifurcation parameter ε along the cochlea. Because emission spectra are relatively stable over time (44), our assumption of static imperfections in ε seems to be plausible. Furthermore, it has been suggested that the bifurcation parameter is kept in close proximity to criticality (ε = 0) by a self-tuning mechanism (3). This implies that the irregularities in the bifurcation parameter should be small compared to the characteristic frequency, i.e., σ ≪ ω(x). Indeed, with our parameter choice, σ/ω(x) < 0.1 for all x, and typically σ/ω(x) < 0.01 in the region where SOAEs are generated.

Irregularities in the physiological equivalent of the bifurcation parameter might arise, for instance, from cell-to-cell variability of the number and geometry of stereocilia (45–47). Other possible sources of variation might be introduced by the self-tuning mechanism or efferent brain activity transmitting signals to outer hair cells. A nonzero correlation length λ of perturbations might result from morphogen gradients or other concentration variations of chemical substances that govern the local activity adjustment during the growth phase of the cochlea.

Values of the longitudinal coupling coefficients can be discussed in the context of cochlear physiology. The coupling contains an elastic and a much weaker viscous component, in line with experimental observations (48). With the parameter values used in our model, the elastic coupling has an approximate strength of K = ακ′b/Δx = 16.5 mN m⁻¹. This is comparable to estimates of coupling strengths mediated by the connecting tissue such as the tectorial membrane in gerbil, where K ≈ 3–30 mN m⁻¹ (38). Note that the value that we used corresponds to the regime of strong coupling in theoretical studies of coupled hair bundles (see, e.g., Dierkes et al. (49)).

Our model predicts that longitudinal coupling governs the interval lengths between neighboring emissions. Thus, modifications of the coupling in vivo are expected to change the interval statistics. Specifically, a weakening of the coupling should result in otoacoustic emissions with a smaller preferred distance. Furthermore, our model implies a correspondence between SOAEs and spontaneous BM vibrations, which has been experimentally demonstrated in one case (50). Hence, the model predicts that for every SOAE there is a spontaneous BM vibration at the position according to the tonotopic map. Last but not least, due to the spatial correlation of the bifurcation parameter, our model suggests that neighboring BM segments exhibit similar levels of spontaneous activity.

Returning to the statistics of SOAEs, we have shown that the cause for the most probable interemission interval of one semitone could be the synchronization of nearby oscillators by a mixture of hydrodynamic, elastic, and viscous interactions, i.e., similar to the mechanism that was suggested to be responsible for a most probable interval in the lizard’s inner ear (21). Hence, synchronization of local oscillators by viscoelastic coupling could be the key to explain the statistics of SOAEs across species.