Induction of Peptide Bond Dipoles Drives Cooperative Helix Formation in the (AAQAA)₃ Peptide

Abstract

Cooperativity is a central feature in the formation of secondary structures in proteins. However, the driving forces behind this cooperativity are poorly understood. The present work shows that the cooperativity of helix formation in the acetyl-(AAQAA)₃-NH₂ peptide is significantly enhanced using an empirical force field that explicitly includes the treatment of electronic polarizability. Polarizable simulations yield helical content consistent with experimental measurements and indicate that the dependence of helical content on temperature is improved over additive models, though further sampling is required to fully validate this conclusion. Cooperativity is indicated by the peptide sampling either the coiled state or long helices with relatively low populations of short helices. The cooperativity is shown to be associated with enhanced dipole moments of the peptide backbone upon helix formation. These results indicate the polarizable force field to more accurately model peptide-folding cooperativity based on its physically realistic treatment of electronic polarizability.

Introduction

Understanding protein folding at an atomic level of detail is challenging (1,2). Toward this goal atomistic force field–based simulations have produced a number of insights (3–8); however, to date additive force fields have not been able to reproduce the cooperativity of helix formation (9–11). Thermodynamically, protein folding cooperativity (12,13) is reflected in the small temperature interval over which a protein goes from the unfolded to folded state. Microscopically, this process involves the presence of partially folded states at very low populations along with fully, or nearly fully folded states. In practical terms, nature utilizes folding cooperativity in proteins to lower the population of partially folded intermediates and thus prevent misfolding and amyloid formation (14,15).

Molecular dynamics (MD) simulation-based methods represent essential theoretical tools to understand the atomic details of protein folding. These include long-time MD simulations (4–6,16), distributed stochastic dynamics simulations (3,17,18), or enhanced sampling techniques such as replica exchange simulations (9,19,20). These methods have been applied to small peptides, including the GB1 hairpin (20–22) and Trp-cage (18,19), up to small proteins, including protein G (4) and ubiquitin (6). Among these is the well-studied helix-forming peptide acetyl-(AAQAA)₃-NH₂ ((AAQAA)₃ herein). Pioneering experimental work by Baldwin and coworkers (23–26) found that short alanine-based peptides form stable helices and characterized the thermodynamics of their helix-coil transition. Shalongo and Stellwagen showed the (AAQAA)₃ peptide to have ∼ 20% helical content at 300 K and reported data on the helical content as a function of residue at several temperatures (27). Computational studies of this peptide using replica exchange simulations with the CHARMM22/CMAP (28,29), AMBER99SB (30), and AMBER03 (31) force fields revealed large deviations with experimental data for three force fields (9). CHARMM22/CMAP and AMBER03 overstabilized the helix (95% and 87% helix at 300 K, respectively) whereas AMBER99SB understabilized the helix (2% at 300 K). This subsequently lead to further optimization of these force fields directly using the helical content of (AAQAA)₃ as target data, resulting in the AMBER03^∗, AMBER99SB^∗, and CHARMM36 force fields (9,32). However, even for these force fields the experimentally measured helical content is only reproduced around 300 K (9,11), whereas the overall temperature dependence of helix formation is significantly underestimated. This was confirmed in a more recent study involving eight different additive protein force fields (10). The best performer in that study was the CHARMM22^∗ force field (5), which overestimated the helical content by ∼ 3% at 300 K but underestimated it by ∼ 12% at 280 K and reported more than 10% helix at 370 K whereas experimental data indicated no helix at 350 K and above. Subsequently, it was shown that the CHARMM36 force field had improved temperature dependence, although the extent of the dependence was significantly less than that observed experimentally. The improved cooperativity was suggested to be attributable to “many-body effects” associated with the form of the backbone CMAP potential designed to reproduce the sampling of the helical region observed in crystal structures (29). However, given the inability of the model to reproduce the experimental folding temperature dependence, the many-body effects introduced by CMAP were still not adequate. Although the lack of cooperativity in current additive force fields may be associated with limitations in their optimization, it may also be attributable to the inherent limitation in the fixed-charge (additive) form of the energy function disallowing variations in the charge distribution that could contribute to the cooperativity of (AAQAA)₃ helix formation.

In this study we report replica exchange simulations of (AAQAA)₃ using a fully polarizable force field based on the Drude oscillator model, Drude-2013 (33). We show that the Drude-2013 polarizable force field, though being a first-generation model and not specifically optimized targeting (AAQAA)₃ helical content, can satisfactorily reproduce the experimentally measured helical content. More importantly, such reproduction is observed for the three temperatures considered, namely 280, 300, and 340 K. Investigation of the conformational properties reveals the peptide to have high propensity for either the coil or for long helical states, indicating a cooperative process in which the helical conformation is propagated throughout the peptide once it is nucleated. Such an atomistic picture of helix formation from a polarizable model contrasts significantly with those observed from additive force fields, indicating that the explicit treatment of electronic polarizability in a force field leads to a fundamentally improved model of the physical forces dictating polypeptide conformational properties.

Materials and Methods

Acetyl-(AAQAA)₃-amide was solvated in a 40 Å cubic water box containing 1943 water molecules and no ions. The starting structure was taken from previous CHARMM36 simulations (32) where the peptide was in the folded state. The system for the Drude simulations was generated by converting TIP3P (34) water molecules into polarizable SWM4 (35) water molecules and adding Drude particles onto nonhydrogen atoms and lone pairs on the hydrogen bond acceptors. MD simulations of 1 ns were then performed in the isothermal-isobaric ensemble (NPT) at the desired temperature T (T = 280, 300, and 340 K) and 1 atmosphere. Hamiltonian replica exchange molecular dynamics (HREMD) simulations were carried out in the canonical ensemble (NVT) using the final volumes from the NPT simulations.

The biasing potential used for HREMD simulations is described by the following:

$${\mathrm{E}}_{\mathrm{replica}}=\beta {\mathrm{E}}_{\mathrm{pp}}+\sqrt{\beta }{\mathrm{E}}_{\mathrm{pw}}+{\mathrm{E}}_{\mathrm{ww}},$$ (1)

as proposed by Wang et al. in the context of replica exchange with solute scaling (36), where E_pp is the peptide intramolecular energy, E_pw is the peptide-water interaction energy, E_ww is the self-interaction energy within the water molecules, and β is a biasing parameter exponentially scaled from 1 (no bias at the 0th replica) to 0.5. Simulations of all replicas are carried out at the same temperature T and exchanged according to the principle of detailed balance. The decomposition and scaling scheme according to Eq. 1 is such that the water-water energy term vanishes from the acceptance criterion. Only the 0th replica (i.e., no modification of the Hamiltonian) is used for analysis, while higher replicas are equivalent to a situation where the intramolecular conformational barriers in the solute correspond to a temperature of T/β emphasizing the Hamiltonian nature of the enhanced sampling methodology.

All the simulations were carried out with CHARMM version c37a2 (37), where the Hamiltonian is biased using the BLOCK facility. Three replica exchange simulations were carried out with the Drude force field (33) to 90 ns at T = 280, 300, and 340 K, each using 12 replicas. Exchange was attempted every 5000 steps and the acceptance ratio is between 20% and 50%. The exchanges of individual replicas in the HREMD simulations are illustrated in Fig. S1 in the Supporting Material. Only the 0th replica was used for analysis and the first 30 ns was considered equilibration and discarded. Simulations at 300 K were further extended to 120 ns to examine the convergence (see Fig. S2). HREMD simulations with the CHARMM36 force field (32) were carried out using the same simulation parameters. Temperature control is performed based on Nose-Hoover thermostats (38,39) and pressure control performed with Andersen barostats (40). For the additive CHARMM36 simulations a thermal piston mass of 2000 kcal/mol • ps² was used, whereas for the polarizable Drude simulations the characteristic response time for the thermostat coupled to non-Drude particles (at temperature T) equals 0.1 ps and for the thermostat coupled to Drude particles (temperature = 1 K) equals 0.005 ps (41). Periodic boundary conditions were applied and Lennard-Jones interactions were truncated at 12 Å with a smoothing function (force switch smoothing for the CHARMM36 simulations and switch smoothing for the Drude) from 10 to 12 Å. The nonbonded interaction lists were generated with a distance cutoff of 16 Å and updated heuristically. Electrostatic interactions were calculated using the particle mesh Ewald method (42) with a real space cutoff of 12 Å on an ∼ 1 Å grid with a sixth-order spline. Covalent bonds to hydrogen atoms were constrained by SHAKE (43). The integration time step equals 1 fs for the Drude and 2 fs for the CHARMM36 simulations, and coordinates were saved every 1 ps.

A residue is defined as being in the α region if it is in the range -100° < ϕ < -30° and -67° < ψ < -7° in the Ramachandran map (Fig. S3). A region of α-helix is defined as at least three consecutive residues being in the α region, as previously performed (9–11,32). Best and Hummer showed that the alternative definition of helix based on helical i, i + 4 hydrogen bonds leads to equivalent results (9). The fraction of helix for a given residue is computed as the fraction of time the residue fulfills the α-helix definition and the fraction of helix for the peptide is computed as the average over all 15 residues. Statistical uncertainties are estimated by block averaging using 10-ns blocks, though we note that the proper derivation of uncertainties from Hamiltonian replica exchange simulations remains an open challenge (44). The peptide is considered to be in coiled states when it contains no residues fulfilling the α-helix definition. A residue is defined as being in a coiled state if the residue is outside the α region in the Ramachandran map as in Lifson-Roig analysis. The α₊ region is a broader region surrounding the α region as defined in Fig. S3.

Results and Discussion

The helical content from the HREMD simulations as a function of temperature is depicted in Fig. 1 for both the Drude-2013 and C36 force fields, together with the experimental NMR data (27) and the previously reported results for C36 obtained from temperature replica exchange simulations (11). The NMR values are based on the carbonyl chemical shift measurements at seven temperatures from 269 to 363 K by Shalongo and Stellwagen, and are computed using Table 1 and Eq. 2 in reference (27). Fraction helix for the individual systems as a function of time is shown in Fig. S1. At 300 K, the Drude simulation predicts a helical content of 25%, which is slightly higher than estimates of 19% and 22% from NMR and circular dichroism measurements (26), respectively. At 280 K, the helical content (34%) is smaller than that obtained from NMR experiments (40%), whereas at the higher temperature (340 K) the deviation is small (4% versus 3%). Qualitatively, the Drude polarizable force field predicts certain amount of helix at 300 K and almost no helix at the higher temperature of 340 K, whereas most additive force fields lead to either helix formation at both temperatures or no helix at both temperatures (9–11). We note that obtaining full convergence of the peptide sampling as required to calculate the helical content is challenging and acknowledge that our results are not fully converged; however, the agreement between the present C36 and previously published temperature replica exchange results for the helical content indicate that the HREMD approach has yielded results that have been representative of the experimental regimen.

Figure 1.

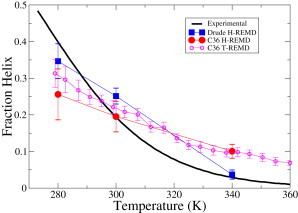
Fraction helix as a function of temperature determined from NMR experiments and replica exchange simulations with the Drude polarizable and the CHARMM36 additive force fields. The C36 T-REMD results were previously reported (11). To see this figure in color, go online.

The consistency with experimental data is also present on a per-residue basis, as shown in Fig. 2. For example, the Drude simulations showing the C-terminal alanine residue to always be in the coiled state is consistent with the experimental NMR chemical shift measurements (27). The helix propensity of the N-terminus is higher than that of the C terminus because of the presence of the acetyl group, which can form an i to i + 4 hydrogen bond that stabilizes the helix as seen in both the simulation and NMR data. This proper treatment of sequence dependence further indicates the quality of the Drude model in treating the coil-helix equilibrium. With C36 the additional helical propensity at the N-terminus is not present, although it was observed in the previous study (32).

Figure 2.

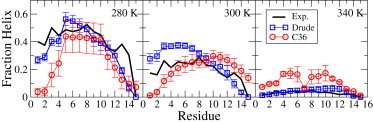
Fraction helix per residue from the Drude and CHARMM36 force fields and from the NMR experimental estimation (27) at 280, 300, and 340 K. To see this figure in color, go online.

Subsequent analysis involved the distribution of the lengths of the helices during the simulations. Fig. 3 presents the probabilities of observing n consecutive residues in the α region. At 340 K, although the Drude model predicts only 4.2% fraction helix, long helical segments are present, with the probability of observing helices with a length of nine residues (1.1%) being higher than that for a seven-residue helix. Such a probability distribution is more prominent at 300 K, with a maximum at 12 residues, which corresponds to the average helix length in proteins (45). At 280 K, the maximum in the helices is slightly shorter than that at 300 K, though the cooperative nature of folding is still evident given the prominence of helices of 8 to 10 residues over shorter helices. In the additive simulations distributions with higher sampling for longer helices are not observed at any temperature, with short helices being the most populated. However, some evidence of cooperativity is present at 280 and 300 K as indicated by presence of small peaks in the distributions at n = 10. These results indicate that the Drude model has a significantly greater amount of folding cooperativity than the additive C36 model.

Figure 3.

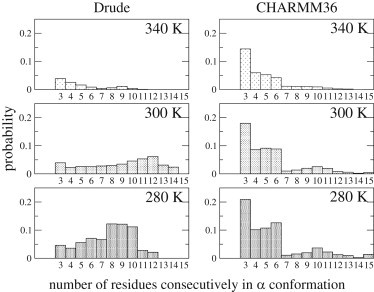
Probabilities of observing n consecutive residues in the α region (as a helix of length n) during the polarizable Drude and additive CHARMM36 simulations at 280, 300, and 340 K.

It should also be emphasized that the total average fraction helix equals the sum of the probabilities (as presented in Fig. 3) multiplied by the respective helix lengths, such that longer helices make a much larger contribution to the reported helical content in the polarizable model. For example, for the Drude model at 300 K helical segments with a length of 10 residues or more account for 78% of the helix observed, whereas these long helices only contribute 25% with the C36 force field. These results further supports a situation with the polarizable force field in which once a helix is nucleated it has higher tendency to elongate, yielding the more pronounced increase in the sampling of long helices shown in Fig. 3.

Although the Drude model has a higher propensity to form helical states as compared with the additive model, it also favors more extended unfolded states. This is indicated by the average radius of gyration of (AAQAA)₃ for coiled states (i.e., those that do not contain any α-helix) being 10.9 Å and 10.0 Å for the Drude and C36 simulations at 300 K, respectively. This is associated with the Drude model yielding a more pronounced bimodal distribution of the radius of gyration compared with the C36 model, as shown in Fig. S4. These results further indicate the cooperativity of helix formation in the polarizable Drude force field.

To understand the strong folding cooperativity with the Drude polarizable force field at a microscopic level, we analyzed the backbone ϕ, ψ distributions for the helical residues, as this sampling was used to explain the enhanced temperature dependence brought by C36’s CMAP potential as compared with other additive force fields (11,32). The average population of residues in the broad α_R region, α₊ (see Fig. S2), in the more strict α region, and in helical segments (%α-helix), as defined by three consecutive helical residues, are listed in Table 1 for the 300 K simulations. Although the polarizable force field yields the highest fraction helix based on both %α and %α-helix, it has lowest population of residues in the broad α₊ region. Accordingly, the ratios of the α/α₊ and α-helix/α populations are higher in the Drude than in the C36 simulation, indicating that once a residue is in the α₊ region it has a larger probability of sampling the more strict, helix-forming α region. Furthermore, once a residue is in the α region it has larger probability of participating in a stretch of three or more consecutive residues in the α region, i.e., forming a helical structure. This indicates a steep funnel-like energy landscape. Similar trends are observed at both the lower and higher temperature as shown in Table S1.

Table 1.

Population of selected conformational regions with the Drude and CHARMM36 force fields at 300 K

	%α+	%α	%α-helix	α/α+	α-helix/α
Drude	36.3	33.0	25.1	0.91	0.76
C36	40.2	30.0	19.8	0.75	0.66

The extent of cooperativity with the additive C36 force field was attributed to many-body effects associated with the CMAP potential that allows for cooperativity of the ϕ and ψ dihedrals to be explicitly parametrized into the model. For the residues in the helical segments, simulations with C36 results in a much narrower free energy basin in their ϕ, ψ distributions (Fig. 4). This tight helical minimum is related to the empirical adjustment of the CMAP term directly targeting a PDB distribution (29) with subsequent optimization of CMAP yielding C36 based on shifting overall regions of CMAP to improve the overall fraction helix of (AAQAA)₃ (11). Imposing such specific optimization in the sampling of ϕ, ψ phase space may be a necessity for additive force fields, whereas this is not required in the Drude force field, as evidenced by the broader ϕ, ψ distribution (Fig. 4) because the additional, electronic degrees of freedom incorporated in the polarizable model yield the observed cooperativity.

Figure 4.

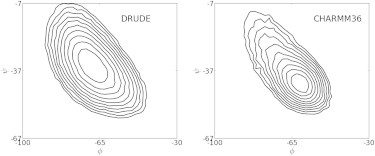
Distributions of backbone ϕ, ψ dihedral angles of residues in α-helical segments of three or more residues from the 300 K simulations with the Drude and CHARMM36 force fields. Results are presented as –kTlnP where P is the probability density plotted in contour lines relative to the lowest value in the region of interest shown. The contour lines are draw from 0 to 2 kcal/mol with an interval of 0.2 kcal/mol.

Verification of the contribution of the electrostatic polarizability to cooperativity involved analysis of peptide backbone dipole moments, computed as the ensemble average from the simulations for the different conformational ranges. The results in Table 2, in the rows labeled “Total,” show that the polarizable Drude model leads to much larger dipole moments than the additive C36 model, as previously observed in MD simulations of proteins and other peptide systems, with the extended conformations having larger dipoles than the helical conformations in the polarizable model (33). To illustrate how the environment affects the dipoles, intrinsic dipoles were obtained for the gas-phase alanine tripeptide as detailed in the supporting information. These values are reported in Table 2 as “Intrinsic,” with the difference between the total and intrinsic dipoles yielding the “Enhancement” of the peptide dipoles because of the full environment comprised of the remainder of the peptide and the surrounding solvent. As is evident, the dipole moments of peptide groups are enhanced significantly with Drude-2013 whereas for the additive force field, as expected, there is no significance difference between condensed and gas phases. The slight enhancement of peptide dipoles observed in the C36 simulations (∼ 0.03 D) is associated with the elongation of peptide C = O bonds because of hydrogen bonding interactions. In the Drude simulations the enhanced dipole is larger for those residues in the α conformation (∼ 1.0 D) than outside that region (∼ 0.6 D). To separate the induction effects of solvent from intrapeptide interactions, we computed the average dipole moments after removing all water molecules from the MD trajectories and then relaxing the Drude particles yielding the “intramolecular enhancement” values. Comparing those with the overall enhancement values shows a significant difference in the intrapeptide enhancement when a residue occupies coiled states (∼ 0.25 D) versus the “α (not in α-helix)”states (0.52 D) versus the α-helical states (0.76 D). If we assume the induction from adjacent residues (i - 1 and i + 1) contributes a 0.39 D enhancement, based on the “α₊ (not in α)” value, then for helical residues the remaining 0.37 D may be attributed to the hydrogen bonding between the i and i+4 residues, which is the unique feature of helical structure. Interestingly, quantum chemistry calculations of model systems indicate that electron density redistribution accounts for half of the helix formation cooperativity (46) and the cooperative stabilizing effect within a helix because of the intrahelical hydrogen bonds is stronger than that between the helix and water associated with hydrogen bonds between the carbonyl groups and water (47), consistent with the present observation.

Table 2.

Backbone peptide dipole moments for residues in different conformational regions from the 300 K simulations with Drude polarizable and CHARMM36 additive force fields

Dipole moment (D)		α-helix	α (not in helix)	α+ (not in α)	PPII	β
Drude	Total	4.91	4.93	5.09	5.07	5.40
	Intrinsic	3.87	3.92	4.28	4.49	4.86
	Enhancement	1.04	1.01	0.81	0.58	0.54
	Intramolecular enhancement	0.76	0.52	0.39	0.27	0.21
C36	Total	3.87	3.91	3.77	3.88	3.75
	Intrinsic	3.84	3.88	3.71	3.84	3.72
	Enhancement	0.03	0.03	0.06	0.04	0.03

Values of α₊ are reported for residues in the α₊ but not in the α conformation (α₊ (not in α)), and of α for those in the α conformation but not forming helices (α (not in α-helix)). The statistical errors are below 0.01 D in all the cases. See the text for more details.

The replica exchange simulation results can be discussed in the context of helix-coil theory using the Lifson-Roig model. Following the protocol outlined by Best and Hummer (9), the Lifson-Roig w, v parameters were computed for both the Drude and C36 simulations. The resulting values are listed in Table 3 together with the experimental values determined from by Rohl and Baldwin (25,26). The temperature independent parameter v describes the propensity for helix nucleation, and the simulations result in values of 0.11 and 0.17 for the Drude and C36 force fields, respectively, compared with the experimental estimation of 0.04. The differences indicate that in the MD simulations residues too readily convert from a coil conformation to an α conformation, though the results with the Drude model are improved over the additive model. The overestimation of the v parameter in simulations is compensated by their underestimation of the w parameter, which describes helix extension, to achieve similar fraction helix observed in experiments. The w parameter for the Drude model are larger than the C36 model at 280 and 300 K, being in better agreement with the experimental data. However, the values at 340 K are smaller than with C36, and in poorer agreement with experiment. Thus, the Drude model is in better agreement for the majority of the analyzed Lifson-Roig terms, consistent with the improved cooperativity in the model.

Table 3.

Lifson-Roig coefficients w and v from the Drude and CHARMM36 simulations, compared with experimental data

	Drude	C36	Experimental data
w at 280 K	1.24	1.11	1.49
w at 300 K	1.17	1.03	1.28
w at 340 K	0.70	0.87	0.99
v	0.11	0.17	0.04

Experimental data taken from previous studies (25,26).

Conclusions

In this study atomistic simulations of solvated (AAQAA)₃ were performed using the first-generation Drude polarizable and additive C36 protein force fields. The fraction helix at 300 K is comparable with experimental data for both force fields, indicating that both satisfactorily balance the helix-coil equilibrium at this temperature. The result is particularly encouraging as the polarizable force field was not optimized targeting the (AAQAA)₃ data as was C36. More importantly, almost no helix is observed at the higher temperature of 340 K in the Drude model, consistent with the experimental measurement. With the polarizable force field, relatively low populations of the short helices are observed whereas higher populations of longer helices are observed, a feature typical of a highly cooperative process (13). Analysis of the simulations indicates that the ability to capture folding cooperativity is attributable to the polarizable model itself instead of the particular parametrization. This is in contrast with the C36 force field, which has been previously shown to yield the largest amount of cooperativity of the additive force fields tested to date because of the many-body effects incorporated by empirical adjustment in its CMAP potential (11). However, it is anticipated that further optimization of the Drude model will lead to improved agreement with experiment on the folding of (AAQAA)₃.

The presented results cumulatively include more than 3 ms of simulation time performed with the Drude-2013 force field. This and the presented results illustrate that the Drude force field represents a more physically valid yet still computationally efficient model for the study of polypeptide folding as well as other phenomena (33). In conclusion, the polarizable Drude force field represent a significant improvement in the reproduction of the temperature dependence and cooperativity of peptide folding over available additive force fields and highlights the advantage of using polarizable force fields in general (48–50) because of their microscopically more physical treatment of electrostatics.

Supporting Citations

Reference (51) appears in the Supporting Material.