Abstract
Actin is ubiquitous globular protein that polymerizes into filaments and forms networks that participate in the force generation of eukaryotic cells. Such forces are used for cell motility, cytokinesis, and tissue remodeling. Among those actin networks, we focus on the actin cortex, a dense branched network beneath the plasma membrane that is of particular importance for the mechanical properties of the cell. Here we reproduce the cellular cortex by activating actin filament growth on a solid surface. We unveil the existence of a sparse actin network that emanates from the surface and extends over a distance that is at least 10 times larger than the cortex itself. We call this sparse actin network the “actin cloud” and characterize its mechanical properties with optical tweezers. We show, both experimentally and theoretically, that the actin cloud is mechanically relevant and that it should be taken into account because it can sustain forces as high as several picoNewtons (pN). In particular, it is known that in plant cells, actin networks similar to the actin cloud have a role in positioning the nucleus; in large oocytes, they play a role in driving chromosome movement. Recent evidence shows that such networks even prevent granule condensation in large cells.
Introduction
The actin cytoskeleton plays a major role in cellular mechanics (1), force generation (2), and cell motility (3). Its mechanical properties have been extensively studied in the past decades (4). The detailed characterization and modeling of the actin cytoskeleton has proven to be a complex task, mainly due to the different structures formed by the actin biopolymer in cells. A major experimental approach to understand the architecture and detailed properties of the actin cytoskeleton is to reconstitute the structures commonly found in cells using purified components (5–8). Such controlled in vitro studies gave detailed insights into the mechanical properties of cytoskeletal structures like actin bundles (9), actin stress fibers (10), and cortical actin networks (7,11).
Of particular importance is the mechanical contribution of the actin cortex, which provides a mechanical barrier supporting the plasma membrane against extracellular forces, but also acts as a steric obstacle for intracellular organelles. The actin cortex in cells was estimated to extend over a thickness of a few hundred nanometers underneath the cell membrane (12,13). However, actin structures connected with the actin cortex appear to be key elements for organelle positioning in plant cells (14,15) and nuclear positioning in oocytes (14,16). Moreover, nuclear actin dynamics is involved in the movement of chromosomal foci in large cells like oocytes (17). A recent study shows that such networks can even prevent the condensation of nuclear droplets in large cells (18). How these actin networks could be connected to the cortex, and can we envision that they could emanate from the actin cortex, are the questions we address here.
How this cortical actin network is nucleated at the membrane is still a debate (19). Although fluorescence techniques did not allow detection of the presence of the Arp2/3 complex and formins as a nucleating agent of the actin network at the membrane (20), the branched structure that is observed under the plasma membrane hints for a contribution of Arp2/3 (12). Therefore, it is important to understand how networks produced by the Arp2/3 complex branching mechanism can impact cell mechanics and behavior. Such a branched and entangled actin network can be reproduced at the surface of beads covered with an activator of the Arp2/3 complex (11). The thickness of such an actin network was detected by epifluorescence microscopy and defined as the distance of the bead surface from the half-maximum intensity position along a radial profile. However, in these experiments, the drop of fluorescence away from the bead is not abrupt as shown in Fig. 1, A and B (11). This is what we explore here, by characterizing the mechanical and structural organization of this actin network further away from the zone detected by fluorescence. Our experimental system, based on the high force sensitivity of optical tweezers (see Fig. 1 C), allows detection of a mechanically relevant actin network that is inaccessible to direct visualization. This actin network emanates from the epifluorescence-visible part, which represents only 1/10 of the full network size, and opposes resistance to indentation, thus revealing its important mechanical role.
Figure 1.
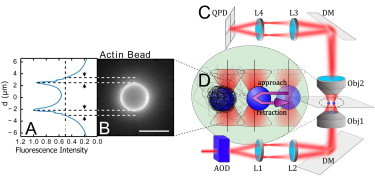
Sketch describing the experimental situation: (A) Normalized intensity profile of the fluorescent actin cortex shown in panel B, taken along the bead diameter. Arrowheads indicate Gel thickness measured as the half-maximal intensity of the epifluorescence signal. (B) Fluorescence image of a 4.3 μm actin bead, 25 nM Arp2/3, 10 nM CP after 30 min. Bar is 5 μm. (C) To probe the mechanics of the actin cloud, we use multiplexed optical tweezers generating two traps. A 1W infrared fiber laser (λ = 1064 nm; IPG Photonics, Oxford, MA) is steered by two acousto-optical deflectors (AODs) and multiplexed by time-sharing. The resulting beams are imaged in the back focal plane of a water immersion objective (Obj1, 60×, NA = 1.2), by a twofold magnification telescope (with focal measurement of the Lx lenses being fL1 = 10 cm, fL2 = 20 cm). The light is coupled in the optical path of a model No. IX71 microscope (Olympus, Melville, NY) by a dichroic mirror (DM). After interaction with the beads, the light is collected by a water immersion objective (Obj2, 40×, NA = 0.9) and the back focal plane of Obj2 is imaged onto a quadrant-photodiode (QPD) via two lenses (fL3 = 6 cm, fL4 = 3 cm). (D) The lasers trap the actin bead (left) and the probe bead. During the experiments, the probe bead is approaching the actin bead and moved from an initial position (transparent, right) to a final position at a velocity v, resting 3 s at the closest proximity (middle) and retracting back to the original position (movement indicated by the purple arrow). The displacement of the two beads from their respective trap center (marked by a straight line) is recorded by the QPD during the whole time. Optical forces are calculated using the calibrated trap stiffness.
The originality of our work is that we show the Arp2/3 complex can give rise to a mechanically resistant actin cloud that spans over distances larger than the dense and branched network close to the Arp2/3 activation. We characterize its mechanical parameters and show that this actin cloud allows sustaining forces able to displace objects on a cellular length-scale. Our findings suggest that even a few filaments that may emanate from the actin cortex can lead to sufficient resistance and can generate forces that may explain the role of actin in organelle positioning within the cell. Similar filaments have been recently described to emanate from a nuclear actin cortex in starfish oocytes (21).
Materials and Methods
Proteins
Products are obtained from Sigma-Aldrich (St. Louis, MO), unless stated otherwise. Actin and the Arp2/3 complex are purchased from Cytoskeleton (Denver, CO), and used without further purification. Fluorescent Alexa-488 actin is obtained from Molecular Probes (Eugene, OR). Capping Protein (CP), profilin, and pVCA are purified as previously described in Bernheim-Groswasser et al. (5) and Paluch et al. (22). Monomeric actin containing 10% molar of labeled Alexa-488 actin in G-Buffer (2 mM Tris, 0.2 mM CaCl2, and 0.2 mM DTT, at pH 8.0) at a concentration of 40 μM is obtained by keeping the solution one night on ice at 4°C before experiments.
Bead coating
Carboxylated polystyrene beads (Polysciences, Philadelphia, PA) of 4.34 ± 0.239 μm (standard deviation, SD) diameter were used for actin and probe beads.
Probe beads
Polystyrene beads are incubated for 20 min at 20°C under agitation with 10 mg/mL BSA at room temperature for 30 min in the working buffer (pH 7.4, 10 mM HEPES, 100 mM KCl, 1 mM MgCl2, 0.1 mM CaCl2, 1.8 mM ATP, and 1 mg/mL BSA), and stored for a few days at 4°C.
Actin beads
Polystyrene beads are first incubated for 20 min at 20°C under agitation with 2 μM pVCA and stored in working buffer (as above) for the day. Then they are placed in the polymerization mix, which is a solution of 4 μM G-actin, 12 μM profilin, and 25 nM of Arp2/3 complex and various concentrations of CP (0–50 nM) in the working buffer. A quantity of 15 μL of this mix is sealed between coverslips.
Experimental procedure and data analysis
For the bead approach experiments, the pVCA-coated beads, which will later polymerize actin, are mixed with BSA-passivated probe beads. Polymerization of actin on the beads is triggered by adding the bead mixture to the polymerization mix. Approximately 15 μL of the mix is sealed between two coverslips and observed in an inverse microscope (model No. IX71; Olympus, Melville, NY) using a 60× water immersion objective (NA = 1.2). Optical tweezers are used to trap and manipulate the beads in three dimensions by the gradient forces of a focused infrared fiber laser (λ = 1064 μm, YLP-1-1064; IPG Photonics, Oxford, MA). The XY position and trapping forces are controlled by acousto-optical deflectors (AA-Opto Electronic, Orsay, France). Multiple traps are realized by time-sharing where the laser is switched within ≈6 μs between two positions, while resting 20 μs on each position. Position and force applied on each bead are measured using a quadrant photodiode (QPD) positioned in the back focal plane of the condenser (Fig. 1).
The trap stiffness is calibrated using the power spectral density of trapped beads (23), and determined to be 34 pN/μm with the laser power of 119 mW as used during all experiments. The signal from the QPD is recorded with a sampling rate of 500 kHz using a commercial data acquisition card (NI PCIe-6363; National Instruments, Austin, TX), and processed using the software LABVIEW (National Instruments) and the software MATLAB (The MathWorks, Natick, MA). Data acquisition and trap positioning are synchronized to recover the individual data for each bead. The signal from the QPD is converted to both the force exerted by the trap on the bead, and the bead position in the trap, thanks to previous calibration.
To measure the viscoelastic properties, we perform a force-indentation experiment. An actin and a probe bead are selected, trapped, and checked for compromising adhesion to the upper or lower coverslip. The presence of the actin network is confirmed using fluorescence microscopy (200-W mercury lamp; Osram, Munich, Germany). All measurements are made on the dynamically polymerizing system, before symmetry breaking of the actin network.
To avoid too-strong forces on the beads, which could push them out of the trap, single approach/retraction cycles were done while decreasing the minimal approach distance stepwise by 0.2–0.5 μm until the maximum force reached 8–10 pN. In these conditions, the experimental protocol was stable and multiple consecutive approach experiments were done.
For the approach phase, the three fit parameters (α, β, and δ) are estimated using a Levenberg-Marquardt algorithm as provided by MATLAB. To facilitate stability in the fit algorithms, distances are expressed in micrometers and forces in pN.
Phenomenological fit of retraction curve
To fit the retracting part, we introduce the function with which corresponds to the elastic part of the actin-cloud, and is hence the discussed forces-distance curve (Eq. 2) scaled with the relaxation R, as described in the main text (see Fig. S4, dashed line in the Supporting Material, and Eq. 9). A(d) is fully determined from the approach and the relaxation data. For the plot in the retraction phase, we use the difference between the actual data and the expected elastic forces A(d) to estimate the force that results from the actin cloud that has closed behind the bead. This is attributed to a second power-law function (see Fig. S4, red), which is fitted to the difference between the measured force during the retraction and A(d) for the long distance (after force minimum is when the retraction phase was reached).
To determine the curve plotted later in Fig. 4, we smoothly converge from A(d) to B(d) by using a the smoothing function which corresponds to a convolution between the projected bead area and a linear ramp function L that is 0 for t ≤ 0 and 1 for t ≥ 1. The final model then reads:
| (1) |
Figure 4.
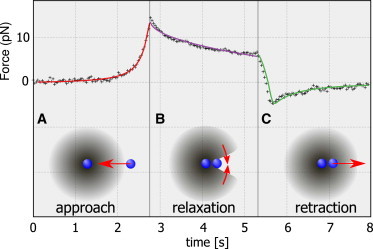
Model and example of a full fit for the measured force-evolution. (A) (Red) While approaching, the bead deforms the full actin cloud between the two beads leading to the measured forces that are fitted by the model of polymer elasticity including the discussed nonlinear Young’s modulus. (B) (Violet) Subsequent viscoelastic relaxation of the network between the two beads, following the theory of polymer relaxation of sparse actin networks given in Eq. 9. To understand the negative forces in the retracting phase, we imply that the network behind the bead is starting to relax into the void created by the bead during the approach phase (red arrows). (C) (Green) This leads to an additional elastic constraint while the bead returns to the initial position, which explains the negative force during the return phase.
Results
Bead system
Polystyrene beads of 4.3 μm diameter are first coated with a nucleation-promoting factor, pVCA, which is the VCA domain of N-WASP with the addition of a proline-rich region (24). Beads coated with pVCA are then placed in the mix of purified proteins, containing 25 nM of the Arp2/3 complex, 4 μM actin, 12 μM profilin, and various amounts of CP. In these conditions, a network of actin filaments grows from the bead surface. In the following, these beads, once covered with their actin network, are called “actin beads” (Fig. 2 A).
Figure 2.
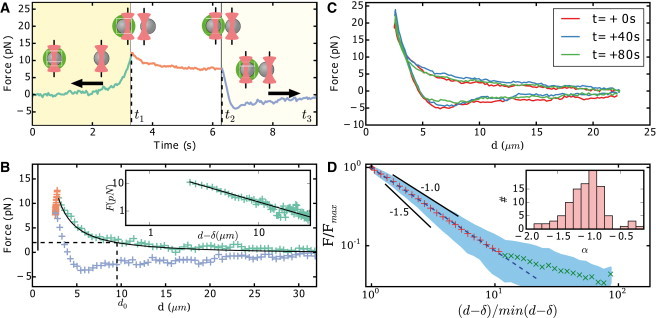
(A) Force of an actin bead as a function of time in the presence of 30 nM CP. The values t1 and t2, respectively, correspond to the beginning of the relaxation and retraction phases. Here, the sample is measured 12 min after adding actin to the bead mix. Color of the points marks the different phases: approach (green), relaxation (red), and retraction (blue). (B) Force on an actin bead as a function of the distance d between bead surfaces of the data presented in panel A. The zero force is fixed by the average of force at a large distance. The value d0 is the distance at which the mean force is higher than the SD measured for the resting bead (before the approach). We use this distance, d0, as the actin cloud size for the presented analysis. However, it should be noted that this measure may depend on the measurement method and the size of the probe beads. The color code used corresponds to panel A. The sample was measured 17 min after adding actin to the bead mix. (Straight black line) δ, the distance at which the force extrapolated by the fit would be infinite. (Inset) Power-law fit of the approach (solid line) and log-log representation. Examples of graphs A and B for different amounts of Capping Protein are available in Fig. S5, Fig. S6, and Fig. S7 in the Supporting Material. (C) Repeated approach-retraction experiments (three out of eight shown) give reproducible data. The example shown was acquired under 10 nM CP concentration. (D) Log-log representation of the rescaled experimental data. (Red and green crosses) Mean values. (Solid blue area) Average plus/minus SD for each averaged bin. (Blue dashed line) Linear fit of the data, (d − δ)/(d − δ)min < 10, and slope is −1.06. Slopes of −1,−1.5 are represented as visual guides. (Inset) Distribution of power-law exponent values obtained for each approach experiment for all CP concentration values (n = 103). We excluded 24 experiments out of 127, which gave fit results with negative and nonphysical value for δ.
In the absence of CP, actin filaments grow with their barbed ends away from the surface (24). The presence of CP limits the filament growth. In a spherical geometry of a bead, a stress builds up because new branches are formed at the surface of the bead, and symmetry breaks in a concentration range of CP from 15 to 35 nM (11,25).
The choice of a bead diameter of 4.3 μm allows us to perform measurements on an actin network that is homogeneous in the angular direction—hence, before the appearance of heterogeneities that are a signature of symmetry breaking (Fig. 1 B). A characteristic symmetry-breaking time for those beads is indeed ∼20 min (11). Because our experiments are performed before symmetry-breaking, both the actin gel and the actin cloud are still growing, and no steady state has been reached. However, as previously investigated (11), the growth velocity is small, with ∼0.1 μm/min, so that during the 2 min required for the approach experiments the actin-gel growth of ∼200 nm is negligible compared to the typical distances of ∼10 μm studied in this work.
Experiment description
Using optical tweezers, the probe bead is moved toward an actin bead. The forces on each bead are monitored, as shown in Fig. 1 C. Time-shared optical tweezers are used to trap the probe- and actin-beads (see Materials and Methods for more details (26)). The displacement of each bead from its trap center is recorded using a QPD, as shown in Fig. 1 C. For further analysis, we exclusively use forces determined from the stationary trap that holds the actin bead to avoid systematic errors that might arise from the trap displacement. The absence of interaction between bead and glass coverslip is probed before each experiment by moving it in all directions using the tweezers. A typical experiment starts as follows: the distance between traps is at least set to 20 μm, and beads are positioned at the trap centers. Then, the probe trap approaches the actin bead at a constant velocity of v = 10 μm/s (0 ≤ t ≤ t1; Fig. 2 A, left). During this process, as soon as the actin bead feels the force exerted by the probe bead, it becomes off-centered in its trap (Fig. 2 A, t ≲ t1).
The approach phase is followed by two other phases, a relaxation phase (t1 < t < t2; Fig. 2 A, center, white background), and a retraction phase (t2 < t < t3; Fig. A, right, light yellow background). During the retraction phase, the probe bead returns to its initial position with the same absolute velocity of 10 μm/s as in the approach phase. The duration of the relaxation phase (t2 − t1 = 3 s) is chosen to be long enough to allow relaxation to happen, and short enough for actin polymerization not to change the properties of the network. The time-dependent force on the actin bead (Fig. 2 A) is converted into a force-distance curve as shown in Fig. 2, B and C, where d is the distance between the surfaces of the actin bead and the probe bead. The force distance curve Fig. 2 B reads as follows: i) (t ≤ t1) the force between beads starts from an asymptotic zero value at long distance and increases as the distance decreases (green points). ii) (t1 ≤ t ≤ t2) the probe bead stops and relaxation occurs. During the relaxation, the force decreases with a very little distance decrease (red points, top left in Fig. 2 B). iii) (t2 ≤ t ≤ t3) the force decreases, becomes negative, and eventually reaches asymptotically zero again when distance increases (blue points).
Those curves are repeatable and show only small changes if multiple approach-retraction cycles are probed (see Fig. 2 C). Previous experiments suggest that for frequencies >0.1 Hz, viscous relaxation becomes comparable to the elastic properties (27). To check the importance of stress relaxation during the approach phase, we verify that the probe trap velocity did not affect the force-distance curves, by performing experiments at variable velocities ranging from 5 to 30 μm/s (see Fig. S1). These experiments did not show any striking differences in the recorded measurements; hence, for the analysis of the approach phase, we use an elastic model.
Experimental Observations
Approach phase
The bead system provides a way to reconstruct actin cortices in vitro. Moreover, these reconstituted systems can be manipulated to investigate three-dimensional mechanical properties of a biomimetic actin cortex in experimental conditions inaccessible to other microscopy techniques that are typically used to investigate single actin filament dynamics, like total internal reflection. Optical tweezer and force measurements on the bead allow us to precisely probe for the actin network emanating from a bead in a three-dimensional environment. To approximate the size of the actin cloud, we determine the distance d0 (Table 1, Fig. 2 B, dotted lines) where the forces on the probed bead become higher than the experimental noise of the force detection (2 pN). The found values for d0 remain large compared to the fluorescent actin gel thickness. Indeed, the probe bead already feels the presence of actin filaments at a distance from 13 to ∼4 μm (Fig. 1, A and B; Table 1). This distance depends on CP concentration (Table 1), but is always much larger than 1 μm. This has been established as an upper estimation of the actin network thickness e, previously measured as the distance of half-maximum fluorescence intensity (11) and Fig. 1 A.
Table 1.
Listing of the fit parameters found for different CP concentrations
| CP [nM] | 0 | 10 | 30 | 50 |
| N | 13 | 29 | 31 | 30 |
| α | −1.2 ± 0.1 | −0.9 ± 0.2 | −1.1 ± 0.2 | −1.2 ± 0.5 |
| β[pNμm] | 24.3 ± 10.7 | 18.7 ± 8.1 | 16.9 ± 16.0 | 6.1 ± 5.9 |
| δ[μm] | 0.5 ± 0.6 | 2.2 ± 0.7 | 1.2 ± 0.6 | 1.0 ± 0.5 |
| ν | 0.1 ± 0.05 | 0.2 ± 0.06 | 0.1 ± 0.07 | 0.1 ± 0.2 |
| E1μm [Pa] | 1.93 ± 1.05 | 1.24 ± 0.78 | 1.39 ± 1.61 | 0.59 ± 0.76 |
| ξ0[nm] | 310 | 397 | 350 | 376 |
| d0[μm] | 8.6 ± 2.9 | 13.3 ± 2.4 | 6.5 ± 3.1 | 3.7 ± 6.3 |
| lf[μm] | 10.8 ± 2.2 | 9.1 ± 5.5 | 2.5 ± 0.5 | 3.1 ± 3.8 |
| Median (R2) | 0.982 | 0.989 | 0.936 | 0.850 |
N represents the number of data-points for each CP concentration. Exponent of the model α, prefactor in the model β, distance offset δ, and E1μm is the elastic modulus at a distance of 1 μm. The value ξ0 is the average mesh size as calculated for an homogeneous network. The value ν is the Poisson’s ratio. The value d0 is the distance at which the average force is >2 pN. The viscoelastic model used also allows prediction of the average filament length lf from the relaxation behaviors. The median R2 values are given to quantify the fit quality for the different conditions.
As the bead distance decreases, the force gradually increases, until the trap stops at the minimal displacement distance. The force-distance data are fitted by a power-law with fit parameters β, α, and δ (Fig. 2, A and B),
| (2) |
where we obtain a high fit quality measured by a median R2 = 0.97. Because the power-law exponent, α, is found to be negative (Table 1), δ corresponds to the offset distance between bead surfaces at which the force would diverge (vertical black line in Fig. 2 B).
We experimentally find a negative power-law exponent close to −1 with a statistical distribution of 〈α〉 = −1.10 ± 0.38 (n = 103, mean ± SD) for all CP concentrations probed (Fig. 2 D, inset).
This inverse relation hints for a far-reaching network, or actin cloud, which is mechanically evidenced here. In our experiments, it is detectable over distances that are larger than the fluorescence-estimated thickness of ∼1 μm (see Movie S1 in the Supporting Material).
Due to the scale invariance of the power-law, we can collapse all 103 experimental curves into a single master curve by normalizing the force with the point of maximal force (Fmax) reached at t1, and the distance between bead surface at the minimal approach (dt1, Fig. 2 D). This rescaling procedure allows us to determine the power-law exponent of all averaged data curves to be (αrs = −1.06), which confirms the −1 exponent.
Nonlinear elastic modulus
To determine the Young’s modulus from the force-distance curves, we use its definition as given by Hooke’s law: E = σ/u, where σ = F/(πR2) is the stress on the projected bead surface, R is the bead radius, u = (dc – x)/dc is the strain where we define dc = (d – δ), and x is the experimentally controlled bead position for the small deformations. Hence du = −dx/dc, where the minus sign reflects the choice of the coordinate system for the deformation, which has to be consistent with the direction of the force to ensure a positive elastic modulus. Here we study the situation in which a predeformation of the gel of dc is applied, and then we apply a stress σ and strain u when displacing the probe bead by a small distance. In such a situation, the global Young’s modulus as function of dc reads E(dc) = (dσ/du)|dc. The deformation-dependent Young’s modulus can hence be expressed as the derivative of the force, with respect to the deformation at the distance dc, to yield
| (3) |
| (4) |
where E0 = −αβ/(πR2). In this expression, we use the fit function of Eq. 2 to calculate the derivative. Interestingly, using the strain at a position dc gives rise to the same power-law between the nonlinear Young’s modulus and the measured force. It should be noted that, experimentally, we can only access the average mechanical properties between the probe- and the actin bead. Hence, all reported values present mean values of the material between these two beads. The discussed model describes the reported mean values, and assumes an effectively averaged Young’s modulus. Here E(dc) is then this global Young’s modulus that measures the material properties of the actin cloud that is confined between the two beads. These values (Table 1) are three orders-of-magnitude smaller than the elasticity of the actin gel generated from an Arp2/3-activated bead (known to be ≈1 kPa (28)). This large difference in rigidity might explain why the actin cloud was not observed in previous mechanical measurements such as micropipette, microneedle deformation, or atomic-force microscopy indentation that were sensitive to large forces in the nanoNewton (nN) regime. However, such small moduli are commonly found in loosely entangled actin networks (27). It also shows that the actin cloud is of a fundamentally different network type, resulting in such a drastic change of mechanical properties compared to the dense actin gel found at the bead surface. Optical tweezers are the optimal measurement technique to determine such small elastic parameters.
Relaxation phase
In the 3 s resting phase, we observe that the beads move toward the center of their traps, corresponding to a force relaxation (Fig. 2 A, central) during which the beads get closer to each other (Fig. 2 A, t = t1 and t = t2). The force-drop during the relaxation is typically of 20% (see Fig. S3).
Retraction phase
We observe a rapid decrease of the force toward negative forces, leading to two different behaviors that may add up:
-
1.
A general tendency is that the rapid drop of the force is followed by a slow force increase through an inflection point (Fig. 2 B, lower curve), and
-
2.
In ≈25% of the experiments, we find evidence of rapid detachments that are identified by a sawtooth shape of the force-distance curve (see Fig. S2).
Irreversibility
An important finding is that the approach phase does not superimpose with the relaxation and retraction phases, which indicates dissipation of energy during a cycle of approach and retraction. Apart from the relaxation phase, a contribution to this dissipation is the negative force that is reminiscent of the sticky behavior similar to atomic-force microscopy indentation/retraction experiments.
Influence of Capping Protein (CP) concentration
Actin filament length is controlled by the amount of CP in the protein mix (24). To check the influence of the CP concentration on the actin cloud we analyze experiments at 0, 10, 30, and 50 nM CP. As shown in Fig. 3 and Table 1, the value of the power-law exponent α does not change significantly with CP concentration. In contrast, we find that the distance offset δ changes under variable conditions and the parameter β decreases fivefold when CP concentration increases from 0 to 50 nM.
Figure 3.
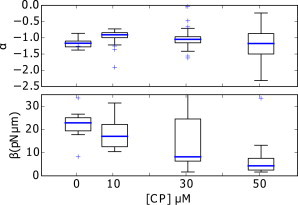
Distribution of power exponent α and prefactor β for different concentrations in CP (see Table 1). (Box plot, blue line) Mean; (box limit) first (q1) and third (q3) quartiles; (whiskers) extension to the most extreme data point within the 1.5 × (q3–q1) data range. None of the values of α are statistically different than the value for [CP] = 50 μM.
Discussion
Approach phase: interpretation of the power-law
To further investigate this power-law exponent (of ≃−1), we model the deformation of the actin cloud by the established theory of semiflexible, entangled polymer networks (29–31). In the approach phase, we focus on the elastic properties quantified by the deformation-dependent Young’s modulus E(dc) and neglect any viscous term, given that the force in this phase does not depend significantly on the approach speed. The Young’s modulus E of semiflexible filaments is well studied and can be expressed as a function of filament contour length density ρ and the entanglement length Le as E = 2·(1 + ν)·7· kBT ρ/(5Le) (31). The prefactor is model-dependent and includes the transition from shear to Young’s modulus using the Poisson ratio. Previous studies have investigated the nonlinear stiffening of actin gels for large deformations comparable to the presented approach protocol (32). For actin concentrations similar to the concentration used in our study, these previous experiments show that a linear description holds, and hence the proposed model should correctly describe the mechanics of the polymer network.
The entanglement length itself can be expressed as a function of density ρ and persistence length Lp as Le ≈ Lp1/5ρ−2/5 (31). For the general case of a compressible material, the only variable that might change under the strong deformation is ρ → ρ(dc). Hence, we can express the Young’s modulus as a function of density ρ that depends on the compression of the network, therefore noted ρ(dc):
| (5) |
Using the experimentally found power-law, Eq. 5 allows us to infer a relation for the density ρ ∝ dc5/7×α. Using the scaling arguments that at the distance d0, which corresponds to the undeformed actin cloud, the density is ρ0, we can directly express ρ (dc) = ρ0(dc/d0) 5/7×α. These changes in the density can be also used to estimate the Poisson’s ratio of the actin cloud, which connects the distance-dependent density and the deformation by ρ (dc) = ρ0(dc/d0) 2ν−1. Hence, we infer for Poisson’s ratio: ν = 1/2(1 + 5/7α). Due to the definition of ρ that corresponds to the filament contour length per unit volume, we can determine the average mesh-size ξ0 of the undeformed network by ρ0 = 1/ξ20. Combining these expressions then leads to
| (6) |
| (7) |
To determine the expected mesh-size, we can set E0 as found in Eq. 3, equal to Eq. 6:
| (8) |
The resulting values of ξ0 are listed in Table 1, which are ∼0.3–0.4 μm. Such average values are consistent with other rheology experiments and have been described in Morse (31). Unlike previous studies of bulk actin networks that find a bulk Poisson ratio of 0.5 for actin gels formed at actin concentration of 21.5 μM (27), we find that the actin cloud can almost collapse under the applied forces, with approximated Poisson’s ratio of 0.1–0.2. The difference may be explained by the lower actin concentration (4 μM) or by the geometrical arrangement of the actin network used in our experiments.
Approach phase: interpretation of distance offset δ
The third fit parameter in the power-law of Eq. 2 is δ, which marks the position at which the power-law diverges. Because the actin network around the bead is known to have an elastic modulus of ≈1 kPa (28,33), the forces provided by our optical tweezers (maximum 30 pN) are unable to deform this network. This suggests that in our measurements, the actin network close to the bead acts as a rigid object, which in turn suggests interpreting δ as the thickness of the actin network defined by epifluorescence (Fig. 1 B). As shown in Table 1, δ decreases with increasing CP concentration. The determined values of ≈1–2 μm are consistent with previous measurements of the actin thickness e by fluorescence microscopy (11). This general dependence is not found in the absence of CP, where the system is in a completely different regime because the filament growth away from the bead is only limited by the amount of G-actin. Indeed, in the absence of Capping Protein, filaments grow mainly away from the bead (11), leading to the absence of symmetry breaking. Therefore, without CP it remains difficult to define an actin shell thickness. The increasing number of filaments growing away from the bead surface changes the overall structure of the gel, which does not allow interpretation of δ.
Relaxation phase
The apparent mechanical effect of the actin cloud shows a dominant elastic component, while the force-distance plot gives a significant dissipation marked by the hysteresis. The repeatable approach-retraction excludes a significant plastic deformation, like breakage of the filaments or rupture of the sparse actin network. To understand the relaxation and the retraction behavior, we further follow the approach inspired by Morse (31), and investigate the proposed relaxation function χ(t), which determines the time dependence of E(t) = E × χ(t),
| (9) |
where In this model, the relaxation is a sum of exponential decays with well-defined decay times for a reptation-dominated relaxation. The unknown parameters are the diffusion constant for filament reptation Drep and the filament length lf, which are combined in the single fit parameter (τrep). We limit the fit to the first 40 terms of the sum in Eq. 9, because the higher modes relax faster that can be observed with the experimental resolution. Such a sum of exponentials remains consistent with the common finding of a power-law behavior of the shear modulus in in vitro actin networks (27) and the relaxation behavior found in cells (34).
To check whether the resulting fit parameter gives realistic values, we estimate where is the friction coefficient per unit length that depends on the solvent viscosity ηs; the mesh-size ξ, which has been estimated in Eq. 8; and the filament diameter df. We can also use ηs = 10−3 Pa × s, df = 7 nm and the mesh-size of ∼400 nm. Knowing the value of the relaxation parameter τrep given by the fit, we can estimate the filament length lf from the two previous expressions in the different CP conditions and determine values of ∼3–8 μm (see Table 1). Interestingly, these values are very close to the size of the actin cloud d0, which we determine independently by the first measurable mechanical signature of the cloud.
Hence, the found values of the fit are directly consistent with the predictions of a decrease of filament length when CP concentration is increased (24). The model of entangled actin filaments can therefore explain both the approach and the relaxation phases.
Retraction phase
During the retraction phase, we observe two types of events:
-
1.
Sticking events (see Fig. S2), where the force becomes abruptly negative until a threshold value is reached and then quickly relaxes; and
-
2.
A continuous decrease of the force that becomes negative after an average retraction of 3.5 μm and returns to zero at large distances.
Although the sticking event can be explained by interaction between the probe bead and the actin, the second case can be modeled phenomenologically by assuming a partial closure of the actin network behind the bead, as sketched in Fig. 4 (right part of the graph). The details of the fit function are given in the Materials and Methods. Briefly, we assume a transition between the elastic force generated by the actin cloud between the two beads and an additional viscoelastic contribution that accounts for the partially closed actin cloud behind the bead during the resting phase.
Biological relevance of the actin cloud emanating from cortical actin
The actin cytoskeleton is involved in many cellular events spanning from setting cell shape to the regulation of gene expression. Further experiments hint for a possible direct mechanical transmission of forces from the outside toward the nucleus via the actin cytoskeleton. Because the actin cytoskeleton is already known to be important in the positioning of the nucleus and presents a force transmission role in cells, it can be speculated that such force transmission may directly or indirectly trigger changes in gene expression. The mechanical link from extracellular environment to the nucleus is established by actin bundles that connect integrins and proteins of the nuclear envelope (35). However, to explain the role of actin in organelle and nucleus positioning (14,15), more than just such actin bundles should be taken into account.
Our experiments highlight that an actin network emanating from the actin cortex can sustain forces in the range of 10 pN. A force of 10 pN is sufficient for dragging organelles inside cells. Moreover, the capacity of Arp2/3 branched networks to reorganize in parallel structure, as well as nucleators as formins (6), can allow a constantly polymerizing cortical network to push throughout the inside of a cell and exert sufficient forces to move organelles and chromosomes (17). Indeed, networks observed inside cells are generally anchored to the cortical actin network (14,36–38). Because we show that mechanical parameters of filaments far away from nucleation sites may sustain forces up to 15 pN, we anticipate that unbranched actin filaments connected to cortical actin may provide a mechanical scaffold for a general mechanism of positioning and long-range interplay between organelles in oocytes (39,40) or even in large-scale systems like Drosophila development (16). Recently, the role of an actin network with similar properties as the here-described actin cloud had been identified in large cells such as Xenopus oocytes, which directly shows the mechanical relevance of the actin cloud in intracellular organization (18).
Conclusion
The transition from a dense actin network, which is polymerized off an Arp2/3 complex-activated surface to the bulk medium, is not abrupt. We identify and characterize a large transition zone, the actin cloud. These actin clouds are very soft compared to the dense actin network that is formed at the location of the Arp2/3 complex activation. Our in vitro experiments show that this actin cloud also gives a mechanical support with a far-reaching mechanical effect that scales inversely to the distance, a property that can be explained by polymer theory. The predicted viscoelastic properties and extracted material properties are in good agreement with our measurements. The actin cloud cannot be ignored in the context of cellular events such as nucleus positioning and oocyte maturation that have been shown to happen on force scales of several pN (18). Moreover, we enlighten a general mechanical feature of sparse actin networks that can serve as a useful mechanism to displace and organize the different cellular compartments.
Acknowledgments
The authors thank Klaus Kroy, Claus Heussinger, and Hervé Isambert for helpful discussions.
K.C. was supported by the Fondation ARC pour la recherche sur le cancer. M.B. and J.L. were supported by the Axa Research Fund. This work was also funded by the Fédération dynamique des systèmes complexes of the University Paris 6 and supported by French Agence Nationale de la Recherche (ANR) grants No. ANR-11-JSV5-0002, No. ANR-09-BLAN-0283, and No. ANR-12BSV5001401, and Fondation pour la Recherche Medicale grant No. DEQ20120323737.
Footnotes
Matthias Bussonnier and Kevin Carvalho contributed equally to this work.
Supporting Material
References
- 1.Fletcher D.A., Mullins R.D. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–492. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lecuit T., Lenne P.-F., Munro E. Force generation, transmission, and integration during cell and tissue morphogenesis. Annu. Rev. Cell Dev. Biol. 2011;27:157–184. doi: 10.1146/annurev-cellbio-100109-104027. [DOI] [PubMed] [Google Scholar]
- 3.Betz T., Koch D., Käs J.A. Growth cones as soft and weak force generators. Proc. Natl. Acad. Sci. USA. 2011;108:13420–13425. doi: 10.1073/pnas.1106145108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Salbreux G., Charras G., Paluch E. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 2012;22:536–545. doi: 10.1016/j.tcb.2012.07.001. [DOI] [PubMed] [Google Scholar]
- 5.Bernheim-Groswasser A., Wiesner S., Sykes C. The dynamics of actin-based motility depend on surface parameters. Nature. 2002;417:308–311. doi: 10.1038/417308a. [DOI] [PubMed] [Google Scholar]
- 6.Reymann A.-C., Martiel J.-L., Théry M. Nucleation geometry governs ordered actin networks structures. Nat. Mater. 2010;9:827–832. doi: 10.1038/nmat2855. [DOI] [PubMed] [Google Scholar]
- 7.Pontani L.-L., van der Gucht J., Sykes C. Reconstitution of an actin cortex inside a liposome. Biophys. J. 2009;96:192–198. doi: 10.1016/j.bpj.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Carvalho K., Lemière J., Sykes C. Actin polymerization or myosin contraction: two ways to build up cortical tension for symmetry breaking. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013;368:20130005. doi: 10.1098/rstb.2013.0005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Strehle D., Schnauss J., Gentry B. Transiently crosslinked F-actin bundles. Eur. Biophys. J. 2011;40:93–101. doi: 10.1007/s00249-010-0621-z. [DOI] [PubMed] [Google Scholar]
- 10.Thoresen T., Lenz M., Gardel M.L. Thick filament length and isoform composition determine self-organized contractile units in actomyosin bundles. Biophys. J. 2013;104:655–665. doi: 10.1016/j.bpj.2012.12.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kawska A., Carvalho K., Sykes C. How actin network dynamics control the onset of actin-based motility. Proc. Natl. Acad. Sci. USA. 2012;109:14440–14445. doi: 10.1073/pnas.1117096109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Morone N., Fujiwara T., Kusumi A. Three-dimensional reconstruction of the membrane skeleton at the plasma membrane interface by electron tomography. J. Cell Biol. 2006;174:851–862. doi: 10.1083/jcb.200606007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Clark A.G., Dierkes K., Paluch E.K. Monitoring actin cortex thickness in live cells. Biophys. J. 2013;105:570–580. doi: 10.1016/j.bpj.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Iwabuchi K., Minamino R., Takagi S. Actin reorganization underlies phototropin-dependent positioning of nuclei in Arabidopsis leaf cells. Plant Physiol. 2010;152:1309–1319. doi: 10.1104/pp.109.149526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stürmer K., Baumann O., Walz B. Actin-dependent light-induced translocation of mitochondria and ER cisternae in the photoreceptor cells of the locust Schistocerca gregaria. J. Cell Sci. 1995;108:2273–2283. doi: 10.1242/jcs.108.6.2273. [DOI] [PubMed] [Google Scholar]
- 16.Huelsmann S., Ylänne J., Brown N.H. Filopodia-like actin cables position nuclei in association with perinuclear actin in Drosophila nurse cells. Dev. Cell. 2013;26:604–615. doi: 10.1016/j.devcel.2013.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kumaran R.I., Thakar R., Spector D.L. Chromatin dynamics and gene positioning. Cell. 2008;132:929–934. doi: 10.1016/j.cell.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Feric M., Brangwynne C.P. A nuclear F-actin scaffold stabilizes ribonucleoprotein droplets against gravity in large cells. Nat. Cell Biol. 2013;15:1253–1259. doi: 10.1038/ncb2830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Smith B.A., Padrick S.B., Gelles J. Three-color single molecule imaging shows WASP detachment from Arp2/3 complex triggers actin filament branch formation. eLife. 2013;2:e01008. doi: 10.7554/eLife.01008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Charras G.T., Hu C.-K., Mitchison T.J. Reassembly of contractile actin cortex in cell blebs. J. Cell Biol. 2006;175:477–490. doi: 10.1083/jcb.200602085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mori M., Somogyi K., Lénárt P. An Arp2/3 nucleated f-actin shell fragments nuclear membranes at nuclear envelope breakdown in starfish oocytes. Curr. Biol. 2014;24:1421–1428. doi: 10.1016/j.cub.2014.05.019. [DOI] [PubMed] [Google Scholar]
- 22.Paluch E., van der Gucht J., Sykes C. Cracking up: symmetry breaking in cellular systems. J. Cell Biol. 2006;175:687–692. doi: 10.1083/jcb.200607159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gittes F., Schmidt C.F. Interference model for back-focal-plane displacement detection in optical tweezers. Opt. Lett. 1998;23:7–9. doi: 10.1364/ol.23.000007. [DOI] [PubMed] [Google Scholar]
- 24.Achard V., Martiel J.-L., Boujemaa-Paterski R. A “primer”-based mechanism underlies branched actin filament network formation and motility. Curr. Biol. 2010;20:423–428. doi: 10.1016/j.cub.2009.12.056. [DOI] [PubMed] [Google Scholar]
- 25.Sykes C., Plastino J. Cell biology: actin filaments up against a wall. Nature. 2010;464:365–366. doi: 10.1038/464365a. [DOI] [PubMed] [Google Scholar]
- 26.Lemire J., Guevorkian K., Betz T. α-hemolysin membrane pore density measured on liposomes. Soft Matter. 2013;9:3181–3187. [Google Scholar]
- 27.Gardel M.L., Valentine M.T., Weitz D.A. Microrheology of entangled F-actin solutions. Phys. Rev. Lett. 2003;91:158302. doi: 10.1103/PhysRevLett.91.158302. [DOI] [PubMed] [Google Scholar]
- 28.Marcy Y., Prost J., Sykes C. Forces generated during actin-based propulsion: a direct measurement by micromanipulation. Proc. Natl. Acad. Sci. USA. 2004;101:5992–5997. doi: 10.1073/pnas.0307704101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Isambert H., Maggs A.C. Dynamics and rheology of actin solutions. Macromolecules. 1996;29:10361040. [Google Scholar]
- 30.MacKintosh F.C., Käs J., Janmey P.A. Elasticity of semiflexible biopolymer networks. Phys. Rev. Lett. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 31.Morse D.C. Viscoelasticity of concentrated isotropic solutions of semiflexible polymers. 2. Linear response. Macromolecules. 1998;31:7044–7067. [Google Scholar]
- 32.Semmrich C., Larsen R.J., Bausch A.R. Nonlinear mechanics of entangled F-actin solutions. Soft Matter. 2008;4:1675–1680. doi: 10.1039/b800989a. [DOI] [PubMed] [Google Scholar]
- 33.Pujol T., du Roure O., Heuvingh J. Impact of branching on the elasticity of actin networks. Proc. Natl. Acad. Sci. USA. 2012;109:10364–10369. doi: 10.1073/pnas.1121238109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fabry B., Maksym G.N., Fredberg J.J. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001;87:148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
- 35.Jaalouk D.E., Lammerding J. Mechanotransduction gone awry. Nat. Rev. Mol. Cell Biol. 2009;10:63–73. doi: 10.1038/nrm2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schuh M., Ellenberg J. A new model for asymmetric spindle positioning in mouse oocytes. Curr. Biol. 2008;18:1986–1992. doi: 10.1016/j.cub.2008.11.022. [DOI] [PubMed] [Google Scholar]
- 37.Chaigne A., Campillo C., Terret M.-E. A soft cortex is essential for asymmetric spindle positioning in mouse oocytes. Nat. Cell Biol. 2013;15:958–966. doi: 10.1038/ncb2799. [DOI] [PubMed] [Google Scholar]
- 38.Lénárt P., Bacher C.P., Ellenberg J. A contractile nuclear actin network drives chromosome congression in oocytes. Nature. 2005;436:812–818. doi: 10.1038/nature03810. [DOI] [PubMed] [Google Scholar]
- 39.Li H., Guo F., Li R. Actin-driven chromosomal motility leads to symmetry breaking in mammalian meiotic oocytes. Nat. Cell Biol. 2008;10:1301–1308. doi: 10.1038/ncb1788. [DOI] [PubMed] [Google Scholar]
- 40.Azoury J., Lee K.W., Verlhac M.-H. Symmetry breaking in mouse oocytes requires transient F-actin meshwork destabilization. Development. 2011;138:2903–2908. doi: 10.1242/dev.060269. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


