Molecular Basis of the Mechanical Hierarchy in Myomesin Dimers for Sarcomere Integrity

Abstract

Myomesin is one of the most important structural molecules constructing the M-band in the force-generating unit of striated muscle, and a critical structural maintainer of the sarcomere. Using molecular dynamics simulations, we here dissect the mechanical properties of the structurally known building blocks of myomesin, namely α-helices, immunglobulin (Ig) domains, and the dimer interface at myomesin’s 13th Ig domain, covering the mechanically important C-terminal part of the molecule. We find the interdomain α-helices to be stabilized by the hydrophobic interface formed between the N-terminal half of these helices and adjacent Ig domains, and, interestingly, to show a rapid unfolding and refolding equilibrium especially under low axial forces up to ∼15 pN. These results support and yield atomic details for the notion of recent atomic-force microscopy experiments, namely, that the unique helices inserted between Ig domains in myomesin function as elastomers and force buffers. Our results also explain how the C-terminal dimer of two myomesin molecules is mechanically outperforming the helices and Ig domains in myomesin and elsewhere, explaining former experimental findings. This study provides a fresh view onto how myomesin integrates elastic helices, rigid immunoglobulin domains, and an extraordinarily resistant dimer into a molecular structure, to feature a mechanical hierarchy that represents a firm and yet extensible molecular anchor to guard the stability of the sarcomere.

Introduction

The M-band is located in the middle of the sarcomere, the muscle’s force-generating unit. It features dark lines in microscopic images formed from fibrils interconnecting the tails of myosin thick fibrils as well as the titin C-terminal portions (1). As an integrating molecular network, the M-band is believed to act as a structural safeguard of the sarcomere (2). Although three-dimensional structures of the M-band have been constructed by single-particle experiments (3), the detailed molecular structure and its way of balancing forces during a force-generating cycle of the sarcomere are still largely unknown.

The interactions between the M-band and other muscle molecules are key to the integration of big fibrils, most importantly myosin and titin, in the sarcomere. Three genetically related molecules have been identified to be responsible for the M-band lines, namely myomesin, M-protein, and myomesin-3 (4). As the most important molecule, being present in all types of striated muscles (5,6), myomesin is a promising candidate for deciphering the mechanical characteristics of the M-band.

Myomesin consists of 13 domains (Fig. 1). It is expressed at a fixed ratio with myosin at different types of muscles, with its special N-terminal domain, my1, connecting to one myosin tail (7). Similar to other muscle proteins, myomesin possesses 12 other domains either as immunoglobulin (Ig) domain or as fibronectin type-III (FNIII) domain. Its fourth-to-sixth domains, my4–my6, interact with titin to firmly accommodate the titin C-terminus in the M-band (8,9), as shown in Fig. 1. One iso-form of myomesin, termed “EH-myomesin”, has an unstructured peptide segment (EH segment) between the sixth and the seventh domains, my6 and my7, which is expressed only in early development of the heart (6). The EH segment has a function similar to PEVK in titin in that it provides a large extensibility to prevent damage upon stretching (10–12). The normal form of myomesin is lacking this critically important elastic EH segment, which raises the question how other segments in myomesin equip this constantly stressed molecule with elasticity.

Figure 1.

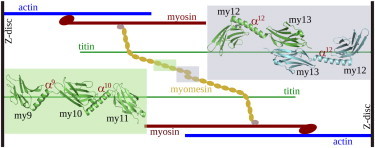
Simplified molecular connections in the M-band of the sarcomere in striated muscle. (Eclipse spheres) Myomesin domains. The two all-atom molecular structures used in this study, my9–my11 and dimeric my12-my13, are shown (insets), with the same coloring as in the scheme to highlight their position within myomesin.

Two myomesin molecules dimerize at their 13th domains, my13. The dimerized myomesins thereby expand from the M4 to the M4′ line in the M-band (1), and thus establishes a regular molecular organization in the sarcomere by connecting two antiparallel myosin molecules and a titin molecule with each other. In this assembly, myomesin acts as a force-transmitting bridge to balance mechanical force between molecules during the sarcomeric force-generating cycles (2). Silencing the function of myomesin resulted in sarcomere damages and muscle weakness (2,13,14). These results have called for an explanation of the molecular basis of myomesin function, in particular as myomesin shares structural similarities with other M-band proteins (4).

Recently, crystal structures of the myomesin C-terminal portion had been resolved (15,16), comprising myomesin’s 9th (my9) to 13th (my13) Ig domains, the latter of which forms a homodimer. Unexpectedly, long α-helices were found to connect each pair of adjacent Ig domains in this portion (Fig. 1). This structure of alternating Ig-domains and α-helices is likely to provide a hierarchy of mechanical responses in the force-generating sarcomere. Investigations of the my12-my13 homodimer by atomic-force microscopy (AFM) experiments combined with molecular-dynamics (MD) simulations showed that the domain-connecting α-helix, α¹², functions as a strain absorber for the molecule (17). Significant mechanical forces of ∼30 pN for helix unfolding were required, and elongations of up to 150% of helical original length could be reached (17). Myomesin Ig domain unfolding followed complete helix extension at much higher forces (>100 pN).

Alpha-helices are among the most ubiquitous secondary structures in proteins. Single molecule stretching experiments and simulations of individual α-helices or α-helical domains such as calmodulin or spectrin had previously revealed the unfolding and refolding dynamics of helices under force (18–21). Other theoretical and experimental studies also had been performed to examine α-helix mechanical properties and even structural transitions (18,19,22–26). A common finding was that α-helical proteins were comparably soft, and unfold at lower forces than the mostly-stiff and force-resistant β-sheet domains. All the myomesin α-helices expressed in the C-terminal portion of the molecule (which orients along the longitudinal axis of the sarcomere and is thus mechanically the most important (1,15)) are critical points for understanding the molecular behavior. Given that their interfacing Ig domains are participating in their folding-unfolding transitions (17), inspection of the mechanics of all these helices and their molecular neighbors can give an overview of the biological functions of the M-band molecules.

How the mechanical properties of the myomesin domains are coupled, and how the hierarchy of mechanical unfolding and refolding events contribute to the integrity of the molecular architecture of the M-band, are the subjects of this study. Whereas former experimental studies concentrated on the C-terminal ends or individual Ig domains (10,17,27), we here expand our focus on the whole C-terminal portion of myomesin, aiming at understanding its subexperimental resolution molecular mechanics. In MD simulations, we found helices to exhibit fast nanosecond-scale unfolding and refolding dynamics under constant force, with the adjacent Ig domain stabilizing the interfacial part of the α-helix. Unexpectedly, small forces of up to ∼5 pN stabilized the α-helix secondary structure, which, in the absence of Ig domains, tended to partially unfold. The Ig domains’ mechanical stability largely exceeded those of the α-helices, and increased toward the dimerized C-terminal my13 domain.

Methods

To explore the conformational dynamics of myomesin under stretching forces, we performed MD simulations of different fragments of the C-terminal portion, which included the helices and Ig domains from my9 to my13. The simulated structures were the following:

• 1.Individual helices, namely the helix between my9 and my10 (α⁹), the helix between my10 and my11 (α¹⁰), and the helix between my12 and my13 (α¹²);
• 2.Combined Ig and helical constructs, namely my9-α⁹-my10-α¹⁰-my11 (also denoted my9–my11) and dimeric my12-α¹²-my13 (denoted (my12-my13)₂); and
• 3.Individual Ig domains, from my9 to my13, as well as the my13 dimer.

Structural equilibration

The x-ray structure of two myomesin C-terminal segments, my9–my11 (PDB:2Y23 (16)) and (my12-my13)₂ (PDB:2R15 (15)) (insets in Fig. 1), were subjected to MD simulations for structural equilibration. The MD and force-probe MD simulations of (my12-my13)₂ (see below) have been already described in Berkemeier et al. (17), where the focus had been on the force-extension behavior of this individual structural unit. We used the WHAT IF (28) package to determine the protonation states of all histidine residues. On solvating the molecular structure with TIP4P water (29) in a simulation box, we ensured the distance between the protein and the box edge to be 1.5 times of the nonbonded interactions cut-off distance of 1.0 nm. We used an ionic concentration of 0.1 mM to mimic the physiological environment. We chose the GROMACS 4.5.x package (30) for all the subsequent MD simulations, and the OPLS-AA force field (31) for the protein. The simulation systems for my9–my11 and (my12-my13)₂ comprised ∼540,000 and ∼630,000 atoms, respectively. In all simulations, we removed artificial boundary effects by employing periodic boundary conditions. We used the particle-mesh Ewald method (32) to account for long-range electrostatics. To use a simulation time step of 2 fs, we used LINCS (33) to constrain all bond vibrations. We simulated an NpT ensemble for all simulations, using a temperature of T = 300 K and a pressure of p = 1 bar. The temperature coupling method was Nosé-Hoover (34,35), with a coupling time constant τ_T = 0.4 ps; the pressure coupling method was Parrinello-Rahman (36), with a coupling time constant of τ_P = 4 ps.

After a simulation time of 50 ns, we cut the final equilibrated structures into different parts, namely the individual helices, the Ig domains my9–my13, and the dimer of two my13 domains, and further solvated them in appropriately sized simulation boxes with the same solvent conditions as described above. We equilibrated the individual helices for 400 ns to ∼2 μs and monitored their secondary structures. We also equilibrated all five individual Ig domains and the my13 dimer for another 10 ns before subjecting them to force-probe MD (FPMD) and force-clamp MD (FCMD) simulations.

Helices under force

All three myomesin helices studied here have a similarly high helical properties, as depicted in Fig. S1 in the Supporting Material. Because the force-extension behavior of α¹² has already been reported in Berkemeier et al. (17), we chose it as a representative helix to investigate its response to a constant pulling force in our FCMD simulations. We used different constant forces ranging from 5 to 100 pN applied to the two ends of α¹². Our FCMD simulation lengths are determined by the responses of the helix under force. For example, higher forces lead to helix unfolding on the nanosecond timescale, which resulted in the termination of our simulations after complete helix unfolding. Meanwhile, reversible unfolding and refolding events of helical turns were observed at lower force range, which were monitored over sampling times of up to 2 μs. We assessed helical structures using the software DSSP (37). Except from the application of a constant pulling force, other simulation parameters in FCMD were those described above for the equilibrium simulations.

Ig domains under force

All individual Ig domains and the (my13)₂ dimer were subjected to forced unfolding or detaching for the first time in FPMD simulations, mimicking the AFM experiments (38). In these simulations, we attached two virtual springs to the two terminal residues of the domain, or to the two N-terminal residues in the My13-dimer. The pulling force was generated by moving these two springs with constant velocity away from the center of the protein. We used a pulling velocity of 0.5 nm × ns⁻¹, and a spring constant of 500 kJ × mol⁻¹ × nm⁻² in all FPMD simulations. To accommodate the extending protein during unfolding, we increased the simulation box dimension along the pulling direction to ∼25.0 nm, resulting in system sizes of ∼160,000 atoms. Other simulation parameters were the same as those listed above for the equilibration simulations. We should note that full forced unfolding of either of the two molecular segments, my9–my11 or (my12-my13)₂, would require simulation box dimensions of ∼80 nm along the axis of force application, which is computationally very demanding.

We also used FCMD simulations to probe the stability of myomesin Ig domains and compared them to those in titin, such as I27 (39). Constant forces in FCMD simulations effectively decrease the energy barrier between folded and unfolded states of these Ig domains, and exponentially correlate with the reciprocal of time needed for energy barrier crossing (40,41). We chose the my12 domain and the my13-dimer for these simulations because of their high rupture force among other Ig domains (see below). We also simulated the titin Ig domain I27 for comparison. These FCMD simulations were continued only until the first unfolding event, allowing the structures to be accommodated in smaller simulation systems. After resolvation, energy reminimization, and solvent equilibration, we finally applied constant forces ranging from 250 to 1328 pN to the termini of the domains (or the two N-termini of the my13-dimer) in opposite directions. We used the same simulation parameters as described above if not otherwise specified. Under mild applied constant forces, the distance between two pulled group shows a plateau before an abrupt increase caused by Ig domain unfolding or dimer detaching in our simulations. We defined the dwell time τ as the time between the initiation of force application and the abrupt increase of the end-to-end distance due to domain unfolding or dimer dissociation. We obtained τ for each of the three proteins at 3–4 different constant forces (between 200 and 800 pN) (Fig. 5 B).

Figure 5.

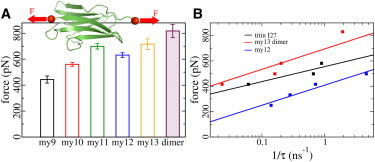
Structural robustness of Ig domains. (A) Forces and standard errors for the unfolding of all five myomesin Ig domains and the detachment force of the myomesin dimer. These forces were obtained by subjecting individual Ig domains (or the my13 dimer) to constant loading applied to the termini (red spheres) in opposite directions (red arrows). (B) Stability comparison of my12, the my13 dimer, and the titin I27 domain. The my13 dimer mechanically outperforms other Ig domains. Rupture times τ were obtained from simulations at varying constant forces. (Solid lines) Bell’s model (40) fits to the data, with F ∼ 1/Δx^≠ × ln 1/τ. The dissociation of the my13 dimer shows a similar distance to the transition state along the pulling direction (Δx^≠ = 0.36 nm) as my12 unfolding (Δx^≠ = 0.51 nm).

Results and Discussion

Myomesin helices in equilibrium

Former studies have demonstrated that the helix α¹² connecting adjacent Ig domains in myomesin serve as a strain absorber in the molecule by providing force-resisting viscosity as well as extensibility (17). However, the atomic detailed and sources of elasticity of α¹² and other myomesin helices under force, especially at the subexperimental resolution scale, have remained unclear. Here we assessed the molecular basis of this elasticity by MD simulations.

The three structurally known helices in myomesin show lengths ranging between 19 and 25 residues. Although they share hardly any sequence similarity, they were predicted to have a relatively high helical propensity in common (see Fig. S1) (42,43). As shown in Fig. 1, they are solvent-exposed for roughly half of the helix length, while the remaining N-terminal half packs itself against the adjacent Ig domain by hydrophobic interactions. We first asked how conformationally flexible the helices were in the context of the myomesin molecule and with external mechanical stress being absent. To restrict the simulation systems to a reasonable size, two segments of the structurally known myomesin molecule were subjected to equilibrium simulations. One contained three Ig domains, my9–my11, and two helices, α⁹ and α¹⁰; the other contained the myomesin dimer consisting of two my12, two my13, and two α¹² helices, as shown in Fig. 1.

Both segments were flexible in simulations. In the 50-ns equilibration, both structures showed a high root mean-square deviation up to 1.2 nm. The root mean-square deviation of individual Ig domains in both segments was only ∼0.2 nm, as expected for a structurally well-defined Ig domain. The high structural deviation was caused by the bending of the helices, as depicted in Fig. 2 A for the example of the my12-my13 dimer. This hinge motion was reversible on the nanosecond timescale. Thus, helices in myomesin can act as flexible linkers by performing hinge motions at the C-terminal solvent-exposed helical section. In contrast, the interactions between the helices and the adjacent Ig domains were firmly maintained throughout the simulations. A large hydrophobic surface area was buried between the helix and the Ig domain. The tight packing between the two was established by large side chains, such as phenyalanine and leucine.

Figure 2.

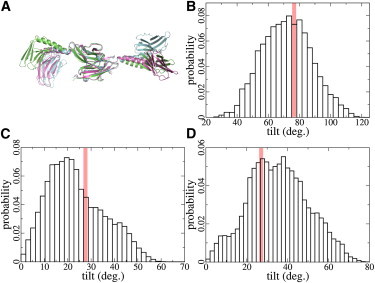
Ig domain tilting angles in structural equilibrium. (A) Representative conformations of the my12-my13 dimer during MD simulations, which differs in its tilting angles between Ig domains. (B) Distribution of tilting angles between my12 and my13 from MD simulation, with an average of 71 ± 16°. (Red bar) 77 ± 7°, average tilt angle observed in multiple crystal structures (16). (C) Distribution of tilting angles between my9 and my10, with an average tilting angle of 23 ± 12° from simulations as compared to the experimental value of 26° (16). (D) Distribution of tilting angles between my10 and my11, with an average tilting angle of 35 ± 14° from simulations as compared to the experimental average of 27 ± 1° (16).

We also monitored the tilting angles between the adjacent Ig domains during the simulations to quantify the hinge motion of each helix. To do so, we measured the direction vector of each Ig domain, which was defined from the first residue to the last one in that domain (16). The tilting angles between vectors across adjacent Ig domains are shown in Fig. 2, B–D. Their average was in good agreement with the tilting angles found in the crystal structures (16). However, they showed strong deviations from the mean with standard deviations between 12 and 17°. This suggests that while the crystal packing prevents such large-scale domain motions, myomesin in solution can in principle show fluctuations of Ig domains relative to each other by helix hinge motions. The pronounced ability of the myomesin helices to form hinges between two neighboring Ig domains might be of physiological importance. In this way, myomesin could buffer shearing forces as they might occur within the sarcomere during the force-generating cycle. Helical hinging allows myomesin to bridge shifted myosin molecules, and as such might be one crucial ingredient for M-band structural integrity.

We next tested whether the hydrophobic interfaces affect the equilibrium stability of the helices, by subjecting the individual helices, namely α⁹, α¹⁰, and α¹², to equilibrium MD simulations for 500 ns to 2 μs in the absence of Ig domains. We then compared the helicity of these supposedly helical fragments with and without hydrophobic protection from the Ig domain, as shown in Fig. 3. The three helices, when embedded into the myomesin molecule, showed helicities of 80–90%, slightly below the helicity of virtually 100% observed in the crystal structures. The hinge motion described above led to a minor unfolding of the helix with respect to the experimental structure. When removing the protection of the N-terminal helix portion from solvent by the Ig domain, the helicity significantly decreased to ∼22% on average (see Fig. S2). Thus, the Ig domains strongly stabilize the secondary structure of myomesin helices, which otherwise quickly and largely unfold.

Figure 3.

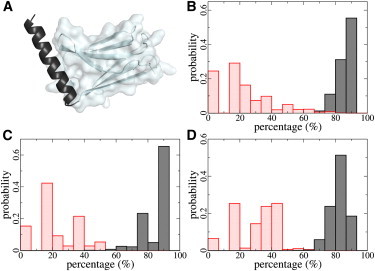
Helicity of myomesin α-helices. (A) Structure of α¹² (black cartoon) and the adjacent my12 (gray cartoon and transparent surface). The N-terminal half of α¹² is protected by the Ig domain via hydrophobic interactions. (B–D) Helicity of α¹² (B), α⁹ (C), and α¹⁰ (D) in the presence (black) and absence (red) of the protection by my12, my9, or my10, respectively.

Our result of a high flexibility and instability of the solvent-exposed helix portions was in line with the finding by Berkemeier et al. (17). Because the other myomesin helices show hydrophobic packing to IG domains similar to α¹², our data suggests the IG domains to be the general factor stabilizing myomesin helices.

Helix elasticity

Although helicity overall decreased when removing the hydrophobic protection from the myomesin Ig domains, all helices occasionally showed refolding events of helical turns in solvent, interestingly—hinting toward a nanosecond scale reversibility of unfolding. This effect is relevant to the mechanical function of myomesin, yet is beyond the capacities of AFM experiments, which showed a lack of hysteresis of force-extension profiles on the millisecond timescale (17). We used DSSP (37) to monitor the secondary structure of the helices in the simulations, as shown in Fig. 4 A for α¹². Blue areas indicate α-helical secondary structure, and white areas any other structure. Although most of the helicity was lost on average, numerous unfolding and refolding events of individual helix turns were observed. Apparently, the preference of α-helical secondary structure and the destabilization of this helix balanced each other such that a dynamic equilibrium of low helical content was established, resulting from the solvent-exposed hydrophobic patches, which within a full myomesin molecule are protected by the Ig domains. This feature of fast helix refolding is likely to be a key function of myomesin elasticity, which is involved in fast-force-generating circles during muscle operation.

Figure 4.

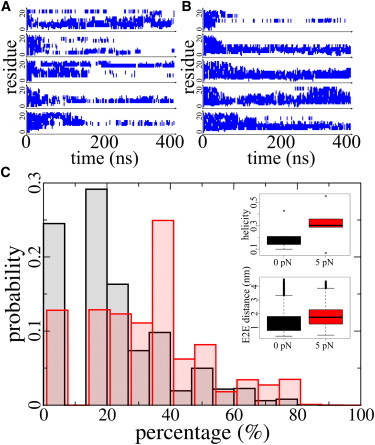
Secondary structure of α¹² in equilibrium and at a pulling force of 5 pN. (A) The α-helical conformation of α¹² along the sequence from the N- (bottom) to the C-terminal side (top) in five independent equilibrium simulations. (B) The α-helical conformation of α¹² in five independent FCMD simulations using a constant pulling force of 5 pN. (C) Percentage of α-helical residues in α¹² in equilibrium (black) and under force (red). (Inset, top) Helicity of α¹² in the second half of five independent simulations. (Inset, bottom) End-to-end distance of α¹² in the final 100 ns of five independent simulations. Secondary structure calculations have been done with DSSP (37). Applying a force of 5 pN moves the conformational ensemble of α¹² toward structures of higher helical content.

In contrast to this scenario of individual helices in water, under physiological conditions, myomesin helices are inserted between two adjacent Ig domains, and thus embedded into the tightly packed M-band of the sarcomere. Consequently, the two ends of the helices are positionally restrained and subjected to stretching. Interestingly, as confirmed by previous AFM experiments, these helices were capable of resisting axial pulling force not only in the first round extension but also after recoiling, which suggested helical structure to reform at millisecond timescales (17). To fully understand how these helices unfold and refold under force, we here applied a range of constant pulling forces to the termini of the α¹² helix in FCMD simulations.

We first compared the α-helical conformation of α¹² in equilibrium and under a stretching force of 5 pN during five 400-ns MD simulations for each case. As shown in Fig. 4 A, α¹² was helical to an only minor extent in equilibrium when the interface to the Ig domain was absent, as discussed above. We determined an average helical content of 23.0% (Fig. 4 C). Counterintuitively, the helical content significantly increased when a pulling force of 5 pN was applied (Fig. 4 B), on average to 31.3% (p-value < 2.2e−16, Wilcoxon test). Thus, more residues preferred an α-helical conformation when α¹² was held at a low force of 5 pN as compared to the absence of force. Apparently, a stretching force enhances helicity in α¹², and supposedly in other myomesin helices too, given their only minor helical propensity (see Fig. S1). The application of 5 pN force leads to an only minor extension of the end-to-end distance of the helix from 1.45 to 1.87 nm (Fig. 4 C (inset, bottom) and see Table S1 in the Supporting Material). This results in an estimate of the work added to the helix by pulling of 1.3 kJ/mol. We interpret this as an ability of α¹² to store mechanical energy before finally fully elongating at higher forces.

To further analyze the numerous events of α-helical turn refolding, we monitored the end-to-end distances of the α¹² as well as its helicity in equilibrium and under forces. As shown in Fig. S3 and Fig. 4 C (inset, top), end-to-end distance of the helix is averagely extended by 5 pN from 1.45 nm in equilibrium to 1.87 nm. The corresponding work by this pulling force through this distance difference is 1.26 kJ/mol. This work is not enough to fully extend the peptide but serves as a counterplay to bending and coiling entropy and prevents peptide fully collapsing, which also increases the probability of forming hydrogen bonds in the backbone and thus helical turns.

If we define the peptide state 1 as <50% of the α¹² residues in helical conformation with state 2 being not less than 50%, we observed the helix dwelled more in state 2 under 5 pN force than in equilibrium. There are 1387 transitions from state 1 to state 2 under this force, compared to 1135 without force in the second-half of our five independent simulations. The longest dwelling time of state 2 is also longer under force, with 13.75 ns compared to 6.45 ns in equilibrium. By cumulatively collecting all the transitions from state 1 to state 2 (see Fig. S4), we estimated a transition rate to the helix-dominated state of 151 ps at 5 pN instead of 168 ps at 0 pN. This estimation was confirmed by the reverse transitions, such as 217 ps at 5 pN compared to 193 ps at 0 pN (see Fig. S4). In summary, a 5-pN pulling force enhances spontaneous turn reforming and helix stability.

We also analyzed α¹² under forces up to 100 pN in FCMD simulations to quantify its mechanical stability. At each force, we monitored the secondary structures and end-to-end distances of the peptide (see Fig. S5), together with a wormlike chain (WLC) model using the same contour and persistence length employed previously for myomesin (17). The accumulated simulation time for this analysis was 7.8 μs to allow for extensive sampling of conformational space at each force. Overall, the helix when not being protected by an Ig domain largely behaved like a WLC in the probed range of forces, agreeing with the overall very minor helical content. For forces of 35 pN and higher, the α-helical content vanished within our nanosecond timescale. In this comparably high-force region, the end-to-end distance closely followed that of an analogous, i.e., unstructured, WLC. Only at forces of 10 pN and lower was a significant fraction of helicity observed, as described above, giving rise to average end-to-end distances of α¹² that were lower than the WLC predictions. We note that two outliers were observed for intermediate forces, namely 20 and 30 pN (see Fig. S5 C). In these two simulations, α¹² was trapped in a coiled state during our submicrosecond timescale, causing a divergence from the WLC curve, which we believed to be an overestimation of the coiling propensity at these forces due to limited sampling.

Taken together, our force-extension data agreed with the previous AFM study that myomesin helices largely followed the behavior of a WLC. We note that experiments had probed the force-extension behavior of myomesin helices between unfolded Ig domains only at forces higher than ≤15 pN (see Fig. S1 in Berkemeier et al. (17)). We found that helical structure was dominant at, and thus can resist, forces of 5 and 10 pN, which were below the experimental force range. They here cause a divergence from a purely WLC behavior. Although with adjacent Ig domains, myomesin helices were primarily helical and showed a distinct plateau in the force-extension curve upon unfolding, the force plateau vanished in the AFM experiments if Ig domains had been unfolded before the helix extension during stretch-relax cycles (17). Our MD simulations of individual helices indicated a lower helicity of these peptides when adjacent Ig domains were absent, suggesting the α-helical conformation and therefore an intact neighboring Ig domain for stabilization to be required for the force resistance observed experimentally. Hence, it is the presence of an interface to an Ig domain that equips myomesin helices with a significantly higher resistance against unfolding up to ∼30 pN.

In all, lower force enhances spontaneous turn formation, probably by restraining the conformational space of the helix ends whereas higher force unfolds helical turns by breaking down hydrogen bonds (Fig. 4 C (inset, top) and see Fig. S5). Previous AFM experiments had demonstrated that stochastic refolding of hydrogen bonds in a stretched single α-helix could cause an increase in molecular stiffness (18,19). The fast refolding of helical turns rendered α¹², and probably the other myomesin helices, highly elastic. This elasticity can give rise to a restoring force within the sarcomere, and therefore can support the reestablishment of relative structural arrangements and the survival of the sarcomere. In this scenario, fast helix refolding is vital to the relaxation period of the force-generating cycle of the sarcomere. It is worth noting that the fast refolding of helices observed here is different from helical nucleation from fully random coils, which is a much slower process on microsecond or even millisecond timescales (44,45). The helical turn refolding in this study is also faster than formerly reported (45), a difference possibly due to the additional pulling forces or due to the limited experimental time-resolution to detect the potential subnanosecond helicity fluctuations observed here.

Myomesin α¹² is considered to provide the extending elements that give elasticity and absorb external stress (17). Our results strongly indicate the same characteristics of other helices studied here. Each single helix can extend to >150% of its initial distance under force, which is critical to the adaptivity of myomesin in the M-band of the sarcomere. Except one of its iso-forms, EH-myomesin, myomesin molecules do not contain an elastic module equivalent to the PEVK segment in titin. Helices in myomesin combine a surprisingly high force resistance against unfolding with a nanosecond-scale refolding propensity, in contrast to disordered protein sequences. As such, they compensate the lack of disordered modules typically employed for facile and reversible extension at low forces. Considering that unfolding of Ig domains are rare physiological events in muscle (as tensile forces are believed to be below critical domain unfolding forces (46)), and the recovery of Ig structures would require seconds, by integrating helices into a molecular structure the myomesin is able to significantly elongate without taking the risk of unfolding its Ig domains.

Mechanical robustness of myomesin Ig domains

The highly elastic helices are inserted in-between Ig domains. This protein domain is also the major component of other muscle proteins such as titin and tenascin, and known to be mechanically very robust (47). All five C-terminal Ig domains in myomesin are structurally known, and are highly homologous both in terms of sequence and structure. As it is being pointed out that these five Ig domains, connected by α-helices, build up the most important part of myomesin for mechanical functions (1), we next asked how their mechanical stability differs among each other and from titin Ig domains and the related fibronectin domains.

To this end, all five known myomesin Ig domains, my9–my13, and the my13 dimer, were independently subjected to a pulling force in FPMD simulations, as shown in Fig. 5 A (top). Average rupture forces of the individual myomesin Ig domains ranged from 440 to 720 pN (Fig. 5 A). We note that the rupture forces obtained in our simulations cannot be directly compared to the much lower forces probed in AFM experiments (17), due to the orders-of-magnitude higher loading rates used here. However, relative mechanical stabilities are likely to be preserved.

We next probed the mechanical stability of the myomesin dimer interface formed by my13. Force was applied to the N-termini of the my13 homodimer, with the same loading rate used for the unfolding simulations. We obtained a detachment force of 818 ± 51 pN in FPMD simulations, which was significantly higher than the forces to unfold the Ig domains of myomesin (Fig. 5 A). The mechanical superiority of the my13 dimer was further confirmed by FCMD simulations, in which different constant forces were used to hold my12, and the my13 dimer (Fig. 5 B). Again, the my13 dimer dissociated after longer dwell-times at a given force, in comparison to the unfolding times of my12. These dwell-times showed a highly similar logarithmic dependency on force (linear fit in Fig. 5 B), so that the same relative stability can be expected at the more relevant low force regime (40). The predicted transition state distances, such as 0.51 nm for my12 and 0.36 nm for my13 dimer, are in line with our simulation results (see Fig. S6).

This hierarchy in mechanical stability had been partially observed in the AFM experiments, where my11 and my12 unfolding preceded dimer disintegration (17). This domain interface even outperformed the robustness of titin I27, one of the most mechanically stable protein domains known, in our simulations at constant forces (Fig. 5 B, black). Also in FPMD simulations, the detachment forces of the my13 dimer were found to be higher than those of Ig domains in titin, such as I1 and I27, when unfolded at comparable loading rates in MD simulations (48). We ascribe the surprisingly high detachment force of the myomesin dimer to the interdomain β-sheet formed across two my13 domains, and also the assisting interdomain polar contacts (see Fig. S7 A). It is established by an extended intermolecular β-sheet formed by the N-terminal β-strand of each my13 (compare Fig. 1), with a strand direction parallel to the direction of force application. This connection is further enhanced by interdomain salt bridges. Detachment required, in total, 16 cross-domain hydrogen bonds and salt bridges, and additional hydrophobic interactions to rupture virtually at once (see Fig. S7 B), explaining the outstanding resilience of the my13 dimer interface.

Interestingly, the my9-13 fragment showed a weak tendency to feature higher mechanical stabilities toward the C-terminus of myomesin, as reflected by the increasing rupture forces from left to right in Fig. 5 A, with the only exception being the my11-my12 pair. This tendency can be expected to prevail throughout myomesin to some extent, as the N-terminal β-sandwich domains are the mechanically less robust FNIII domains (27,49,50). Based on these considerations, we hypothesize that after the elongation of helices, at extremely high forces, myomesin would further elongate by FNIII and Ig domain unfolding, starting at the N-terminal and proceeding to the C-terminal side, on average. In this scenario, the late onset of unfolding events at the C-terminal side of myomesin might represent an additional mechanism of protecting the my13 dimeric interface.

As a consequence of the my13 dimer’s outstanding mechanical stability, the linkage between two myomesin molecules stays intact while the domain-connecting helices unwind, and eventually FNIII/Ig domains unfold upon passive overstretching of the muscle. This mechanical hierarchy enables myomesin to establish a firm yet highly stretchable bridge between two antiparallel myosin fibrils. The importance of the myomesin dimer linkage has been further verified by experiments with myomesin mutants showing decreased dimer stability, which is linked to diseases such as hypertrophic cardiomyopathy (13).

Conclusions

In this study, we used MD simulations to dissect the mechanics of myomesin, trying to understand its function in the M-band of the sarcomere. Myomesin is an important structural molecule for establishing the intricate connective network anchoring muscle fibrils. It uses flexible and elastic α-helices as elastomers to provide molecular extensibility and elasticity. By ultrafast nanosecond-scale refolding, these helices shorten virtually instantaneously in a relaxed sarcomere, and thereby are able to quickly restore the network structure, a key factor in maintaining M-band stability.

Interestingly, small forces of ∼5 pN stabilize the helical structure, suggesting a toughening of the helices by small mechanical loads. In line with this finding, previous studies suggested axial stretching forces at the termini of a helix to reduce peptide terminal vibrations and strand bending, accompanied by a decrease in peptide entropy and an enhancement of helicity (51–53). Because isolated myomesin helices showed significant helicity only at forces smaller than 15 pN, it is the interface to adjacent Ig domains that significantly fosters mechanical resistance of the helices up to 30 pN. Hence, the hydrophobic interface between the Ig and helical building blocks in myomesin is a major molecular prerequisite of the force-buffering function of myomesin.

Myomesin is the only muscle molecule featuring interdomain helices as elastic components. Other elastomeric proteins contain disordered regions, such as the PEVK domain in titin and twitchin (54,55). Instead, myomesin accommodates an intrinsically disordered region, the EH segment, but only in its embryonic isoform. As force buffering regions, helices differ from disordered regions, according to our simulation results, in two aspects:

• 1.The ∼30 pN force plateau at low to intermediate extensions provides a comparably high and constant absorption of mechanical work during loading.
• 2.Myomesin helices ensure a small yet finite resistance to bending, as compared to disordered random coils such as PEVK.

Apparently, these mechanical properties are beneficial for the cross-linking and force-buffering function of myomesin dimers in the M-band.

Finally, myomesin’s dimer interface is tougher than its Ig domains, which ensures antiparallel myosin fibrils to remain intact during the force-generating cycles of the sarcomere. An analogous, yet structurally different case of interdomain association with extraordinary mechanical stability is the sarcomeric titin Z1Z2-telethonin complex (56–58). In both cases, interdomain β-sheets orienting in parallel to the direction of tensile forces acting on the molecule are the basis of the high resistance against rupture (56). Myomesin also uses side-chain salt bridges to further reinforce the interdomain β-sheet. A tendency for rupture forces to increase throughout the myomesin molecule from the fibronectin domains at the N-terminal portion to the mechanically more robust my11 and my12 Ig domains might further aid in protecting the my13 dimer from dissociation. Myomesin dimers are actually experiencing forces in the sarcomere close to that required for possible domain unfolding and dissociation, such as was recently demonstrated for titin (59). Taken together, the molecular composition of myomesin—soft α-helices embedded into a tough dimer—creates a mechanically adaptive molecule for elasticity in muscle through a mechanical hierarchy of its components.