Microvortex for focusing, guiding and sorting of particles

Abstract

We report a microvortex manipulator (MVM) that is a passive, scalable system with great potential for the manipulation and separation of particulate samples in microfluidic environments. The movement of particles is determined by a unique combination of helical flow, buoyant, and gravitational forces. Helical flows are induced by topographically patterned microchannel surfaces, which have previously been used for molecular mixing in microfluidic devices. Here we exploit the behavior of particles in the generated microvortices and present a generic strategy to focus, guide and sort particles. Particles can be focused and guided along arbitrary continuous patterns in a microchannel, which can be easily scaled up to focus multiple streams of particles in parallel. We theoretically illustrate the mechanism of our technique and experimentally demonstrate its applications in passive focusing of beads and cells into parallel streams and guiding of particles and cells. We also explore the application of the unique density-selectivity of microvortex focusing and successfully sort a mixture of two bead populations whose density difference is as small as 0.1 g/cm³.

Introduction

In the last few decades, there has been significant increase in the interest in the development of micro total analysis systems (μTAS)¹ or lab-on-a-chip (LOC) systems². There is a tendency toward miniaturization, since a smaller sample volume allows faster analysis and opens the possibility for highly parallel systems with reduced costs. The applications of these types of microsystems are numerous and special emphasis is given to biological and clinical applications^3–5, for which, particle manipulation represents an important and fundamental step for concentrating, detecting, sorting and focusing particulate samples, such as cells and colloids^6–8.

The versatility of microsystems makes it possible to use a number of different techniques to manipulate and separate particles either passively or actively. Passive manipulation of particles, such as hydrodynamic focusing⁹, size filtration¹⁰, branched structures separation¹¹, and sedimentation¹² are relatively simple but less versatile, since their operation is often dependent on flow conditions and channel geometry. On the contrary, active manipulation techniques using optical forces¹³, magnetism¹⁴, electro-kinetics¹⁵, dielectrophoresis¹⁶, acoustics¹⁷ or their combinations¹⁸, allow a higher degree of particle manipulation. However they require the integration of powered components which add complexity and cost.

Particle focusing applications have also been explored using microscale systems. Particle focusing in continuous flow is an essential operation step in FACS (fluorescence-activated cell sorting) or flow cytometry both in conventional and miniaturized platforms^{19, 20}. Precise positioning of particulate samples is vital for the performance of subsequent process steps. For instance, it is important for particles and cells moving at a consistent velocity to pass through the focal point of a laser beam one at a time for accurate optical detection and cell sorting in FACS. Optical components are expensive and difficult to scale up in conventional FACS systems but can be massively parallelized in microfluidic flow cytometry systems²¹. However, such systems would require a large number of focused parallel particle streams which can not be easily achieved using most existing techniques. For example, for hydrodynamic focusing N focused streams require 2N+1 input channels. Emerging techniques using inertial lift forces in microfluidic flows may be able to address this concern by creating N parallel focused streams of particles from a single input, but this technique is constrained to operation at only very high velocities which may not be suitable for some microfluidic systems²².

Here, we present a generic strategy – microvortex manipulation (MVM) - that is simple and yet allows for highly parallel and precise manipulation of particles. In MVM, the motion of the particle is due to a combination of hydrodynamic, buoyant and gravitational forces. No mechanical or electrical parts are required. Microvortices- helical flows created by surface topologies on the microchannel- were found to have the remarkable ability to focus particles at intended locations. Randomly distributed particles can be continuously focused to single or multiple streamlines following surface patterns. As a result, the MVM has the ability to create arbitrary number of focused particle streams in a single channel which is difficult to achieve using other passive methods. The MVM provides a simple method that is scalable, low-cost and well-suited for focusing a variety of cell types and particles. In addition, the focusing position is density dependent, making it possible for the MVM to separate particles by properly tuning the density of the medium.

Theoretical background and mechanism of microvortex focusing and sorting

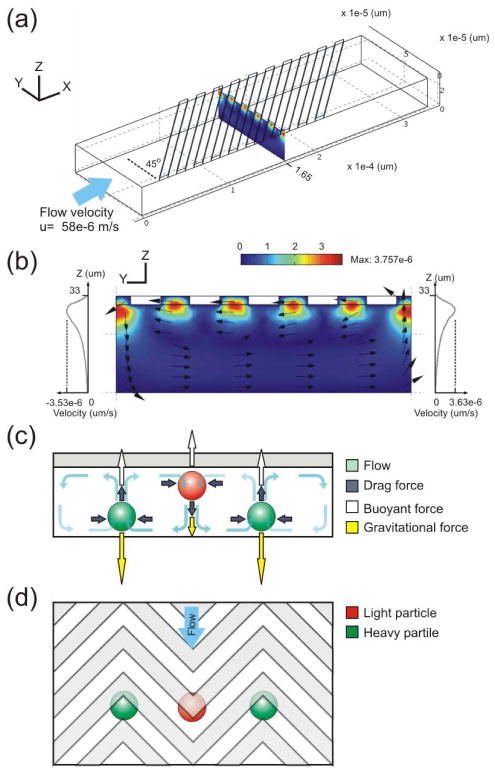
Herringbone and slanted groove micromixers have been a convenient choice for lab-on-a-chip applications requiring rapid mixing of two or more liquids²³. There have been a number of theoretical, experimental, and numerical studies aimed at the characterization and optimization of these micromixers^24–26. Recently, the use of herringbone structures in microchannels has also been suggested for particle separation, where the gap at the end of structure is used as a filter for a particular particle size²⁷. We study the flow pattern in a microchannel with herringbone grooves on the top surface of the channel as shown in Fig. 1d with a three-dimensional finite element computational model. Owing to its symmetric structure with respect to each apex of the herringbone, the computational fluid dynamics analysis can be accomplished by simulating only a portion of the device consisting of one set of slanted grooves as shown in Fig. 1a. One microvortex is created by a set of slanted grooves on the top surface of the microchannel (Fig. 1b). Vorticity in the flow is generated in the streamwise direction due to deflection of fluid by the oblique grooves. That is, the oblique grooves serve to transport fluid laterally from the apex of the groove structure downstream to the groove ends. Due to conservation of mass, fluid near the bottom of the channel will then re-circulate in the opposite direction, and an overall helical flow pattern is created. Symmetric microvortices of alternating circulation direction are created by each set of oblique grooves as schematically shown in Fig. 1c.

Figure 1.

Mechanism of microvortex focusing and sorting. (a) A three-dimensional model of a microchannel containing oblique grooves on its ceiling. The average flow velocity in the channel is 58×10⁻⁶ m/s (Reynolds number ~0.003). (b)Finite element modeling result of cross-sectional flow velocity field induced by flowing fluid through the microchannel. (c) The cross-sectional force diagram and trap locations of particles in a microchannel structured with herringbone grooves on its ceiling as shown in the top-view schematic (d). When focused, the particles’ flow paths follow the apexes of the herringbone grooves as illustrated in (d.)

In addition to the drag force due to fluid flow, gravity and buoyancy are also exerted on particles in MVM. At low Reynolds numbers typical in microfluidic systems, the force of drag experienced by a spherical particle due to a fluid that is moving through can be expressed as:

$$F_d=-6\pi R\eta (v_m-v_p)$$ [1]

where F_d is the drag force, R is the radius of the particle, η is the viscosity of the medium, v_m is the velocity of the flow and v_p is the velocity of the particle²⁸.

The buoyant force on a spherical particle suspended in a medium can be expressed as:

$$F_b=\frac{4}{3}\pi R^3{\rho }_{m}g$$ [2]

while the gravitational force of a spherical particle is expressed as:

$$F_s=\frac{4}{3}\pi R^3{\rho }_{p}g$$ [3]

where ρ_m is the density of the medium and ρ_p is the density of the particle²⁸.

In our system, the microvortices exert drag forces (F_d, indicated as dark blue arrows in Fig. 1c) on particles in both the vertical (along the z-axis) and lateral (along the y-axis) directions whereas the buoyant force (F_b, indicated as white arrows in Fig. 1c) and gravitational force (F_g, indicated as yellow arrows in Fig. 1c) act only in the vertical direction. We find that two trap locations are created at the interfaces where flows from two adjacent counter-rotating microvortices converge. Particles are focused to the interfaces of adjacent microvortices by the lateral flow and trapped if the net force of gravity and buoyancy is large enough to counteract the drag force due to upward/downward circulating flow. For example, particles less dense than the medium (indicated as a red sphere in Fig. 1c–d) are lifted toward the top of the channel after focusing to the interface between two microvortices by lateral drag forces. When the net buoyant force in the vertical direction pushing the particle up at the interface balances downward Stokes drag and gravitational forces, particles are pinned at this trap location. Similarly, “heavy” particles (indicated as a green spheres in Fig. 1c–d) are focused by the same mechanism except they are focused to the bottom of the interface of two microvortices. In order to focus particles to the trap locations in MVM, the magnitude of the z-component of the drag force, F_dz must be smaller than the net force of buoyancy and gravity, which can be represented as:

$$\left|F_{dz}\right|\le \left|F_g-F_b\right|$$ [4]

Therefore the maximal operating flow velocity in the z-direction of MVM can be expressed as:

$$\left|v_{mz}\right|\le \frac{2R^{2}g}{9\eta }\left|{\rho }_p-{\rho }_m\right|,v_{pz}=0$$ [5]

where v_mz and v_pz are the z-velocity of the flow and the particle, respectively. Notably, the amplitude of v_mz is much larger in regions closer to herringbone grooves as indicated by line scans of v_mz at interfaces of the microvortices shown in Fig. 1b. Hence, the focusing of particles denser than the medium can be operated at much higher flow rates compared to the focusing of light particles in a MVM device.

Materials and methods

Device fabrication

Our microfluidic devices were made of Polydimethylsiloxane (PDMS) using softlithography techniques²⁹. Briefly, negative photoresist (SU-8, MicroChem, Newton, MA, USA) was photolithographically patterned on silicon wafers to create masters with two-layer features. The heights of SU-8 features (ranging from 3 – 30 μm) on the masters were measured with a surface profilometer (Dektak ST System Profilometer, Veeco Instruments Inc., Plainview NY). The masters were then used as molds, on which PDMS pre-polymer was poured and allowed to cure in a conventional oven at 65 °C for 24 hours. The cured PDMS replicas were removed from the molds and bonded to glass substrates to form the final devices after a brief oxygen plasma treatment.

Bead and cell experiment setup

Polymethymethacrylate (PMMA) beads (diameter = 10.0 μm, density = 1.15 g/cm³) and fluorescent polystyrene beads (diameter = 9.9 μm, density = 1.05 g/cm³) were purchased from Bangs Laboratories (Bangs Laboratories Inc., Fishers, IN) and Duke Scientific (Duke Scientific Corp., Fremont, CA), respectively. Particles were prepared in desired weight concentrations by dilution in deionized water or a metrizamide solution and stabilized by addition of 0.1% Tween 20. H1650 cells were cultured in RPMI 1640 medium containing 10% FBS and 1% Penstrep. Before experiment, cells were labeled with a fluorescent cellular dye (CellTracker^™ Orange, Invitrogen, Carlsbad, CA) and suspended in PBS. Bead and cell suspensions were loaded into syringes which were connected to the microchannels with Tygon tubings (Small Parts Inc., Mirama. Fl). A syringe pump (PHD 22/2000 Syringe Pump, Harvard Apparatus, Holliston, MA) was used to drive flow. The experiment was performed with the PDMS device mounted on an inverted microscope (TE2000-U, Nikon Inc., Melville, NY). Fluorescent and bright field single and time lapse images were obtained with a CCD camera (Spot RT, Diagnostic Instrument, Steering Height, MI) and a image acquisition software (Spot, Diagnostic Instrument, Steering Height, MI).

Image analysis

The intensity profiles of bead streaks were measured by taking line scans across the microchannel on the images and analyzed using an image processing program (ImageJ, National Institutes of Health). The same program was used to analyze the distribution of beads for the MVM sorting experiment. Briefly, background subtraction followed by thresholding was applied to detect the lateral positions of beads that pass through the end of the herringbone grooves in the sequential images.

Results and discussion

Computational analysis of flow profiles

To predict flow velocity profiles within grooved channels, we used a finite element computational fluid dynamics model. Fig. 1b represents a typical transverse flow velocity profile resulting from the 3D simulation using an inlet velocity of 58 × 10⁻⁶ m/s. As shown in the image, the streamline analysis of flow velocity profiles predicted the formation of one microvortex by a set of slanted grooves on the top surface of the microchannel. To assess the validity of the modeling, we use the experimentally-observed maximal flow rate that allows the focusing of beads that are 9.9 μm in diameter and differ with the medium (η = 10⁻³ Pa.s) by 0.06 g/cm³ in density in the simulation model and found the maximal v_mz is 3.53 × 10⁻⁶ m/s at where light particles are to be focused, which is in a good agreement with calculated v_mz value, 3.2×10⁻⁶ m/s, using eq(5).

From our simulation, the cross-sectional flow pattern shown in Fig. 1b is qualitatively preserved (i.e., flow only changes its amplitude linearly with the change of inlet flow rate) for all Reynolds numbers < 2, thus the inlet flow velocity v_ix is linearly proportional to the maximum z-directional flow velocity v_mz (in the case of Fig. 1b the ratio is $\frac{v_{ix}}{v_{mz}}=15.4$. Based on it, one can obtain the maximal allowable inlet flow velocity based on known maximal allowable v_mz. Since our experimental demonstrations were performed under smaller Reynolds numbers ranging from 10⁻³ – 10⁻², this linear relationship is likely to hold for other applications in most conditions. The effect of flow steering in slanted/herringbone groove micromixers depends on several geometrical parameters, including the angle between the grooves and the axis of the channel (θ), the height of the channel (H), the ratio of the height of grooves to that of the channel (α), the wave number of the grooves (q), where q= 2Π/λ, λ= the periodic length between grooves. As a general guide, it was found that the maximum angle (Ω_max) between the flow and the axis of the channel of occurs when αqH~1 and tan (Ω_max) = αsin(θ)cos(θ)³⁰. However, behaviors of particles in the flow can be complex and depend on many parameters, such as the concentration and rheological properties of particles, and thus may require more advanced mathematical modeling or to be studied empirically.

Microvortex focusing of particles and cells

Parallel focusing of particles is achieved by incorporating multiple sets of herringbone structures in MVM. No external power sources are needed except one flow inlet for introducing the sample solution into the device. Hence, MVM provides a simple strategy for parallel and continuous particle focusing in microchannels.

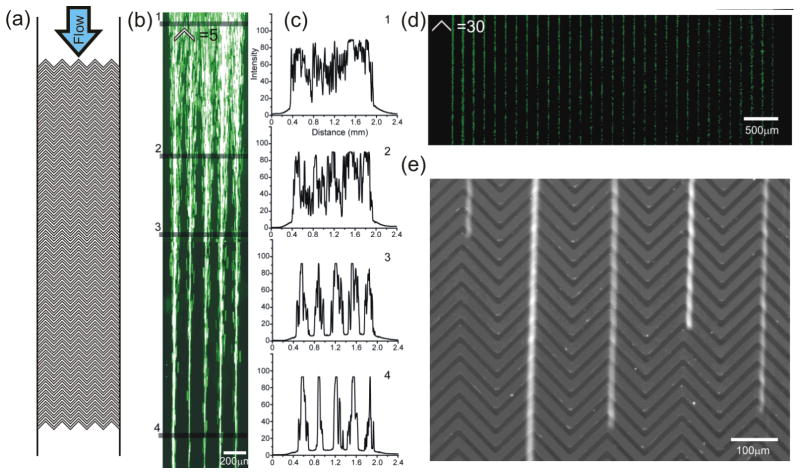
We demonstrate precise and parallel focusing of particles in a MVM device containing five columns of herringbone grooves on its top wall (Fig. 2a). Fluorescent polystyrene beads (diameter = 9.9 μm, density = 1.05 g/cm³) were suspended in deionized water (density = 1.0 g/cm³) and flowed through the channel from a single inlet at an average flow velocity of 20 μm/s. Fluorescent particle streak images (Fig. 2b) clearly show that while flowing through the microchannel, randomly distributed beads are focused into five narrow streams. The distribution of particles at different locations can be assessed by line scans of the fluorescence intensity across the microchannel as shown on the right of Fig. 2b. Since the number of focused particle streams depends on the number of the rows of herringbone grooves in the microchannel, parallelization can be easily achieved by incorporating a lager number of parallel herringbones. Fig. 2d shows a large number of thirty focused streams of the same polystyrene beads within a single microchannel.

Figure 2.

Microvortex focusing of particles and cells. (a) Schematic diagram of a microchannel containing five columns of herringbone-shaped grooves on it ceiling. (b) Trajectory images of fluorescent polystyrene beads focused into five narrow streams when flowing through a microchannel that has the same design as sown in (a). (c) Lines-scan profiles of the bead streaks in from the image in (b). (d) Thirty parallel focused particle streams are formed in a single microchannel containing thirty columns of herringbone grooves. (e) An image of fluorescent streaks obtained from focused H1650 cells flowing in a MVM device. The Reynolds number ~ 0.007 for (b) and ~0.012 for (d) and (e).

Since most mammalian cells are denser than cell buffer solutions, one can expect that mammalian cells in PBS will also be focused with a MVM. To confirm this hypothesis, we conducted a focusing experiment in a MVM device using the human lung cancer cell line H1650 cells suspended in PBS. For these cells a streak image (Fig. 2e and SI movie 1) shows that the focusing with the MVM. It is worth mentioning that particle focusing in MVM can be affected by the collisions of particles. The average of full widths at half maximum (FWHM) of the five fluorescent streaks in the line scan 4 in Fig. 2b is 71 μm. This broadening is mainly a result of multiple beads competing for the same focusing positions. When the concentrations of particles is low as in our cell focusing experiment, the absence of interactions between cells allows focusing of cells into streaks of single cell width as shown in Fig. 2e. We are exploring a more elaborate model incorporating particle-particle interactions that will provide better quantitative predictions of particle behavior in the MVM device.

Microvortex guiding of particles and cells

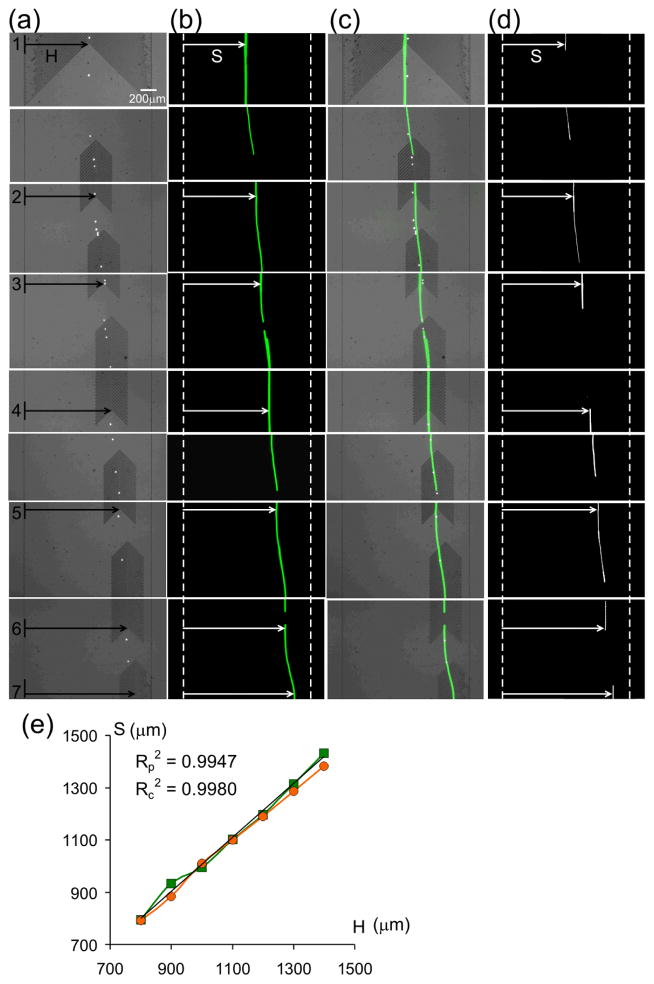
Cell transportation is an essential step in cell-based microfluidic systems in which cells need to be moved to precise locations before or/and after analysis. This need is even more emphasized because modern biology has started to analyze cells at the single-cell level^{31, 32}. As a proof of concept, we use MVM as a “particle-guide” to direct flowing particles in microchannels. When fluorescent polystyrene beads (diameter = 9.9 μm and density = 1.05 g/cm³) in deionized water (density = 1.0 g/cm³) were flowed (average flow velocity = 250 μm/s) through a MVM device containing a single column of herringbone grooves whose lateral position shifts (100 μm distance in each shift) along the microchannel as shown in Fig. 3a, the polystyrene beads were focused into a linear stream and their lateral positions followed those of the herringbone grooves (as shown in the light microscopy images in Fig. 3a and fluorescent particle streak images in Fig. 3b). The lateral position of the particle stream closely overlaps with that of the herringbone grooves (Fig. 3c and 3e), demonstrating that guiding particle flow paths in microchannels can be achieved using MVM. The same experiment was performed with H1650 cells in PBS solution, and a similar guiding result is showed in Fig. 3d and 3e. Additionally, use of externally tunable herringbone structures would allow for on-demand particle position control ³³. Owing to its simplicity and straightforward implementation, MVM may provide a convenient strategy for continuous handling of particles in microfluidic systems.

Figure 3.

Microvortex particle-guideing. (a) Bright-field microscopy, (b) fluorescent trajectories and (c) their superpositioned images of polystyrene beads focused and guided by locally patterned herringbone grooves in a microchannel. (d) Fluorescent trajectories of guided H1650 cells in the same device. (e) The lateral positions of the bead and cell trajectories S closely overlap with the lateral positions of the herringbone grooves H (the green line and red line represent polystyrene beads and H1650 cells respectively. The Reynolds number ~ 0.012 for both bead and cell guiding experiments.

Microvortex particle sorting

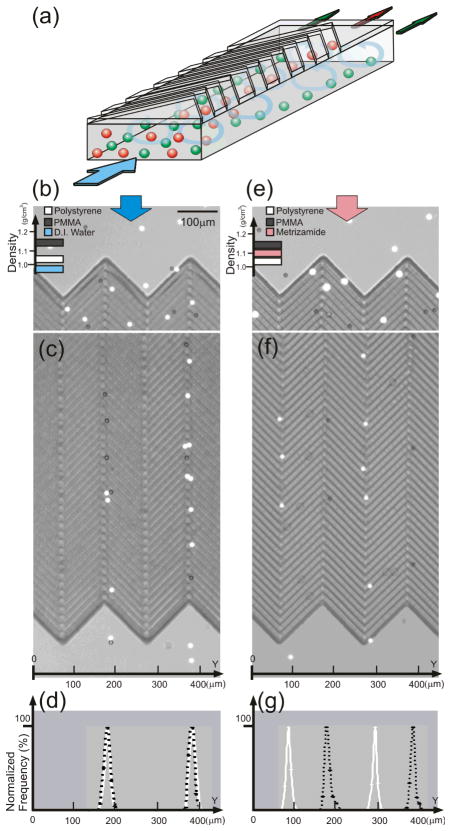
We have theoretically illustrated that locations for microvortex focusing are density-dependent making it possible to use MVM to separate particles based on density. To prove this concept, we prepared and tested two bead suspensions: 1) a mixture of polystyrene (diameter = 9.9 μm and density = 1.05 g/cm³) and PMMA (diameter = 10 μm and density = 1.15 g/cm³) beads in deionized water (density = 1.0 g/cm³, η = 10⁻³ Pa.s), and 2) the same bead mixture in a metrizamide solution (20 % w/v, density = 1.11 g/cm³, η = 10⁻³ Pa.s).

When deionized water is used as the medium (in the case of suspension 1), both polystyrene and PMMA beads are heavier than the medium and therefore both are focused to the same locations (Fig. 4b – c and SI movie 2). When metrizamide solution is used as the medium (suspension 2), polystyrene beads are less dense while PMMA beads remain denser than the medium, resulting in the separation of two bead populations into different positions as predicted (Fig. 4d – e and SI movie 3). We took a series of images at the end of the microchannel during both experiments, and analyzed the distribution of the beads (Fig. 4f – g). The average FWHM of Gaussian fitted distribution profiles of Polystyrene and PMMA beads in Fig. 4d are 11.8±1.3 μm and 11.6±1.6 μm, respectively, while the FWHW of Gaussian fitted distribution profiles of PS and PMMA beads in Fig. 4g are 10.7±0.7 μm and 9.8±0.2 μm, respectively. As the distance between alternating focused bead positions is 100 μm, which is at least 8 times larger than the FWHM, the possibility of finding not pure beads is almost zero statistically. This result demonstrates that two particle populations with a density difference as small as 0.1 g/cm³ can be separated with a very high purity using a MVM device.

Figure 4.

Microvortex particle sorting. (a) Illustration of the operation of density-selective microvortex sorting. (b)– (d) Non-separation focusing and (e)– (g) separaion focusing of polystyrene (density = 1.05 g/cm³) and PMMA (density = 1.15 g/cm³) beads flowing in 1% PBS solution (density = 1.00 g/cm³) and metrizamide solution (density = 1.10 g/cm³); separation occurs when the fluid’s density is between those of the two bead populations. The Reynolds numbers ~ 0.003 for this experiment.

The properties of metrizamide solutions are especially suitable for MVM in terms of density, viscosity and osmolality. Compared to other commonly used density-gradient media, such as Ficoll, sucrose and CsCl, metrizamide forms less viscous solutions than sucrose or Ficoll and causes less change in osmolality than sucrose or CsCl at corresponding concentrations³⁴. For example, for a medium of density 1.11 g/cm³, the Ficoll solution is ~80 times more viscous than the metrizamide solution. From Eq. 5 the maximum operating velocity is inversely proportional to viscosity of the medium. Consequently, the flow rate has to be at least 80 times slower when Ficoll rather than metrizamide is used in MVM. We observed this effect when we ran a sorting experiment substituting metrizamide with Ficoll. Here beads were mixed instead of focused at the same flow rate. The difference in viscosity of CsCl or sucrose solution compared to that of the metrizamide solution is less than 2 folds when the density of the solution is 1.11 g/cm³. Although the maximum operating velocity is only reduced by less than 2 folds, the osmolality of CsCl or sucrose solutions is extremely high at the required densities making them unsuitable for cells or other samples sensitive to changes in the osmotic strength of the medium. To evaluate whether the use of metrizamide solution or the MVM device can impair cell viability is concerned, we conducted a cell viability test and found that both of them do not have adverse effect on the cell viability (see supplementary material: SI_Cell_Viability).

We think the MVM sorting technique may have applications in density-based cell separations such as blood cell separation, stem cell isolation, isolation of fetal cells from maternal blood, and sperm purification which are usually performed with density gradient medium using centrifugation^{35, 36}. However, since the density differences among different cell types and the rigidity of cells are different from those of the beads being demonstrated, further device optimization and operation condition adjustment may be required for cellular applications.

Conclusions

Microvortex focusing has been shown to allow highly parallel operation with reduced device complexity in microfluidic systems. Where locally induced, focusing can be used as a passive particle-guide to straightforwardly place particles at arbitrary positions in microchannels. Additionally, by utilizing density selectivity, microvortex sorting can be used as a generic tool for filtration based on density differences. The utilities of MVM have been demonstrated in focusing and guiding of both polymeric beads and cells while the density-based separation of MVM was only demonstrated with beads and its cellular applications remained to be further investigated. Here we have also provided a simple theoretical analysis and fluidic modeling that permits predictions of the operating flow rates. Unexplored in this work, the equations governing focusing behavior also suggest focusing and separations that are dependent on particle size. Finally, since the flow conditions in microvortex focusing, guiding and sorting are gentle, these techniques may have a large impact in the processing of delicate samples such as cells in a highly parallel manner.